Study on Key Mechanical Parameters of High-Strength Grouting Material

Abstract

In order to better design and calculate in infrastructures, it is necessary to clarify the key mechanical parameters of structural materials, such as axial compressive strength, elastic modulus and Poisson’s ratio. High-strength grouting material (HSGM) have begun to be used as structural materials with the development of large and complex structures. A large number of test dates were used to analyze the relationship between the axial compressive strength and the cubic compressive strength of HSGM in the paper. ABAQUS software was used to model the specimens of axial compressive strength, and the strain cloud maps of concrete and HSGM were compared and analyzed. By considering HSGM as two-phase (sand and paste) composites, the relationship between elastic modulus of HSGM and mechanical parameters of component materials was derived, and the test results of the mechanical properties of HSGM with different ratios of sand to cement were used for verification. The test results show that the axial compressive strength of the HSGM is closer to the cubic strength than that of the concrete material, which accords with the finite element analysis results. The elastic modulus of high-strength grouting material conforms to the theoretical derivation of two-phase material. The material composition is one of the main factors affecting the elastic modulus. Poisson’s ratio range of high-strength grouting material is 0.25 ± 0.01 by statistical analysis.

1. Introduction

Cement-based material such as concrete, mortar and grout are widely used in structures because of its good compression performance and low-cost characteristics [1]. With the rapid development of cement-based material technology, high-strength grouting material can have the properties of large fluidity, super early strength and super high strength [2]. It has been a structural material in important engineering foundations such as offshore wind power connecting section not only a grouting material in equipment leveling [3]. The foremost problem is the fact that, due to the lack of data, high-strength grouting material is often considered as concrete in the design of structural foundations [4]. However, the upper limit of the strength range of conventional concrete is 80 MPa, while the final strength of HSGM can reach 120 MPa or higher [5]. In the foundation structure of major engineering such as offshore wind power, the mechanical parameters under pressure are important to the structural design calculation of the grout joint section [6]. The standard values of concrete axial compressive strength and elastic modulus used in design calculation have a certain model formula conversion relationship with the cubic strength, and Poisson’s ratio also has a specified range [7]. There are obvious differences in composition and properties between the high-strength grouting material and concrete. To our knowledge, few studies have yielded mechanical parameters characteristic of HSGM. Therefore, it is urgent to study the key mechanical parameters of high-strength HSGM.

The standard solution to the problem is based on the verification of a model theoretical calculation and analysis of measured data. It is of interest to know whether HSGM still follows the rules of concrete. For our goal, we focus on three problems: what are the characteristics of HSGM axial compressive strength, what are the characteristics of HSGM elastic modulus and what is the range of PIFs genes he HSGM Poisson’s ratio. In this paper, ABAQUS software is used to simulate the grout material and the concrete material test block, and the resulting stress cloud map is analyzed to clarify the difference between HSGM and concrete under axial compressive strength. The difference was verified by testing the axial compressive strength and cubic compressive strength of high-strength grouting material at different ages, and the formula coefficients between them were amended. The results of the elastic modulus and compressive strength are used to verify the elastic model of grout material which was derived by the Mori–Tanaka method and make clear the characteristics of the elastic modulus of grout material. Poisson’s ratio range was calculated by a large number of test results. All these will provide a certain basis for the subsequent engineering design.

2. Experiments

2.1. Materials

The raw materials employed in this work were P.II 52.5 Portland cement from Conch; the main properties of the cement are given in

Table 1. The main properties of cement.

-	Density	Specific Surface Area	1-Day Compressive Strength	3-Day Compressive Strength	7-Day Compressive Strength	28-Day Compressive Strength
P.II52.5 Portland cement	3.02 g/cm3	394 m2/kg	23.1 MPa	39.3 MPa	50.8 MPa	57.9 MPa

: fine aggregate from Qingdao China with a fineness modulus is 2.6 and elastic modulus of parent rock is 75 GPa. The main properties of the fine aggregate are given in

Table 2. The main properties of fine aggregate.

-	Apparent Density	Bulk Density	Tight Bulk Density	Stone Powder Content	Water Absorption
Fine aggregate	2700 kg/m3	1490 kg/m3	1590 kg/m3	1.5%	1.2%

: high performance powder water-reducing agent from Yingshan PC100T. The main properties of the water reducing agent are given in

Table 3. The main properties of water reducing agent.

-	Appearance	Moisture Content	pH	Bulk Density	Water Reduction Rate
Water reducing agent	Pale yellow to white	0.5%	7.2	450 kg/m3	28%

. A physical drawing of cement, fine aggregate and agent are seen in Figure 1.

2.2. Experiment Design

Due to the high compressive strength, the water binder ratio of high-strength grouting materials is generally low; 0.2 was adopted to be the water-binder ratio in this experiment. The water reducing agent content was 0.4% of the cementing material. The apparent density of high-strength grouting material was set at 2400 kg/m³. The dosage of cement, fine aggregate, water and admixture was calculated according to the apparent density, sand binder ratio and water-binder ratio parameters.

The axial compressive strength and cubic compressive strength of HSGM at different ages was tested. Since the structural grout materials have a higher strength at the later stage, in order to improve the data of the low-strength areas, the early strength data were included in the test range, and the strength of the data at each age of 1 day, 2 days, 3 days, 7 days, 14 days and 28 days were collected. There are many factors affecting the strength data of cement-based materials. In order to increase the accuracy of the data and eliminate the influence of strength fluctuations as far as possible, the test was repeated three times to test the axial compressive strength and cubic strength.

Specimens formed by structural grout materials with different sand binder ratios were used to verify the elastic modulus model which was calculated by two-phase theory. The cubic compressive strength and elastic modulus of HSGM with sand binder ratios of 1.75, 1.55, 1.35, 1.15, 0.95, 0.75, 0.55, 0.35 and 0 (pure pulp) at the age of 7 days were tested, respectively. The design of the experiment is given in

Table 4. The design of the experiment.

No.	Water-Binder Ratio	Sand-Binder Ratio	Water Reducing Agent Content	Test Content
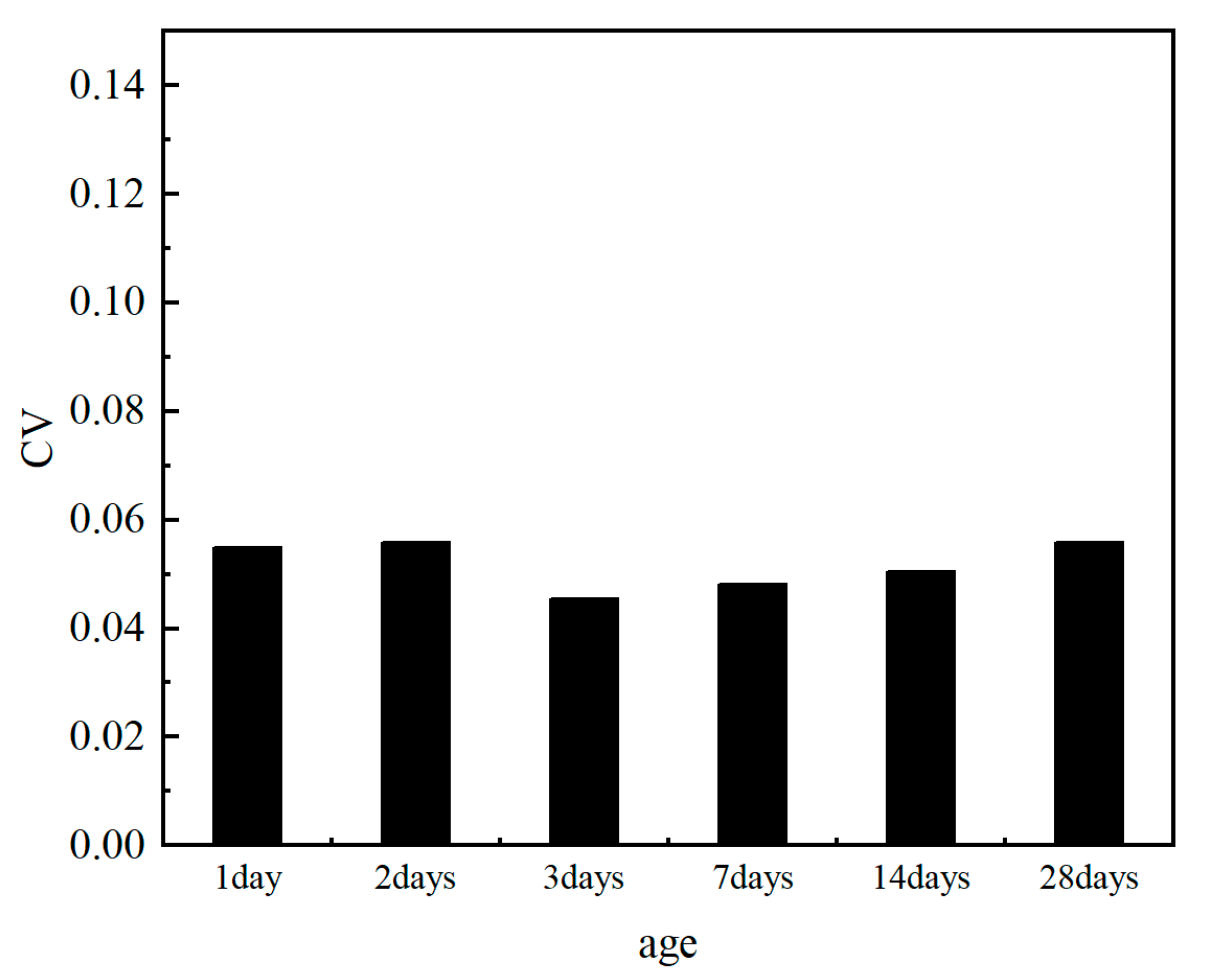
1	0.2	1.15	0.4%	Axial compressive strength, cubic compressive strength and Possion’s ratio at 1 day, 2 days, 3 days, 7 days, 14 days and 28 days, three times
2	0.2	1.75	0.4%	Elastic modulus and cubic compressive strength at 7 days
3	0.2	1.55	0.4%	Elastic modulus and cubic compressive strength at 7 days
4	0.2	1.35	0.4%	Elastic modulus, cubic compressive strength and Possion’s ratio at 7 days
5	0.2	1.15	0.4%	Elastic modulus and cubic compressive strength at 7 days
6	0.2	0.95	0.4%	Elastic modulus, cubic compressive strength and Possion’s ratio at 7 days
7	0.2	0.75	0.4%	Elastic modulus and cubic compressive strength at 7 days
8	0.2	0.55	0.4%	Elastic modulus and cubic compressive strength at 7 days
9	0.2	0.35	0.4%	Elastic modulus and cubic compressive strength at 7 days
10	0.2	0	0.4%	Elastic modulus and cubic compressive strength at 7 days

.

2.3. Methods

The compressive strength test, elastic modulus test and Poisson’s ratio test procedure was based on “Standard of Test Methods for Physical and Mechanical Properties of Concrete” (GB/T50081-2019) [8]. The loading device was the WHY-2000 electro-hydraulic servo pressure testing machine (Figure 2) manufactured by the Shanghai Hualong Test Instruments Corporation. During the elastic modulus and Poisson’s ratio tests, the strain on the transverse and longitudinal deformation of the specimen was collected by a TDS-530 strain collector.

3. Results and Discussion

3.1. Relationship between Axial Compressive Strength and Cubic Compressive Strength of HSGM

3.1.1. Finite Element Modeling

Based on the ABAQUS software (version STANDARD 2020), the POLARIS-MesoConcrete plug-in was used to accomplish random aggregate production, aggregate group generation and aggregate group random delivery [9]. The maximum particle size of HSGM was 5 mm, and the particle size of concrete aggregate was a continuous gradation from 20 mm. The volume of aggregate in the whole specimen is shown in

Table 5. The volume of aggregate in HSGM and concrete.

-	Less Than 5 mm	5 mm–10 mm	10 mm–15 mm	15 mm–20 mm	Totol
Grouting material	42%	/	/	/	42%
Concrete	20%	9%	7%	6%	38%

. Two-dimensional aggregate models of the axial strength samples of grouting material and concrete were generated respectively. The size of the sample is 300 mm × 100 mm.

As is shown in Figure 3, the green color of the base represents the cement paste, different colored spheres represent aggregate and the size of colored spheres is determined by Table 1.

In keeping with the reality, two steel plates were simulated, respectively, on the upper and lower parts of the specimen. A fixed friction force on the contact surface between steel plate and test block was set as 0.3, as shown in Figure 4. A load of 1100 kN was applied to the upper surface. The strain cloud diagram of HSGM and concrete was obtained through finite element analysis. The local image was cut in the middle of the specimen, as shown in Figure 5.

Concrete strength has strong size effect [10]. According to the Weibull distribution theory, when the size of the specimen increases, the volume of concrete increases, and thus the possibility of defects or large defects increases [11]. The damage and failure of concrete are developed from local stress concentration which is easy to occur in the inherent defects of concrete. The larger the structure size, the higher the possibility of large internal defects, the lower the ultimate compressive strength, and the more significant the size effect. For grout materials, its aggregate particle size is small, and at the same time, its flow performance is good, its gas content is low, so it has good filling property with the bubble and is easy to discharge, and the section structure is dense. The probability of large and serious defects is much lower than that of concrete. According to the strain cloud map (Figure 5), the deformation concentration phenomenon occurs more in the concrete test blocks, but less in the grout material test blocks, which is similar to the theoretical analysis results. The size effect of HSGM is lower than concrete, and the theoretical compressive strength of HSGM of different sizes would be much closer.

3.1.2. Formula for the Relationship between Axial Compressive Strength and Cubic Compressive Strength of HSGM

Figure 6 shows the relationship between the axial compressive strength and cubic compressive strength of concrete, ultra-high performance concrete in other papers [12,13,14,15,16,17,18,19,20,21], and also HSGM from Table 1 in this paper. The axial compressive strength of structural grouting increases with the increase in cubic strength, showing a linear growth trend similar to that of concrete. The axial compressive strength of HSGM is generally higher than that of concrete when the cubic compressive strength is the same. As shown in Figure 7, the coefficients of variation (CV) in different ages are close, which reflected the reliability of the data in this paper.

According to the test results, standard deviation processing was carried out on the strength data to determine the fluctuation range of each data. Since most of the concrete material’s axial compressive strength and cubic compressive strength relationship formula adopted a linear relationship formula, the linear formula was used to fit the axial compressive strength and cubic compressive strength data of high-strength grouting material. We used 18 experimental units from Table 4 No.1 to build a linear regression, each experimental unit have three evaluation according to standard test procedure. The fitting results are shown in Figure 8. The fitting has a very high correlation coefficient which is 0.98, indicating that the fitting formula can well characterize the relationship between the axial compressive strength and the cubic strength of HSGM.

Based on the above data analysis and fitting results, within the range of 60~120 MPa, the standard value formula of axial compressive strength of HSGM can be defined as

$$f_{\mathrm{ck}}=0.91f_{\mathrm{cu},\mathrm{k}}+4.1$$

(1)

where f_ck is the axial compressive strength of HSGM; f_cu,k are cubic strength of structural grout material; 0.91 is the reduction coefficient; 4.1 is the correction coefficient.

In general, axial compressive strength is lower than cubic compressive strength in cement-based materials [22]. The gap between axial compressive strength and cubic compressive strength in HSGM is smaller than in concrete, the reduction coefficient of HSGM is higher than concrete which conforms to the finite element simulation results. The model formula of HSGM can better represent the mechanical characteristics of HSGM.

3.2. Relationship between Elastic Modulus and Cubic Compressive Strength of HSGM

3.2.1. Derivation of Elastic Modulus Model

The elastic modulus of HSGM can be deduced by using meso-hierarchy theory based on the distribution and performance parameters of component materials [23]. The grout material can be regarded as the combination of fine aggregate and cement paste. From the meso-level, it is assumed that the fine aggregate and cement paste in the grout material are elastic materials with the same properties in each phase. The bubbles are not considered because there are relatively few bubbles in the grout material. In addition, an interfacial transition zone is not considered because the interfacial transition zone of HSGM is relatively thin and has little effect [24]. The aggregate can be simplified into a sphere because of the aggregate for HSGM is relatively fine and its grain type is round. The aggregate can be seen as a hardened inclusion. The elastic modulus model of structural grout material can be predicted by combining with the theory of multi-phase inclusion.

Mori–Tanaka theory is a widely used multi-phase inclusion theory, which comprehensively considers the influence of distant strain on the interaction between medium [25]. The grout material model uses cement paste as the matrix phase and fine aggregate particles as the inclusion phase. As elastic material, its elastic modulus E, bulk modulus K, shear modulus G and Poisson’s ratio v are related to each other [26]. By inputting the material parameters of aggregate into the model, the model relationship between the elastic modulus of HSGM, the elastic modulus of cement paste and the volume content of aggregate can be obtained:

$$E_c=\frac{9K_c{G}_c}{3K_c+G_c}$$

(2)

where E_c is the elastic modulus of HSGM, GPa; K_c is the volume modulus of HSGM, GPa; G_c is shear modulus of HSGM, GPa.

$$K_c=\frac{\left(18.02+15.35V_r+0.221E_m-0.221V_r{E}_m\right)E_m}{\left(25.96-25.96V_r+0.319E_m+0.375V_r{E}_m\right)}$$

(3)

where K_c is the volume modulus of HSGM, GPa; V_r is aggregate volume content, %; E_m is the elastic modulus of cement paste, GPa.

$$G_c=\frac{\left(5.764+6.236V_r+0.082E_m-0.082V_r{E}_m\right)E_m}{\left(14.52-14.52V_r+0.206E_m+0.191V_r{E}_m\right)}$$

(4)

where G_c is shear modulus of HSGM, GPa; V_r is aggregate volume content, %; E_m is the elastic modulus of cement paste, GPa.

3.2.2. Test Verification of Elastic Modulus

The volume content of aggregate in HSGM with different sand binder ratios can be calculated by density of material. The volume content and the cubic strength and compressive elastic modulus measured in the same age are shown in

Table 6. Strength and elastic modulus of grout materials with different sand to paste ratios.

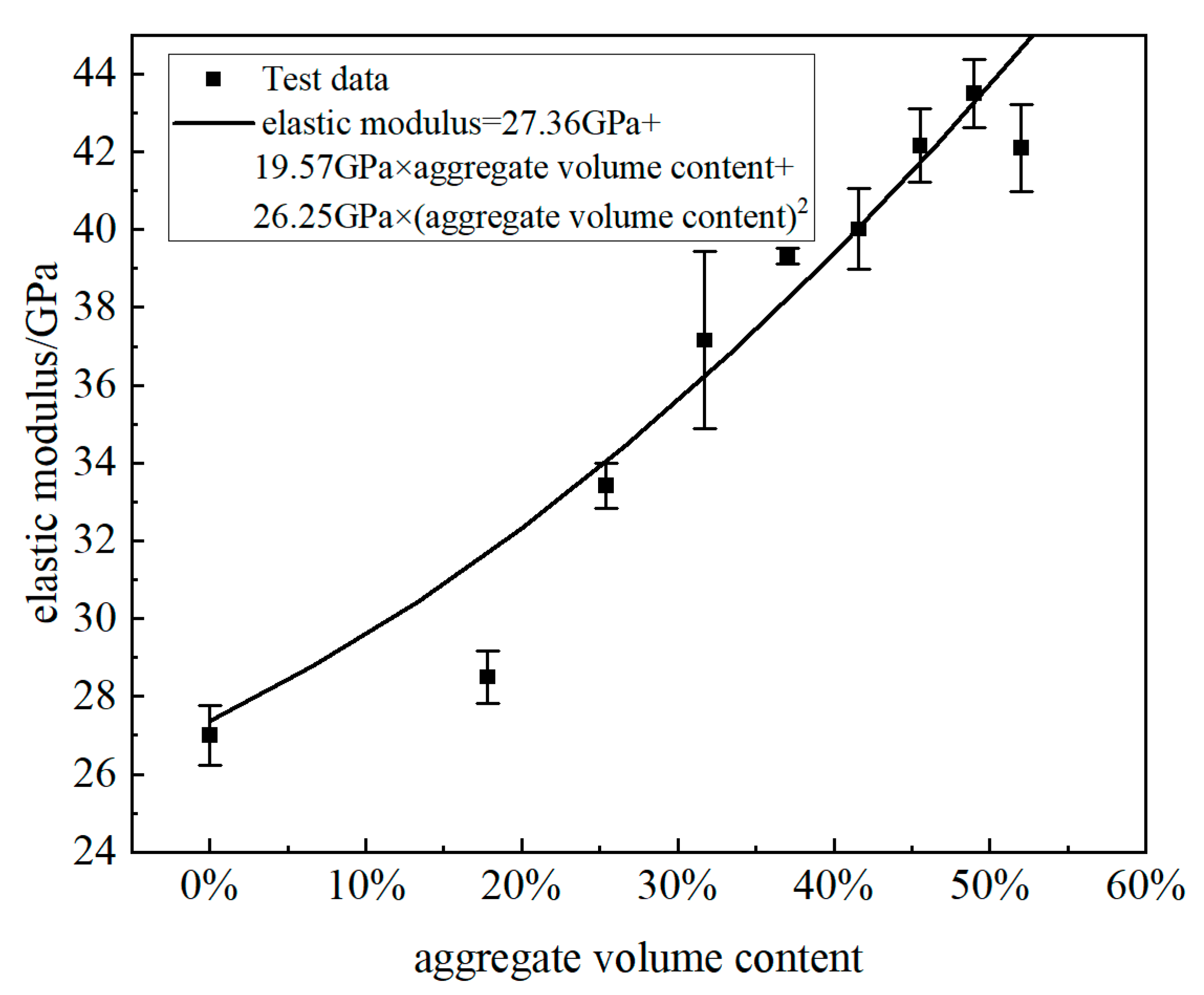
No.	Sand to Paste Ratios	Volume Contents of Aggregate	Cubic Strength/MPa	Elastic Modulus/GPa
1	1.75	52%	114.7	42.1
2	1.55	49%	115.2	43.5
3	1.35	46%	109.1	42.2
4	1.15	42%	115.3	40.0
5	0.95	37%	115.4	39.3
6	0.75	32%	117.6	37.3
7	0.55	25%	116.1	33.4
8	0.35	18%	114.5	28.5
9	0	0%	116.5	27.0

. It can be seen from the data in the table that the cubic strength of the specimen does not change significantly under different aggregate content, and the strength is basically around 115 MPa. This indicates that the volume content of aggregate has little influence on the strength at a low water binder ratio. Although the transition zone increased by the volume content of aggregate, the strength did not decrease, which verifies that the interfacial transition zone is no longer a weak area for HSGM.

The elastic modulus and Poisson’s ratio of pure cement paste obtained in the test were substituted into Formula (5); the model relationship between the elastic modulus of structural grout material and the volume content of aggregate can be written as

$$E_c=26.25\times V_r^2+19.57\times V_r+27.36$$

(5)

where E_c is the elastic modulus of structural grout material, GPa; V_r is aggregate volume content, %.

The derived model Formula (5) was placed in the elastic modulus and strength data graphs obtained by testing with different sand binder ratios, as shown in Figure 9.

Figure 9 is the result of 10 experimental units from Table 4, where each experimental unit contains three evaluated units. The average error rate is the average value of error rate contained in all experimental units. The error rate is calculated by the difference between the predicted value and the measured value divides the predicted value. As can be seen from Figure 9, when using the same material and aggregate with different volume contents, the model derived from the material property mechanism is close to the experimental data with the average error rate of just 3%, which proves the accuracy of the elastic modulus model of structural grout materials. At the same time, it also indicates that the elastic modulus is closely related to the aggregate content. The main reason is that the elastic modulus essentially reflects the load-deformation condition of the material at the elastic stage and the content change of its component materials will affect the overall deformation condition. It has been verified in the mechanical test of HSGM, indicating that the component materials of grouting material have a greater influence on the elastic modulus. Therefore, the strength should not be only considered when designing the elastic modulus in structural design, but also the composition and distribution of materials.

3.3. Selection of Poisson’s Ratio

Poisson’s ratio is the ratio of transverse deformation to longitudinal deformation when material is under stress. Most scholars believe that the compressive strength and tensile strength Poisson’s ratio of concrete materials are the same, and Poisson’s ratio is generally closely related to the composition of materials [27,28]. Poisson’s ratio will fluctuate within a range around a certain point. Poisson’s ratio of concrete in the specification is 0.2 [29]. The regression statistical method was adopted to make statistics on the compressive and tensile Poisson’s ratio data obtained in the experiment in this paper, as shown in

Table 7. Poisson’s ratio statistics of structural grout materials.

No.	Compressive Poisson’s Ratio	Tensile Poisson’s Ratio
1	0.244	0.271
2	0.242	0.259
3	0.241	0.257
4	0.243	0.256
5	0.242	0.255
6	0.240	0.257
7	0.239	0.243
8	0.245	0.259
9	0.242	0.259
10	0.244	0.271
11	0.239	0.267
12	0.251	0.237
13	0.247	0.259
14	0.259	0.242
15	0.248	0.234
16	0.257	0.246
17	0.248	0.236
18	0.254	0.244
19	0.273	0.240
20	0.266	0.261
average value	0.248	0.253
standard deviation	0.009	0.011

. By standard deviation analysis and weighted average calculate, a representative value range was obtained. The calculation formula of sample standard deviation was as follows:

$$\mathrm{S}=\sqrt{\frac{\sum {\left(X_i-\overline{X}\right)}^2}{n-1}}$$

(6)

where S is the sample standard deviation, X_i is the ith data, $\overline{X}$ is the average value of the whole data, and n is the number of the whole samples.

The standard deviation of the compressive Poisson’s ratio is 0.009 and the mean value of the compressive Poisson’s ratio is 0.248. The standard deviation of the tensile Poisson’s ratio is 0.011 and the mean value of the tensile Poisson’s ratio is 0.253. After the combining of compressive and tensile Poisson’s ratios, an average range of 0.25 ± 0.01 can be obtained. Comparing this range with actual data, as show in Figure 10. It can be seen from the figure that more than 95% points fall in this range, which is highly representative.

4. Discussion and Conclusions

The axial compressive strength is important to the main structural force of the whole structure in structural design. Because the axial compressive strength test is not convenient, the cubic compressive strength test is commonly used in the construction process. Concrete is the most commonly used cement-based structure material, and the relationship between the axial compressive strength and cube compressive strength of concrete is relatively clear. HSGM has obvious differences in strength and maximum aggregate particle size to concrete.

The stress concentration phenomenon under pressure in HSGM is significantly less than that in concrete by the finite element analysis of HSGM and concrete axial compressive strength specimens under stress. Test dates show that the axial compressive strength of HSGM is generally higher than that of concrete when the cubic compressive strength is the same; the size effect of HSGM is not as obvious as concrete. The standard value formula between the axial compressive strength and cubic strength of high-strength grouting material can be defined.

The elastic modulus and Poisson’s ratio reflect the deformation characteristics before specimen failure, and they can affect the deformation of the whole structure in the structure design. Under the same pressure, the deformation characteristics of aggregate and paste are different. The Mori–Tanaka model is very successful in predicting the effective properties of two-phase composites.

The relationship model between the elastic modulus of HSGM and the volume content of aggregate is given, by using cement paste as the matrix phase and fine aggregate particles as the inclusion phase with the theory of multi-phase inclusion. The results verify the accuracy of the model with the average error rate of just 3%. In elastic modulus design and calculation, the influence of material composition should be considered in high-strength grouting material.

Based on a large number of Poisson’s ratio data of HSGM, the Poisson’s ratio suitable for structural grout materials is given by statistical analysis, which is 0.25 ± 0.01. Poisson’s ratio covers more than 95% of the measured data, and it is suggested to be used as Poisson’s ratio for HSGM in structure design.