Corrosion Rate of Steel in Liquid Zn, Zn-Bi and Zn-Sn Baths
Abstract
:1. Introduction
2. Views on the Mechanism of Dissolution of Solid Metals in Liquid Metals
- -
- The formation of intermetallic phases on the solid metal surface;
- -
- Creating solutions;
- -
- Mass transfer under the influence of a temperature gradient;
- -
- Reaction with impurities.
- -
- The transition of atoms (ions) or molecules of solid metal into the liquid;
- -
- Transferring the mass of the dissolved metal into the volume of the alloy.
- -
- Diffusion, in which the rate of dissolution depends on the rotational speed of the disc according to the equation:
- -
- Kinetic, in which the rate of dissolution does not depend on the rotational speed of the disc according to the equation:
3. Materials and Methods
- -
- A resistance furnace with an alumina crucible with a capacity of 0.6 dm3 with a furnace chamber filled with quartz sand to increase the heat capacity and temperature stability;
- -
- An adjustable drive system of the sample centrifugation;
- -
- Temperature and rotation speed measurement and control systems.

4. Results and Discussion
4.1. Calculation of the Error of the Weight Measurements
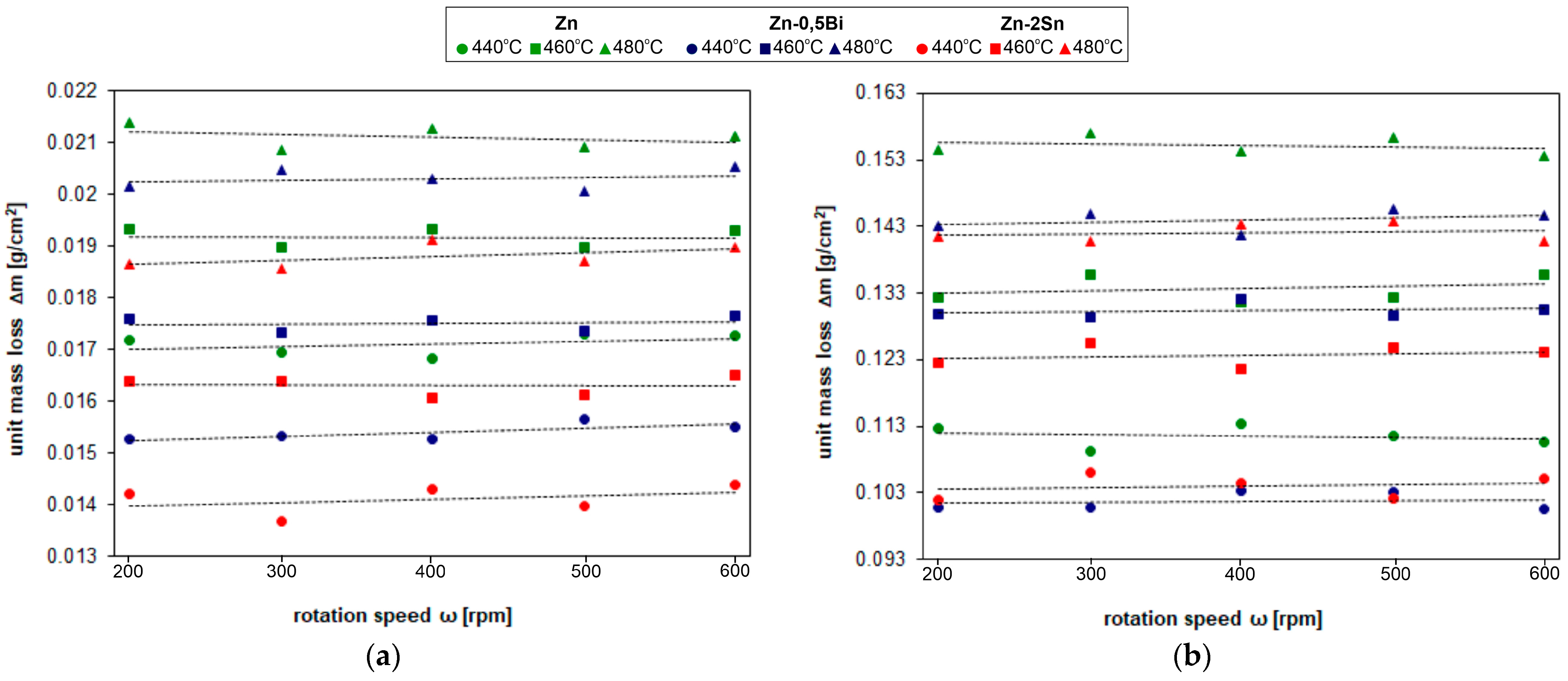

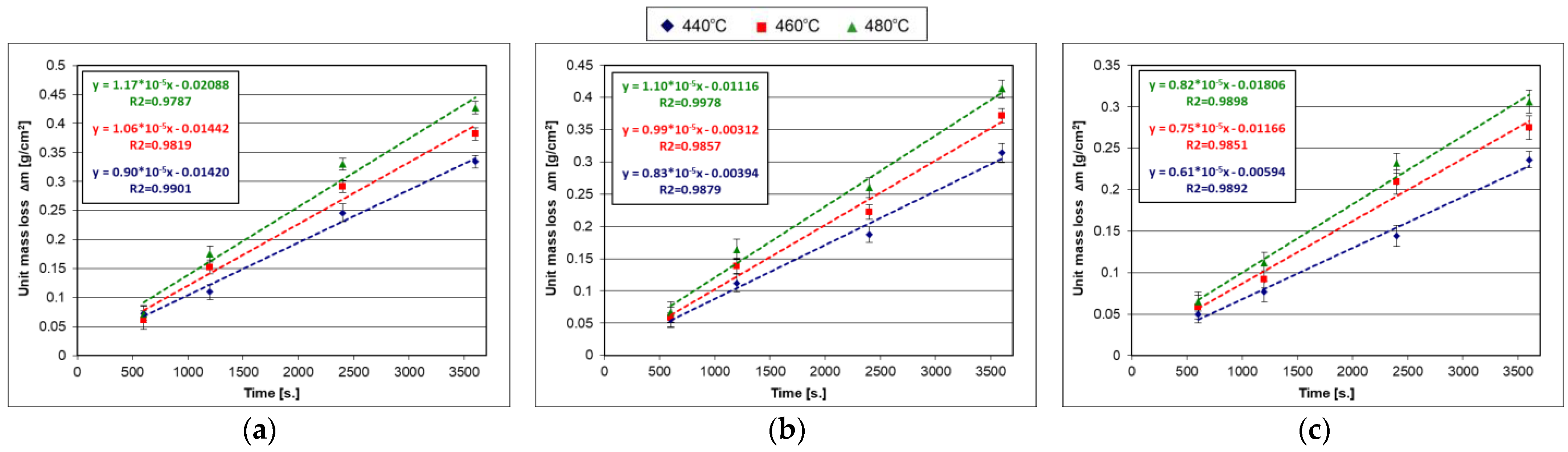
4.2. Kinetics of Dissolution Steel in Zinc Bath
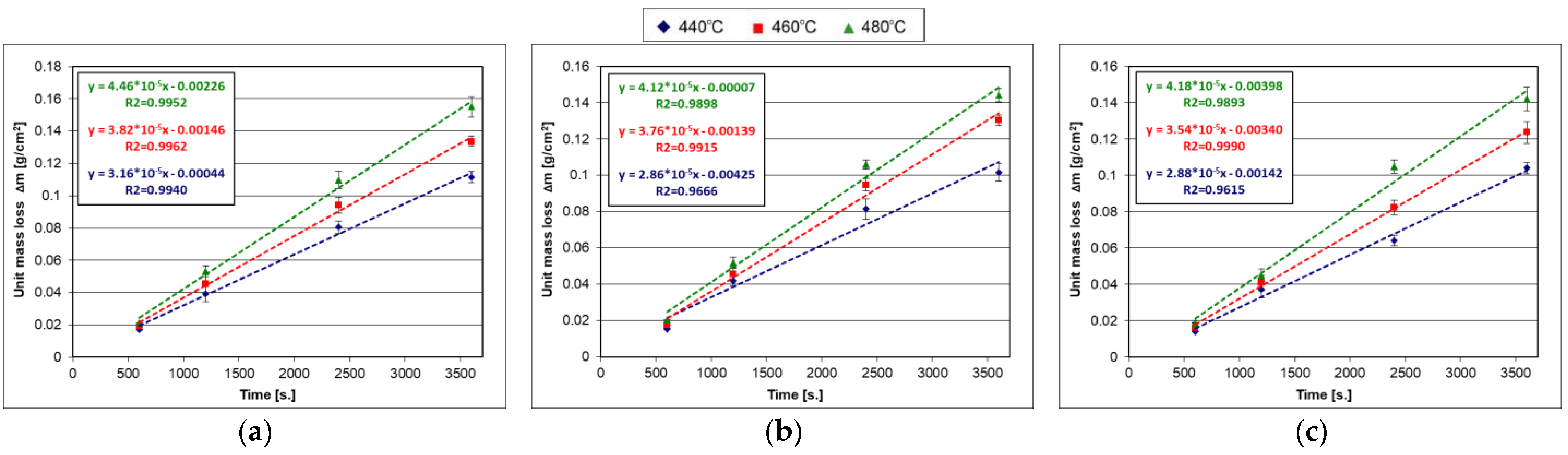
4.2.1. Low-Silicon Steel
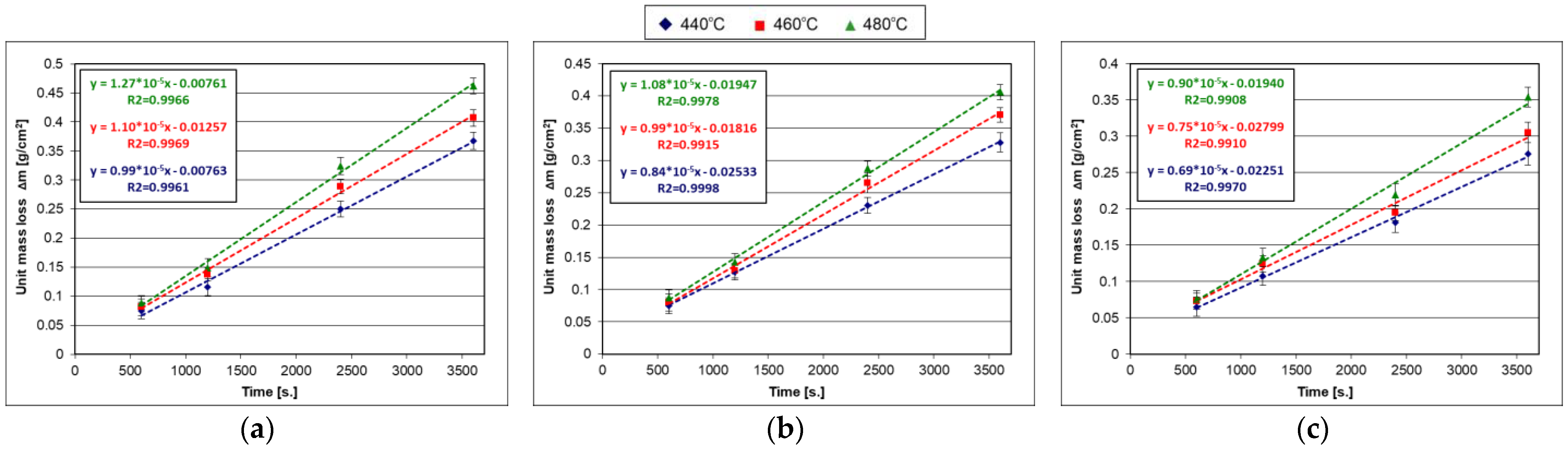
4.2.2. Sandelin’s Steel
4.2.3. Sebisty’s Steel

4.2.4. High-Silicon Steel
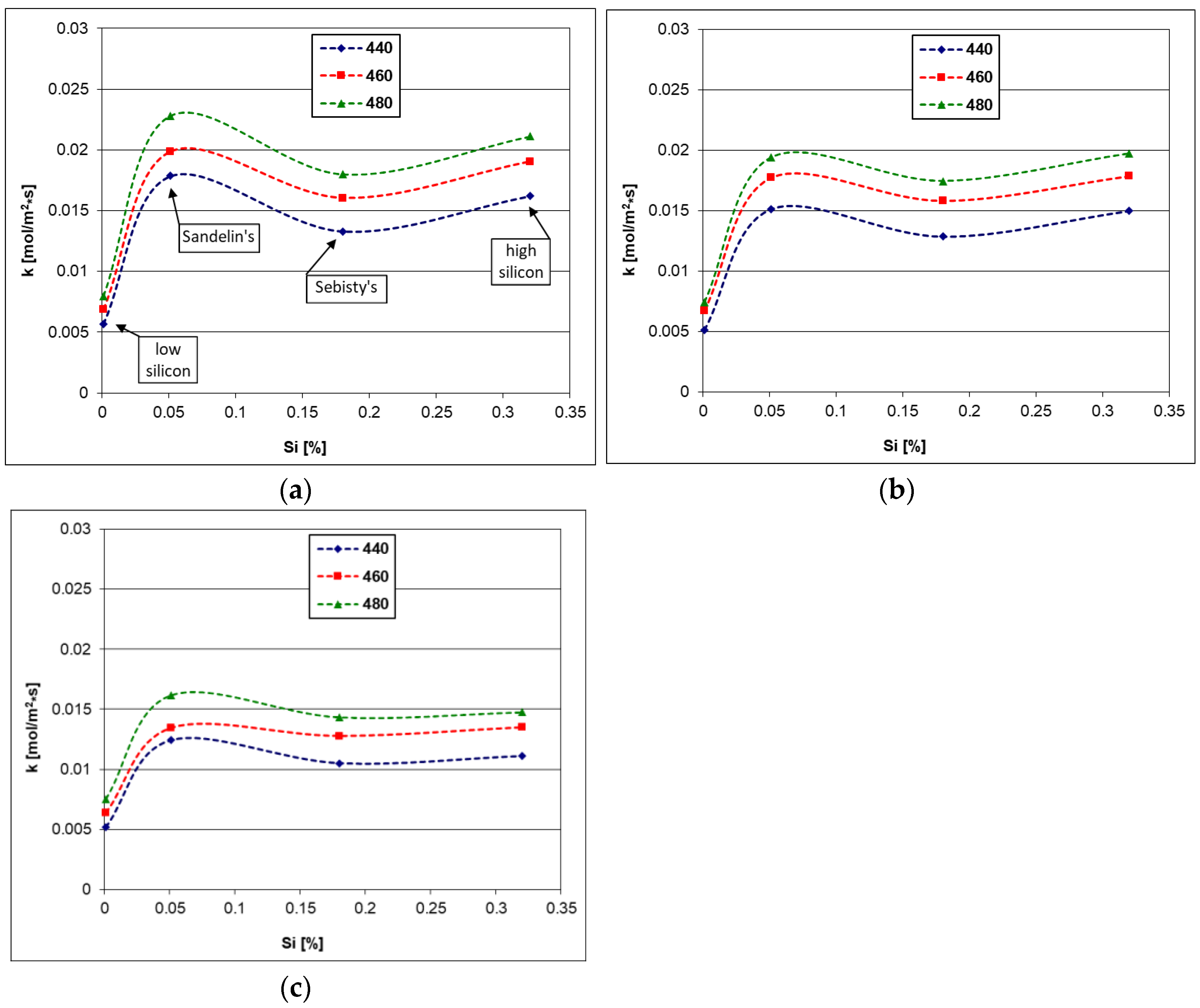
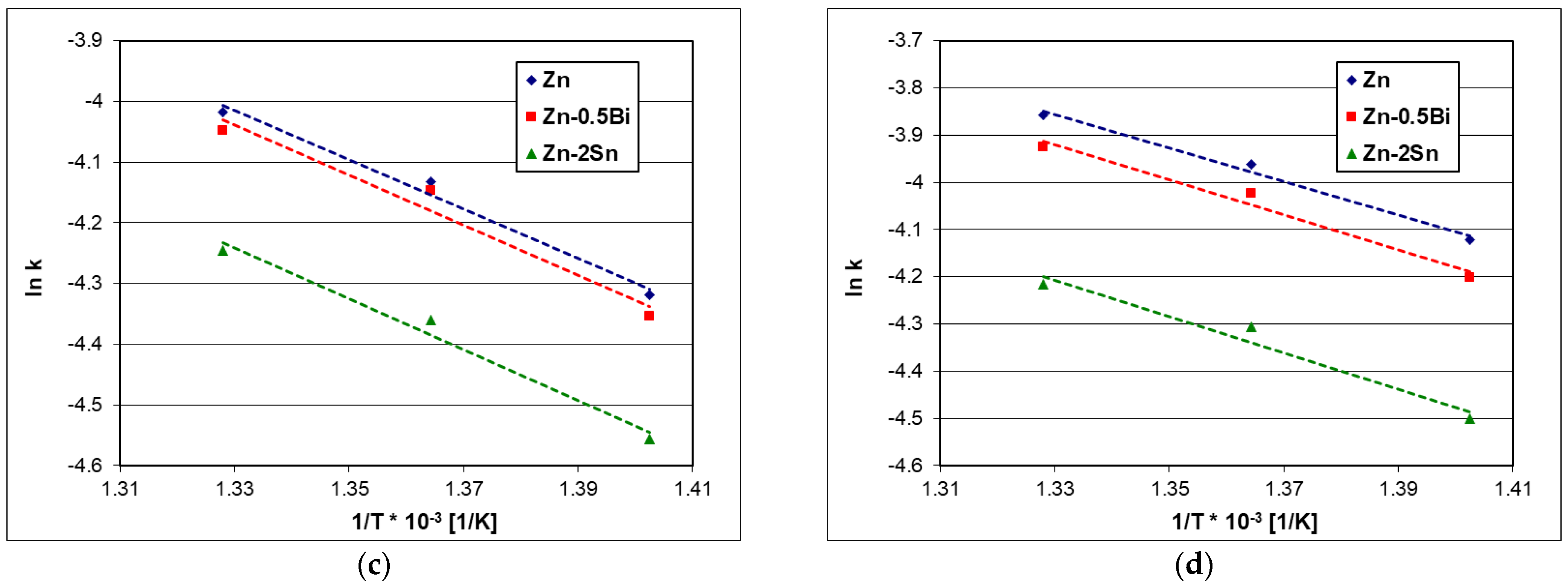
4.3. Activation Energy of Dissolution

5. Conclusions
- The process of steel dissolution under the conditions of kinetic tests using the rotating-disc method was characterized by a linear law, and in the tested range of 200–600 rpm, it did not depend on the rotation speed of disc. This allowed for the determining of the kinetic dissolution constant, which characterizes the dissolution rate of steel in liquid zinc.
- In the tested temperature range of 440–480 °C, the value of the kinetic dissolution constant increased with increasing the temperature, reaching the highest values in the Zn bath. The additions of Bi and Sn to the zinc bath lowered the value of the kinetic dissolution constant and may have acted as an inhibitor of Fe dissolution in the liquid zinc.
- In the temperature range of 440–480 °C, the additions of Bi and Sn increased the value of the activation energy of the dissolution, which reduced the intensity of Fe transfer to the zinc bath.
- The values of the dissolution constant “k” and the activation energy of the kinetic dissolution reflected the increased reactivity in the Fe-Zn system due to the presence of Si. The Sandelin’s steel had the highest solubility in the Zn, Zn-0.5Bi and Zn-2Sn baths.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kania, H.; Saternus, M. Evaluation and Current State of Primary and Secondary Zinc Production—A Review. Appl. Sci. 2023, 13, 2003. [Google Scholar] [CrossRef]
- Liberski, P. Anticorrosive Hot Dip Coatings; Silesian University of Technology: Gliwice, Poland, 2013. (In Polish) [Google Scholar]
- Jędrzejczyk, D. Effect of High Temperature Oxidation on Structure and Corrosion Resistance of the Zinc Coating Deposited on Cast Iron. Arch. Metall. Mater. 2012, 57, 145–154. [Google Scholar] [CrossRef]
- Šmak, M.; Kubíček, J.; Kala, J.; Podaný, K.; Vaněrek, J. The Influence of Hot-Dip Galvanizing on the Mechanical Properties of High-Strength Steels. Materials 2021, 14, 5219. [Google Scholar] [CrossRef] [PubMed]
- Suliga, M.; Wartacz, R.; Hawryluk, M. Evolution of zinc coatings during drawing process of steel wires. Arch. Civ. Mech. 2023, 23, 120. [Google Scholar] [CrossRef]
- Courouau, J.-L.; Feron, D. Corrosion of structural materials by liquid metals used fusion, fission and spallation. In Proceedings of the 1st IAEA Workshop on Challenges for Coolants in Fast Spectrum System, Vienne, Austria, 5–7 July 2017. [Google Scholar]
- Blakey, S.G.; Beck, S.B.M. The effect of combined radiation and convection on hot dip galvanizing kettle wear. Appl. Therm. Eng. 2004, 24, 1301–1319. [Google Scholar] [CrossRef]
- Borishansky, V.M. Liquid Metal Coolants; Atomizdat: Moscow, Russia, 1967. [Google Scholar]
- Schulz, W.D.; Thiele, M. Feuerverzinken von Stückgut; Eugen Leuze Verlag: Bad Saulgau, Germany, 2008. [Google Scholar]
- Sandelin, R.W. Galvanizing Characteristics of Dierent Types of Steels. Wire Wire Prod. 1940, 15, 655–676. [Google Scholar]
- Sebisty, J.J.; Palmer, R.H. Hot dip galvanizing with less common bath additions. In 7th International Conference on Hot Dip Galvanizing, Paris, 1964; ILZRO: Durham, NC, USA, 1964; pp. 235–265. [Google Scholar]
- Kuklik, V.; Kudláček, J. Hot-Dip Galvanizing of Steel Structures; Elsevier Ltd.: Boston, MA, USA, 2016. [Google Scholar]
- Kania, H.; Mendala, J.; Kozuba, J.; Saternus, M. Development of bath chemical composition for batch hot-dip galvanizing-A Review. Materials 2020, 13, 4168. [Google Scholar] [CrossRef] [PubMed]
- Reumont, G.; Perrot, P. Fundamental study of lead additions in industrial zinc. In Proceedings of the 18th International Galvanizing Conference, Birmingham, UK, 8–11 June 1997. [Google Scholar]
- Zhang, J.; Hosemann, P.; Maloy, S. Models of liquid metal corrosion. J. Nucl. Mater. 2010, 404, 82–96. [Google Scholar] [CrossRef]
- Eremenko, V.N.; Natanzon, Y.V. Kinetics of External Dissolution of Metals in Metallic Melts—Review. Sov. Powder Metall. Met. Ceram. 1970, 8, 39–54. [Google Scholar] [CrossRef]
- Dybkov, V.I. Reaction Diffusion and Solid State Chemical Kinetics; IPMS Publications: Kyiv, Ukraine, 2002. [Google Scholar]
- Liberski, P. Physicochemical Basic of Rational Shaping of Aluminium Dip Coatings on Iron; Silesian University of Technology: Gliwice, Poland, 2002. [Google Scholar]
- Eremenko, V.N.; Natanzon, Y.V.; Dybkov, V.I. The effect of dissolution on the growth of the Fe2Al5 interlayer in the solid iron-liquid aluminium system. J. Mater. Sci. 1981, 16, 1748–1756. [Google Scholar] [CrossRef]
- Eremenko, V.N.; Natanzon, Y.V.; Ryabov, V.R. Investigation of the kinetics of Dissolution of solid metals in metal melts by the rotating disc method iron-aluminium system. Phys.-Chem. Mech. Mater. 1968, 4, 286–290. [Google Scholar]
- Levich, V.G. Physicochemical Hydrodynamics; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1962. [Google Scholar]
- Chuchmarev, S.K.; Pokhmurskii, V.I.; Raevskii, Y.A.; Dmitriev, Y.G.; Lizun, O.Y. Kinetics of iron dissolution in liquid zinc. Sov. Mater. Sci. 1985, 21, 17–19. [Google Scholar]
- Beguin, P.; Bosschaerts, M.; Dhaussy, D.; Pankert, R.; Gilles, M. Galveco a Solution for Galvanizing Reactive Steel. In Proceedings of the 19th International Galvanizing Conference, Berlin, German, 1–8 March 2000. [Google Scholar]
- Pankert, R.; Dhaussy, D.; Beguin, P.; Gilles, M. Three years industrial experience with the Galveco alloy. In Proceedings of the 20th International Galvanizing Conference Intergalva 2003, Amsterdam, The Netherlands, 1–4 June 2003. [Google Scholar]
- Kania, H.; Saternus, M.; Kudláček, J. Impact of Bi and Sn on microstructure and corrosion resistance of zinc coatings obtained in Zn-AlNi bath. Materials 2020, 13, 3788. [Google Scholar] [CrossRef]
- Kania, H.; Saternus, M.; Kudláček, J.; Svoboda, J. Microstructure characterization and corrosion resistance of zinc coating obtained in a Zn-AlNiBi galvanizing bath. Coatings 2020, 10, 758. [Google Scholar] [CrossRef]
- Fries, S.G.; Lukas, H.L. System Sn–Zn. In Thermochemical Database for Light Metal Alloys; Ansara, I., Dinsdale, A.T., Rand, M.H., Eds.; Ocial Publications of the European Communitie: Luxemburg, 1998; Volume 2, p. 288. [Google Scholar]
- Malakhov, D.V. Thermodynamic assessment of the Bi-Zn system. Calphad 2000, 24, 1–14. [Google Scholar] [CrossRef]
- Tatarek, A.; Kania, H.; Liberski, P.; Podolski, P. Diffusion dissolution of reactive steels in a zinc bath with the addition of tin. Inżynieria Mater. 2010, 5, 1362–1365. [Google Scholar]
- Tatarek, A.; Saternus, M. Investigation of the Diffusion Dissolution of Reactive Steels in a Zinc Bath with the Addition of Bismuth. Ochr. Przed Koroz. 2018, 7, 186–190. [Google Scholar]
- Tatarek, A. Analysis of Physicochemical Phenomena at the Solid-Liquid Interface during the Hot-Dip Galvanizing Process. Ph.D. Thesis, Silesian University of Technology, Gliwice, Poland, 2007. [Google Scholar]
- Pistofidis, N.; Vourlias, G.; Konidaris, S.; Stergioudis, G. The effect of bismuth on the structure of zinc hot-dip galvanized coatings. Mater. Lett. 2007, 61, 994–997. [Google Scholar] [CrossRef]
- Avettand-Fènoël, M.-N.; Reumont, G.; Perrot, P. The effect of tin on the reactivity of silicon-containing steels. In Proceedings of the 21st International Galvanizing Conference Intergalva 2006, Naples, Italy, 12–14 June 2006. [Google Scholar]

| Bath | Content [wt.%] | ||||||
|---|---|---|---|---|---|---|---|
| Cd | Fe | Al | Cu | Bi | Sn | Zn and Others | |
| Zn | 0.003 | 0.0004 | 0.001 | 0.0001 | 0.001 | 0.001 | balance |
| Zn-0.5Bi | 0.002 | 0.0003 | 0.001 | 0.0001 | 0.54 | 0.001 | balance |
| Zn-2Sn | 0.003 | 0.0004 | 0.002 | 0.0004 | 0.001 | 1.97 | balance |
| Grade | Steel Type | Content [wt.%] | |||||
|---|---|---|---|---|---|---|---|
| C | Si | Mn | S | P | Fe and Others | ||
| 04 | Low silicon | 0.03 | 0.001 | 0.14 | 0.010 | 0.013 | balance |
| S250 GD | Sandelin’s | 0.06 | 0.052 | 0.71 | 0.0074 | 0.0057 | balance |
| B500SP | Sebisty’s | 0.19 | 0.18 | 0.65 | 0.021 | 0.072 | balance |
| S355JR | High silicon | 0.13 | 0.34 | 1.12 | 0.013 | 0.015 | balance |
| Steel | Trend Line Equation | tg α * | ~α * [°] | Mass Loss [g/cm2] | Relative Mass Loss [%] |
|---|---|---|---|---|---|
| After 10 min Pickling Time | |||||
| Low silicon | y = −1.47 × 10−5x + 16.65 | −0.0000147 | ~179.9992 | 0.0000273 | 0.00016 |
| Sandelin’s | y = −1.27 × 10−5x + 16.72 | −0.0000127 | ~179.9993 | 0.0000225 | 0.00013 |
| Sebisty’s | y = −1.51 × 10−5x + 16.68 | −0.0000151 | ~179.9991 | 0.0000275 | 0.00016 |
| High silicon | y = −1.35 × 10−5x + 16.74 | −0.0000135 | ~179.9992 | 0.0000237 | 0.00014 |
| Bath | Temp. [°C] | Trend Line Equation | tg α * | ~α * [°] | Average Mass Loss [g/cm2] | Standard Deviation [g/cm2] |
|---|---|---|---|---|---|---|
| Dissolution Time 10 min | ||||||
| 440 | y = 0.5 × 10−6 + 0.016 | 0.0000005 | ~0.00001 | 0.017 | 0.00021 | |
| Zn | 460 | y = −0.2 × 10−7 + 0.019 | −0.00000002 | ~1,799,999 | 0.019 | 0.00019 |
| 480 | y = −0.5 × 10−6 + 0.021 | −0.0000005 | ~1,799,999 | 0.021 | 0.00023 | |
| 440 | y = 0.8 × 10−6 + 0.015 | 0.0000008 | ~0.00001 | 0.015 | 0.00016 | |
| Zn-0.5Bi | 460 | y = 0.1 × 10−6 + 0.017 | 0.0000001 | ~0.00001 | 0.018 | 0.00013 |
| 480 | y = 0.3 × 10−6 + 0.020 | 0.0000003 | ~0.00001 | 0.020 | 0.00020 | |
| 440 | y = 0.6 × 10−6 + 0.013 | 0.0000006 | ~0.00001 | 0.014 | 0.00024 | |
| Zn-2Sn | 460 | y = −0.7 × 10−7 + 0.016 | −0.00000007 | ~1,799,999 | 0.016 | 0.00018 |
| 480 | y = 0.7 × 10−7 + 0.018 | 0.00000007 | ~0.00001 | 0.019 | 0.00023 | |
| Dissolution Time 60 min | ||||||
| 440 | y = −1.9 × 10−6 + 0.112 | −0.0000019 | ~1,799,999 | 0.112 | 0.00357 | |
| Zn | 460 | y = 3.4 × 10−6 + 0.132 | 0.0000034 | ~0.00001 | 0.134 | 0.00303 |
| 480 | y = −2.3 × 10−6 + 0.158 | −0.0000023 | ~1,799,999 | 0.155 | 0.00648 | |
| 440 | y = 1.6 × 10−6 + 0.101 | 0.0000016 | ~0.00001 | 0.102 | 0.00503 | |
| Zn-0.5Bi | 460 | y = −1.6 × 10−6 + 0.129 | −0.0000016 | ~1,799,999 | 0.130 | 0.00290 |
| 480 | y = 3.8 × 10−6 + 0.142 | 0.0000038 | ~0.00001 | 0.144 | 0.00355 | |
| 440 | y = 2.5 × 10−6 + 0.103 | 0.0000025 | ~0.00001 | 0.104 | 0.00320 | |
| Zn-2Sn | 460 | y = 2.4 × 10−6 + 0.122 | 0.00000024 | ~1,799,999 | 0.124 | 0.00593 |
| 480 | y = 1.7 × 10−6 + 0.141 | 0.00000017 | ~0.00001 | 0.142 | 0.00644 | |
| Bath | Temp. [°C] | tg α (1) | k [g/m2*s] | k [mol/m2*s] |
|---|---|---|---|---|
| 440 | 0.00003161 | 0.316 | 0.00566 | |
| Zn | 460 | 0.00003824 | 0.382 | 0.00685 |
| 480 | 0.00004464 | 0.446 | 0.00799 | |
| 440 | 0.00002865 | 0.287 | 0.00513 | |
| Zn-0.5Bi | 460 | 0.00003764 | 0.376 | 0.00674 |
| 480 | 0.00004124 | 0.412 | 0.00739 | |
| 440 | 0.00002887 | 0.289 | 0.00517 | |
| Zn-2Sn | 460 | 0.00003549 | 0.355 | 0.00636 |
| 480 | 0.00004188 | 0.419 | 0.00750 |
| Bath | Temp. [°C] | tg α (1) | k [g/m2*s] | k [mol/m2*s] |
|---|---|---|---|---|
| 440 | 0.00009970 | 0.997 | 0.01785 | |
| Zn | 460 | 0.00011085 | 1.109 | 0.01985 |
| 480 | 0.00012738 | 1.274 | 0.02281 | |
| 440 | 0.00008443 | 0.844 | 0.01512 | |
| Zn-0.5Bi | 460 | 0.00009900 | 0.990 | 0.01773 |
| 480 | 0.00010827 | 1.083 | 0.01939 | |
| 440 | 0.00006931 | 0.693 | 0.01241 | |
| Zn-2Sn | 460 | 0.00007506 | 0.751 | 0.01344 |
| 480 | 0.00009044 | 0.904 | 0.01619 |
| Bath | Temp. [°C] | tg α (1) | k [g/m2*s] | k [mol/m2*s] |
|---|---|---|---|---|
| 440 | 0.00007429 | 0.743 | 0.01330 | |
| Zn | 460 | 0.00008958 | 0.896 | 0.01604 |
| 480 | 0.00010054 | 1.005 | 0.01800 | |
| 440 | 0.00007175 | 0.718 | 0.01285 | |
| Zn-0.5Bi | 460 | 0.00008838 | 0.884 | 0.01583 |
| 480 | 0.00009746 | 0.975 | 0.01745 | |
| 440 | 0.00005859 | 0.586 | 0.01049 | |
| Zn-2Sn | 460 | 0.00007131 | 0.713 | 0.01277 |
| 480 | 0.00008006 | 0.801 | 0.01434 |
| Bath | Temp. [°C] | tg α (1) | k [g/m2*s] | k [mol/m2*s] |
|---|---|---|---|---|
| 440 | 0.00009054 | 0.905 | 0.01621 | |
| Zn | 460 | 0.00010632 | 1.063 | 0.01904 |
| 480 | 0.00011788 | 1.179 | 0.02111 | |
| 440 | 0.00008362 | 0.836 | 0.01497 | |
| Zn-0.5Bi | 460 | 0.00009981 | 0.998 | 0.01787 |
| 480 | 0.00011017 | 1.102 | 0.01973 | |
| 440 | 0.00006195 | 0.619 | 0.01109 | |
| Zn-2Sn | 460 | 0.00007531 | 0.753 | 0.01349 |
| 480 | 0.00008240 | 0.824 | 0.01476 |
| Steel | Bath | Trend Line Equation | R2 | E [kJ/mol] |
|---|---|---|---|---|
| Zn | y = −4635.8x + 1.33 | 0.9981 | 38.54 | |
| Low silicon | Zn-0.5Bi | y = −4909.8x + 1.64 | 0.9318 | 40.82 |
| Zn-2Sn | y = −4994.3x + 1.74 | 0.9977 | 41.52 | |
| Zn | y = −3283.5x + 0.57 | 0.9913 | 27.30 | |
| Sandelin’s | Zn-0.5Bi | y = −3345.7x + 0.51 | 0.9792 | 27.81 |
| Zn-2Sn | y = −3556.3x + 0.58 | 0.9420 | 29.56 | |
| Zn | y = −4067.9x + 1.39 | 0.9856 | 33.82 | |
| Sebisty’s | Zn-0.5Bi | y = −4122.5x + 1.44 | 0.9644 | 34.27 |
| Zn-2Sn | y = −4199.4x + 1.34 | 0.9825 | 34.91 | |
| Zn | y = −3548.6x + 0.86 | 0.9881 | 29.50 | |
| High silicon | Zn-0.5Bi | y = −3710.3x + 1.01 | 0.9786 | 30.84 |
| Zn-2Sn | y = −3841.0x + 0.90 | 0.9628 | 31.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kania, H. Corrosion Rate of Steel in Liquid Zn, Zn-Bi and Zn-Sn Baths. Coatings 2023, 13, 993. https://doi.org/10.3390/coatings13060993
Kania H. Corrosion Rate of Steel in Liquid Zn, Zn-Bi and Zn-Sn Baths. Coatings. 2023; 13(6):993. https://doi.org/10.3390/coatings13060993
Chicago/Turabian StyleKania, Henryk. 2023. "Corrosion Rate of Steel in Liquid Zn, Zn-Bi and Zn-Sn Baths" Coatings 13, no. 6: 993. https://doi.org/10.3390/coatings13060993
APA StyleKania, H. (2023). Corrosion Rate of Steel in Liquid Zn, Zn-Bi and Zn-Sn Baths. Coatings, 13(6), 993. https://doi.org/10.3390/coatings13060993






