Influence of Tuning Potential Parameters on Wettability of Smooth Copper Plate: A Molecular Dynamic Study

Abstract

The influences of interactions between copper plate and nano-water droplets on wettability with different solid–liquid potential parameters were studied, and the spread of droplets was compared and analyzed using the molecular dynamics method. The diameter of droplet spreading and the amount of water molecules adsorbed on the copper gradually increased with the potential parameters, whereas the absolute potential energy value between copper and water also increased. Negative potential energy represents the attraction force between solid atoms and liquid molecules, and the attraction grows stronger with the large absolute value of negative potential energy. The heat transfer performance of the wettability surface can be explained by analyzing the force of solid and liquid from the perspective of energy. These results are of great significance for establishing the wettability model of a smooth plate correctly and the design and manufacture of a special functional surface.

1. Introduction

The wettability of a solid surface is defined as the ability of one liquid to adhere or spread on a solid surface [1,2], which is one of these surfaces’ important characteristics. The essence of solid wettability is that the free energy of the system changes when the solid–liquid interface replaces the gas–liquid and gas–solid interface. The chemical composition and microscopic geometry of solid surfaces are important factors that affect their wettability [3]. At nanoscale, some wettability surfaces were manually controlled and prepared with special functions, which were widely used in tribology, nanofluidic devices, heat transfer, and self-cleaning [4,5]. Especially anisotropic wettability surfaces, which have great application prospects in the fields of microreactors, biomedical devices, and sensors [6].

To study the specific function of the wettability interface, scientists have conducted many relevant studies. In their experiment, Bourdon et al. [7] demonstrated the significant impact of ultra-smooth surface wettability on boiling heat transfer. Liu et al. [8] studied the special bouncing behavior of water droplets at different interfaces. Chen et al. [9] found that adjusting the wettability of the interface could effectively strengthen the boiling efficiency of the interface. However, the mechanism of these special functional interfaces at nanoscale remains unclear.

Some scholars have attempted to elucidate the mechanism of special functions by studying the influencing factors of wettability. Through experimental research, Misyura [10] showed that the static contact angle on the structured surface for the steady equilibrium was dependent on the droplet shape and initial diameter. Comparing a simulation and an experiment, Abdullah et al. [11] proved that the surface heat transfer performance of droplet adhesion on a micro-post array surface changed accordingly. This indicated that droplet size and interface structure were the main factors affecting wettability. However, Wen et al. [12] proved that the wettability of nanostuctured surfaces changed with the condensing condition induced by the experiment. Kim et al. [13] found that the wettability of metallic nanostructures increased following the application of electrical potential. In fact, the interaction mechanism between solid and liquid was the foundation for understanding the change in wettability on a solid surface at nano scale [14]. Molecular dynamics simulation, which can describe the physical process from the atomic level, is an effective method for describing the liquid behavior near a solid wall at nanoscale [15,16]. The dynamic and static contact states of water droplets on a solid surface had been successfully simulated by molecular dynamics [17]. Xu et al. [18] studied the wettability of defective graphene oxide film via molecular dynamics simulations, whereas Chen et al. [19] studied the mechanism of surface nanostructure changing wettability using the molecular dynamics method.

The behavior of liquid droplets between nanoscale and the macro level is significantly different due to the large difference in surface-to-volume ratios. It is necessary to adjust the simulation conditions to match the experimental results. Barisik et al. [20] showed that the interaction parameters for the silicon–water system should be properly tuned in order to recover the wettability behavior measured during experiments.

In this paper, the wettability of smooth copper plates is studied by adjusting the copper–water potential parameters, excluding the effect of roughness. The solid–liquid potential energy and the diameter of the solid–liquid contact surface under different potential energy parameters are analyzed, and the reason for wettability is explained from the perspective of energy analysis, which explains the special functional principle of wettable materials from the perspective of molecular potential energy. It is of great significance for the design and manufacture of wetted surfaces with special functions.

2. Simulation Models and Methods

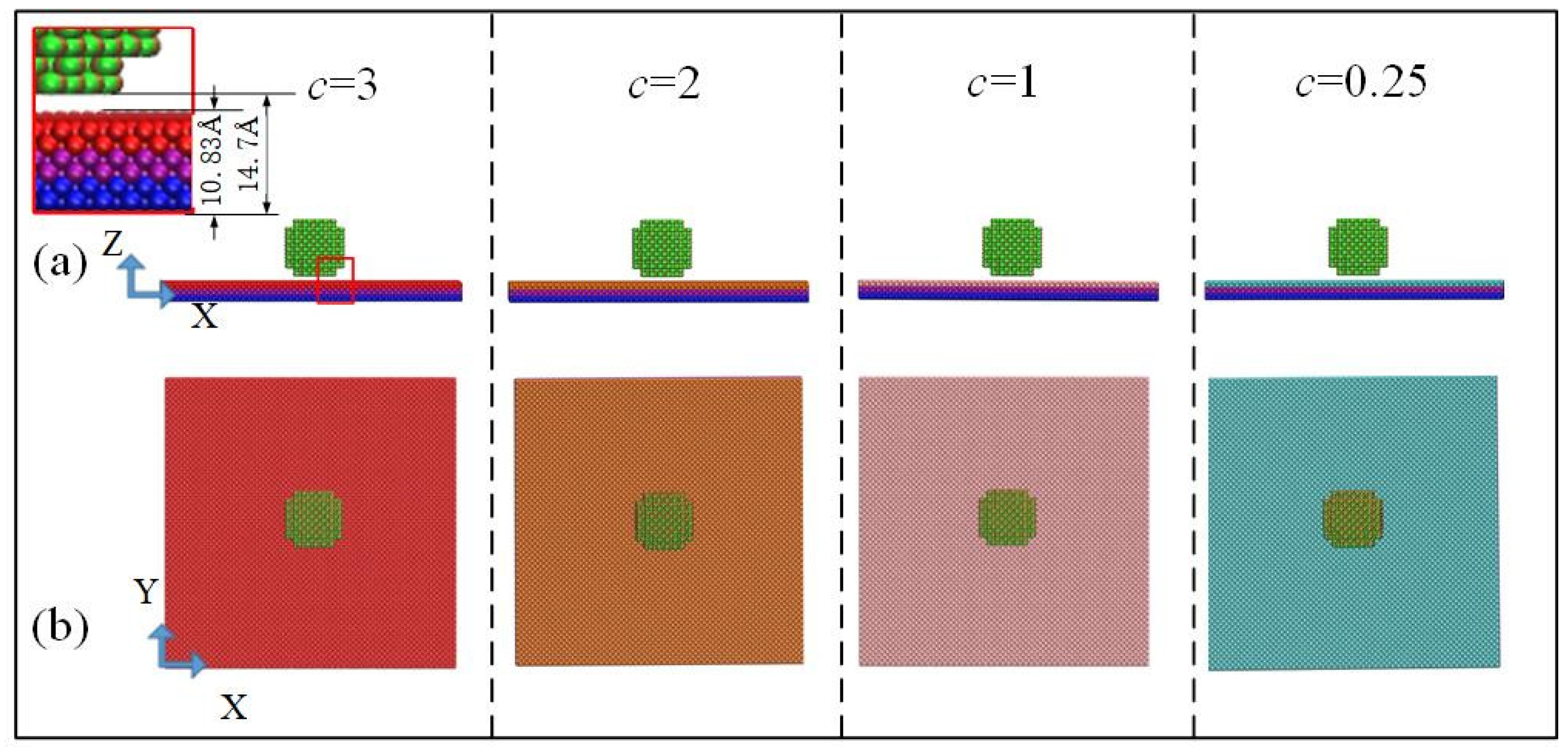
A simulation box [18.05 nm (x) × 18.05 nm (y) × 36.1 nm (z)] was built. Four initial configurations of the simulation systems with different value of potential parameters are presented in Figure 1.

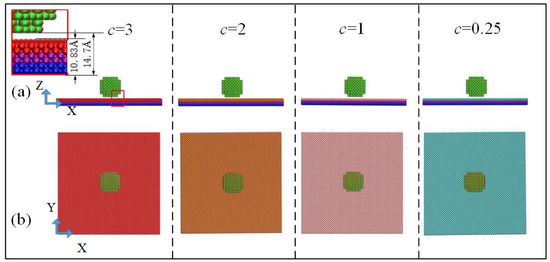
Figure 1. Schematic diagram of initial configuration system for four surfaces with different potential parameters: (a) X–Z two-dimensional view and (b) X–Y two-dimensional view.

A same-size water droplet was modeled using a four-site water model (TIP4P) with a lattice constant of 4.9 Å corresponding to its density of 1.0 g/cm³ and was placed on a copper plate with different potential energy. The lattice constant of the copper plate, which consisted of six layers of copper atoms, was 3.61 Å, corresponding to a density of 8.9 g/cm³. For these surfaces, the bottom two layers of atoms were fixed to prevent atom migrations [21]. The middle two layers were set as “phantom atoms” [22]; the heat source was maintained at 298 K by a Langevin thermostat [23]. As shown in Figure 1a, the center height of the spherical droplet was six lattice lengths, 29.4 Å, and its radius was three lattice lengths, 14.7 Å. The thickness of the copper atomic layer was 10.83 Å, and the lowest point of the nano water drop was 14.7 Å away from the bottom of the copper atomic layer. There was no interference between copper atoms and water molecules.

In this study, all classical molecular dynamics simulations were performed using LAMMPS (version 16 Mar 2018), and visualization of data was conducted using VMD [24]. Potential functions related to the nature of the molecular force are usually used to describe the forces between atoms. In these simulations, Lennard–Jones (L-J) potential function was used to represent the interaction between copper–oxygen atoms and copper–copper atoms, as follows:

$$\mathrm{U}=4\epsilon \left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right]$$

(1)

where ε is the distance of the potential well and σ is the finite length, where the potential energy is zero. The interactions between H-Cu atoms and H-H atoms were ignored and assumed to be zero. For interactions between copper atom and oxygen atom, ε and σ were given as:

$${\sigma }_{Cu-o}=\frac{1}{2}\left({\sigma }_{Cu}+{\sigma }_o\right)$$

(2)

$${\epsilon }_{Cu-o}=c\sqrt{{\epsilon }_{Cu}{\epsilon }_o}$$

(3)

The wettability of copper plate surface was obtained by regulating the value of the potential parameter c, which described the interaction strength of copper and water [25]. The contact angle of solid surface increased with the decrease in parameter c [26]. Copper atoms and water molecules show actual interaction when the value of c is equal to 1.

L-J with long-range Coulombic interactions was successfully used to present the interaction force between hydrogen atoms, oxygen atoms, or hydrogen and oxygen [27]:

$$U_{ab}=\sum _i^a\sum _j^b\frac{k_c{q}_{a_i}{q}_{b_j}}{r_{a_i{b}_j}}+\sum _i^a\sum _j^{b}4{\epsilon }_{a_i{b}_j}\left[{\left(\frac{{\sigma }_{a_i{b}_j}}{r_{a_i{b}_j}}\right)}^{12}-{\left(\frac{{\sigma }_{a_i{b}_j}}{r_{a_i{b}_j}}\right)}^6\right]$$

(4)

where subscripts a and b represented two different atom types. Subscripts i and j denoted oxygen or hydrogen atoms in a single TIP4P water molecule. Parameter q_i is the charge of site i, and r_aibj is the distance between the two atoms. k_c is the electrostatic constant. Long-range effect effects are expressed as PPPM (particle–particle particle–mesh) with an accuracy of 10⁻⁶ due to electrostatic potential.

The whole calculation process was divided into two steps. First, the energy of the whole system was minimized, and the droplet was relaxed by the Langevin thermostat (298 K) alone for 500 ps, then the solid atoms interacted with the liquid water molecules for 100 ps. The time step was 0.001 fs, and the output data were 100 fs at a time. The pair potential between oxygen atoms was considered with a cutoff radius of 12 Å. Furthermore, the rigidity of the water molecules was maintained by implementing the SHAKE [28] algorithm. The L-J potential parameters of copper and water potential parameters are shown in Table 1.

Table 1. L-J potential parameters for copper–oxygen and water potential parameters.

Parameters	Values	Units
${\epsilon }_{O-O}$	0.006998	eV
${\sigma }_{O-O}$	3.16438	Å
$q_O$	−1.04	e
$q_H$	0.52	e
${\epsilon }_{Cu-O}$	0.06387	eV
${\sigma }_{Cu-O}$	2.7172	Å
E	274–306	GPa
d	3.615	Å

3. Results and Discussion

3.1. The Wettability and Spreading Behavior of Droplets

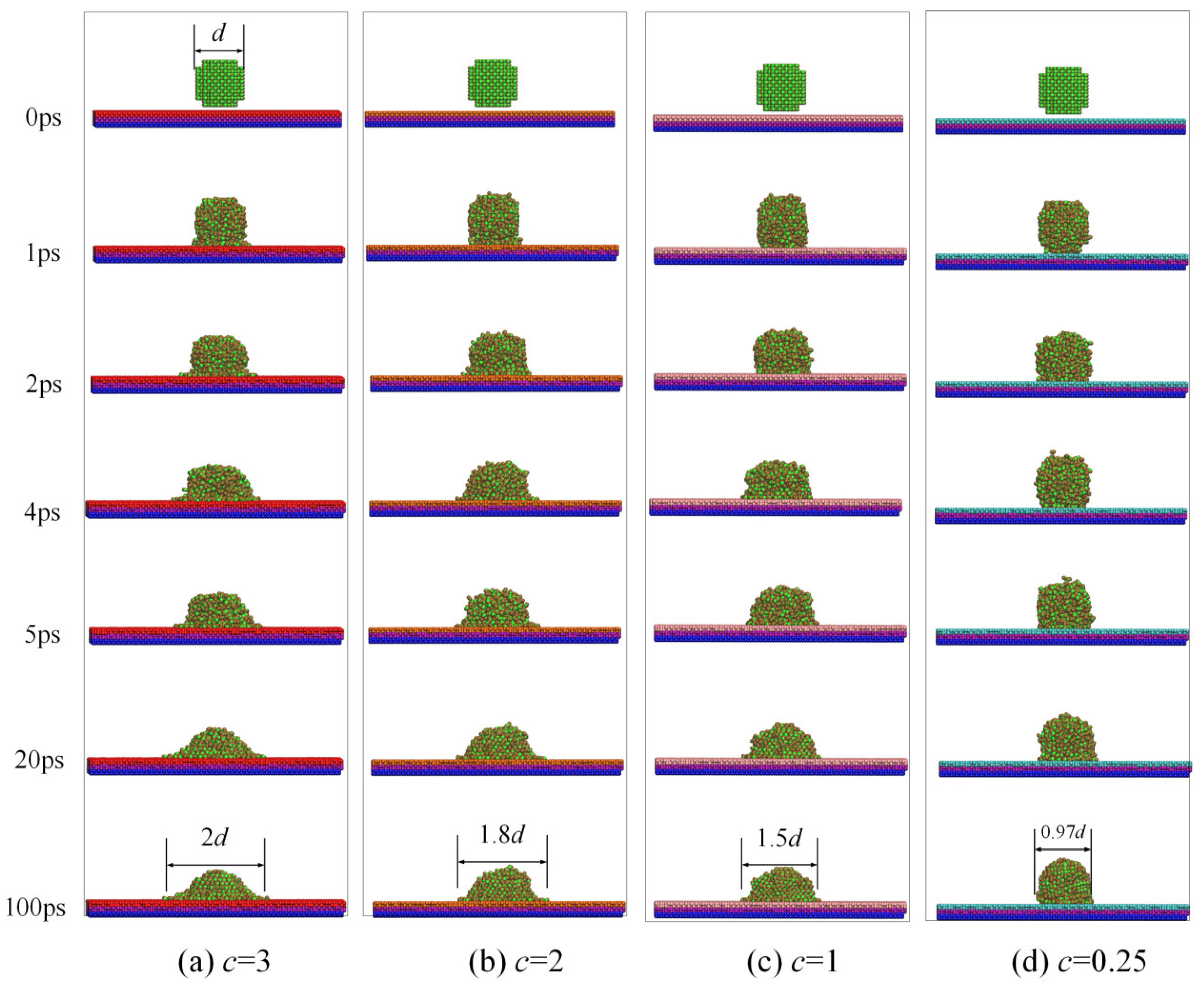
To explicitly show the wettability and spreading behavior of a nano-water droplet on the copper plate, X–Z two-dimensional view snapshots of water droplets’ wettability and spreading on surfaces with different potential parameters are presented in Figure 2.

Figure 2. The wettability and spreading snapshot of droplets on different solid surfaces.

At the beginning of the simulation, droplets of the same size were placed above four different copper plates with different values of c, respectively. The nano-water droplet quickly dropped on the copper plate and began to spread out in all simulations under the action of potential energy at 1 ps once the simulation started. The mass of the droplet was ignored in these simulations.

From 1 ps to 20 ps, water droplets gradually spread to the copper surface, but it was evident that the area of water droplets spreading was larger with the larger value of c. After 20 ps, the system was stabilized. The diameters of water droplets spreading were measured as 2, 1.8, 1.5, and 0.97 times those of the original diameters of water droplets on different surfaces at 100 ps.

3.2. Contact Angle Measurements and Analysis

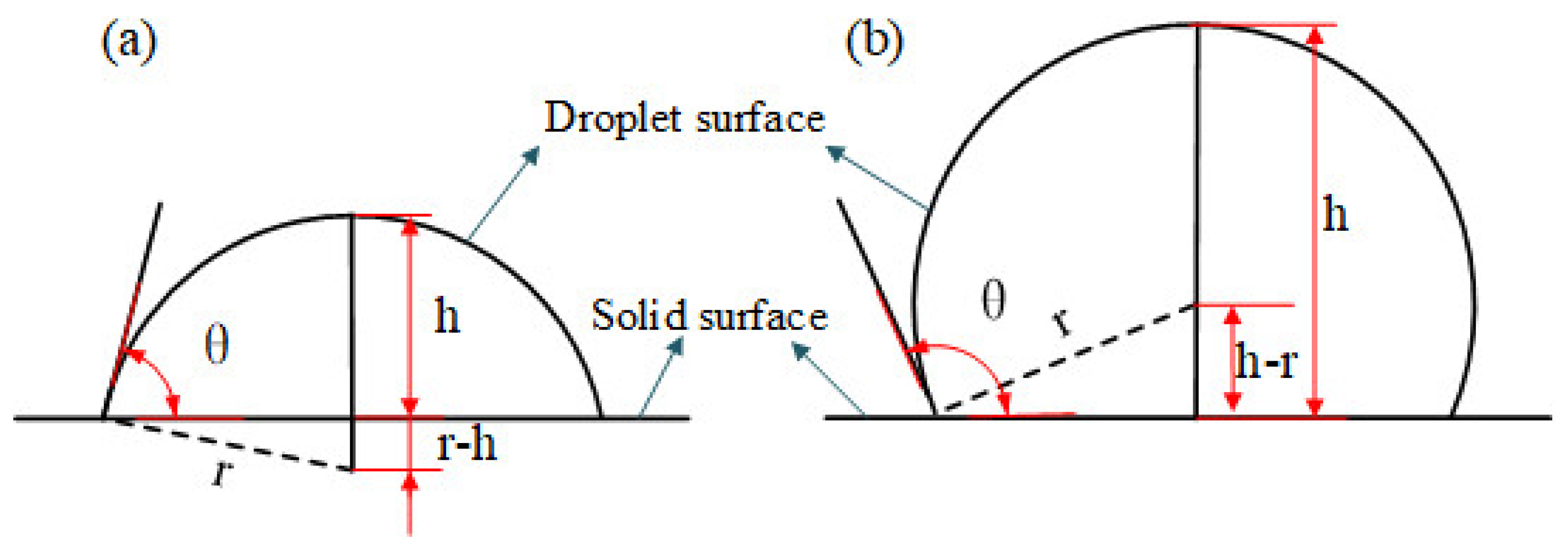
In order to quantitatively analyze the surface wettability of different potential well depth parameters, it is necessary to calculate the solid–liquid contact angle. The schematic diagram of contact angle calculation is shown in Figure 3, where θ is the static contact angle between solid and liquid, h is the droplet height, and r is the droplet radius.

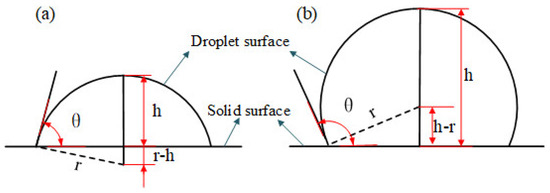
Figure 3. Diagram of contact angle calculation: (a) h < r and (b) h > r.

According to the trigonometric function theorem, the value of static contact angle $\theta$ can be calculated as follows [29]:

$$\left\{\begin{array}{c}\theta =\arccos \left(1-\frac{h}{r}\right)(h<r)\\ \theta =\frac{\pi }{2}+\arcsin \left(\frac{h}{r}-1\right)(h>r)\end{array}\right.$$

(5)

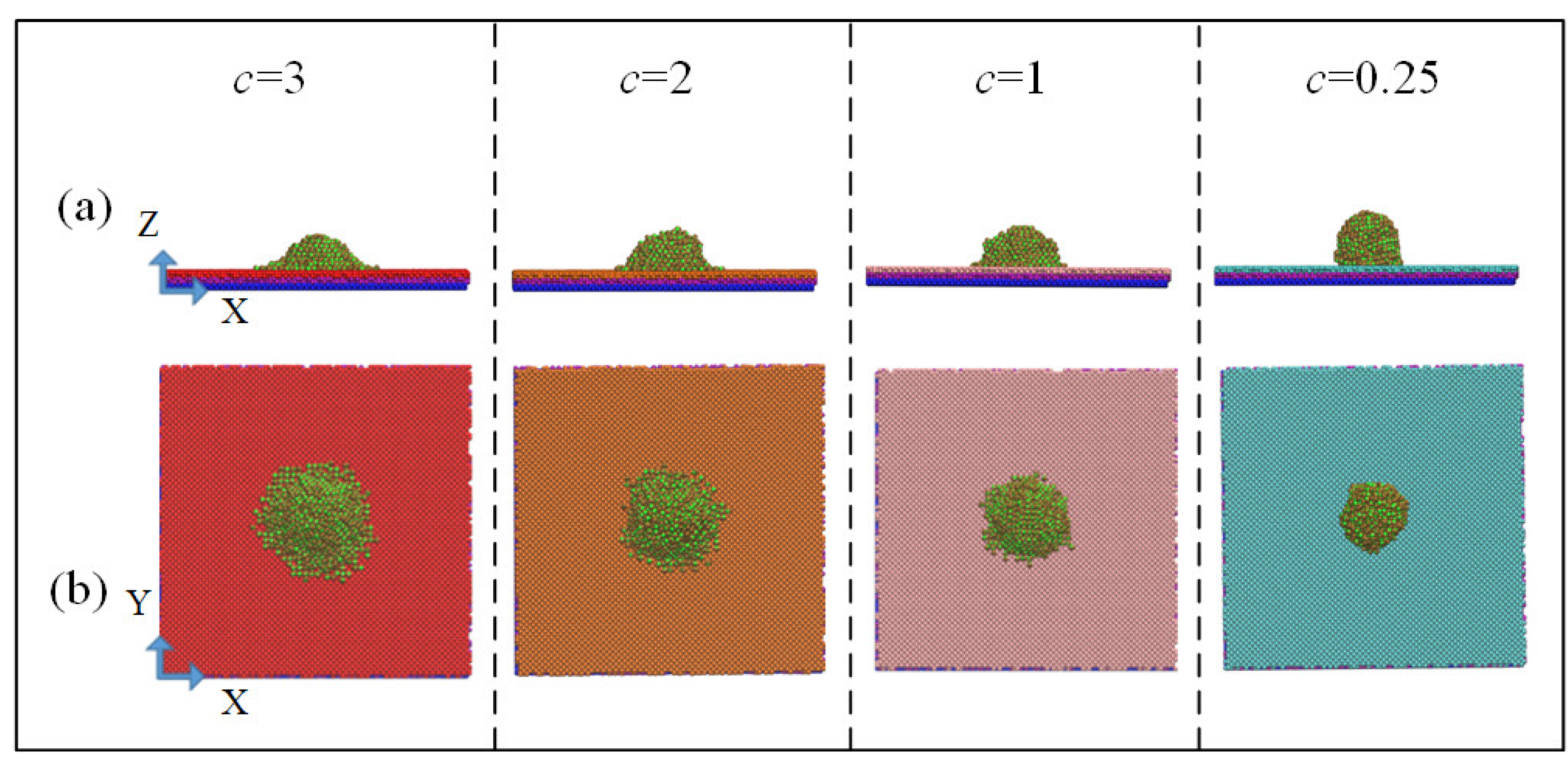
In order to determine the width and height of water droplet laying, the simulation boxes were divided into 1702 bins at 1 nm and 0.4 nm intervals in the z and x directions, respectively. The position of each bin and the number of water molecules in the bin were available, from which width and height of the droplet laying were obtained. Snapshots of the spreading state of the droplets after simulated equilibrium were shown in Figure 4; as shown in Equation (6), when the values of potential parameter c were 3, 2, 1, and 0.25, the measured static contact angles were 50.8°, 75.3°, 87°, and 119.9°, respectively.

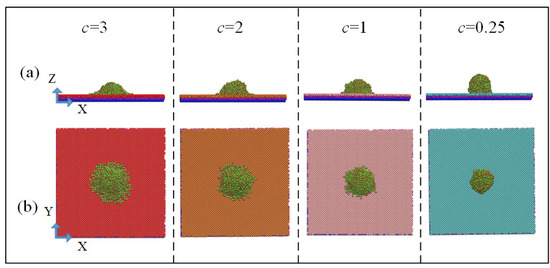
Figure 4. Snapshots of the spreading state of the droplets after simulated equilibrium: (a) X–Z two-dimensional view and (b) X–Y two-dimensional view.

To determine the contact angles of water and copper plates, a contact angle measuring instrument was used to measure these angles on a smooth copper surface. In Figure 5, contact angles were measured for four common sizes (3 μL, 6 μL, 9 μL, and 12 μL) on five smooth copper plates using a DropMeter A-300. The contact angle measurements were repeated 3–5 times for each surface and each droplet size, and the average values of all measurements were recorded. The contact angle of the smooth copper surface was approximately 76°. This was smaller than the simulated value; that is to say, the actual solid plane could not reach the ideal smooth plane, and the rough surface reduced the contact angle and increased hydrophilicity [29].The results also showed that the establishment of the model was valid and correct.

Figure 5. Contact angle measurement of smooth copper plate.

3.3. The Influence of Tuning Potential Parameters on Potential Energy and Spreading Behavior of Water Droplets

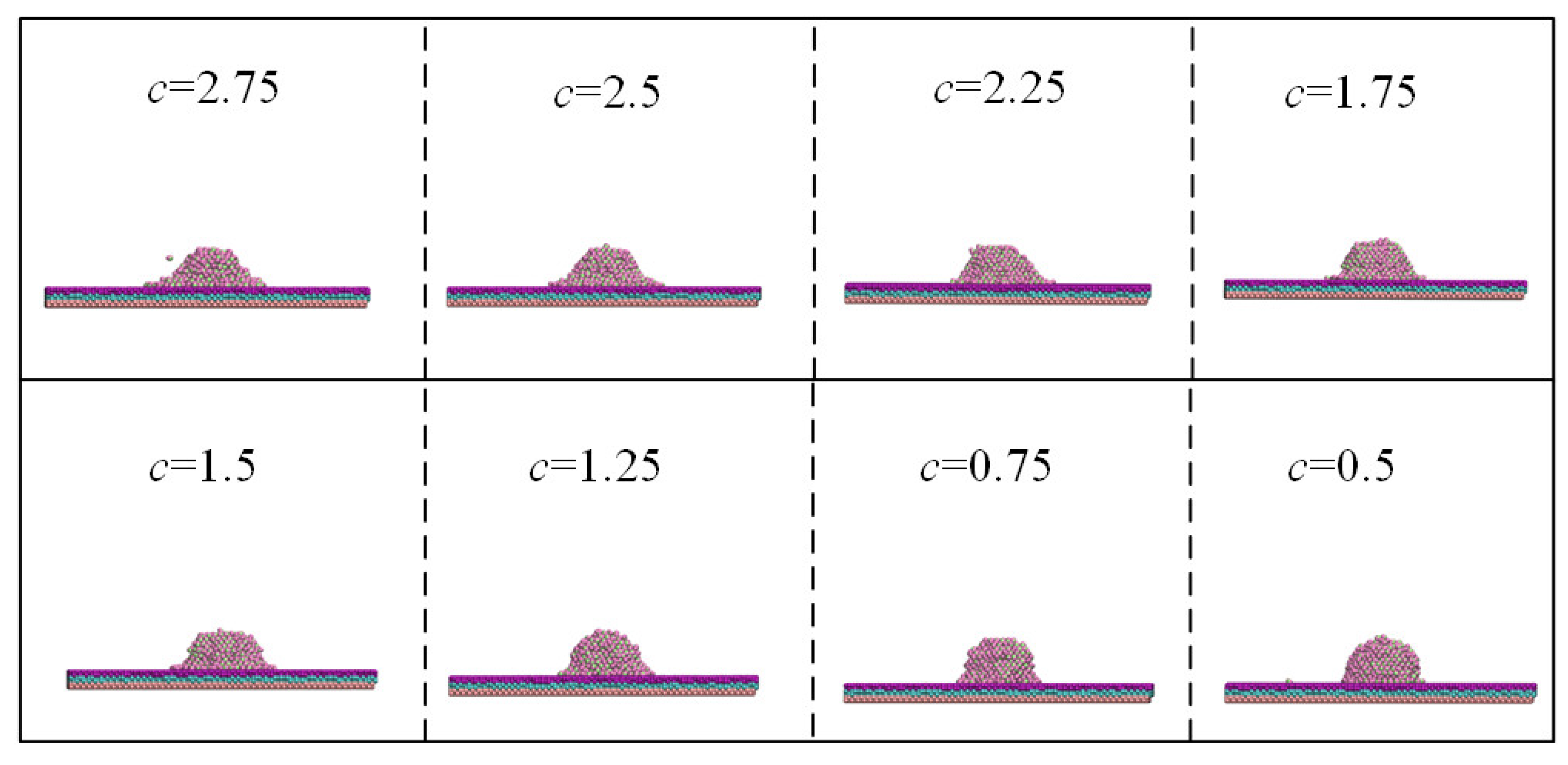
To clarify the influence of tuning potential parameters on the potential energy and spreading behavior of water droplets, the values of c ranged from 0.25 to 3, and the widths and heights of the droplet laying of other surfaces obtained at intervals of 0.25 are shown in Figure 6. The diameter of solid–liquid contact increased, and the contact angle reduced with the increase in the c value.

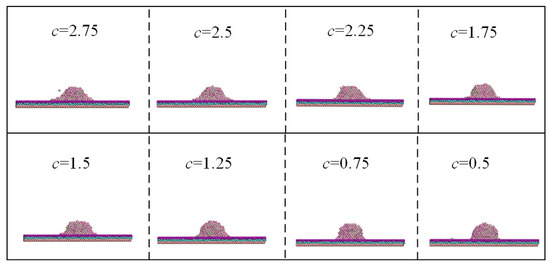
Figure 6. Spreading behavior of water droplet with different values of c.

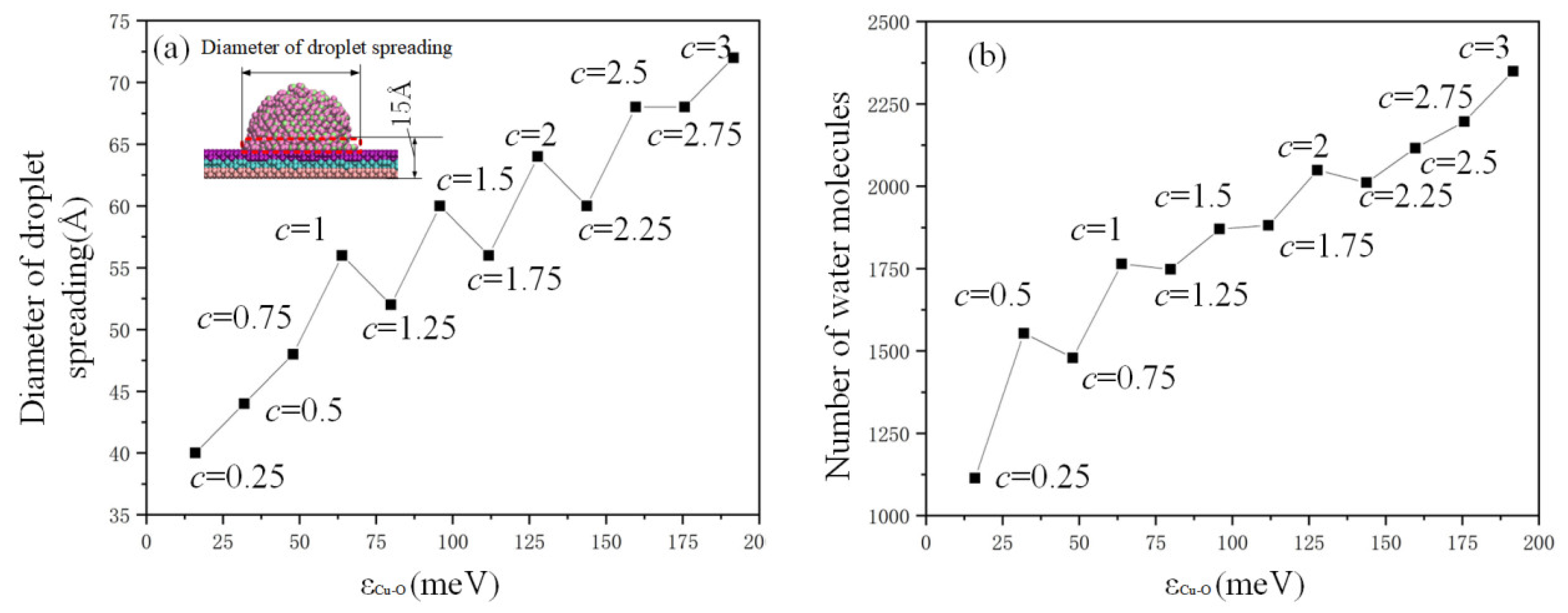
The behaviors of droplet spreading in relation to different copper–oxygen potential parameters are analyzed in Figure 7. The distance of potential well (${\epsilon }_{Cu-o}$) increased with the increase in c value. The diameter of droplet spreading and the number of water molecules on the copper plate in the red dotted box (the height is 15 Å) increased with the value of ${\epsilon }_{Cu-o}$, and the change curve did not always appear as a straight line but sometimes as a zigzag change with the value of c from 0.5 to 2.25. In Figure 7a, three values (c = 1.25, 1.75, 2.25) are observed to be abnormal. The reason is that the effective rank of c is down to the percentile, and the order of magnitude of ${\epsilon }_{Cu-o}$ is too small, resulting in the unstable sensitivity of the simulation system. In general, the droplet diameter showed a consistent upward trend, except these three values.

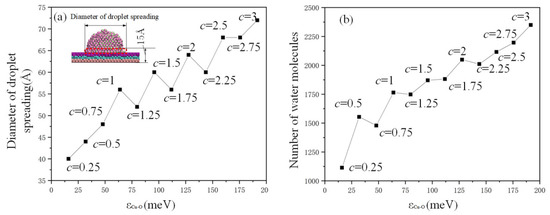
Figure 7. Analysis of the (a) diameter and (b) quantity of droplet spreading.

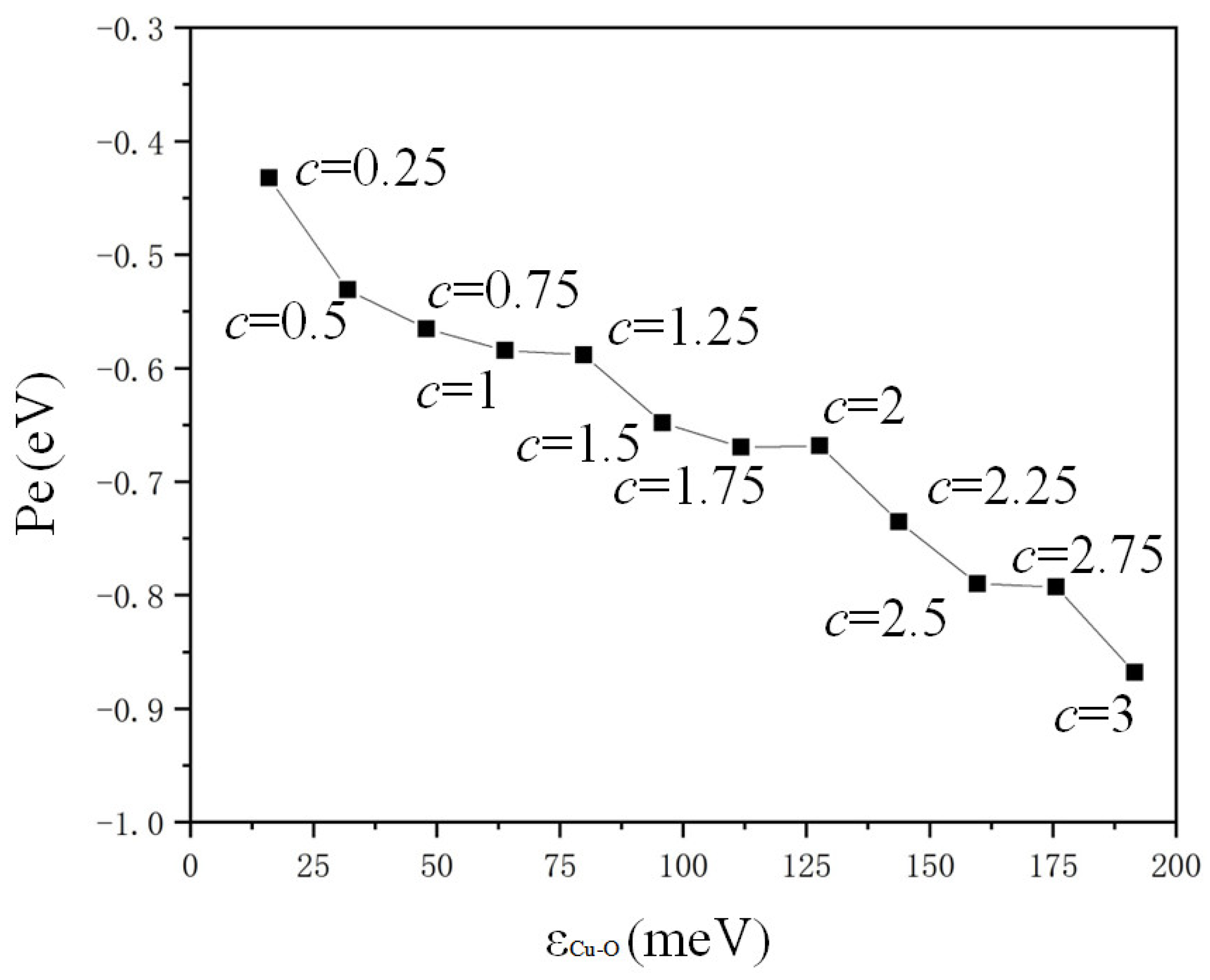
The potential energy changes in water molecules in the red dotted line box in Figure 7a on the copper surface are calculated in Figure 8. The negative values of potential energy (Pe) represent attractive force. The potential energy of water molecules on a copper surface showed a regular trend in variation with the value of c. Furthermore, the attractive force was greater for the region with a larger absolute value of potential energy. The surface was more hydrophilic if the value of c was bigger due to the superior attractive force of solid atoms and liquid molecules. The smaller absolute value of the potential energy resulted in reduced attraction of water and copper, and the surface was hydrophobic. The properties of hydrophilic and hydrophobic heat transfer could be explained by molecular potential energy. The critical heat flux [30,31] was high on a hydrophilic surface with small solid–liquid attraction due to the significant attractive force ensuing sufficient solid–liquid contact. The boiling heat transfer coefficient was high on the hydrophobic surface [32,33] due to the reduced attractive force promoting the formation of bubbles.

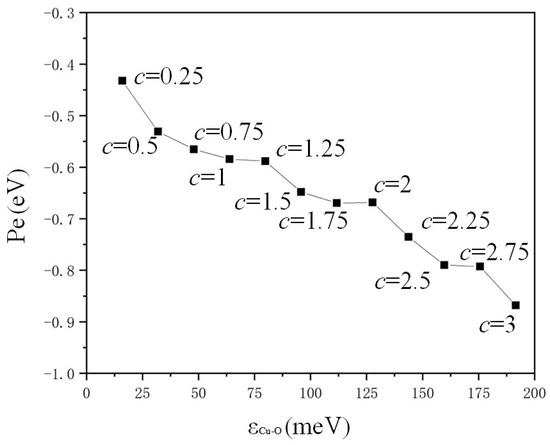
Figure 8. Dependence of potential energy on the distance of potential well (${\epsilon }_{Cu-o}$).

4. Conclusions

Molecular dynamics simulations were carried out to investigate the wettability of nano-water droplet on a smooth copper plate. For all cases studied, the behavior of nano-water droplet spreading above the copper plate was analyzed. The simulation results showed that the diameter of droplet spreading and the number of water molecules on the copper plate increased with the increase in the potential parameters. Meanwhile, the attractive force between liquid and solid increased with the value of ${\epsilon }_{Cu-o}$. The principle of surface wettability of a copper plate is the change in the potential energy of liquid molecules. The heat transfer properties of hydrophilic and hydrophobic surfaces can also be explained by the difference in the potential energy of the liquid molecules. This makes it possible to explain the mechanism of wetting surfaces with special functions from the perspective of liquid molecular energy and provides a basis for the design of wetting surfaces with special functions from the perspective of energy.