A Study on Poly(ethylene oxide)-Based Supercapacitors Doped with Various Dopants
Abstract
:1. Introduction
2. Experimental Methods
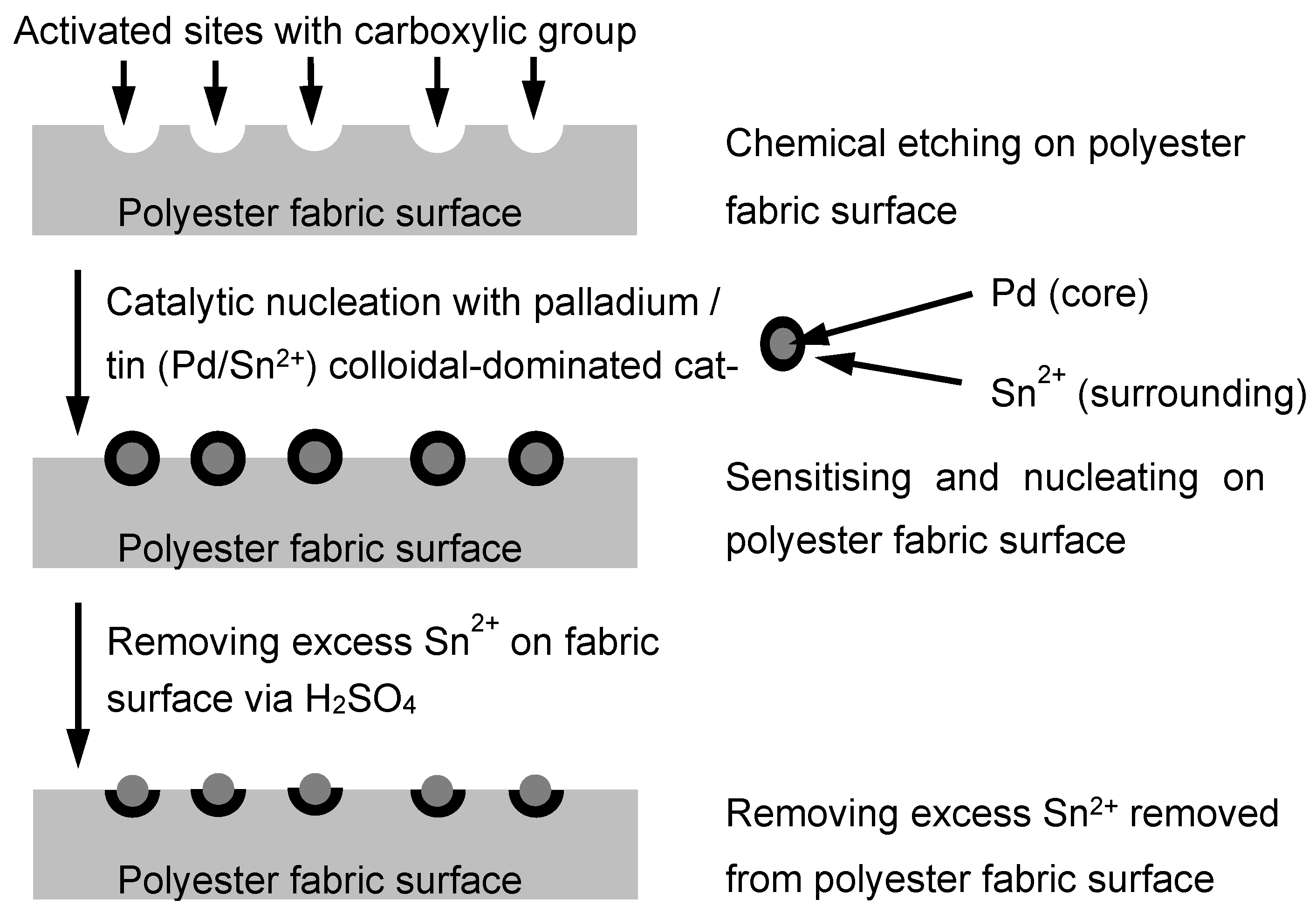
2.1. Polyester Fabric Metallisation
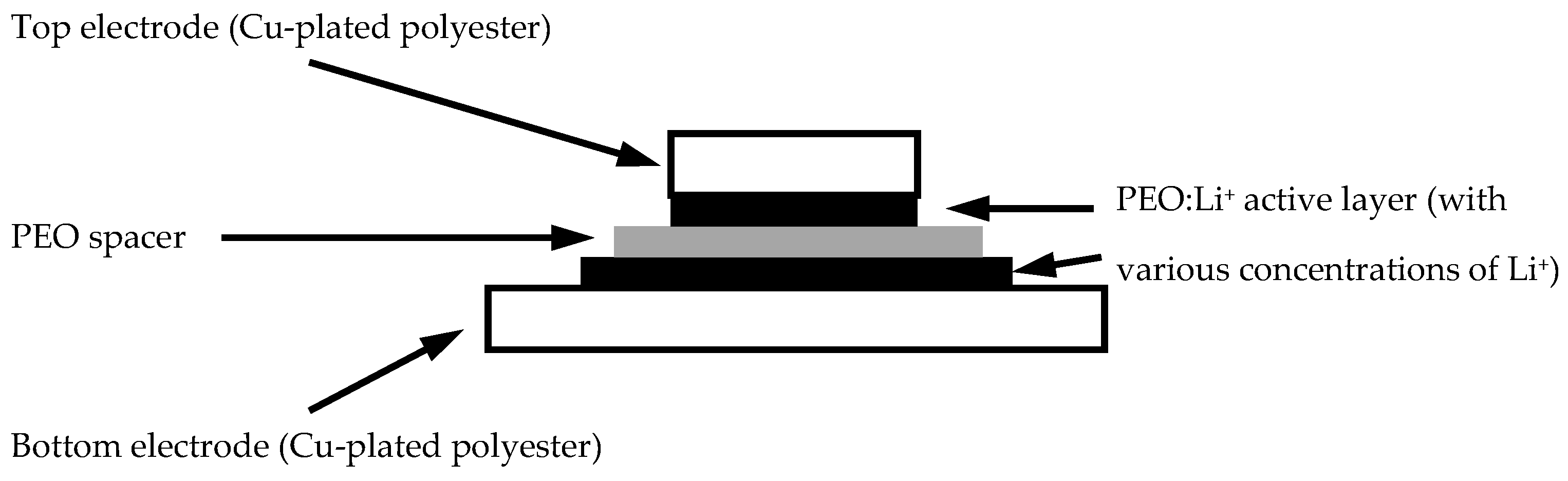
2.2. Fabrication of EDL Capacitors with Various Dopants
2.2.1. Preparation of Flexible Current-Collecting Polyester Fabrics
2.2.2. Preparation of PEO Dielectric Spacer
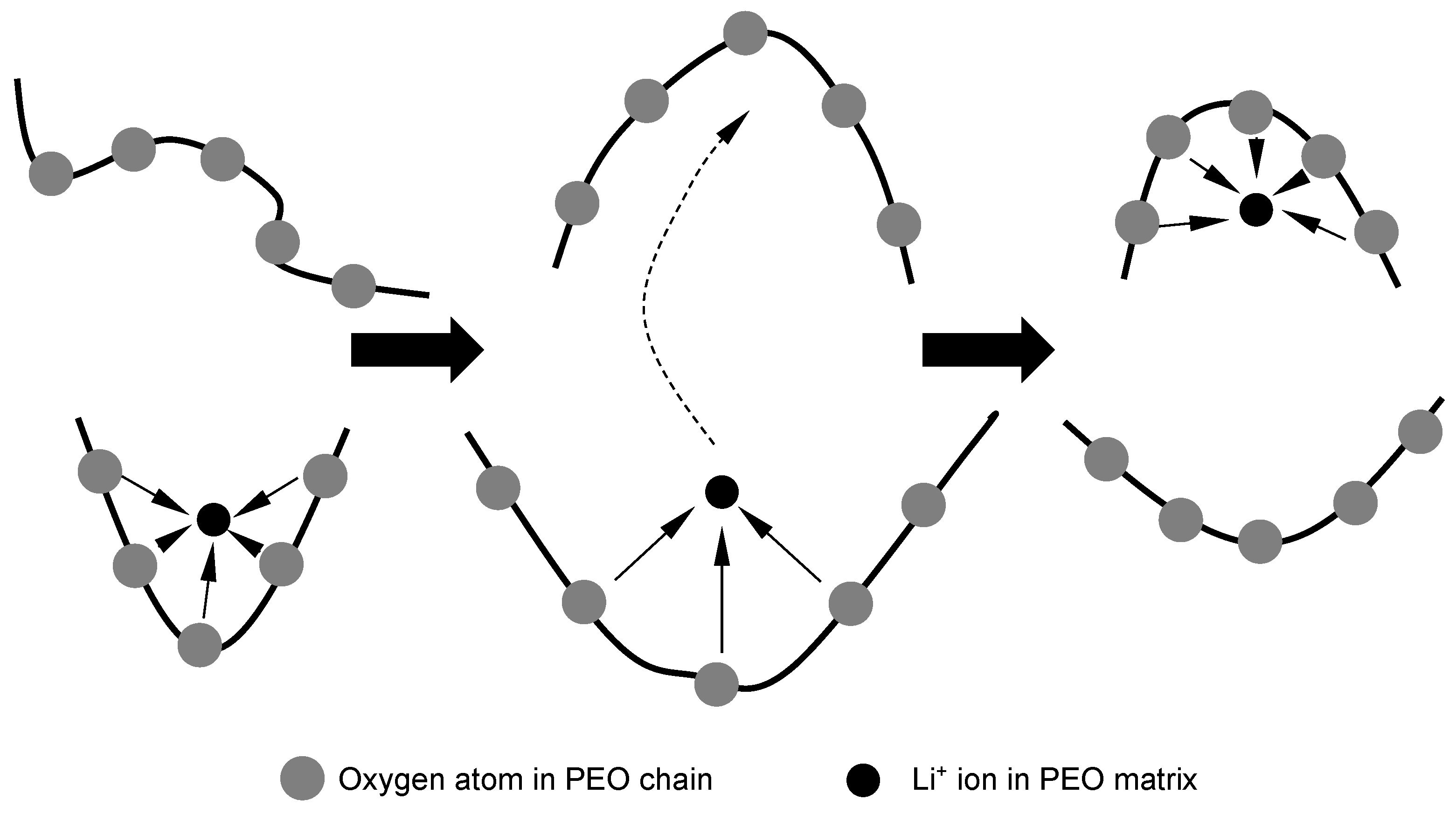
2.2.3. Preparation of PEO:Li+ EDL Capacitors with Different LiClO4 Concentrations
2.2.4. Preparation of PEO:nanocarbon EDL Capacitors with Different Types of Nanocarbons
3. Results and Discussion
3.1. Surface Morphology of Metallised Polyester Fabrics
3.2. Thickness Estimation of Different PEO-Casted Polyester Fabric Samples
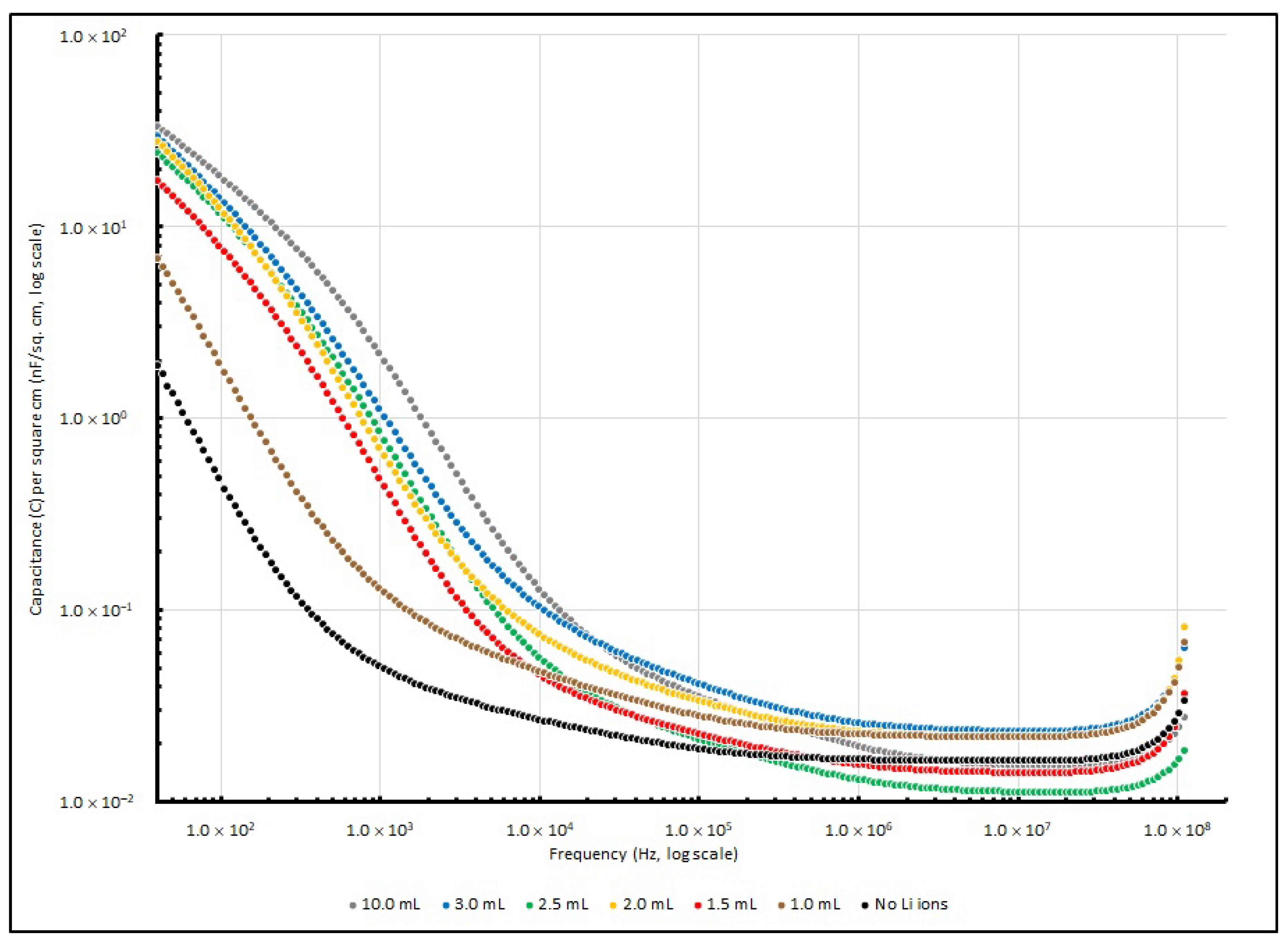
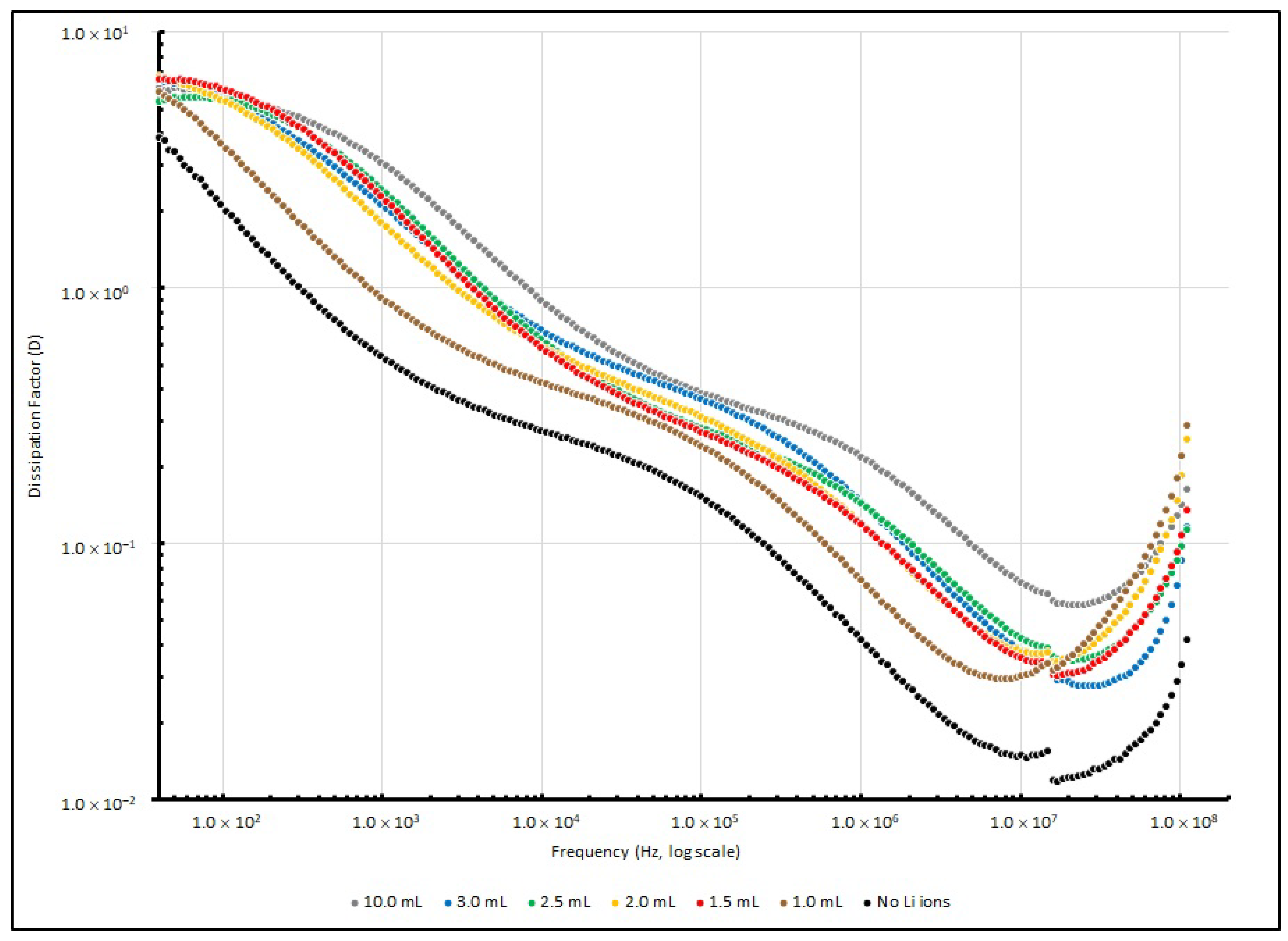
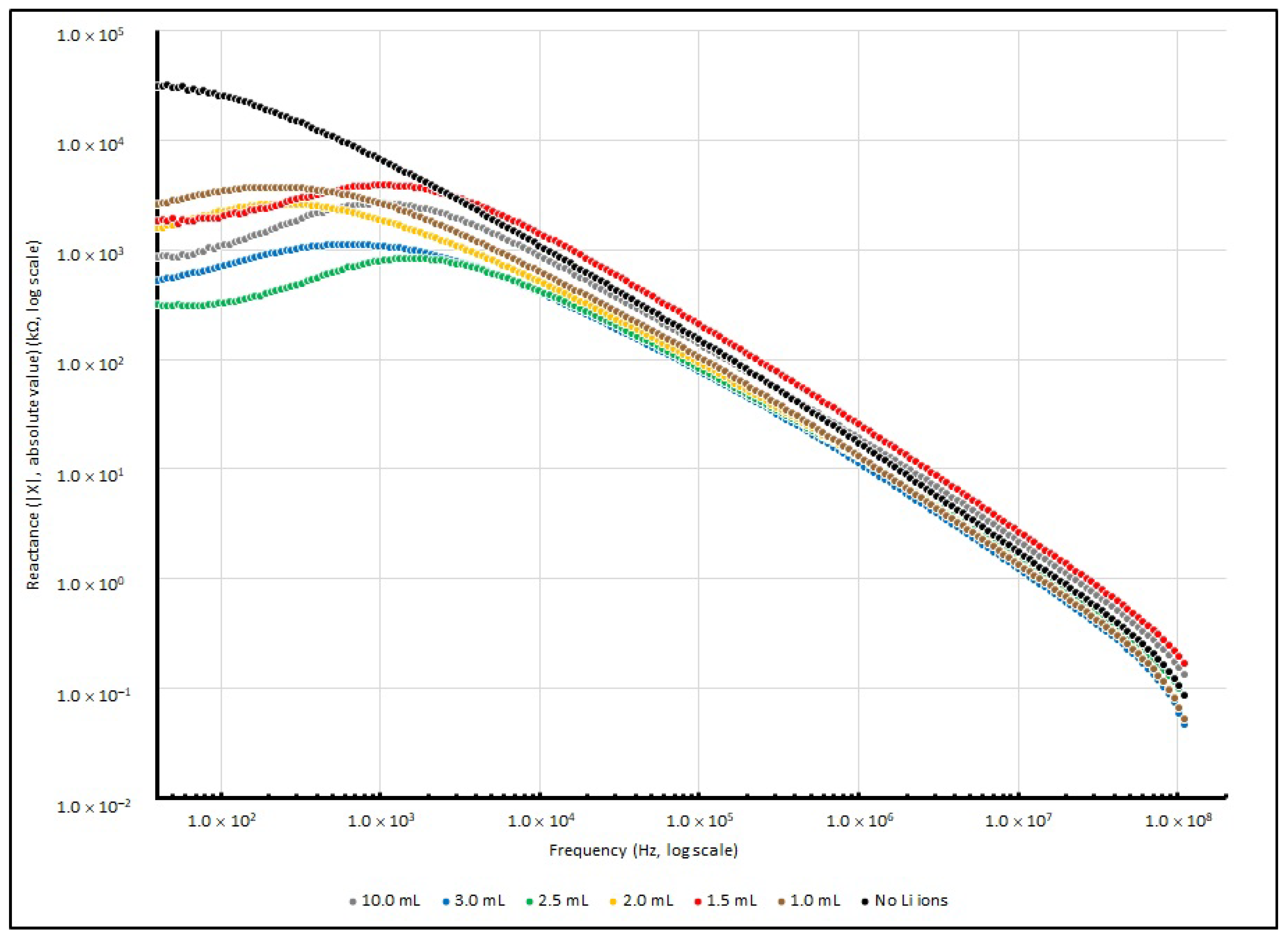
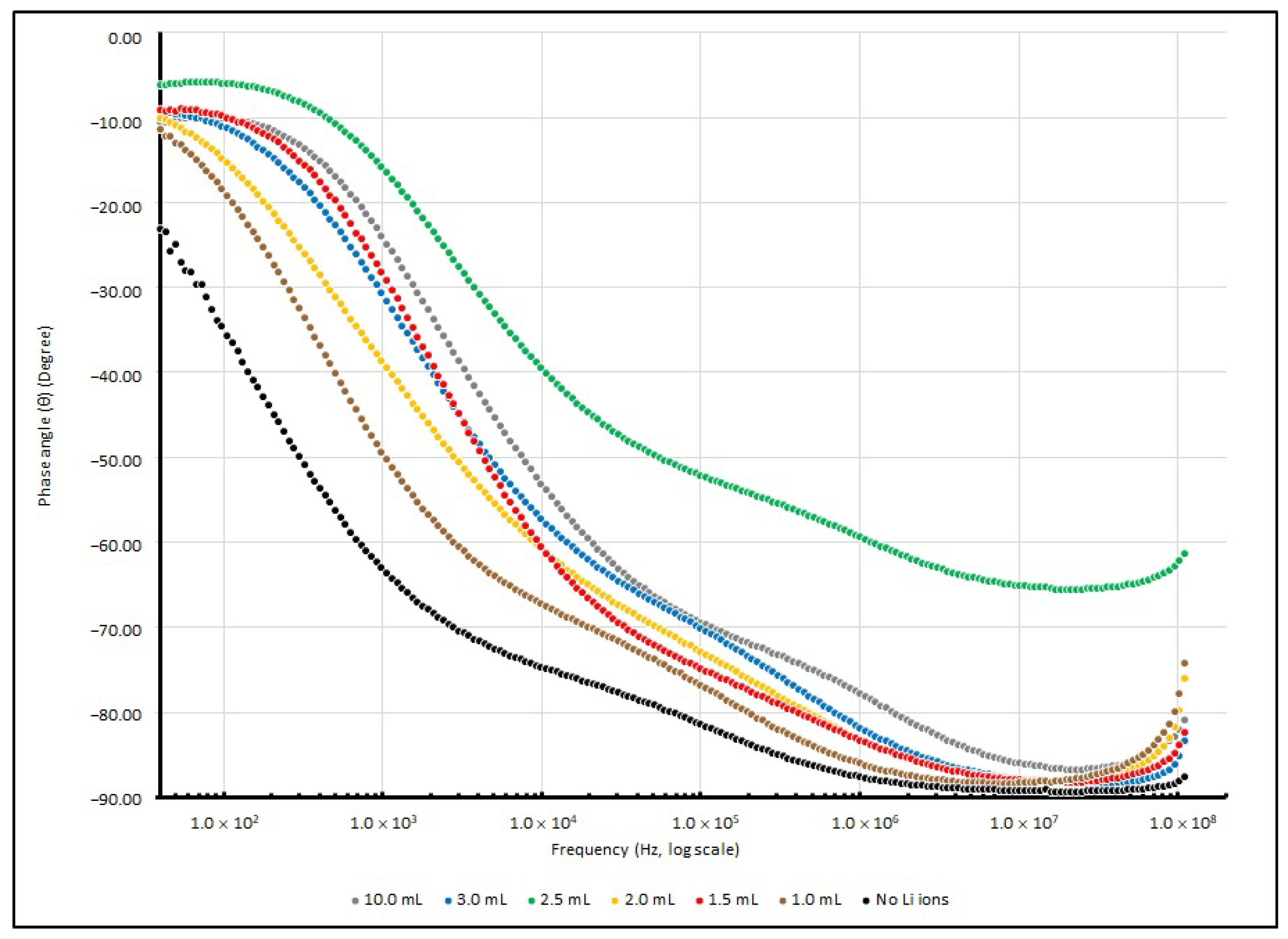
3.3. Frequency Responses of PEO-Based EDL Capacitors with Various LiClO4 Concentrations
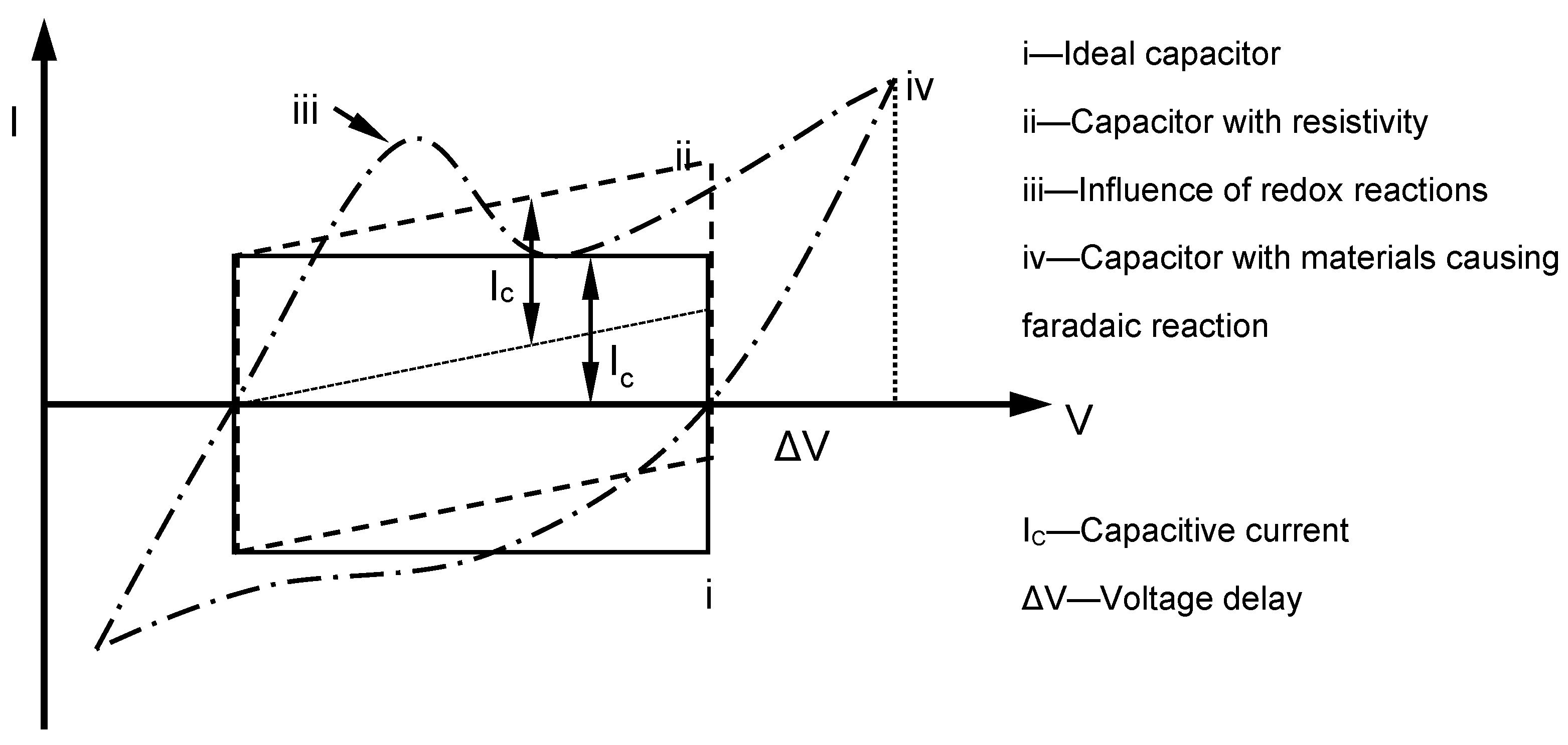
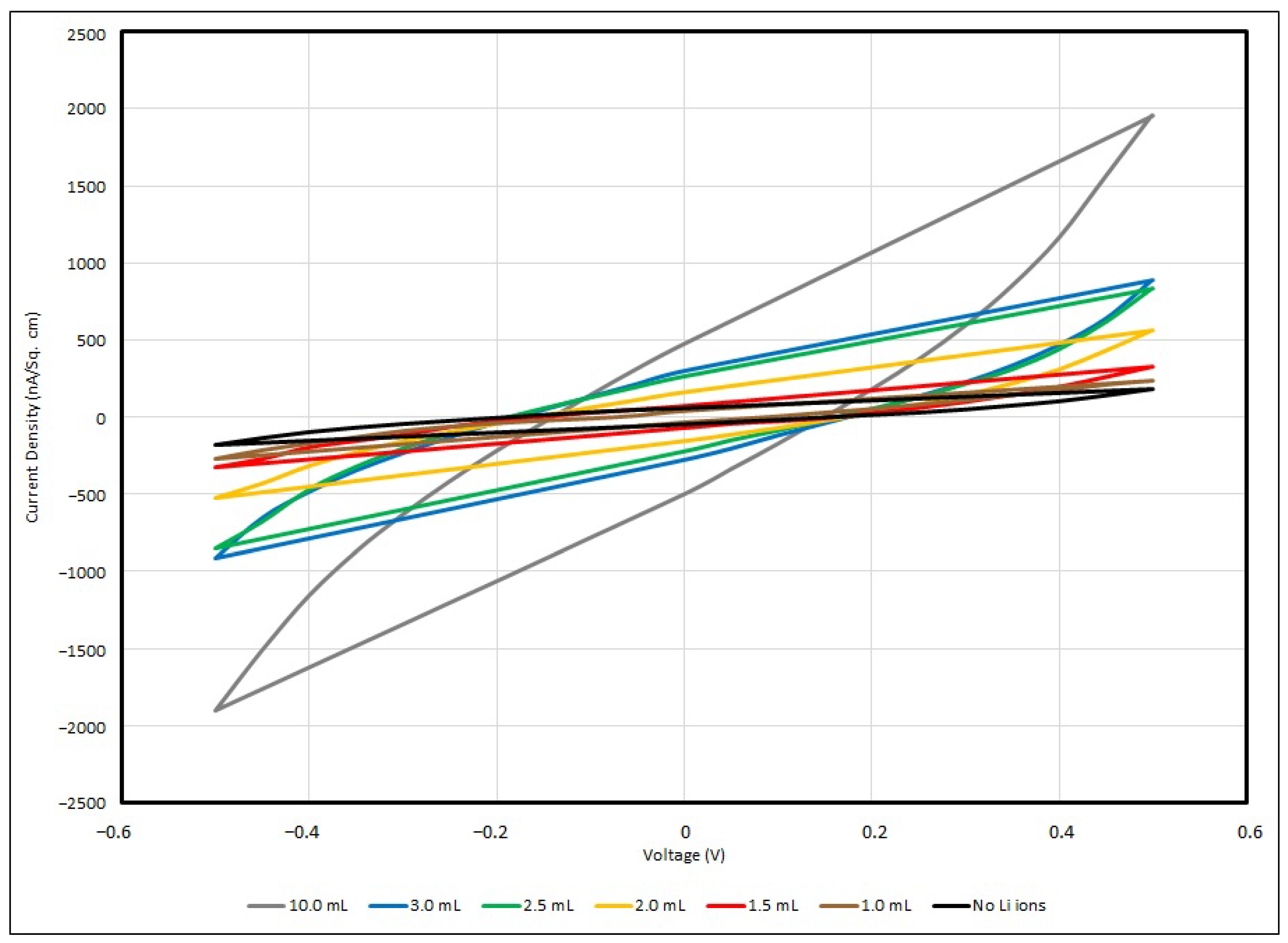
3.4. Cyclic Voltammetry of PEO-Based EDL Capacitors with Various LiClO4 Concentrations
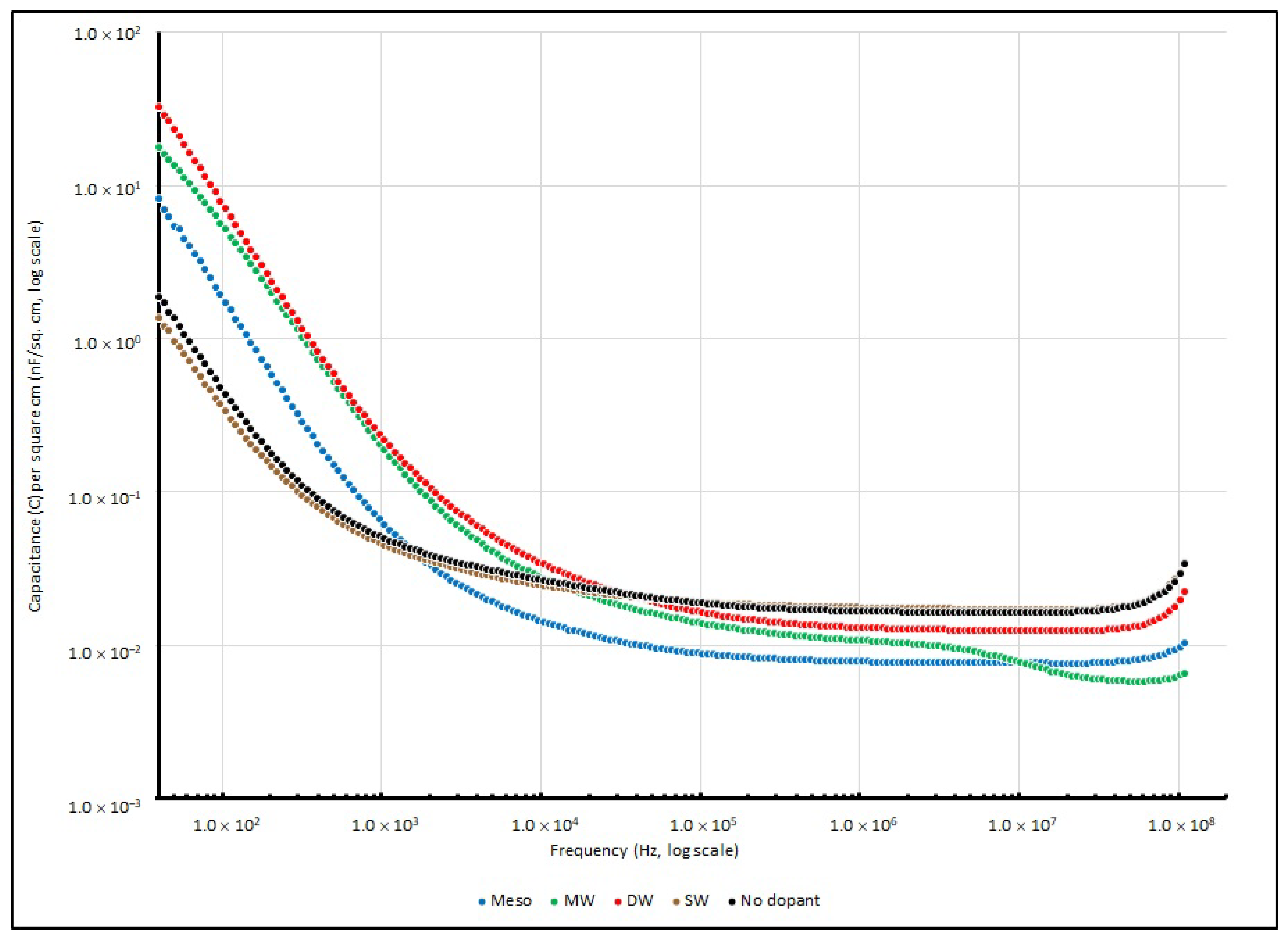
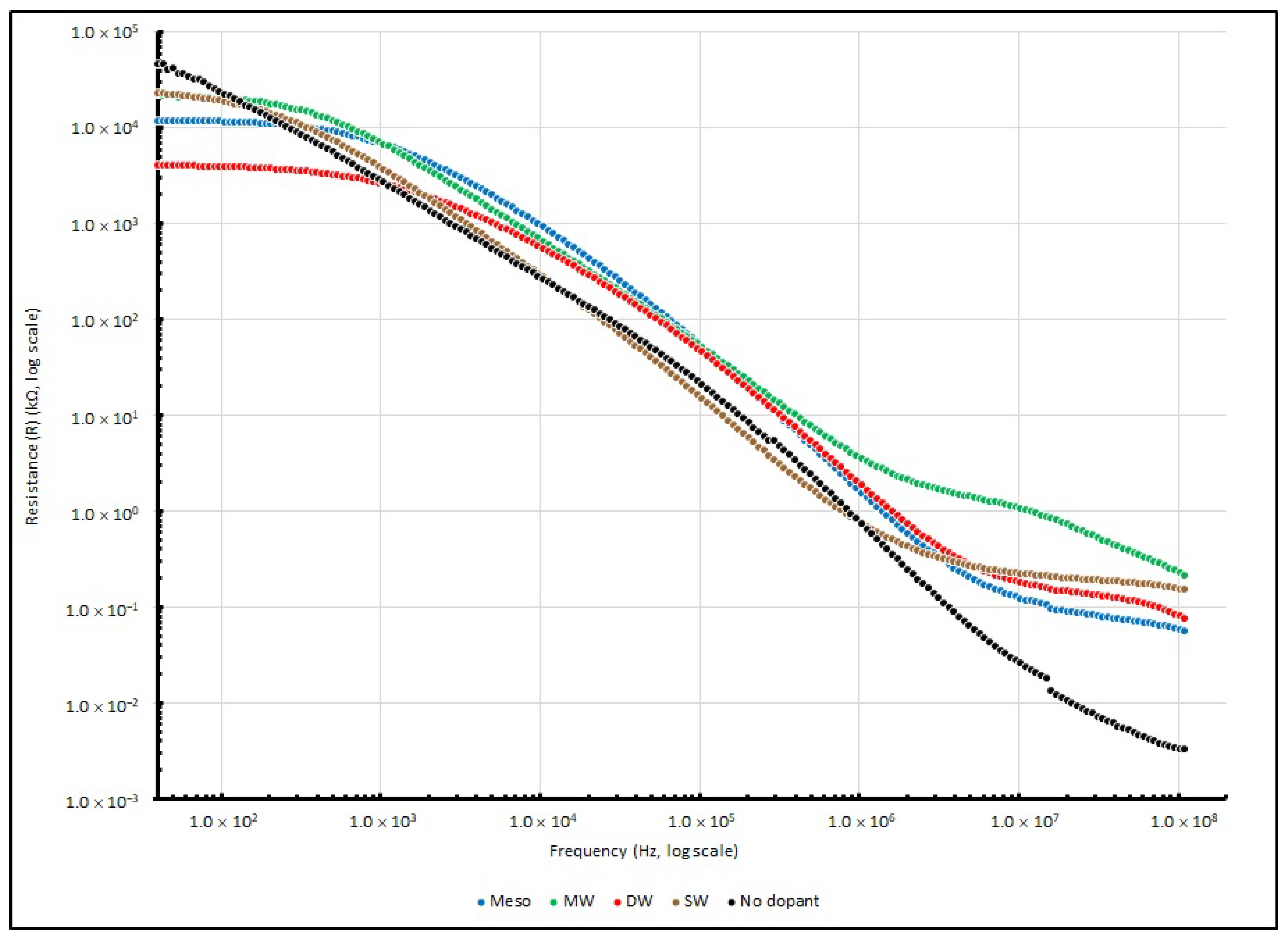
3.5. Frequency Responses of PEO-Based EDL Capacitors with Various Types of Nanocarbons
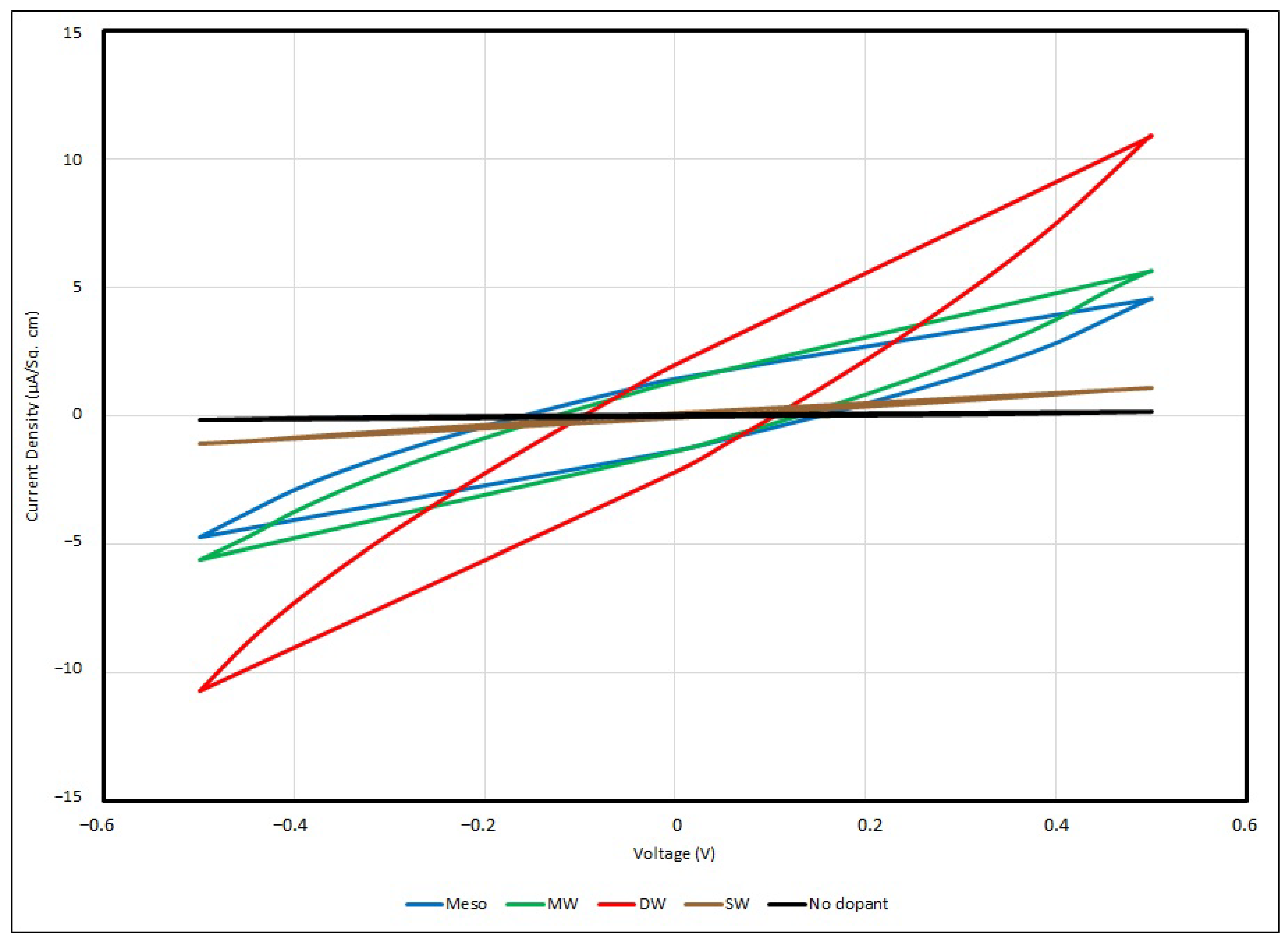
3.6. Cyclic Voltammetry of PEO-Based EDL Capacitors with Various Types of Nanocarbons
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, C.G.; Yu, Z.N.; Neff, D.; Zhamu, A.; Jang, B.Z. Graphene-based supercapacitor with an ultrahigh energy density. Nano Lett. 2010, 10, 4863–4868. [Google Scholar] [CrossRef]
- Balducci, A.; Dugas, R.; Taberna, P.; Simon, P.; Plee, D.; Mastragostino, M.; Passerini, S. High temperature carbon-carbon supercapacitor using ionic liquid as electrolyte. J. Power Sources 2007, 165, 922–927. [Google Scholar] [CrossRef] [Green Version]
- Mastragostino, M.; Arbizzani, C.; Soavi, F. Polymer-based supercapacitors. J. Power Sources 2001, 97–98, 812–815. [Google Scholar] [CrossRef]
- Pandolfo, A.G.; Hollenkamp, A.F. Carbon properties and their role in supercapacitors. J. Power Sources 2006, 157, 11–27. [Google Scholar] [CrossRef]
- Snook, G.A.; Kao, P.; Best, A.S. Conducting-polymer-based supercapacitor devices and electrodes. J. Power Sources 2011, 196, 1–12. [Google Scholar] [CrossRef]
- Zhang, L.L.; Zhao, X.S. Carbon-based materials as supercapacitor electrodes. Chem. Soc. Rev. 2009, 38, 2520–2531. [Google Scholar] [CrossRef]
- Frackowiak, E.; Khomenko, V.; Jurewicz, K.; Lota, K.; Beguin, F. Supercapacitors based on conducting polymers/nanotubes composites. J. Power Sources 2006, 153, 413–418. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, B.S.; Chen, S.; Yang, S.H.; Hammond, P.T. Layer-by-layer assembly of all carbon nanotube ultrathin films for electrochemical applications. J. Am. Chem. 2009, 131, 671–679. [Google Scholar] [CrossRef]
- Jost, K.; Perez, C.R.; McDonough, J.K.; Presser, V.; Heon, M.; Dion, G.; Gogotsi, Y. Carbon coated textiles for flexible energy storage. Energy Environ. Sci. 2011, 4, 5060–5067. [Google Scholar] [CrossRef]
- Huang, Y.; Hu, H.; Huang, Y.; Zhu, M.; Meng, W.; Liu, C.; Pei, Z.; Hao, C.; Wang, Z.; Zhi, C. From industrially weavable and knittable highly conductive yarns to large wearable energy storage textiles. ACS Nano 2015, 9, 4766–4775. [Google Scholar] [CrossRef]
- Dong, L.; Xu, C.; Li, Y.; Wu, C.; Jiang, B.; Yang, Q.; Zhou, E.; Kang, F.; Yang, Q. Simultaneous production of high-performance flexible textile electrodes and fiber electrodes for wearable energy storage. Adv. Mater. 2016, 28, 1675–1681. [Google Scholar] [CrossRef]
- Gan, X.P.; Wu, Y.T.; Liu, L.; Shen, B.; Hu, W.B. Electroless copper plating on PET fabrics using hypophosphite as reducing agent. Surf. Coat. 2007, 201, 7018–7023. [Google Scholar] [CrossRef]
- Liu, X.; Osaka, T. Properties of electric double-layer capacitors with various polymer gel electrolytes. J. Electrochem. Soc. 1997, 144, 3066–3071. [Google Scholar] [CrossRef]
- Lim, B.H.; Kim, J.M.; Nguyen, V.; Kim, H.; Park, C.W.; Lee, J.K.; Lee, C.; Yoo, J.; Min, B.K.; Kim, S.K. Functionalized methyl cellulose/LiClO4 composite as an environmentally friendly quasi-solid polymer electrolyte for solid-state electrochromic devices and cellulose-based supercapacitors. Mater. Today Energy 2023, 33, 101263. [Google Scholar] [CrossRef]
- Hashmi, S.A.; Latham, R.J.; Linford, R.G.; Schlindwein, W.S. Studies on all solid state electric double layer capacitors using proton and lithium ion conducting polymer electrolytes. J. Chem. Soc. Faraday Trans. 1997, 93, 4177–4182. [Google Scholar] [CrossRef]
- Borges, R.S.; Miquita, D.R.; Silva, G.G. Electrochemical study of double-walled carbon nanotube electrode/block polyether-lithium bis(trifluorosulphonyl)imide salt polymer electrolyte interface. Electrochim. Acta 2011, 56, 4650–4656. [Google Scholar] [CrossRef]
- Lust, E.; Nurk, G.; Jänes, A.; Arulepp, M.; Nigu, P.; Möller, P.; Kallip, S.; Sammelselg, V. Electrochemical properties of nanoporous carbon electrodes in various nonaqueous electrolytes. J. Solid State Electrochem. 2003, 7, 91–105. [Google Scholar] [CrossRef]
- Gan, X.P.; Wu, Y.T.; Liu, L.; Shen, B.; Hu, W.B. Electroless plating of Cu-Ni-P alloy on PET fabrics and effect of plating parameters on the properties of conductive fabrics. J. Alloys Compd. 2008, 455, 308–313. [Google Scholar] [CrossRef]
- Han, E.G.; Kim, E.A.; Oh, K.W. Electromagnetic interference shielding effectiveness of electroless Cu-plated PET fabrics. Synth. Met. 2001, 123, 469–476. [Google Scholar] [CrossRef]
- Gasana, E.; Westbroek, P.; Hakuzimana, J.; De Clerck, K.; Priniotakis, G.; Kiekens, P.; Tseles, D. Electroconductive textile structures through electroless deposition of polypyrrole and copper at polyaramide surfaces. Surf. Coat. 2006, 201, 3547–3551. [Google Scholar] [CrossRef]
- Park, N.W.; Kim, I.W.; Kim, J.Y. Copper Metallization of poly(ethylene terephthalate) Fabrics via Intermediate Polyaniline Layers. Fibers Polym. 2009, 10, 310–314. [Google Scholar] [CrossRef]
- Shoji, E.; Takagi, S.; Araie, H. Novel conducting fabric polymer composites as stretchable electrodes: One-step fabrication of chemical actuators. Polym. Adv. Technol. 2009, 20, 423–426. [Google Scholar] [CrossRef]
- Lu, Y.X.; Xue, L.L.; Li, F. Silver nanoparticle catalyst for electroless Ni deposition and the promotion of its adsorption onto PET substrate. Surf. Coat. 2010, 205, 519–524. [Google Scholar] [CrossRef]
- Kofod, G.; Stoyanov, H.; Gerhard, R. Multilayer coaxial fibre dielectric elastomers for actuation and sensing. Appl. Phys. A 2011, 102, 577–581. [Google Scholar] [CrossRef]
- Zheng, Z.R.; Gu, Z.Y.; Huo, R.T.; Ye, Y.H. Superhydrophobicity of polyvinylidene fluoride membrane fabricated by chemical vapour deposition from solution. Appl. Surf. Sci. 2009, 255, 7263–7267. [Google Scholar] [CrossRef]
- Das, R.N.; Rosser, S.G.; Papathomas, K.I.; Poliks, M.D.; Lauffer, J.M.; Markovich, V.R. Resin coated copper capacitive (RC3) nanocomposites for multilayer embedded capacitors. In Proceedings of the 2008 58th Electronic Components and Technology Conference, Lake Buena Vista, FL, USA, 27–30 May 2008; pp. 729–735. [Google Scholar]
- Das, R.N.; Rosser, S.G.; Papathomas, K.I.; Antesberger, T.; Markovich, V.R. Resin coated copper capacitive (RC3) nanocomposites for multilayer embedded capacitors: Towards system in a package (SiP). Circuit World 2009, 35, 31–39. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Li, X.; Gandhi, J.; Luo, S.J.; Jiang, T. Adhesion improvement for polymer dielectric to electrolytic-plated copper. In Proceedings of the 2010 Proceedings 60th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 1–4 June 2010; pp. 1106–1111. [Google Scholar]
- Armand, M. Polymers with ionic conductivity. Adv Mater. 1990, 2, 278–286. [Google Scholar] [CrossRef]
- Xi, J.; Qiu, X.; Zhu, W.; Tang, X. Enhanced electrochemical properties of poly(ethylene oxide)-based composite polymer electrolyte with ordered mesoporous materials for lithium polymer battery. Microporous Mesoporous Mater. 2006, 88, 1–7. [Google Scholar] [CrossRef]
- Gadjourova, Z.; Andreev, Y.G.; Tunstall, D.P.; Bruce, P.G. Ionic conductivity in crystalline polymer electrolytes. Nature 2001, 412, 520–523. [Google Scholar] [CrossRef]
- Edman, L.; Ferry, A.; Doeff, M.M. Slow recrystallization in the polymer electrolyte system poly(ethylene oxide)n–LiN(CF3SO2)2. J. Mater. Res. 2000, 15, 1950–1954. [Google Scholar] [CrossRef]
- Strawhecker, K.E.; Manias, E. Crystallization behavior of poly(ethylene oxide) in the presence of Na+ montmorillonite fillers. Chem. Mater. 2003, 15, 844–849. [Google Scholar] [CrossRef]
- Bac, A.; Ciosek, M.; Bukat, M.; Siekierski, M.; Wieczorek, W. The effect of salt concentration on the PEO-LiClO4-lithium electrode interfacial resistivity. J. Power Sources 2006, 159, 438–442. [Google Scholar] [CrossRef]
- Hadjichristov, G.B.; Ivanov, T.E.; Marinov, Y.G.; Koduru, H.K.; Scaramuzza, N. PEO-PVP-NaIO4 ion-conducting polymer electrolyte: Inspection for ionic space charge polarization and charge trapping. Phys. Status Solidi A 2019, 216, 1800739. [Google Scholar] [CrossRef]
- Meyer, W.H. Polymer Electrolytes for Lithium-Ion Batteries. Adv. Mater. 1998, 10, 439–448. [Google Scholar] [CrossRef]
- Frackowiak, E.; Béguin, F. Carbon materials for the electrochemical storage of energy in capacitors. Carbon 2001, 39, 937–950. [Google Scholar] [CrossRef]
- Moradian, R.; Azadi, S.; Refii-tabar, H. When double-wall carbon nanotubes can become metallic or semiconducting. J. Condens. Matter Phys. 2007, 19, 176209. [Google Scholar] [CrossRef]
- Villalpando-Paez, F.; Son, H.; Nezich, D.; Hsieh, Y.P.; Kong, J.; Kim, Y.A.; Shimamoto, D.; Muramatsu, H.; Hayashi, T.; Endo, M.; et al. Raman spectroscopy study of isolated double-walled carbon nanotubes with different metallic and semiconducting configurations. Nano Lett. 2008, 8, 3879–3886. [Google Scholar] [CrossRef]
- Shen, C.; Brozena, A.H.; Wang, Y.H. Double-walled carbon nanotubes: Challenges and opportunities. Nanoscale 2011, 3, 503–518. [Google Scholar] [CrossRef]










| Research Groups | Electrode Materials | Electrolytes Used | Dopants Applied |
|---|---|---|---|
| Liu et al. [13] | HDC | PEO/PMMA/PAN mixed with EC and PC | LiClO4 |
| Lim et al. [14] | WO3 on ITO glass | LiClO4-LiMC, LiClO4-PEO, LiClO4-LiSMC | LiClO4 |
| Hashmi et al. [15] | (1) High-density graphite sheets (2) Activated carbon fabrics | PVA-H3PO4, (PEO)9-LiCF3SO3 | LiCF3SO3 |
| Jost et al. [9] | Various types of activated carbon impregnation on polyester microfibre and cotton lawn | Na2SO4-Li2SO4 | CXV, YP17, carbon onions |
| Borges et al. [16] | DWCNT-COOH/PE-b-PEO-LiTFSI | PE-b-PEO-LiTFSI | DWCNT-COOH |
| Lust et al. [17] | Nanoporous carbon on Al foil | LiClO4, LiBF4, Et4NBF4, Et3MeNBF4, EtMe3NBF4 | Nanoporous carbon |
| Solution | PEO Amount (in g) | LiClO4 Amount (in mg) | LiClO4 Amount (in mL) | PEO to LiClO4 (Ratio in Weight) |
|---|---|---|---|---|
| A | 1.0 | 1.0 | 1.0 | 1000:1 |
| B | 1.0 | 1.5 | 1.5 | ~667:1 |
| C | 1.0 | 2.0 | 2.0 | 500:1 |
| D | 1.0 | 2.5 | 2.5 | 400:1 |
| E | 1.0 | 3.0 | 3.0 | ~333:1 |
| F | 1.0 | 10.0 | 10.0 | 100:1 |
| R | 1.0 | N.A. | N.A. | Control |
| Item | Dimension of Nanocarbons | Density (g/cm3) at 25 °C |
|---|---|---|
| Meso | <500 nm particle size | 1.887 |
| MW | Length: 2.5–20 μm, O.D.: 6–13 nm | 2.1 |
| DW | Length: 50 μm, I.D.: 1.3–2.0 nm, O.D.: 5 nm | 1.7–2.1 |
| SW | Diameter: 0.7–1.3 nm | 1.7–1.9 |
| Stages of Treatment | Average Diameter of the Fibre |
|---|---|
| Untreated | 15 μm |
| Palladium-coated | 15 μm |
| Nickel-coated | 17 μm |
| Copper-coated | 20 μm |
| Samples | Thickness (μm) |
|---|---|
| Metallised polyester fabrics with copper | 65 |
| Pure PEO spacer and control sample | 25 |
| Samples casted with different concentrations of PEO:Li+ | 20 |
| Samples casted with different types of PEO:nanocarbons | 50 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Li+ Added (in mL) | 40 | 1 K | 100 K | 100 MHz |
| Nil | 1.89 | 0.05 | 0.02 | 0.03 |
| 1.0 | 6.86 | 0.12 | 0.03 | 0.05 |
| 1.5 | 17.32 | 0.44 | 0.02 | 0.03 |
| 2.0 | 27.92 | 0.64 | 0.03 | 0.06 |
| 2.5 | 24.23 | 0.77 | 0.02 | 0.02 |
| 3.0 | 29.67 | 1.02 | 0.04 | 0.05 |
| 10.0 | 33.56 | 2.00 | 0.04 | 0.02 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Li+ Added (in mL) | 40 | 1 K | 100 K | 100 MHz |
| Nil | 3.87 | 0.52 | 0.15 | 0.03 |
| 1.0 | 5.86 | 0.89 | 0.24 | 0.22 |
| 1.5 | 6.54 | 2.19 | 0.27 | 0.11 |
| 2.0 | 6.69 | 1.73 | 0.31 | 0.18 |
| 2.5 | 5.40 | 2.34 | 0.28 | 0.10 |
| 3.0 | 6.49 | 2.04 | 0.37 | 0.09 |
| 10.0 | 6.05 | 3.00 | 0.39 | 0.14 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Li+ Added (in mL) | 40 | 1 K | 100 K | 100 MHz |
| Nil | 46,373.67 | 2712.78 | 23.18 | 0.01 |
| 1.0 | 10,099.36 | 2054.68 | 25.06 | 0.01 |
| 1.5 | 10,156.82 | 5105.76 | 39.65 | 0.02 |
| 2.0 | 7110.52 | 1620.95 | 27.25 | 0.01 |
| 2.5 | 2346.95 | 1442.97 | 28.81 | 0.01 |
| 3.0 | 3387.20 | 1377.66 | 26.02 | 0.01 |
| 10.0 | 7070.60 | 3303.59 | 34.84 | 0.02 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Li+ Added (in mL) | 40 | 1 K | 100 K | 100 MHz |
| Nil | −31,325.38 | −6471.99 | −152.31 | −0.11 |
| 1.0 | −2581.87 | −2608.91 | −105.89 | −0.07 |
| 1.5 | −1849.45 | −3888.73 | −210.13 | −0.20 |
| 2.0 | −1569.23 | −1842.49 | −93.09 | −0.07 |
| 2.5 | −316.90 | −812.02 | −83.64 | −0.10 |
| 3.0 | −522.57 | −1084.45 | −78.46 | −0.06 |
| 10.0 | −850.10 | −2692.39 | −138.93 | −0.15 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Li+ Added (in mL) | 40 | 1 K | 100 K | 100 MHz |
| Nil | 56,727.70 | 7149.97 | 154.26 | 0.11 |
| 1.0 | 10,384.77 | 3341.51 | 108.60 | 0.07 |
| 1.5 | 10,328.40 | 6454.05 | 215.02 | 0.20 |
| 2.0 | 7318.01 | 2543.76 | 97.63 | 0.07 |
| 2.5 | 2368.53 | 1669.78 | 88.93 | 0.10 |
| 3.0 | 3428.50 | 1783.19 | 82.95 | 0.06 |
| 10.0 | 7124.34 | 4294.57 | 144.79 | 0.16 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Li+ Added (in mL) | 40 | 1 K | 100 K | 100 MHz |
| Nil | −23.11 | −63.55 | −81.34 | −88.06 |
| 1.0 | −11.40 | −50.26 | −76.78 | −77.80 |
| 1.5 | −9.15 | −29.15 | −74.81 | −83.89 |
| 2.0 | −10.07 | −39.51 | −72.84 | −79.77 |
| 2.5 | −6.15 | −16.49 | −52.12 | −62.10 |
| 3.0 | −9.31 | −31.57 | −70.06 | −85.13 |
| 10.0 | −10.54 | −24.92 | −69.39 | −81.99 |
| Scan Rate (in mV/s) | ||||
|---|---|---|---|---|
| Li+ Added (in mL) | 100 | 50 | 20 | 10 |
| Nil | 177 | 172 | 87 | 71 |
| 1.0 | 243 | 191 | 136 | 102 |
| 1.5 | 351 | 279 | 205 | 189 |
| 2.0 | 562 | 475 | 347 | 186 |
| 2.5 | 883 | 538 | 385 | 377 |
| 3.0 | 924 | 695 | 510 | 313 |
| 10.0 | 1844 | 1304 | 876 | 330 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Nanocarbons Added | 40 | 1 K | 100 K | 100 MHz |
| SW | 1.353 | 0.046 | 0.019 | 0.030 |
| DW | 32.798 | 0.238 | 0.016 | 0.020 |
| MW | 17.806 | 0.206 | 0.014 | 0.006 |
| Meso | 8.238 | 0.066 | 0.009 | 0.010 |
| No dopant | 1.890 | 0.050 | 0.020 | 0.030 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Nanocarbons Added | 40 | 1 K | 100 K | 100 MHz |
| SW | 4.45 | 0.64 | 0.10 | 1.71 |
| DW | 17.75 | 2.14 | 0.27 | 0.46 |
| MW | 11.70 | 1.87 | 0.24 | 0.46 |
| Meso | 14.06 | 1.58 | 0.17 | 0.21 |
| No dopant | 3.87 | 0.52 | 0.15 | 0.03 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Nanocarbons Added | 40 | 1 K | 100 K | 100 MHz |
| SW | 23,241.52 | 4016.48 | 15.01 | 0.16 |
| DW | 4078.95 | 2694.65 | 46.00 | 0.08 |
| MW | 22,366.81 | 7258.65 | 51.32 | 0.23 |
| Meso | 12,060.08 | 7037.73 | 52.26 | 0.06 |
| No dopant | 46,373.67 | 2712.78 | 23.18 | 0.01 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Nanocarbons Added | 40 | 1 K | 100 K | 100 MHz |
| SW | −5239.97 | −6302.44 | −144.30 | −0.09 |
| DW | −243.79 | −1315.14 | −169.59 | −0.16 |
| MW | −2228.80 | −7974.92 | −275.94 | −0.49 |
| Meso | −858.95 | −4453.04 | −311.58 | −0.28 |
| No dopant | −31,325.38 | −6471.99 | −152.31 | −0.11 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Nanocarbons Added | 40 | 1 K | 100 K | 100 MHz |
| SW | 23,826.51 | 7474.36 | 145.07 | 0.18 |
| DW | 4086.41 | 3004.90 | 175.79 | 0.18 |
| MW | 22,478.09 | 10,944.02 | 282.84 | 0.54 |
| Meso | 12,090.74 | 8328.22 | 315.93 | 0.29 |
| No dopant | 56,727.70 | 7149.97 | 154.26 | 0.11 |
| Frequency (in Hz) | ||||
|---|---|---|---|---|
| Nanocarbons Added | 40 | 1 K | 100 K | 100 MHz |
| SW | −12.71 | −57.56 | −84.05 | −30.47 |
| DW | −3.34 | −25.64 | −74.94 | −65.55 |
| MW | −5.00 | −34.30 | −76.43 | −65.23 |
| Meso | −4.08 | −32.32 | −80.48 | −78.33 |
| No dopant | −23.11 | −63.55 | −81.34 | −88.06 |
| Scan Rate (in mV/s) | ||||
|---|---|---|---|---|
| Nanocarbons Added | 100 | 50 | 20 | 10 |
| SW | 1.11 | 1.01 | 0.50 | 0.41 |
| DW | 10.51 | 8.36 | 6.56 | 5.30 |
| MW | 5.56 | 4.91 | 2.36 | 0.99 |
| Meso | 4.68 | 3.32 | 1.57 | 1.32 |
| No dopant | 0.18 | 0.17 | 0.09 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hui, C.-Y.; Kan, C.-W.; Chau, K.-H. A Study on Poly(ethylene oxide)-Based Supercapacitors Doped with Various Dopants. Coatings 2023, 13, 1373. https://doi.org/10.3390/coatings13081373
Hui C-Y, Kan C-W, Chau K-H. A Study on Poly(ethylene oxide)-Based Supercapacitors Doped with Various Dopants. Coatings. 2023; 13(8):1373. https://doi.org/10.3390/coatings13081373
Chicago/Turabian StyleHui, Chi-Yuen, Chi-Wai Kan, and Kam-Hong Chau. 2023. "A Study on Poly(ethylene oxide)-Based Supercapacitors Doped with Various Dopants" Coatings 13, no. 8: 1373. https://doi.org/10.3390/coatings13081373
APA StyleHui, C.-Y., Kan, C.-W., & Chau, K.-H. (2023). A Study on Poly(ethylene oxide)-Based Supercapacitors Doped with Various Dopants. Coatings, 13(8), 1373. https://doi.org/10.3390/coatings13081373









