Effects of Nitrogen Doping on Pulling Rate Range of Defect-Free Crystal in CZ Silicon
Abstract
:1. Introduction
2. Experimental Section
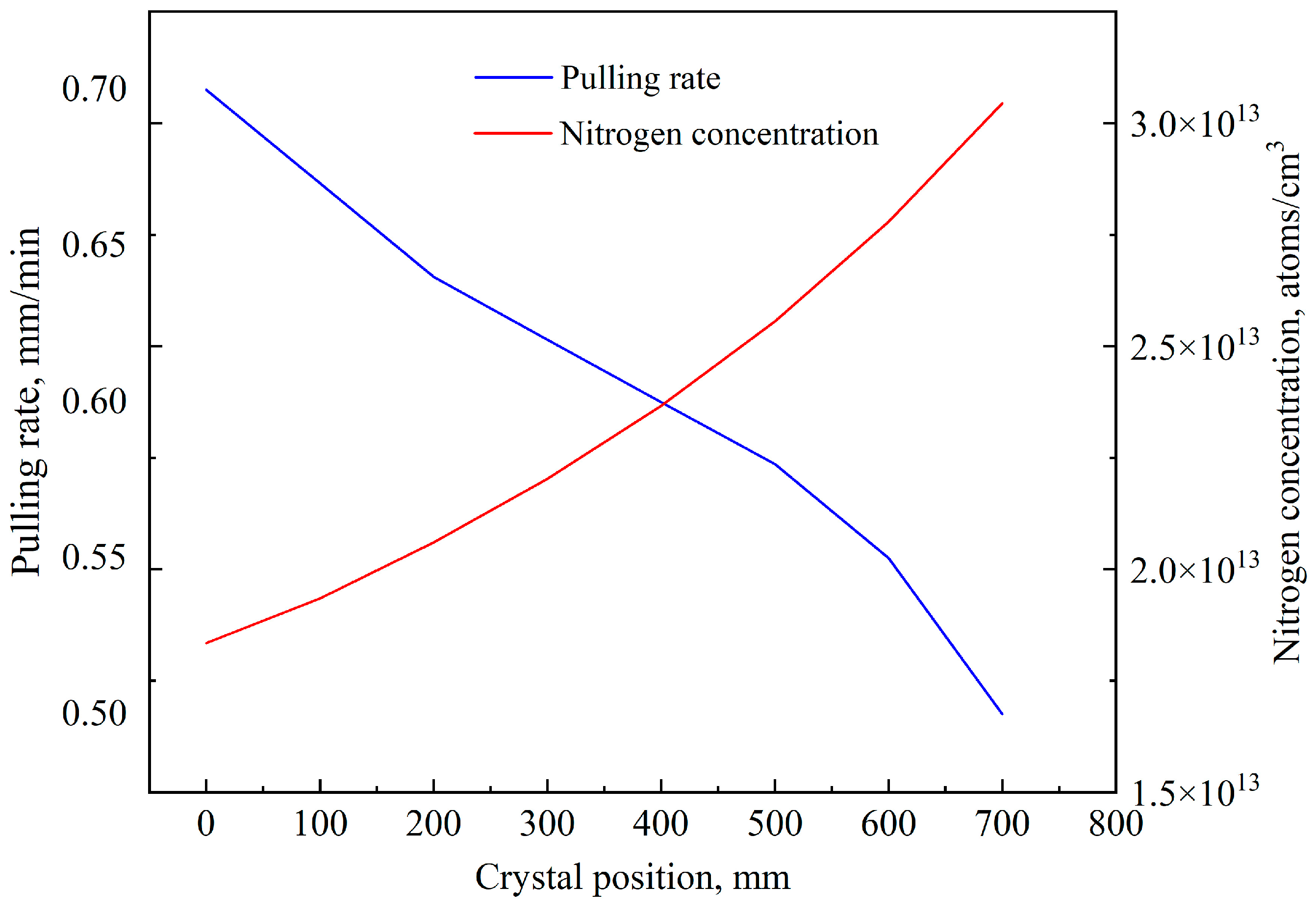
2.1. Experimental Details
2.2. Experimental Results and Discussions
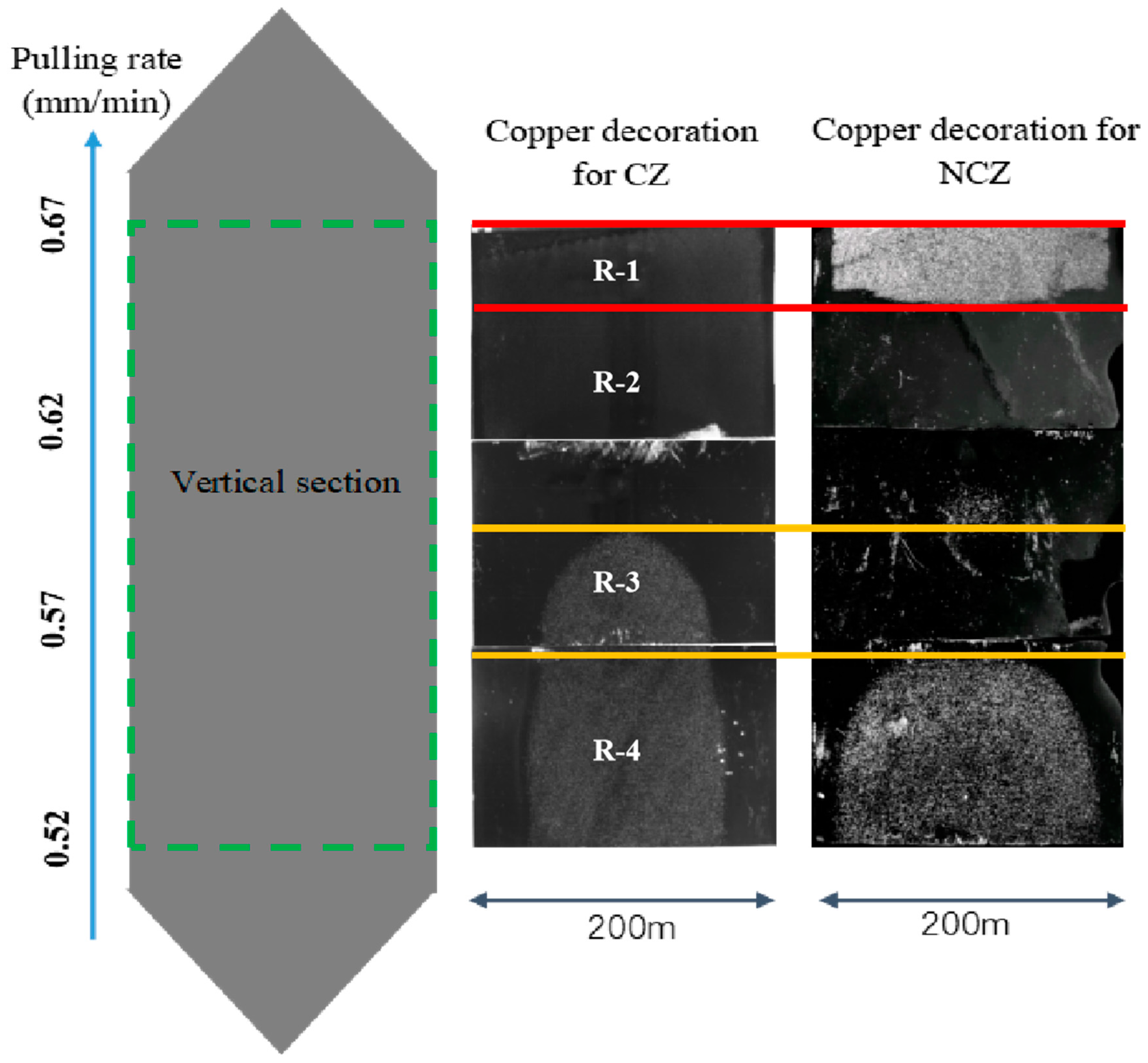
2.2.1. Copper Decoration Analysis
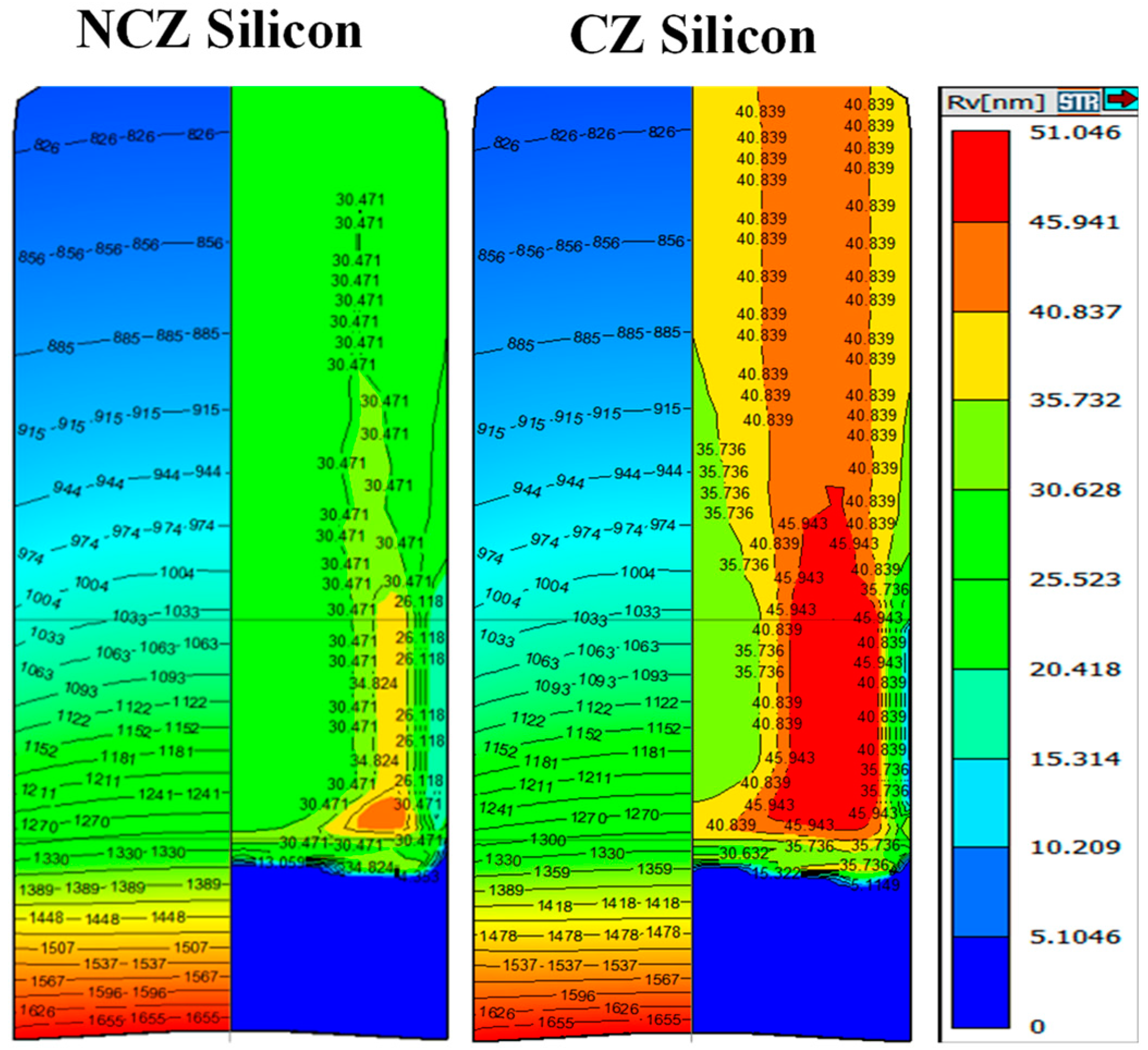
2.2.2. COPs and FPDs Analysis of Polish Wafer
3. Numerical Simulation Section
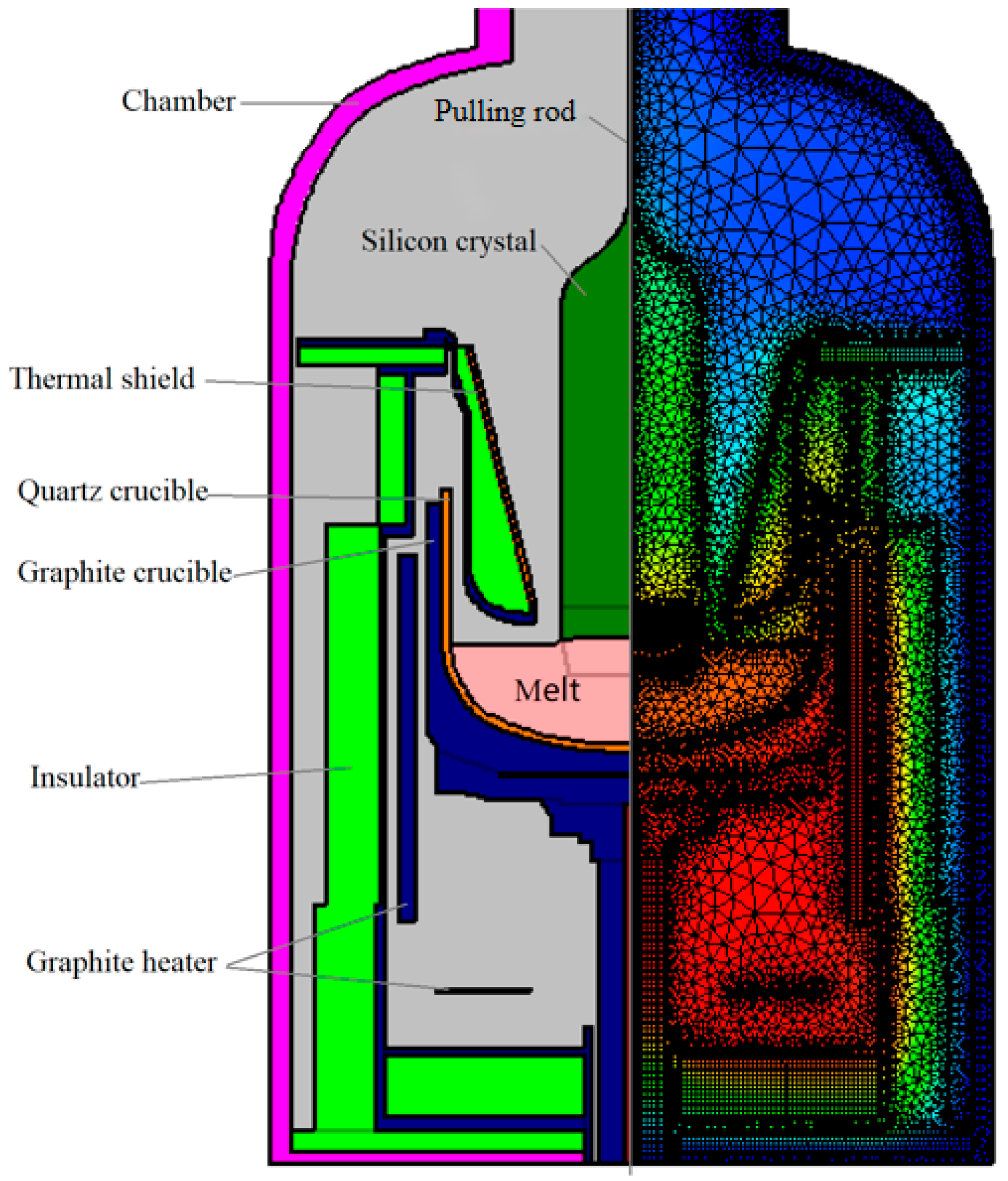
3.1. Numerical Simulation Setup
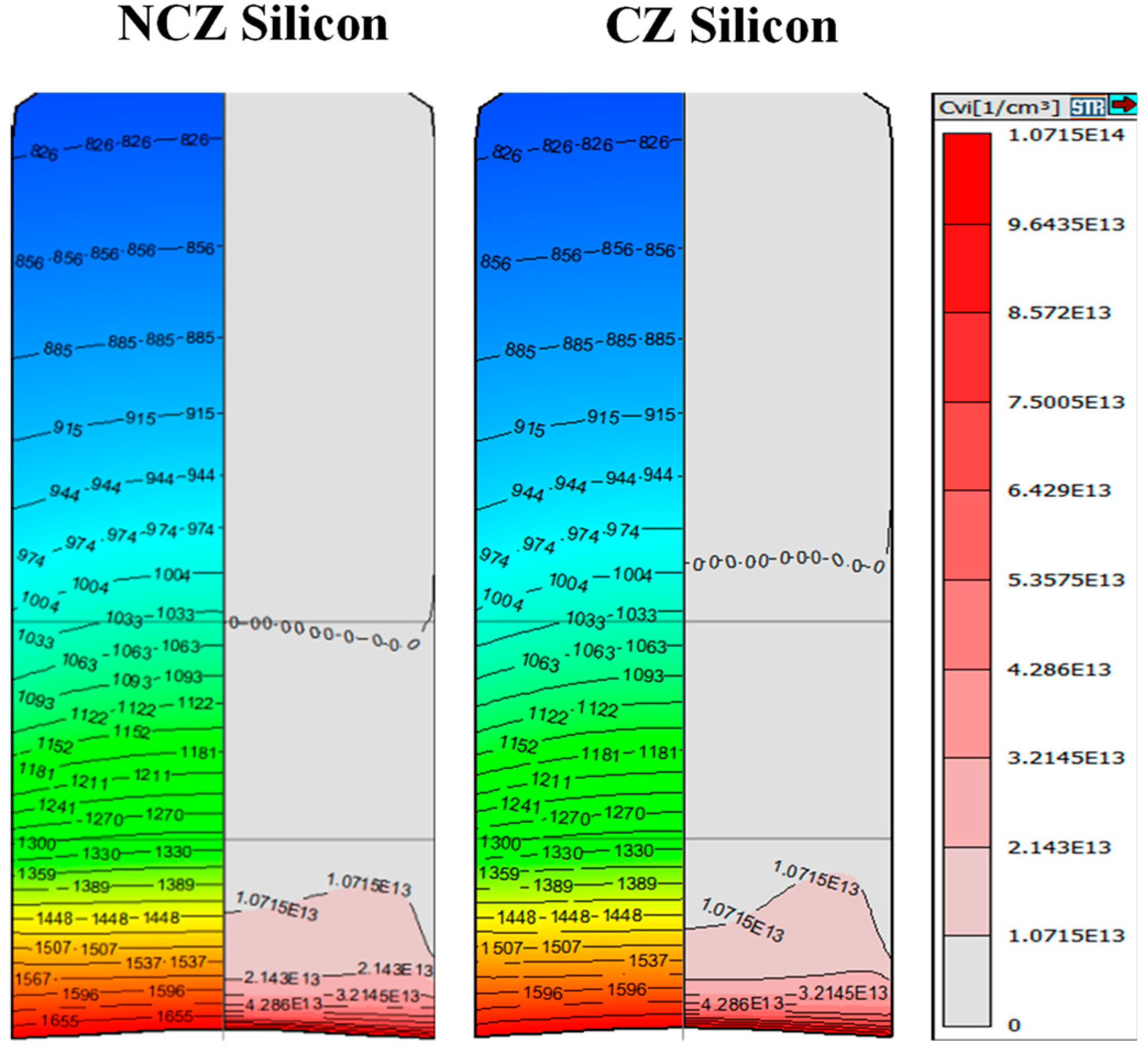
3.2. V/G Value Based on the Different Growth Rates
3.3. Defects for CZ and NCZ Crystal
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, S.; Li, H.; Huang, H.; Kang, R. Grinding and Lapping Induced Surface Integrity of Silicon Wafers and Its Effect on Chemical Mechanical Polishing. Appl. Surf. Sci. 2022, 599, 153982. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, B.; Hou, H.; Chen, W.; Wang, M. Phase-Field Simulation for the Evolution of Solid/Liquid Interface Front in Directional Solidification Process. J. Mater. Sci. Technol. 2019, 35, 1044–1052. [Google Scholar] [CrossRef]
- Voronkov, V. The mechanism of swirl defects formation in silicon. J. Cryst. Growth 1982, 59, 625–643. [Google Scholar] [CrossRef]
- Voronkov, V. Vacancy and self-interstitial concentration incorporated into growing silicon crystals. J. Appl. Phys 1999, 86, 5975–5982. [Google Scholar] [CrossRef]
- Yu, X.; Chen, J.; Ma, X.; Yang, D. Impurity engineering of Czochralski silicon. Mater. Sci. Eng. R Rep. 2013, 74, 1–33. [Google Scholar] [CrossRef]
- Vanhellemont, J.; Kamiyama, E.; Sueoka, K. Silicon Single Crystal Growth from a Melt: On the Impact of Dopants on the v/G Criterion. ECS J. Solid State Sci. Technol. 2013, 2, P166–P179. [Google Scholar] [CrossRef]
- Taniguchi, M.; Sueoka, K.; Hourai, M. Density Functional Theory Study on Concentration of Intrinsic Point Defects in Growing N-Doped Czochralski Si Crystal. J. Cryst. Growth 2021, 571, 126249. [Google Scholar] [CrossRef]
- Kajiwara, K.; Torigoe, K.; Harada, K.; Hourai, M.; Nishizawa, S. Oxygen concentration dependence of as-grown defect formation in nitrogen-doped Czochralski silicon single crystals. J. Cryst. Growth 2021, 570, 126236. [Google Scholar] [CrossRef]
- Berg Rasmussen, F.; Öberg, S.; Jones, R.; Ewels, C.; Goss, J.; Miro, J.; Deák, P. The nitrogen-pair oxygen defect in silicon. Mater. Sci. Eng. 1996, B36, 91–95. [Google Scholar] [CrossRef]
- Park, B.M.; Seo, G.H.; Kim, G. Nitrogen-Doping Effect in a Fast-Pulled Cz-Si Single Crystal. J. Cryst. Growth 2001, 222, 74–81. [Google Scholar] [CrossRef]
- Yu, X.; Yang, D.; Ma, X.; Yang, J.; Li, L.; Que, D. Grown-in Defects in Nitrogen-Doped Czochralski Silicon. J. Appl. Phys. 2002, 92, 188–194. [Google Scholar] [CrossRef]
- Zeng, Y.; Chen, J.; Ma, M.; Wang, W.; Yang, D. Enhancement effect of nitrogen co-doping on oxygen precipitation in heavily phosphorus-doped Czochralski silicon during high-temperature annealing. J. Cryst. Growth 2009, 311, 3273–3277. [Google Scholar] [CrossRef]
- Umeno, S.; Ono, T.; Tanaka, T.; Asayama, E.; Nishikawa, H.; Hourai, M.; Katahama, H.; Sano, M. Nitrogen Effect on Grown-in Defects in Czochralski Silicon Crystals. J. Cryst. Growth 2002, 236, 46–50. [Google Scholar] [CrossRef]
- Yang, D.; Ma, X.; Fan, R.; Zhang, J.; Li, L.; Que, D. Oxygen precipitation in nitrogen-doped Czochralski silicon. Phys. B Condens. Matter 1999, 273–274, 308–311. [Google Scholar] [CrossRef]
- Mule’Stagno, L. A Technique For Delineating Defects in Silicon. Solid State Phenom. 2002, 82–84, 753–758. [Google Scholar] [CrossRef]
- Kulkarni, M.S.; Libbert, J.; Keltner, S.; Muléstagno, L. A Theoretical and Experimental Analysis of Macrodecora-tion of Defects in Monocrystalline Silicon. J. Electrochem. Soc. 2002, 149, G153. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, C.; Zhou, Q.; Wang, J.; Hao, Q.; Zhang, H.; Li, Y. Evolution of Flow Pattern Defects in Bo-ron-Doped <100> Czochralski Silicon Crystals during Secco Etching Procedure. J. Cryst. Growth 2004, 269, 310–316. [Google Scholar] [CrossRef]
- Xu, W.; Chen, J.; Ma XYang, D.; Gong, L.; Tian, D. Flow pattern defects in germanium-doped Czochralski silicon crystals. Appl. Phys. A 2011, 104, 349–355. [Google Scholar] [CrossRef]
- Chen, J.-C.; Chiang, P.-Y.; Nguyen, T.H.T.; Hu, C.; Chen, C.-H.; Liu, C.-C. Numerical Simulation of the Oxygen Concentration Distribution in Silicon Melt for Different Crystal Lengths during Czochralski Growth with a Trans-verse Magnetic Field. J. Cryst. Growth 2016, 452, 6–11. [Google Scholar] [CrossRef]
- Mukaiyama, Y.; Sueoka, K.; Maeda, S.; Iizuka, M.; Mamedov, V.M. Numerical Analysis of Effect of Thermal Stress Depending on Pulling Rate on Behavior of Intrinsic Point Defects in Large-Diameter Si Crystal Grown by Czochralski Method. J. Cryst. Growth 2020, 531, 125334. [Google Scholar] [CrossRef]
- Nguyen, T.H.T.; Chen, J.C.; Hu, C.; Chen, C.H. Numerical Simulation of Heat and Mass Transfer during Czo-chralski Silicon Crystal Growth under the Application of Crystal-Crucible Counter- and Iso-Rotations. J. Cryst. Growth 2019, 507, 50–57. [Google Scholar] [CrossRef]
- Von Ammon, W.; Dornberger, E.; Oelkrug, H.; Weidner, H. The Dependence of Bulk Defects on the Axial Tem-perature Gradient of Silicon Crystals during Czochralski Growth. J. Cryst. Growth 1995, 151, 273–277. [Google Scholar] [CrossRef]
- Muhammad, I.; Ali, A.; Zhou, L.; Zhang, W.; Wong, P.K.J. Vacancy-Engineered Half-Metallicity and Magnetic Anisotropy in CrSI Semiconductor Monolayer. J. Alloys Compd. 2022, 909, 164797. [Google Scholar] [CrossRef]
- Von Ammon, W.; Hölzl, R.; Virbulis, J.; Dornberger, E.; Schmolke, R.; Gräf, D. The Impact of Nitrogen on the Defect Aggregation in Silicon. J. Cryst. Growth 2001, 226, 19–30. [Google Scholar] [CrossRef]



| Crystal Type | Nitrogen Concentration (Atoms/cm3) | Pulling Rate (mm/min) | Diameter, mm |
|---|---|---|---|
| CZ | 0 | 0.67→0.5 | 200 |
| NCZ | 1.9 × 1013~3 × 1013 | 0.67→0.5 | 200 |
| R-1 | R-2 | R-3 | R-4 | |
|---|---|---|---|---|
| COP Distribution at 0.065 μm (CZ) | 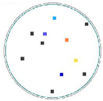 |  |  | 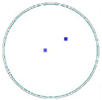 |
| COP Distribution at 0.065 μm (NCZ) | 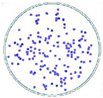 |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Lou, Z.; Ai, X.; Xue, Z.; Zhang, H.; Chen, G. Effects of Nitrogen Doping on Pulling Rate Range of Defect-Free Crystal in CZ Silicon. Coatings 2023, 13, 1637. https://doi.org/10.3390/coatings13091637
Sun C, Lou Z, Ai X, Xue Z, Zhang H, Chen G. Effects of Nitrogen Doping on Pulling Rate Range of Defect-Free Crystal in CZ Silicon. Coatings. 2023; 13(9):1637. https://doi.org/10.3390/coatings13091637
Chicago/Turabian StyleSun, Chenguang, Zhongshi Lou, Xingtian Ai, Zixuan Xue, Hui Zhang, and Guifeng Chen. 2023. "Effects of Nitrogen Doping on Pulling Rate Range of Defect-Free Crystal in CZ Silicon" Coatings 13, no. 9: 1637. https://doi.org/10.3390/coatings13091637
APA StyleSun, C., Lou, Z., Ai, X., Xue, Z., Zhang, H., & Chen, G. (2023). Effects of Nitrogen Doping on Pulling Rate Range of Defect-Free Crystal in CZ Silicon. Coatings, 13(9), 1637. https://doi.org/10.3390/coatings13091637






