Investigation of Oxygen Behavior under Different Melt Flow, Diffusion Boundary Layer, and Crystal-Melt Interface in a 300 mm Silicon Crystal Growth with Cusp Magnetic Field
Abstract
:1. Introduction
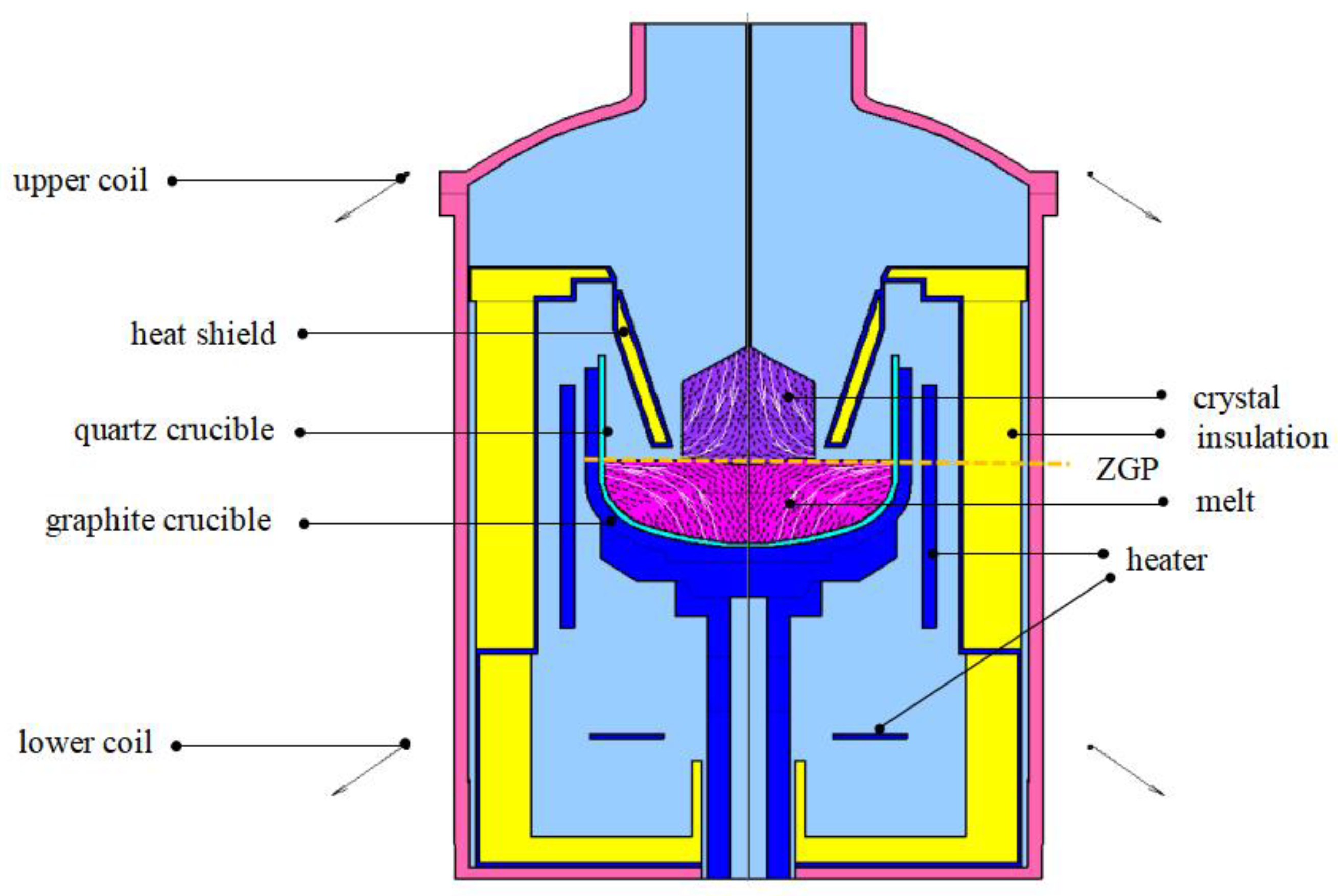
2. Experimental Setup and Modeling Approach
3. Description of Cusp Magnetic Field
4. Results and Discussion
4.1. CMF Effects on the Silicon Melt Convection
4.2. CMF Effects on the Oxygen Transport
4.3. CMF Effects on Growth Interface
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schulze, H.-J.; Ofner, H.; Niedernostheide, F.-J.; Lukermann, F.; Schulz, A. Fabrication of IGBTs using 300 mm magnetic Czochralski substrates. IET Power Electron. 2019, 12, 3870–3873. [Google Scholar] [CrossRef]
- Kalaev, V.; Sattler, A.; Kadinski, L. Crystal twisting in Cz Si growth. J. Cryst. Growth 2015, 413, 12–16. [Google Scholar] [CrossRef]
- Bok-Cheol, S.; In-Kyoo, L.; Kwang-Hun, K.; Hong-Woo, L. Oxygen concentration in the Czochralski-grown crystals with CUSP-magnetic field. J. Cryst. Growth 2005, 275, 455–459. [Google Scholar]
- Liu, X.; Liu, L.; Li, Z.; Wang, Y. Effects of CUSP-shaped magnetic field on melt convection and oxygen transport in an industrial CZ-Si crystal growth. J. Cryst. Growth 2012, 354, 101–108. [Google Scholar] [CrossRef]
- Kakimoto, K.; Liu, X.; Nakano, S. Analysis of the Effect of CUSP-Shaped Magnetic Fields on Heat, Mass, and Oxygen Transfer Using a Coupled 2D/3D Global Model. Cryst. Res. Technol. 2022, 57, 2100092. [Google Scholar] [CrossRef]
- Koichi, K.; Kyung-Woo, Y.; Minoru, E. Oxygen transfer during single silicon crystal growth in Czochralski system with vertical magnetic fields. J. Cryst. Growth 1996, 163, 238–242. [Google Scholar]
- Liu, X.; Liu, L.; Li, Z.; Wang, Y. Effects of static magnetic fields on thermal fluctuations in the melt of industrial CZ-Si crystal growth. J. Cryst. Growth 2012, 360, 38–42. [Google Scholar] [CrossRef]
- Borisov, D.; Artemyev, V.; Kalaev, V.; Smirnov, A.; Kuliev, A.; Zobel, F.; Kunert, R.; Turan, R.; Aydin, O.; Kabacelik, I. Advanced approach for oxygen transport and crystallization front calculation in Cz silicon crystal growth. J. Crystal Growth 2022, 583, 126493. [Google Scholar] [CrossRef]
- Nguyen, T.-H.; Chen, J.-C.; Hu, C.; Chen, C.-H. Effects of crystal-crucible iso-rotation and a balanced/unbalanced cusp magnetic field on the heat, flow, and oxygen transport in a Czochralski silicon melt. J. Cryst. Growth 2020, 531, 125373. [Google Scholar] [CrossRef]
- Gunjal, P.R.; Ramachandran, P.A. Tailoring the oxygen distribution in 300 mm Czochralski crystal of pure silicon using cusp magnetic field. Prog. Comput. Fluid Dyn. Int. J. 2010, 10, 307–318. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Purans, J.; Popov, A.I.; Jia, R. Tendencies in ABO3 perovskite and SrF2, BaF2 and CaF2 bulk and surface F-center Ab initio computations at high symmetry cubic structure. Symmetry 2021, 13, 1920. [Google Scholar] [CrossRef]
- Ding, J.; Li, Y.; Liu, L. Effect of CUSP magnetic field on the turbulent melt flow and crystal melt interface during large-size Czochralski silicon crystal growth. Int. J. Therm. Sci. 2021, 170, 107137. [Google Scholar] [CrossRef]
- Chen, J.C.; Guo, P.C.; Chang, C.H.; Teng, Y.Y.; Hsu, C.; Wang, H.M.; Liu, C.C. Numerical simulation of oxygen transport during the Czochralski silicon crystal growth with a CUSP magnetic field. J. Cryst. Growth 2014, 401, 888–894. [Google Scholar] [CrossRef]
- Raufeisen, A.; Breuer, M.; Botsch, T.; Delgado, A. Prediction of the three-phase boundary movement in Czochralski crystal growth. J. Cryst. Growth 2010, 312, 2297–2299. [Google Scholar] [CrossRef]
- Smirnova, O.V.; Durnev, N.V.; Shandrakova, K.E.; Mizitov, E.L.; Soklakov, V.D. Optimization of furnace design and growth parameters for Si Cz growth, using numerical simulation. J. Cryst. Growth 2008, 310, 2185–2191. [Google Scholar] [CrossRef]
- Murgai, A. Mechanisms of oxygen incorporation in Czochralski-grown silicon. In Semiconductor Silicon 1981 (Proceedings of the 4th International Symposium on Silicon Materials Science and Technology, Electrochemical Society PV 81-5); Huff, Y.T.H., Kriegler, R., Eds.; The Electrochemical Society: Pennington, NJ, USA, 1981; p. 11. [Google Scholar]
- Hoshikawa, K.; Hirata, H.; Nakanishi, H.; Ikuta, K. Control of oxygen concentration in Cz silicon growth. In Semiconductor Silicon 1981 (Proceedings of the 4th International Symposium on Silicon Materials Science and Technology, Electrochemical Society PV 81-5); Huff, Y.T.H., Kriegler, R., Eds.; The Electrochemical Society: Pennington, NJ, USA, 1981; p. 101. [Google Scholar]
- Carlberf, T.; King, T.B.; Witt, A.F. Dynamic Oxygen Equilibrium in Silicon Melts during Crystal Growth by the Czochralski Technique. J. Electrochem. Soc. 1982, 129, 189. [Google Scholar] [CrossRef]
- Moody, J.W. Oxygen precipitation in Czochralski silicon. In Semiconductor Silicon 1981 (Proceedings of the 4th International Symposium on Silicon Materials Science and Technology, Electrochemical Society PV 81-5); Huff, Y.T.H., Kriegler, R., Eds.; The Electrochemical Society: Pennington, NJ, USA, 1981; p. 100. [Google Scholar]
- Brice, J.C.; Laudise, R.A. The Growth of Crystals from Liquids; North-Holland Publishing Company: Amsterdam, The Netherlands, 1973; Chapter 4. [Google Scholar]












| Parameter | Value |
|---|---|
| Furnace pressure, Pa | 2000 |
| Argon gas flow rate, slpm (standard liter per minute) | 95 |
| Crystal pulling rate, mm/h | 24.5 |
| The ratio of crystal to crucible rotation rate | 6:−1 |
| Magnetic field strength, T | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Ai, X.; Zhang, H.; Chou, H.; Lyu, H.; Chen, G. Investigation of Oxygen Behavior under Different Melt Flow, Diffusion Boundary Layer, and Crystal-Melt Interface in a 300 mm Silicon Crystal Growth with Cusp Magnetic Field. Coatings 2023, 13, 1634. https://doi.org/10.3390/coatings13091634
Sun C, Ai X, Zhang H, Chou H, Lyu H, Chen G. Investigation of Oxygen Behavior under Different Melt Flow, Diffusion Boundary Layer, and Crystal-Melt Interface in a 300 mm Silicon Crystal Growth with Cusp Magnetic Field. Coatings. 2023; 13(9):1634. https://doi.org/10.3390/coatings13091634
Chicago/Turabian StyleSun, Chenguang, Xingtian Ai, Hui Zhang, Hungpang Chou, Huiyun Lyu, and Guifeng Chen. 2023. "Investigation of Oxygen Behavior under Different Melt Flow, Diffusion Boundary Layer, and Crystal-Melt Interface in a 300 mm Silicon Crystal Growth with Cusp Magnetic Field" Coatings 13, no. 9: 1634. https://doi.org/10.3390/coatings13091634
APA StyleSun, C., Ai, X., Zhang, H., Chou, H., Lyu, H., & Chen, G. (2023). Investigation of Oxygen Behavior under Different Melt Flow, Diffusion Boundary Layer, and Crystal-Melt Interface in a 300 mm Silicon Crystal Growth with Cusp Magnetic Field. Coatings, 13(9), 1634. https://doi.org/10.3390/coatings13091634






