Surface Mechanical Property Prediction and Process Optimization of 18CrNiMo7-6 Carburized Steel Stator Guide Based on Radial Basis Function Neural Network and NSGA-II Algorithm
Abstract
:1. Introduction
2. Numerical Model
2.1. Carburizing Model
2.2. Temperature Field Model
2.3. Phase Transition Model
2.3.1. Mathematical Modeling of Austenitization
2.3.2. Mathematical Modeling of Martensitization
2.3.3. Hardness Field Model
3. Model Validation
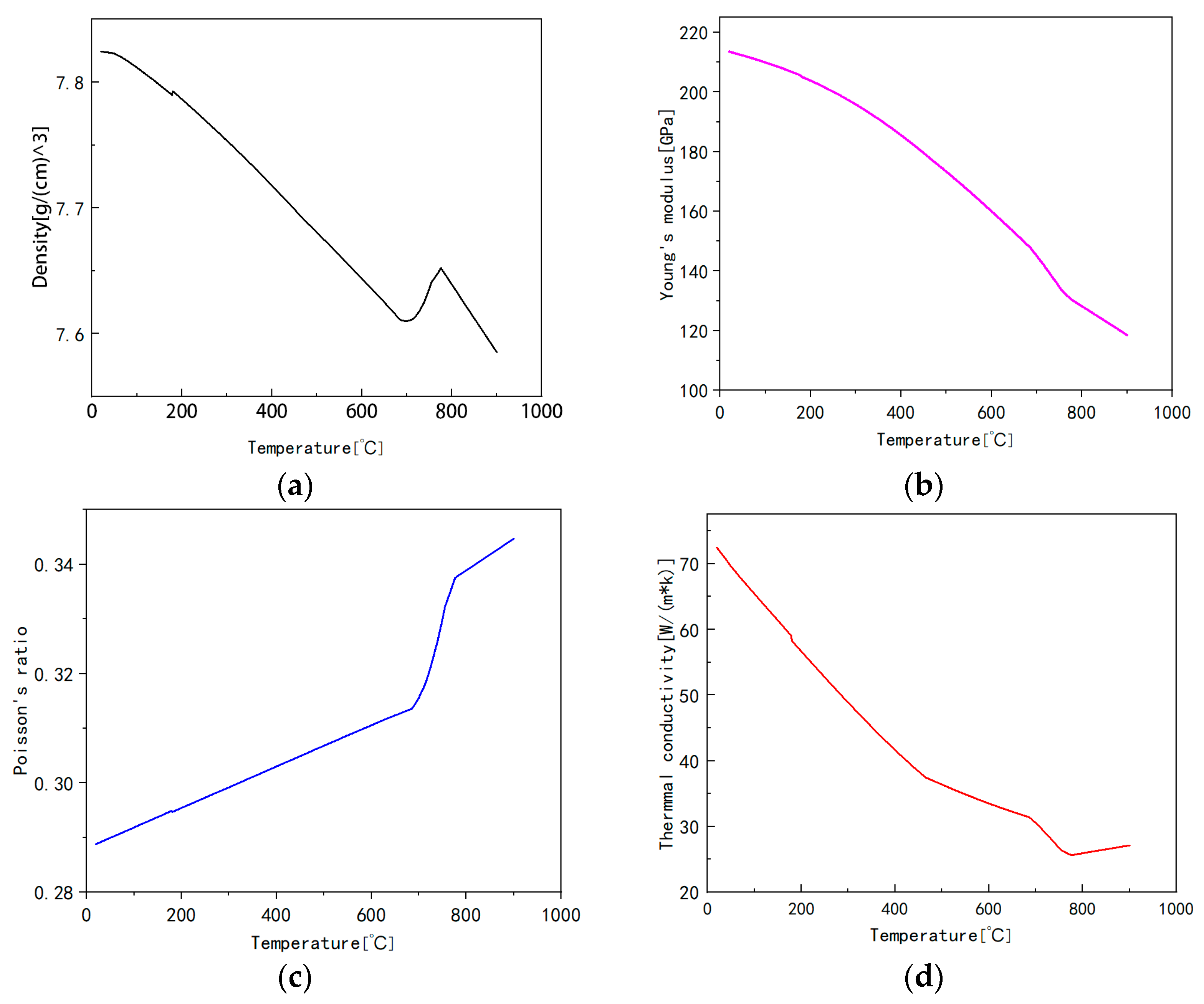
3.1. Stator Guide 18CrNiMo7-6 Carburizing Steel Composition and Thermal Properties
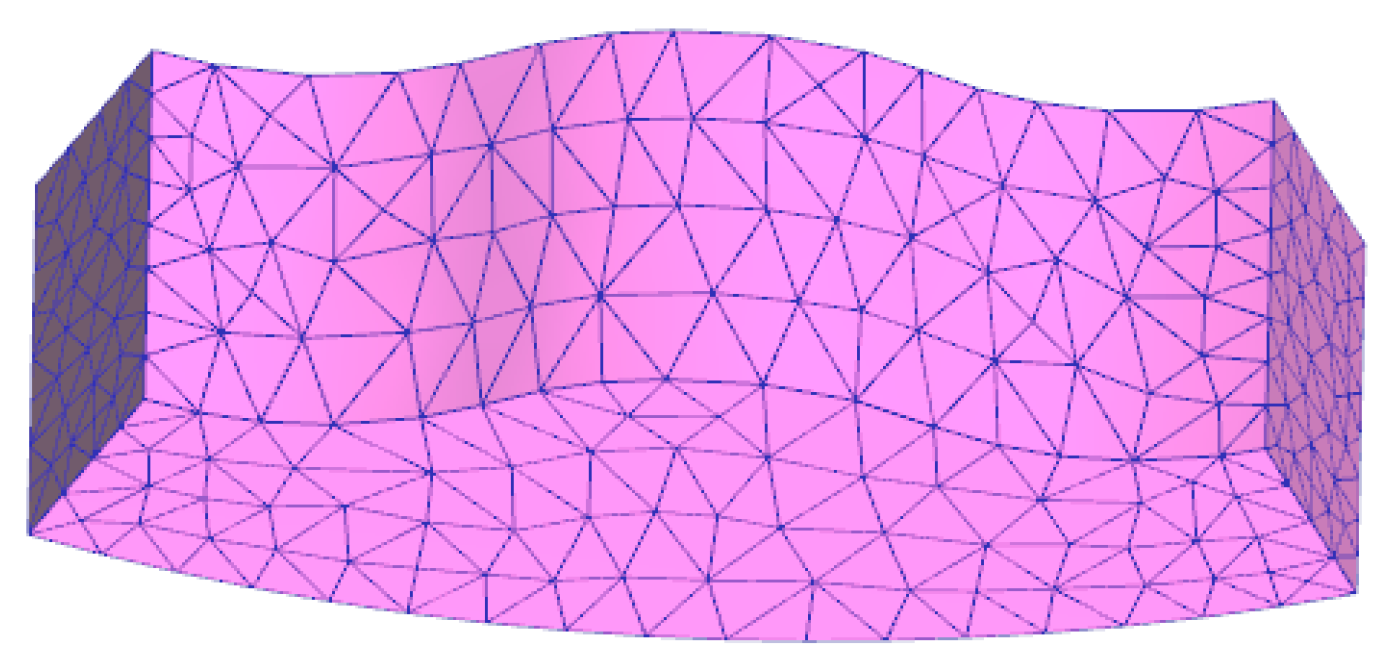
3.2. Finite Element Model
3.3. Numerical Simulation and Experimental Validation of the Carburizing Process for the Stator Guide
4. Mechanical Performance Prediction and Parameter Optimization
4.1. Mechanical Property Prediction Based on RBF Neural Network
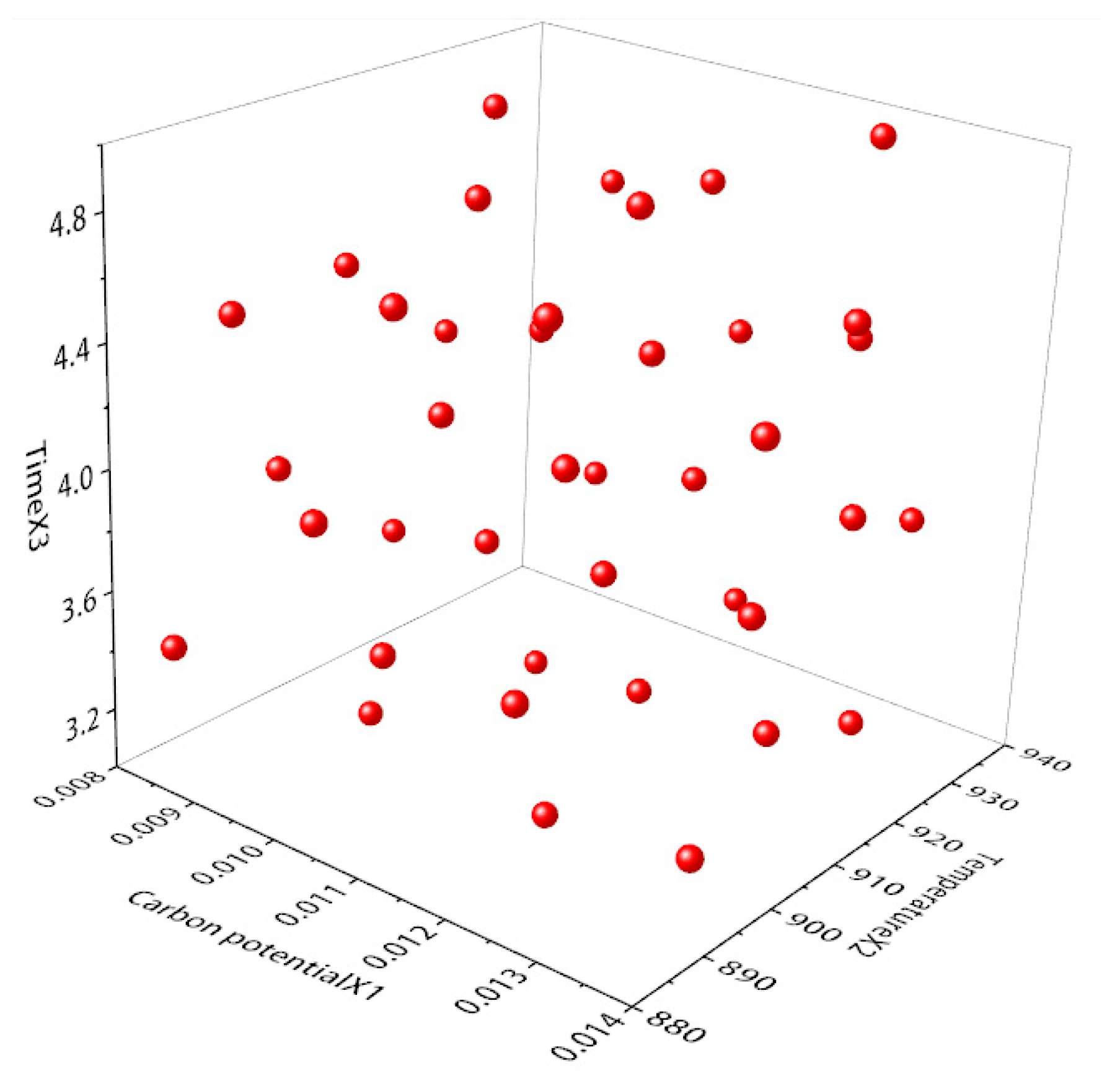
4.1.1. DEFORM-ISIGHT-Based DOE Experimental Design
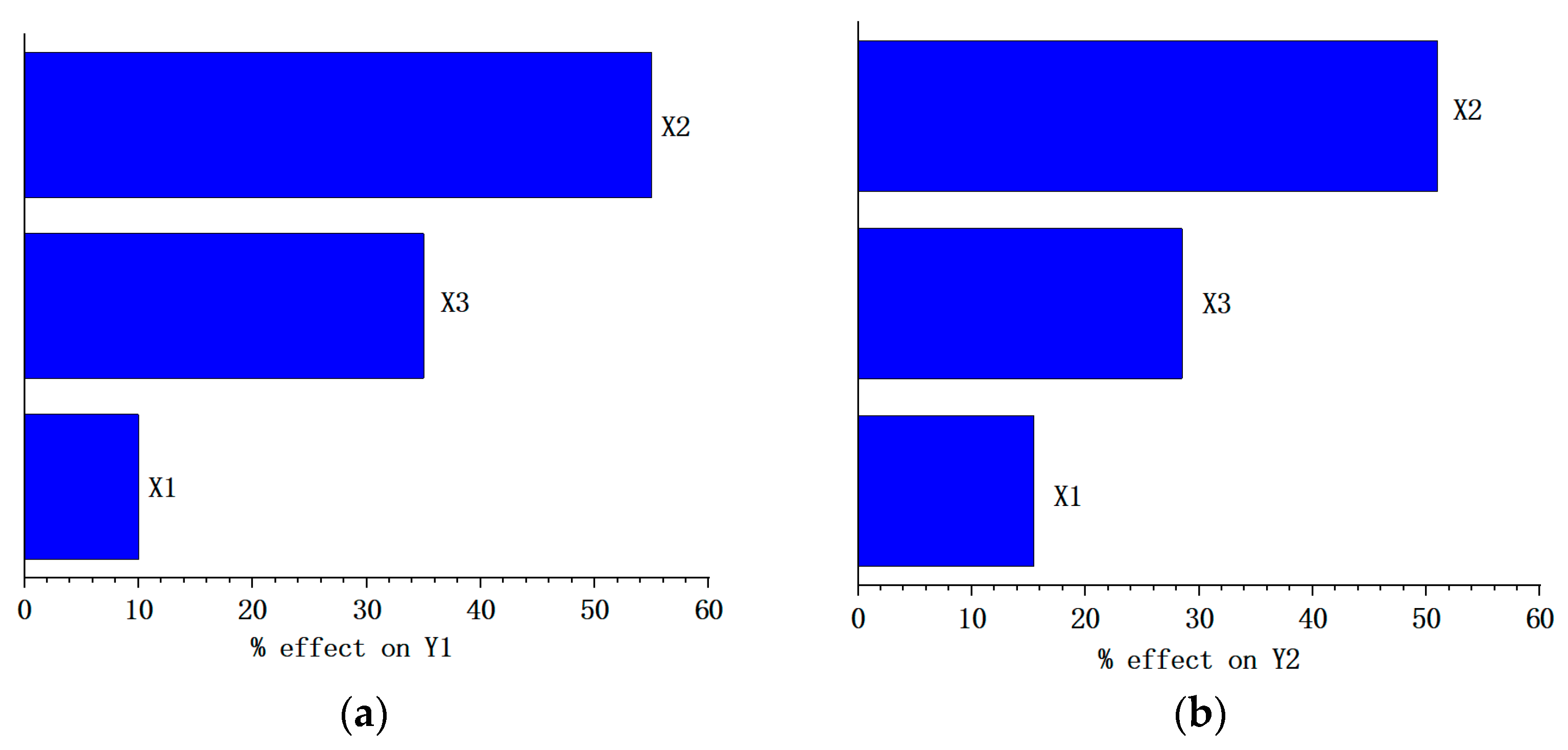
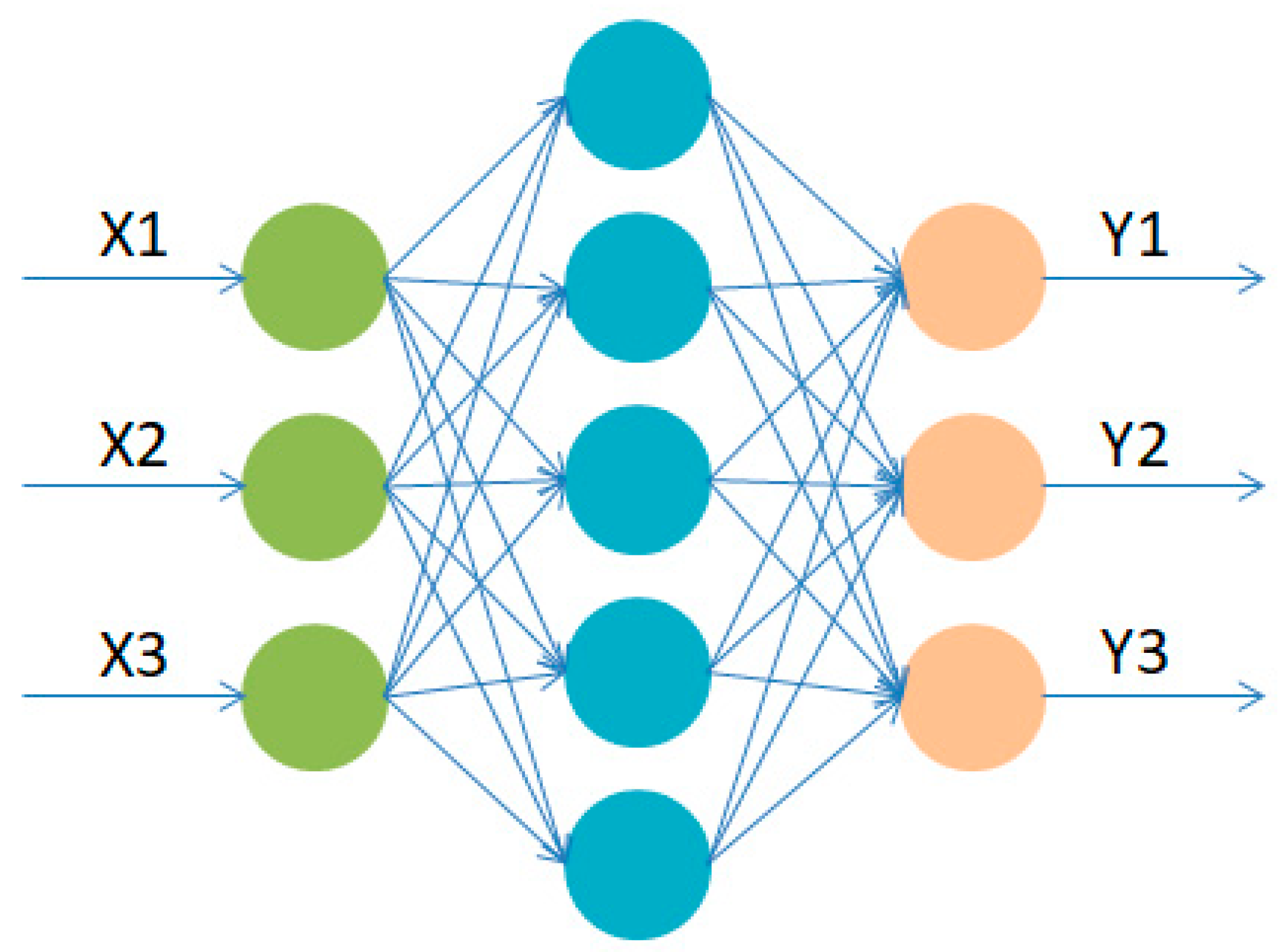
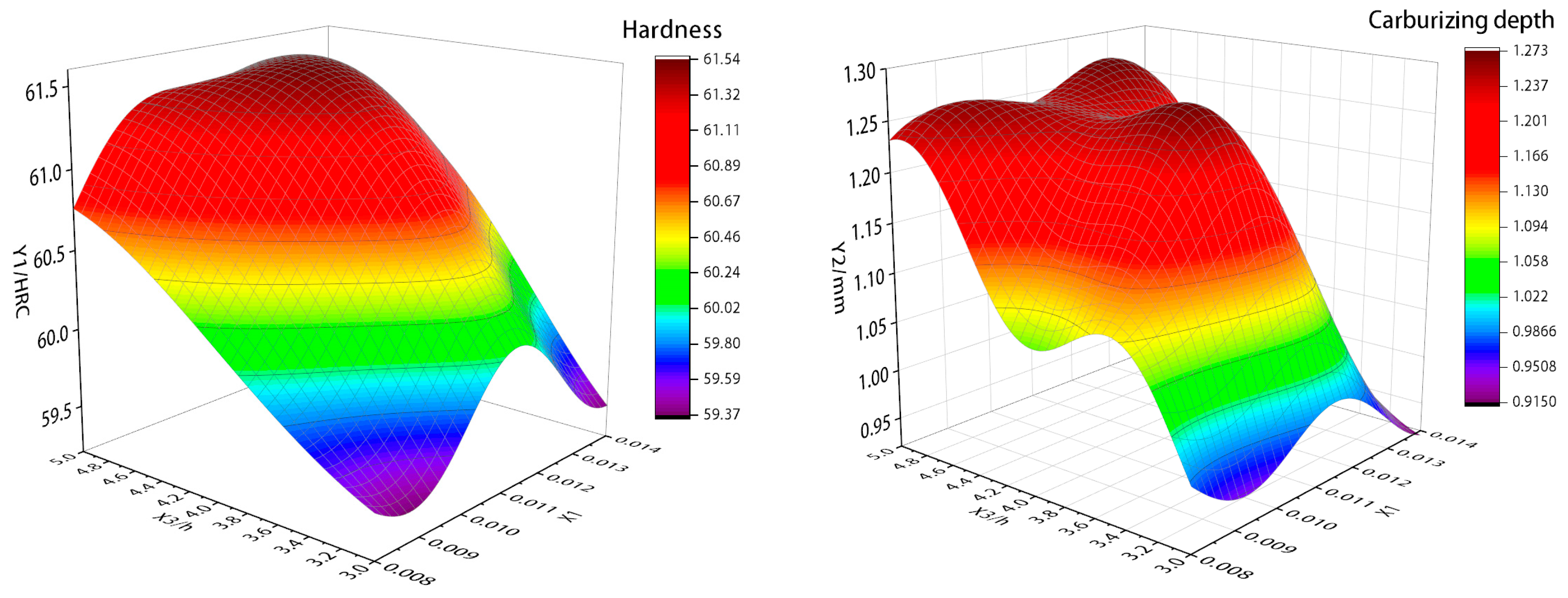
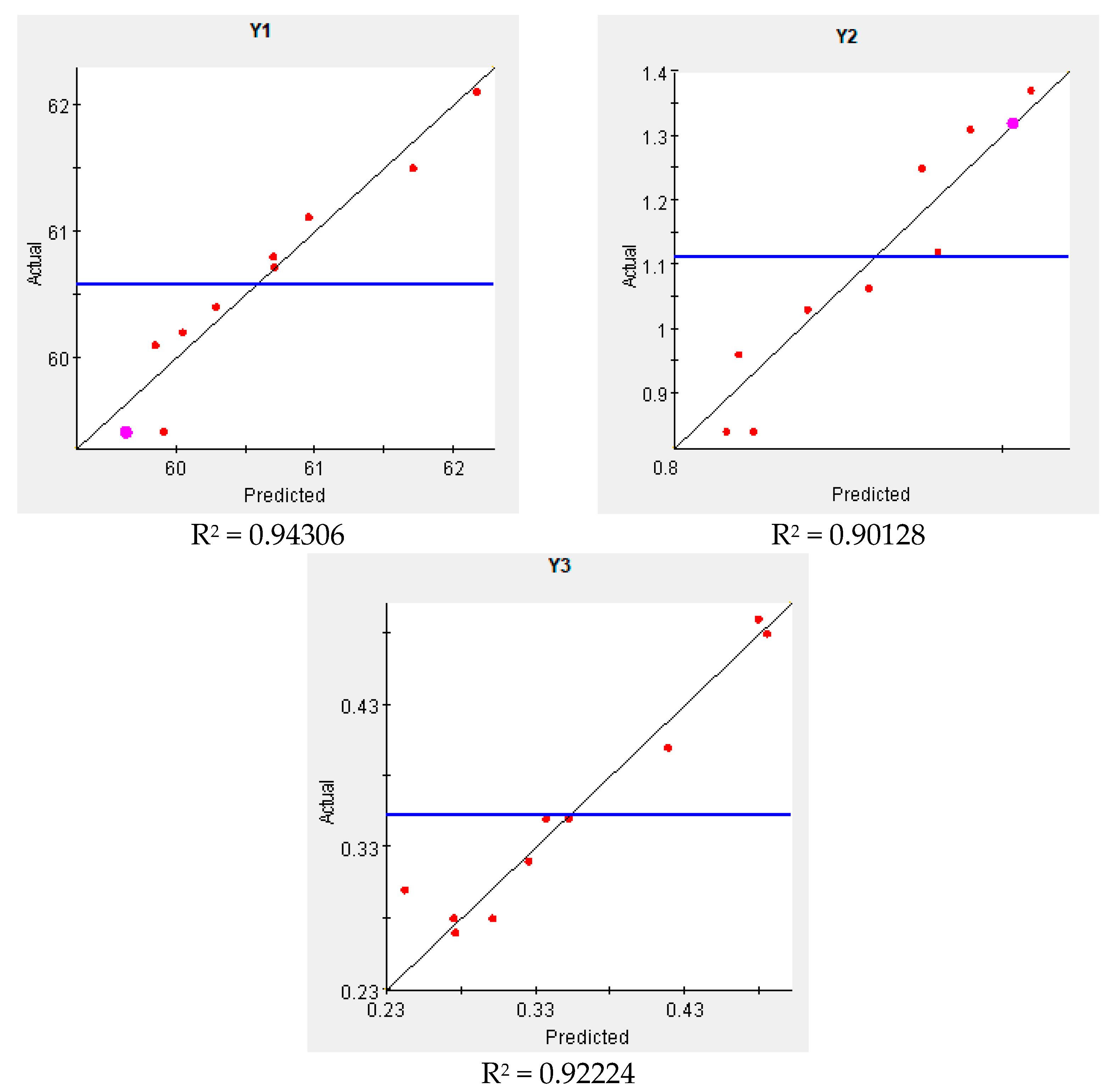
4.1.2. Approximate Modeling Based on RBF Neural Network
4.1.3. Optimization of Stator Guide Carburizing Process Parameters for Hydraulic Motor Based on NSGA-II Algorithm
5. Conclusions
- (1)
- Using DEFORM software, the stator guide carburizing model was established; it can simulate the carburizing process and predict the indicated hardness, deformation, and depth of the carburized layer of the workpiece after carburizing. By simulating the actual working conditions, the simulation results and experimental results for hardness were compared; the error range is within 4.5%, which verifies the correctness of the establishment of the finite element model.
- (2)
- A DOE full factorial test design was carried out for the carburizing process, and carburizing potential, temperature, and time were selected as design variables. The approximate model was established by the RBF neural network, and it was found that the approximate model has high precision and can replace the finite element model analysis and greatly improve the optimization efficiency; the prediction accuracy is greater than 90%.
- (3)
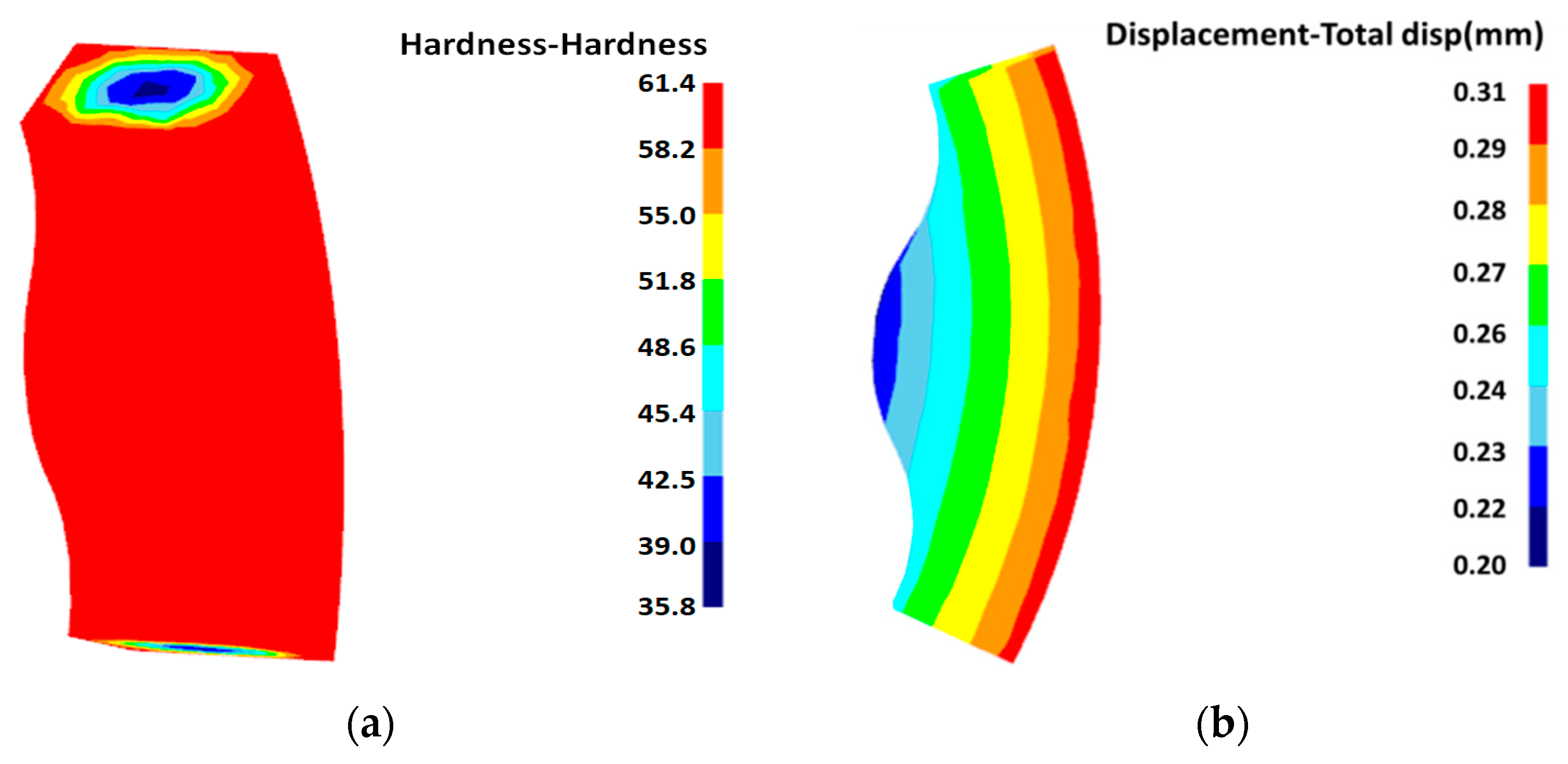
- On the basis of the approximation model, the NSGA-II algorithm was used to carry out multi-objective optimization, and the optimized carburization parameters were a carbon potential of 1.35%, a temperature of 900 °C, and a time of 4.1 h. The surface hardness increased from 59 HRC to 61.25 HRC, and the depth of carburization increased from 1.23 mm to 1.29 mm, which is an increase of 4.2% and 5.1%, and at the same time, the amount of deformation decreased to 0.31 mm. Finally, the optimized parameters were substituted into the finite element model, and the simulation results were found to be highly consistent with the optimization results, which verified the correctness of the optimization.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, C.; Wei, X.; Yi, Z.; Li, Z.; Zhu, C.; Ma, Z. Strength Analysis and Structure Optimization of the Crankshaft of an Opposed-Power Reciprocating Pump. Machines 2023, 11, 123. [Google Scholar] [CrossRef]
- Liu, Z.-J.; Zhao, Y.-C.; Gan, Z.-Q.; Hui, D.-L. Driving shaft fatigue optimization design of Ω type profile twin-screw pumps. J. Mech. Sci. Technol. 2018, 32, 5089–5096. [Google Scholar] [CrossRef]
- Zhu, J.; Cao, J.; Guo, W. Three-dimensional fatigue crack growth based method for fatigue reliability of metallic materials. Int. J. Fatigue 2023, 173, 107697. [Google Scholar] [CrossRef]
- Klevtsov, G.V.; Valiev, R.Z.; Klevtsova, N.y.A.; Tyurkov, M.N.; Pigaleva, I.N.; Aksenov, D.A. Fracture Kinetics and Mechanisms of Ultrafine-Grained Materials during Fatigue Tests in the Low-Cycle Fatigue Region. Metals 2023, 13, 709. [Google Scholar] [CrossRef]
- Goo, B.-C. Effect of post-weld heat treatment on the fatigue behavior of medium-strength carbon steel weldments. Metals 2021, 11, 1700. [Google Scholar] [CrossRef]
- Réger, M.; Horváth, R.; Széll, A.; Réti, T.; Gonda, V.; Felde, I. The relationship between surface and in-depth hardness for the nitrocarburizing treatment process. Metals 2021, 11, 812. [Google Scholar] [CrossRef]
- Wolff, S.J.; Gan, Z.; Lin, S.; Bennett, J.L.; Yan, W.; Hyatt, G.; Ehmann, K.F.; Wagner, G.J.; Liu, W.K.; Cao, J. Experimentally validated predictions of thermal history and microhardness in laser-deposited Inconel 718 on carbon steel. Addit. Manuf. 2019, 27, 540–551. [Google Scholar] [CrossRef]
- Hu, X.; Li, J.; Wang, Z.; Wang, J. A microstructure-informatic strategy for Vickers hardness forecast of austenitic steels from experimental data. Mater. Des. 2021, 201, 109497. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, M.; Yan, Y. Hardness prediction of grind-hardening layer based on integrated approach of finite element and cellular automata. Materials 2021, 14, 5651. [Google Scholar] [CrossRef]
- Ko, D.-H.; Ko, D.-C.; Kim, B.-M. Novel method for predicting hardness distribution of hot-stamped part using Fe-simulation coupled with quench factor analysis. Metall. Mater. Trans. B 2015, 46, 2072–2083. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, X.; Yang, C.; Wang, X.; Zhang, Y.; Li, Y.; Xue, H.; Zheng, Z. A multiphysics model for predicting microstructure changes and microhardness of machined AerMet100 steel. Materials 2022, 15, 4395. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Hong, K.-M.; Katinas, C.; Shin, Y.C. Multiphysics modeling of phase transformation and microhardness evolution in laser direct deposited Ti6Al4V. J. Manuf. Process. 2019, 45, 579–587. [Google Scholar] [CrossRef]
- Umemoto, M.; Ohtsuka, H. Mechanical Properties of Cementite. ISIJ Int. 2022, 62, 1313–1333. [Google Scholar] [CrossRef]
- Savrai, R.A.; Skorynina, P.A.; Makarov, A.V.; Osintseva, A.L. Effect of Liquid Carburizing at Lowered Temperature on the Micromechanical Characteristics of Metastable Austenitic Steel. Phys. Met. Metallogr. 2020, 121, 1015–1020. [Google Scholar] [CrossRef]
- Deng, Y.; Qiao, L.; Zhu, J.; Yang, B. Mechanical Performance and Microstructure Prediction of Hypereutectoid Rail Steels Based on BP Neural Networks. IEEE Access 2020, 8, 41905–41912. [Google Scholar] [CrossRef]
- Wei, Y.; Yu, X.; Wang, S.; Shen, X.; Zhao, W.; Su, Y.; Yang, Y.; Feng, X. Effect of Short-Time Carburizing Treatment on Microstructure and Mechanical Properties of M50 Steel. Met. Mater. Int. 2023, 29, 1586–1595. [Google Scholar] [CrossRef]
- Yan, Y.; Liu, K.; Luo, Z.; Wang, M.; Wang, X. Effect of cryogenic treatment on microstructure, mechanical properties and distortion of carburized gear steels. Metals 2021, 11, 1940. [Google Scholar] [CrossRef]
- Fang, D.; Lu, J.; Dou, H.; Zhou, Z.; Yan, J.; Li, Y.; He, Y. Effect of Post-Plasma Nitrocarburized Treatment on Mechanical Properties of Carburized and Quenched 18Cr2Ni4WA Steel. Lubricants 2024, 12, 153. [Google Scholar] [CrossRef]
- Long, J.B.; Li, X.B.; Zhong, Y.C.; Peng, D. Application of BP Neural Networks on the Thickness Prediction of Sherardizing Coating. Trans. Indian Inst. Met. 2019, 72, 2443–2448. [Google Scholar] [CrossRef]
- Sirin, S.Y.; Nal, M. Artificial neural network approach to predict ion nitrided case depth and surface hardness of AISI 4340 steel. Mater. Test. 2019, 61, 567–572. [Google Scholar] [CrossRef]
- Wang, X.; Li, D.; Li, P. Analysis and Optimization of Carburizing–Quenching Distortion on Locomotive Gear Ring. JOM 2023, 75, 2441–2450. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, J.-y.; Zhang, X.-r. An optimized hardness model for carburizing-quenching of low carbon alloy steel. J. Cent. South Univ. 2017, 24, 9–16. [Google Scholar] [CrossRef]
- Wang, H.; Wang, B.; Wang, Z.; Tian, Y.; Misra, R. Optimizing the low-pressure carburizing process of 16Cr3NiWMoVNbE gear steel. J. Mater. Sci. Technol. 2019, 35, 1218–1227. [Google Scholar] [CrossRef]
- Yang, Z.; Wei, J.; Liu, T.; Liu, S.; Fang, D.; Li, Z. Influence of carbon layer hardness characteristics on RCF performance of carburized bearing steel and optimization of heat treatment process. Eng. Fail. Anal. 2024, 160, 108164. [Google Scholar] [CrossRef]
- Miao, S.; Ju, D.-Y.; Chen, Y.; Liu, Y.-q. Optimization based on orthogonal experiment design and numerical simulation for carburizing quenching process of helical gear. Mater. Perform. Charact. 2019, 8, 66–79. [Google Scholar] [CrossRef]
- Luo, A.; Lei, M.; Song, W.; Wan, M.; Chen, G.; Qu, Z. Enhanced Friction and Wear Performance of 297A-Hybridsteel Carburized Layer through Pre-tempering Optimization. J. Mater. Eng. Perform. 2024, 1–9. [Google Scholar] [CrossRef]
- LSalawu, E.Y.; Adediran, A.A.; Ajayi, O.O.; Inegbenebor, A.O.; Dirisu, J.O. On the analyses of carbon atom diffused into grey cast iron during carburisation process. Sci. Rep. 2022, 12, 18303. [Google Scholar]
- Wei, L.; Meng, W.-D.; Sun, L.-C.; Cao, X.-F.; Pu, X.-Y. Measurement and verification of concentration-dependent diffusion coefficient: Ray tracing imagery of diffusion process. Chin. Phys. B 2020, 29, 084206. [Google Scholar] [CrossRef]
- Liang, R.; Wang, Z.; Yang, S.; Chen, W. Study on hardness prediction and parameter optimization for carburizing and quenching: An approach based on FEM, ANN and GA. Mater. Res. Express 2021, 8, 116501. [Google Scholar] [CrossRef]
- Wen, G.; Du, C. Research on Key Technology of Finite Element Simulation of 12CrNi3 Helical Gear Carburizing and Quenching Process. New Technol. New Process 2019, 06, 20–26. [Google Scholar]
- Sugianto, A.; Narazaki, M.; Kogawara, M.; Shirayori, A.; Kim, S.-Y.; Kubota, S. Numerical simulation and experimental verification of carburizing-quenching process of SCr420H steel helical gear. J. Mater. Process. Technol. 2009, 209, 3597–3609. [Google Scholar] [CrossRef]
- Tong, D.; Gu, J.; Yang, F. Numerical simulation on induction heat treatment process of a shaft part: Involving induction hardening and tempering. J. Mater. Process. Technol. 2018, 262, 277–289. [Google Scholar] [CrossRef]
- Khan, D.; Gautham, B. Integrated modeling of carburizing-quenching-tempering of steel gears for an ICME framework. Integr. Mater. Manuf. Innov. 2018, 7, 28–41. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Fu, J.; Sun, H.; Li, J.; Liu, H. Research on microstructure evolution and mechanical properties of steering shaft teeth after pre-heat treatment and carburizing-quenching processes. In Proceedings of the 2021 7th International Forum on Manufacturing Technology and Engineering Materials (IFEMMT 2021), Dali, China, 18–20 June 2021; IOP Publishing: Bristol, UK, 2021; Volume 1965, p. 012051. [Google Scholar]
- Wang, Z.; Feng, Y.; Yang, Y.; Wang, J.; Xu, S.; Qin, J. Multi-objective optimization of rectangular cooling channel design using Design of Experiments (DOE). Appl. Therm. Eng. 2024, 242, 122507. [Google Scholar] [CrossRef]
- Guo, S.; Li, C.; Shi, J.; Luan, F.; Song, X. Effect of quenching media and tempering temperature on fatigue property and fatigue life estimation based on RBF neural network of 0.44% carbon steel. Mech. Sci. 2019, 10, 273–286. [Google Scholar] [CrossRef]
- Piepho, H.P. An adjusted coefficient of determination (R2) for generalized linear mixed models in one go. Biom. J. 2023, 65, 2200290. [Google Scholar] [CrossRef]
- Liu, S.; Yang, Z.; Liu, T.; Li, Z.; Cong, T. Effect of Case Depth and Hardness Distribution on the Rolling Contact Fatigue Performance of G20CrNi2MoA Carburized Steel. Steel Res. Int. 2024, 95, 2300875. [Google Scholar] [CrossRef]





| Heat Treatment State | Heat Transfer Coefficient [J/(S∙mm∙°C)] |
|---|---|
| heating stage | 0.1 |
| carburizing stage | 0.05 |
| C | Si | Mn | S | P | Cr | Ni | Mo | Fe |
|---|---|---|---|---|---|---|---|---|
| 0.21 | 0.34 | 0.72 | 0.004 | 0.01 | 1.58 | 1.4 | 0.26 | Bal. |
| Heat Treatment | Process | T [°C] | Time [s] | Carbon Potential [%] | Type of Cooling |
|---|---|---|---|---|---|
| Carburization | Intensive carburizing | 930 | 14,400 | 1.2 | - |
| Quenching | Oil quenching | 25 | 1440 | 0.6 | Oil cooling |
| Tempering | Low tempering | 180 | 720 | - | Air cooling |
| Variable Name | Lower Value | Initial Value | Upper Value |
|---|---|---|---|
| Carbon Potential X1 | 0.8% | 1.1% | 1.4% |
| Temperature X2 | 880 °C | 920 °C | 940 °C |
| Time X3 | 3 h | 4 h | 5 h |
| Test Number | Carbon Potential X1 | Temperature X2/[°C] | Time X3/[h] |
|---|---|---|---|
| 1 | 0.954 | 923.08 | 3 |
| 2 | 0.815 | 916.92 | 3.41 |
| 3 | 0.923 | 901.54 | 3.051 |
| 4 | 1.323 | 909.23 | 3.359 |
| 5 | 1.031 | 890.77 | 3.513 |
| 6 | 0.862 | 881.54 | 3.462 |
| 7 | 1.246 | 932.31 | 4.333 |
| 8 | 1 | 906.15 | 4.795 |
| 9 | 1.123 | 924.62 | 3.821 |
| 10 | 1.092 | 929.23 | 4.744 |
| 11 | 1.262 | 930.77 | 5 |
| 12 | 1.154 | 912.31 | 4.385 |
| 13 | 1.185 | 895.38 | 3.103 |
| 14 | 1.169 | 904.62 | 3.769 |
| 15 | 0.985 | 910.77 | 3.615 |
| 16 | 1.077 | 886.15 | 4.692 |
| 17 | 0.831 | 907.69 | 4.436 |
| 18 | 1.338 | 918.46 | 3.974 |
| 19 | 1.308 | 926.15 | 3.154 |
| 20 | 1.015 | 900 | 4.179 |
| 21 | 1.108 | 935.38 | 3.256 |
| 22 | 1.231 | 884.62 | 3.667 |
| 23 | 0.877 | 887.69 | 4.487 |
| 24 | 1.4 | 893.85 | 4.538 |
| 25 | 1.262 | 883.08 | 4.846 |
| 26 | 0.8 | 926.15 | 4.026 |
| 27 | 1.2 | 903.08 | 4.949 |
| 28 | 0.969 | 920 | 4.231 |
| 29 | 0.846 | 896.92 | 3.872 |
| 30 | 1.138 | 915.38 | 3.205 |
| 31 | 0.892 | 921.54 | 4.897 |
| 32 | 1.354 | 913.85 | 4.641 |
| 33 | 1.369 | 898.46 | 3.923 |
| 34 | 1.062 | 940 | 4.128 |
| 35 | 0.938 | 933.85 | 3.564 |
| 36 | 1.292 | 936.92 | 3.718 |
| 37 | 1.215 | 892.31 | 4.282 |
| 38 | 1.385 | 889.23 | 3.308 |
| 39 | 1.046 | 880 | 4.077 |
| 40 | 0.908 | 938.46 | 4.538 |
| Test Number | Carbon Potential X1 | Temperature X2/[°C] | Time X3/[h] | Hardness Y1/[HRC] | Carburizing Depth Y2/[mm] | Deformation Y3/[mm] |
|---|---|---|---|---|---|---|
| 1 | 923.08 | 3 | 59.5 | 0.95 | 0.29 | 0.954 |
| 2 | 916.92 | 3.41 | 60.4 | 1.07 | 0.35 | 0.815 |
| 3 | 901.54 | 3.051 | 58.6 | 0.78 | 0.25 | 0.923 |
| 4 | 909.23 | 3.359 | 60.2 | 1.07 | 0.34 | 1.323 |
| 5 | 890.77 | 3.513 | 58.5 | 0.83 | 0.27 | 1.031 |
| 6 | 881.54 | 3.462 | 58.3 | 0.84 | 0.25 | 0.862 |
| 7 | 932.31 | 4.333 | 61.7 | 1.29 | 0.42 | 1.246 |
| 8 | 906.15 | 4.795 | 60.4 | 1.12 | 0.33 | 1 |
| 9 | 924.62 | 3.821 | 61.2 | 1.28 | 0.37 | 1.123 |
| 10 | 929.23 | 4.744 | 61.6 | 1.3 | 0.44 | 1.092 |
| 11 | 930.77 | 5 | 61.8 | 1.31 | 0.45 | 1.262 |
| 12 | 912.31 | 4.385 | 60.5 | 1.13 | 0.36 | 1.154 |
| 13 | 895.38 | 3.103 | 58.8 | 0.81 | 0.27 | 1.185 |
| 14 | 904.62 | 3.769 | 60.1 | 1.09 | 0.34 | 1.169 |
| 15 | 910.77 | 3.615 | 60.2 | 1.08 | 0.35 | 0.985 |
| 16 | 886.15 | 4.692 | 60 | 1.12 | 0.32 | 1.077 |
| 17 | 907.69 | 4.436 | 60.3 | 1.14 | 0.35 | 0.831 |
| 18 | 918.46 | 3.974 | 60.8 | 1.04 | 0.38 | 1.338 |
| 19 | 926.15 | 3.154 | 59.7 | 0.98 | 0.28 | 1.308 |
| 20 | 900 | 4.179 | 60.1 | 1.04 | 0.32 | 1.015 |
| 21 | 935.38 | 3.256 | 61.5 | 1.25 | 0.4 | 1.108 |
| 22 | 884.62 | 3.667 | 58.6 | 0.84 | 0.25 | 1.231 |
| 23 | 887.69 | 4.487 | 58.7 | 0.88 | 0.26 | 0.877 |
| 24 | 893.85 | 4.538 | 58.9 | 0.87 | 0.28 | 1.4 |
| 25 | 883.08 | 4.846 | 58.8 | 0.88 | 0.27 | 1.262 |
| 26 | 926.15 | 4.026 | 60 | 1.06 | 0.32 | 0.8 |
| 27 | 903.08 | 4.949 | 60.3 | 1.06 | 0.35 | 1.2 |
| 28 | 920 | 4.231 | 61.1 | 1.21 | 0.37 | 0.969 |
| 29 | 896.92 | 3.872 | 58.6 | 0.82 | 0.26 | 0.846 |
| 30 | 915.38 | 3.205 | 60.5 | 1.06 | 0.36 | 1.138 |
| 31 | 921.54 | 4.897 | 61.2 | 1.25 | 0.38 | 0.892 |
| 32 | 913.85 | 4.641 | 60.4 | 1.14 | 0.36 | 1.354 |
| 33 | 898.46 | 3.923 | 60 | 1.04 | 0.31 | 1.369 |
| 34 | 940 | 4.128 | 62.1 | 1.32 | 0.49 | 1.062 |
| 35 | 933.85 | 3.564 | 61.5 | 1.27 | 0.41 | 0.938 |
| 36 | 936.92 | 3.718 | 61.8 | 1.28 | 0.45 | 1.292 |
| 37 | 892.31 | 4.282 | 59 | 0.88 | 0.32 | 1.215 |
| 38 | 889.23 | 3.308 | 58.8 | 0.84 | 0.31 | 1.385 |
| 39 | 880 | 4.077 | 58.4 | 0.8 | 0.3 | 1.046 |
| 40 | 938.46 | 4.538 | 62 | 1.3 | 0.48 | 0.908 |
| Type of Result | Carbon Potential | Temperature/°C | Time/h | Surface Hardness/HRC | Carburizing Depth/mm | Deformation/mm |
|---|---|---|---|---|---|---|
| Preliminary design | 1.1 | 920 | 4 | 59.0 | 1.23 | 0.39 |
| Optimized forecasting | 1.35 | 900 | 4.1 | 61.25 | 1.29 | 0.31 |
| Simulation verification | 1.35 | 900 | 4.1 | 61.4 | 1.28 | 0.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Tang, Y.; Chen, J.; Xia, Z. Surface Mechanical Property Prediction and Process Optimization of 18CrNiMo7-6 Carburized Steel Stator Guide Based on Radial Basis Function Neural Network and NSGA-II Algorithm. Coatings 2024, 14, 1369. https://doi.org/10.3390/coatings14111369
Li C, Tang Y, Chen J, Xia Z. Surface Mechanical Property Prediction and Process Optimization of 18CrNiMo7-6 Carburized Steel Stator Guide Based on Radial Basis Function Neural Network and NSGA-II Algorithm. Coatings. 2024; 14(11):1369. https://doi.org/10.3390/coatings14111369
Chicago/Turabian StyleLi, Chunjin, Yongjie Tang, Jianzhi Chen, and Zhengwen Xia. 2024. "Surface Mechanical Property Prediction and Process Optimization of 18CrNiMo7-6 Carburized Steel Stator Guide Based on Radial Basis Function Neural Network and NSGA-II Algorithm" Coatings 14, no. 11: 1369. https://doi.org/10.3390/coatings14111369
APA StyleLi, C., Tang, Y., Chen, J., & Xia, Z. (2024). Surface Mechanical Property Prediction and Process Optimization of 18CrNiMo7-6 Carburized Steel Stator Guide Based on Radial Basis Function Neural Network and NSGA-II Algorithm. Coatings, 14(11), 1369. https://doi.org/10.3390/coatings14111369






