Numerical Analysis of Thermal Flow Dynamics of Arc Plasma and Molten Pool in Hollow Cathode Arc Welding with Oxygen Content
Abstract
1. Introduction
2. Mathematical Model
2.1. Assumptions
- The shielding gas is in the Local Thermodynamic Equilibrium (LTE) state;
- The multiphase fluids (gas, liquid) are incompressible with a laminar flow;
- The Marangoni effect of Fe-O alloy is determined by both temperature and oxygen content [2].
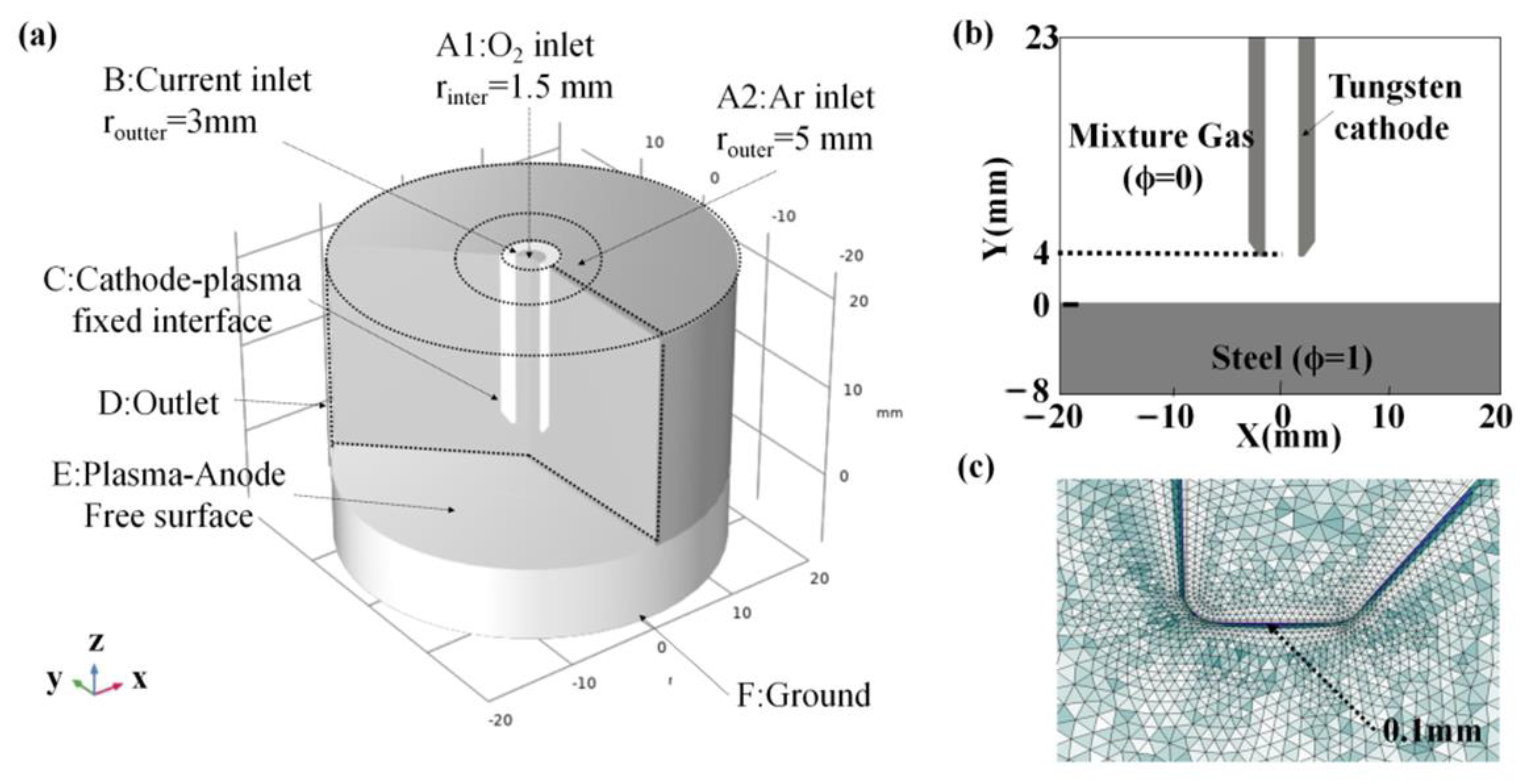
2.2. Boundary Conditions and Meshes
2.3. Numerical Procedure
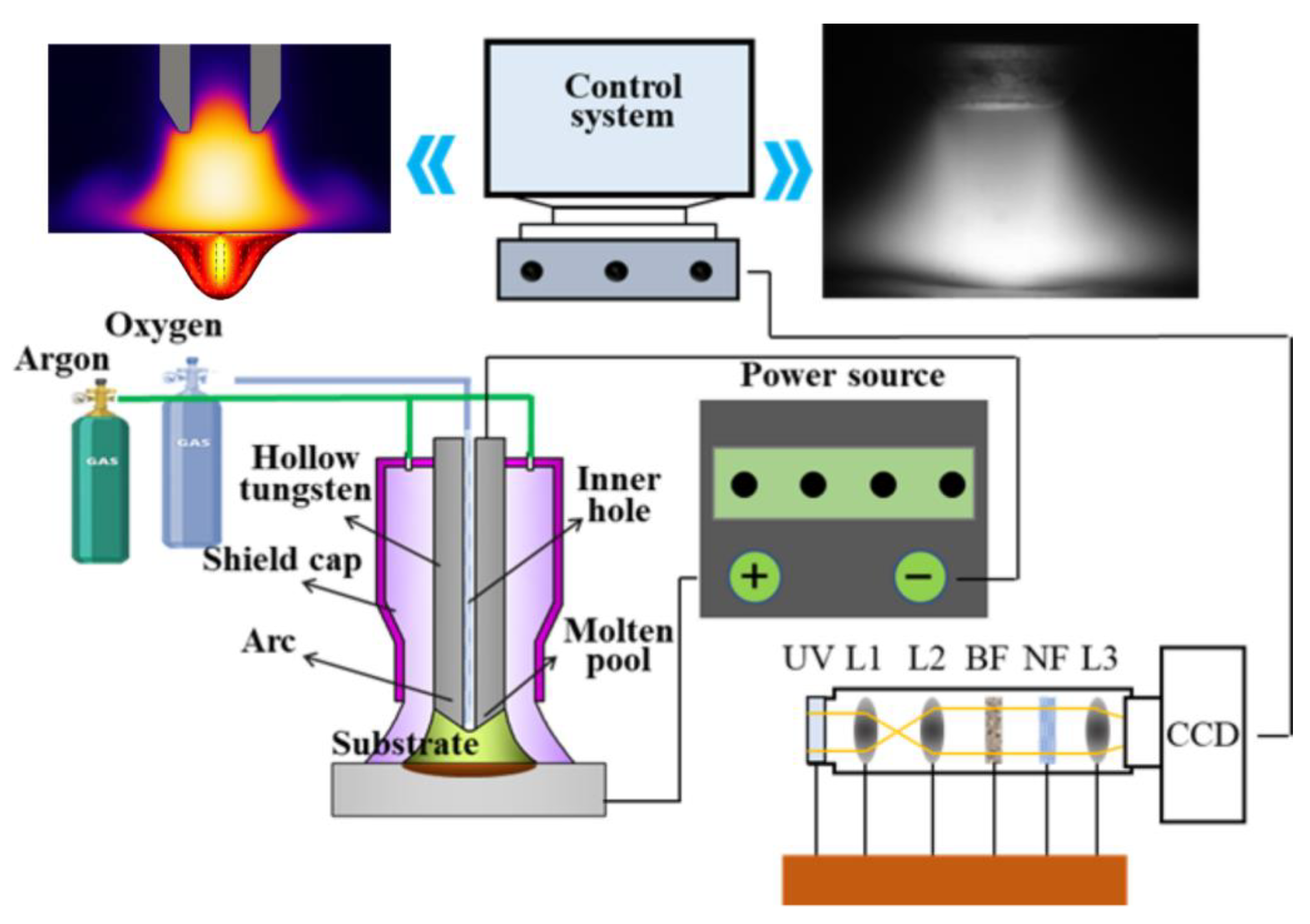
3. Experimental Procedure
4. Results and Discussion
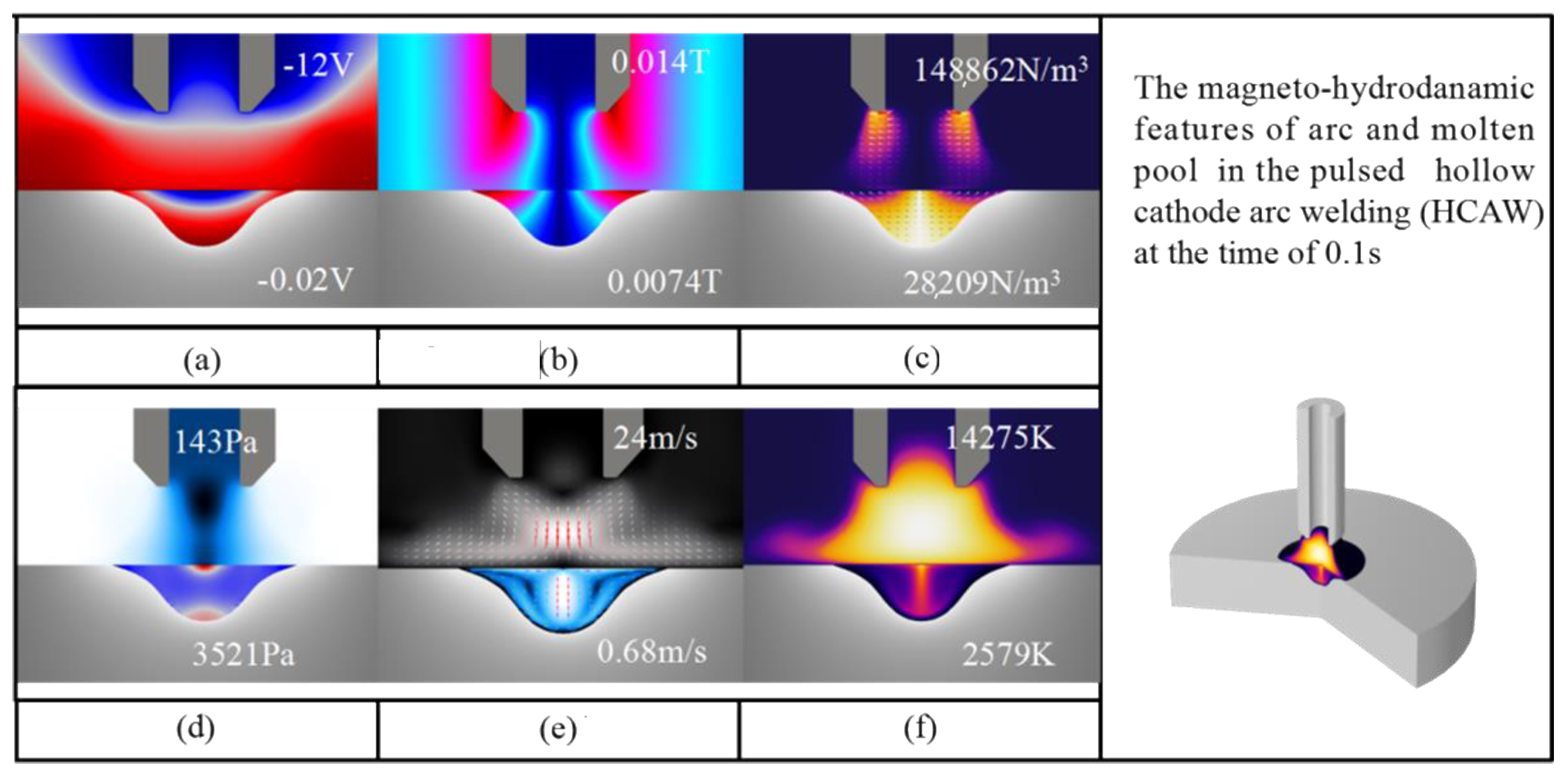
4.1. The Magneto-Hydro Dynamic Characteristics of Arc Plasma and Weld Pool in HCAW (t = 0.1 s, O2 wt% = 0.1)
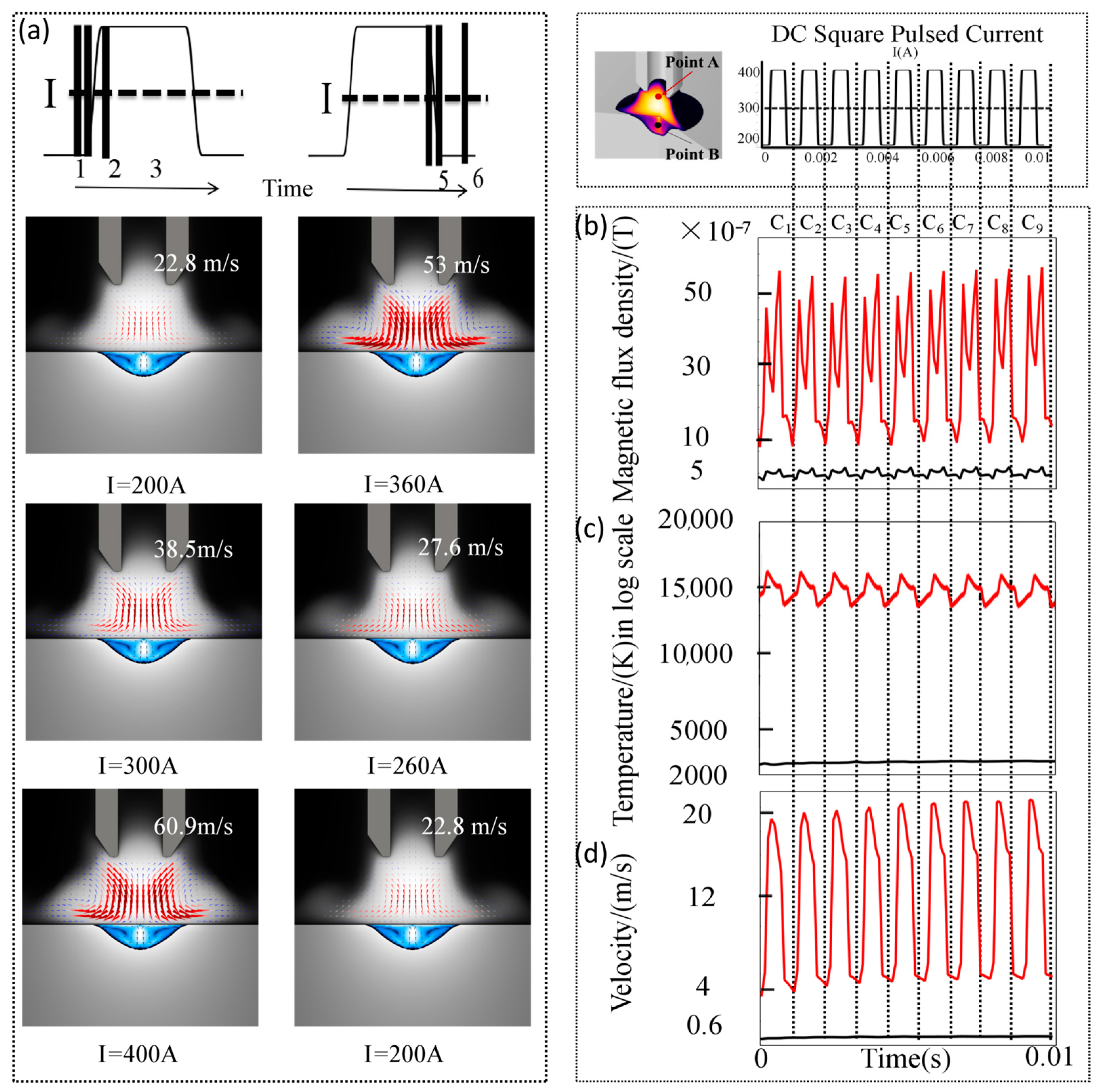
4.2. The Magneto-Hydro Dynamic Characteristics of HCAW in Ten Circles (t = 0~0.01 s, O2 wt% = 0.1)
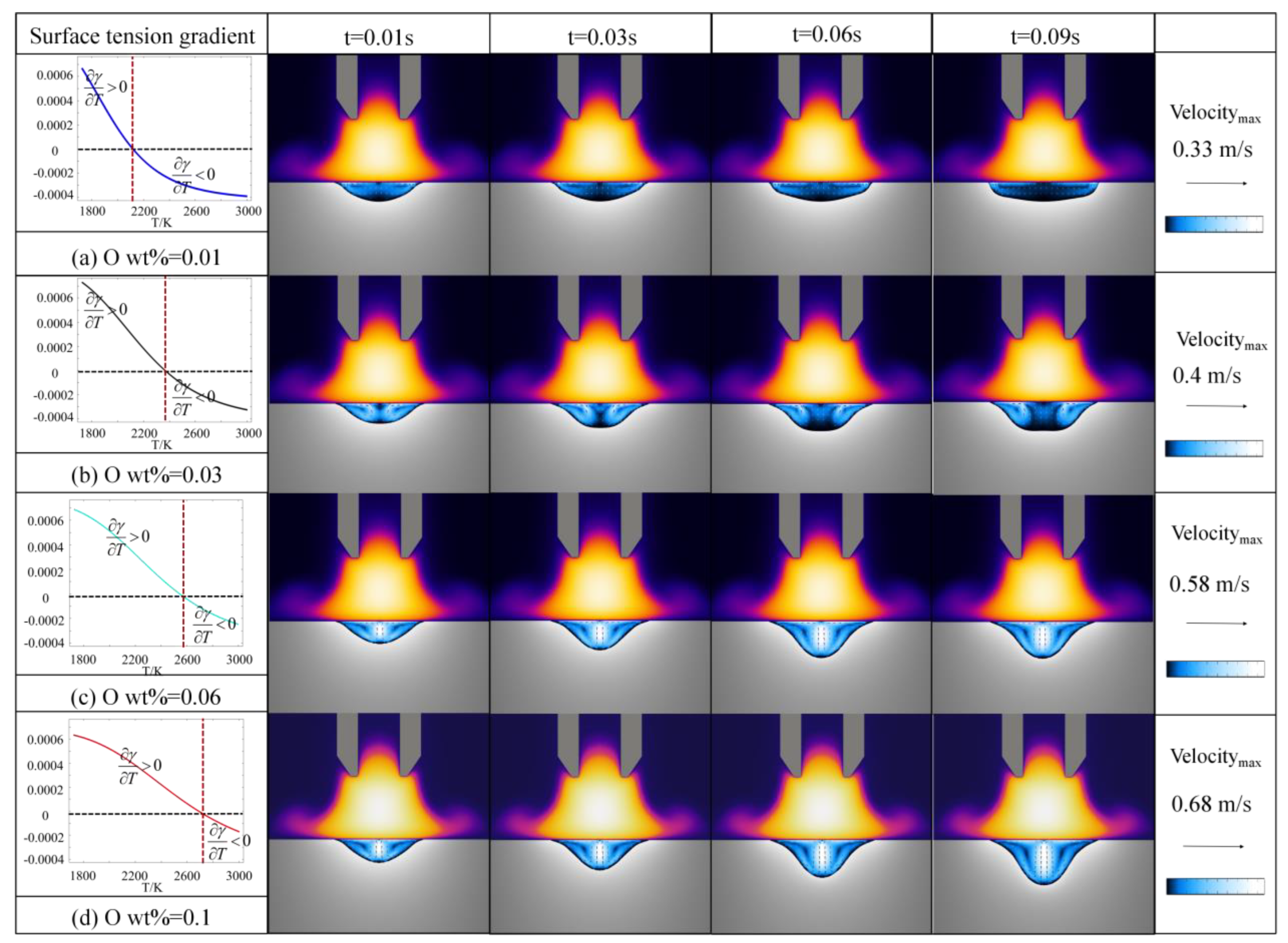
4.3. Influence of Oxygen Content on the Molten Pool Dynamics (t = 0–0.1 s, O2 wt% = 0.01~0.1)
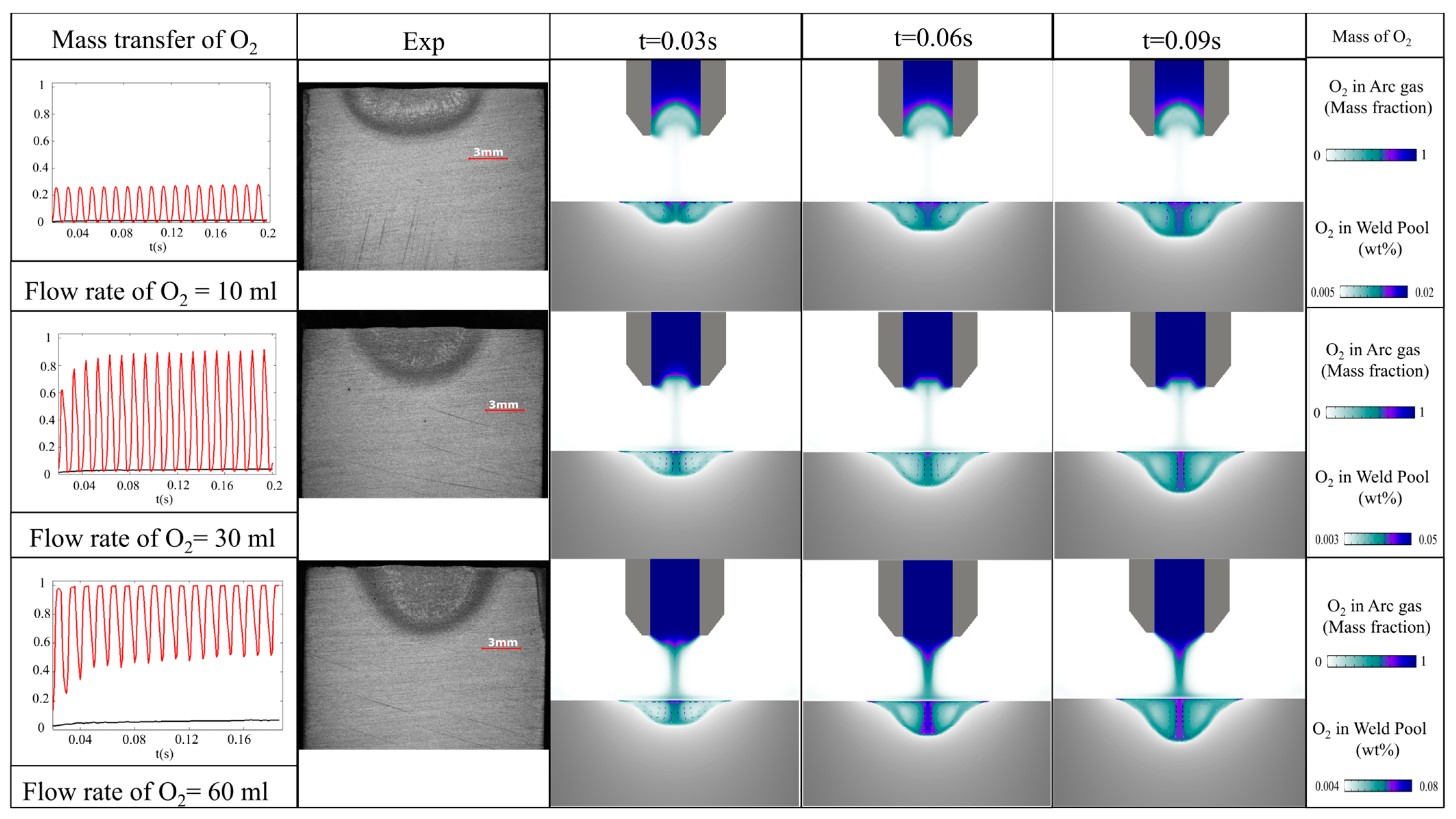
4.4. Mass Transfer of Oxygen in Arc Plasma and Melt Pool (t = 0–0.1 s, Flow Rate O2 = 0.01 L~0.06 L)
4.5. Experimental Validation
5. Conclusions
- Compared to the solid cathode GTAW process, the hollow cathode leads to a less intensive arc flow and a more uniform temperature field in the arc plasma, and the intensity of electromagnetic fields is comparatively weakened by the design of a hollow cathode.
- The momentum sources from plasma jets and Lorentz force could be neglected in the high-frequency pulsing current arc welding process; the Marangoni effect is predominant in the flow dynamics of molten pools in HCAW. The explanation of electromagnetic-induced string is not appropriate for describing flow dynamics in the high-frequency pulsed current arc welding process.
- The flow dynamics of molten pools are sensitive to oxygen content in HCAW; as the oxygen content increases from 0.01 wt% to 0.1 wt%, there is a transition of internal flow patterns from upward–outward melt flow, resulting in a shallow weld pool, to inward–downward melt flow, resulting in a deep finger-like weld pool; we could promote penetration by increasing O2 content in HCAW.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nerovnyi, V.M.; Khakhalev, A.D. Hollow cathode arc discharge as an effective energy source for welding processes in vacuum. J. Phys. D Appl. Phys. 2008, 41, 035201. [Google Scholar] [CrossRef]
- Nishikawa, H.; Yoshida, K.; Maruyama, T.; Ohji, T.; Suita, Y.; Masubuchi, K. Gas hollow tungsten arc characteristics under simulated space environment. Sci. Technol. Weld. Join. 2013, 6, 12–16. [Google Scholar] [CrossRef]
- Shobako, S.; Ota, M.; Oji, T. Characteristics of an arc column in a hollow cathode arc. Weld. Int. 2006, 20, 111–115. [Google Scholar] [CrossRef]
- Cho, D.W.; Lee, S.H.; Na, S.J. Characterization of welding arc and weld pool formation in vacuum gas hollow tungsten arc welding. J. Mater. Process. Technol. 2013, 213, 143–152. [Google Scholar] [CrossRef]
- Nishikawa, H.; Shobako, S.; Ohta, M.; Ohji, T. Heat input properties of hollow cathode arc as a welding heat source. J. Phys. D Appl. Phys. 2005, 38, 3451–3456. [Google Scholar] [CrossRef]
- Chen, S.; Yan, Z.; Jiang, F.; Lu, Z. The pressure distribution of hollow cathode centered negative pressure arc. J. Manuf. Process. 2016, 23, 21–28. [Google Scholar] [CrossRef]
- Jiang, F.; Yan, Z.; Chen, S.; Lu, Z. The energy distribution of electrode in hollow cathode centered negative pressure arc. J. Manuf. Process. 2016, 24, 138–144. [Google Scholar] [CrossRef]
- Tashiro, S.; Tanaka, M.; Nakatani, M.; Tani, K.; Furubayashi, M. Numerical analysis of energy source properties of hollow cathode arc. Surf. Coat. Technol. 2007, 201, 5431–5434. [Google Scholar] [CrossRef]
- Saifutdinov, A.I.; Timerkaev, B.A.; Ibragimov, A.R. Numerical Simulation of Temperature Fields in a Direct-Current Plasma Torch. Tech. Phys. Lett. 2018, 44, 164–166. [Google Scholar]
- Baeva, M.; Zhu, T.; Kewitz, T.; Testrich, H.; Foest, R. Self-Consistent Cathode-Plasma Coupling and Role of the Fluid Flow Approach in Torch Modeling. J. Therm. Spray Technol. 2021, 30, 1737–1750. [Google Scholar] [CrossRef]
- Lidsky, L.M.; Rothleder, S.D.; Rose, D.J.; Yoshikawa, S.; Michelson, C.; Mackin, R.J., Jr. Highly Ionized Hollow Cathode Discharge. J. Appl. Phys. 1962, 33, 2490–2497. [Google Scholar] [CrossRef]
- Limmaneevichitr, C.; Kou, S. Visualization of Marangoni convection in simulated weld pools containing a surface-active agent. Weld. J. 2000, 79, 324–330. [Google Scholar]
- Aucott, L.; Dong, H.; Mirihanage, W.; Atwood, R.; Kidess, A.; Gao, S.; Wen, S.; Marsden, J.; Feng, S.; Tong, M.; et al. Revealing internal flow behaviour in arc welding and additive manufacturing of metals. Nat. Commun. 2018, 9, 5414. [Google Scholar] [CrossRef] [PubMed]
- Mills, K.C.; Keene, B.J.; Brooks, R.F.; Shirali, A. Marangoni effects in welding. Philos. Trans. A Math. Phys. Eng. Sci. 1998, 356, 911–925. [Google Scholar] [CrossRef]
- Sahoo, P.; DebRoy, T.; McNallan, M.T. Surface tension of binary metal surface active solute systems under conditions relevant to welding metallurgy. Metall. Trans. B 1988, 19B, 483–491. [Google Scholar] [CrossRef]
- Mishra, S.; Lienert, T.J.; Johnson, M.Q.; DebRoy, T. An experimental and theoretical study of gas tungsten arc welding of stainless steel plates with different sulfur concentrations. Acta Mater. 2008, 56, 2133–2146. [Google Scholar] [CrossRef]
- Ko, S.H.; Choi, S.K.; Yoo, C.D. Effects of surface depression on pool convection and geometry in stationary GTAW. Weld. J. 2001, 80, 39–45. [Google Scholar]
- Savage, W.F.; Nippes, E.F.; Agusa, K. Effect of arc force on defect formation in GTA welding. Weld. J. 1979, 58, s212–s224. [Google Scholar]
- Kim, W.H.; Na, S.J.; Fan, H.G. Effect of various driving forces on heat and mass transfer in arc welding. Numer. Heat Transf. Part A Appl. 1997, 32, 633–652. [Google Scholar] [CrossRef]
- Wang, D.; Lu, H. Numerical analysis of internal flow of molten pool in pulsed gas tungsten arc welding using a fully coupled model with free surface. Int. J. Heat Mass Transf. 2021, 165, 120572. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Y.; Liu, W.; Hua, C.; Yu, C.; Lu, H. Multiscale investigation of microstructure optimization in the arc additive manufacturing and arc welding by self-induced ultrasound. Int. J. Heat Mass Transf. 2021, 180, 121790. [Google Scholar] [CrossRef]


| Symbol | Nomenclature | Value | Unit |
|---|---|---|---|
| I0 | Continuous current | 400 | A |
| Ie | Pulsed current | 200 | A |
| f | Frequency | 900 | HZ |
| T0 | Temperature | 300 | K |
| Ugas | Gas inflow rate | 15 | L/min |
| ρl(T)/ρAr(T)/ρO2(T) | Density of liquid/Ar/O2 | 7015~6712/1.7~0.008/0.78~0.004 | kg/m3 |
| kl(T)/kAr(T)/kO2(T) | Thermal conductivity of liquid/Ar/O2 | 46~5/5~0.1/4.9~0.04 | W/(m·K) |
| σl(T)/σAr(T)/σO2(T) | Electrical conductivity of liquid/Ar/O2 | 6.77 × 105~6.27 × 105/1 × 104~1/1.4 × 104~0 | S/m |
| μ(T)/μAr(T)/μO2(T) | Viscosity of liquid/Ar/O2 | (5.8~4.7) × 10−3/(2.5~1.2) × 10−5/(29~3) × 10−5 | Pa·s |
| Cpl/CAr/CO2 | Specific enthalpy of liquid/Ar/O2 | 475/824/8000~800 | J/(kg·K) |
| Lf | Latent heat of fusion | 2.54 × 105 | J/kg |
| αo | Activity of oxygen | 0.01~0.1 | wt% |
| Aγ | Constant in surface tension gradient | 4.3 × 10−4 | N/(m·K) |
| Rg | Gas constant | 8314.3 | J/(kg·mol) |
| ΔH0 | Standard heat of absorption | −1.46 × 108 | J |
| t | Total time of heating duration | 0.1 | S |
| Np | Number of thermal circles | 90 | kg/m3 |
| σt(T) | Electrical conductivity of tungsten cathode | 4.8 × 107~1 × 106 | S/m |
| Ct | Specific enthalpy of tungsten cathode | 130~290 | Pa·s |
| ks | Thermal conductivity of solid steel | 44.5 | J/(kg·K) |
| Boundary (Surface) | ||||
| B (Current inlet) | ~ | |||
| A1 (O2 inlet) | ||||
| A2 (Ar inlet) | ||||
| C (Interface) | ||||
| E (Interface) | ||||
| D (Outlet) | ||||
| F (Ground) | ~ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Du, B.; Huang, J.; Lei, Z.; Xu, F.; Sun, Q.; Wei, P.; Wang, D. Numerical Analysis of Thermal Flow Dynamics of Arc Plasma and Molten Pool in Hollow Cathode Arc Welding with Oxygen Content. Coatings 2024, 14, 382. https://doi.org/10.3390/coatings14040382
Yang Y, Du B, Huang J, Lei Z, Xu F, Sun Q, Wei P, Wang D. Numerical Analysis of Thermal Flow Dynamics of Arc Plasma and Molten Pool in Hollow Cathode Arc Welding with Oxygen Content. Coatings. 2024; 14(4):382. https://doi.org/10.3390/coatings14040382
Chicago/Turabian StyleYang, Yicheng, Bing Du, Jihua Huang, Zhen Lei, Fujia Xu, Qian Sun, Pengyu Wei, and Daqing Wang. 2024. "Numerical Analysis of Thermal Flow Dynamics of Arc Plasma and Molten Pool in Hollow Cathode Arc Welding with Oxygen Content" Coatings 14, no. 4: 382. https://doi.org/10.3390/coatings14040382
APA StyleYang, Y., Du, B., Huang, J., Lei, Z., Xu, F., Sun, Q., Wei, P., & Wang, D. (2024). Numerical Analysis of Thermal Flow Dynamics of Arc Plasma and Molten Pool in Hollow Cathode Arc Welding with Oxygen Content. Coatings, 14(4), 382. https://doi.org/10.3390/coatings14040382






