Machine Learning-Based Predictions of Porosity during Cold Spray Deposition of High Entropy Alloy Coatings
Abstract
:1. Introduction
2. Methods
2.1. Data Collection
2.2. Machine Learning
3. Results and Discussion
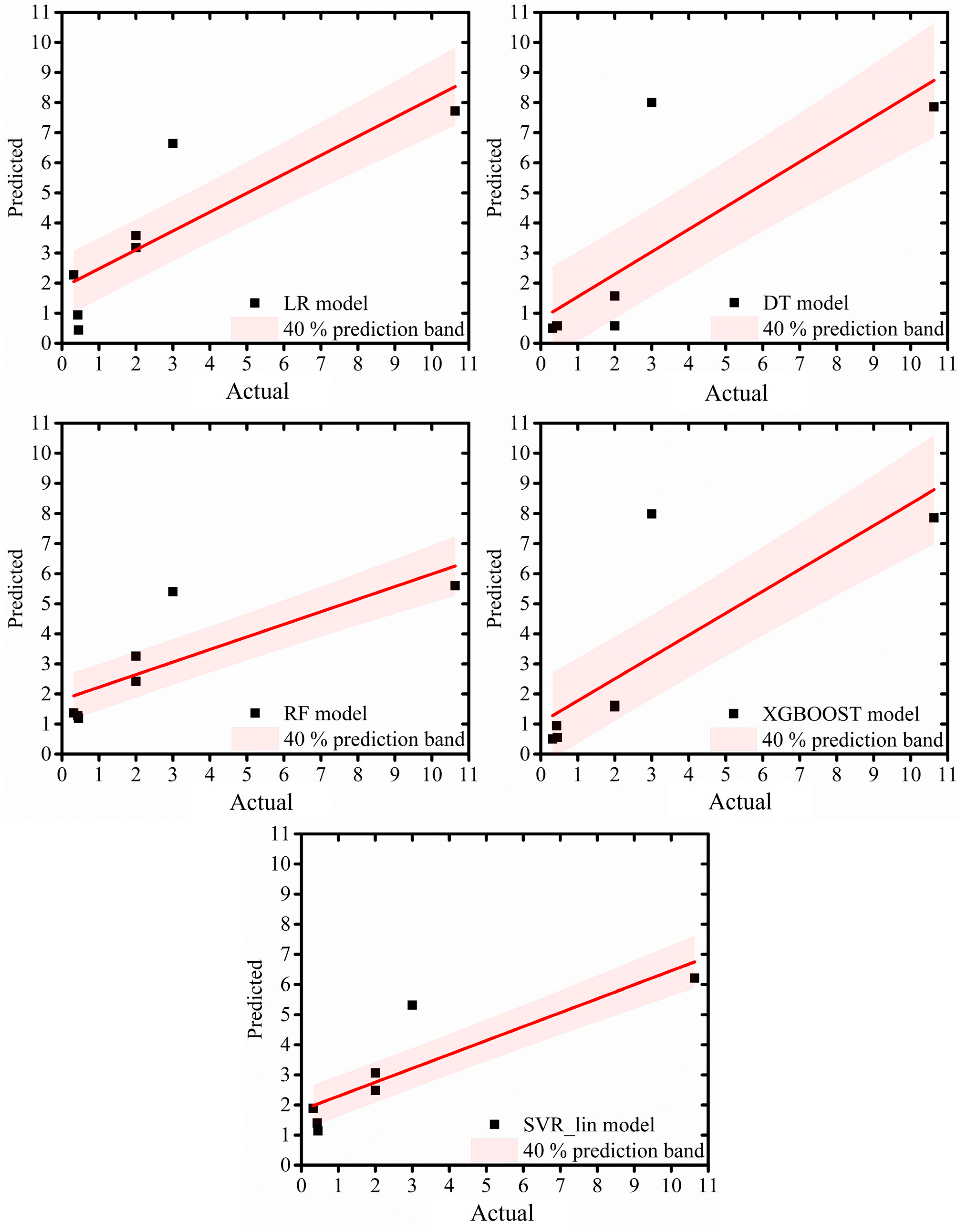
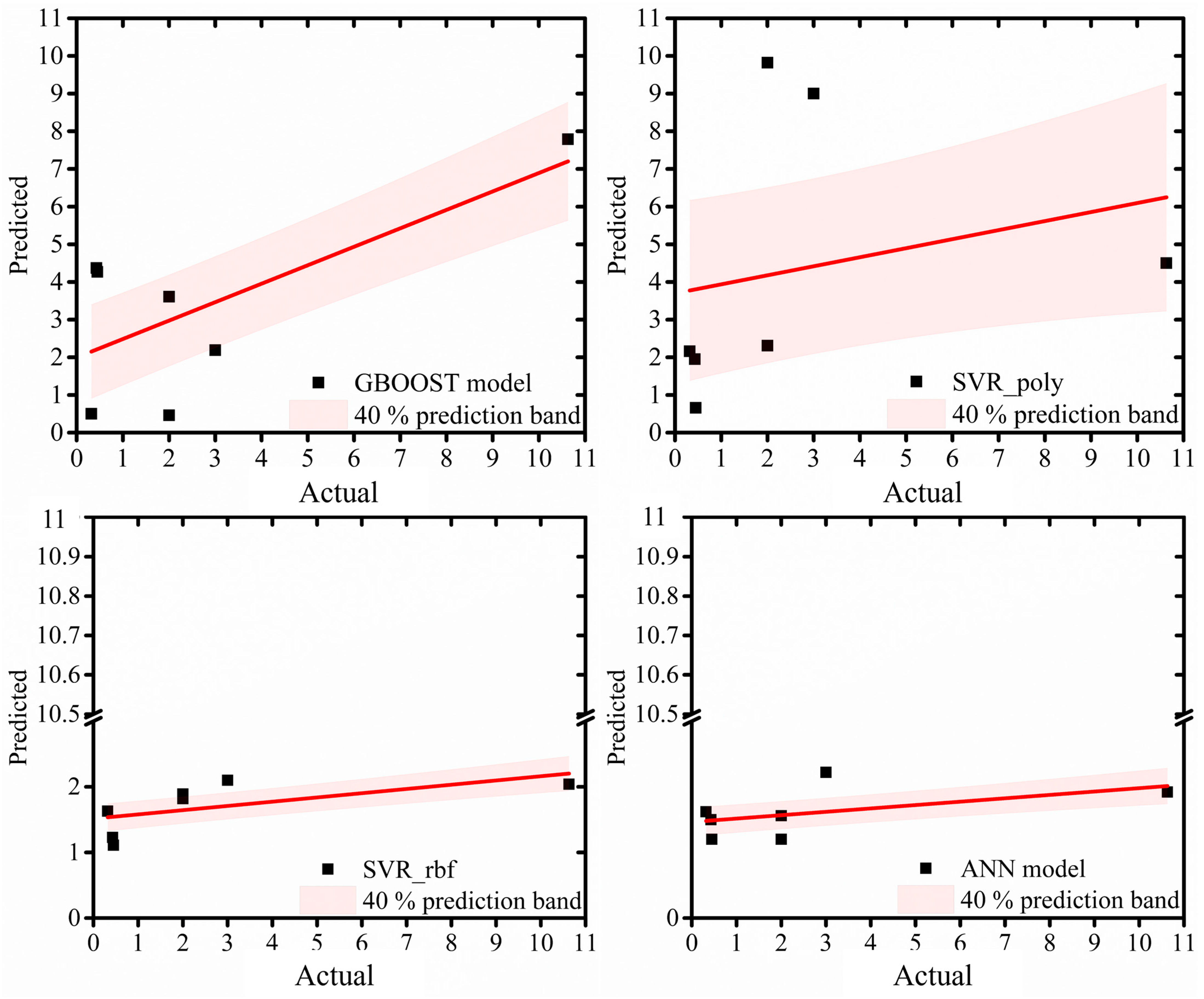
3.1. Performance of All Models
3.2. Hierarchical Impact of Input Features
3.3. Performance of Top Five Models with Top Four Input Features
3.4. Best Models
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Assadi, H.; Kreye, H.; Gärtner, F.; Klassen, T. Cold spraying—A materials perspective. Acta Mater. 2016, 116, 382–407. [Google Scholar] [CrossRef]
- Tam, J.; Yu, B.; Li, W.; Poirier, D.; Legoux, J.G.; Giallonardo, J.D.; Howe, J.; Erb, U. The effect of annealing on trapped copper oxides in particle-particle interfaces of cold-sprayed Cu coatings. Scr. Mater. 2022, 208, 114333. [Google Scholar] [CrossRef]
- Zou, Y. Cold Spray Additive Manufacturing: Microstructure Evolution and Bonding Features. Acc. Mater. Res. 2021, 2, 1071–1081. [Google Scholar] [CrossRef]
- Poza, P.; Garrido-Maneiro, M.Á. Cold-sprayed coatings: Microstructure, mechanical properties, and wear behaviour. Prog. Mater. Sci. 2022, 123, 100839. [Google Scholar] [CrossRef]
- Hassani-Gangaraj, M.; Veysset, D.; Champagne, V.K.; Nelson, K.A.; Schuh, C.A. Adiabatic shear instability is not necessary for adhesion in cold spray. Acta Mater. 2018, 158, 430–439. [Google Scholar] [CrossRef]
- Weiller, S.; Delloro, F. A numerical study of pore formation mechanisms in aluminium cold spray coatings. Addit. Manuf. 2022, 60, 103193. [Google Scholar] [CrossRef]
- Oladijo, O.P.; Obadele, B.A.; Venter, A.M.; Cornish, L.A. Investigating the Effect of Porosity on Corrosion Resistance and Hardness of WC-Co Coatings on Metal Substrates. Afr. Corros. J. 2016, 2, 37–44. [Google Scholar]
- Alonso, L.; Poza, P. A study of the parameters affecting the particle velocity in cold-spray: Theoretical results and comparison with experimental data. Addit. Manuf. 2023, 67, 103479. [Google Scholar] [CrossRef]
- Satish, V.; Johnson, K.W.; Ozdemir, O.C.; Crawford, G.A. Influence of feedstock powder and cold spray processing parameters on microstructure and mechanical properties of Ti-6Al-4V cold spray depositions. Surf. Coat. Technol. 2018, 335, 1–12. [Google Scholar]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Zeng, Z.; Xiang, M.; Zhang, D.; Shi, J.; Wang, W.; Tang, X.; Tang, W.; Wang, Y.; Ma, X.; Chen, Z.; et al. Mechanical properties of Cantor alloys driven by additional elements: A review. J. Mater. Res. Technol. 2021, 15, 1920–1934. [Google Scholar] [CrossRef]
- Chen, T.K.; Shun, T.T.; Yeh, J.W.; Wong, M.S. Nanostructured nitride films of multi-element high-entropy alloys by reactive DC sputtering. Surf. Coat. Technol. 2004, 188–189, 193–200. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A. 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Akisin, C.J.; Dovgyy, B.; Bennett, C.J.; Pham, M.S.; Venturi, F.; Hussain, T. Microstructural Study of Cold-Sprayed CoCrFeNiMn High Entropy Alloy. J. Therm. Spray Technol. 2023, 32, 2539–2562. [Google Scholar] [CrossRef]
- Ahn, J.E.; Kim, Y.K.; Yoon, S.H.; Lee, K.A. Tuning the Microstructure and Mechanical Properties of Cold Sprayed Equiatomic CoCrFeMnNi High-Entropy Alloy Coating Layer. Met. Mater. Int. 2021, 27, 2406–2415. [Google Scholar] [CrossRef]
- Xu, Y.; Li, W.; Qu, L.; Yang, X.; Song, B.; Lupoi, R.; Yin, S. Solid-state cold spraying of FeCoCrNiMn high-entropy alloy: An insight into microstructure evolution and oxidation behavior at 700–900 °C. J. Mater. Sci. Technol. 2021, 68, 172–183. [Google Scholar] [CrossRef]
- Silvello, A.; Cavaliere, P.; Yin, S.; Lupoi, R.; Garcia Cano, I.; Dosta, S. Microstructural, Mechanical and Wear Behavior of HVOF and Cold-Sprayed High-Entropy Alloys (HEAs) Coatings. J. Therm. Spray Technol. 2022, 31, 1184–1206. [Google Scholar] [CrossRef]
- Cavaliere, P.; Perrone, A.; Silvello, A.; Laska, A.; Blasi, G.; Cano, I.G. Fatigue Bending of V-Notched Cold-Sprayed FeCoCrNiMn Coatings. Metals 2022, 12, 780. [Google Scholar] [CrossRef]
- Feng, S.; Guan, S.; Story, W.A.; Ren, J.; Zhang, S.; Te, A.; Gleason, M.A.; Heelan, J.; Walde, C.; Birt, A.; et al. Cold Spray Additive Manufacturing of CoCrFeNiMn High-Entropy Alloy: Process Development, Microstructure, and Mechanical Properties. J. Therm. Spray Technol. 2022, 31, 1222–1231. [Google Scholar] [CrossRef]
- Wu, D.; Xu, Y.; Li, W.; Yang, Y.; Liu, K.; Wan, W.; Qi, Z. Process optimisation of cold spray additive manufacturing of FeCoNiCrMn high-entropy alloy. Sci. Technol. Weld. Join. 2023, 8, 540–547. [Google Scholar] [CrossRef]
- Yang, C.; Ren, C.; Jia, Y.; Wang, G.; Li, M.; Lu, W. A machine learning-based alloy design system to facilitate the rational design of high entropy alloys with enhanced hardness. Acta Mater. 2022, 222, 117431. [Google Scholar] [CrossRef]
- Sai, N.J.; Rathore, P.; Chauhan, A. Machine learning-based predictions of fatigue life for multi-principal element alloys. Scr. Mater. 2023, 226, 115214. [Google Scholar] [CrossRef]
- Wieczerzak, K.; Groetsch, A.; Pajor, K.; Jain, M.; Müller, A.M.; Vockenhuber, C.; Schwiedrzik, J.; Sharma, A.; Klimashin, F.F.; Michler, J. Unlocking the potential of CuAgZr metallic glasses: A comprehensive exploration with combinatorial synthesis, high-throughput characterization, and machine learning. Adv. Sci. 2023, 10, 2302997. [Google Scholar] [CrossRef] [PubMed]
- Chollet, F. Deep Learning with Python; Manning Shelter Island: New York, NY, USA, 2021. [Google Scholar]
- Roy, S.; Ravi, K. A Machine Learning Based Approach for Cold Spray Deposition Porosity Prediction from Processing Parameters. In Proceedings of the Thermal Spray 2022: Proceedings from the International Thermal Spray Conference, Vienna, Austria, 4–6 May 2022; pp. 961–976. [Google Scholar]
- Liu, M.; Yu, Z.; Zhang, Y.; Wu, H.; Liao, H.; Deng, S. Prediction and analysis of high velocity oxy fuel (HVOF) sprayed coating using artificial neural network. Surf. Coat. Technol. 2019, 378, 124988. [Google Scholar] [CrossRef]
- Fukumoto, M.; Wada, Y.; Umemoto, M.; Okane, I. Effect of connected pores on the corrosion behavior of plasma sprayed alumina coatings. Surf. Coat. Technol. 1989, 39–40, 711–720. [Google Scholar] [CrossRef]
- Hansson, C.M. The impact of corrosion on society. Metall. Mater. Trans. A 2011, 42, 2952–2962. [Google Scholar] [CrossRef]
- Gallagher, J. The importance of being porous. Nat. Energy 2019, 4, 630. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. Historical commentary NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Muller, A.C.; Guido, S. Introduction to Machine Learning with Python: A Guide for Data Scientists; O’Reilly Media: Sebastopol, CA, USA, 2016. [Google Scholar]
- Sarker, I.H. Deep Learning: A Comprehensive Overview on Techniques, Taxonomy, Applications and Research Directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef]
- Gramegna, A.; Giudici, P. SHAP and LIME: An Evaluation of Discriminative Power in Credit Risk. Front. Artif. Intell. 2021, 4, 752558. [Google Scholar] [CrossRef]
- Silvello, A.; Cavaliere, P.D.; Albaladejo, V.; Martos, A.; Dosta, S.; Cano, I.G. Powder properties and processing conditions affecting cold spray deposition. Coatings 2020, 10, 91. [Google Scholar] [CrossRef]
- Villafuerte, J. Modern Cold Spray Materials, Process, and Applications; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Zahiri, S.H.; Fraser, D.; Gulizia, S.; Jahedi, M. Effect of processing conditions on porosity formation in cold gas dynamic spraying of copper. J. Therm. Spray Technol. 2006, 15, 422–430. [Google Scholar] [CrossRef]
- Gilmore, D.L.; Dykhuizen, R.C.; Neiser, R.A.; Roemer, T.J.; Smith, M.F. Particle velocity and deposition efficiency in the cold spray process. J. Therm. Spray Technol. 1999, 8, 576–582. [Google Scholar] [CrossRef]
- Zhan, Z.; Li, H. Machine learning based fatigue life prediction with effects of additive manufacturing process parameters for printed SS 316L. Int. J. Fatigue 2021, 142, 105941. [Google Scholar] [CrossRef]
- Tan, A.W.Y.; Sun, W.; Phang, Y.P.; Dai, M.; Marinescu, I.; Dong, Z.; Liu, E. Effects of traverse scanning speed of spray nozzle on the microstructure and mechanical properties of cold-sprayed Ti6Al4V coatings. J. Therm. Spray Technol. 2017, 26, 1484–1497. [Google Scholar] [CrossRef]
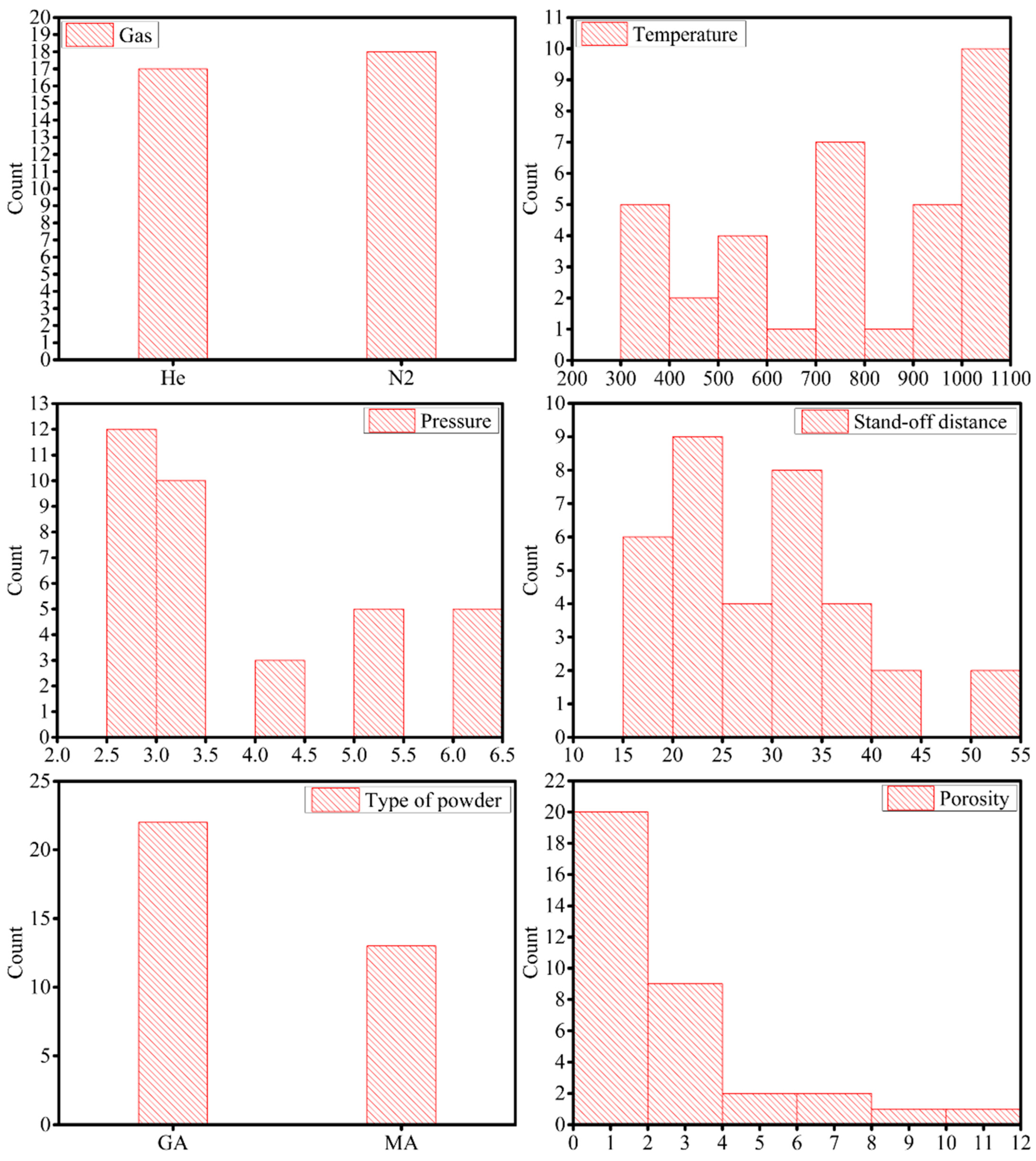



| S. no. | Gas | Temperature (°C) | Pressure (MPa) | Stand-Off Distance (mm) | Type of Powder | Porosity (%) | Reference |
|---|---|---|---|---|---|---|---|
| From the literature | |||||||
| 1 | He | 300 | 3.0 | 30 | GA | 0.32 | [15] |
| 2 | He | 300 | 3.0 | 30 | GA | 0.5 | [16] |
| 3 | He | 400 | 3.0 | 20 | GA | 1.20 | [19] |
| 4 | He | 500 | 3.0 | 20 | GA | 1.11 | [19] |
| 5 | He | 600 | 3.0 | 20 | GA | 0.85 | [19] |
| 6 | He | 700 | 3.0 | 20 | GA | 0.58 | [19] |
| 7 | He | 800 | 3.0 | 20 | GA | 0.66 | [19] |
| 8 | N2 | 1000 | 5.0 | 30 | GA | 8.0 | [17] |
| 9 | N2 | 1000 | 6.0 | 30 | GA | 3.0 | [17] |
| 10 | N2 | 700 | 2.5 | 15 | GA | 7.86 | [20] |
| 11 | N2 | 700 | 2.5 | 25 | GA | 10.63 | [20] |
| 12 | N2 | 700 | 2.5 | 35 | GA | 6.35 | [20] |
| 13 | He | 300 | 2.5 | 15 | GA | 1.01 | [20] |
| 14 | He | 500 | 2.5 | 15 | GA | 0.74 | [20] |
| 15 | He | 700 | 2.5 | 15 | GA | 0.45 | [20] |
| 16 | He | 300 | 2.5 | 25 | GA | 1.76 | [20] |
| 17 | He | 500 | 2.5 | 25 | GA | 1.46 | [20] |
| 18 | He | 700 | 2.5 | 25 | GA | 0.43 | [20] |
| 19 | He | 300 | 2.5 | 35 | GA | 5.67 | [20] |
| 20 | He | 500 | 2.5 | 35 | GA | 1.77 | [20] |
| 21 | He | 700 | 2.5 | 35 | GA | 0.77 | [20] |
| 22 | He | 400 | 3.3 | 20 | GA | 2.4 | [14] |
| From experiments | |||||||
| 23 | N2 | 1000 | 3.0 | 15 | MA | 2.1 | |
| 24 | N2 | 1000 | 3.0 | 50 | MA | 2 | |
| 25 | N2 | 1000 | 6.0 | 15 | MA | 2.2 | |
| 26 | N2 | 1000 | 6.0 | 50 | MA | 2 | |
| 27 | N2 | 900 | 4.0 | 20 | MA | 1.63 | |
| 28 | N2 | 900 | 5.0 | 30 | MA | 2.9 | |
| 29 | N2 | 900 | 5.0 | 30 | MA | 2.89 | |
| 30 | N2 | 900 | 4.0 | 40 | MA | 5.53 | |
| 31 | N2 | 1000 | 6.0 | 30 | MA | 0.82 | |
| 32 | N2 | 1000 | 5.0 | 40 | MA | 1.57 | |
| 33 | N2 | 1000 | 4.0 | 30 | MA | 1.78 | |
| 34 | N2 | 1000 | 5.0 | 20 | MA | 2.41 | |
| 35 | N2 | 900 | 6.0 | 20 | MA | 1.27 | |
| ML Model | |||
|---|---|---|---|
| LR | 0.056 | 2.73 | 3.49 |
| DT | 0.3 | 2.16 | 3.58 |
| RF | −0.018 | 2.38 | 3.41 |
| GBOOST | 0.29 | 3.21 | 4.23 |
| XGBOOST | NAN | 2.24 | 3.38 |
| SVR_lin | −0.02 | 2.24 | 3.5 |
| SVR_poly | −0.078 | 5.73 | 8.211 |
| SVR_rbf | −0.35 | 2.02 | 3.63 |
| ANN | −0.02 | 2.21 | 3.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, D.; Boruah, D.; Bakir, A.A.; Ameen, A.; Paul, S. Machine Learning-Based Predictions of Porosity during Cold Spray Deposition of High Entropy Alloy Coatings. Coatings 2024, 14, 404. https://doi.org/10.3390/coatings14040404
Sharma D, Boruah D, Bakir AA, Ameen A, Paul S. Machine Learning-Based Predictions of Porosity during Cold Spray Deposition of High Entropy Alloy Coatings. Coatings. 2024; 14(4):404. https://doi.org/10.3390/coatings14040404
Chicago/Turabian StyleSharma, Deepak, Dibakor Boruah, Ali Alperen Bakir, Ahamed Ameen, and Shiladitya Paul. 2024. "Machine Learning-Based Predictions of Porosity during Cold Spray Deposition of High Entropy Alloy Coatings" Coatings 14, no. 4: 404. https://doi.org/10.3390/coatings14040404
APA StyleSharma, D., Boruah, D., Bakir, A. A., Ameen, A., & Paul, S. (2024). Machine Learning-Based Predictions of Porosity during Cold Spray Deposition of High Entropy Alloy Coatings. Coatings, 14(4), 404. https://doi.org/10.3390/coatings14040404








