Comparison of Fatigue Properties of Porous Polyurethane and Porous Asphalt Mixtures Considering the Influence of Immersion Conditions
Abstract
1. Introduction
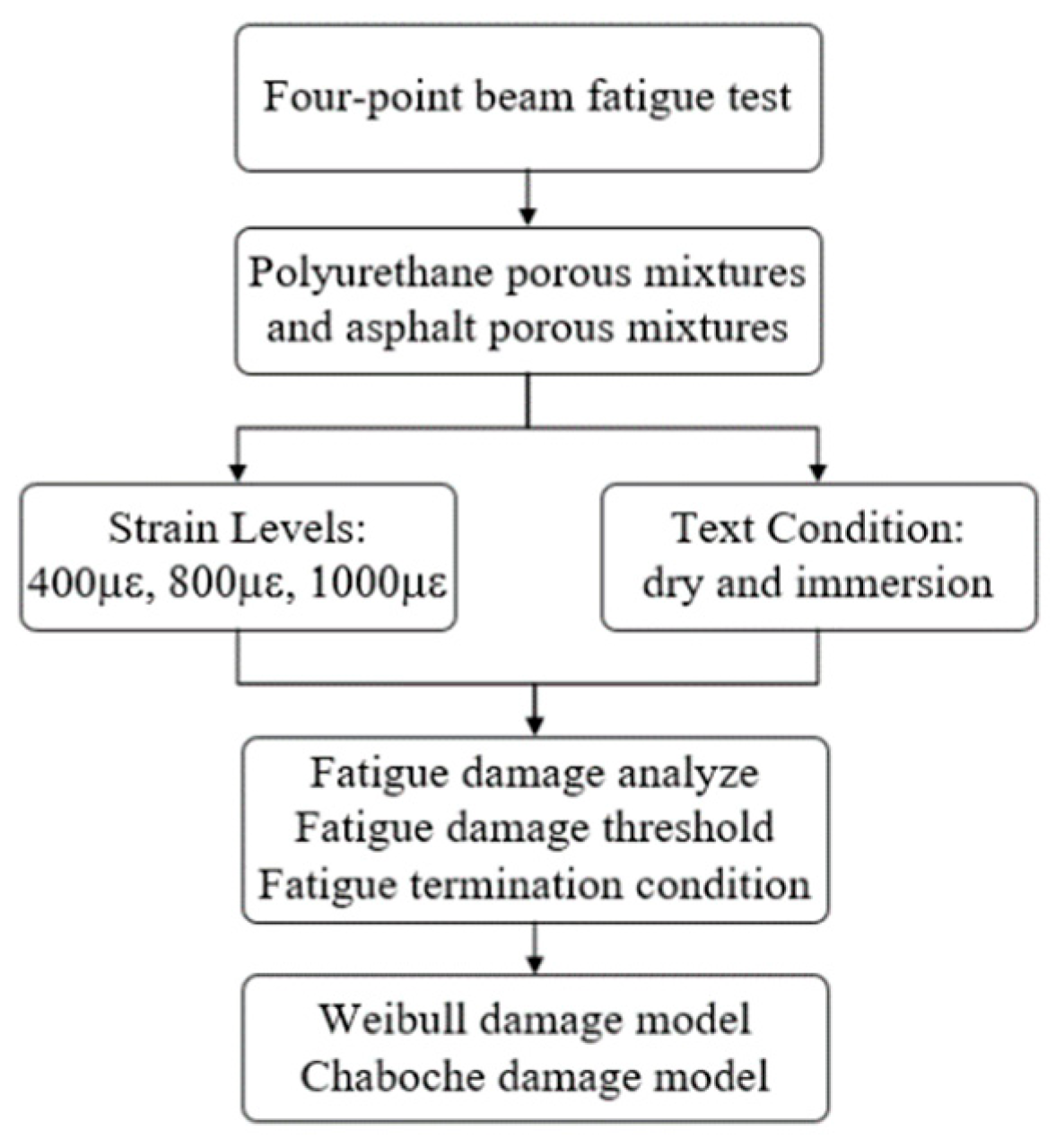
2. Objectives and Scope
3. Materials and Methods
3.1. Materials
3.2. Methods
4. Results and Discussion
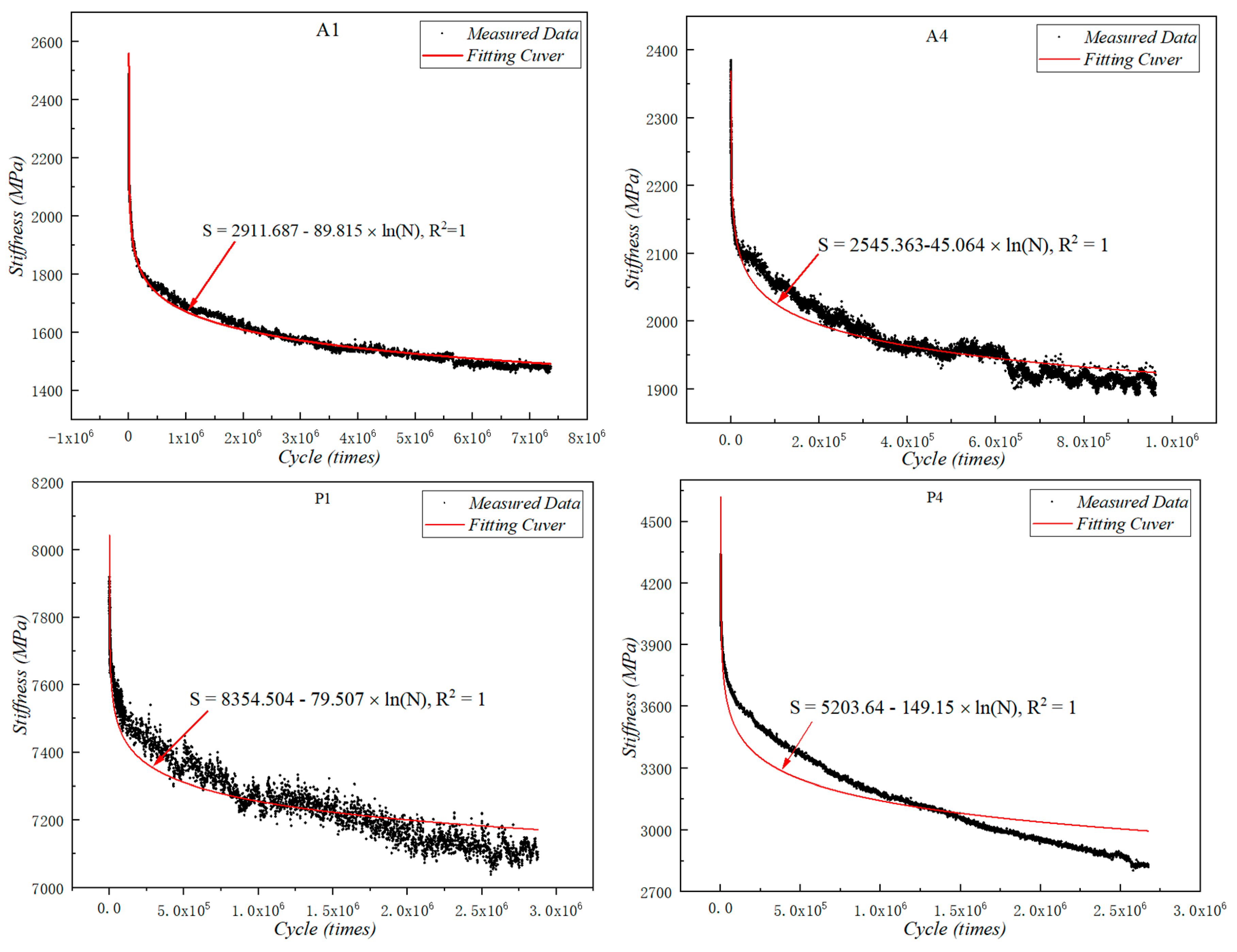
4.1. Analysis of the Initial Stiffness and Fatigue Life
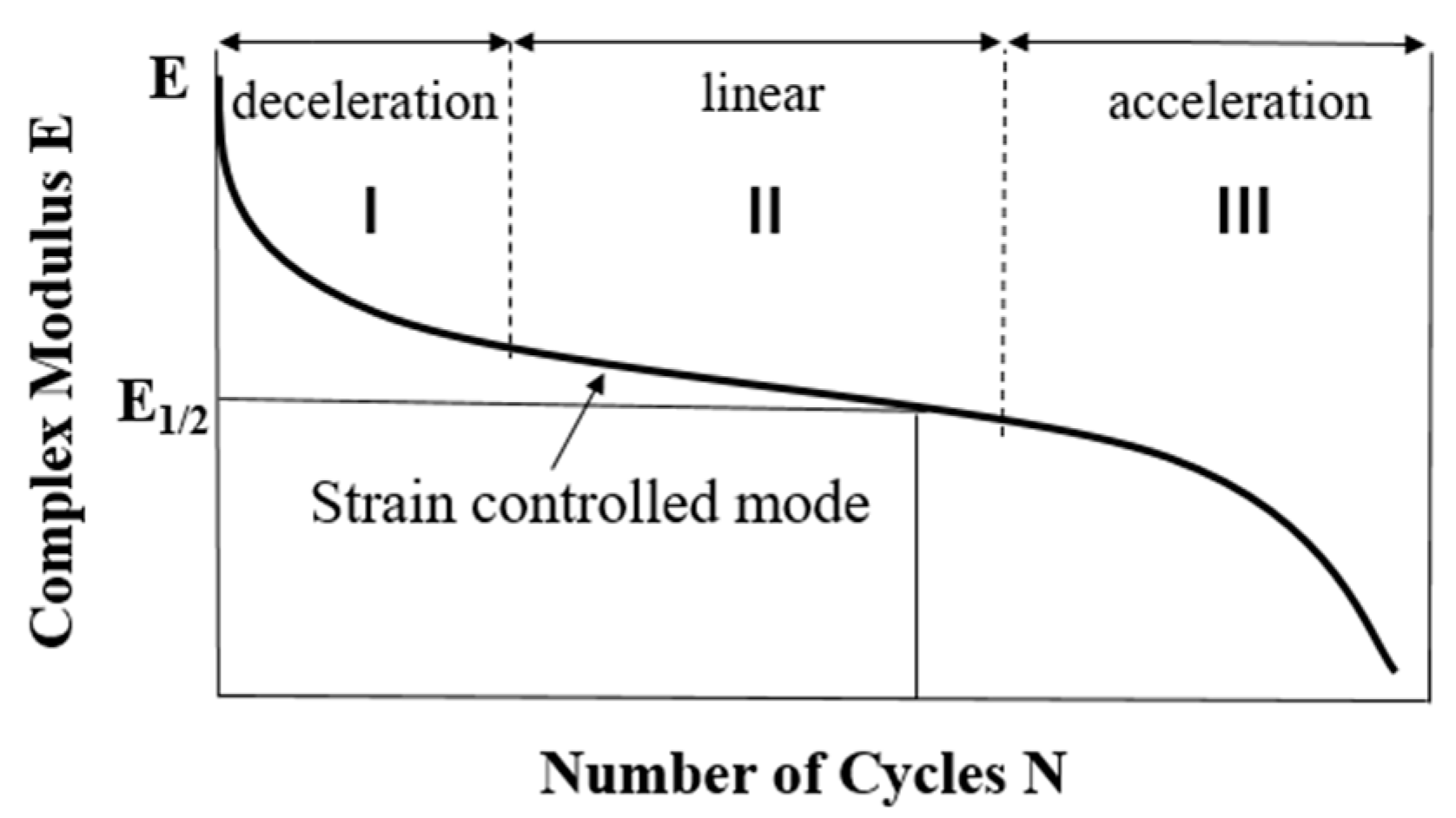
4.2. Analysis of the Fatigue Characteristics
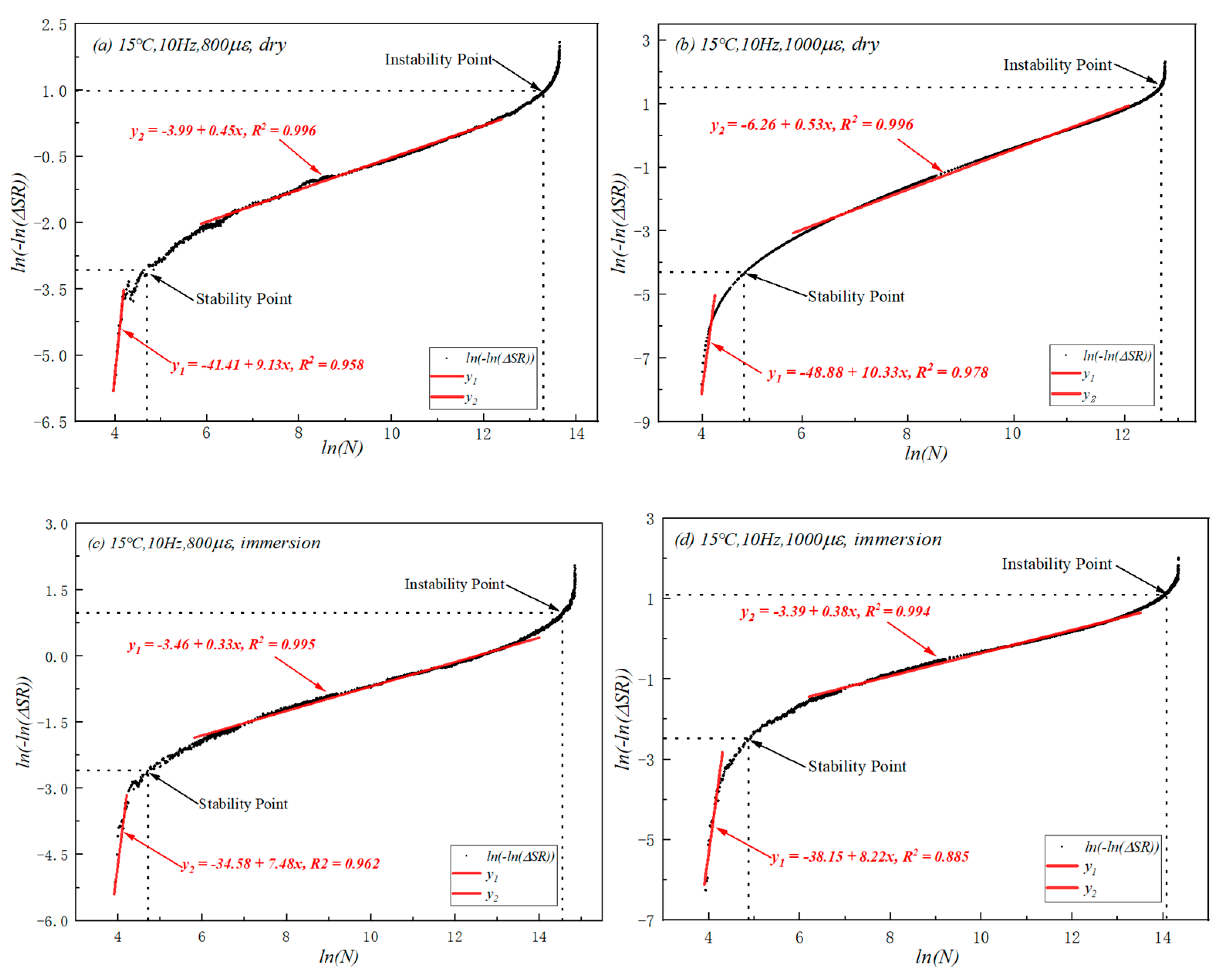
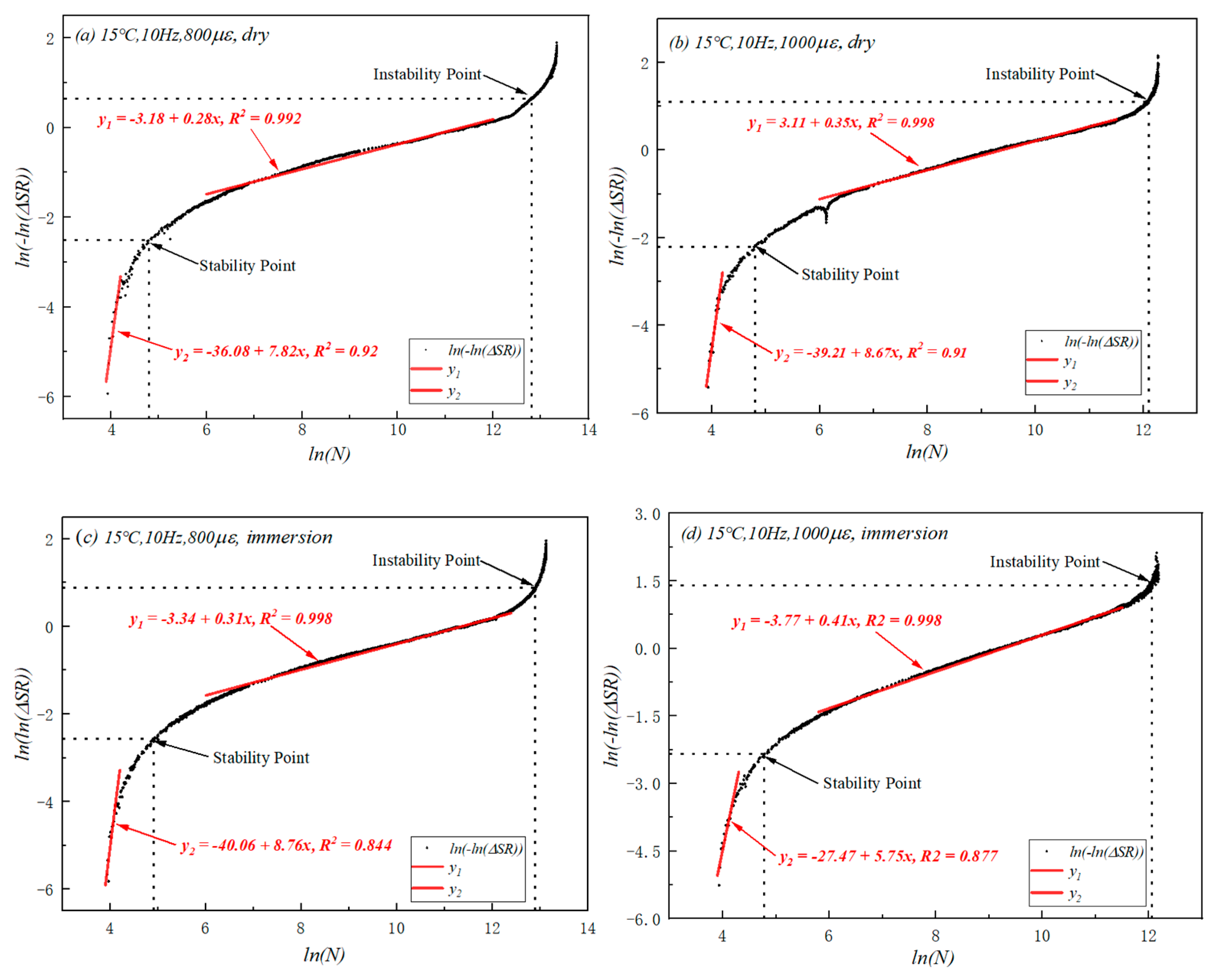
4.2.1. Introduction of Fatigue Damage and Weibull Distribution Function
4.2.2. The Analysis of Fatigue Damage Using the Weibull Distribution Function
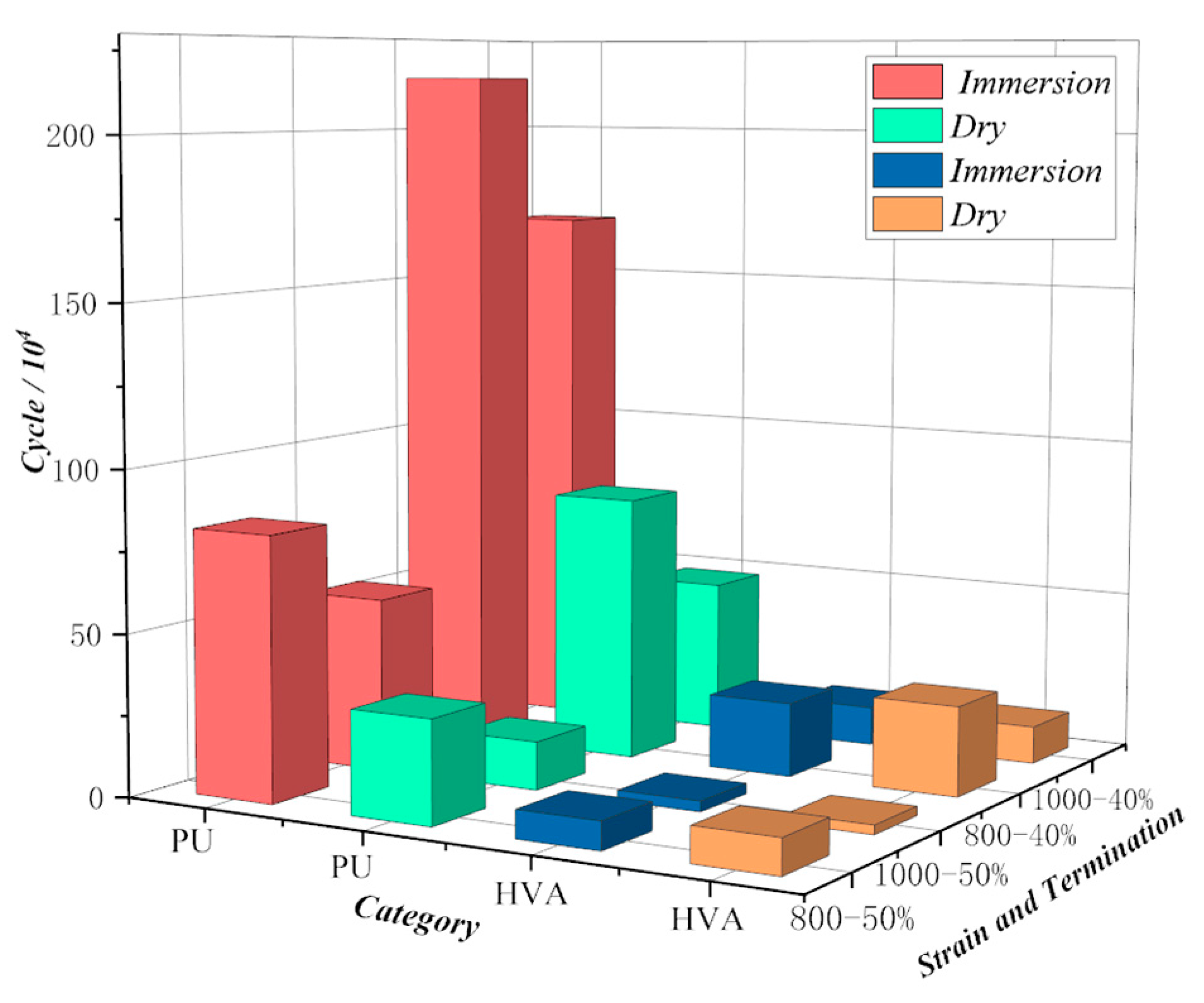
4.3. The Analysis of the Fatigue Threshold Using the Weibull Distribution Function
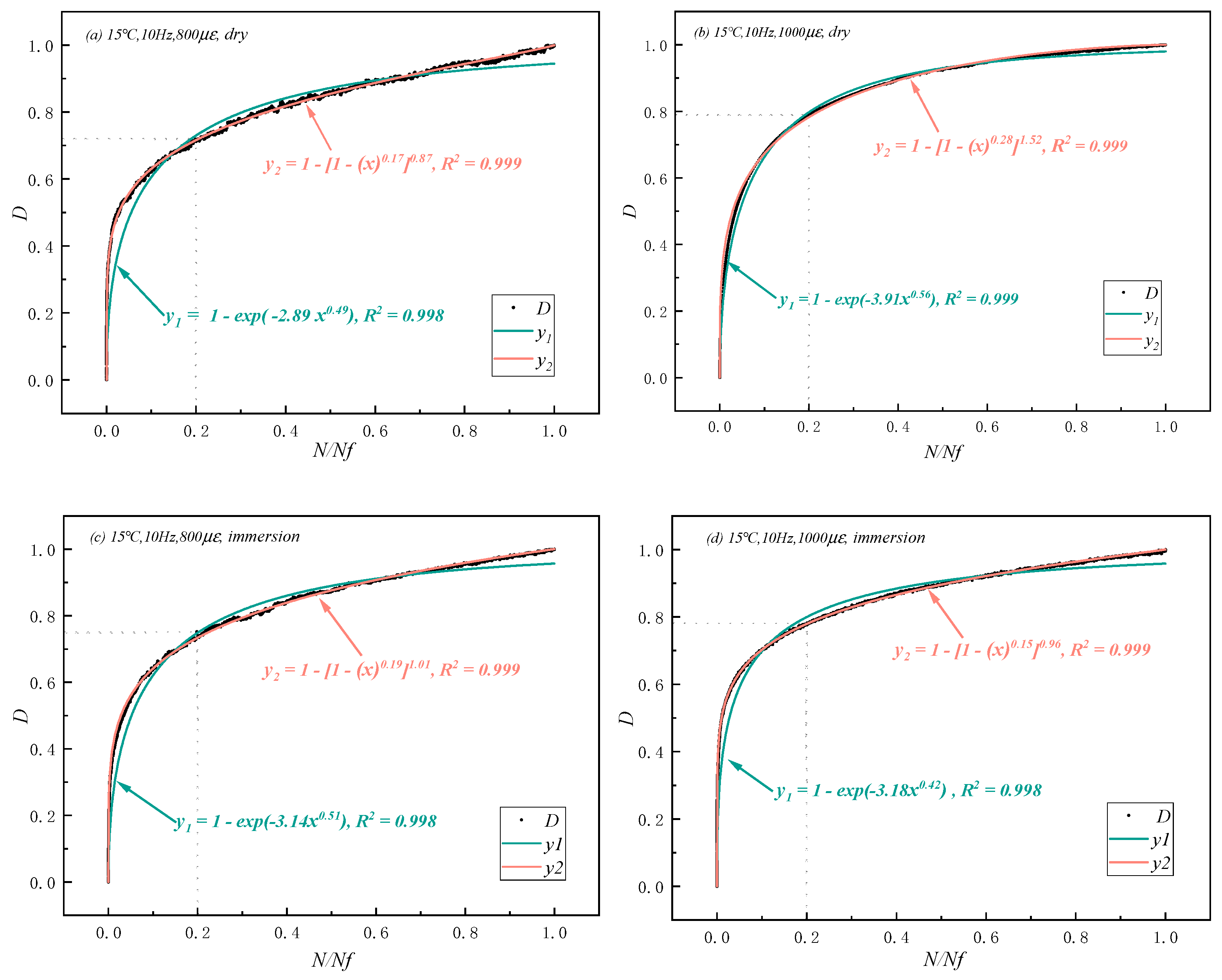
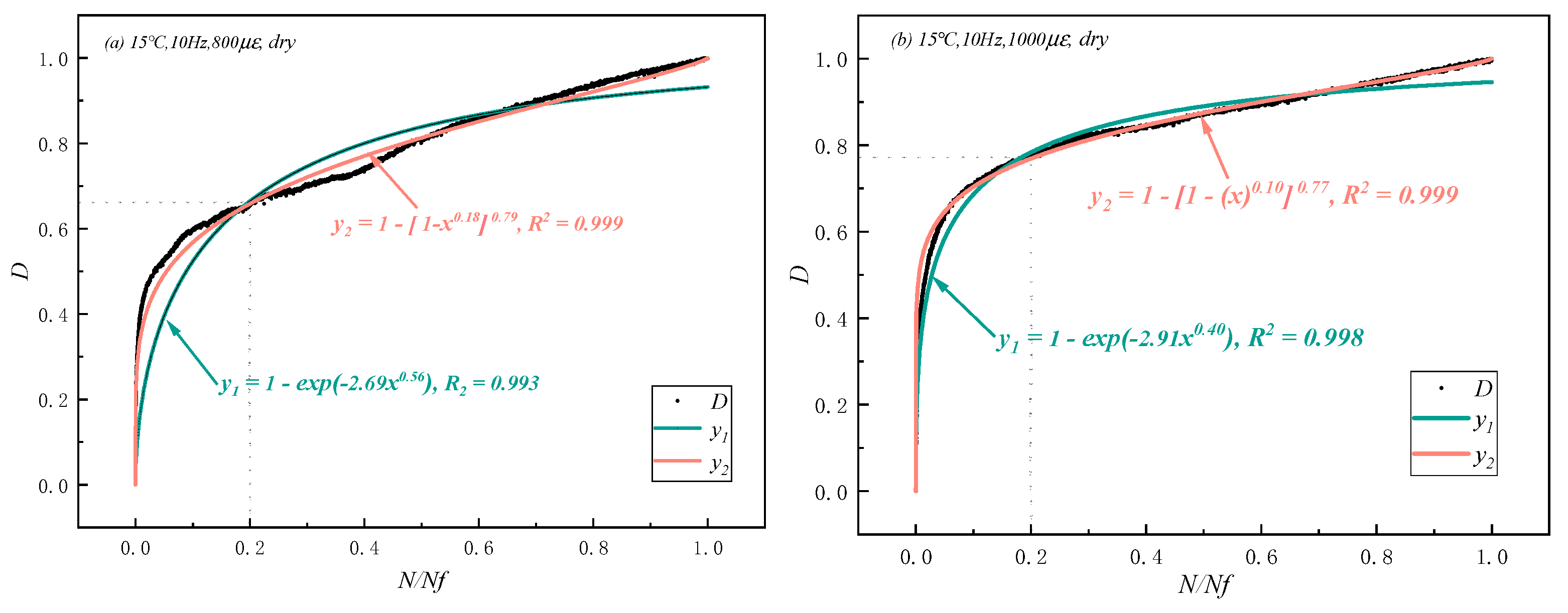
4.4. Comparison of Fatigue Damage Function
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hong, B.; Xian, G. Ageing of a thermosetting polyurethane and it spultruded carbon fiber plates subjected to sea water immersion. Constr. Build. Mater. 2018, 165, 514–522. [Google Scholar] [CrossRef]
- Lu, G.; Liu, P.; Wang, G.; Tekampe, S. Development of a sustainable pervious pavement material using recycled ceramic aggregate and bio-based polyurethane binder. J. Clean. Prod. 2019, 220, 1052–1060. [Google Scholar] [CrossRef]
- Xu, S.; Xu, M.; Zhang, Y.; Cheng, G. AnIndoor Laboratory Simulation and Evaluation on the Aging Resistance of Polyether Polyurethane Concrete for Bridge Deck Pavement. Front. Mater. 2020, 7, 237. [Google Scholar] [CrossRef]
- Lu, G.; Renken, L.; Li, T.; Wang, D.; Li, H.; Oeser, M. Experimental study on the polyurethane-bound pervious mixture in the application of permeable pavements. Constr. Build. Mater. 2019, 202, 838–850. [Google Scholar] [CrossRef]
- Siddaraju, S. Laboratory investigation of open graded friction course mixes with construction and demolition waste aggregates. In Proceedings of the 5th Colloquiumon Transportation Systems Engineering and Management (CTSEM2018), Hanamkonda, India, 17–19 May 2018. [Google Scholar]
- Alvarez, A.E.; Martin, A.E.; Estakhri, C. A review of mix design and evaluation research for permeable friction course mixture. Constr. Build. Mater. 2011, 25, 1159–1166. [Google Scholar] [CrossRef]
- Shen, W.; Shan, L.; Zhang, T.; Ma, H.; Cai, Z. Investigation on polymer–rubber aggregate modified porousconcrete. Constr. Build. Mater. 2013, 38, 667–674. [Google Scholar] [CrossRef]
- Li, H.; Harvey, J.T.; Holland, T.J.; Kayhanian, M. Corrigendum: The use of reflective and permeable pavements as a potential practice for heat island mitigation and stormwater management. Environ. Res. Lett. 2013, 8, 015023. [Google Scholar] [CrossRef]
- Tennis, P.D.; Leming, M.L.; Akers, D.J. Pervious Concrete Pavements. Deten. Basins 2004. [Google Scholar]
- Cong, L.; Wang, T.; Tan, L.; Yuan, J.; Shi, J. Laboratory evaluation on performance of porous polyurethane mixture and OGFC. Constr. Build. Mater. 2018, 169, 436–442. [Google Scholar] [CrossRef]
- Chen, J.; Yin, X.; Wang, H.; Ding, Y. Evaluation of Durability and Functional Performance of Porous Polyurethane Mixture in Porous Pavement. J. Clean. Prod. 2018, 188, S0959652618309788. [Google Scholar] [CrossRef]
- Hong, B.; Lu, G.; Gao, J.; Dong, S.; Wang, D. Green tunnel pavement: Polyurethane ultra-thin friction course and its performance characterization. J. Clean. Prod. 2020, 289, 125131. [Google Scholar] [CrossRef]
- Chen, J.; Ma, X.; Wang, H.; Xie, P.; Huang, W. Experimental study on anti-icing and deicing performance of polyurethane concrete as road surface layer. Constr. Build. Mater. 2018, 161, 598–605. [Google Scholar] [CrossRef]
- Underwood, B.S.; Kim, Y.R.; Guddati, M.N. Improved calculation method of damage parameter in viscoelastic continuum damage model. Int. J. Pavement Eng. 2010, 11, 459–476. [Google Scholar] [CrossRef]
- Wang, Y.; Norouzi, A.; Kim, Y.R. Comparison of Fatigue Cracking Performance of Asphalt Pavements Predicted by Pavement ME and LVECD Programs. Transp. Res. Rec. 2016, 2590, 44–55. [Google Scholar] [CrossRef]
- Wang, Y.; Kim, R.Y. Development of a pseudo strain energy-based fatigue failure criterion for asphalt mixture. Int. J. Pavement Eng. 2019, 20, 1182–1192. [Google Scholar] [CrossRef]
- Bodin, D.; Pijaudier-Cabot, G.; de La Roche, C.; Piau, J.M.; Chabot, A. Continuum Damage Approach to Asphalt Concrete Fatigue Modeling. J. Eng. Mech. 2004, 130, 700–708. [Google Scholar] [CrossRef]
- Hou, T.; Shane Underwood, B.; Richard Kim, Y.; Guddati, M.N. Fatigue Performance Prediction of North Carolina Mixture Using the Simplified Viscoelastic Continuum Damage Model. J. Assoc. Asph. Paving Technol. 2010, 79, 35–79. [Google Scholar]
- Zhang, J.; David Wang, Y.; Su, Y.; Fu, G. Fatigue damage evolution model of asphalt mixture considering influence of loading frequency. Constr. Build. Mater. 2019, 218, 712–720. [Google Scholar] [CrossRef]
- Tsai, B.W.; Harvey, J.T.; Monismith, C.L. Application of Weibull Theory in Prediction of Asphalt Concrete Fatigue Performance. Transp. Res. Rec. 2003, 1832, 121–130. [Google Scholar] [CrossRef]
- Tsai, B.W.; Harvey, J.T.; Monismith, C.L. Using the Three-Stage Weibull Equation and Tree-Based Model to Characterize the Mix Fatigue Damage Process. Transp. Res. Rec. 2005, 1929, 227–237. [Google Scholar] [CrossRef]
- Zou, X.; Ding, B.; Peng, Z.; Li, H. Damage analysis four-point bending fatigue tests on stone matrix asphalt using dissipated energy approaches. Int. J. Fatigue 2020, 133, 105453. [Google Scholar] [CrossRef]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. J. Eng. Mater. Technol. -Trans. ASME 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Chaboche, J.-L. Continuum damage mechanics: Part I—General concepts. J. Appl. Mech. 1988, 55, 59–64. [Google Scholar] [CrossRef]
- Shen, S.H.; Chiu, H.M.; Huang, H. Characterization of Fatigue and Healing in Asphalt Binders. J. Mater. Civ. Eng. 2010, 22, 846–852. [Google Scholar] [CrossRef]
- Anderson, D.A.; Le Hir, Y.M.; Marasteanu, M.O.; Planche, J.P.; Martin, D.; Gauthier, G. Evaluation of fatigue criteria for asphalt binders. Transp. Res. Rec. 2001, 1766, 48–56. [Google Scholar] [CrossRef]
- Mo, L.T. Damage development in the adhesive zone and mortar of porous asphalt concrete. Astron. Data Anal. Softw. Syst. XIX 2010. [Google Scholar] [CrossRef]
- Hagos, E.T. The effect of aging on binder proporties of porous asphalt concrete. Bitum. Pavements 2008. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=b733b501f855bbaa6dd1569a6ed98c1a&site=xueshu_se&hitarticle=1, (accessed on 8 July 2024).
- Mo, L.T.; Huurman, M.; Wu, S.P.; Molenaar, A.A. Bitumen–stone adhesive zone damage model for the meso-mechanical mixture design of ravelling resistant porous asphalt concrete. Int. J. Fatigue 2011, 33, 1490–1503. [Google Scholar] [CrossRef]
- AASHTO T 321-03; Standard Method of Test for Determining the Fatigue Life of Compacted Hot-Mix Asphalt (HMA) Subjected to Repeated Flexural Bending. AASHTO: Washington, DC, USA, 2003.
- Rabotnov, Y.N. On the Equation of State of Creep, Proceedings of the Institution of Mechanical Engineers; SAGE Publications: London, UK, 1963; pp. 117–122. [Google Scholar]
- Lemaitre, J. A Course on Damage Mechanics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Kachanov, L.M. Rupture Time Under Creep Conditions. Int. J. Fract. 1999, 97, 11–18. [Google Scholar] [CrossRef]
- Sudarsanan, N.; Kim, Y.R. A critical review of the fatigue life prediction of asphalt mixture and pavements. J. Traffic Transp. Eng. (Engl. Ed.) 2022, 9, 808–835. [Google Scholar] [CrossRef]
- Mannan, U.A.; Islam, R. Tarefder R A.Effects of recycled asphalt pavements on the fatigue life of asphalt under different strain levels and loading frequencies. Int. J. Fatigue 2015, 78, 72–80. [Google Scholar] [CrossRef]
- Ye, Y.; Li, G.; Zhuang, C.; Zhao, S.; Guo, H. Study on fatigue damage evolution and model prediction of asphalt pavement in the end-stage of service. Case Stud. Constr. Mater. 2023, 19, e02377. [Google Scholar] [CrossRef]




| Index | Unit | Result |
|---|---|---|
| Viscosity (25 °C) | Mpa·s | 1708 |
| Dry time (30 °C, 90% RH) | min | 70 |
| Tensile strength | Mpa | 24.1 |
| Breaking elongation | % | 208 |
| Density (15 °C) | g/cm3 | 1.108 |
| Index | Unit | Results | Test Method |
|---|---|---|---|
| Penetration (25 °C, 5 s, 100 g) | 0.1 mm | 46 | T 0604 |
| Ductility (5 °C, 5 cm/min) | cm | 37 | T 0605 |
| Softening point TR&B | °C | 92 | T 0606 |
| Dynamic viscosity (60 °C) | Pa·s | 58,600 | T 0620 |
| Flash point | °C | 358 | T 0611 |
| Density (15 °C) | g/cm3 | 1.065 | T 0603 |
| Number | Category | Strain/με | Immersion | Number | Category | Strain/με | Immersion |
|---|---|---|---|---|---|---|---|
| P1 | PPM | 400 | − | A1 | PAM | 400 | − |
| P2 | 800 | − | A2 | 800 | − | ||
| P3 | 1000 | − | A3 | 1000 | − | ||
| P4 | 400 | + | A4 | 400 | + | ||
| P5 | 800 | + | A5 | 800 | + | ||
| P6 | 1000 | + | A6 | 1000 | + |
| Test Number | Initial Stiffness/(MPa) | 50% Fatigue Life/Times | 40% Fatigue Life/Times | Test Number | Initial Stiffness/(MPa) | 50% Fatigue Life/Times | 40% Fatigue Life/Times |
|---|---|---|---|---|---|---|---|
| P1 | 7860.85 | \ | \ | A1 | 2489.14 | \ | \ |
| P2 | 7258.23 | 320,000 | 830,000 | A2 | 2414.77 | 109,000 | 279,000 |
| P3 | 7086.84 | 150,000 | 325,000 | A3 | 2412.21 | 29000 | 117,000 |
| P4 | 4341.43 | \ | \ | A4 | 2382.47 | \ | \ |
| P5 | 4229.82 | 815,000 | 2,170,000 | A5 | 2469.15 | 87,000 | 231,000 |
| P6 | 3178.85 | 540,000 | 1,690,000 | A6 | 2159.68 | 32,900 | 122,000 |
| Category | Strain/με | Condition | Slope | Category | Strain/με | Condition | Slope | ||
|---|---|---|---|---|---|---|---|---|---|
| Stage 1 | Stage 2 | Stage 1 | Stage 2 | ||||||
| PPM | 800 | dry | 9.13 | 0.45 | PAM | 800 | dry | 7.82 | 0.28 |
| 1000 | dry | 10.33 | 0.53 | 1000 | dry | 8.67 | 0.35 | ||
| 800 | immersion | 7.48 | 0.33 | 800 | immersion | 8.76 | 0.31 | ||
| 1000 | immersion | 8.22 | 0.38 | 1000 | immersion | 5.75 | 0.41 | ||
| Category | Strain/με | Condition | Steady Point (ln(N)) | Instability Point (ln(N)) | Threshold/104 | SR |
|---|---|---|---|---|---|---|
| PPM | 800 | dry | 4.71 | 13.31 | 60.30 | 0.468 |
| 1000 | dry | 4.86 | 12.63 | 30.55 | 0.455 | |
| 800 | immersion | 4.71 | 14.56 | 210.54 | 0.437 | |
| 1000 | immersion | 4.85 | 14.08 | 130.28 | 0.438 | |
| PAM | 800 | dry | 4.86 | 12.82 | 36.95 | 0.417 |
| 1000 | dry | 4.78 | 12.08 | 17.63 | 0.383 | |
| 800 | immersion | 4.91 | 12.93 | 41.25 | 0.397 | |
| 1000 | immersion | 4.81 | 12.05 | 17.11 | 0.395 |
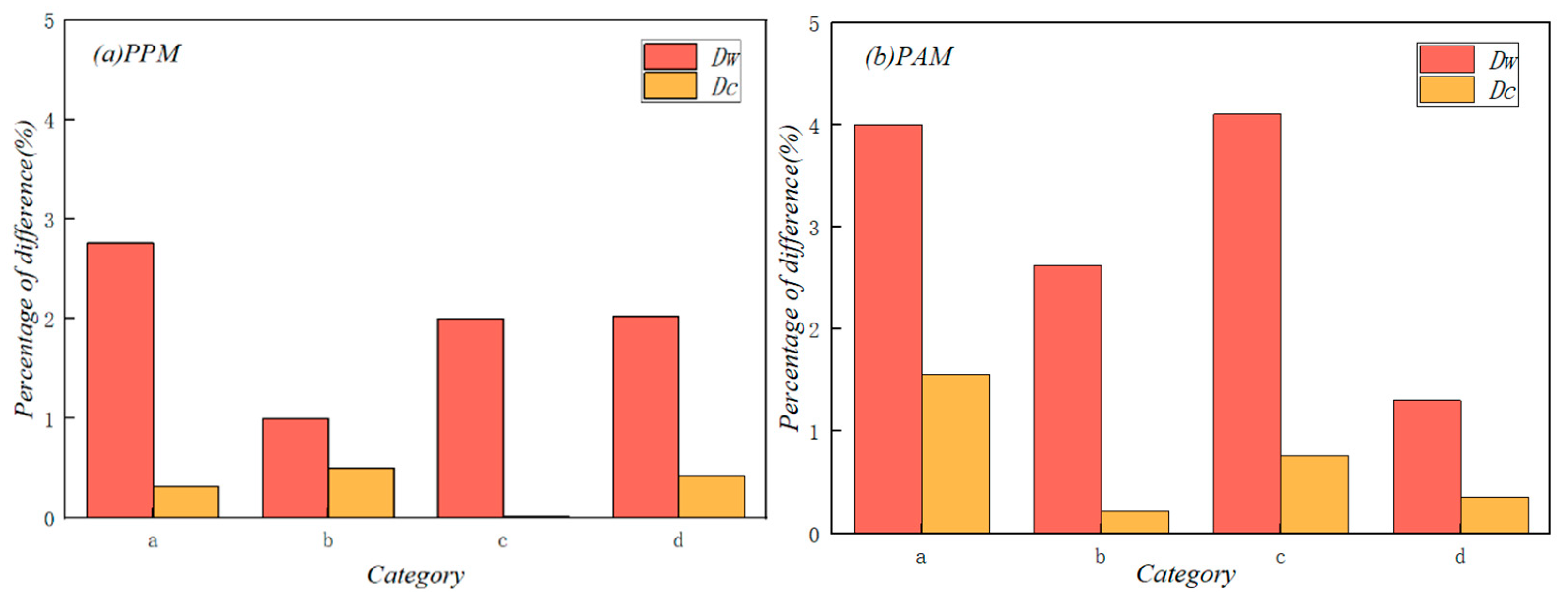
| Test Condition | PPM | PAM | ||
|---|---|---|---|---|
| Dw | Dc | Dw | Dc | |
| a (800 , dry) | 2.76 | 0.32 | 4.00 | 1.56 |
| b (1000 , dry) | 1.00 | 0.5 | 2.62 | 0.22 |
| c (800 , immersion) | 2.00 | 0 | 4.10 | 0.76 |
| d (1000 , immersion) | 2.02 | 0.42 | 1.30 | 0.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Ye, Y.; Zhao, H.; Zhang, Q.; Zhao, S.; Zhuang, C.; Zhang, P. Comparison of Fatigue Properties of Porous Polyurethane and Porous Asphalt Mixtures Considering the Influence of Immersion Conditions. Coatings 2024, 14, 867. https://doi.org/10.3390/coatings14070867
Li G, Ye Y, Zhao H, Zhang Q, Zhao S, Zhuang C, Zhang P. Comparison of Fatigue Properties of Porous Polyurethane and Porous Asphalt Mixtures Considering the Influence of Immersion Conditions. Coatings. 2024; 14(7):867. https://doi.org/10.3390/coatings14070867
Chicago/Turabian StyleLi, Gen, Yali Ye, Haisheng Zhao, Qi Zhang, Shuqian Zhao, Chuanyi Zhuang, and Peiyu Zhang. 2024. "Comparison of Fatigue Properties of Porous Polyurethane and Porous Asphalt Mixtures Considering the Influence of Immersion Conditions" Coatings 14, no. 7: 867. https://doi.org/10.3390/coatings14070867
APA StyleLi, G., Ye, Y., Zhao, H., Zhang, Q., Zhao, S., Zhuang, C., & Zhang, P. (2024). Comparison of Fatigue Properties of Porous Polyurethane and Porous Asphalt Mixtures Considering the Influence of Immersion Conditions. Coatings, 14(7), 867. https://doi.org/10.3390/coatings14070867






