Study on Characterization of Phase Transition in Continuous Cooling of Carbon Steel Using In Situ Thermovoltage Measurement
Abstract
:1. Introduction
2. Experimental Materials and Methods
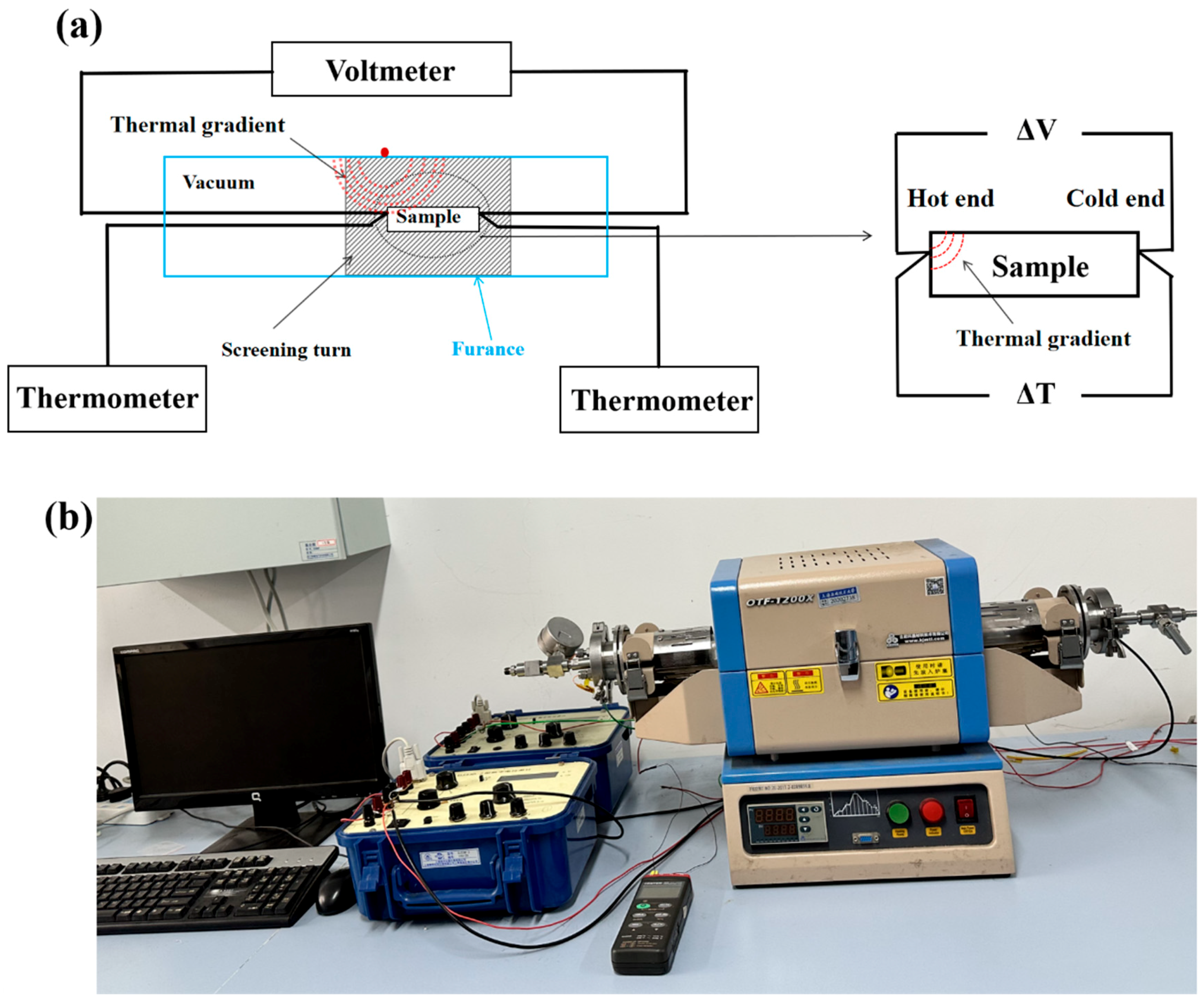
2.1. Principle of Thermovoltage Measurement
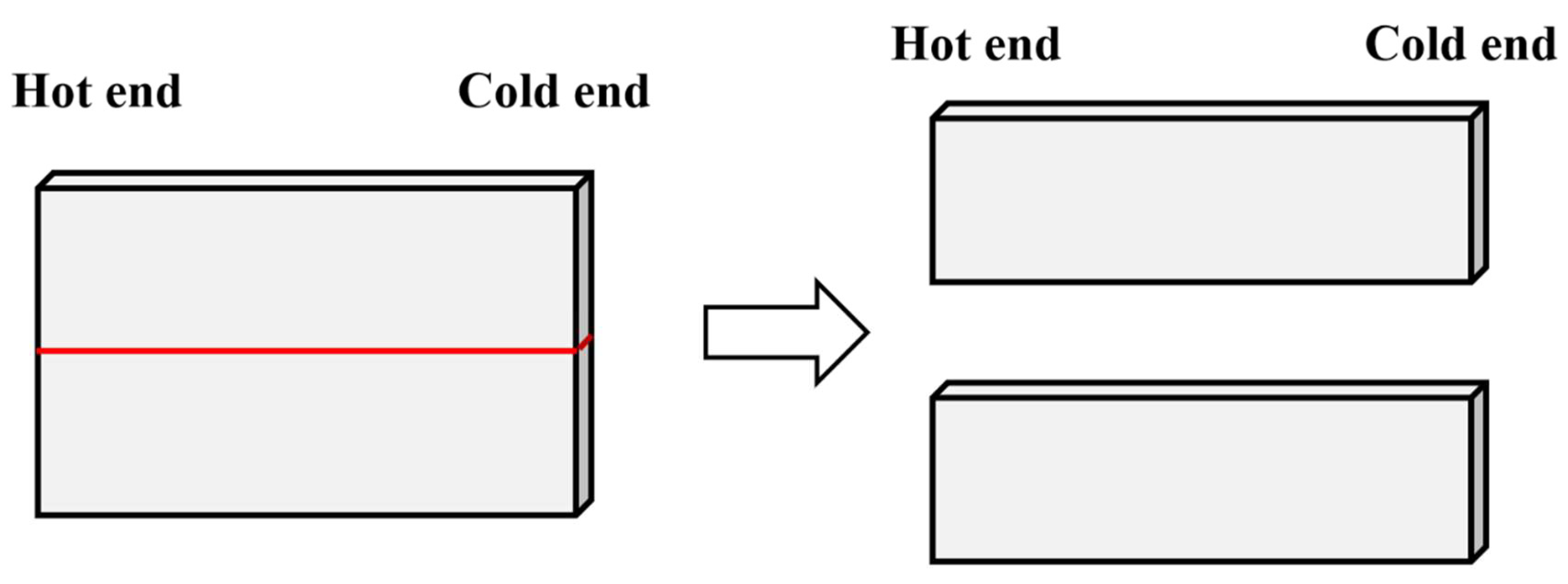
2.2. Experimental Methods
3. Experimental Results and Discussion
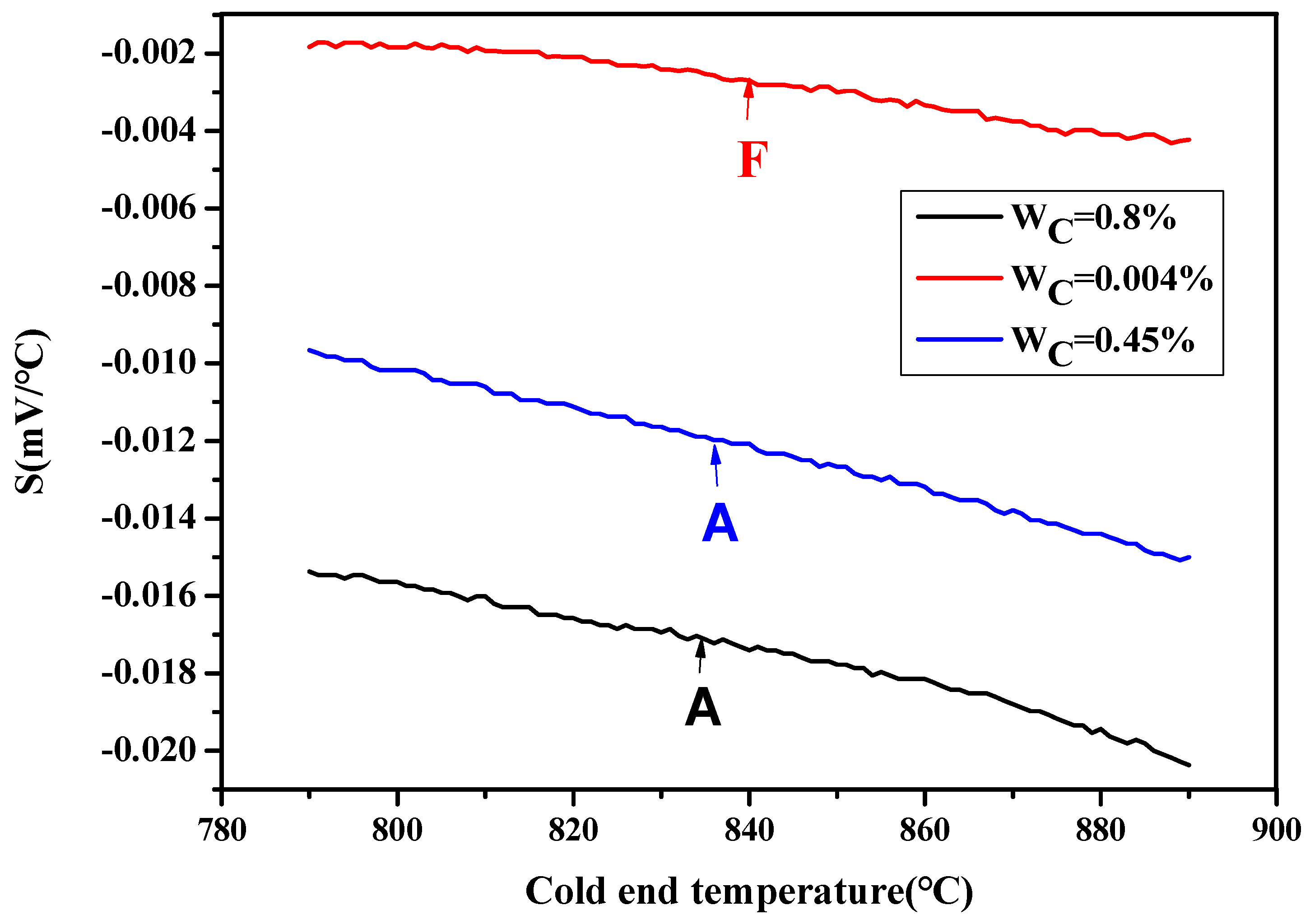
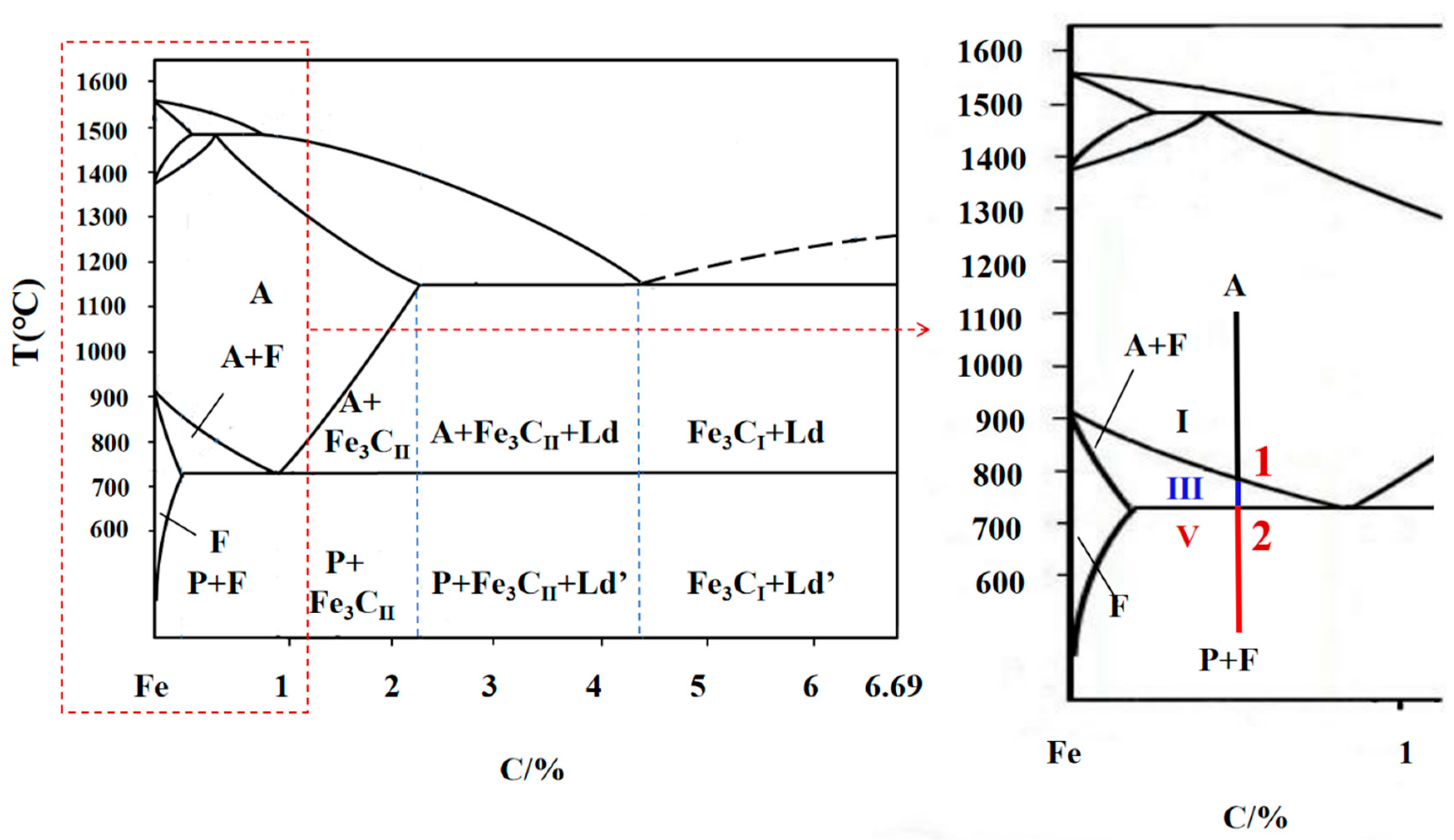
3.1. In Situ Thermovoltage Analysis of Single-Phase Austenite/Ferrite with Different Solid Solution Carbon Contents during Cooling without Transformation
3.2. In Situ Thermovoltage Analyses during Continuous Cooling of 45 Steel
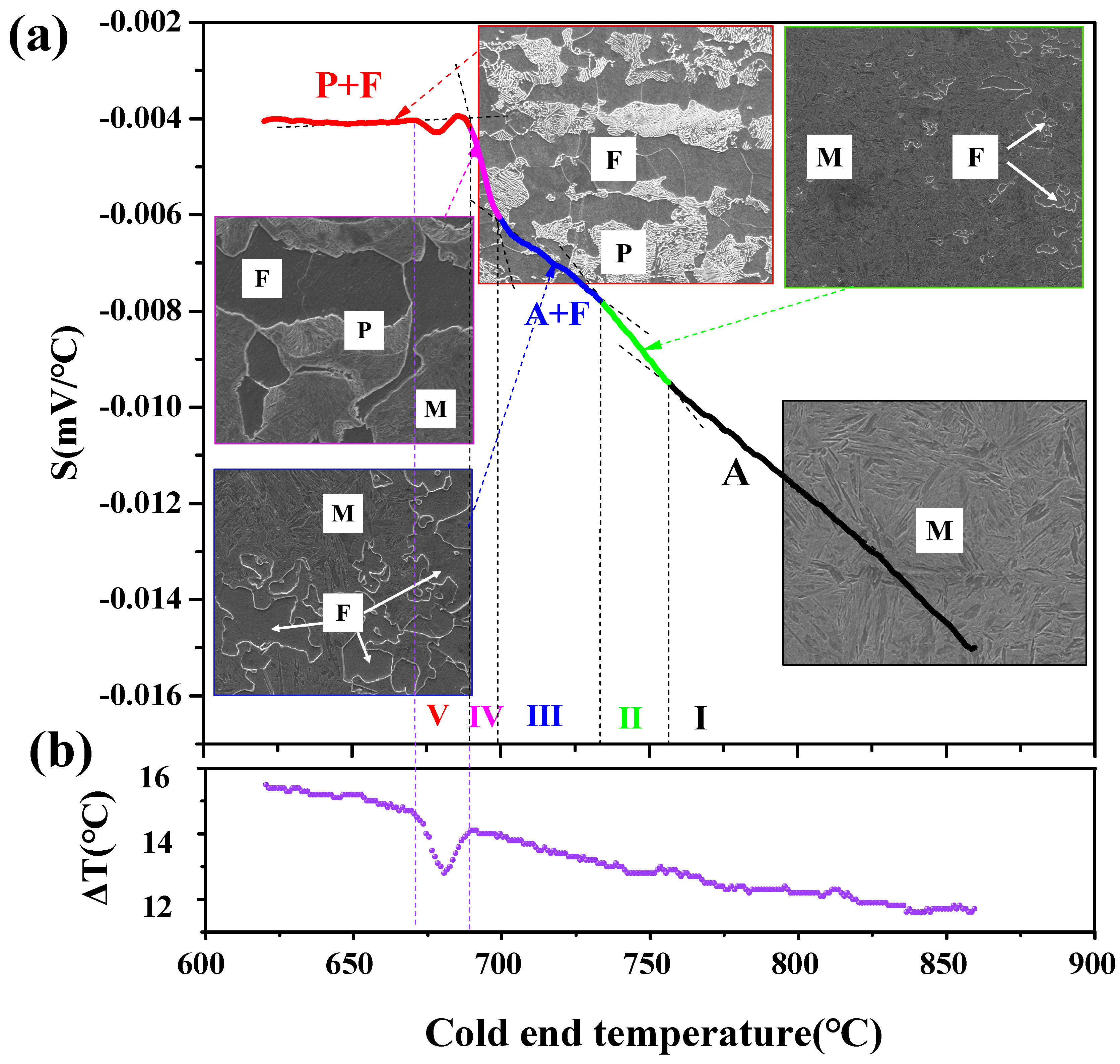
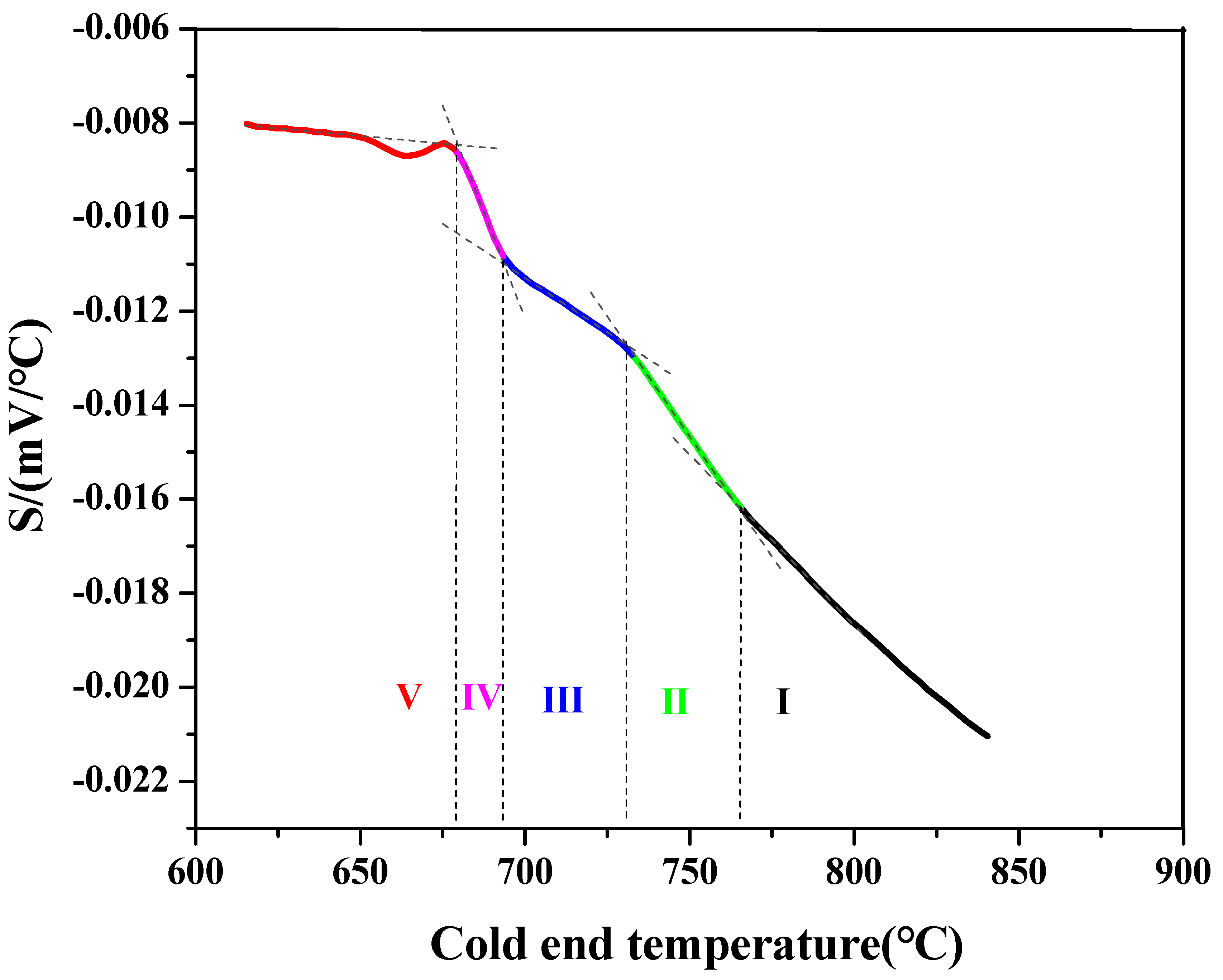
3.2.1. In Situ Thermovoltage Curve and Analyses
- (1)
- In situ thermovoltage curves and analysis during continuous cooling at 0.02 °C/s
- (2)
- Further discussion of the thermovoltage curve in the phase transition region
3.2.2. Comparative Analysis of In Situ Thermovoltage Curves at Different Cooling Rates
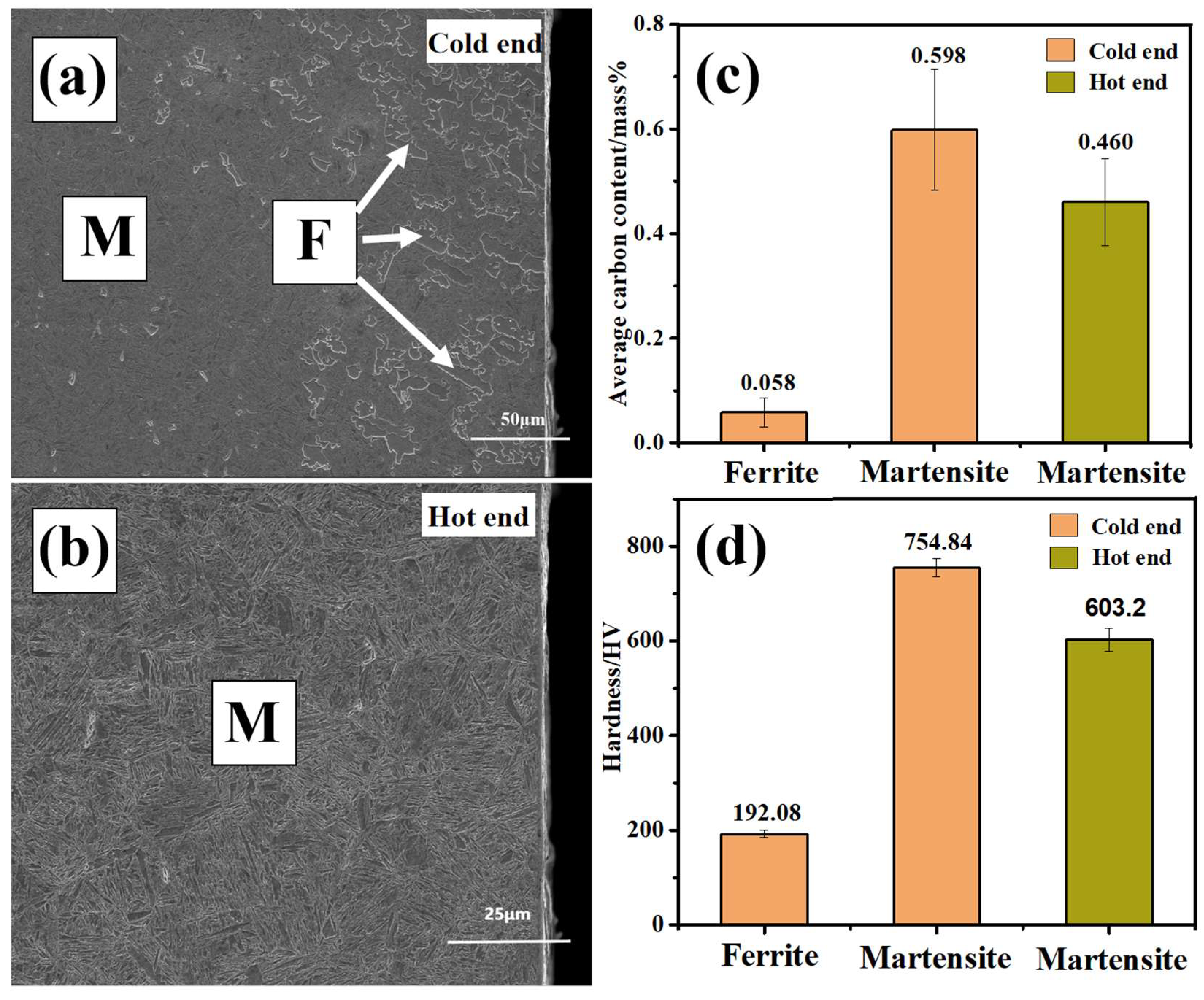
3.3. Analysis of Results of Quenching Experiments at Phase Transition Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, W.; Zhou, Y.; Ma, Y.; Liu, K.; Wang, L.; Chen, K. The Ferrite layer on the surface of carbon steel obtained by precisely designed cooling rate heat treatment and its microstructure analysis. Coatings 2022, 12, 541. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Jiao, S.H.; Ding, J.H.; Wan, D.; Liu, Z.; Wang, G. Super long-range diffusion of carbon during proeutectoid ferrite transformation. J. Cent. South Univ. 2019, 26, 560–566. [Google Scholar] [CrossRef]
- Xu, Z.Y. Phase transition of materials and its applications. J. Shanghai Jiao Tong Univ. 2001, 323–330. [Google Scholar]
- Tian, Z.H.; Zhang, X.H.; Tian, Z.G. Application of X-ray diffraction technique in material analysis. Eng. Test. 2009, 49, 40–42. [Google Scholar]
- Shi, X.X.; Yan, C.L. Application of Thermal Expansion Instrument in the Study of Steel Materials. Shougang Sci. Technol. 2011, 50–53. [Google Scholar]
- He, W.; Du, X.P.; Ma, H.Z.; Hui, X.Y.; Sun, X.F. Determination and analysis of phase transition temperature of TC4 titanium alloy. Phys. Chem. Insp. Phys. Div. 2014, 461–464. [Google Scholar]
- Zhang, Y.M.; Tang, Y.L.; Chen, W.Z. Determination of martensitic phase transition temperature in copper-based alloys. Mater. Dev. Appl. 1994, 9, 16–19. [Google Scholar]
- Zhen, R. Common measurement methods of phase transition temperature in shape memory alloys. J. Nanjing Eng. Inst. Nat. Sci. Ed. 2006, 4, 27–32. [Google Scholar]
- Li, W.J. Application of Differential Thermal Analysis to Metallic Materials. J. Anshan Iron Steel Inst. 1993, 4, 24–27. [Google Scholar]
- Qian, H.Z.; Zhang, J.Q.; Cui, L.X. Characterization of thermal expansion of steel in cast state. J. Iron Steel Res. 2011, 23, 44–49. [Google Scholar]
- Lasseigne, A.N.; Olson, D.L.; Kleebe, H.J.; Boellinghaus, T. Microstructural assessment of nitrogen-strengthened austenitic stainless-steel welds using thermoelectric power. Metall. Mater. Trans. A 2005, 36, 3031–3039. [Google Scholar] [CrossRef]
- Mott, N.F.; Jones, H. The Theory of the Properties of Metals and Alloys; Oxford University Press: Oxford, UK, 1945. [Google Scholar]
- Borrelly, R.; Merle, P.; Adami, L. Study of the solubility of iron in zirconium by thermoelectric power measurements. J. Nucl. Mater. 1990, 170, 147–156. [Google Scholar] [CrossRef]
- Brachet, J.C. Correlation between thermoelectric power (TEP) and martensite start temperature (Ms) measurements of 9Cr-WV-(Ta) martensitic steels. J. Phys. IV 1995, 5, 339–344. [Google Scholar]
- Kim, S.; Hong, H.S.; Oh, Y.M. Study of the thermoelectric power evolution of Zr-based alloys with Nb additions. J. Nucl. Mater. 2002, 306, 194–201. [Google Scholar]
- Samran, T.; Termsuksawad, P. An investigation of microstructural change of low alloy steel AISI 4150 by Seebeck coefficient. J. Met. Mater. Miner. 2010, 20, 21–26. [Google Scholar]
- Szabó, A.; Lovas, A. The study of transformations in glassy and crystalline alloys using thermoelectric power measurements. Acta Electrotech. Inform. 2010, 10, 71–74. [Google Scholar]
- Perez, M.; Sidoroff, C.; Vincent, A.; Esnouf, C. Microstructural evolution of martensitic 100Cr6 bearing steel during tempering: From thermoelectric power measurements to the prediction of dimensional changes. Acta Mater. 2009, 57, 3170–3181. [Google Scholar] [CrossRef]
- Radelytskyi, I.; Pękała, M.; Szymczak, R.; Gawryluk, D.J.; Berkowski, M.; Fink-Finowicki, J.; Diduszko, R.; Dyakonov, V.; Szymczak, H. Magnetocaloric effect in Ni2MnGa single crystal in the vicinity of the martensitic phase transition. J. Magn. Magn. Mater. 2017, 430, 16–21. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Q.; Yang, W.; Liu, K.; Wang, L.; Chen, K. Study on the characterization of surface ferrite transformation in carbon steel using in-situ thermovoltage measurement. Vacuum 2023, 213, 112111. [Google Scholar] [CrossRef]
- Gao, M.; Zhang, J.Y.; Rowe, V.H. Temperature Difference Electrical Conversion and Its Application; Ordnance Industry Press: Beijing, China, 1996. [Google Scholar]
- Ortiz, N.; Curiel, F.F.; López, V.H.; Ruiz, A. Evaluation of the intergranular corrosion susceptibility of UNS S31803 duplex stainless steel with thermoelectric power measurements. Corros. Sci. 2013, 69, 236–244. [Google Scholar] [CrossRef]
- GB/T 4340.1-2009; Metallic Material-Vickers Hardness Test-Part 1: Test Method. China Standard Publishing House: Bjing, China, 2009.
- Sherby, O.D.; Wadsworth, J.; Lesuer, D.R.; Syn, C.K. Structure and hardness of martensite in quenched Fe-C steels. Mater. Sci. Forum 2010, 638, 160–167. [Google Scholar] [CrossRef]
- Sherby, O.D.; Wadsworth, J.; Lesuer, D.R.; Syn, C.K. Martensite in quenched Fe–C steels and Engel–Brewer electron theory of crystal structures. Mater. Sci. Technol. 2012, 28, 471–480. [Google Scholar] [CrossRef]
- Caballero, F.G.; Capdevila, C.; Alvarez, L.F.; de Andres, C.G. Thermoelectric power studies on a martensitic stainless steel. Scr. Mater. 2004, 50, 1061–1066. [Google Scholar] [CrossRef]
- Dayal, P.; Darken, L.S. Migration of carbon in steel under the influence of direct current. JOM 1950, 2, 1156–1158. [Google Scholar] [CrossRef]
- Morinaga, M.; Yukawa, N.; Adachi, H.; Mura, T. Electronic stability effect on local strain in martensite. J. Phys. F Met. Phys. 1987, 17, 2147. [Google Scholar] [CrossRef]
- Chen, J. Relationship between physical properties and atomic structure of precious metals. Strateg. Study Chin. Acad. Eng. 2000, 66–73. [Google Scholar]
| Steels | C | Si | Mn | P | S | Fe |
|---|---|---|---|---|---|---|
| 45 | 0.45 | 0.18 | 0.65 | 0.020 | 0.004 | Bal. |
| T8 | 0.79 | 0.17 | 0.24 | 0.012 | 0.005 | Bal. |
| pure iron | 0.004 | 0.04 | 0.15 | 0.009 | 0.003 | Bal. |
| Cooling Rate (°C/s) | Wtidth of Zone II (°C) | Width of Zone IV (°C) | The Width Ratio of Zone II to Zone IV |
|---|---|---|---|
| 0.02 | 22 | 10 | 2.20 |
| 0.05 | 34 | 14 | 2.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Chen, K.; Liu, K.; Wang, L.; Chu, Y.; Xie, B. Study on Characterization of Phase Transition in Continuous Cooling of Carbon Steel Using In Situ Thermovoltage Measurement. Coatings 2024, 14, 980. https://doi.org/10.3390/coatings14080980
Wang Q, Chen K, Liu K, Wang L, Chu Y, Xie B. Study on Characterization of Phase Transition in Continuous Cooling of Carbon Steel Using In Situ Thermovoltage Measurement. Coatings. 2024; 14(8):980. https://doi.org/10.3390/coatings14080980
Chicago/Turabian StyleWang, Qihui, Kun Chen, Kejia Liu, Lianbo Wang, Yu Chu, and Bichen Xie. 2024. "Study on Characterization of Phase Transition in Continuous Cooling of Carbon Steel Using In Situ Thermovoltage Measurement" Coatings 14, no. 8: 980. https://doi.org/10.3390/coatings14080980
APA StyleWang, Q., Chen, K., Liu, K., Wang, L., Chu, Y., & Xie, B. (2024). Study on Characterization of Phase Transition in Continuous Cooling of Carbon Steel Using In Situ Thermovoltage Measurement. Coatings, 14(8), 980. https://doi.org/10.3390/coatings14080980






