Ultra High Efficiency Solar Capture Device Based on InAs Nanoring Microstructure
Abstract
:1. Introduction
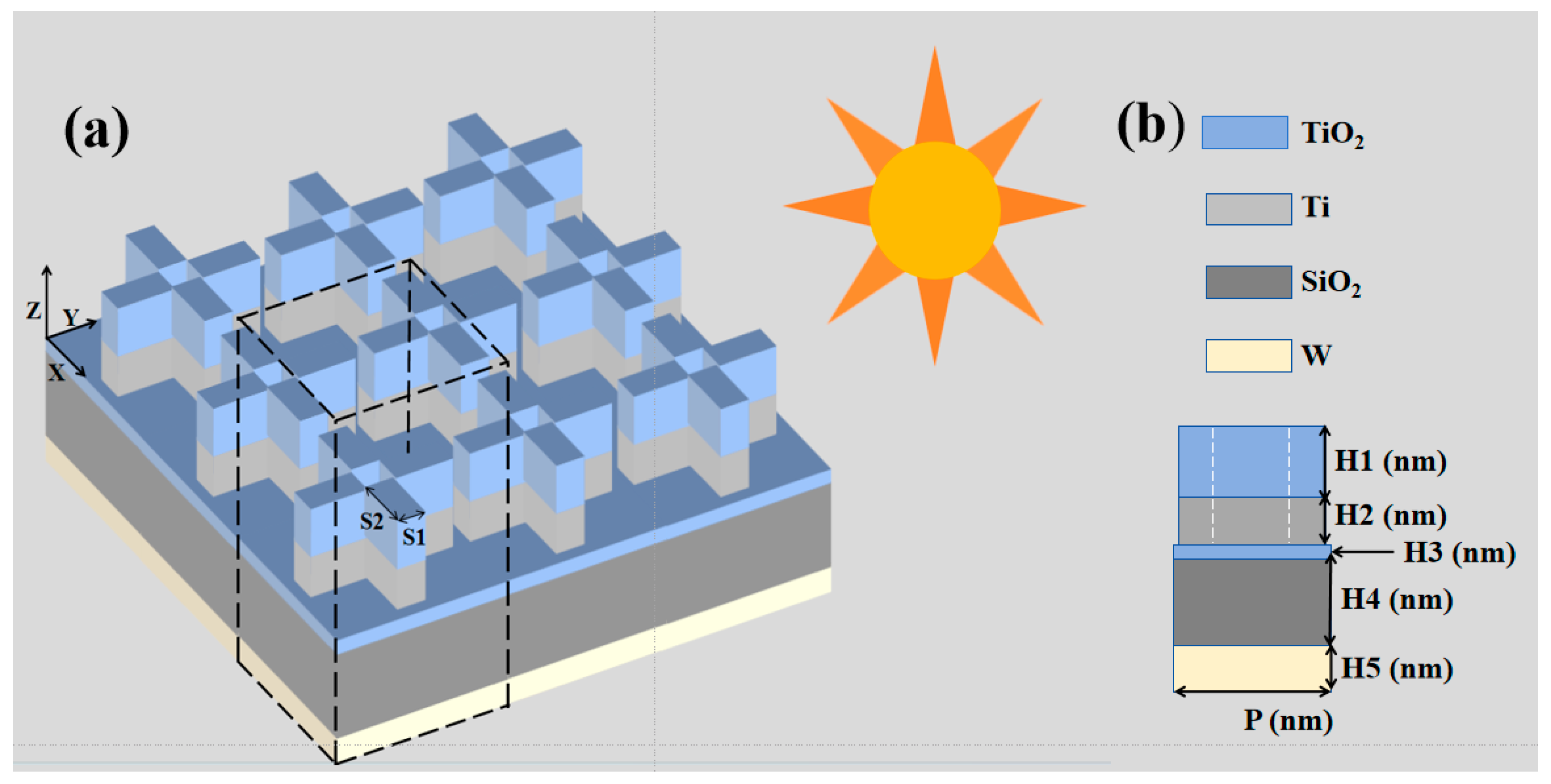
2. Structural Arrangement
3. Analysis and Discussion of Results
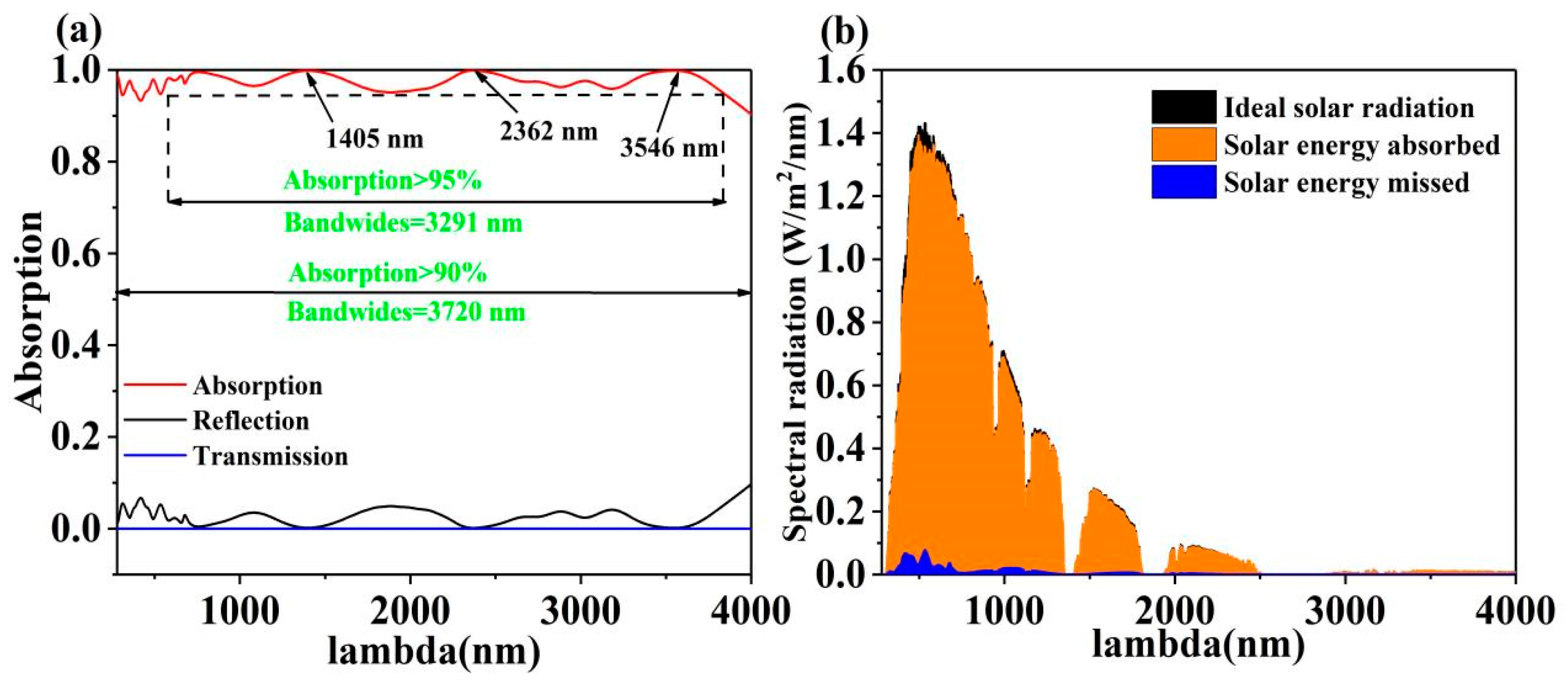
3.1. Broadband Absorption and Air Mass 1.5 Conditions
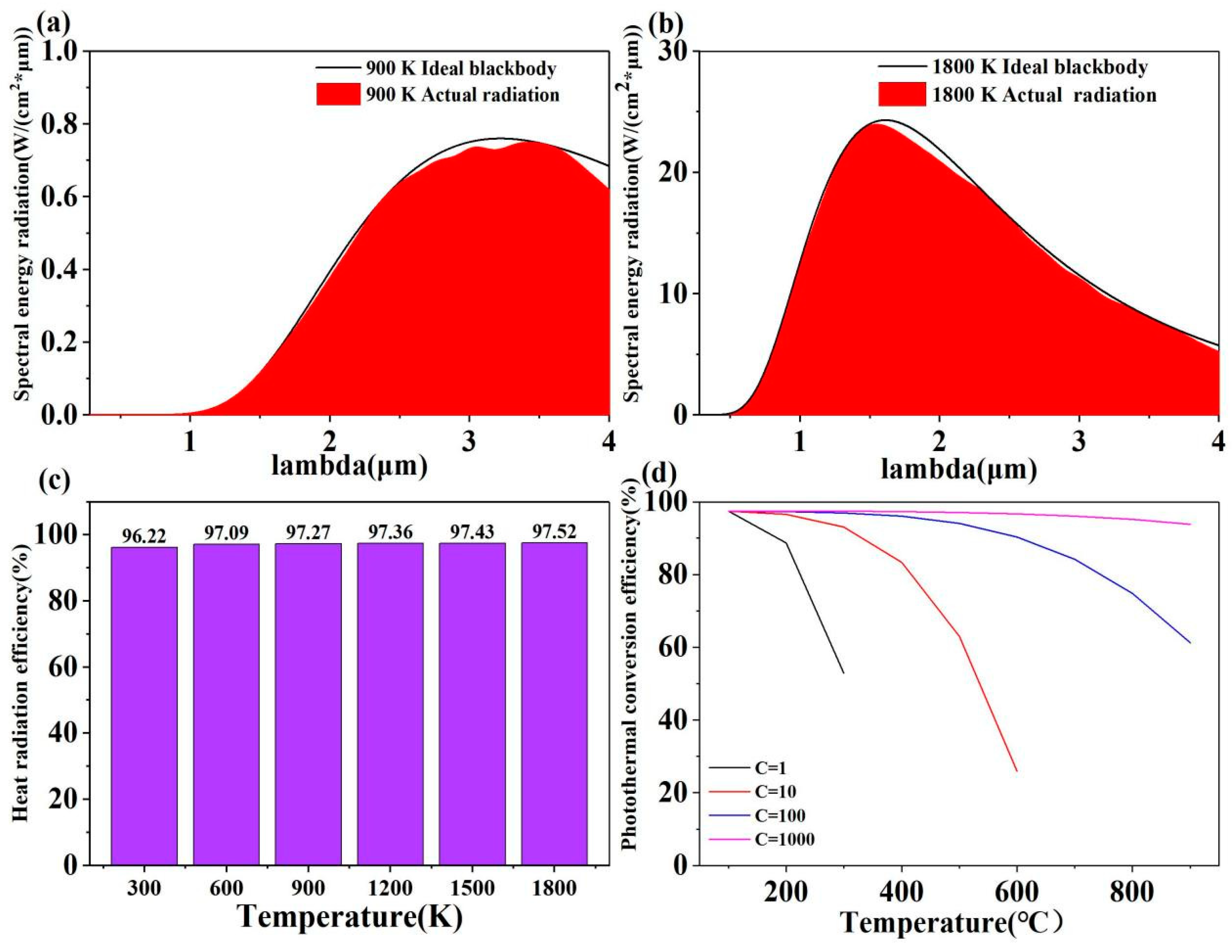
3.2. Thermal Radiation Efficiency and the pc Efficiency
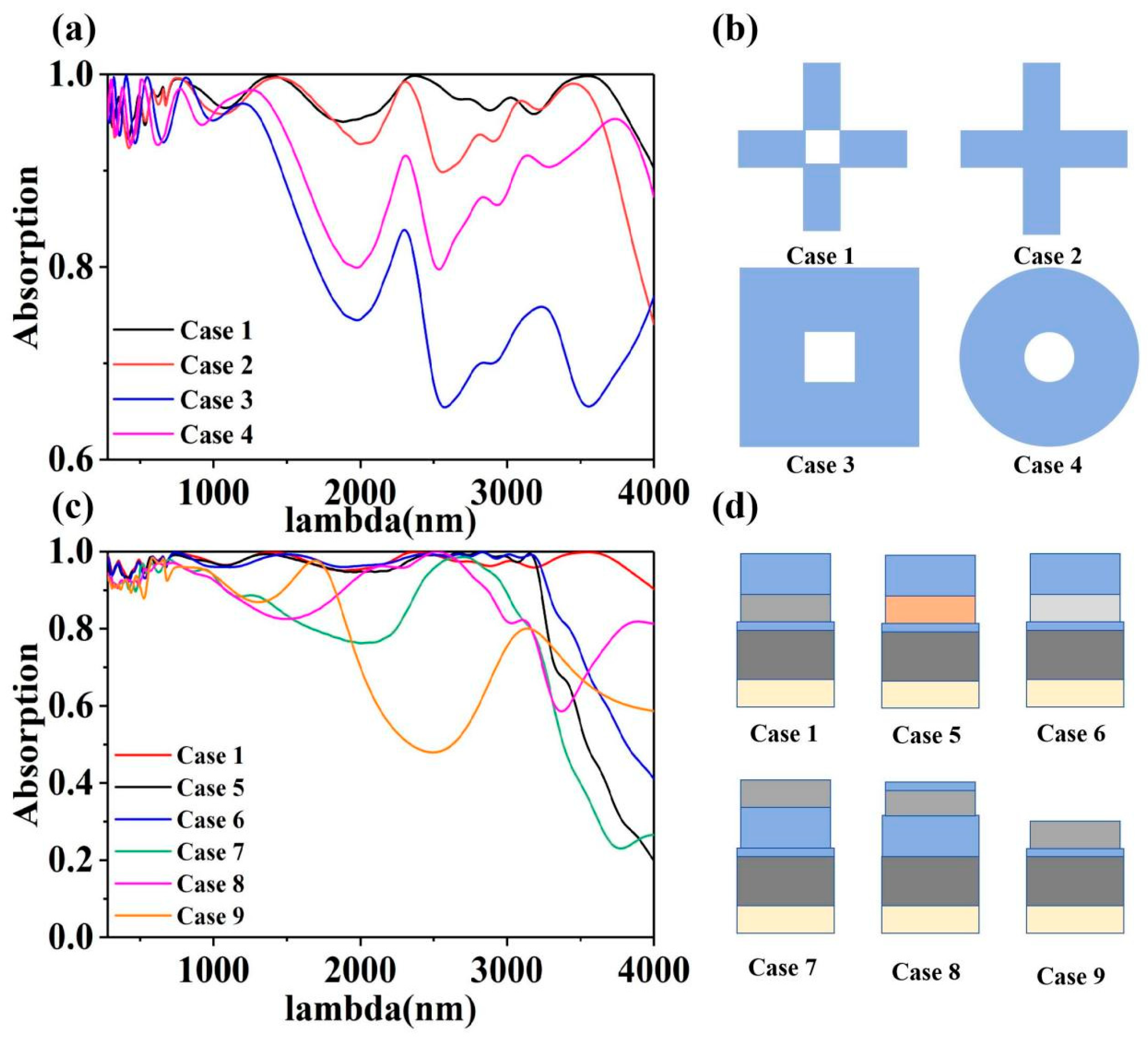
3.3. Different Structures Yield Distinct Outcomes
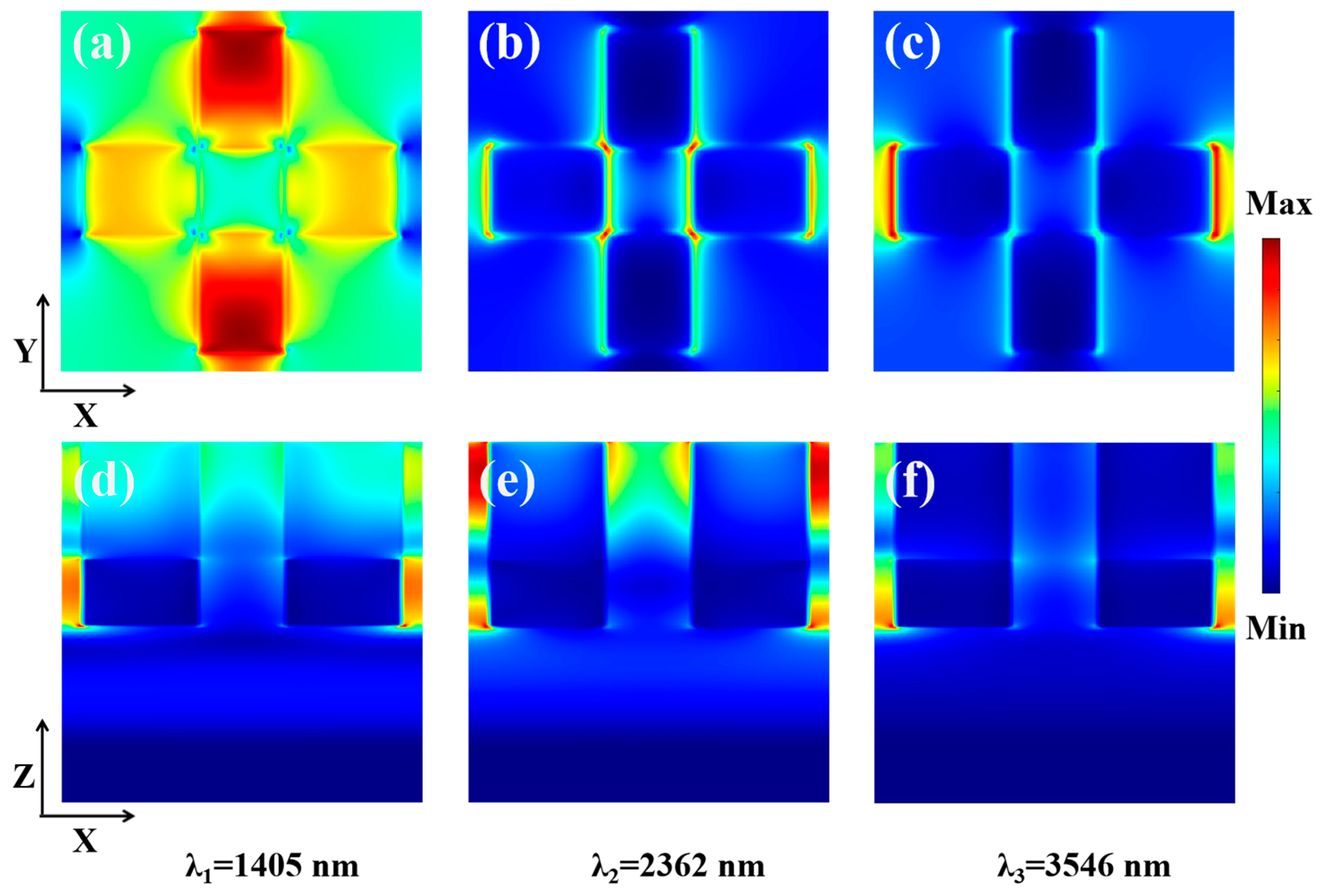
3.4. Field Strength Distribution
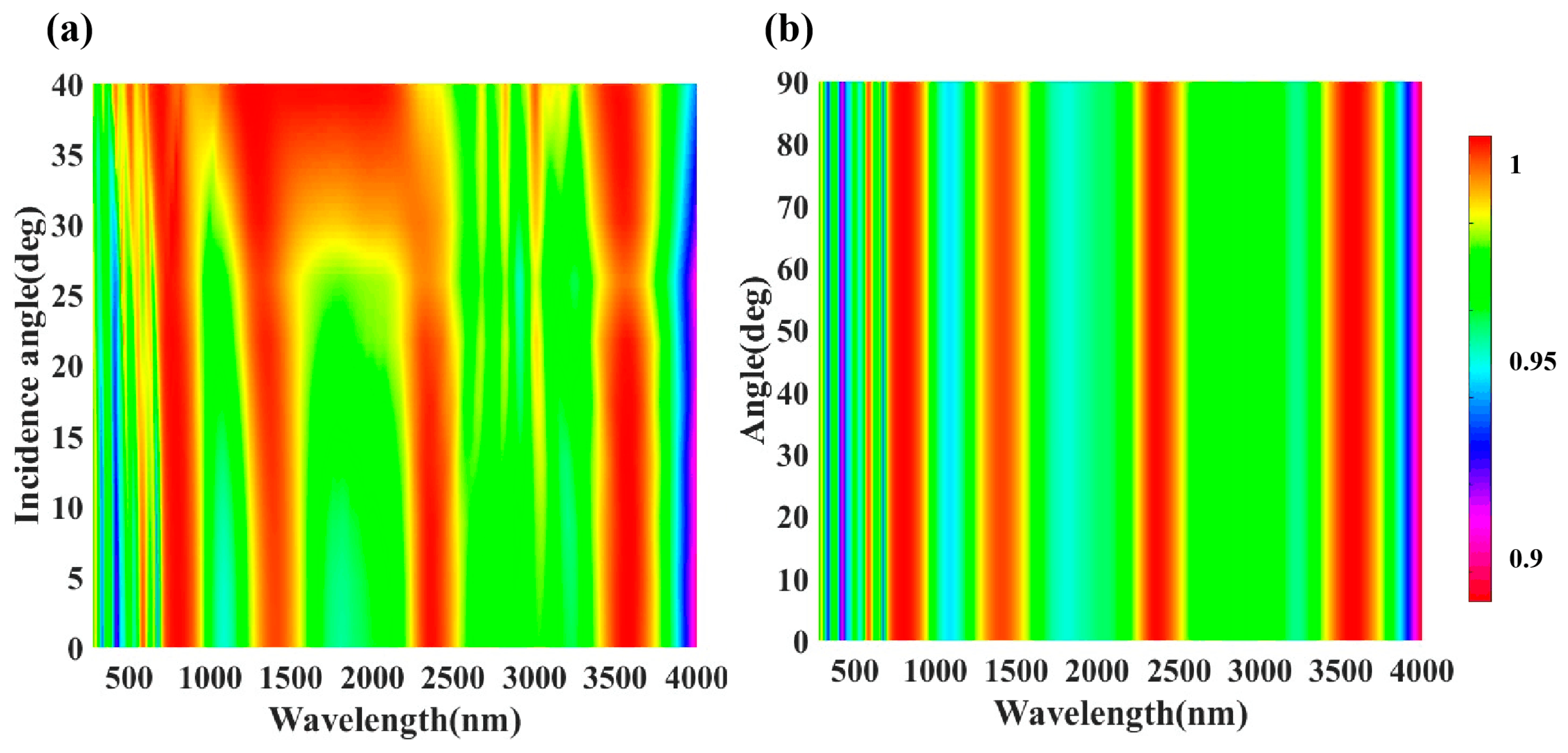
3.5. Angle Scanning
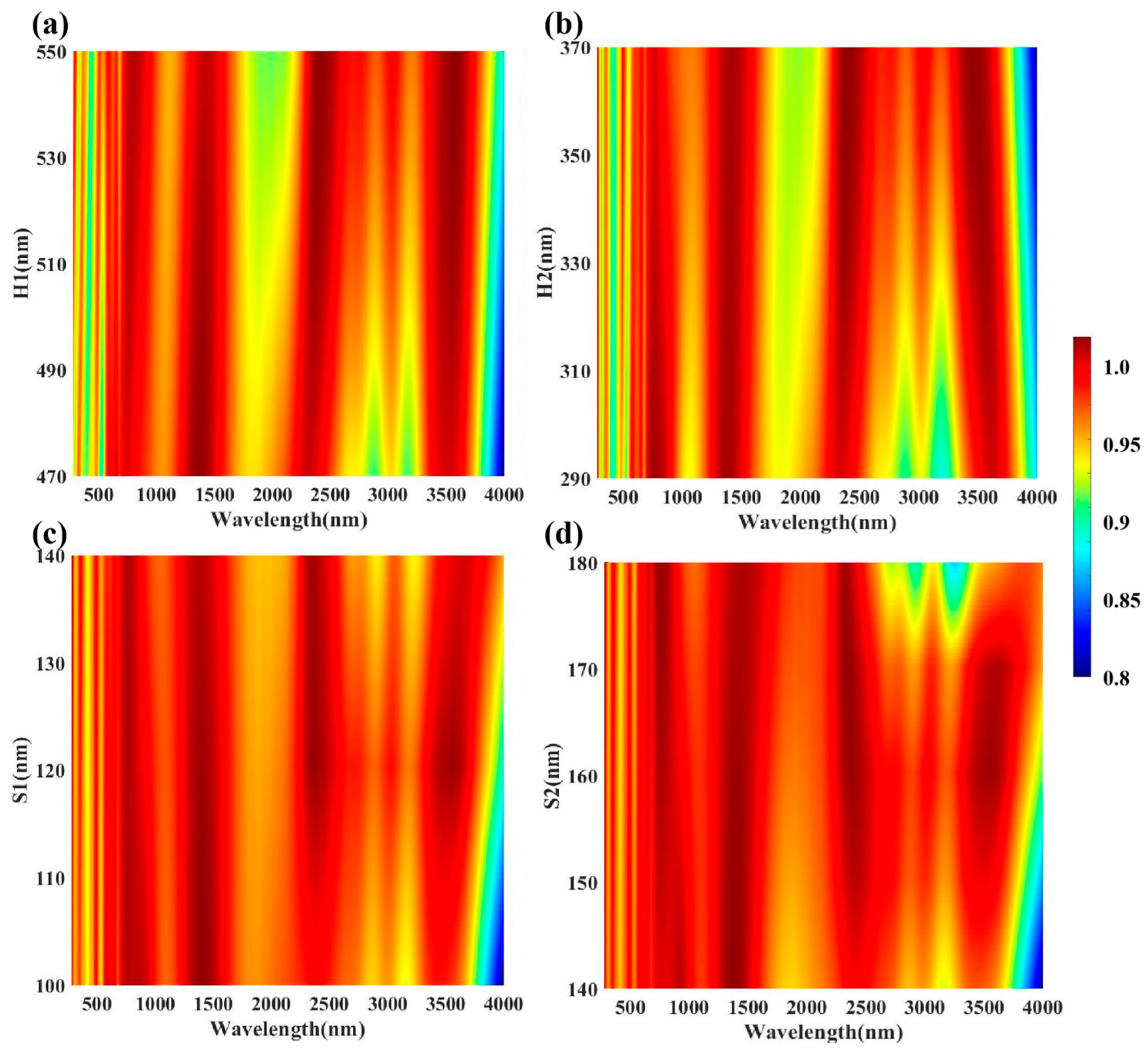
3.6. Different Structural Parameters Have Different Effects
4. Error Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, S.; Wu, X.H.; Fu, C.J. Active tuning of anisotropic phonon polaritons in natural van der Waals crystals with negative permittivity substrates and its application in energy transport. Opto-Electron. Sci. 2024, 3, 240002. [Google Scholar] [CrossRef]
- Baeva, M.; Gets, D.; Polushkin, A.; Vorobyov, A.; Goltaev, A.; Neplokh, V.; Mozharov, A.; Krasnikov, D.V.; Nasibulin, A.G.; Mukhin, I.; et al. ITO-free silicon-integrated perovskite electrochemical cell for light-emission and light-detection. Opto-Electron. Adv. 2023, 6, 220154. [Google Scholar] [CrossRef]
- Creutzig, F.; Agoston, P.; Goldschmidt, J.C.; Luderer, G.; Nemet, G.; Robert, C.P. The underestimated potential of solar energy to mitigate climate change. Nat. Energy 2017, 2, 17140. [Google Scholar] [CrossRef]
- Xiao, T.X.; Tu, S.; Liang, S.Z.; Guo, R.J.; Tian, T.; Müller-Buschbaum, P. Solar cell-based hybrid energy harvesters towards sustainability. Opto-Electron. Sci. 2023, 2, 230011. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, L.; Wang, F.Y.; Liu, M.Z.; Zhang, Y.Y.; Zhu, J.; Lu, Y.; Xu, T. Janus aramid nanofiber aerogel incorporating plasmonic nanoparticles for high-efficiency interfacial solar steam generation. Opto-Electron. Adv. 2023, 6, 220061. [Google Scholar] [CrossRef]
- Colmenares-Quintero, R.F.; Rojas, N.; Colmenares-Quintero, J.C.; Stansfield, K.E.; Villar-Villar, S.S.; Albericci-Avendaño, S.E. Design of an Integral Simulation Model for Solar-Powered Seawater Desalination in Coastal Communities: A Case Study in Manaure, La Guajira, Colombia. Sustainability 2025, 17, 1505. [Google Scholar] [CrossRef]
- Basit, M.A.; Imran, M.; Anwar-Ul-Haq, T.; Yan, C.-F.; Breaz, D.; Cotîrlă, L.-I.; Danciu, A. Advancing Renewable Energy Systems: A Numerical Approach to Investigate Nanofluidics’ Role in Engineering Involving Physical Quantities. Nanomaterials 2025, 15, 261. [Google Scholar] [CrossRef]
- Xiao, Y.F.; Ma, C.; Sun, T.Y.; Song, Q.J.; Bian, L.; Yi, Z.; Hao, Z.Q.; Tang, C.J.; Wu, P.H.; Zeng, Q.D. Investigation of a high-performance solar absorber and thermal emitter based on Ti and InAs. J. Mater. Chem. A 2024, 12, 29145. [Google Scholar] [CrossRef]
- Esposito, S.; D’Angelo, A.; Diletto, C.; Rossi, G.; Volpe, R.; Guglielmo, A.; De Girolamo Del Mauro, A.; Prestigiacomo, C.; Lanchi, M. Solar Selective Absorber Coating with Ag Infrared Reflector for Receiver Tubes Operating at 550 °C. Energies 2025, 18, 880. [Google Scholar] [CrossRef]
- Sun, Y.B.; Yang, L.L.; Wang, J.X.; Cheng, Y.Z.; Luo, H.; Chen, F.; Li, X.C. Microstrip antenna loaded with focusing metasurface for high-gain dual-polarization and bidirectional radiation. J. Appl. Phys. 2025, 137, 013104. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Luo, M.H.; Ju, X.W.; Hu, J.Y. Ultra-narrow dual-band perfect absorber based on double-slotted silicon nanodisk arrays. J. Phys. D Appl. Phys. 2024, 57, 345104. [Google Scholar] [CrossRef]
- Gu, X.; Liu, X.; Yan, X.F.; Du, W.J.; Lin, Q.; Wang, L.L.; Liu, G.D. Polaritonic coherent perfect absorption based on self-hybridization of a quasi-bound state in the continuum and exciton. Opt. Express 2023, 31, 4691–4700. [Google Scholar] [CrossRef]
- Jo, Y.; Park, H.; Yoon, H.; Kim, I. Advanced biological imaging techniques based on metasurfaces. Opto-Electron. Adv. 2024, 7, 240122. [Google Scholar] [CrossRef]
- Tan, Z.Q.; Lin, Q.; Du, W.J.; Wang, L.L.; Liu, G.D. Simultaneously enhance electric and magnetic Purcell factor by strong coupling between toroidal dipole quasi-BIC and electric dipole. J. Appl. Phys. 2025, 137, 033103. [Google Scholar] [CrossRef]
- Wang, H.Y.; Ma, R.; Liu, G.D.; Wang, L.L.; Lin, Q. Optical force conversion and conveyor belt effect with coupled graphene plasmon waveguide modes. Opt. Express 2023, 31, 32422. [Google Scholar] [CrossRef]
- Li, W.X.; Cheng, S.B.; Yi, Z.; Zhang, H.F.; Song, Q.J.; Hao, Z.Q.; Sun, T.Y.; Wu, P.H.; Zeng, Q.D.; Raza, R. Advanced optical reinforcement materials based on three-dimensional four-way weaving structure and metasurface technology. Appl. Phys. Lett. 2025, 126, 033503. [Google Scholar] [CrossRef]
- Li, B.X.; Liu, M.L.; Wen, R.Q.; Wei, Y.; Zeng, L.L.; Deng, C.S. Dynamic control of Fano-like interference in the graphene periodic structure. J. Phys. D Appl. Phys. 2023, 56, 115104. [Google Scholar] [CrossRef]
- Liu, M.L.; Li, B.X.; Zeng, L.L.; Wei, Y.; Wen, R.Q.; Zhang, X.J.; Deng, C.S. Dynamic tunable narrow-band perfect absorber for fiber -optic communication band based on liquid crystal. J. Phys. D Appl. Phys. 2023, 56, 505102. [Google Scholar] [CrossRef]
- Hu, J.Y.; Tan, C.X.; Bai, W.D.; Li, Y.M.; Lin, Q.; Wang, L.L. Dielectric nanocavity-coupled surface lattice resonances for high-efficiency plasmonic sensing. J. Phys. D Appl. Phys. 2022, 55, 075105. [Google Scholar] [CrossRef]
- Wang, Q.S.; Fang, Y.; Meng, Y.; Hao, H.; Li, X.; Pu, M.; Ma, X.; Luo, X. Vortex-field enhancement through high-threshold geometric metasurface. Opto-Electron. Adv. 2024, 7, 240112. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Lin, Q.; Yan, X.Q.; Wang, L.L.; Liu, G.D. Flat-band Friedrich-Wintgen bound states in the continuum based on borophene metamaterials. Opt. Express 2024, 32, 10669–10678. [Google Scholar] [CrossRef]
- Yang, J.P.; Tang, A.; Lian, B.W.; Xiong, Z.J.; Ma, Z.B.; Gu, N.T. Optimal multi-spectrum polarization detection with full-Stokes in a single channel by using standard retarders. Measurement 2025, 242, 116052. [Google Scholar] [CrossRef]
- He, M.Y.; Wang, Q.Q.; Zhang, H.; Xiong, J.; Liu, X.P.; Wang, J.Q. Analog electromagnetic induced transparency of T-type Si-based metamaterial and its applications. Phys. Scr. 2024, 99, 035506. [Google Scholar] [CrossRef]
- Wang, J.Q.; Sun, J.Y.; Sun, S.; Zhang, H.; Wang, Q.Q.; Yang, J.Y.; Mei, Y.W. Numerical simulation of electromagnetically induced transparency in composite metamaterial. Phys. Scr. 2025, 100, 025512. [Google Scholar] [CrossRef]
- Tang, C.J.; Nie, Q.M.; Cai, P.G.; Liu, F.X.; Gu, P.; Yan, Z.D.; Huang, Z.; Zhu, M.W. Ultra-broadband near-infrared absorption enhancement of monolayer graphene by multiple-resonator approach. Diam. Relat. Mater. 2024, 141, 110607. [Google Scholar] [CrossRef]
- He, Z.; Fang, D.; Yi, Y. Design of a Tunable Metamaterial Absorption Device with an Absorption Band Covering the Mid-Infrared Atmospheric Window. Photonics 2025, 12, 148. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Cheng, S.B.; Zhang, H.F.; Yi, Z.; Tang, B.; Chen, J.; Zhang, J.G.; Tang, C.J. Ultra wideband absorption absorber based on Dirac semimetallic and graphene metamaterials. Phys. Lett. A 2024, 517, 129675. [Google Scholar] [CrossRef]
- Li, Y.M.; Tan, C.X.; Hu, J.Y.; Bai, W.D.; Zhang, R.L.; Lin, Q.; Zhang, Y.; Wang, L.L. Ultra-narrow band perfect absorbance induced by magnetic lattice resonances in dielectric dimer metamaterials. Results Phys. 2022, 39, 105730. [Google Scholar] [CrossRef]
- Xiang, T.; Sun, Z.; Wang, L.L.; Lin, Q.; Liu, G.D. Polarization independent perfect absorption of borophene metamaterials operating in the communication band. Phys. Scr. 2024, 99, 085519. [Google Scholar] [CrossRef]
- Hung, C.-C.; Lin, X.-Y.; Wu, T.-L.; Liao, S.-H.; Chen, H.-S.; Yang, C.-F. Investigation of an Ultra-Wideband Optical Absorber with the Bandwidth from Ultraviolet C to Middle Infrared. Photonics 2025, 12, 83. [Google Scholar] [CrossRef]
- Shen, Z.; Ni, J. Multi-Resonant Full-Solar-Spectrum Perfect Metamaterial Absorber. Nanomaterials 2024, 14, 1959. [Google Scholar] [CrossRef] [PubMed]
- Li, X.T.; Cai, X.D.; Liu, C.; Kim, Y.; Badloe, T.; Liu, H.; Rho, J.; Xiao, S. Cascaded metasurfaces enabling adaptive aberration corrections for focus scanning. Opto-Electron. Adv. 2024, 7, 240085. [Google Scholar] [CrossRef]
- Drymiskianaki, A.; Viskadourakis, Z.; Kenanakis, G. Hybrid Microwave/Solar Energy Harvesting System Using 3D-Printed Metasurfaces. Materials 2024, 17, 5969. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Y.; Lin, Q.; Wang, L.L.; Liu, G.D. Dynamic control of polarization conversion based on borophene nanostructures in optical communication bands. Phys. Scr. 2024, 99, 085531. [Google Scholar] [CrossRef]
- Jung, J.; Yoon, S.; Kim, B.; Kim, J.B. Development of High-Performance Flexible Radiative Cooling Film Using PDMS/TiO2 Microparticles. Micromachines 2023, 14, 2223. [Google Scholar] [CrossRef]
- Li, B.X.; Zeng, L.L.; Wen, R.Q.; Zhang, X.J. Dynamic Regulation of Multiple Fano Resonances Based on Liquid Crystal. IEEE Photonics J. 2023, 15, 2200506. [Google Scholar] [CrossRef]
- Zeng, L.L.; Li, B.X.; Wen, R.Q.; Zhang, X.J. Plasmonic Sensor Based on Multi Fano Resonance in Inverse T Shape Structure for Detection of CO2 Concentration. IEEE Photonics J. 2023, 15, 2201805. [Google Scholar] [CrossRef]
- Abdulkarem, H.M.A.; Dhruvik, A.; Shobhit, K.P.; Muhammad, I.; Khaled, A.; Meshari, A.; Ammar, A. Structural investigation of ultra–Broadband disk-shaped resonator solar absorber structure based on CNT–TiC composites for solar energy harvesting. Int. J. Therm. Sci. 2023, 192, 108414. [Google Scholar] [CrossRef]
- Yu, Z.; Li, M.; Xing, Z.; Gao, H.; Liu, Z.; Pu, S.; Mao, H.; Cai, H.; Ma, Q.; Ren, W.; et al. Genetic algorithm assisted meta-atom design for high-performance metasurface optics. Opto-Electron. Sci. 2024, 3, 240016. [Google Scholar] [CrossRef]
- Hu, J.Y.; Bai, W.D.; Tan, C.X.; Li, Y.M.; Lin, Q.; Wang, L.L. Highly electric field enhancement induced by anapole modes coupling in the hybrid dielectric-metal nanoantenna. Opt. Commun. 2022, 511, 127987. [Google Scholar] [CrossRef]
- Wang, B.X.; Wu, C.Y.; Duan, G.Y.; Xu, W.; Pi, F.W. Review of broadband metamaterial absorbers: From principles, design strategies, and tunable properties to functiona applications. Adv. Funct. Mater. 2023, 33, 2213818. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, H.; Xiong, J.; Liu, X.P.; Wang, Q.Q.; Wang, J.Q. Controlling of spontaneous emission of quantum dots based on hyperbolic metamaterials. J. Phys. D Appl. Phys. 2024, 57, 255111. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, S.M.; Tian, Y.; Li, C.; Huang, W.; Liu, Y.; Jin, Y.; Fang, B.; Hong, Z.; Jing, X. Focus control of wide-angle metalens based on digitally encoded metasurface. Opto-Electron. Adv. 2024, 7, 240095. [Google Scholar] [CrossRef]
- Li, Z.T.; Cheng, S.B.; Zhang, H.F.; Yang, W.X.; Yi, Z.; Yi, Y.G.; Wang, J.Q.; Ahmad, S.; Raza, R. Ultrathin broadband terahertz metamaterial based on single-layer nested patterned graphene. Phys. Lett. A 2025, 534, 130262. [Google Scholar] [CrossRef]
- Luo, M.H.; Hu, J.Y.; Li, Y.M.; Bai, W.D.; Zhang, R.L.; Lin, Q.; Wang, L.L. Anapole-assisted ultra-narrow-band lattice resonance in slotted silicon nanodisk arrays. J. Phys. D Appl. Phys. 2023, 56, 375102. [Google Scholar] [CrossRef]
- Kang, D.H.; Heo, H.S.; Yang, Y.H.; Seong, J.; Kim, H.; Kim, J.; Rho, J. Liquid crystal-integrated metasurfaces for an active photonic platform. Opto-Electron. Adv. 2024, 7, 230216. [Google Scholar] [CrossRef]
- Yan, X.F.; Lin, Q.; Wang, L.L.; Liu, G.D. Tunable strong plasmon–exciton coupling based modulator employing borophene and deep subwavelength perovskite grating. J. Phys. D Appl. Phys. 2023, 56, 435106. [Google Scholar] [CrossRef]
- Xiong, H.; Yang, Q.; Huang, Y.Z.; Deng, J.H. High-Efficiency Microwave Wireless Power Transmission via Reflective Phase Gradient Metasurfaces and Surface Wave Aggregation. ACS Appl. Mater. Interfaces 2024, 16, 60189–60196. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Deng, J.H.; Xiong, H. Tri-Band Metamaterial Absorber Based on a Three-Ring Coupled Structure. ACS Appl. Electron. Mater. 2024, 6, 9184–9193. [Google Scholar] [CrossRef]
- Deng, M.; Kanwal, S.; Wang, Z.; Cai, C.; Cheng, Y.; Guan, J.; Hu, G.; Wang, J.; Wen, J.; Chen, L. Dielectric Metasurfaces for Broadband Phase-Contrast Relief-Like Imaging. Nano Lett. 2024, 24, 14641–14647. [Google Scholar] [CrossRef]
- Yu, P.; Yang, H.; Chen, X.; Yi, Z.; Yao, W.; Chen, J.; Yi, Y.; Wu, P. Ultra-wideband solar absorber based on refractory titanium metal. Renew. Energy 2020, 158, 227–235. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, T.; Zhong, Q.; Yan, R.; Huang, X. A Near-Ideal Solar Selective Absorber with Strong Broadband Optical Absorption from UV to NIR. Nanotechnology 2020, 31, 315202. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.J.; He, Y.R. Plasmonic nanostructures for broadband solar absorption based on the intrinsic absorption of metals. Solar Energy Mater. Sol. Cells 2018, 188, 156–163. [Google Scholar] [CrossRef]
- Qin, F.; Xu, F.; Liu, J.W.; Hu, P.F.; Yi, Z.; Liu, L.; Yang, H.; Zhang, J.G.; Pan, M.; Wu, P.H. Broadband solar absorbers with excellent thermal radiation efficiency based on W–Al2O3 stack of cubes. Int. J. Therm. Sci. 2022, 179, 107683. [Google Scholar] [CrossRef]
- Zeng, Z.L.; Liu, H.F.; Zhang, H.F.; Cheng, S.B.; Yi, Y.G.; Yi, Z.; Wang, J.Q.; Zhang, J.G. Tunable ultra-sensitive four-band terahertz sensors based on Dirac semimetals. Photonics Nanostruct. Fundam. Appl. 2025, 63, 101347. [Google Scholar] [CrossRef]
- Li, Z.T.; Li, X.; Liu, G.D.; Wang, L.L.; Lin, Q. Analytical investigation of unidirectional reflectionless phenomenon near the exceptional points in graphene plasmonic system. Opt. Express 2023, 31, 30458. [Google Scholar] [CrossRef] [PubMed]
- Zun, J.; Wu, Z.; Fu, D.; Lu, G.; Hu, H. Novel optical switch and four-to-one data selector utilizing an MIM waveguide structure based on surface plasmon polaritons. Measurement 2025, 241, 115681. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.T.; Wang, L.L.; Lin, Q. Unidirectional reflectionless propagation in borophene plasmonic metamaterials. J. Phys. D Appl. Phys. 2023, 57, 015103. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, L.G.; Zeng, Y.; Liu, G.D.; Wang, L.L.; Lin, Q. Extreme enhancement of optical force via the acoustic graphene plasmon mode. Opt. Express 2023, 31, 482723. [Google Scholar] [CrossRef]
- Cheng, S.B.; Li, W.X.; Zhang, H.F.; Akhtar, M.N.; Yi, Z.; Zeng, Q.D.; Ma, C.; Sun, T.Y.; Wu, P.H.; Ahmad, S. High sensitivity five band tunable metamaterial absorption device based on block like Dirac semimetals. Opt. Commun. 2024, 569, 130816. [Google Scholar] [CrossRef]
- Ling, Z.X.; Zeng, Y.; Liu, G.D.; Wang, L.L.; Lin, Q. Unified model for plasmon-induced transparency with direct and indirect coupling in borophene-integrated metamaterials. Opt. Express 2022, 30, 21966. [Google Scholar] [CrossRef] [PubMed]
- Berhe, A.M.; As’ham, K.; Al-Ani, I.; Hattori, H.T.; Miroshnichenko, A.E. Strong coupling and catenary field enhancement in the hybrid plasmonic metamaterial cavity and TMDC monolayers. Opto-Electron. Adv. 2024, 7, 230181. [Google Scholar] [CrossRef]
- Li, W.; Cheng, S.; Zhang, H.; Yi, Z.; Tang, B.; Ma, C.; Wu, P.; Zeng, Q.; Raza, R. Multi-functional metasurface: Ul-tra-wideband/multi-band absorption switching by adjusting guided mode resonance and local surface plasmon resonance effects. Commun. Theor. Phys. 2024, 76, 065701. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, G.D.; Wang, L. Active modulation of quasi-bound state in the continuum based on bulk Dirac semimetals metamaterial. Appl. Phys. Express 2022, 15, 032006. [Google Scholar] [CrossRef]
- Yang, C.; Lin, Q.; Du, W.J.; Wang, L.L.; Liu, G.D. Bi-tunable absorber based on borophene and VO2 in the optical telecom-munication band. J. Opt. Soc. Am. B 2022, 39, 2969–2974. [Google Scholar] [CrossRef]
- Li, W.; Yi, Y.; Yang, H.; Cheng, S.; Yang, W.X.; Zhang, H.; Yi, Z.; Yi, Y.; Li, H. Active Tunable Terahertz Band-width Absorber Based on single layer Graphene. Commun. Theor. Phys. 2023, 75, 045503. [Google Scholar] [CrossRef]
- Zeng, Y.; Ling, Z.X.; Liu, G.D.; Wang, L.L.; Lin, Q. Tunable plasmonically induced transparency with giant group delay in gain-assisted graphene metamaterials. Opt. Express 2022, 30, 455954. [Google Scholar] [CrossRef]
- Yan, X.; Lin, Q.; Wang, L.; Liu, G.D. Active absorption modulation by employing strong coupling between magnetic plasmons and borophene surface plasmons in the telecommunication band. J. Appl. Phys. 2022, 132, 063101. [Google Scholar] [CrossRef]
- Xiao, Y.T.; Chen, L.W.; Pu, M.B.; Xu, M.F.; Zhang, Q.; Guo, Y.; Chen, T.; Luo, X. Improved spatiotemporal resolution of an-ti-scattering super-resolution label-free microscopy via synthetic wave 3D metalens imaging. Opto-Electron. Sci. 2023, 2, 230037. [Google Scholar] [CrossRef]
- Alsaif, H.; Muheki, J.; Ben Ali, N.; Ghachem, K.; Surve, J.; Patel, S.K. Thin-Film Solar Energy Absorber Structure for Window Coatings for Self-Sufficient Futuristic Buildings. Micromachines 2023, 14, 1628. [Google Scholar] [CrossRef] [PubMed]

| Member | Absorption Bandwidth with a Rate Exceeding 90% | Absorption Efficiency | Thermal Radiation Efficiency |
|---|---|---|---|
| [52] | 1900 nm (100–2000 nm) | 93.17% (100–2000 nm) | / |
| [53] | 712 nm (354–1066 nm) | 97% (354–1066 nm) | / |
| [39] | 2800 nm (200–3000 nm) | 93.8% (280–2030 nm) | / |
| [54] | 1200 nm (300–1500 nm) | 91% (300–1500 nm) | 83.26% (1000 K) |
| [55] | 1692 nm (420–2112 nm) | 93.16% (280–2500 nm) | 91.47% (2000 K) |
| proposed | 3720 nm (280–4000 nm) | 97.38% (280–4000 nm) 97.75% (542–3833 nm) | 97.27% (900 K) 97.52% (1800 K) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, Z.; Yao, X.; Song, Q.; Wu, X. Ultra High Efficiency Solar Capture Device Based on InAs Nanoring Microstructure. Coatings 2025, 15, 243. https://doi.org/10.3390/coatings15020243
Yi Z, Yao X, Song Q, Wu X. Ultra High Efficiency Solar Capture Device Based on InAs Nanoring Microstructure. Coatings. 2025; 15(2):243. https://doi.org/10.3390/coatings15020243
Chicago/Turabian StyleYi, Zao, Xiangchao Yao, Qianju Song, and Xianwen Wu. 2025. "Ultra High Efficiency Solar Capture Device Based on InAs Nanoring Microstructure" Coatings 15, no. 2: 243. https://doi.org/10.3390/coatings15020243
APA StyleYi, Z., Yao, X., Song, Q., & Wu, X. (2025). Ultra High Efficiency Solar Capture Device Based on InAs Nanoring Microstructure. Coatings, 15(2), 243. https://doi.org/10.3390/coatings15020243







