Heat Transfer Characteristics of Electrical Heating Deicing and Snow-Melting Asphalt Pavement Under Different Operating Conditions
Abstract
1. Introduction
2. Methods
2.1. Heat Transfer Model
2.2. Entransy Dissipation Analysis
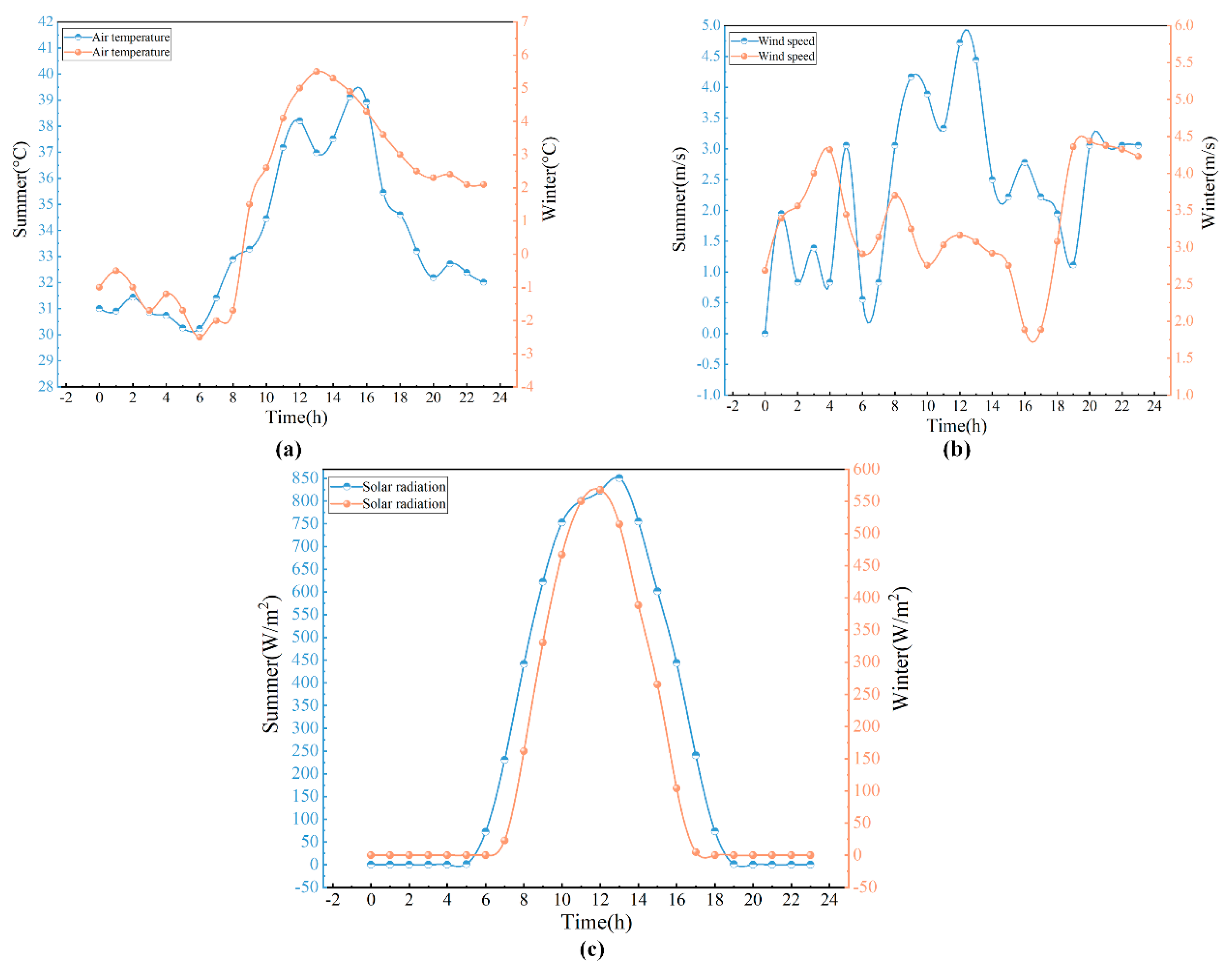
3. Field Experiment and Model Verification
3.1. Outdoor Test Model Making
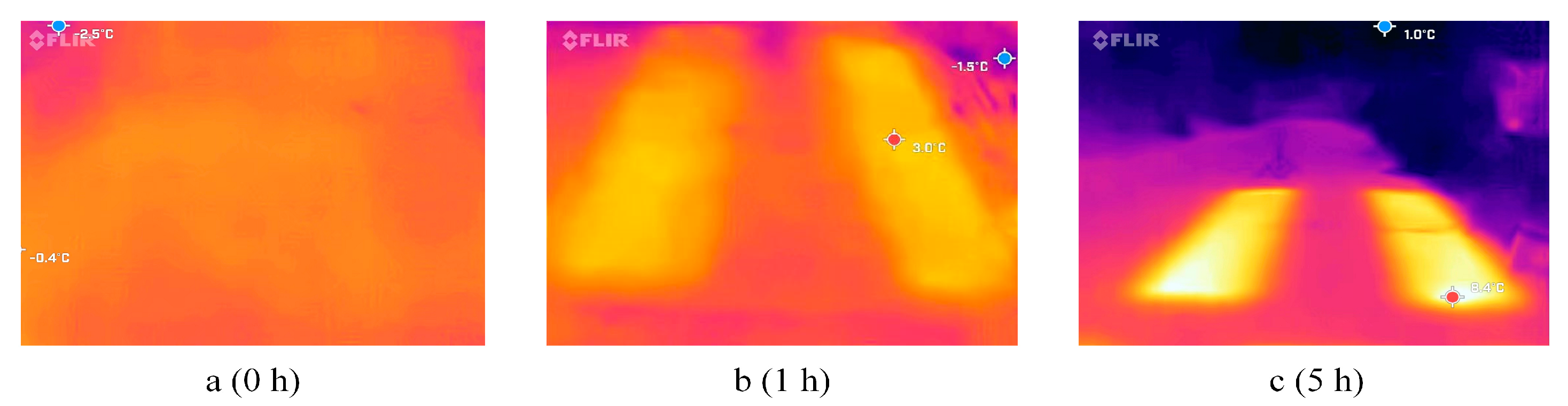
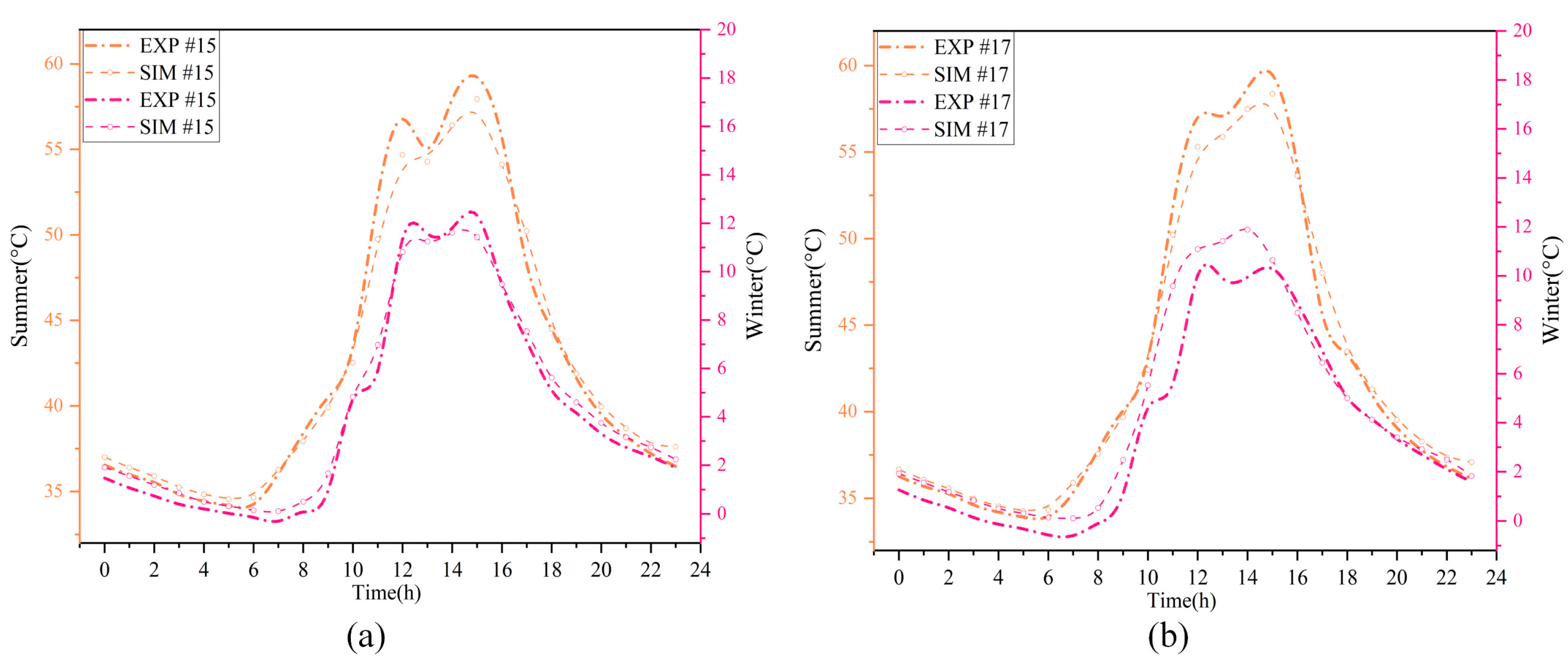
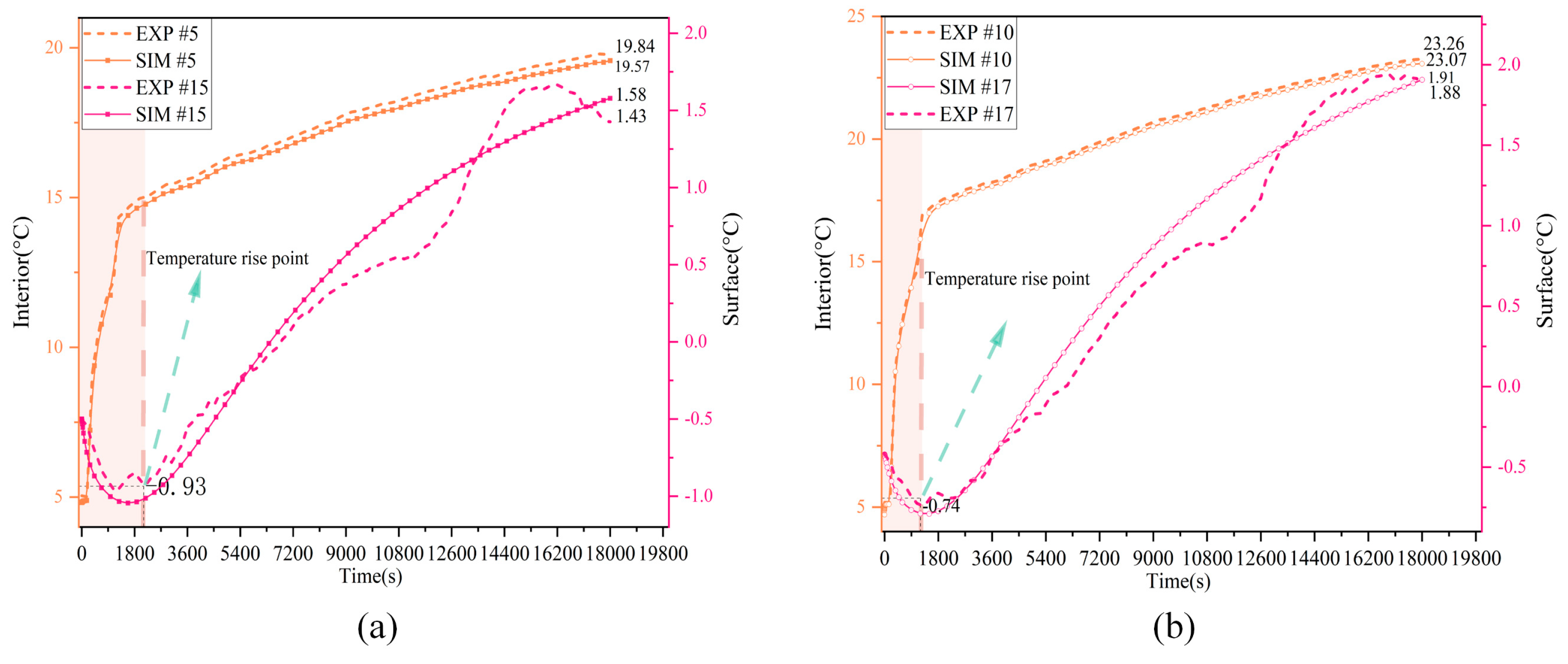
3.2. Experimental Results and Verification
4. Results and Discussion
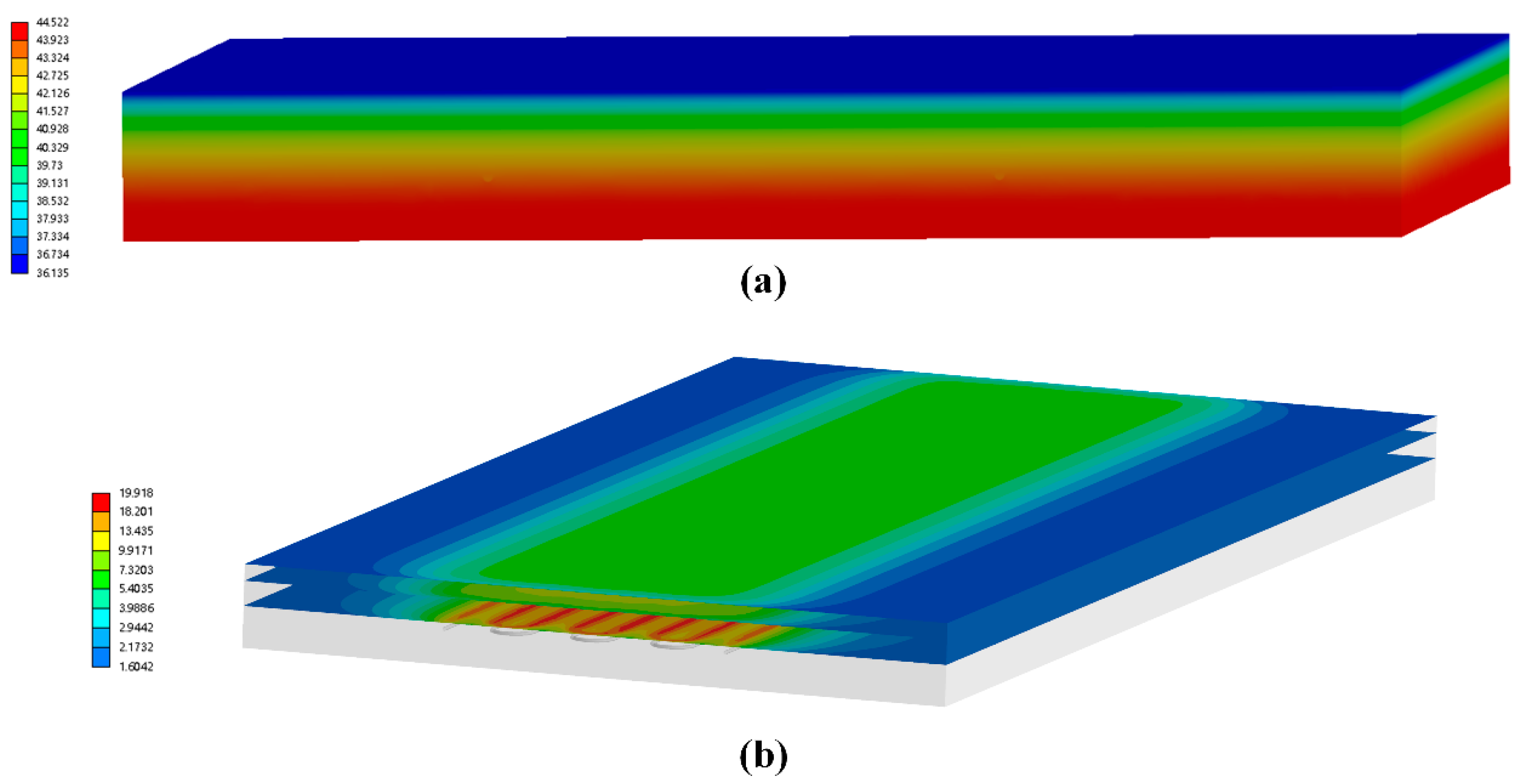
4.1. Temperature Field Distribution Characteristics
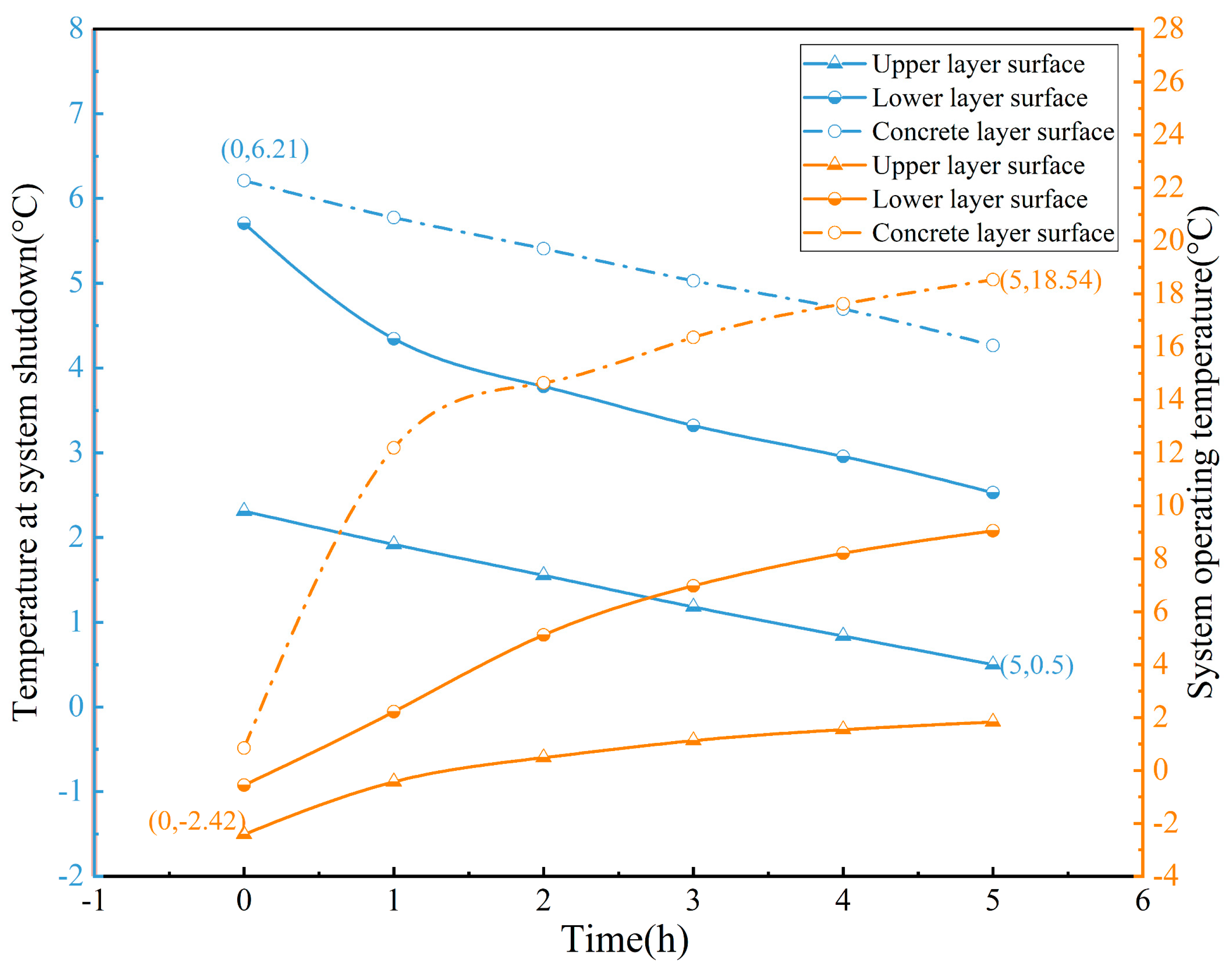
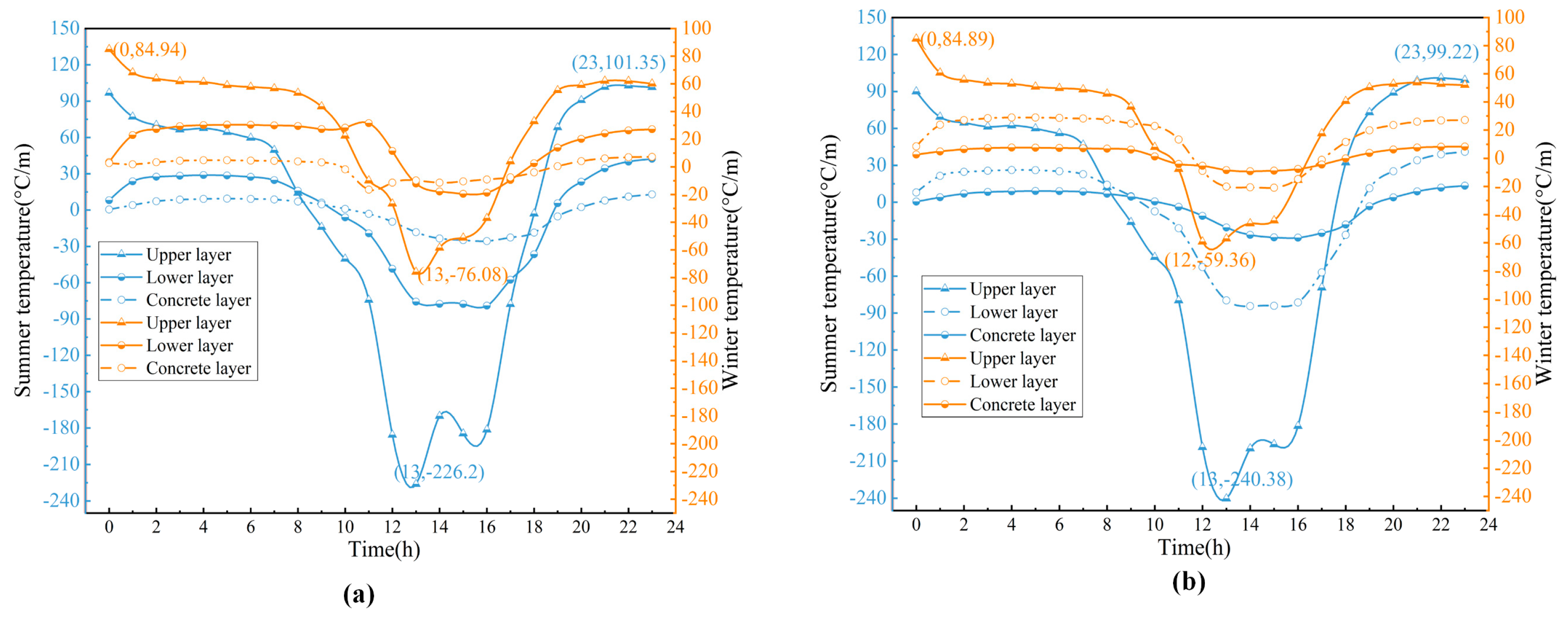
4.1.1. Analysis of Temperature Distribution Characteristics
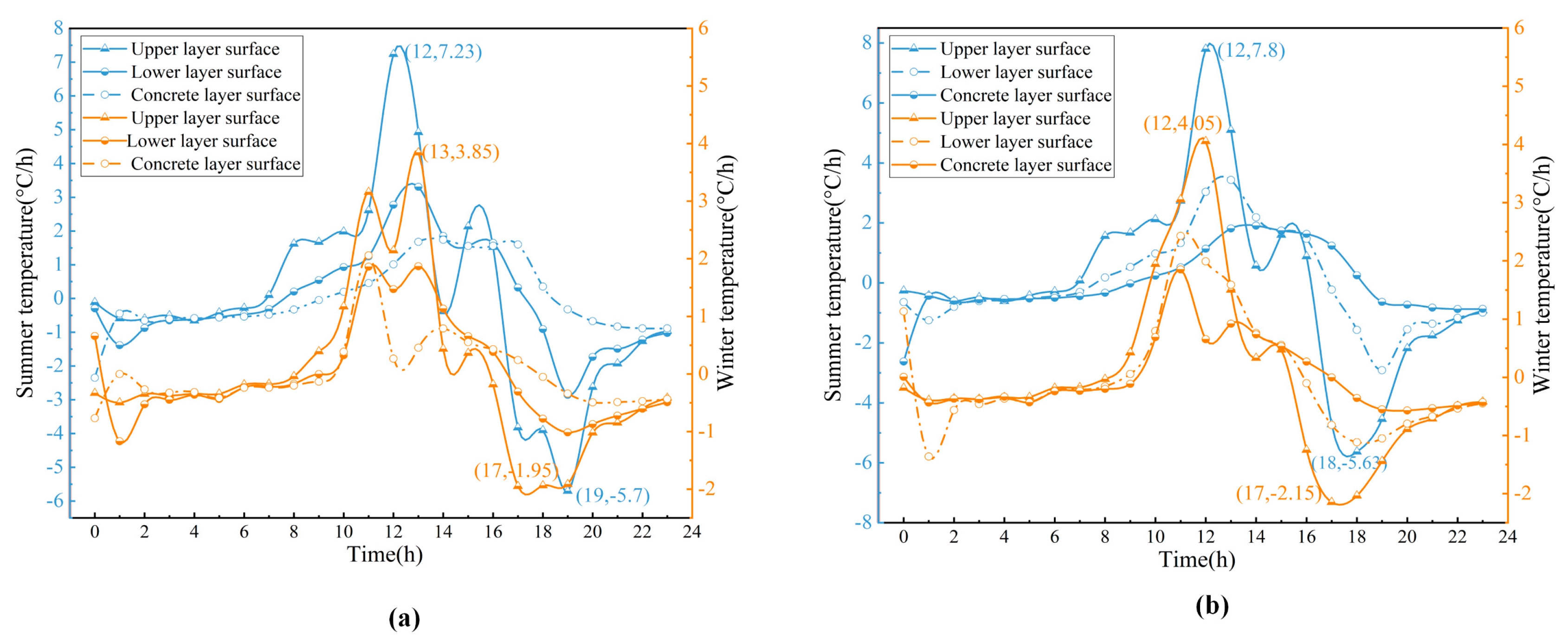
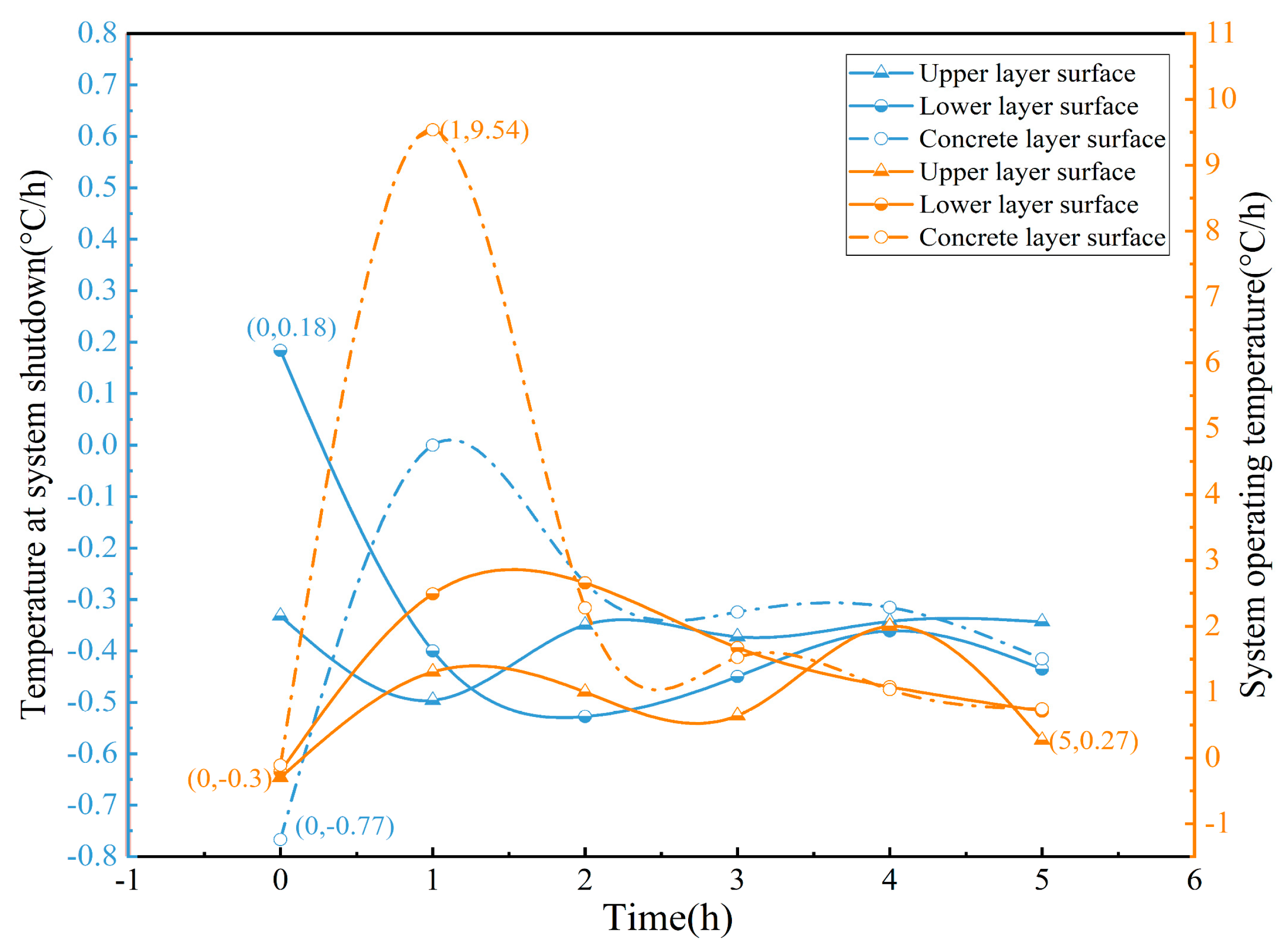
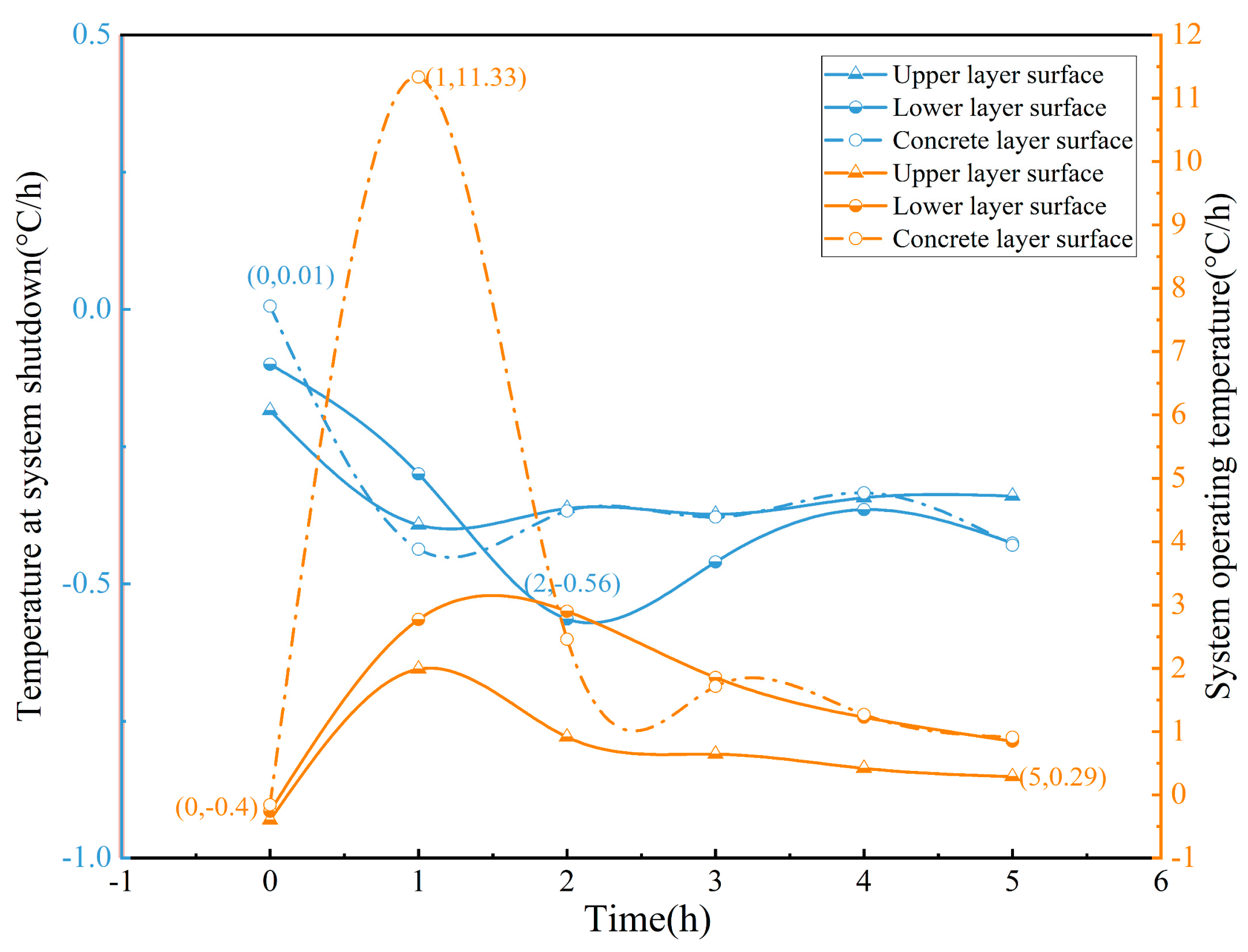
4.1.2. Temperature Change Rate Analysis
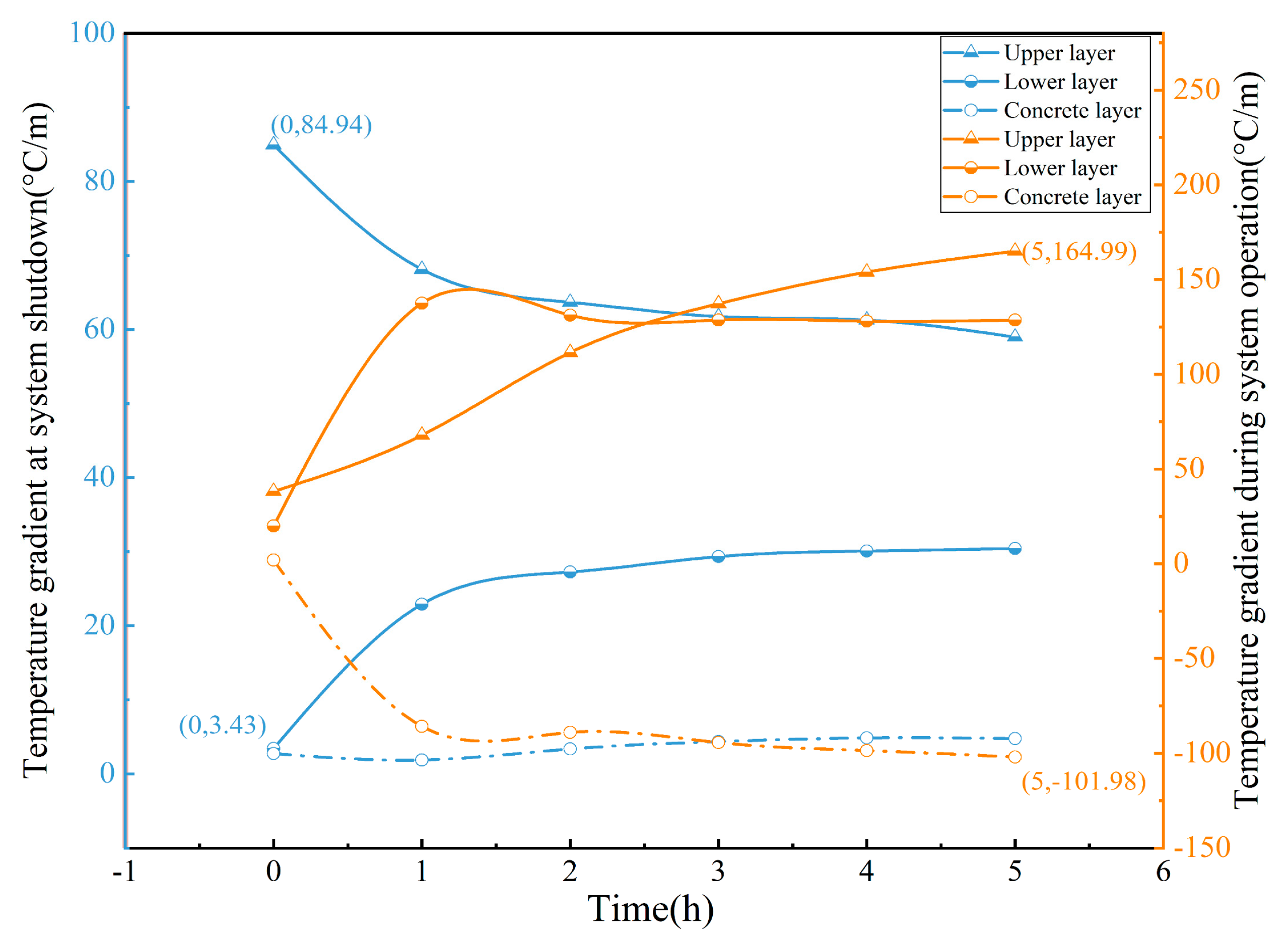
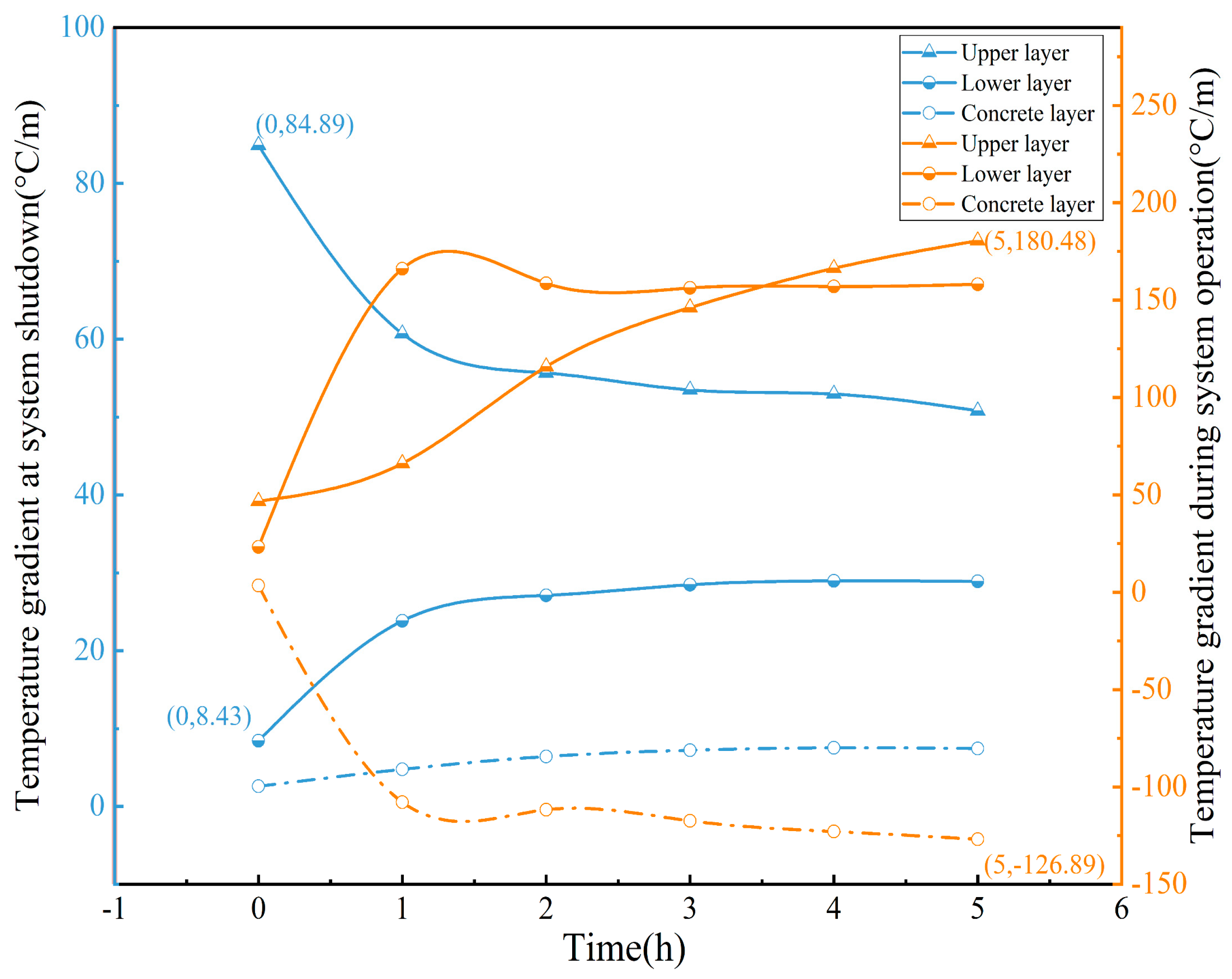
4.1.3. Analysis of Temperature Gradient Variation
4.2. Analysis of Heat Transfer Entransy Dissipation
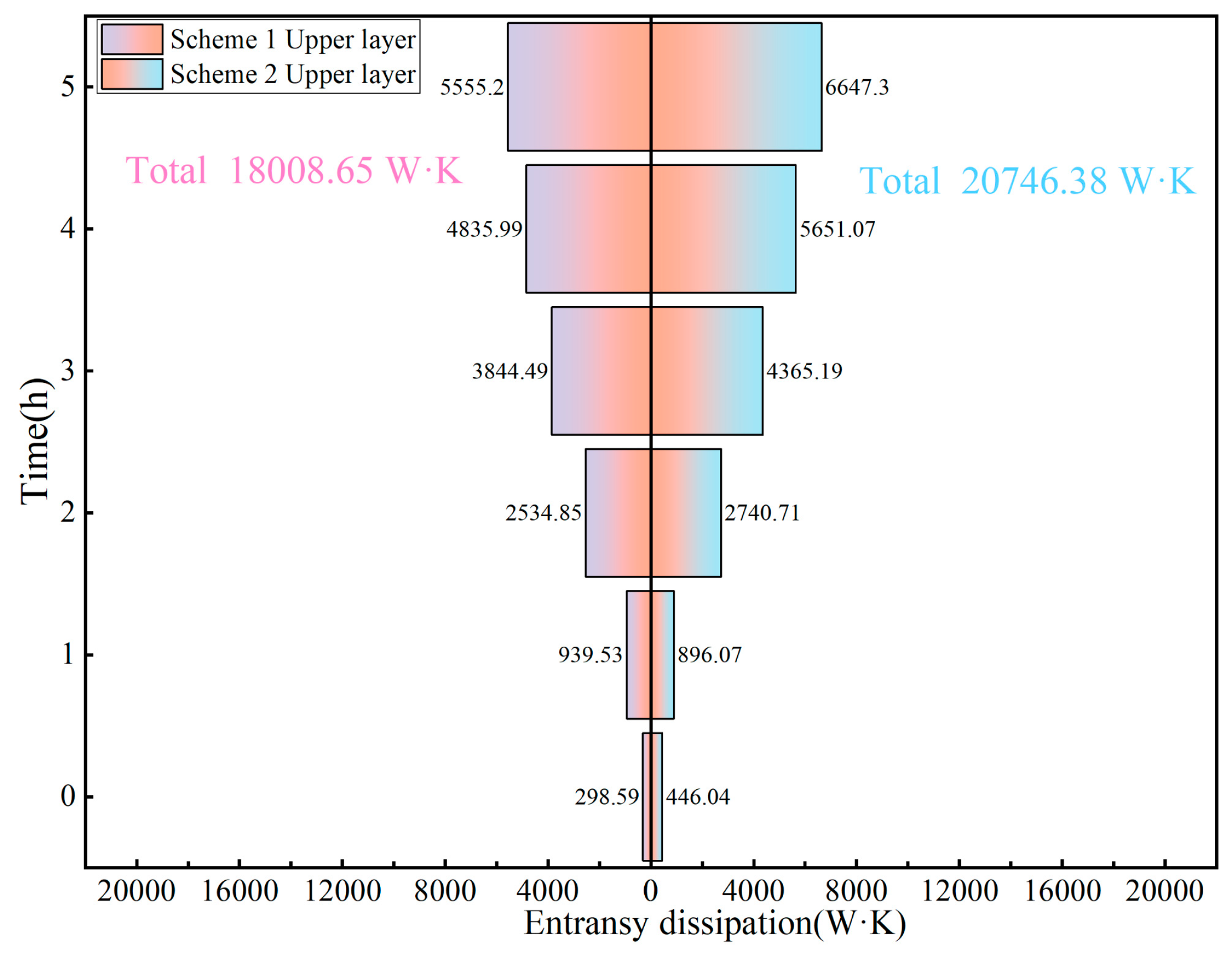
4.2.1. Heat Transfer Entransy Dissipation in Summer
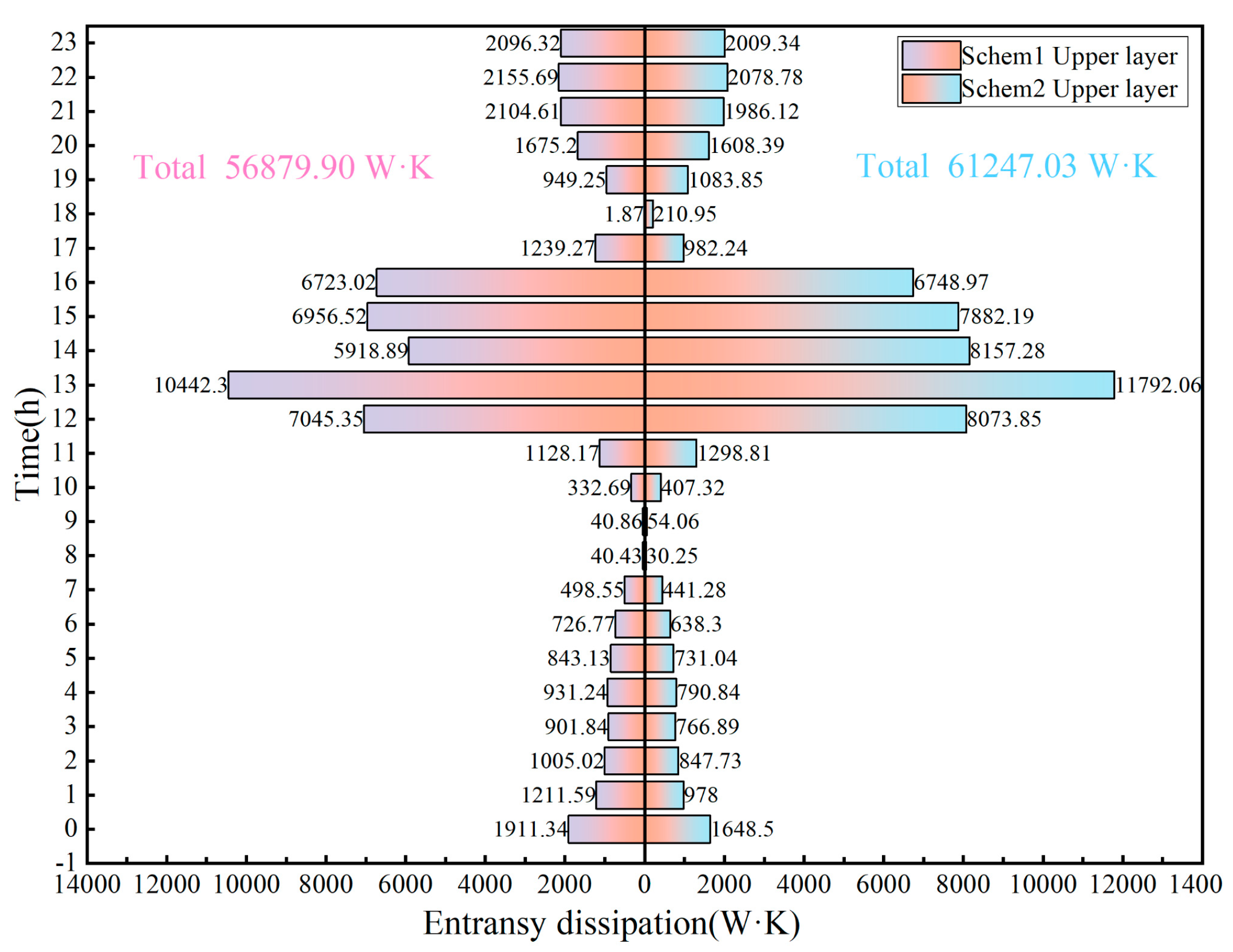
4.2.2. Heat Transfer Entransy Dissipation in Winter
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Liu, X.; Wei, D. Asphalt Mixture with Nucleus-Shell Structural Microwave Enhanced Aggregate: Structure Design, Preparation and Performance. Case Stud. Constr. Mater. 2023, 19, e02248. [Google Scholar] [CrossRef]
- Hussein, A.K.; Rashid, F.L.; Togun, H.; Sultan, H.S.; Homod, R.Z.; Sadeq, A.M.; Attia, M.E.H.; Ali, B.; Biswal, U.; Rout, S.K.; et al. A Review of Design Parameters, Advancement, Challenges, and Mathematical Modeling of Asphalt Solar Collectors. J. Therm. Anal. Calorim. 2024, 149, 41–61. [Google Scholar] [CrossRef]
- Rahman, M.L.; Malakooti, A.; Ceylan, H.; Kim, S.; Taylor, P.C. A Review of Electrically Conductive Concrete Heated Pavement System Technology: From the Laboratory to the Full-Scale Implementation. Constr. Build. Mater. 2022, 329, 127139. [Google Scholar] [CrossRef]
- Tang, C.; Liu, J.; Lu, Z.; Zhao, Y.; Zhang, J.; Feng, Y. Dynamic Thermo-Mechanical Responses of Road-Soft Ground System Under Vehicle Load and Daily Temperature Variation. J. Rock Mech. Geotech. Eng. 2024, 16, 1722–1731. [Google Scholar] [CrossRef]
- Xu, J.; Yao, X.; Xu, T. Heat Conduction Behaviors in Semiflexible Pavements Using Discrete-Element Method. J. Transp. Eng. Part B: Pavements 2023, 149, 8001–8015. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Q.; Du, Z.; Wu, H.; Sun, Y. Snow-Melting Pavement Design Strategy with Electric Cable Heating System Balancing Snow Melting, Energy Conservation, and Mechanical Performance. Resour. Conserv. Recycl. 2022, 177, 105970. [Google Scholar] [CrossRef]
- Sha, A.; Zhang, J.; Jia, M.; Jiang, W.; Jiao, W. Development of Polyurethane-Based Solid-Solid Phase Change Materials for Cooling Asphalt Pavements. Energy Build. 2022, 259, 111873. [Google Scholar] [CrossRef]
- Golden, J.S.; Kaloush, K.E. Mesoscale and Microscale Evaluation of Surface Pavement Impacts on the Urban Heat Island Effects. Int. J. Pavement Eng. 2006, 7, 37–52. [Google Scholar]
- Yaghoobian, N.; Kleissl, J. An Indoor–Outdoor Building Energy Simulator to Study Urban Modification Effects on Building Energy Use—Model Description and Validation. Energy Build. 2012, 54, 407–417. [Google Scholar] [CrossRef]
- Feng, J.; Yin, G. Thermal Analyses and Responses of Bridge Deck Hydronic Snow Melting System. Adv. Civ. Eng. 2019, 2019, 8172494. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, J.; Zhan, L.; Ma, F.; Yan, J.; Wang, T. Study on Groundwater Recharge Based on Chloride Mass Balance and Hydrochemistry in the Irrigated Agricultural Area, North China Plain. Environ. Earth Sci. 2023, 82, 70. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, X.; Guo, D.; Wang, F.; Xie, H. The Interlaminar Shear Failure Characteristics of Asphalt Pavement Coupled Heating Cables. Mater. Struct. 2018, 51, 67. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Q.; Chen, L.; Du, Z. Mechanical Response of Hydronic Asphalt Pavement Under Temperature–Vehicle Coupled Load: A Finite Element Simulation and Accelerated Pavement Testing Study. Constr. Build. Mater. 2021, 272, 121884. [Google Scholar] [CrossRef]
- Huang, C.; Li, J.; Xiao, H.; Gan, S.; Xie, X. Experimental Study of Ice Melting of Concrete Permeable Brick Sidewalks Using Embedded Carbon Fibre Heating Wire. Road Mater. Pavement Des. 2024, 25, 1191–1210. [Google Scholar] [CrossRef]
- Chen, J.; Wang, H.; Xie, P.; Najm, H. Analysis of Thermal Conductivity of Porous Concrete Using Laboratory Measurements and Microstructure Models. Constr. Build. Mater. 2019, 218, 90–98. [Google Scholar] [CrossRef]
- Luo, Y.; Wu, H.; Song, W.; Yin, J.; Zhan, Y.; Yu, J.; Abubakar Wada, S. Thermal Fatigue and Cracking Behaviors of Asphalt Mixtures Under Different Temperature Variations. Constr. Build. Mater. 2023, 369, 130623. [Google Scholar] [CrossRef]
- Chen, J.; Wang, H.; Xie, P. Pavement Temperature Prediction: Theoretical Models and Critical Affecting Factors. Appl. Therm. Eng. 2019, 158, 113755. [Google Scholar] [CrossRef]
- Qin, Y.; Hiller, J.E. Understanding Pavement-Surface Energy Balance and Its Implications on Cool Pavement Development. Energy Build. 2014, 85, 389–399. [Google Scholar] [CrossRef]
- Du, Y.; Dai, M.; Deng, H.; Deng, D.; Wei, T.; Li, W. Evaluation of Thermal and Anti-Rutting Behaviors of Thermal Resistance Asphalt Pavement with Glass Microsphere. Constr. Build. Mater. 2020, 263, 120609. [Google Scholar] [CrossRef]
- Du, Y.; Wang, J.; Deng, H.; Liu, Y.; Tian, J.; Wu, X. Using Steel Fibers to Accelerate the Heat Conduction in Asphalt Mixture and Its Performance Evaluation. Constr. Build. Mater. 2021, 282, 122637. [Google Scholar] [CrossRef]
- Xu, X.; Chen, J.; Zhou, J.; Li, B. Thermal Conductivity of Polymers and Their Nanocomposites. Adv. Mater. 2018, 30, 1705544. [Google Scholar] [CrossRef]
- Wang, F.; Fu, C.; Liu, K.; Huang, S.; Gao, Y.; Xie, H. Experimental Study and Numerical Simulation of Concrete Pavement Electrical Heating for Snow Melting. Constr. Build. Mater. 2024, 442, 137611. [Google Scholar] [CrossRef]
- Jiao, W.; Sha, A.; Liu, Z.; Jiang, W.; Hu, L.; Qin, W. Analytic Investigations of Snow Melting Efficiency and Temperature Field of Thermal Conductive Asphalt Concrete Combined with Electrical-Thermal System. J. Clean. Prod. 2023, 399, 136622. [Google Scholar] [CrossRef]
- Liu, K.; Xie, H.; Jin, C.; Huang, S.; Wang, F. The Equivalent Plasticity Strain Analysis of Snow-Melting Heated Pavement Concrete Exposed to Inner Elevated Temperatures. Constr. Build. Mater. 2017, 137, 66–75. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, G.; Tao, X.; Xiao, H.; Liu, K.; Chen, Z. Experimental Study on Snow Melting and Deicing of Carbon Fiber Heating Roads Considering Thermal Insulation Conditions. Case Stud. Therm. Eng. 2024, 60, 104806. [Google Scholar] [CrossRef]
- Fu, C.; Liu, K.; Zhi, W.; Liu, P.; Oeser, M. Comprehensive Evaluation of Thermally Conductive Functional Layer on Snow-Melting Performance for Electric Heating Bridge System. Cold Reg. Sci. Technol. 2024, 219, 104099. [Google Scholar] [CrossRef]
- Zhu, J. A Three-Cell Effective Thermal Conductivity Model of Two-Phase Porous Media. Int. J. Heat Mass Transf. 2023, 209, 124127. [Google Scholar] [CrossRef]
- Sheng, Y.; Li, C.; Wang, J.; Xia, X.; Weng, G.J.; Su, Y. Multiscale Modeling of Thermal Conductivity of Hierarchical CNT-Polymer Nanocomposite System with Progressive Agglomeration. Carbon 2023, 201, 785–795. [Google Scholar] [CrossRef]
- Kumar, A.; Wojciechowski, K.T. Effect of Interface Thermal Resistance on Thermoelectric Properties of Acoustically Mismatched Composite. J. Eur. Ceram. Soc. 2022, 42, 4227–4232. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Zhang, X. Heat Transfer Mechanism of Asphalt Pavement Based on Entransy Dissipation Analysis. J. Therm. Anal. Calorim. 2024, 149, 8001–8015. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X. Entransy Dissipation Thermal Resistance for Asphalt Pavement and Application in Optimization of Cooling Structure. J. Therm. Anal. Calorim. 2024, 149, 2665–2681. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Liu, X.B.; Tao, W.Q.; Shah, R.K. Effectiveness–Thermal Resistance Method for Heat Exchanger Design and Analysis. Int. J. Heat Mass Transf. 2010, 53, 2877–2884. [Google Scholar] [CrossRef]
- Chen, Q.; Liang, X.-G.; Guo, Z.-Y. Entransy Theory for the Optimization of Heat Transfer—A Review and Update. Int. J. Heat Mass Transf. 2013, 63, 65–81. [Google Scholar] [CrossRef]
- Guo, Z.-Y.; Zhu, H.-Y.; Liang, X.-G. Entransy—A Physical Quantity Describing Heat Transfer Ability. Int. J. Heat Mass Transf. 2007, 50, 2545–2556. [Google Scholar] [CrossRef]
- Chen, L. Progress in Entransy Theory and Its Applications. Chin. Sci. Bull. 2012, 57, 4404–4426. [Google Scholar] [CrossRef]
- Xu, B.; Lu, S.; Jia, W.; Du, H.; Fan, M.; Wang, R. Thermodynamic Study on Charge-Discharge Processes and Cycle of Cascaded Latent Heat Storage in Heating System. Energy Build. 2021, 249, 111216. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, Y. Optimization of Double-Stage Latent Heat Storage Unit in Whole Cycle with Entransy Analysis. Int. J. Heat Mass Transf. 2017, 114, 1013–1024. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, P.; Wang, T.; Liu, C. Variabilities and Their Upper and Lower Bounds of the Equivalent Thermal Conductivity and Resistance Defined by the Entransy Dissipation Rate. Int. J. Heat Mass Transf. 2021, 170, 120990. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, L.; Du, Y.; Wang, H.; Dan, H. Three-Dimensional Microstructure Based Model for Evaluating the Coefficient of Thermal Expansion and Contraction of Asphalt Concrete. Constr. Build. Mater. 2021, 284, 122764. [Google Scholar] [CrossRef]
- Chen, J.-Q.; Li, L.; Wang, H. Analytical Prediction and Field Validation of Transient Temperature Field in Asphalt Pavements. J. Cent. South Univ. 2015, 22, 4872–4881. [Google Scholar] [CrossRef]
- Simoncelli, M.; Zucca, M.; Stochino, F. Fire Resistance of Steel Rack Frames: Assessment, Reinforcement and Collapse Mitigation Strategies. Fire Technol. 2024, 1–23. [Google Scholar] [CrossRef]
- Yiqiu, T.; Chi, Z.; Huijie, L.; Hao, S.; Huining, X. Experimental and Numerical Analysis of the Critical Heating Strategy for Hydronic Heated Snow Melting Airfield Runway. Appl. Therm. Eng. 2020, 178, 115508. [Google Scholar] [CrossRef]
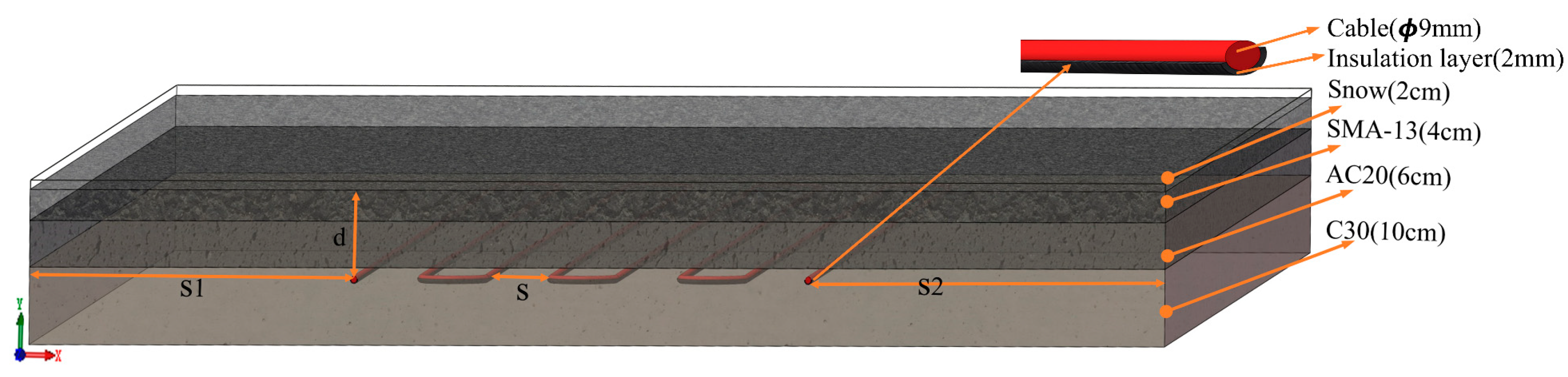












| Material | Thickness (mm) | Density (kg/m3) | Thermal Conductivity (W/(m·k)) | Specific Heat Capacity (J/(kg·k)) | Poisson’s Ratio (-) |
|---|---|---|---|---|---|
| Cable | Diameter 9 mm | 7930 | 24.5 | 510 | 0.3 |
| Upper layer | 40 | 2300 | 0.833 | 1000 | 0.35 |
| Lower layer | 60 | 2400 | 1.583 | 970 | 0.35 |
| C30 | 100 | 2380 | 1.74 | 925 | 0.24 |
| Snow | 20 | 450 | 2.2 | 2050 | - |
| Insulation layer | 2 | 400 | 0.18 | 400 | 0.26 |
| Parameters | Embedding Depth (d/mm) | Thermal Insulation Layer/mm | Snow Thickness/mm |
|---|---|---|---|
| Scheme 1 | 115 | 0 | 20 |
| Scheme 2 | 115 | 2 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Chen, Z.; Xiao, H.; Zhu, M.; Wang, Z. Heat Transfer Characteristics of Electrical Heating Deicing and Snow-Melting Asphalt Pavement Under Different Operating Conditions. Coatings 2025, 15, 367. https://doi.org/10.3390/coatings15040367
Xu K, Chen Z, Xiao H, Zhu M, Wang Z. Heat Transfer Characteristics of Electrical Heating Deicing and Snow-Melting Asphalt Pavement Under Different Operating Conditions. Coatings. 2025; 15(4):367. https://doi.org/10.3390/coatings15040367
Chicago/Turabian StyleXu, Kai, Zhi Chen, Henglin Xiao, Mengjun Zhu, and Zhiyong Wang. 2025. "Heat Transfer Characteristics of Electrical Heating Deicing and Snow-Melting Asphalt Pavement Under Different Operating Conditions" Coatings 15, no. 4: 367. https://doi.org/10.3390/coatings15040367
APA StyleXu, K., Chen, Z., Xiao, H., Zhu, M., & Wang, Z. (2025). Heat Transfer Characteristics of Electrical Heating Deicing and Snow-Melting Asphalt Pavement Under Different Operating Conditions. Coatings, 15(4), 367. https://doi.org/10.3390/coatings15040367





