Analysis of Electromagnetic Wave Propagation in Carbon Nanotube-Coated Metamaterials in Terms of Backward Electromagnetic Waves
Abstract
:1. Introduction
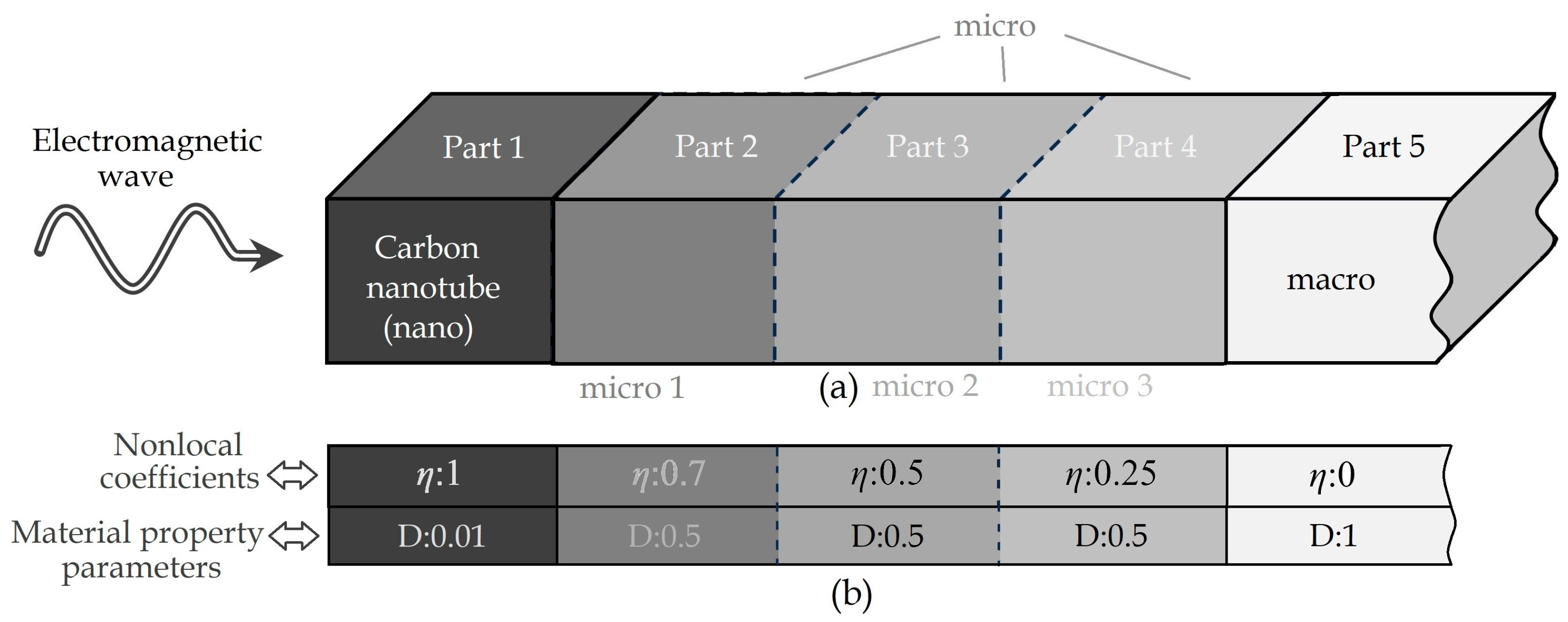
2. Materials and Methods
3. Results
- -
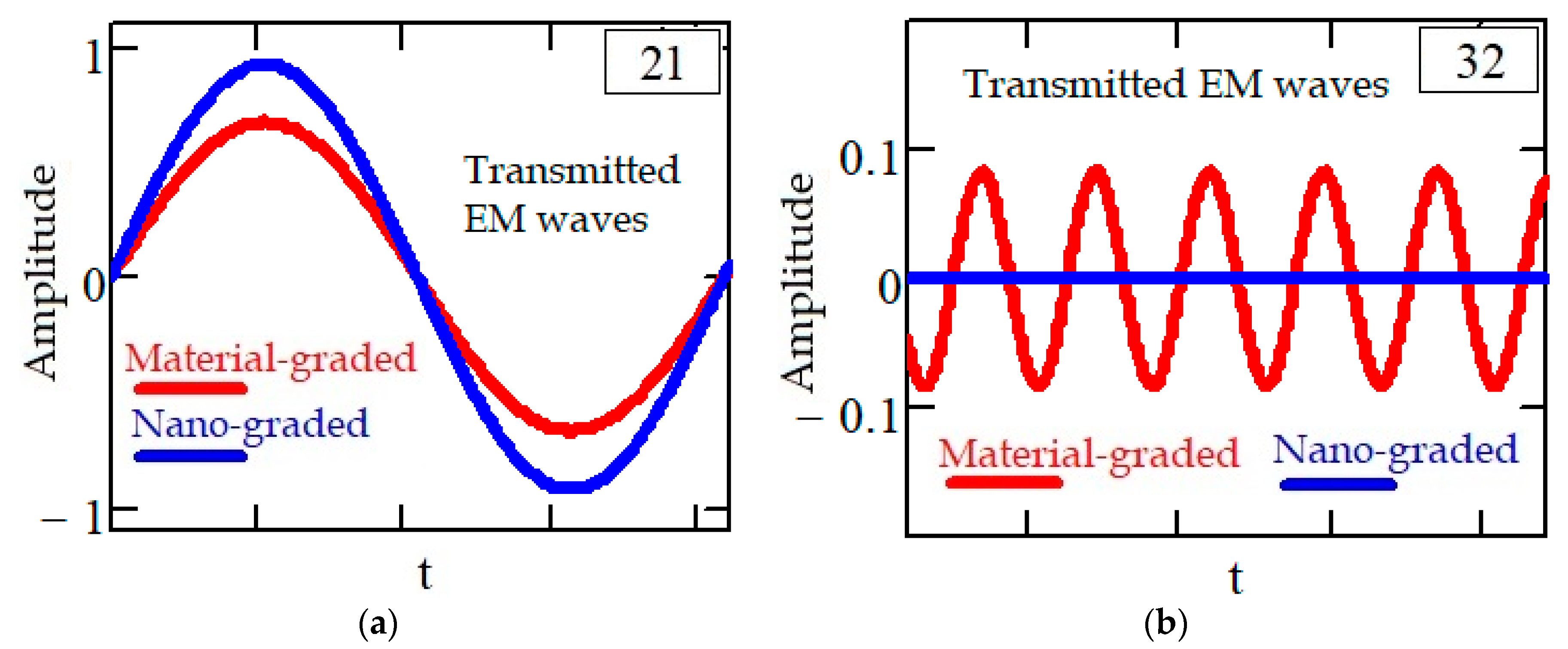
- The EM wave traveling from Part 1 to Part 2 is denoted as 21.
- -
- The EM wave traveling from Part 2 to Part 3 is indicated by 32.
- -
- The EM wave traveling from Part 3 to Part 4 is represented by 43.
- -
- The EM wave traveling from Part 4 to Part 5 is labeled 54.
| Electromagnetic Waves | Nano-Graded (%) | Material-Graded (%) |
|---|---|---|
| 21 | 92.310 | 66.942 |
| 32 | 0 | 8.264 |
| 43 | 0 | 3.966 |
| 54 | 0 | 0.648 |
| 4534 | 0 | 0.544 |
| 3423 | 0.087 | 0.457 |
| 2312 | 0.065 | 0.151 |
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cornwell, D. Space-based laser communications break threshold. Opt. Photonics News 2016, 27, 24–31. [Google Scholar] [CrossRef]
- Araki, K.; Arimoto, Y.; Shikatani, M.; Toyoda, M.; Toyoshima, M.; Takahashi, T.; Kanda, S.; Shiratama, K. Performance evaluation of laser communication equipment onboard the ETS-VI satellite. In Proceedings of the SPIE—The International Society for Optical Engineering, San Jose, CA, USA, 22 April 1996. [Google Scholar] [CrossRef]
- Tan, J.; Zhao, Z.; Wang, Y.; Zhang, Z.; Liu, J.; Zhu, N. 12.5 Gb/s multi-channel broadcasting transmission for free-space optical communication based on the optical frequency comb module. Opt. Express 2018, 26, 2099. [Google Scholar] [CrossRef] [PubMed]
- Poyanco, J.-M.; Pizarro, F.; Roja-Iglesias, E. 3D-Printing for transformation optics in electromagnetic high-frequency lens applications. Materials 2020, 13, 2700. [Google Scholar] [CrossRef] [PubMed]
- Zengerle, R. Light propagation in singly and doubly periodic planar waveguides. J. Mod. Opt. 1987, 34, 1589–1617. [Google Scholar] [CrossRef]
- Karakilinc, O.O.; Dinleyici, M.S. Design of dual-mode dual-band photonic crystal bandpass filters for terahertz communication applications. Microw. Opt. Technol. Lett. 2015, 57, 1806–1810. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 2008; pp. 1–43. [Google Scholar]
- Boyd, R.W. Nonlinear Optics; Academic Press: London, UK, 2020; pp. 1–135. [Google Scholar]
- Gorur, A.K.; Karpuz, C.; Ozek, A.; Emur, M. Metamaterial based dual-band bandpass filter design for WLAN/WiMAX applications. Microw. Opt. Technol. Lett. 2014, 56, 2211–2214. [Google Scholar] [CrossRef]
- Sohoo, A.A.; Seman, F.C.; Al-Gburi, A.J.A.; Ahmad, H.; Khee, Y.S.; Ishak, N.S.B.; Alghamdi, T.A.H.; Alathbah, M. Exploiting surface plasmon with dielectric coating in copper wires waveguide for the propagation of terahertz waves. Coatings 2023, 13, 1857. [Google Scholar] [CrossRef]
- Basmaci, A.N. Characteristics of electromagnetic wave propagation in a segmented photonic waveguide. J. Optoelectron. Adv. Mater. 2020, 22, 452–460. [Google Scholar]
- Fomenko, S.I.; Golub, M.V.; Zhang, C.; Bui, T.Q.; Wang, Y.-S. In-plane elastic wave propagation and band-gaps in layered functionally graded phononic crystals. Int. J. Solids Struct. 2014, 51, 2491–2503. [Google Scholar] [CrossRef]
- Jahani, S.; Jacob, Z. All-dielectic metamaterials. Nat. Nanotechnol. 2016, 11, 23–36. [Google Scholar] [CrossRef]
- El Haddad, A. Exact analytical solution for the electromagnetic wave propagation in a photonic band gaps material with sinusoidal periodicity of dielectric permittivity. Optik 2016, 127, 1627–1629. [Google Scholar] [CrossRef]
- Elakkiya, A.; Radha, S.; Sreeja, B.S.; Manikandan, E. Terahertz metamaterial absorber with sensing capabilities. J. Optoelectron. Adv. Mater. 2020, 22, 360–364. [Google Scholar]
- Fathallah, W.; Sakli, H.; Aguili, T. Electromagnetic wave propagation in anisotropic metamaterial waveguides. Int. J. Numer. Model. 2014, 28, 479–486. [Google Scholar] [CrossRef]
- Chen, J.; Dai, Y.; Yan, L.; Zhao, H. Steady bound electromagnetic eigenstate arises in a homogeneous isotropic linear metamaterial with zero-real-part-of-impedance and nonzero-imaginary-part-of-wave-vector. Opt. Commun. 2018, 413, 167–171. [Google Scholar] [CrossRef]
- Kaya, N.; Delihacioglu, K. Reflection and transmission coefficients from chiral nihility slab. J. Optoelectron. Adv. Mater. 2014, 16, 859–863. [Google Scholar]
- Tu, W.; Zhong, S.; Zhang, Q.; Huang, Y.; Luo, M. Improved numerical modelling of terahertz wave propagation in epoxy coating with the finite-difference time-domain method. Coatings 2023, 13, 1593. [Google Scholar] [CrossRef]
- Deng, L.; Han, M. Microwave absorbing performances of multiwalled carbon nanotube composites with negative permeability. Appl. Phys. Lett. 2007, 91, 023119. [Google Scholar] [CrossRef]
- Gama, A.M.; Rezende, M.C. Complex permeability and permittivity variation of radar absorbing materials based on MnZn ferrite in microwave frequencies. Mater. Res. 2013, 16, 997–1001. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703. [Google Scholar] [CrossRef]
- Hajdo, L.E.; Eringen, A.C. Application of nonlocal theory to electromagnetic dispersion. Lett. Appl. Eng. Sci. 1979, 17, 785–791. [Google Scholar] [CrossRef]
- Keller, O.; Pedersen, J.H. A nonlocal description of the dispersion relation and the energy flow associated with surface electromagnetic waves on metals. Scatt. Diffr. 1988, 1029, 18–726. [Google Scholar] [CrossRef]
- Mikki, S. Directive properties of radiating source systems in massive electromagnetism. Results Phys. 2022, 42, 105886. [Google Scholar] [CrossRef]
- Basmaci, A.N.; Filiz, S. Electromagnetic wave propagation behavior of conjoined carbon nanotubes. J. Optoelectron. Adv. Mater. 2023, 25, 580–585. [Google Scholar]
- Zhou, S.; Bi, K.; Li, Q.; Mei, L.; Niu, Y.; Fu, W.; Han, S.; Zhang, S.; Mu, J.; Tan, L.; et al. Patterned graphene-based metamaterials for terahertz wave absorption. Coatings 2023, 13, 59. [Google Scholar] [CrossRef]
- Munalli, D.; Dimitrakis, G.; Chronopoulos, D.; Greedy, S.; Long, A. Electromagnetic shielding effectiveness of carbon fibre reinforced composites. Compos. B Eng. 2019, 173, 106906. [Google Scholar] [CrossRef]
- Kolanowska, A.; Janas, D.; Herman, A.P.; Jedrysiak, R.G.; Gizewski, T.; Boncel, S. From blackness to invisibility—Carbon nanotubes role in the attenuation of and shielding from waves radio waves for stealth technology. Carbon 2018, 126, 31–52. [Google Scholar] [CrossRef]
- Zohuri, B. Radar Energy Warfare and the Challenges of Stealth Technology; Springer Nature: Cham, Switzerland, 2020; pp. 205–310. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, H.; Hu, X.; Ju, D. A novel processing for cnt-reinforced Mg-matrix laminated composites to enhance the electromagnetic shielding property. Coatings 2021, 11, 1030. [Google Scholar] [CrossRef]
- Sun, H.; Che, R.; You, X.; Jiang, Y.; Yang, Z.; Deng, J.; Qiu, L.; Peng, H. Cross-stacking aligned carbon-nanotube films to tune microwave absorption frequencies and increase absorption intensities. Adv. Mater. 2014, 26, 8120–8125. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2012; pp. 1–47. [Google Scholar]
- Cheng, D.K. Field and Wave Electromagnetics; Pearson New International Edition: London, UK, 2013; pp. 307–347. [Google Scholar]
- Basmaci, A.N. Characteristics of electromagnetic waves propagating in 2d photonic crystals. In Engineering Sciences Innovative Approaches; Asci, Y., Ed.; Livre de Lyon: Lyon, France, 2021; pp. 1–23. [Google Scholar]
- Basmaci, A.N. The bahavior of electromagnetic wave propagation in photonic crystals with or without a defect. Appl. Comput. Electromagn. Soc. J. 2021, 36, 632–641. [Google Scholar] [CrossRef]
- Zheng, H.; Fan, Z.; Li, J. Simulation of electromagnetic wave propagations in negative index materials by the localized RBF-collocation method. Eng. Anal. Bound. Elem. 2022, 136, 204–212. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basmaci, A.N.; Filiz, S. Analysis of Electromagnetic Wave Propagation in Carbon Nanotube-Coated Metamaterials in Terms of Backward Electromagnetic Waves. Coatings 2025, 15, 455. https://doi.org/10.3390/coatings15040455
Basmaci AN, Filiz S. Analysis of Electromagnetic Wave Propagation in Carbon Nanotube-Coated Metamaterials in Terms of Backward Electromagnetic Waves. Coatings. 2025; 15(4):455. https://doi.org/10.3390/coatings15040455
Chicago/Turabian StyleBasmaci, Ayse Nihan, and Seckin Filiz. 2025. "Analysis of Electromagnetic Wave Propagation in Carbon Nanotube-Coated Metamaterials in Terms of Backward Electromagnetic Waves" Coatings 15, no. 4: 455. https://doi.org/10.3390/coatings15040455
APA StyleBasmaci, A. N., & Filiz, S. (2025). Analysis of Electromagnetic Wave Propagation in Carbon Nanotube-Coated Metamaterials in Terms of Backward Electromagnetic Waves. Coatings, 15(4), 455. https://doi.org/10.3390/coatings15040455






