Evaluation of Hydrogen Trapping Capability at Interfaces Between Vanadium Carbide and Vanadium Nitride Nanoprecipitates with α-Fe by Density Functional Theory
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Geometric Structure
3.2. Stability of Different Structures
3.2.1. Formation Enthalpy
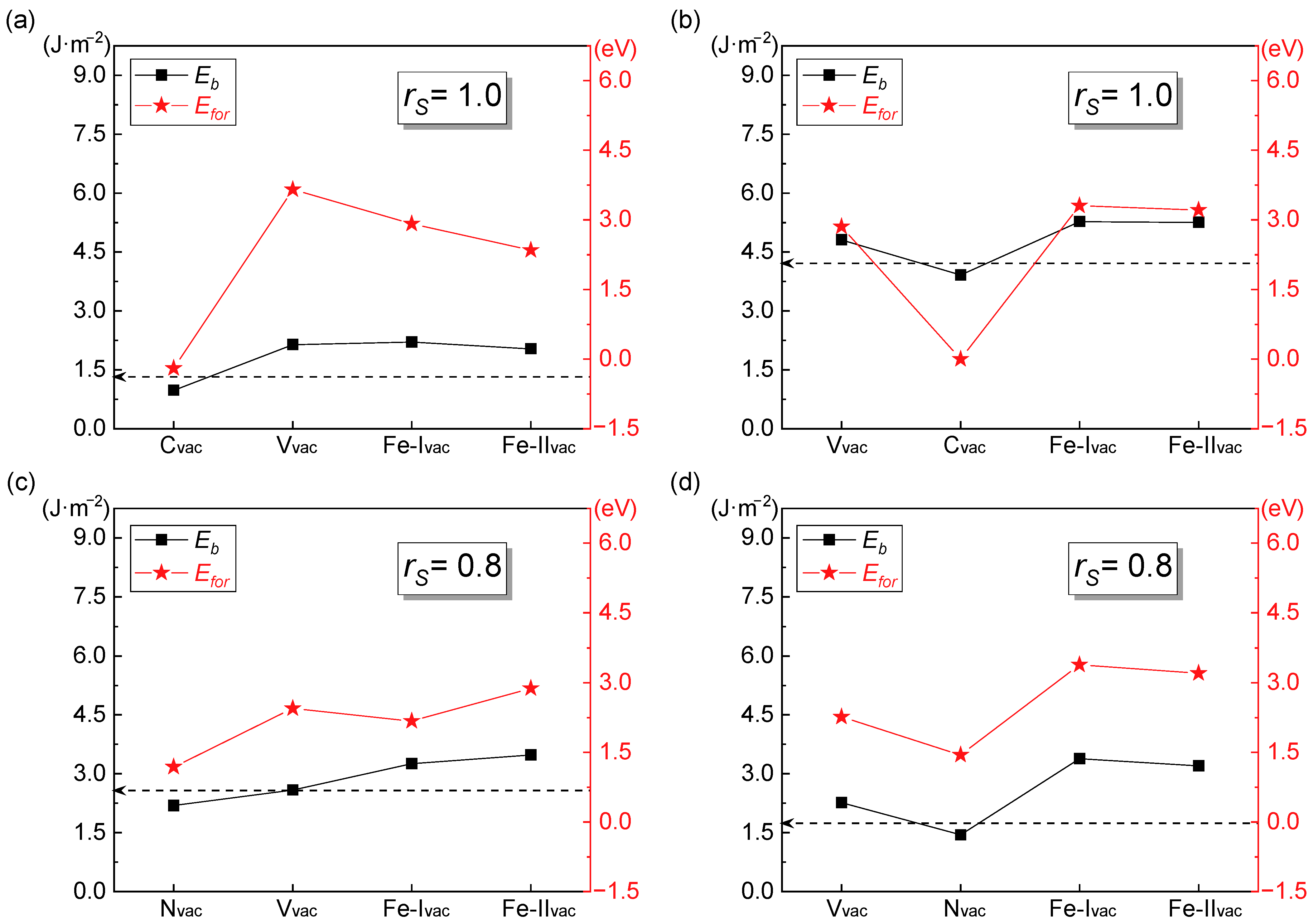
3.2.2. Interfacial Binding Energy
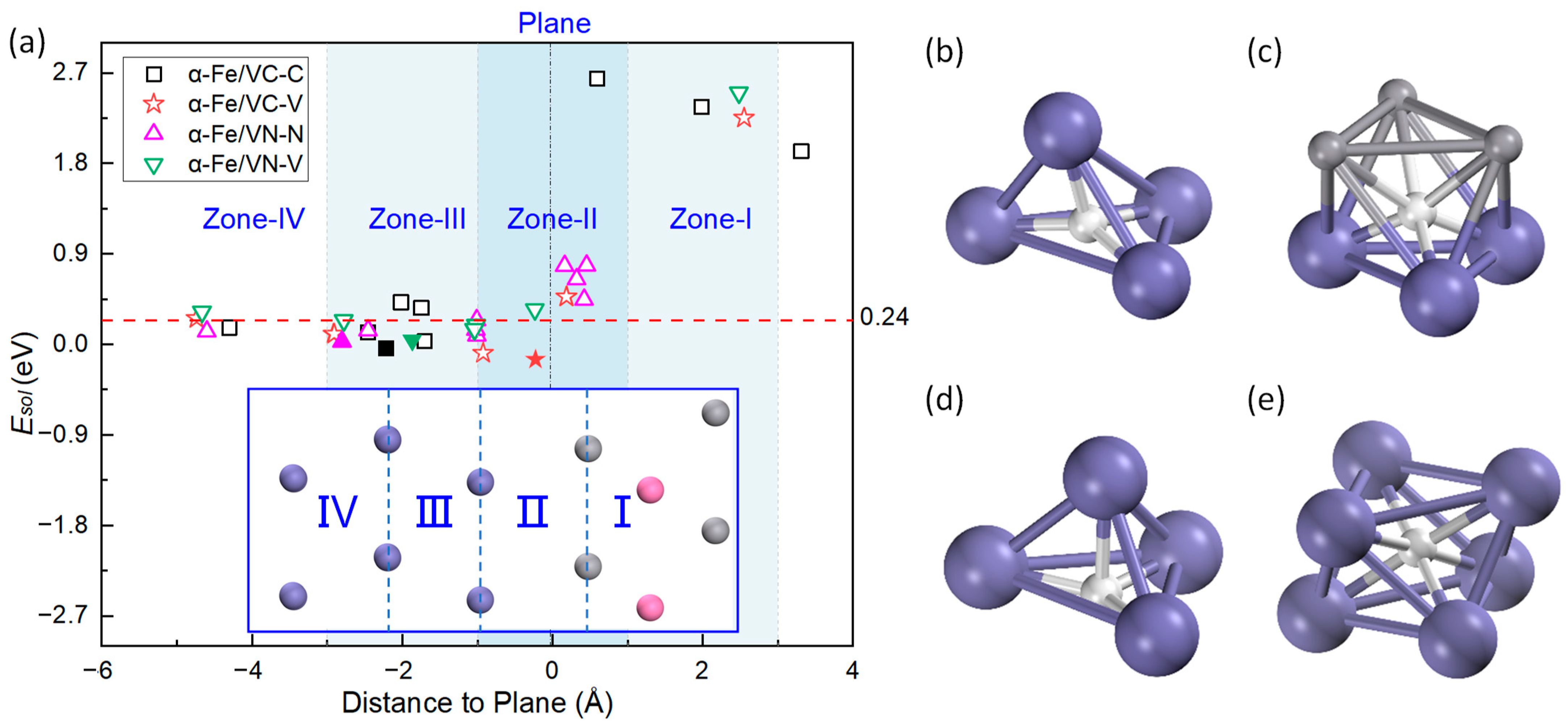
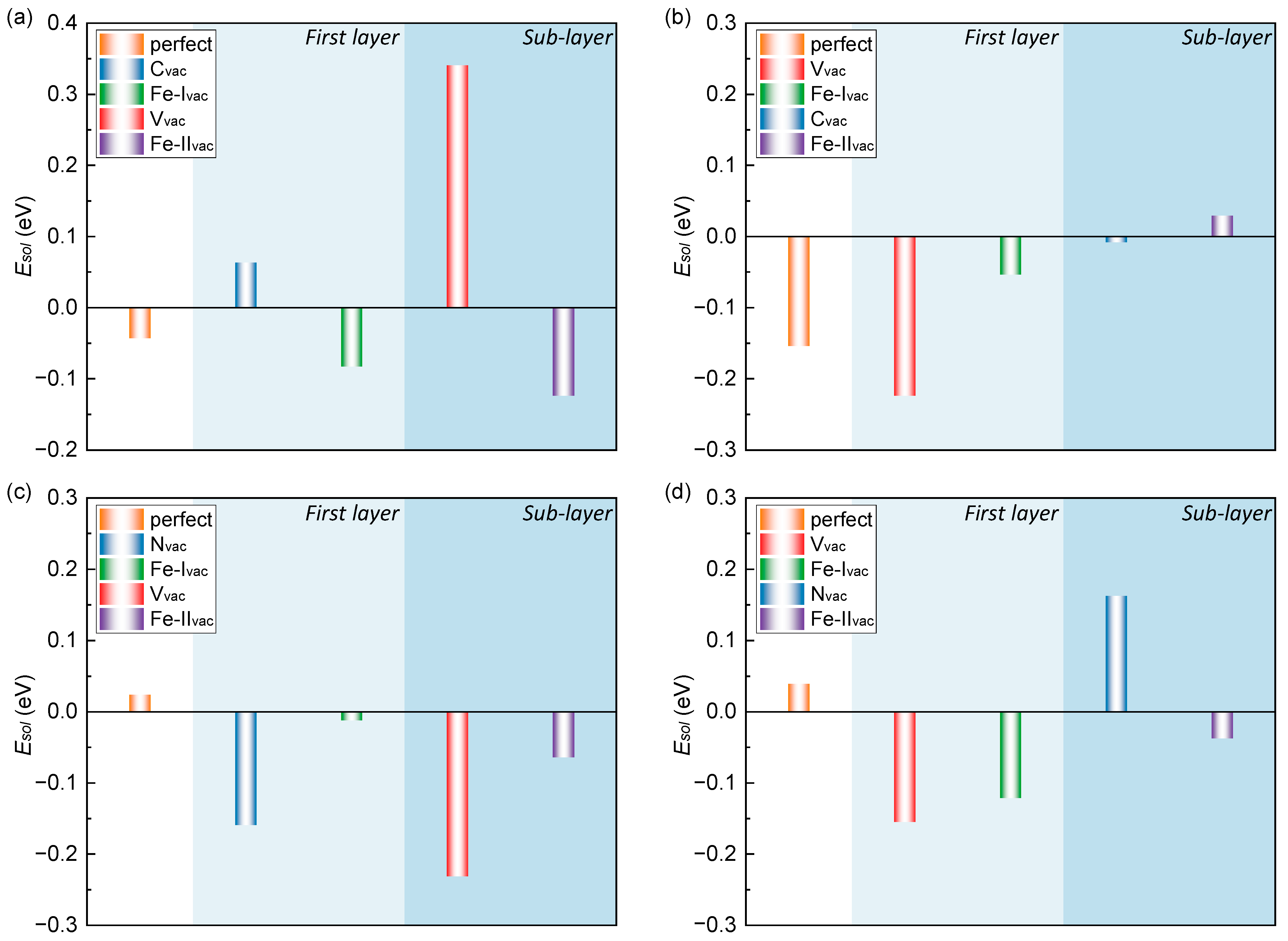
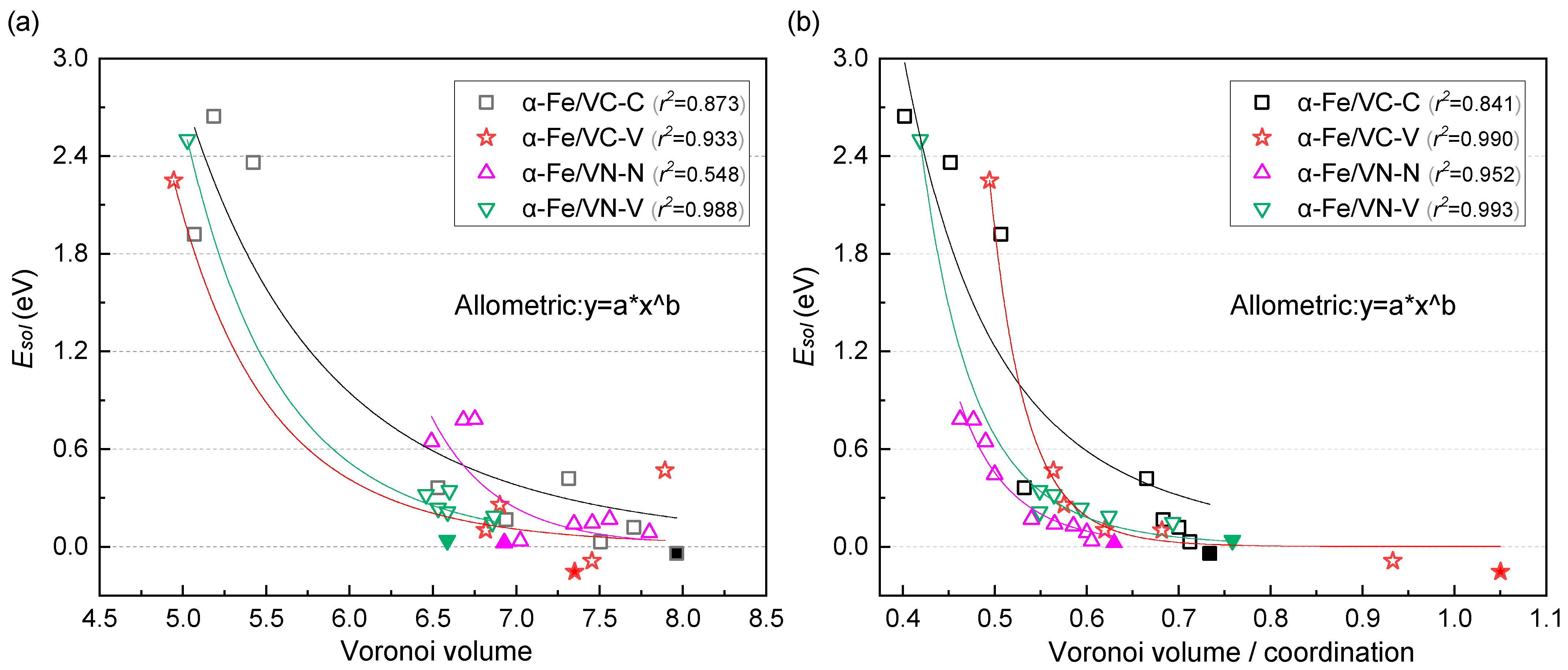
3.3. H Interaction with the Interface Solubility
4. Discussion
4.1. Influence of Vacancy on Interfacial Stability
4.2. Segregation of H in the Interface
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| K-S | Kurdjumov–Sachs |
| B-N | Baker–Nutting |
| APT | atom probe tomography |
| DFT | density functional theory |
| GGA | generalized gradient approximation |
| BCC | body-centered cubic |
| TIS | tetrahedral interstitial site |
| OIS | octahedral interstitial site |
| LDOS | local density of states |
| PDOS | projected density of states |
References
- Bosque, A.; Fernández-Arias, P.; Vergara, D. Advancements in Hydrogen Storage Vessels: A Bibliometric Analysis. Sci 2025, 7, 21. [Google Scholar] [CrossRef]
- Shin, D.H.; Kim, S.J. Effect of hydrogen embrittlement on mechanical characteristics of DLC-coating for hydrogen valves of FCEVs. npj Mater. Degrad. 2024, 8, 47. [Google Scholar] [CrossRef]
- Sun, B.; Zhao, H.; Dong, X.; Teng, C.; Zhang, A.; Kong, S.; Zhou, J.; Zhang, X.; Tu, S. Current challenges in the utilization of hydrogen energy-a focused review on the issue of hydrogen-induced damage and embrittlement. Adv. Appl. Energy 2024, 14, 100168. [Google Scholar] [CrossRef]
- Meda, U.S.; Bhat, N.; Pandey, A.; Subramanya, K.N.; Raj, M.L.A. Challenges associated with hydrogen storage systems due to the hydrogen embrittlement of high strength steels. Int. J. Hydrogen Energy 2023, 48, 17894–17913. [Google Scholar] [CrossRef]
- Yu, H.; Díaz, A.; Lu, X.; Sun, B.; Ding, Y.; Koyama, M.; He, J.; Zhou, X.; Oudriss, A.; Feaugas, X.; et al. Hydrogen embrittlement as a conspicuous material challenge—Comprehensive review and future directions. Chem. Rev. 2024, 124, 6271–6392. [Google Scholar] [CrossRef]
- Meng, B.; Gu, C.; Zhang, L.; Zhou, C.; Li, X.; Zhao, Y.; Zheng, J.; Chen, X.; Han, Y. Hydrogen effects on X80 pipeline steel in high-pressure natural gas/hydrogen mixtures. Int. J. Hydrogen Energy 2017, 42, 7404–7412. [Google Scholar] [CrossRef]
- Dwivedi, S.K.; Vishwakarma, M. Hydrogen embrittlement in different materials: A review. Int. J. Hydrogen Energy 2018, 43, 21603–21616. [Google Scholar] [CrossRef]
- Giannini, L.; Razavi, N.; Alvaro, A.; Paltrinieri, N. Embrittlement, degradation, and loss prevention of hydrogen pipelines. MRS Bull. 2024, 49, 464–477. [Google Scholar] [CrossRef]
- Ilyushechkin, A.; Schoeman, L.; Carter, L.; Hla, S.S. Material challenges and hydrogen embrittlement assessment for hydrogen utilisation in industrial scale. Hydrogen 2023, 4, 599–619. [Google Scholar] [CrossRef]
- Sezgin, J.G.; Bosch, C.; Montouchet, A.; Perrin, G.; Wolski, K. Modelling of hydrogen induced pressurization of internal cavities. Int. J. Hydrogen Energy 2017, 42, 15403–15414. [Google Scholar] [CrossRef]
- Xie, D.; Li, S.; Li, M.; Wang, Z.; Gumbsch, P.; Sun, J.; Ma, E.; Li, J.; Shan, Z. Hydrogenated vacancies lock dislocations in aluminium. Nat. Commun. 2016, 7, 13341. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Curtin, W.A. Atomic mechanism and prediction of hydrogen embrittlement in iron. Nat. Mater. 2013, 12, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Troiano, A.R. The role of hydrogen and other interstitials in the mechanical behavior of metals. Metallogr. Microstruct. Anal. 2016, 5, 557–569. [Google Scholar] [CrossRef]
- Li, X.; Ma, X.; Zhang, J.; Akiyama, E.; Wang, Y.; Song, X. Review of hydrogen embrittlement in metals: Hydrogen diffusion, hydrogen characterization, hydrogen embrittlement mechanism and prevention. Acta Metall. Sin. (Engl. Lett.) 2020, 33, 759–773. [Google Scholar] [CrossRef]
- Wang, S.; Martin, M.L.; Sofronis, P.; Ohnuki, S.; Hashimoto, N.; Robertson, I.M. Hydrogen-induced intergranular failure of iron. Acta Mater. 2014, 69, 275–282. [Google Scholar] [CrossRef]
- Martin, M.L.; Fenske, J.A.; Liu, G.S.; Sofronis, P.; Robertson, I.M. On the formation and Nature of quasi-cleavage fracture surfaces in hydrogen embrittled steels. Acta Mater. 2011, 59, 1601–1606. [Google Scholar] [CrossRef]
- Djukic, M.B.; Bakic, G.M.; Zeravcic, V.S.; Sedmak, A.; Rajicic, B. The synergistic action and interplay of hydrogen embrittlement mechanisms in steels and iron: Localized plasticity and decohesion. Eng. Fract. Mech. 2019, 216, 106528. [Google Scholar] [CrossRef]
- Oriani, R.A. The diffusion and trapping of hydrogen in steel. Acta Metall. 1970, 18, 147. [Google Scholar] [CrossRef]
- Counts, W.A.; Wolverton, C.; Gibala, R. First-principles energetics of hydrogen traps in α-Fe: Point defects. Acta Mater. 2010, 58, 4730–4741. [Google Scholar] [CrossRef]
- Haas, P.; Tran, F.; Blaha, P. Calculation of the lattice constant of solids with semilocal functionals. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 79, 085104. [Google Scholar] [CrossRef]
- Davey, W.P. Precision measurements of the lattice constants of twelve common metals. Phys. Rev. 1925, 25, 753. [Google Scholar] [CrossRef]
- Li, M.; Zhang, H.; Henein, H.; Liu, J. Hydrogen traping in precipitates of high-strength steel: Insights into various coherent and stress conditions. Int. J. Hydrogen Energy 2024, 92, 1356–1365. [Google Scholar] [CrossRef]
- Wang, H.; Ren, H.; Han, L.; Jin, Z.; Sun, H. Microstructure and texture comparison of an acicular ferrite pipeline steel with different hot rolling process. Adv. Mat. Res. 2012, 399, 264–267. [Google Scholar] [CrossRef]
- Wei, F.G.; Hara, T.; Tsuzaki, K. Nano-Preciptates Design with Hydrogen Trapping Character in High Strength Steel. In Advanced Steels; Springer: Berlin/Heidelberg, Germany, 2011; pp. 87–92. [Google Scholar] [CrossRef]
- Kirchheim, R. Changing the interfacial composition of carbide precipitates in metals and its effect on hydrogen trapping. Scr. Mater. 2019, 160, 62–65. [Google Scholar] [CrossRef]
- Wei, F.G.; Tsuzaki, K. Quantitative analysis on hydrogen trapping of TiC particles in steel. Metall. Mater. Trans. A 2006, 37, 331–353. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Cui, Y.; Djukic, M.B.; Feng, H.; Wang, Y. Review of the hydrogen embrittlement and interactions between hydrogen and microstructural interfaces in metallic alloys: Grain boundary, twin boundary, and nano-precipitate. Int. J. Hydrogen Energy 2024, 72, 74–109. [Google Scholar] [CrossRef]
- Vojvodic, A.; Ruberto, C. Trends in bulk electron-structural features of rocksalt early transition-metal carbides. J. Phys. Condens. Matter Inst. Phys. J. 2010, 22, 375501. [Google Scholar] [CrossRef]
- Nakamura, K.; Yashima, M. Crystal structure of NaCl-type transition metal monocarbides MC (M = V, Ti, Nb, Ta, Hf, Zr), a neutron powder diffraction study. Mater. Sci. Eng. B 2008, 148, 69–72. [Google Scholar] [CrossRef]
- Zhukov, V.; Gubanov, V. The study of the energy band structures of TiC, VC, Ti4C3 and V4C3 by the LMTO-ASA method. J. Phys. Chem. Solids 1987, 48, 187–195. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Y.; Ye, J. Mechanical properties and electronic structures of VC, V4C3 and V8C7 from first principles. Phys. Scr. 2013, 88, 015301. [Google Scholar] [CrossRef]
- Ravi, C. First-principles study of ground-state properties and phase stability of vanadium nitrides. Calphad 2009, 33, 469–477. [Google Scholar] [CrossRef]
- Carlson, O.N.; Smith, J.F.; Nafziger, R.H. The vanadium-nitrogen system: A review. Metall. Mater. Trans. A 1986, 17, 1647–1656. [Google Scholar] [CrossRef]
- Lee, J.; Lee, T.; Kwon, Y.J.; Mun, D.J.; Yoo, J.Y.; Lee, C.S. Effects of vanadium carbides on hydrogen embrittlement of tempered martensitic steel. Met. Mater. Int. 2016, 22, 364–372. [Google Scholar] [CrossRef]
- Takahashi, J.; Kawakami, K.; Tarui, T. Direct observation of hydrogen-trapping sites in vanadium carbide precipitation steel by atom probe tomography. Scr. Mater. 2012, 67, 213–216. [Google Scholar] [CrossRef]
- Ma, Y.; Shi, Y.; Wang, H.; Mi, Z.; Liu, Z.; Gao, L.; Yan, Y.; Su, Y.; Qiao, L. A first-principles study on the hydrogen trap characteristics of coherent nano-precipitates in α-Fe. Int. J. Hydrogen Energy 2020, 45, 27941–27949. [Google Scholar] [CrossRef]
- Sagar, S.; Sluiter, M.H.F.; Dey, P. First-Principles study of hydrogen-Carbide interaction in bcc Fe. Int. J. Hydrogen Energy 2024, 50, 211–223. [Google Scholar] [CrossRef]
- Hammer, P.; Romaner, L.; Razumovskiy, V.I. Hydrogen trapping in mixed carbonitrides. Acta Mater. 2024, 268, 119754. [Google Scholar] [CrossRef]
- Zhang, B.; Su, J.; Wang, M.; Liu, Z.; Yang, Z.; Militzer, M.; Chen, H. Atomistic insight into hydrogen trapping at MC/BCC-Fe phase boundaries: The role of local atomic environment. Acta Mater. 2021, 208, 116744. [Google Scholar] [CrossRef]
- Baker, T.N. Titanium microalloyed steels. Ironmak. Steelmak. 2019, 46, 1–55. [Google Scholar] [CrossRef]
- Chen, J.; Lü, M.; Tang, S.; Liu, Z.; Wang, G. Microstructure, mechanical properties and interphase precipitation behaviors in V-Ti microalloyed steel. Acta Metall. Sin. 2014, 50, 524–530. Available online: https://www.ams.org.cn/EN/Y2014/V50/I5/524 (accessed on 10 December 2024).
- Li, X.; Wang, Z. Interphase precipitation behaviors of nanometer-sized carbides in a Nb-Ti-bearing low-carbon microalloyed steel. Acta Metall. Sin. 2015, 51, 417–424. Available online: https://www.ams.org.cn/EN/Y2015/V51/I4/417 (accessed on 10 December 2024).
- Restrepo, S.E.; Di Stefano, D.; Mrovec, M.; Paxton, A.T. Density functional theory calculations of iron-vanadium carbide interfaces and the effect of hydrogen. Int. J. Hydrogen Energy 2020, 45, 2382–2389. [Google Scholar] [CrossRef]
- Hartford, J. Interface energy and electron structure for Fe/VN. Phys. Rev. B 2000, 61, 2221–2229. [Google Scholar] [CrossRef]
- Davenport, A.T.; Honeycomhe, R.W.K. The secondary hardening of tungsten steels. Met. Sci. 1975, 9, 201–208. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zurob, H.S. The precipitation of NbC on dislocations in austenite. Appl. Phys. A 2002, 74, 1213–1215. [Google Scholar] [CrossRef]
- Van Aswegen, J.S.; Honeycombe, R.W.K.; Warrington, D.H. Precipitation on stacking faults in Cr-Ni austenitic steels. Acta Metall. 1964, 12, 1–13. [Google Scholar] [CrossRef]
- Eom, H.J.; Shin, J.H.; Kong, B.S.; Jeong, C.; Jang, C.; Ahn, D.; Jang, D. Dissolution of nanosized NbC precipitates in austenite matrix during elastic deformation-Deleterious effect of high number density. Mater. Sci. Eng. A 2022, 833, 142506. [Google Scholar] [CrossRef]
- Lee, C.; Nambu, S.; Inoue, J.; Koseki, T. Ferrite formation behaviors from B1 compounds in steels. ISIJ Int. 2011, 51, 2036–2041. [Google Scholar] [CrossRef]
- Shi, R.; Ma, Y.; Wang, Z.; Gao, L.; Yang, X.; Qiao, L.; Pang, X. Atomic-scale investigation of deep hydrogen trapping in NbC/α-Fe semi-coherent interfaces. Acta Mater. 2020, 200, 686–698. [Google Scholar] [CrossRef]
- Chai, J.; Dong, H.; Zhang, J.; Shen, K.; Yang, Z.; Chen, H. On the role of interfacial coherency and carbon in niobium segregation at ferrite/austenite interface: An atomistic study. Scr. Mater. 2024, 247, 116109. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133e8. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Siegel, D.J.; Hector, L.G., Jr.; Adams, J.B. First-principles study of metal-carbide/nitride adhesion: Al/VC vs. Al/VN. Acta Mater. 2002, 50, 619–631. [Google Scholar] [CrossRef]
- Jang, J.H.; Lee, C.H.; Heo, Y.U.; Suh, D.W. Stability of (Ti, M) C (M = Nb, V, Mo and W) carbide in steels using first-principles calculations. Acta Mater. 2012, 60, 208–217. [Google Scholar] [CrossRef]
- Chong, X.; Jiang, Y.; Zhou, R.; Feng, J. Electronic structures mechanical and thermal properties of V-C binary compounds. RSC Adv. 2014, 4, 44959–44971. [Google Scholar] [CrossRef]
- Du, Y.A.; Ismer, L.; Rogal, J.; Hickel, T.; Neugebauer, J.; Drautz, R. First-principles study on the interaction of H interstitials with grain boundaries in α-and γ-Fe. Phys. Rev. B 2011, 84, 144121. [Google Scholar] [CrossRef]
- Jiang, D.E.; Carter, E.A. Diffusion of interstitial hydrogen into and through bcc Fe from first principles. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 70, 064102. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Xu, Y.; Lei, Y.; Xie, Z.; Wang, X.; Fang, Q.; Liu, C.; Wu, X. Hydrogen trapping, desorption and clustering in heterophase interfaces of W-ZrC alloy. Acta Mater. 2023, 242, 118469. [Google Scholar] [CrossRef]
- Bowles, J.S.; Wayman, C.M. The bain strain, lattice correspondences, and deformations related to martensitic transformations. Metall. Trans. 1972, 3, 1113–1121. [Google Scholar] [CrossRef]
- Wang, B.; Gu, N.; Guo, S.; Ma, X. The mathematical description of the K-S mechanism and Bain correspondence. Acta Metall. Sin. 2002, 38, 474–478. Available online: https://www.ams.org.cn/CN/Y2002/V38/I5/474 (accessed on 10 December 2024).
- Ramasubramaniam, A.; Itakura, M.; Ortiz, M.; Carter, E. Effect of atomic scale plasticity on hydrogen diffusion in iron: Quantum mechanically informed and on-the-fly kinetic Monte Carlo simulations. J. Mater. Res. 2008, 23, 2757–2773. [Google Scholar] [CrossRef]
- Miwa, K.; Fukumoto, A. First-principles study on 3d transition-metal dihydrides. Phys. Rev. B 2002, 65, 155114. [Google Scholar] [CrossRef]
- Norsko, J.K. Chemisorption on metal surfaces. Rep. Prog. Phys. 1990, 53, 1253. [Google Scholar] [CrossRef]
- Christmann, K. Hydrogen adsorption on metal surfaces. In Atomistics of Fracture; Springer: Boston, MA, USA, 1983; pp. 363–389. [Google Scholar] [CrossRef]



| Present Work | Previous Works | |
|---|---|---|
| α-Fe | 2.830 | 2.830 (th.) [19]; 2.853 (expt.) [20]; 2.833 (th.) [20]; 2.858 (expt.) [21]; 2.836 (th.) [43] |
| VC | 4.182 | 4.164 (th.) [28]; 4.163 (expt.) [29]; 4.169 (expt.) [30] |
| VN | 4.128 | 4.130 (th.) [44]; 4.140 (expt.) [44] |
| Present Work | Previous Works | |
|---|---|---|
| VC | −0.477 | −0.494 [31]; −0.435 [43]; −0.405 [58] |
| VN | −1.210 | −1.039 [32]; −1.120 [33] |
| Interface Types | Interfacial Binding Energy (J/m 2) | Average Bond Length (Å) |
|---|---|---|
| α-Fe/VC–C | 1.324 | 1.819 (Fe–C bonds) |
| α-Fe/VC–V | 4.214 | 2.647 (Fe–V bonds) |
| α-Fe/VN–N | 2.577 | 1.842 (Fe–N bonds) |
| α-Fe/VN–V | 1.742 | 2.449 (Fe–V bonds) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Zhu, Y.; Wang, C.; Li, R.; Hu, J.; Chen, Z. Evaluation of Hydrogen Trapping Capability at Interfaces Between Vanadium Carbide and Vanadium Nitride Nanoprecipitates with α-Fe by Density Functional Theory. Coatings 2025, 15, 466. https://doi.org/10.3390/coatings15040466
Yang S, Zhu Y, Wang C, Li R, Hu J, Chen Z. Evaluation of Hydrogen Trapping Capability at Interfaces Between Vanadium Carbide and Vanadium Nitride Nanoprecipitates with α-Fe by Density Functional Theory. Coatings. 2025; 15(4):466. https://doi.org/10.3390/coatings15040466
Chicago/Turabian StyleYang, Shuaijun, Yucheng Zhu, Chaoming Wang, Ruidong Li, Jun Hu, and Zhong Chen. 2025. "Evaluation of Hydrogen Trapping Capability at Interfaces Between Vanadium Carbide and Vanadium Nitride Nanoprecipitates with α-Fe by Density Functional Theory" Coatings 15, no. 4: 466. https://doi.org/10.3390/coatings15040466
APA StyleYang, S., Zhu, Y., Wang, C., Li, R., Hu, J., & Chen, Z. (2025). Evaluation of Hydrogen Trapping Capability at Interfaces Between Vanadium Carbide and Vanadium Nitride Nanoprecipitates with α-Fe by Density Functional Theory. Coatings, 15(4), 466. https://doi.org/10.3390/coatings15040466








