A Micropitting Study Considering Rough Sliding and Mild Wear

Abstract

Micropitting is a typical surface contact fatigue in rolling–sliding contact. The kinematic sliding is of great significance in the initiation and progression of micropitting. A numerical surface fatigue model considering rolling–sliding contact and surface evolution is developed based on mixed-EHL (elastohydrodynamic lubrication) theory, rainflow cycle counting method and Archard’s law. Surface evolution is evaluated using Archard’s wear law based on measured teeth surface topography. Surface damage is determined via the Palmgren–Miner line rule and Goodman diagrams. The effect of rolling speed and surface roughness are discussed in detail. Results show that stress micro-cycles are introduced by rough sliding in the rolling–sliding contact. The mild wear reduces the height of asperities, the maximum pressure and alleviates subsurface stress concentration. For rolling–sliding contact, the faster moving surface dominates the composite height of asperities, then decides the fluctuations of pressure, as well as stress ranges. The combination of surface topography should be considered in the surface design.

1. Introduction

Micropitting is a typical surface contact damage widely reported in operating bearings and gears. If left unchecked, micropitting can further lead to pitting, spalling or tooth flank breakage. Moreover, the progression of micropitting promotes noise and vibration and decreases load capacity and service life. It is understood that micropitting is highly associated with rolling–sliding motion, surface topography as well as lubricant condition. As a type of contact fatigue at roughness asperity level, micropitting is heavily affected by severe stress concentration near the surface, in both the magnitude, as well as cycles, of stresses [1]. Meanwhile, the interaction of lubricants and asperities, the presence of sliding, and the variation in geometry generate micro-contacts at the interface that can greatly influence the stress cycles [2]. As such, a micropitting model should incorporate the effects of kinematical sliding and mixed lubrication. In addition, the surface roughness changes during the repeated contact of the wear process, which further affects the contact behavior. The coupled effect of the surface roughness evolution and damage accumulation is of great importance for micropitting analysis.

Most recently, Liu et al. [3] reviewed micropitting studies, which supports that the combined effect of the wear process and surface fatigue failure damages is of great significance on successful micropitting modelling. In particular, a competition mechanism between surface contact fatigue and mild wear has been revealed gradually over the last decade. Investigation of this competition mechanism can be traced back to pioneering works of Olver and coworkers [4,5]. They concluded that anti-wear (AW) additives tend to promote micropitting by impairing the wearing-in approach. In their micropitting tests, mild wear is a ‘beneficial effect’ because the asperity height is reduced. Based on this view, Morales-Espejel et al. [6,7,8] developed a numerical model considering the concurrent influence of mild wear and surface damage. They verified this model with many triple-contact roller-disc tests and predicted the micropitting rate on gear tooth flanks. Brandao et al. [9] investigated gear micropitting with the Dang Van fatigue criterion. The results were compared to FZG gear test results, suggesting that most mass loss is caused by wear. Zhou et al. [10] studied the influence of contact severity on micropitting, and the results of simulation and experiment illustrated that the final surface damage is influenced by the combination of micropitting and mild wear. Lately, a series of in-situ measurements of micropitting performed by Ueda et al. [11] strongly supported this competition mechanism. It is presented that higher Zinc Dialkyldithiophosphate (ZDDP) concentrations cause more micropitting and less surface wear. The earlier AW tribo-film formation prevents proper running-in and leads to higher subsurface stress. The importance of stress cycles is highlighted throughout the discussions mentioned above. The quantitative description of stress micro-cycles and amplitudes is necessary. However, it was simplified in most existing numerical models.

The development of deterministic elastohydrodynamic lubrication (EHL) models [12] and discrete convolution and fast Fourier transform (DC-FFT) algorithm [13] provides effective ways for better modelling of lubricated contact. The mixed EHL model developed by Zhu and Wang [14] is widely accepted in many EHL contact fatigue studies [15,16,17]. These models solve for the pressure and the stress through the EHL approach, then evaluate the fatigue performance using multiaxial fatigue criteria. Li and Kahraman [18] proposed a micropitting model and compared with gear fatigue experiments. The results show that the characteristic plane criterion is relatively accurate to predict the crack initial life and the location of failure. Evans el al. [19] performed a micro-EHL simulation of gear tooth contact in micropitting tests. They suggested that super-finishing can significantly improve the micropitting resistance of gears. These studies investigated micropitting based on mixed EHL and multiaxial criteria, and the fatigue lives were evaluated according to the stress field at one contact point, which failed to simulate the rolling–sliding contact. The work presented by Pu et al. [20] highlighted that the increased number of stress cycles due to asperity contacts might accelerate fatigue failure. The stress cycle counting method, however, must still be improved to take real measured surface topography into account.

In this study, a numerical model incorporating stress micro-cycles and surface evolution is proposed to simulate micropitting in rolling–sliding contact. The mixed EHL formulation along series of timesteps are implemented in the model to capture the effects of kinematic sliding and surface roughness. Rainflow cycle counting is performed for the consideration of stress micro-cycles. The surface damage accumulation is described using the Palmgren–Miner rule. Surface roughness evolution at each instant is determined by Archard’s wear law. Furthermore, the effect of entrainment speed and surface roughness are discussed in detail. With the help of this study, more insight into the competition mechanism between micropitting and mild wear can be obtained. Although this micropitting model can be further advanced, such as with consideration of the crack propagation, it provides a new approach where the number of cycles and amplitudes of stress micro-cycles can be quantified in fatigue analysis.

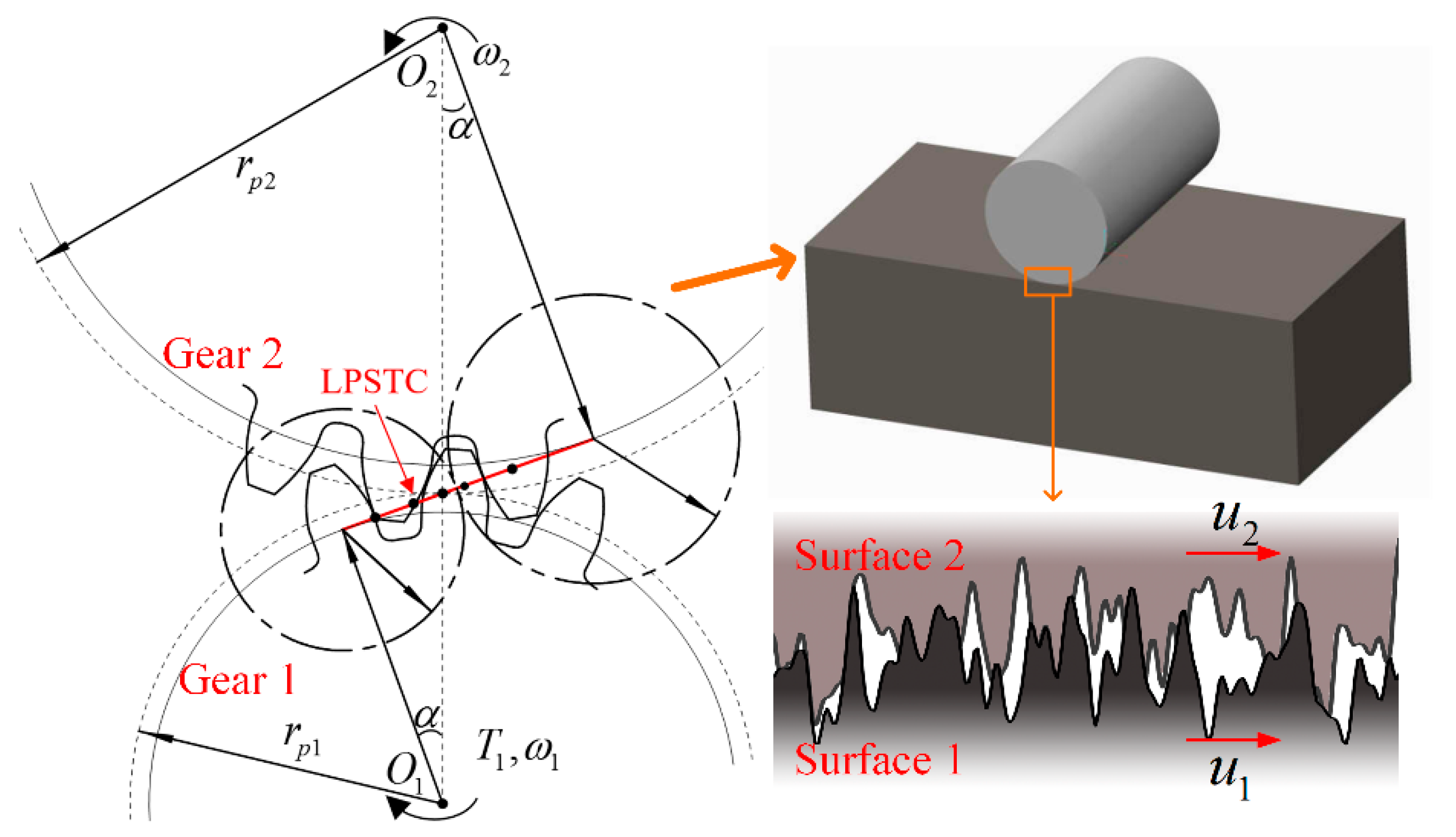
2. Methodology

The model is developed based on three-dimensional (3D) line contact that simulates gear contact during engagement, as shown in Figure 1. The surface micro-topography is superimposed on both Surfaces 1 and 2. Due to the wear process the surface roughness will update at every instant. This updated topography is used to calculate the pressure and stress field at the next moment. The stress history is obtained after one loading passage, then the number of stress cycles is counted and damage accumulation is determined. The technical diagram is depicted in Figure 2.

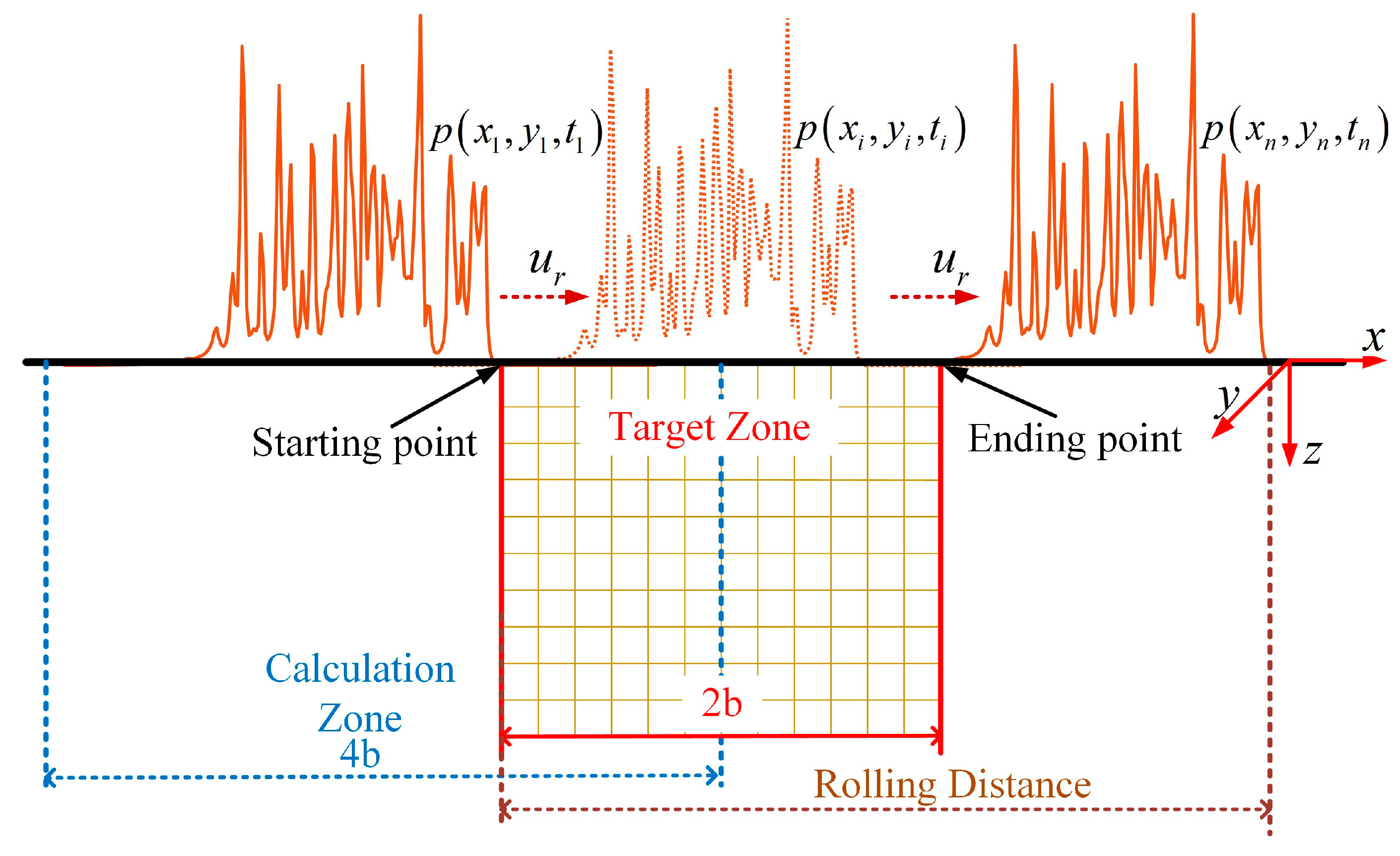
2.1. EHL Equations

The basic EHL approach has been discussed in many works [10,21,22]. However, for clarity, the core equations are briefly presented in the following. The 3D line contact EHL approach is governed by the generalized Reynolds equation [23].

$$\frac{\partial }{\partial x}\left(\frac{\rho h^3}{12{\eta }^{*}}\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{\rho h^3}{12{\eta }^{*}}\frac{\partial p}{\partial y}\right)=\frac{\partial \left(\rho uh\right)}{\partial x}+\frac{\partial \left(\rho h\right)}{\partial t},$$

(1)

The pressure $p$ is equilibrated with total load in the entire computation domain.

$${{\displaystyle \iint }}^{}p\left(x,y\right)\mathrm{d}x\mathrm{d}y=W_n.$$

(2)

Under the isothermal assumption, the pressure–density $\left(\rho \right)$ and pressure–viscosity $\left(\eta \right)$ relationships are empirically described by the Dowson–Higginson equation [24] and Roeland equation [25], respectively, as follows,

$$\{\begin{array}{l}\rho ={\rho }_0\left(0.59\times {10}^9+1.34p\right)/\left(0.59\times {10}^9+p\right)\\ \eta ={\eta }_0\exp \left\{\left(\ln {\eta }_0+9.67\right)\left[{\left(1+5.1\times {10}^{-9}p\right)}^{z_e}-1\right]\right\}\end{array},$$

(3)

where ${\rho }_0$ and ${\eta }_0$ are the ambient density and viscosity, respectively; $z_e$ is the calculated pressure–viscosity coefficient $z_e=\alpha /\left[5.1\times 10{ }^{-9}\left(\ln {\eta }_0+9.67\right)\right]$. The effective viscosity ${\eta }^{*}$ is used to describe the non-Newtonian behavior as,

$${\eta }^{*}=\eta \left(\frac{\tau }{{\tau }_0}\right)/\sin \mathrm{h}\left(\frac{\tau }{{\tau }_0}\right),$$

(4)

where $\tau$ is the film shear stress and ${\tau }_0$ is the characteristic stress given as ${\tau }_0=5 \mathrm{MPa}$.

The time dependent film thickness is given as,

$$h=h_0\left(t\right)+h_g+V_e\left(x,y,t\right)+S_1\left(x,y,t\right)+S_2\left(x,y,t\right),$$

(5)

where $h_0\left(t\right)$ and $h_g$ are the initial separation and geometry gap between two surfaces, respectively; $V_e$ is the elastic deformation determined by the Boussinesq equation and the DC-FFT algorithm [26]. $S_1\left(x,y,t\right)$ and $S_2\left(x,y,t\right)$ denote the time-varying roughness profiles for Surfaces 1 and 2, respectively. Once the surface pressure is obtained, the stress field can be calculated efficiently through the DC-FFT algorithm with predetermined influence coefficient [26,27].

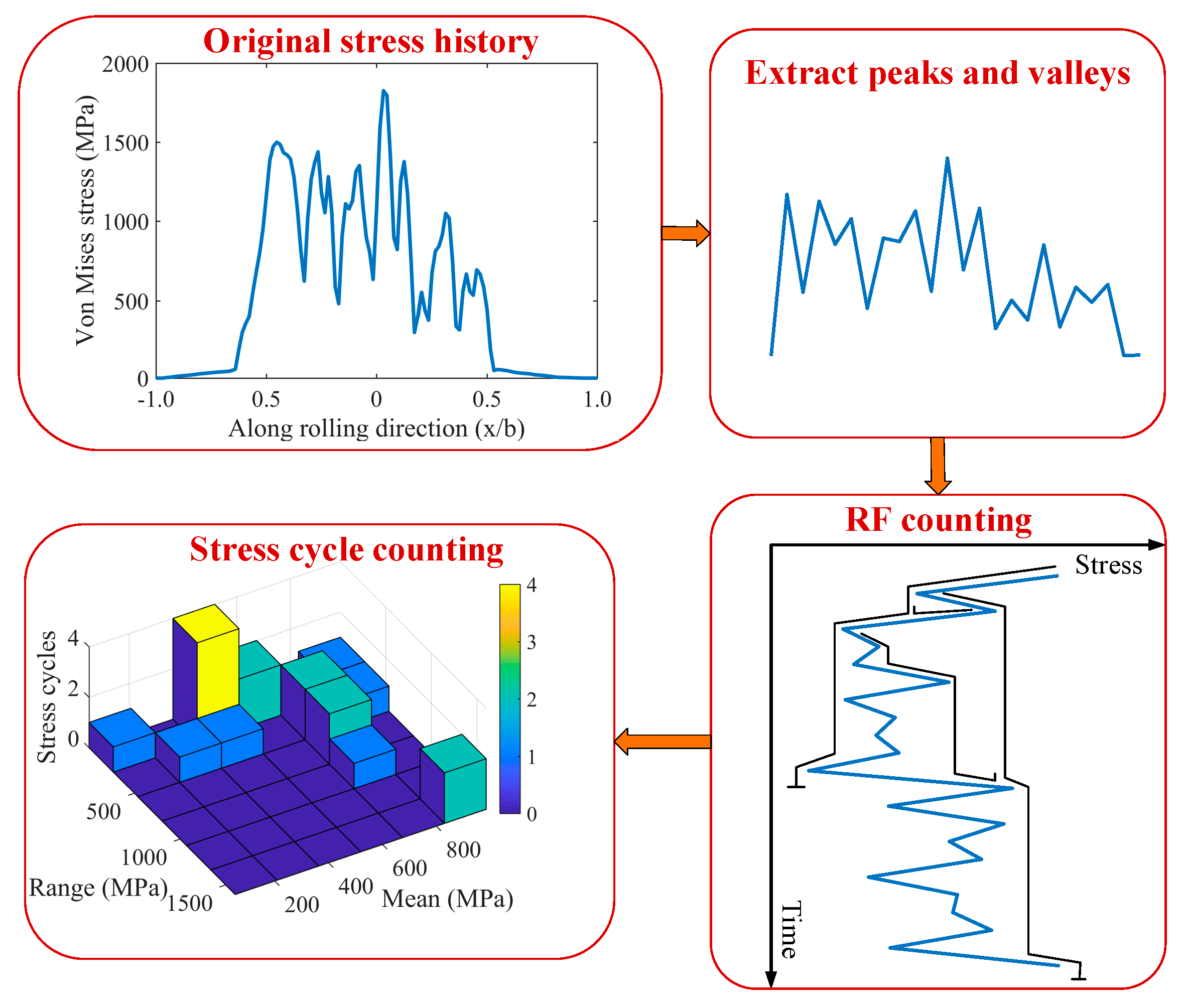
2.2. Stress History and Damage Accumulation Rule

Once the surface pressure and traction are obtained via the EHL approach, the sub-surface stress can be calculated. The stress history is determined via the moving stress field caused by the surface roughness and rolling–sliding contact. For gear contact, the stress history differs greatly at each point during a mesh cycle. Herein, the contact procedure is discretized to multiple timesteps. The stress field is documented at each timestep, then a complete stress history of every point is obtained. Details of the numerical process are presented in Section 2.4.

The stress fluctuations introduce stress micro-cycles. For high cycle fatigue, the rainflow (RF) method is widely accepted for cycle counting [28]. This method corresponds to the stable cyclic stress/strain behavior in that all strain ranges counted as cycles will form closed strain hysteresis loops [29]. Thus, the stress history can be accounted for in a consistent way. In the paper, the rainflow counting method is applied based on the ASTM E1049-85 standard [30]. Generally, there are always some peaks and valleys unmatched at the ends of time-series. These so-called ‘half-cycles’ can be treated as half of a full cycle in the damage evaluation [31]. The flowchart of rainflow cycle counting is shown in Figure 3. The range, mean and number of stress cycles can be obtained with the predetermined stress history and RF counting. The overall effects of mean stress and range is evaluated according to modified Goodman diagrams as,

$$\frac{{\mathsf{\sigma }}_a}{\Delta {\mathsf{\sigma }}_e}+{\left(\frac{{\mathsf{\sigma }}_m}{{\mathsf{\sigma }}_b}\right)}^2=1,$$

(6)

where ${\mathsf{\sigma }}_m$ and ${\mathsf{\sigma }}_a$ are the mean and range of stress cycle, respectively; $\Delta {\mathsf{\sigma }}_e$ is the equivalent stress amplitude; ${\mathsf{\sigma }}_b$ denotes bending strength limit. The damage accumulation is accounted for by applying the Palmgren–Miner linear damage accumulation rule.

$$\mathrm{D}={\displaystyle \sum }_{i=1}^{n}1/N_i,$$

(7)

where $N_i$ is the fatigue life corresponding to a single stress cycle. It can be calculated based on the general S–N curve which takes the form of a power law fit as [32],

$$\frac{{\left(\Delta {\mathsf{\sigma }}_e\right)}_i}{2}={\mathsf{\sigma }}_{\mathrm{f}}{}^{\prime }{\left(2N_i\right)}^c,$$

(8)

where $c$ is fatigue strength component and ${\mathsf{\sigma }}_{\mathrm{f}}{}^{\prime }$ is the axial fatigue strength coefficient. For typical gear steels, the empirical formula summarized by Boller and Seeger [33] can be used to determine the fatigue parameters as,

$${\mathsf{\sigma }}_{\mathrm{f}}{}^{\prime }=1.5{\mathsf{\sigma }}_b;c=-0.087.$$

(9)

2.3. Wear Model

From an engineering point of view, mild wear often results in a surface that is smoother than the original surface. The surface topography changes gradually during the contact cycles, as the asperities are removed due to the wear process. Archard’s wear law is extensively applied to evaluate the wear volume. Despite the complex impact of the different physical mechanisms, many wear criteria can be reduced to an Archard equation form, with elaborated wear coefficient calculations [8]. The general Archard’s wear law is [34],

$$\Delta V=k\frac{F_n{D}_s}{H_a},$$

(10)

where $F_n$ is total load,$D_s$ is sliding distance in a certain time, $H_a$ is the material hardness and $k$ denotes wear coefficient. Considering the sliding distance and the contact area in a certain time, the removed layer height $h_w$ is,

$$h_w=k\frac{\overline{p}{u}_{s}t}{H_a},$$

(11)

where $\overline{p}$ denotes the mean pressure defined as the ratio of normal load to contact area, $u_s$ is the relative sliding speed. One can replace the time by the contact length $L_c$, the grid pressure $p\left(x,y\right)$ and the speed of the current surface $u_1$, so the equation becomes

$$h_w\left(x,y\right)=k\frac{p\left(x,y\right)L_c}{H_a}\left(\frac{u_s}{u_1}\right),$$

(12)

In this work, the contact length is approximately equal to the Hertzian contact width ($2\mathrm{b}$). The local wear coefficient is given as $k_{lub}$ and $k_{dry}$ based on the lubrication region. According to existing papers [7], the ratio of $k_{dry}/k_{lub}=5$ is assumed and the wear coefficient in the fully lubrication region is $k_{lub}=1\times {10}^{-11}$.

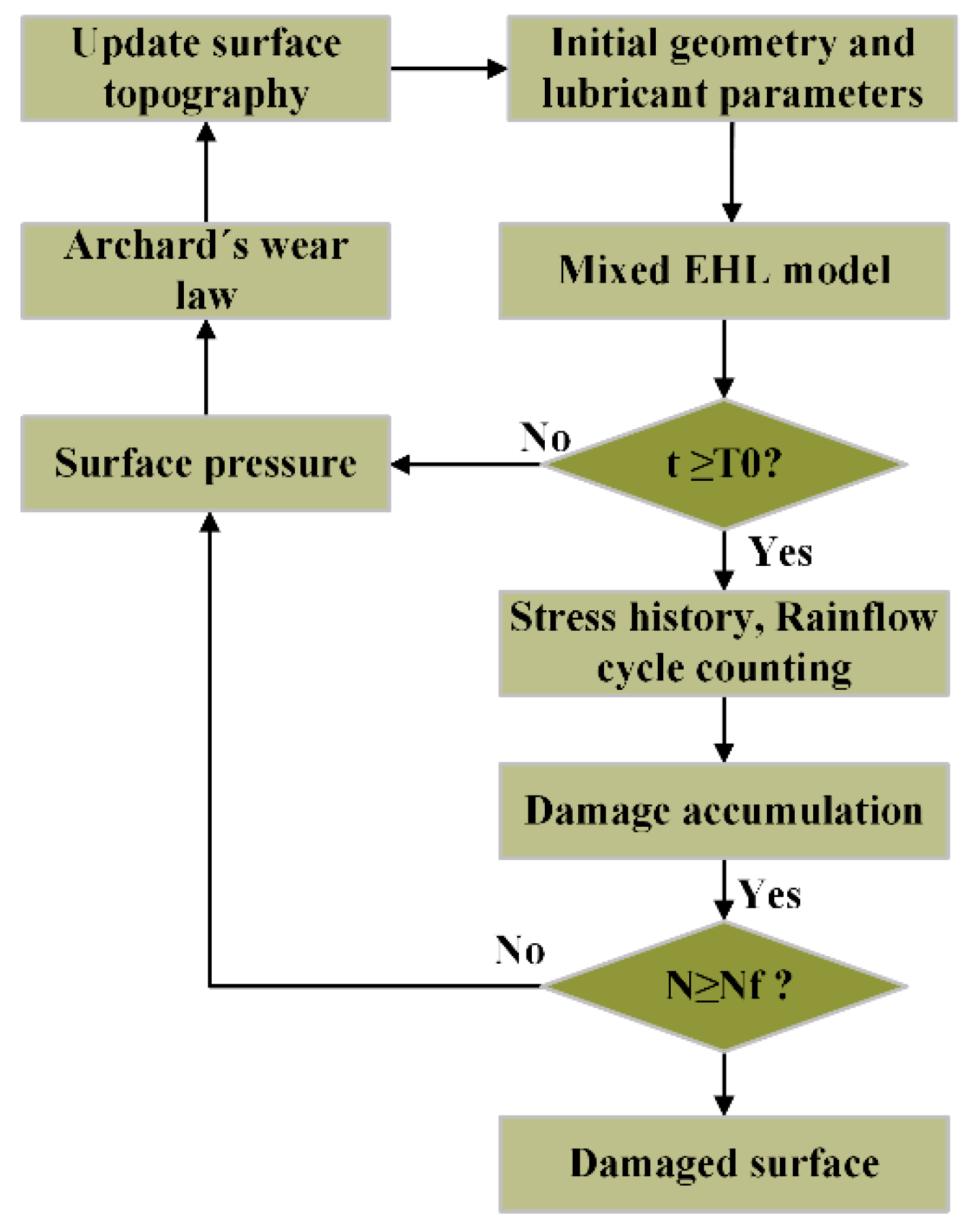
2.4. Numerical Procedure

To simulate the rolling–sliding contact and capture the variation of stress, the moving path and computation zone are designed as shown in Figure 4. The width of the computation domain is $-2\le x/b\le 2$, $-0.5\le y/l\le 0.5$, where $b$ is the Hertzian half-width and $l$ is the width of the contact zone. It is discretized into a $256\times 128$ grid. The target zone (TZ) is the area where the pressure, stress and roughness are documented. The grid number of the TZ is $128\times 128$ with a width of $2b$. One loading cycle is defined as the period between the contact zone entering and exiting the target zone. The entire contact cycle is divided into 128 contact timesteps. At every instant, the wear height at the current position is calculated based on the solved pressure, and then the surface topography is updated. The stress history is obtained after 128 timesteps, and then the rainflow counting is performed. Damage accumulation is calculated with the determined stress spectrum and material parameters. It is time-consuming to calculate the wear and damage in each loading cycle. Here, the jump-in-cycle is applied based on the assumption that the damage and topography change very little within a life block. Then the wear height and damage accumulation are multiplied by the interval to determine the total volume. The life interval is given as $\Delta N=1.0\times {10}^6.$ Because micropitting can be found in the early stage of contact, the total cycle ($N_f$) in the simulation is assumed to be $10$ million cycles.

The surface topography coming from a generating grinding tooth is measured through an optical measurement system (InfiniteFocus, Alicona, Graz, Austria), as shown in Figure 5. The surface roughness of Surfaces 1 and 2 are sampled from the measured topography with different intervals. These surfaces move through the TZ with different speed to simulate the rolling–sliding contact. Parameters of the simulated gear pair and lubricant are listed in

Table 1. Gear and lubricant parameters.

Parameters	Values
Number of teeth	${\mathit{Z}}_1=121,{\mathit{Z}}_2=24$
Normal module	${\mathit{m}}_0=0.011 m$
Face width	${\mathit{b}}_{\mathit{w}}=0.295 m$
Pressure Angle	${\mathit{\alpha }}_0=20°$
Poisson’s ratio	${\mathit{\nu }}_{1,2}=0.3$
Elastic modules	${\mathit{E}}_{1,2}=210 \mathrm{GPa}$
Gear shifting coefficients	${\mathit{x}}_1=0.0034,{\mathit{x}}_2=0.4$
Rated input torque	${\mathit{T}}_1=282768 Nm$
Input speed	${\mathit{N}}_1=154 r/\min$
Ambient density	${\mathit{\rho }}_0=870 \mathrm{kg}/m^3$
Ambient dynamic viscosity	${\mathit{\eta }}_0=0.08 pa·s$
Viscosity-pressure coefficient	$2.1\times {10}^{-8} p{a}^{-1}$
Kinematic viscosity at 40 °C	$220 m{m}^2/s$
Kinematic viscosity at 100 °C	$28.5 m{m}^2/s$

. The velocity of Surface 2 is higher than Surface 1 and the slide-to-roll ratio stays the same, since the analysis just focuses on the lowest point of single tooth contact (LPSTC).

3. Results and Discussion

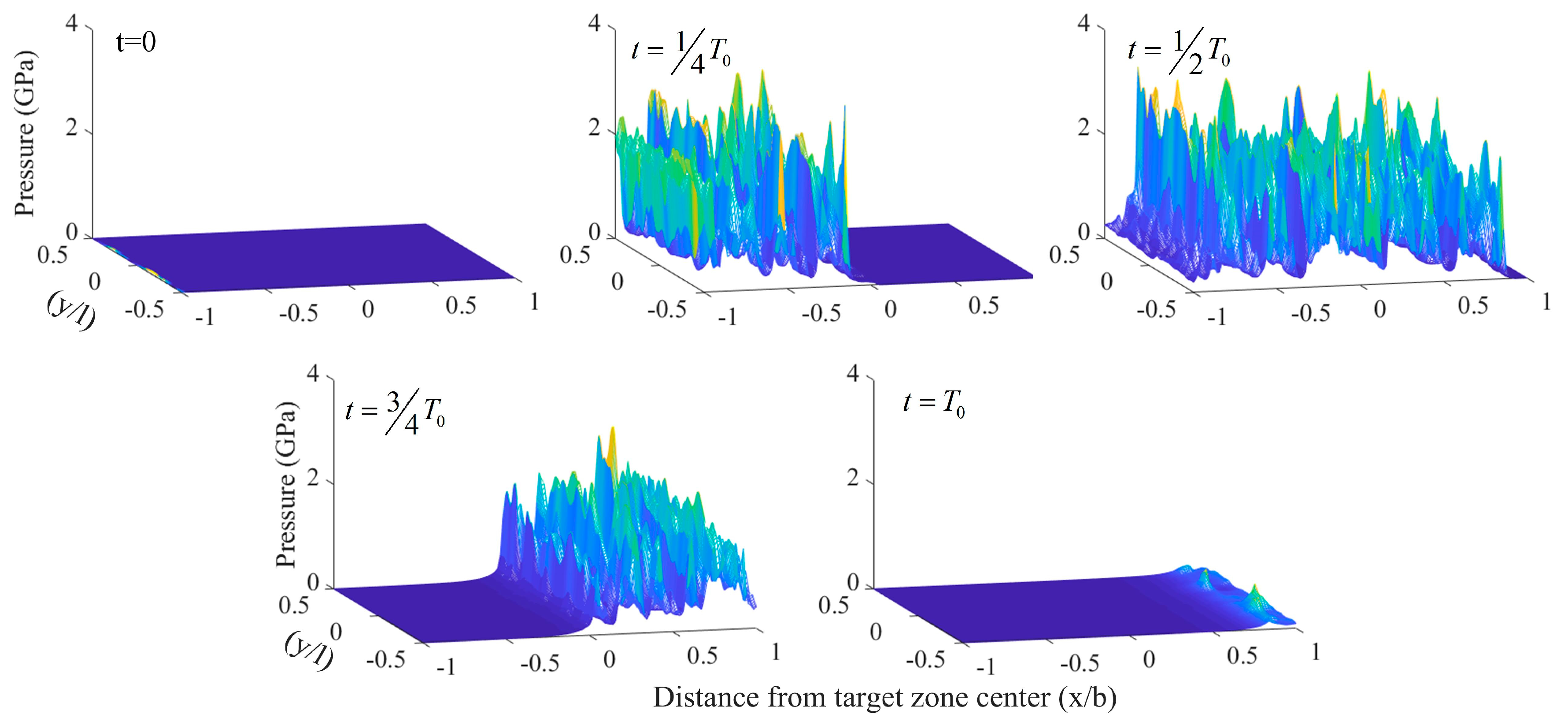
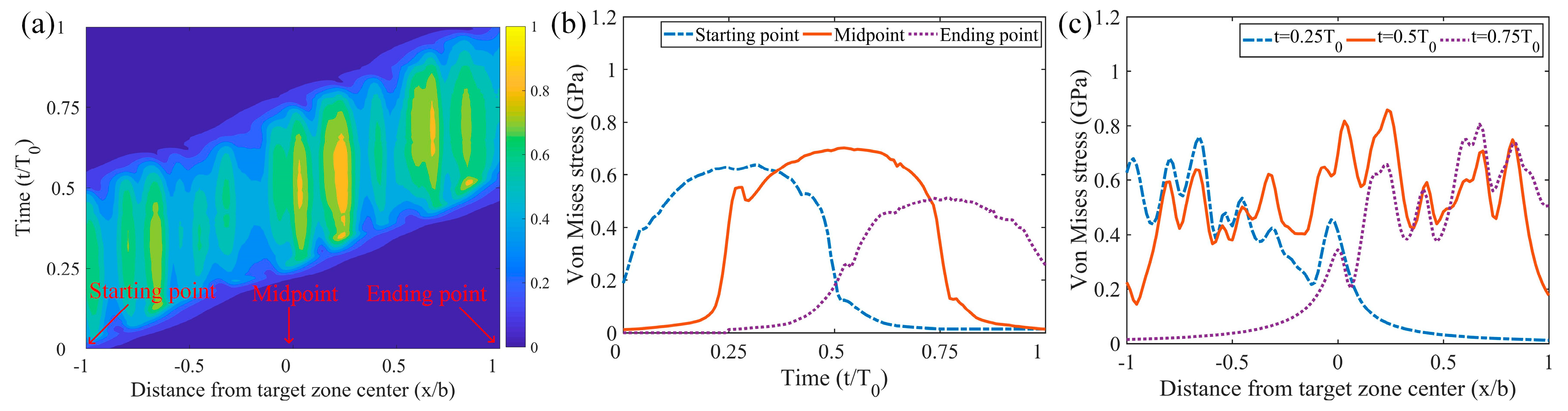
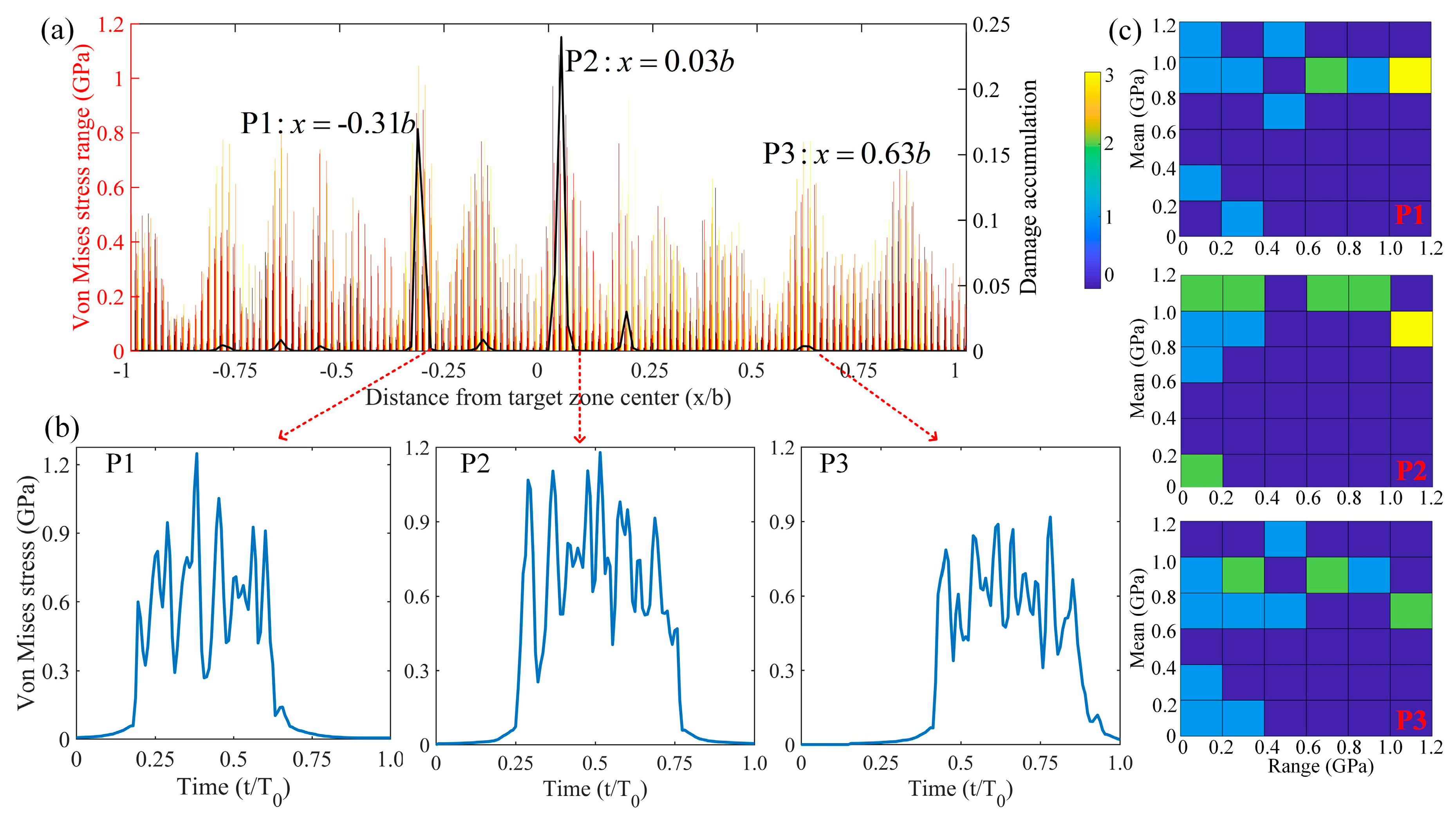
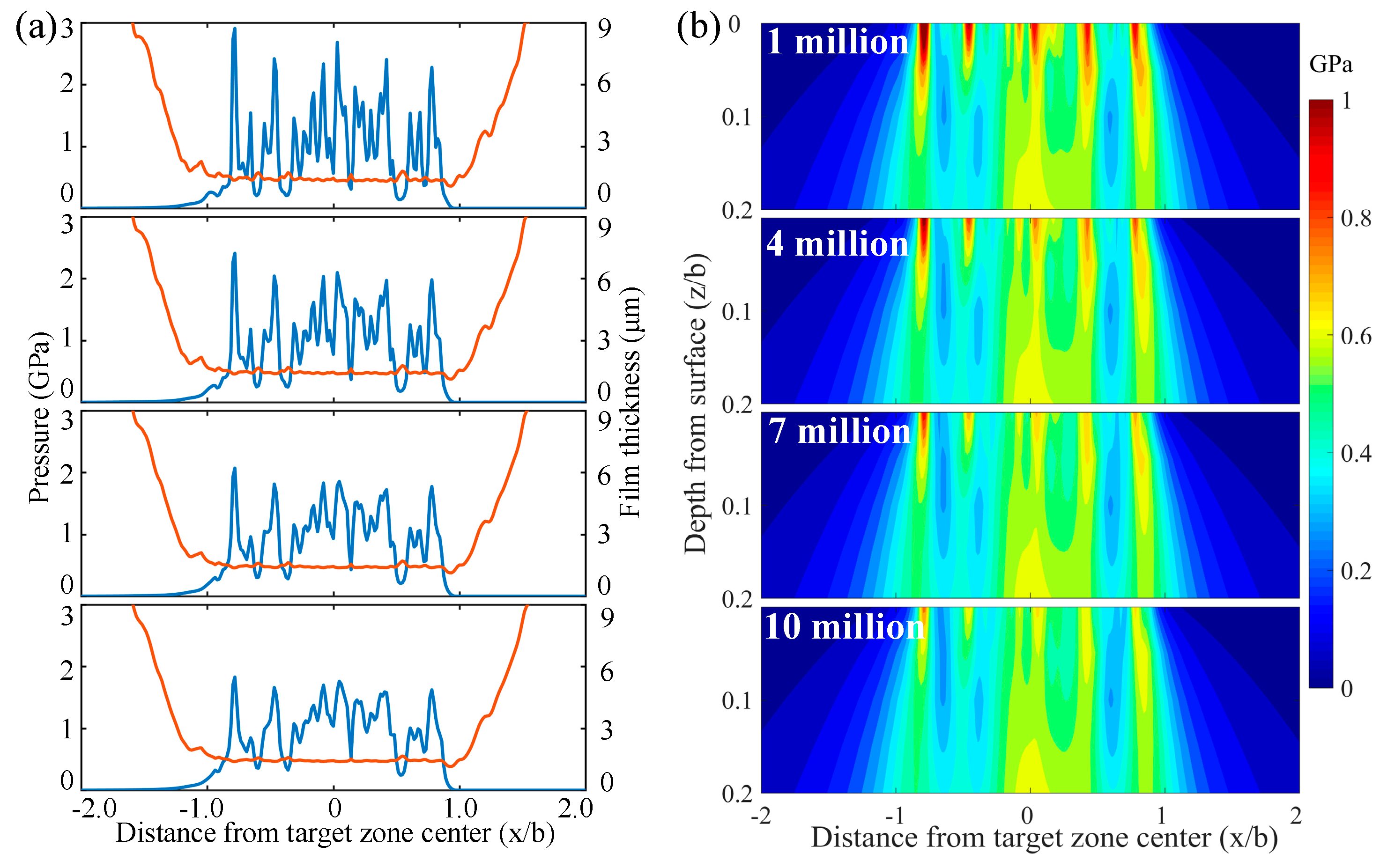
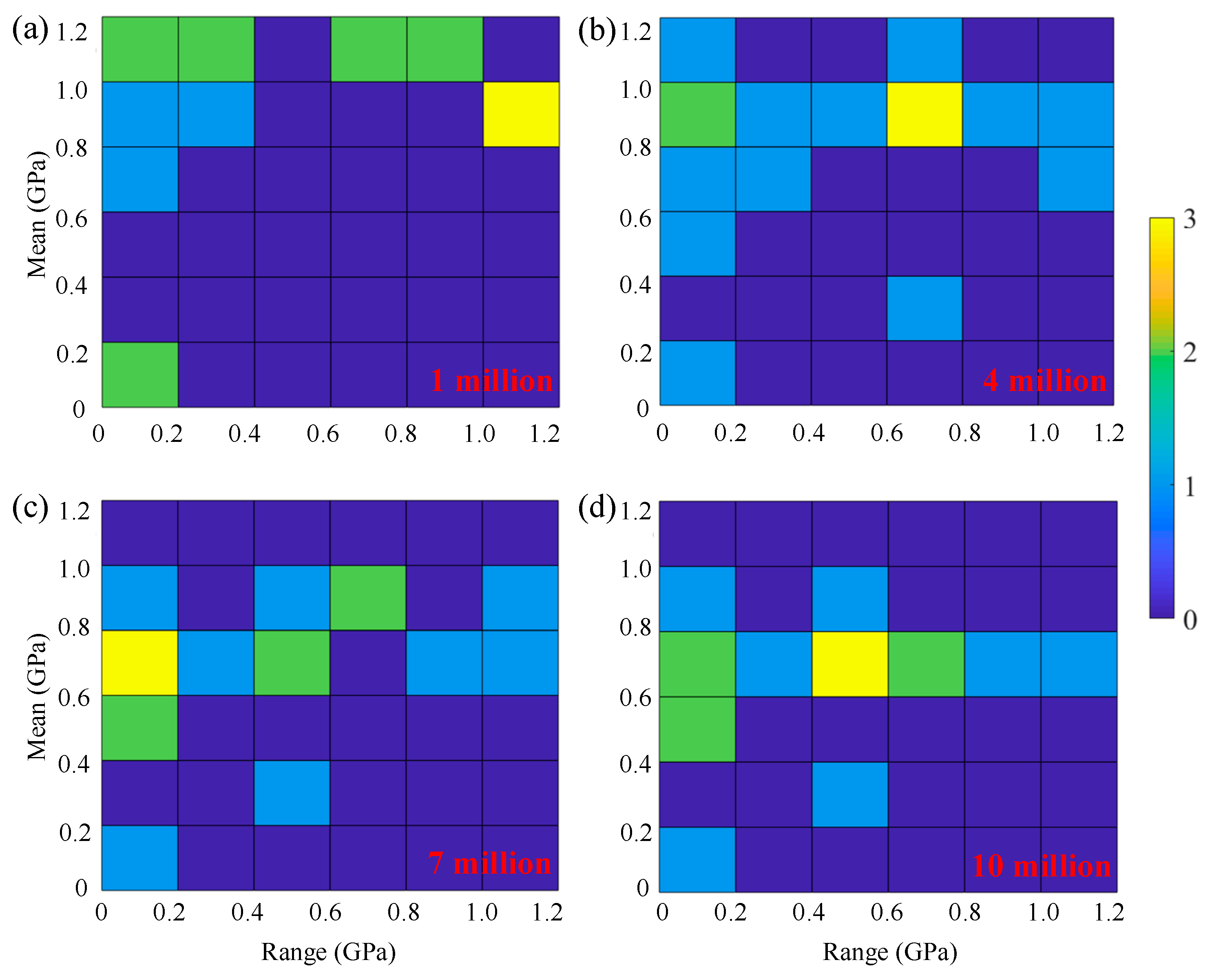
3.1. The Effect of Stress Micro-Cycles

Figure 6 depicts the distributions of surface pressure in the target zone (TZ) during a full loading passage. As mentioned above, one loading cycle starts from the moment that the contact zone enters the TZ. The pressure variation reflects the movement of the contact zone. The pressure is almost invisible at $\mathrm{t}=0$, while several waves remain at the end of the passage. This coincides with the typical distribution of EHL pressure [35], since these two locations are the outlet and inlet regions of the first and last contact point, respectively. At the instant of $\mathrm{t}=1/2T_0$, the contact zone completely covers the TZ. The surface topography characteristic is directly reflected in the distribution of pressure. The ridge-like grinding lays, as shown in Figure 5, correspond to the peaks and valleys of pressure. Moreover, due to the existence of asperities, the peaks of pressure reach up to $2.5-3.5\mathrm{GPa}$, which are $2-3$ times higher than the maximum Hertzian pressure.

Fluctuations of surface pressure can change the distribution sub-surface stress and give rise to stress concentration at or near the surface. The latter is regarded as one of the main causes of micropitting [36]. To illustrate the variations of stress, the X-O-Z cross section (mid-plane, y = 0) is selected as the reference section. Figure 7a shows the distribution of von Mises stress along space and time at the layer of $\mathrm{z}=0.05\mathrm{b}$. The yellow patches denote the distinctive high stresses introduced by the asperities. According to Olver et al. [2], the stress history depends on the relative position of the surface asperities. It is readily to seen that there is a trace of the peak stress, which implies the trajectory of the asperities on the surface. Specifically, due to the analysis focused on Surface 1, which underwent negative sliding ($u_1<u_2$), the movements of the asperities are in the opposite direction of rolling contact. Figure 7b,c are the X and Y sections of the contour plot, respectively. Figure 7b shows stress-time plots at different positions. In a complete loading passage, one material element experiences several stress peaks. These sequenced peaks and valleys can be treated as the superposition of alternating stress and mean stress. It is illustrated that the interested elements could undergo numbers of stress cycles. This agrees well with the stress micro-cycles described in References. [2,6].

To investigate the causes of stress micro-cycles in the rolling–sliding contact. The stress history of a pure-rolling case with the same loading condition and surface roughness is presented in Figure 8. The local stress peaks become contiguous high-stress area in the pure rolling contact. Moreover, the stress-time profiles are obviously different. Figure 8b depicts a relatively smooth profile of stress history, in which the peaks vanish and just one cycle remains. However, the instantaneous stress plots show similar profiles at the same instant, as shown in Figure 7c and Figure 8c. One can consider that in the pure rolling condition, an element of material always faces the same asperity, whereas the counter-surface moves in the presence of sliding. Therefore, the roughness and sliding greatly increase the number of stress cycles of which the element at or close to the surface experiences in the rolling–sliding contact.

Figure 9 presents the typical results of rainflow cycle counting and damage accumulation in the mid-plane. As shown in Figure 9a, the ranges of von Mises stress are represented by colored bars at each point, and the black line denotes damage accumulation. The positions of peak values of damage are basically consistent with those of the high stress ranges. The maximum damage occurs around $x=0.03b$ where the greatest concentration of high stress is observed. The main reason is that the exponential stress-life relationship is sensitive to the high stress. To further observe the influence of stress micro-cycles, the stress history and the corresponding stress cycles of three different locations are illustrated in Figure 9b,c. The maximum values of location P1 and P2 are $1.65\mathrm{GPa}$ and $1.58\mathrm{GPa}$, respectively, whereas that of P3 is only $1.2\mathrm{GPa}$. Compared with location P1, more high stress peaks can be found at P2 in the time-stress profiles.

Figure 9c shows the simplified stress spectra. Most of the cycles are found at the area where the mean stress exceeds $0.6\mathrm{GPa}$. There are three cycles whose stress range is higher than $1\mathrm{GPa}$ at both locations P1 and P2. However, the cycles whose mean stress exceeds $1\mathrm{GPa}$ at location P2 are much more than those of P1. The range and mean stress of cycles at P3 are relatively lower than the others. This agrees with the observation of peak-valley profiles in Figure 9b. This implies that the higher number of stress cycles and equivalent stress amplitudes lead to the higher damage accumulation, which is consistent with results reported by Pu et al. [20].

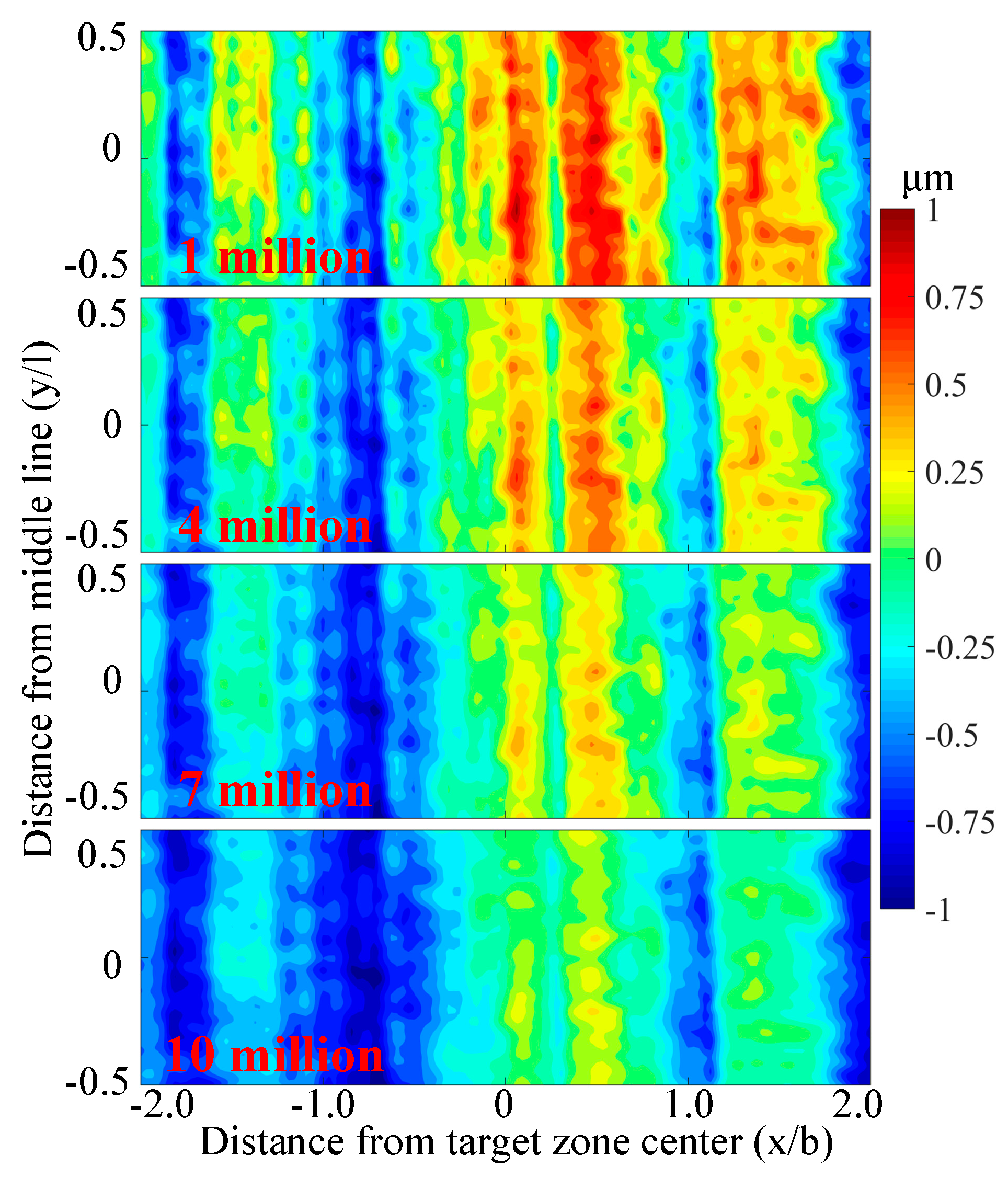
3.2. The Effect of Mild Wear

To study the effect of mild wear, ten loading passages were performed based on the jump-in-cycles method. Figure 10 presents the surface evolution within 10 million cycles. The roughness peaks are removed due to the wear procedure, while the valleys remain. The significant variation of topography can be found from 1 million to 7 million cycles, and it changes little from 7 to 10 million cycles. After 10 million cycles, most of the asperities are smoothed, while the macro waviness remains. This agrees with the surface topography measured by Roy et al. [37].

Figure 11 shows the distribution of pressure, film thickness and von Mises stress at the mid-plane within 10 million cycles. The maximum pressure is close to $3\mathrm{GPa}$ at 1 million cycles, and reduces to $1.8\mathrm{GPa}$ after 10 million cycles. The pressure peaks are reduced, and the fluctuation of film thickness is flattened. As shown in Figure 11b, the concentrated stress can be found near the surface at 1 million cycles. However, it is greatly mitigated from 1 to 10 million cycles. And the stress distribution at the deeper layer, see $z=0.1b$, changes little. Thus, the mild wear reduces the roughness level noticeably, then decreases the maximum pressure and relieves the sub-surface stress concentration.

Figure 12 illustrates the variation of stress cycles during ten loading passages. The number of high stress cycles decreases. There are 13 cycles whose mean stress exceeds $0.8\mathrm{GPa}$ at 1 million cycles. This reduces to 11, 4 and 2 at 4, 7, and 10 million cycles, respectively. The cycles change little in the low stress region where the mean stress is less than $0.4\mathrm{GPa}$. It is remarkable that the stress amplitudes, as well as the number of stress cycles, significantly decreases as the life increases. This implies that the risk of micropitting is reduced as the cycle goes on. This finding supports the competition mechanism between micropitting and mild wear: mild wear tends to suppress the micropitting by smoothing the surface. However, micropitting manifests itself as a deterioration of the surface, i.e., the microcracks and micropits. These flaws lead to a harsher topography, then intensify the wear process by aggravating the contact conditions. To summarize, the interaction between mild wear and micropitting has a significant influence on the overall level and type of surface damage, which is in line with existing numerical discussion [7] and experimental observations [10].

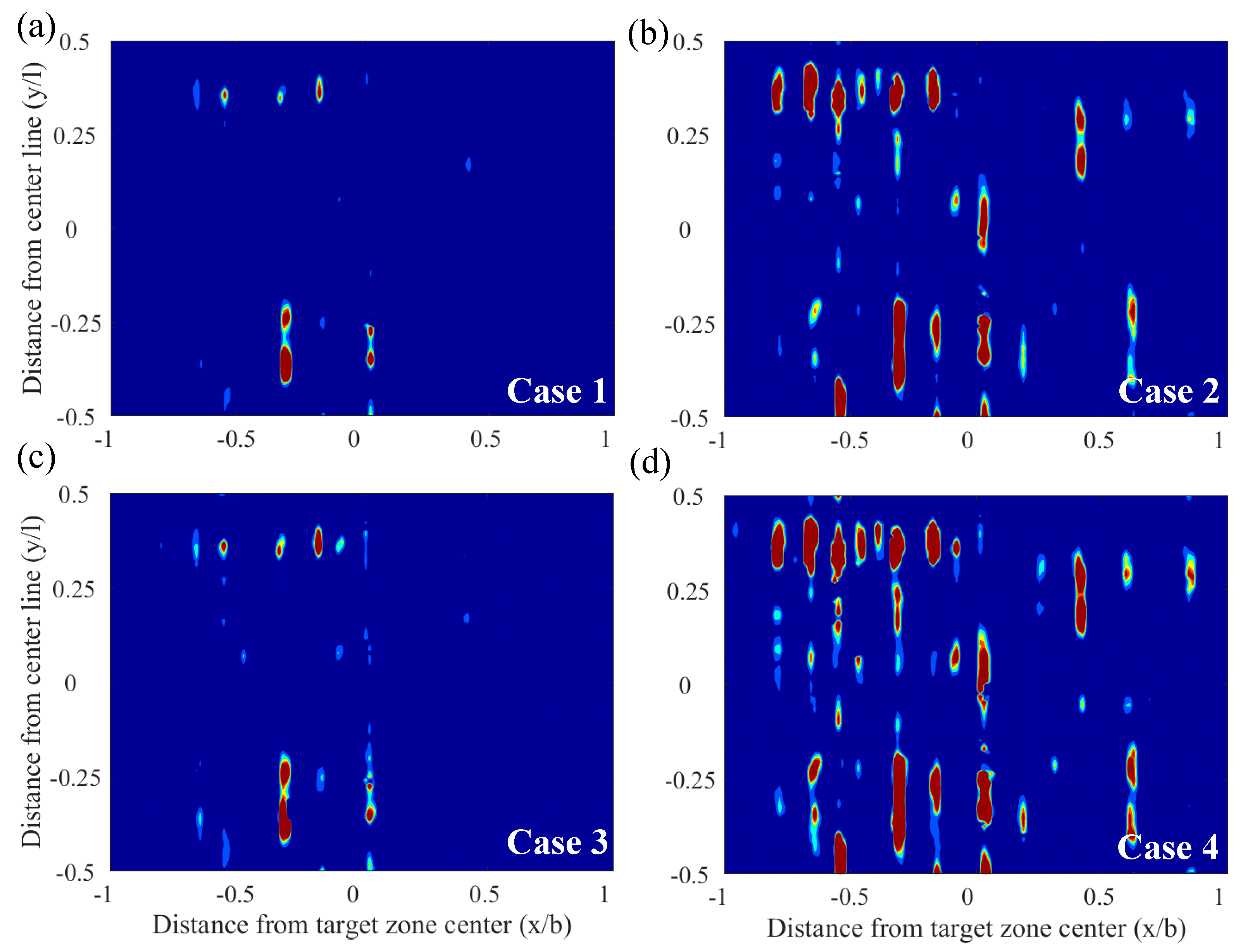
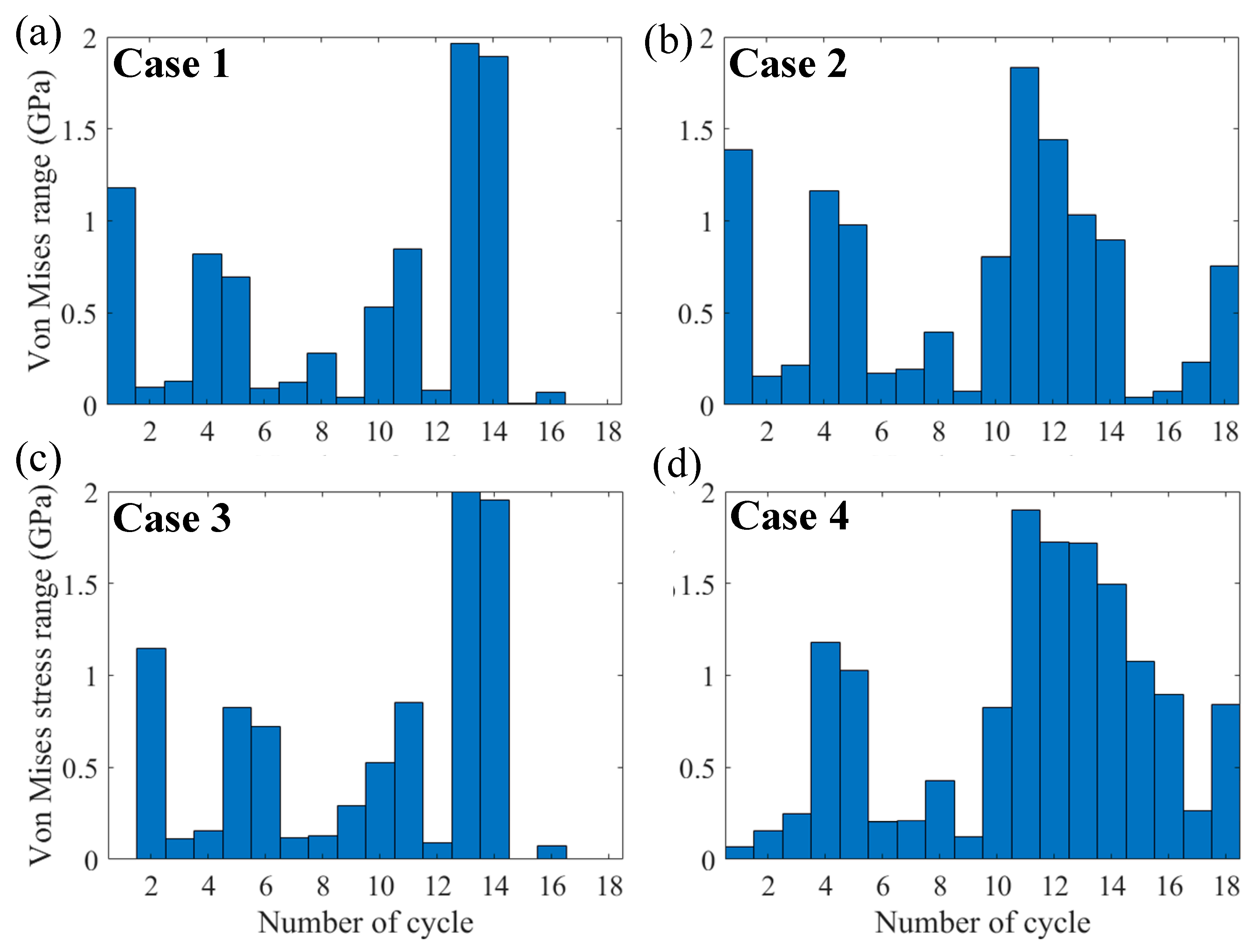
3.3. The Effect of Surface Roughness and Speed

To evaluate the influence of different roughnesses, the topography on Surfaces 1 and 2 was scaled as $S_{1\mathrm{h}}\left(x,y\right)=1.5\ast S_1(x,y)$, $S_{2\mathrm{h}}\left(x,y\right)=1.5\ast S_2(x,y)$.

Table 2. Four cases of different roughness and speed.

Case #	${\mathit{u}}_{\mathit{r}}(\mathbf{m}/\mathbf{s})$	Surface 1 Ra	Surface 2 * Ra	Damage Area Ratio
1	3.0	$\mathbf{0.42} \mathsf{\mu }m$	$\mathbf{0.28} \mathsf{\mu }m$	0.26%
2	3.0	$\mathbf{0.28} \mathsf{\mu }m$	$\mathbf{0.42} \mathsf{\mu }m$	1.88%
3	1.5	$\mathbf{0.42} \mathsf{\mu }m$	$\mathbf{0.28} \mathsf{\mu }m$	0.32%
4	1.5	$\mathbf{0.28} \mathsf{\mu }m$	$\mathbf{0.42} \mathsf{\mu }m$	3.05%

* denotes the surface with the higher speed.

presents four different cases with different rolling speeds and surface roughnesses, while other work conditions remain unchanged. The comprehensive damage risk of four cases after ten loading passages are shown in Figure 13. The surface damage shows the ‘patch-like’ pattern and longitudinal distribution, which is consistent with the aforementioned characteristic of surface topography. The damage area ratios of Cases 1–4 are 0.26%, 1.88%, 0.32% and 3.05%, respectively. Comparing cases with the same roughness condition, Cases 1 and 2 experience less damage. The possible reason is that the lower rolling speed leads to a thinner lubricant film, as well as the higher pressure.

In the cases where Surface 2 has the higher roughness, more damage area can be observed. The damage patches in Case 4 are larger than Case 2. It is postulated that when the rougher surface moves faster it induces more damage on the counter-surface. One can consider that with two surfaces having different roughness in rolling–sliding contact, the faster one dominates the composite height of asperities. Because the faster surface takes more asperities into contact. That is to say, the faster one will dominate the contact condition, then decides the fluctuations of pressure, as well as stress ranges. Furthermore, considering cases with the same rolling speed and composite roughness, the only difference is that one surface is rougher than the other. Apparently, the damage risk in Cases 2 and 4 is far higher than in Cases 1 and 3, respectively.

Figure 14 illustrates the range of von Mises stress of Cases 1–4 at the same position. Cases 2 and 4 experience more high-stress cycles. The maximum range, $2\mathrm{GPa}$, occurs in Case 3. If the contact fatigue life is based on the maximum stress amplitude, Case 3 will have the earliest failure. However, more damage is observed in Case 4. It is suggested that for the design of rolling–sliding contact surface, not only the composite roughness needs to be considered, but the combination of topography should be taken into account in terms of the specific surface speed to improve service life.

4. Conclusions

In this study, a method for micropitting evaluation is proposed by considering the stress micro-cycles and rough surface evolution. The influence of surfaces with different roughness on surface damage is discussed in detail. The main conclusions are summarized as follows:

• In rolling–sliding contact, stress micro-cycles are introduced by sliding kinematics and surface roughness. The fluctuations in stress history is caused by the relative motion of surface asperities. More stress cycles and higher equivalent stress amplitude both lead to a higher damage accumulation.
• Surface asperities are smoothed due to the wear process, while the macro waviness of the topography remains. Mild wear reduces the roughness noticeably, and consequently decreases the maximum pressure and alleviates the sub-surface stress concentration. The number of high-stress cycles decreases as the life cycles increase.
• In rolling–sliding contact, the faster surface dominates the composite height of asperities, then determines the fluctuations of pressure, as well as stress ranges. Under the same composite roughness and rolling speed, the faster and rougher surface may induce more damage on the counter-surface. The service life can be improved by optimizing the combination of surface topography.
• The interaction between initiated micropits and mild wear would be incorporated in the future work. Thus, the further understanding of competition mechanism between surface contact fatigue and mild wear can be explored, by evaluating the rate of micropitting initiation and progression then comparing it with wear rate.