Abstract
In this work, a new approach to solving problems of optimal control of manufacture procedures for the production of silica optical fiber are proposed. The procedure of silica tubes alloying by the Modified Chemical Vapor Deposition (MCVD) method and optical fiber drawing from a preform are considered. The problems of optimal control are presented as problems of controlling distributed systems with objective functionals and controls of different types. Two problems are formulated and solved. The first of them is the problem of the temperature field optimizing in the silica tubes alloying process in controlling the consumption of the oxygen–hydrogen gas mixture (in the one- and two-dimensional statements), the second problem is the geometric optimization of fiber shape in controlling the drawing velocity of the finished fiber. In both problems, while using an analog to the method of Lagrange, the optimality systems in the form of differential problems in partial derivatives are obtained, as well as formulas for finding the optimal control functions in an explicit form. To acquire optimality systems, the qualities of lower semicontinuity, convexity, and objective functional coercivity are applied. The numerical realization of the obtained systems is conducted by using Comsol Multiphysics.
1. Introduction
Nowadays, fiber optics have solidly taken leading positions among various branches of science and technology [1]. Fiber-optic technologies are widely used in long-distance and local communication systems, instrument engineering, and scientific research [2]. At the same time, plenty of information in this area of science is either insufficiently or fragmentarily studied, mostly out of reach, not reliable enough, or not even reproducible. Such a situation leads us to the fact that to improve the characteristics of the fiber, we have to put out a lot of effort and resources. First of all, this applies to optical fibers, for which there is a need for significant improvement. Thereby, research of the technology features and fiber production is a well-timed and relevant objective.
It is known that the main optical and mechanical characteristics of optical fibers are determined by the structure and quality of the initial billet [3]. However, the determination of these indicators largely depends on the alloying regimes (vapor deposition) and fiber drawing. In the alloying process, such parameters as the pressure and temperature of the reagents at the tube inlet, the speed of the burner, the temperature of the outer surface of the silica tube in the reaction zone, the tube diameter, the tube deflection, and a number of other parameters are controlled. The quality control of preform parameters includes measurements of the refractive index, core diameter, the outer diameter of the preform, and concentricity. In the process of fiber drawing, the speed and strength of the drawing, the outer diameter of the fiber, the concentricity and thickness of the coating, as well as the temperature of the preform surface at one point, when the preform is in the high-temperature furnace, are controlled. After drawing, the optical fiber is subjected to the final quality control of the target characteristics. One of the key methods for the final quality control of special anisotropic fibers is reflectometry. Reflectometric control makes it possible to determine changes in the fiber diameter and fiber refractive index by an indirect sign (optical power dissipation) [4].
Thus, the methods of mathematical modeling, as well as the research of optical fiber production from the standpoint of the distributed systems theory, are especially relevant. Moreover, this is particularly important for the effective optimal control system construction.
The most widely used methods to obtain silica multimode and single-mode optical fibers with extremely low losses and a wide passband (>1 GHz·km) are vapor-phase methods, the essence of which is the oxidation or hydrolysis of silicon tetrachloride vapors and halides of alloying components (GeCl4, BBr3, POC13) [5]. The advantage of these methods is the possibility of obtaining pure or doped silicon dioxide containing impurities of the “coloring” metals (Fe, Cu, Mn, Co, Cr, Ni) at a level of <10−7 wt%, which virtually eliminates losses associated with the absorption of light in the range of 0.63 to 1.55 μm [6]. The production of such pure oxides is considered because of the use of especially pure starting halides [7] (in which the concentration of impurities of these metals is at a level of 10−7–10−8 wt%, and hydrogen-containing compounds at a level of 10−4–10−7 wt%) [8]. Additional purification occurs during their evaporation, since the “coloring” metal halides have a significantly higher boiling point than the above-listed halides and, accordingly, lower saturated vapor pressure at the working temperature of the bubblers. The vapor-phase methods for the preparation of preforms by the nature of the formation and deposition of the resulting silicon oxides and alloying components are divided as follows [9]:
- MCVD is the modified chemical vapor deposition;
- OVD is the outside vapor deposition;
- VAD is the vapor axial deposition;
- plasma-chemical methods (PMCVD, PCVD, etc.).
Motivation
Nowadays, the problems of distributed systems’ optimal control gain particular interest because they describe various high-tech production processes, including all the main technological cycles of the silica optical fibers’ production. Under the main production cycles, we understand both the process of forming a silica preform (according to MCVD technology for our work) and fiber drawing (the final stage of production). The mathematical modeling of these technological processes is widely researched [10,11,12]. The authors of various literature analyze the features of models that describe the production of different types of special fibers [13,14] and the mutual influence of model parameters; numerical results of these calculations are obtained. The authors of this research did not aim to improve the existing mathematical models or their parameters. The general objective of this work is to restrict the research to the available models that describe the main stages of optical fiber production so we can formulate, justify, obtain, and analyze the results of optimal control problems’ numerical solutions for the chosen processes.
The approach proposed in this work is based on two main ideas:
- (a)
- To control and manage the allowing processes by the MCVD method and the drawing of optical fibers not by measuring the temperature and fiber diameter at only one point, as it is done now, but by measuring these parameters over extended sections (by length). In other words, to conduct a distributed observation;
- (b)
- To control the process not with the help of PID controllers, as it is done now, but based on the theory of the optimal control of distributed systems.
2. Distributed Optimal Control of the Heat Source in Vapor Deposition Processes
2.1. One-Dimensional Mathematical Model of MCVD Process
The main problem is the difficulty in controlling the temperature of the reaction zone, where physical and chemical processes take place. At the same time, the temperature distribution field in the zone of oxide formation is not limited to determining just the size and concentration of the coagulated particles but the direction of their motion under the influence of thermophoresis forces, since the thermophoretic force acting on each particle is proportional to the temperature field gradient at a given point [15]. In MCVD practice, the temperature on the surface of a silica tube is monitored using non-contact infrared pyrometers.
We developed a mathematical model for heating a silica tube with a movable heat source that will describe the temperature field with sufficient accuracy in the silica tube formed during a real technological process. The mathematical model was obtained under the following assumptions: the temperature field of the silica tube is axisymmetric (this is ensured by the rotation of the pipe); the heat exchange with the external environment and gas flowing inside the pipe is described by Newton’s law; the radiation from the outer surface of the pipe obeys the Stefan–Boltzmann law.
The model includes the energy equation (in our case, the heat equation) and the model of the moving source, that is, a description of the shape and power of the supplied heat flux, as well as the source motion law [16,17]. The heat flux from the plume changes along the z-axis and is described by the following Gauss function:
where v(ξ) is burner moving speed, H is a form parameter (heat, flow, width), qmax is the burner intensity (power), t is time, and z is a spatial variable.
Then, the heat equation for a silica tube in a cylindrical coordinate system has the following form:
where —temperature; , , are the density, specific heat, and thermal conductivity of silica, respectively. In general, these characteristics are a function of temperature ; r and z are spatial variables, and, moreover , , and , where is the pipe’s inner radius, R is the pipe’s outer radius, is the length of the pipe, and T is the deposition process duration.
The effective thermal conductivity of silica as a material transparent to thermal radiation consists of two components: conductive and radiant . Since the medium is optically thick, the Rosseland approximation was used to estimate the radiation component of the thermal conductivity coefficient as follows:
The initial and boundary conditions on the pipe surfaces have the following form:
where and are the heat transfer coefficients of gas and the environment (air), respectively, and are gas and ambient temperatures, respectively, is the black ratio, and is the Stefan–Boltzmann constant. Furthermore, we will omit the arguments when writing functions if this entry is not fundamentally important.
Temperature changes along the pipe cross-section are small compared to temperature changes along the z-axis due to the axial symmetry of the temperature field and the small thickness of the pipe wall. That is why we replace the temperature values in the cross-section with the average value over the region . We integrate both sides of Equation (2) over the indicated region as follows:
Then, the first integral on the right side of the last equation takes the following form when paying attention to conditions (4) and (5):
After averaging the remaining terms over domain D and dividing both sides of the equation by , we obtain the following equation of the following form with properties that depend on temperature:
where:
Equation (8) is supplemented by the initial and boundary conditions similar to (3), (6), and (7), as follows:
If the output of the object can be considered small deviations of from some temperature , while assuming that , then with fairly smooth dependencies , Equation (8) can be linearized in the vicinity of temperature by expanding nonlinear dependencies into a Taylor series. We use this technique in Equation (8), which is a one-dimensional second-order differential equation with a nonlinear operator calculated as follows:
Let this equation also describe the state of the object , where is small variation with respect to a certain state , which corresponds to a certain external influence . At the same time, and satisfy Equation (9), that is:
Assuming that the function A is twice continuously differentiable by the totality of arguments, we can obtain a linear equation for (perform linearization procedure), which is called the equation in variations [18] as follows:
These notations are introduced here where symbol “*” corresponds to the state of the system.
Derivatives in the Equation (10) present in the following form:
Considering the introduced notations, we obtain:
Divide both sides of the resulted equation by to obtain:
Then, we have the following:
where:
Note that if the temperature depends only on the coordinate z, then in expression , the first term turns to zero. In the case , then in , the first three terms equal to zero and .
Similarly, we linearize the boundary and initial conditions, as a result of which we obtain the following boundary and initial conditions for the linearized problem:
Thus, the linear distributed differential problem (11), (12) is formulated, described by the one-dimensional heat equation, simulating the heat transfer of the MCVD process.
2.2. Solution of the Distributed Optimal Control Problem
In general, the goal of influence heat source optimal stabilizing control during vapor deposition is to select such source parameters as power qmax, speed of his movement v(ξ), and shape parameter (heat flux width) H, for which the temperature of the silica tube is kept in the vicinity of a given state. We formulate the optimal control problem considering the linearization of the initial model and the further transition to the research of temperature deviations. Consider the problem of distributed control and a distributed monitoring system (11), (12) [19]. Let the function from the right side of the equation be the control function (further noted as ), and observation is a function of the state of the system at every point in space and time. As a control space, we consider the space , and as a space of solutions consider space , where is the process control time. Notice that the value generally does not match the value T, defined above.
We define a target functional of an integral type that explicitly depends on the control function and has the property of coercivity, which will allow us to use the technique of obtaining an optimization system in the future and determine the optimal control function in the following explicit form:
Functional F is a mixed integral criterion with an integrand that gives the average phase deviations and the total energy costs. Here is a positive numerical parameter (control price), which is estimated in advance or selected from the solutions of test problems.
Since control Δu(t, z) is included in the task (11), (12) linearly, then we can talk about linear operator acting on , with values in the state space , where Note that the Gato differential (the first variation of the mapping) on the increment matches the value of the operator itself, due to linearity , since
We introduce the following notation: ; the value will be called the conjugate state to the state of the system . We vary the initial differential problem (11), (12) and obtain a differential problem with respect to the conjugate state function of the following form:
Multiply the right and left sides of the problem Equation (14) by an arbitrary function and integrate over a given region to obtain the following:
We obtain the following result after carrying out equivalent transformations:
We require that the arbitrary p(t, z) function must satisfy the differential problem with the inverse time:
Considering (16), the relation (15) transforms into the following:
According to one of the consequences of the optimality criterion for distributed systems with compromise control [4], we have the following:
where is the first functional variation (13), Δu is minimizing element (optimal control function), and is a variation of element Δu.
Note that because of the notation introduced earlier, the integral of the first term in (18) exactly coincides with the integral on the left side of relation (17). With this in mind, Equation (18) can be rewritten as follows:
Since, by definition, variation the optimal control function can be represented by an explicit dependence as follows:
Thus, considering the forms of differential problems (11), (12), (16), and the relation for the optimal control function (19), we can write the optimality system in strong form, i.e., in the form of a system of boundary value problems for the original function and the adjoint function in the following form:
2.3. General Results
The optimality system (20) is a differential problem that is inconsistent in time. The state of the system is particularly described by a boundary-value problem. It is correct in time forward, and the conjugate state is correct in backward time, which leads to some implementation difficulties: It is not possible to count in a certain direction in time. In this regard, solution (20) was carried out by the iterative method. In particular, knowing the values of the conjugate function p(t, z) at the i-th step, and hence the optimal control at the i-th step (i = 0, 1, 2, …), we can solve the boundary-value problem that describes state of the system (in this case, we find the i-th approximation of the function ΔΘ(t, z)). The obtained solution allows us to solve the boundary value problem for finding (i + 1)th conjugate state approximations, where as a function ΔΘ(t, z), the i-th approximation is taken. The (i + 1)th optimal control approximation through the values of the conjugate function in the (i + 1)th approximation. A zero function approximation p(t, z) was chosen arbitrarily.
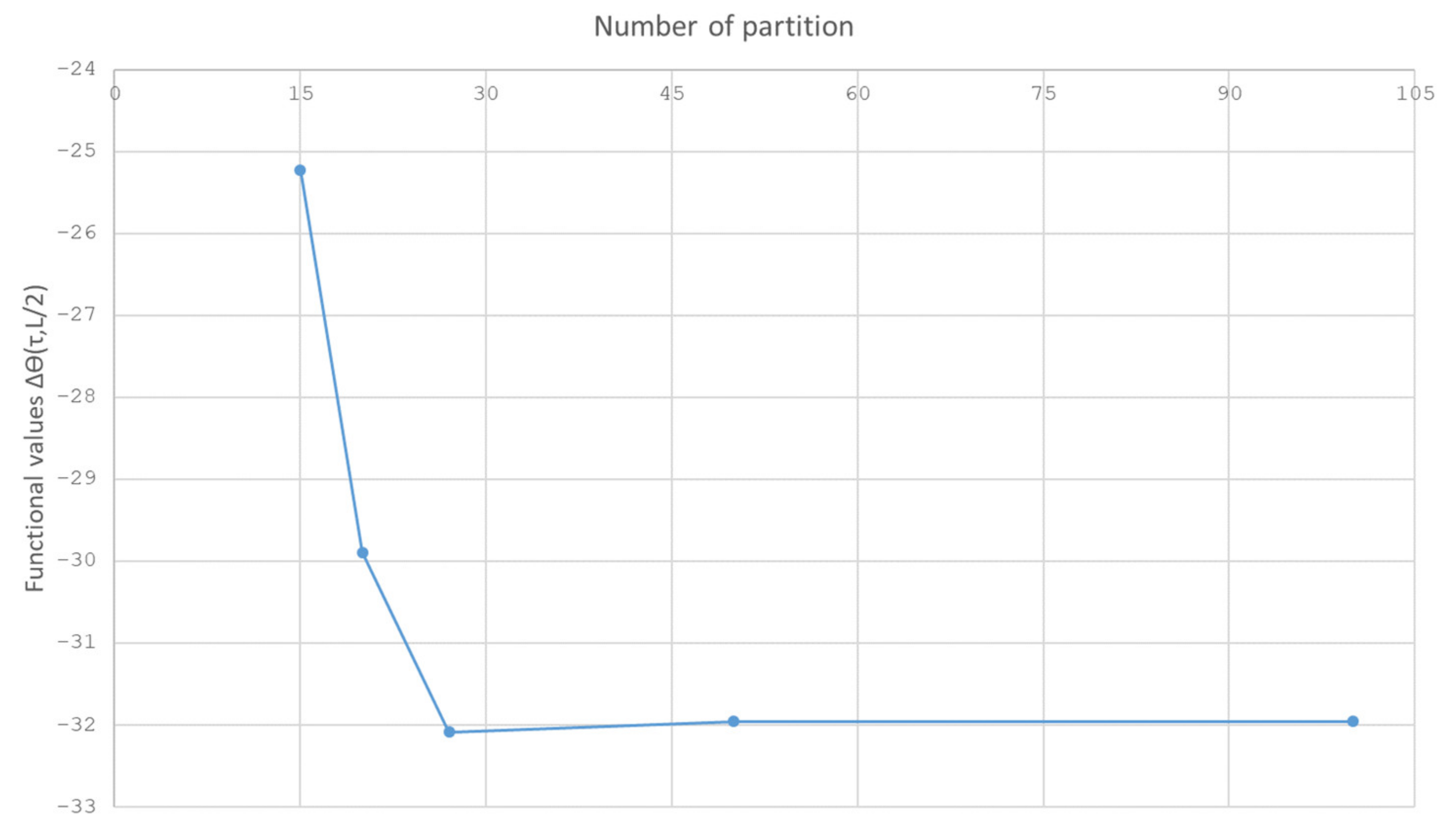
Each boundary value problem was solved by the finite element method implemented in the Comsol Multiphysics computing system. All physical functions and constants, which are the thermophysical parameters of the problem, were taken from the Material Library Comsol Multiphysics. To solve boundary value problems describing the state of the system and the conjugate state, a uniform grid in the spatial variable z was used. A study was conducted regarding the effect of the grid pitch on the resulting solutions. Moreover, when grinding the steps of the grid with respect to the spatial variable, starting from a certain value, the establishment of solutions was observed—the values of the desired functions changed very little (Figure 1).

Figure 1.
Dependence of the function values ΔΘ(τ, L/2) on the number of partitions.
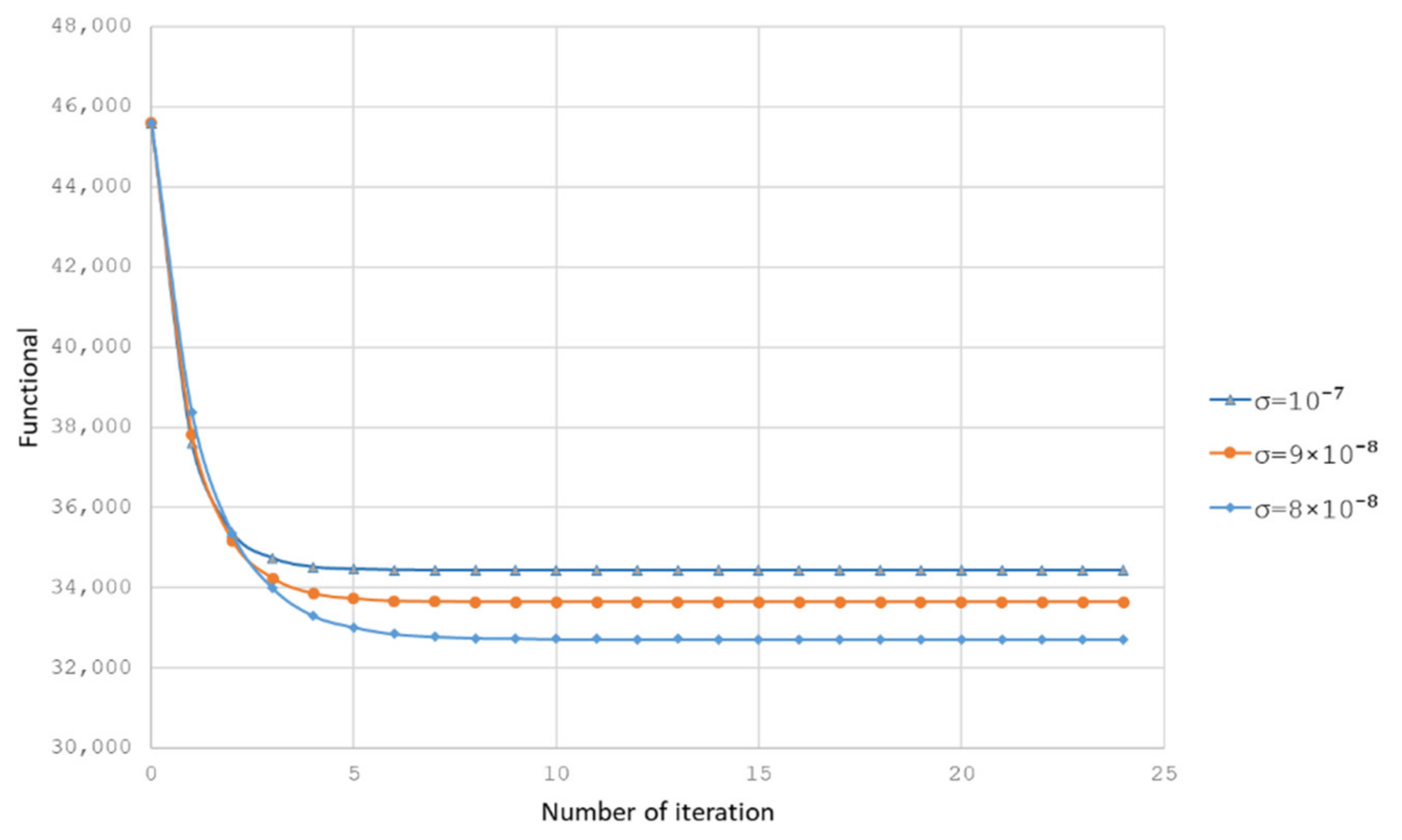
The dependence graph of the target functional on the iteration number, shown in Figure 2 is also interesting. It can be seen that starting from the seventh iteration, the functional decreases slightly and is set near the value F = 32,750 (for the value σ = 8 × 10−8).

Figure 2.
Dependence of the target functional on the iteration number.
It is assumed that the temperature distribution along the heating surface of the silica cylinder is controlled by a scanning pyrometer, which allows you to simultaneously record the temperature distribution over a length of 100 mm. Temperature measurements take place at regular intervals of time τ. The values of τ are selected considering the features of the MCVD process and physical capabilities to carry out the adjustment of the task parameters. Within the borders of this formulation, the system control time τ values were chosen equal to 1, 3, and 5 s. A corrective control was calculated according to Equation (19) from the solution of the system. Therefore, the heat source power qmax is found, which is necessary to stabilize the process within the estimated time (0, τ). Note that the stabilizing control found will only act for the specified time period, after which the process repeats. A new temperature measurement takes place, the optimal control problem is solved again, the heat source power is corrected again, etc.
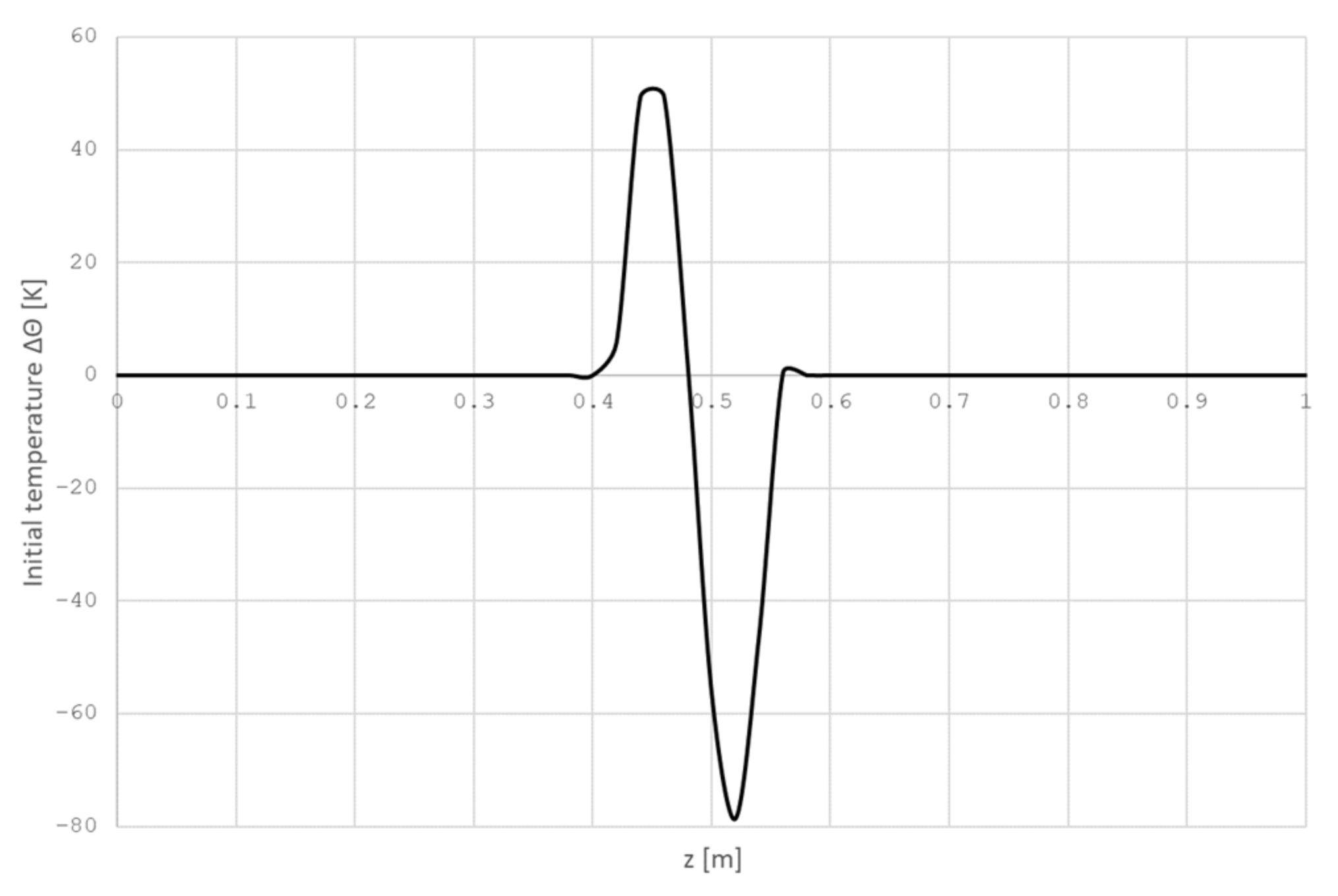
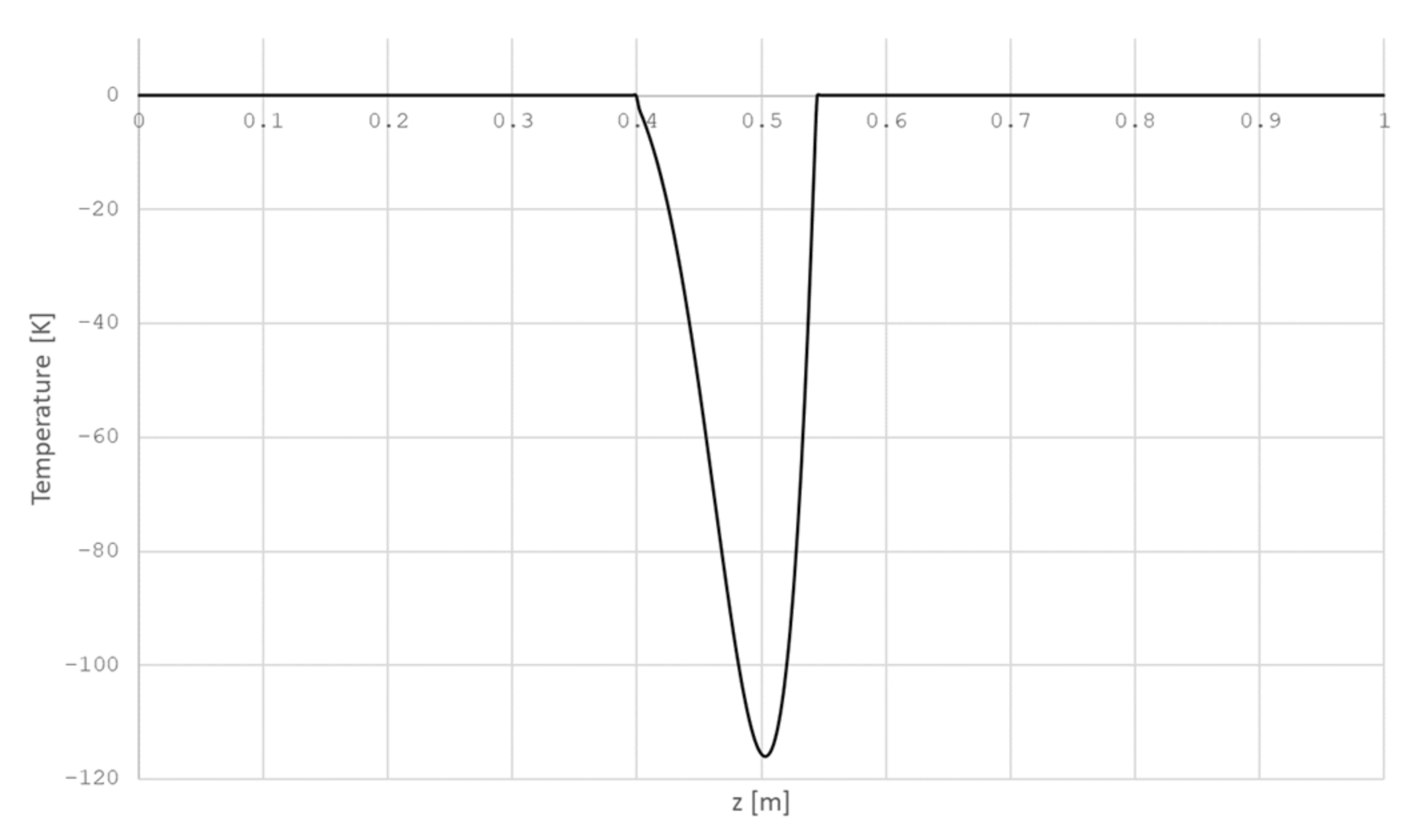
The scanning pyrometer takes readings in the heating zone only. As a demonstration example, we consider the difference between the real (determined using a pyrometer) and program temperature at a time corresponding to the coordinate z = L/2. We take the values of these differences as the initial conditions for the heat equation of the optimality system (20) (Figure 3).

Figure 3.
Initial temperature distribution .
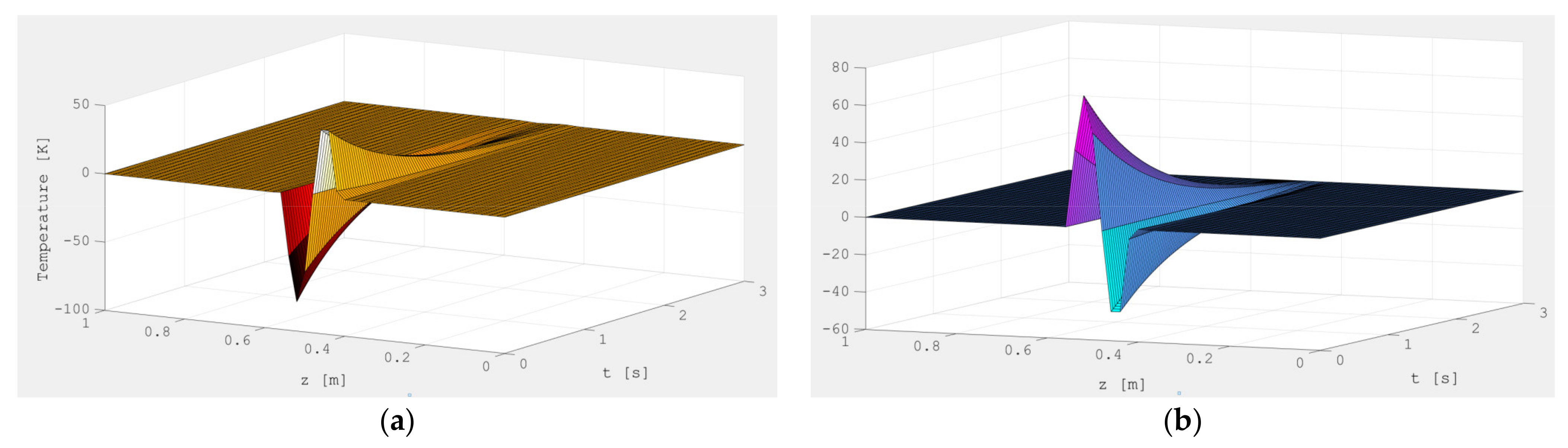
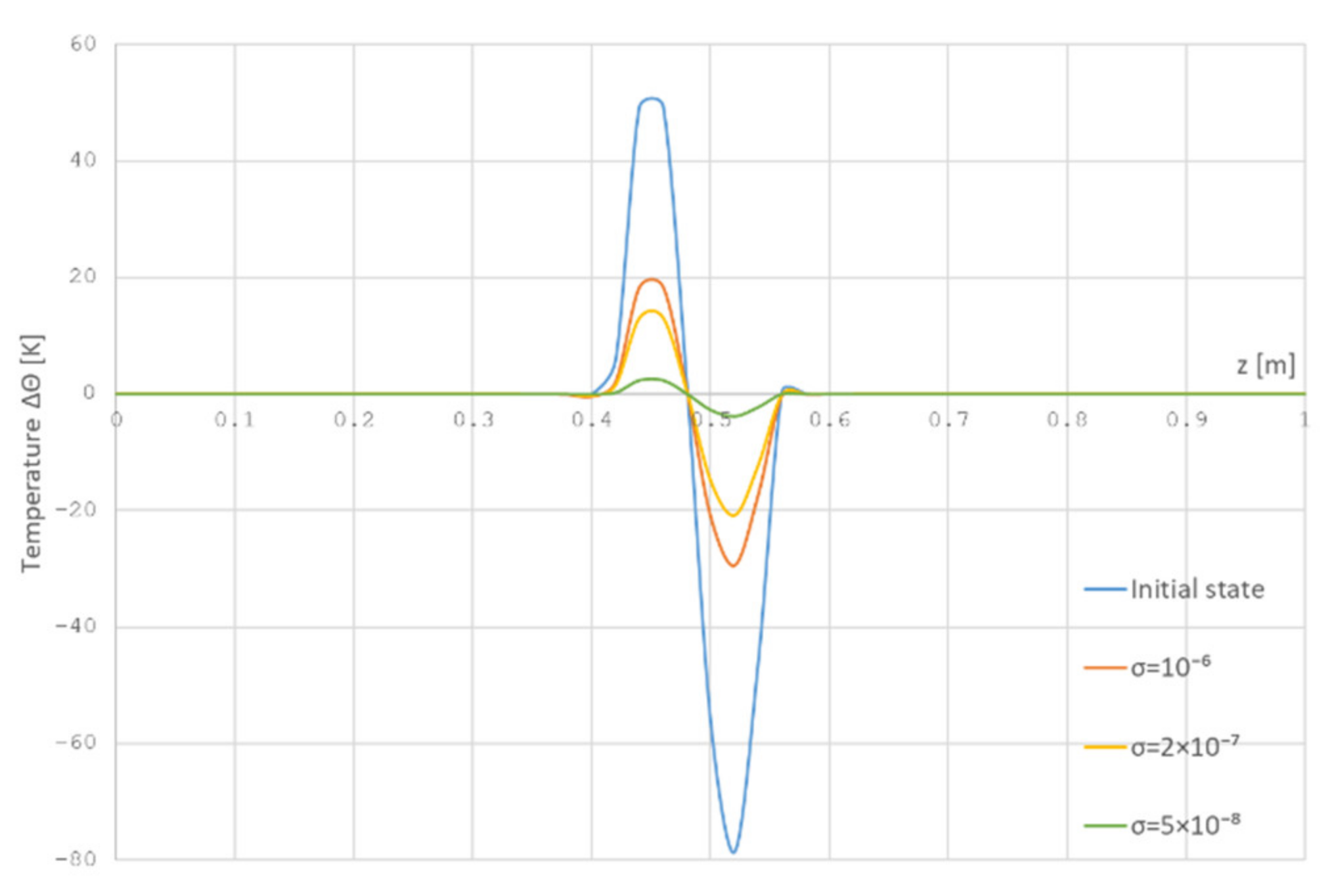
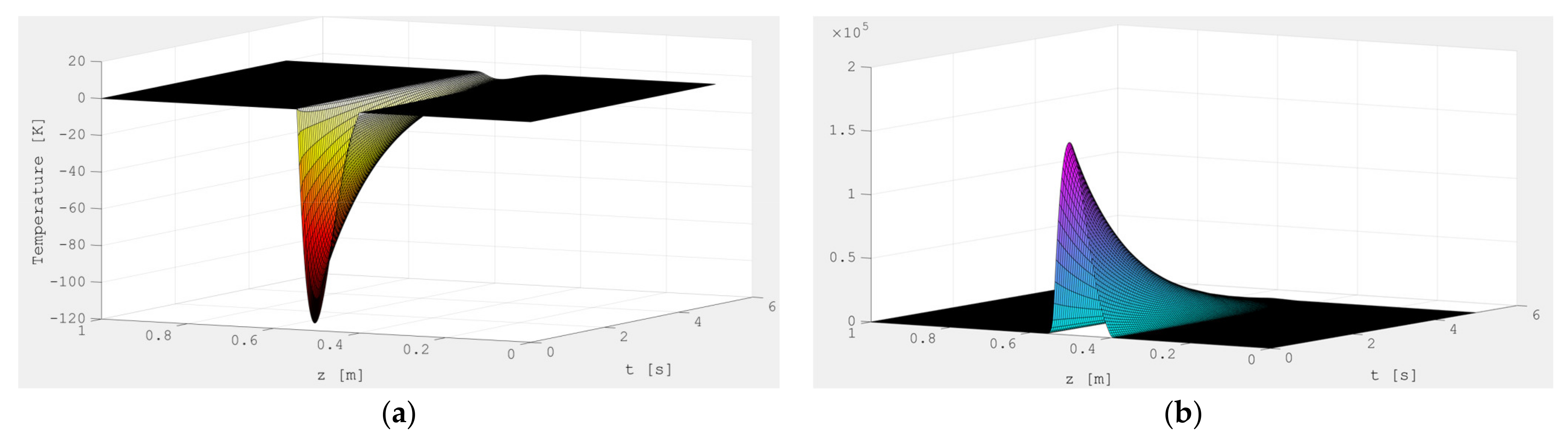
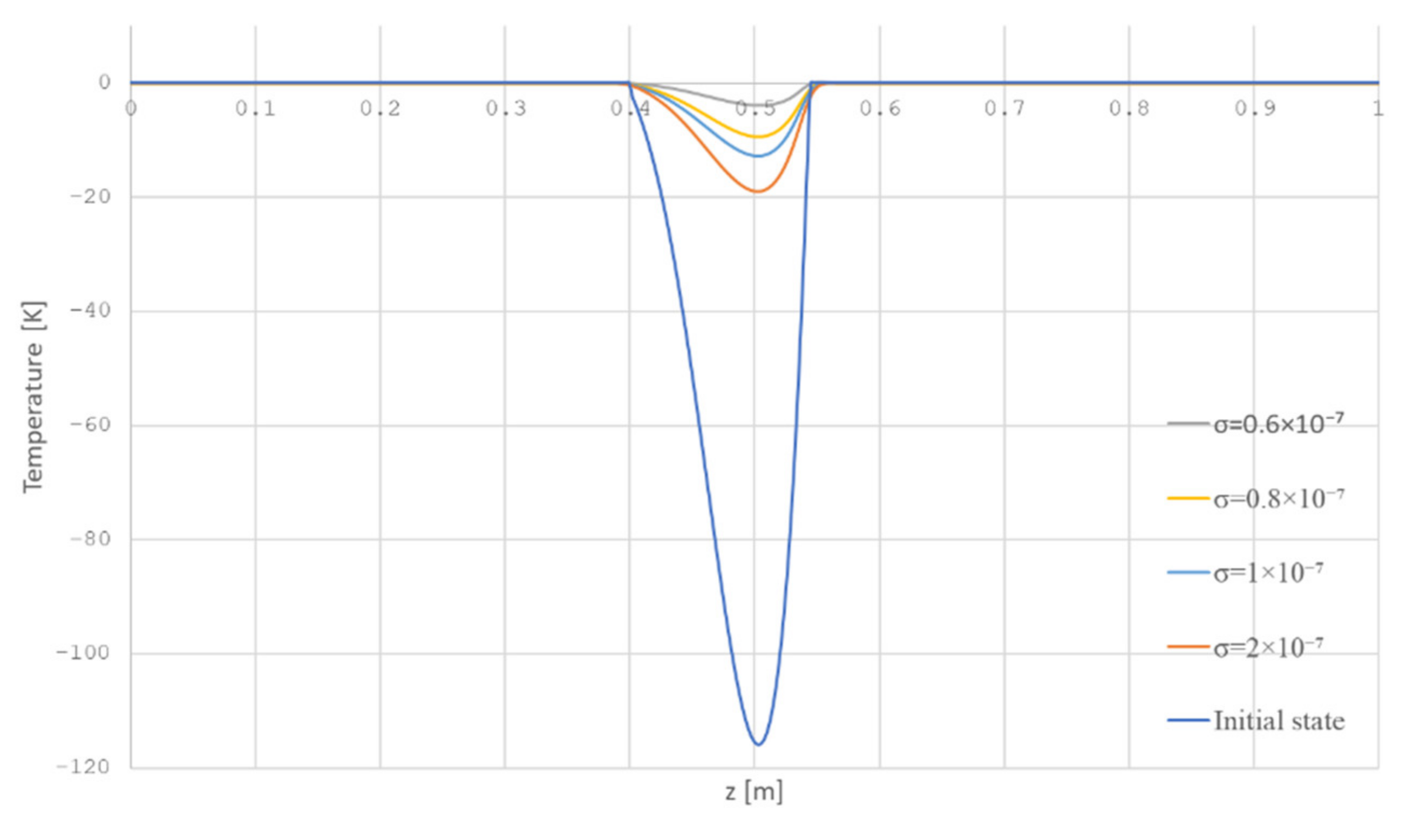
Figure 4 shows the surface of the temperature distribution and control (heat flux) obtained as a result of solving the optimality system (20). The control price is the parameter, as noted above, that can vary. The values are selected from considerations of the method practical implementation. In our case, the choice of this value depends on the measurement error with a pyrometer. The used pyrometers have an instrumental error of 0.5%, so the control price parameter σ was selected on the assumption that the temperature measurement error is no more than 8 °C. Based on this, the problem was calculated for various values of the parameter σ (Figure 5), and the green color shows the temperature profile, corresponding to the value of the error stated above.

Figure 4.
Surface graphs: (a) deviation of the silica temperature ΔΘ(t, z); (b) optimal control Δuopt(t, z) at τ = 3 [s].

Figure 5.
The dependence of the temperature distribution on the value of the parameter .
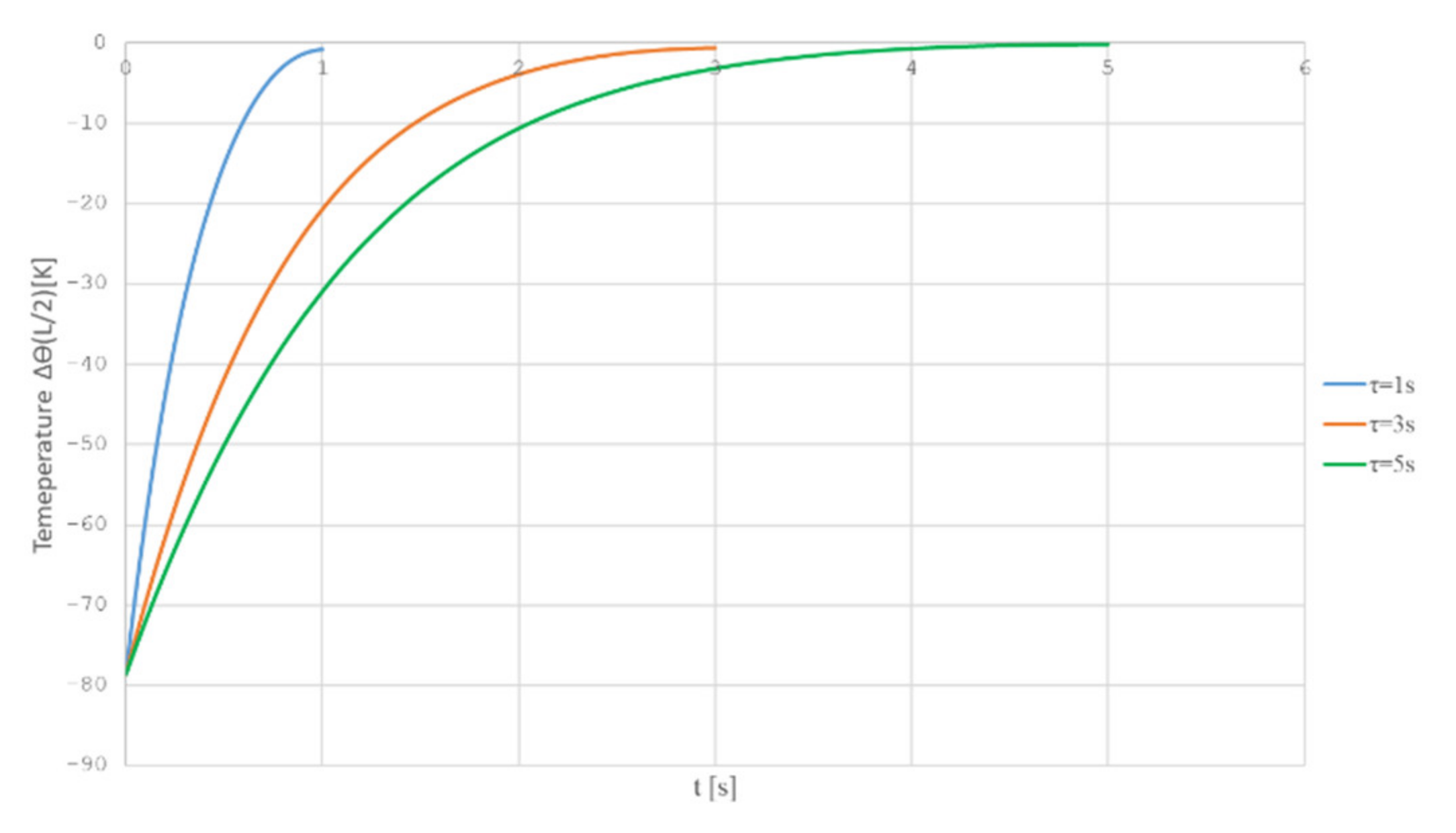
Numerical experiments were conducted covering the influence of control time τ on the distribution of the optimal temperature (temperature , corresponding to optimal control ). From the graphs presented in Figure 6, it is obvious that with increasing control time, the temperature values are decreasing. The initial state of the system was chosen unchanged within the calculations.

Figure 6.
Temperature dependence from time to time in various time modes control τ; z coordinate is fixed by z = L/2 (m).
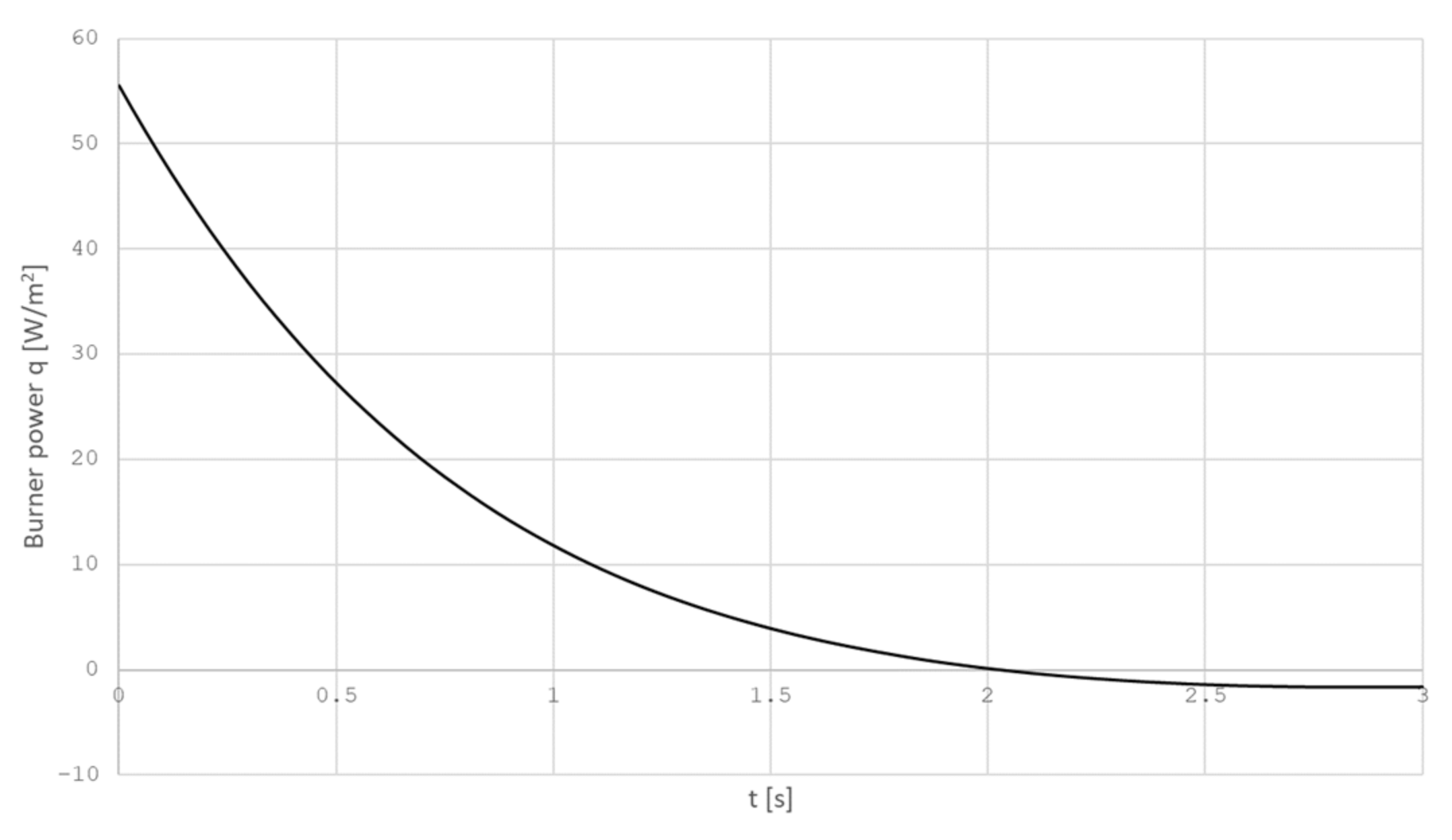
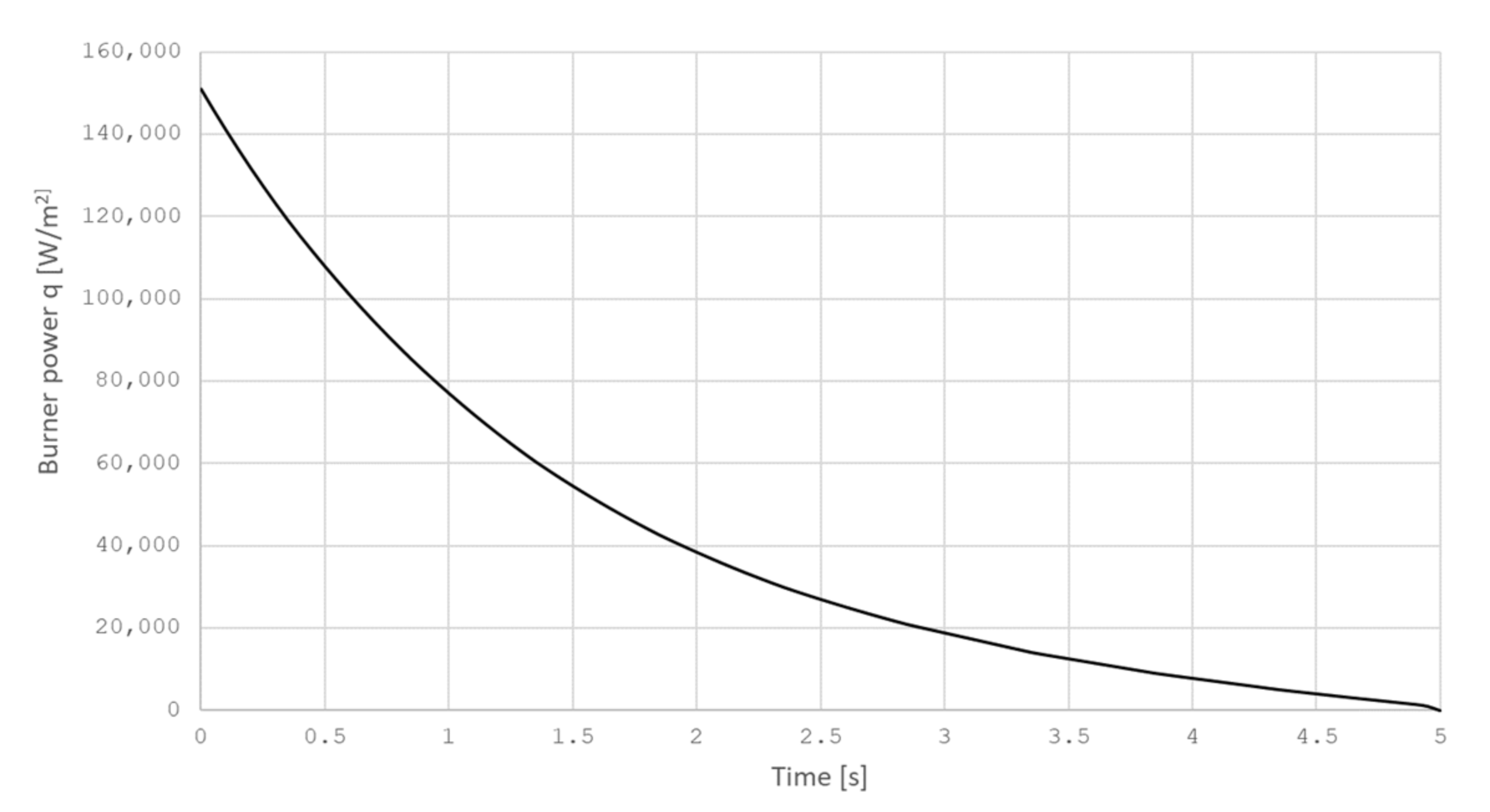
The heat flux of the torch noted above by Equation (1) is described by the Gauss function. The heat source power qmax was calculated according to the found values . The approximation result for the control time τ = 3 [s] is shown in Figure 7.

Figure 7.
The heat source power dependence qmax on time t.
3. Boundary Optimal Control of the Heat Source in Vapor Deposition Processes
3.1. Two-Dimensional (Axisymmetric) Mathematical Model of MCVD Process
We consider the MCVD optimal control problem in a two-dimensional (axisymmetric) formulation. The thermal state of the system, as before, will be described by Equation (2) from the beginning and boundary conditions (3) to (7). Then, we proceed to the two-dimensional model linearization. The linearization technique described above will look like the following:
where is with little variation regarding distribution , which meets external influences caused by the operation of a heat source (1) on the boundary .
If the function G is differentiable (at least twice) in the totality of arguments, then the linearization procedure leads to the following linear differential equation of the form concerning :
We obtain the values of the corresponding derivatives:
Based on the foregoing, the linearized equation takes the following form:
or
Define functional operators , , depending on the functions and first derivatives of the function in spatial variables by the following relations:
Similarly, we linearize the initial and boundary conditions:
Then, the boundary and initial conditions of the linearized differential problem take the following form:
So, the linear differential problem (22)–(27) is formulated, which is described by the two-dimensional axisymmetric heat equation.
3.2. Solution of the Boundary Optimal Control Problem
As noted above, the decisive role in the process of vapor deposition is played by the temperature distribution in the thermophoresis zone. In this regard, the most natural statement of the MCVD process optimal control problem is to obtain the temperature closest to the desired (specified) in the silica tube by controlling the burner power and/or speed.
In the scope of this statement for the optimal control function, we use the notation similar to the previous one-dimensional statement. The Δu(t, z) optimal control function is renamed. In this case, it implies the power of the heat flux from the Δq(t, z) heat source obtained by the system from the burner in contact with the outer surface of the silica tube (boundary r = R). The optimal control function Δu(t, z) must be found from the condition of minimizing the functional of the integral form, under the condition that the positive parameter σ (control prices) is limited as follows:
So, a functional of the form (28) minimizes temperature deviations from the programmed (specified) state on the outer cylindrical surface of the silica tube. At the same time, the control function is small in norm, and this means that the corrective actions on the system are small. The control efficiency in problem (22)–(28) consists in timely stabilization by adjusting the temperature regime supplied by the burner to the outer cylindrical surface of the silica tube. The control function here is the power of the heat flux from the burner, therefore, at the boundary r = R, the heat flux is set, and all types of heat exchange with the environment are considered. The system is also monitored on this part of the boundary; however, the parameter that is being observed is the temperature distribution on the surface of the cylinder. The stabilizing control problem formulated in this way is a problem with boundary control and boundary observation; the objective functional (28) for this problem, as before, clearly depends on the control function.
Based on the known variational principles and using the previously described algorithm for obtaining the necessary solvability conditions, as well as skipping a series of standard actions similar to those described earlier, we obtain an optimization system for the two-dimensional formulation of (22) to (28).
The optimality system is obtained in the strong form, i.e., in the form of a system of boundary value problems for the original function and conjugate state function and has the following form:
The optimal control function is determined by the following formula:
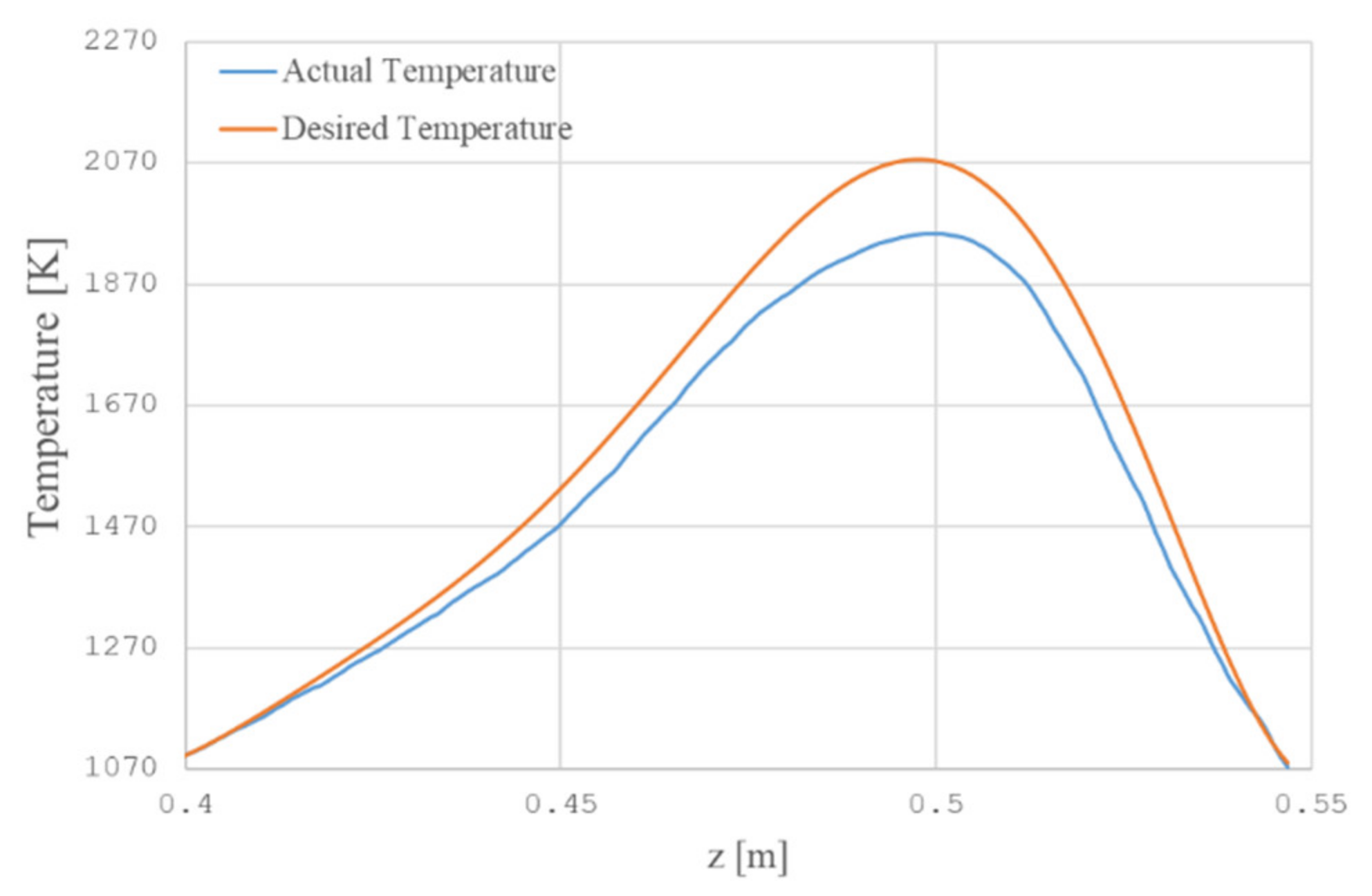
We assume that we know the desired temperature distribution in a cylindrical pipe in advance. This distribution can be obtained, for example, from experimental data or any other considerations. To obtain the temperature field closest to the desired in a silica tube, the following control algorithm is proposed. We measure the temperature field using a scanning pyrometer at equal intervals of time τ. As an initial condition for the problem of stabilizing optimal control (29), we consider the difference between the desired and actual temperatures. From the solution of the problem, we find the optimal value of the increment in the heat source power qmax. This control will be valid only for the time interval (0, τ), after which a new temperature measurement takes place, etc. The objective of optimal control is to find a level of increase (decrease) in the power of the heat source at which the difference between the current temperature distribution and the program would be minimal. As a simulation object, we take a pipe made of synthetic silica with an external radius of R = 14 mm, an internal radius of r0 = 12 mm, and a length of L = 1000 mm. Using a scanning pyrometer, we will measure the temperature. Figure 8 shows the profile of desired and actual (obtained by the measurement) temperature.

Figure 8.
Actual and desired temperature at time t = 225 [s].
The difference in these temperatures will be the initial condition for the problem of stabilizing optimal control (Figure 9).

Figure 9.
Temperature distribution at the initial time.
We decide the optimality system based on the obtained data. As a result of the solution, we obtain the optimal value of the heat source power increment qmax. We will perform calculations using the COMSOL Multiphysics software product, as well as the MatLab and Maple software packages. To calculate the optimality system, we will use the simple iteration method with a constant control time τ and control cost σ. As a result of solving the optimality system (29), we obtained the temperature and power distribution of the burner over the time interval (0, τ).
Furthermore, from the obtained power function, it is necessary to obtain the optimal value of the power increment of the heat source qmax. As noted earlier, the thermal flux of the MCVD flare is described by the Gauss function (1). In this regard, the burner physically cannot produce the heat flux described in Figure 10b, and the function Δu must be approximated by a function that describes the shape of the heat source. As a result of approximation, we obtain the following law of change qmax from the time (Figure 11).

Figure 10.
Surface graphs: (a) change in temperature ΔΘ; (b) burner power Δu at τ = 5 (s).

Figure 11.
Values qmax versus time.
Furthermore, the obtained values of the power source increment of the heat source must be converted to the corresponding values of the hydrogen flow rate at the MCVD installation. The resulting function will operate over time τ, after which a new temperature measurement will be made, etc. We also note that one of the key parameters affecting the control process is the control price σ. By changing this parameter, it is possible to accelerate the process of minimizing the module ΔΘ (Figure 12).

Figure 12.
The dependence of the control price on temperature at time τ.
3.3. Adjustment and Experimental Determination of the Parameters of a Moving Exposure Source
To determine the correspondence between the power of the heat source and the hydrogen flow rate, we carry out a series of experiments on heating silica pipes with a burner flame and measure using a scanning pyrometer at fixed intervals of the temperature distribution on the outer surface of the pipe. According to the received information, it is possible to select the desired values qmax and H so that when they are substituted into Equations (22)–(27), the solution of the latter would give the temperature distribution on the outer surface of the pipe, which coincides with the experimentally obtained values. We assume that we know the law of motion of the source, i.e., the change in speed v(t) is known in advance (Equation (1)).
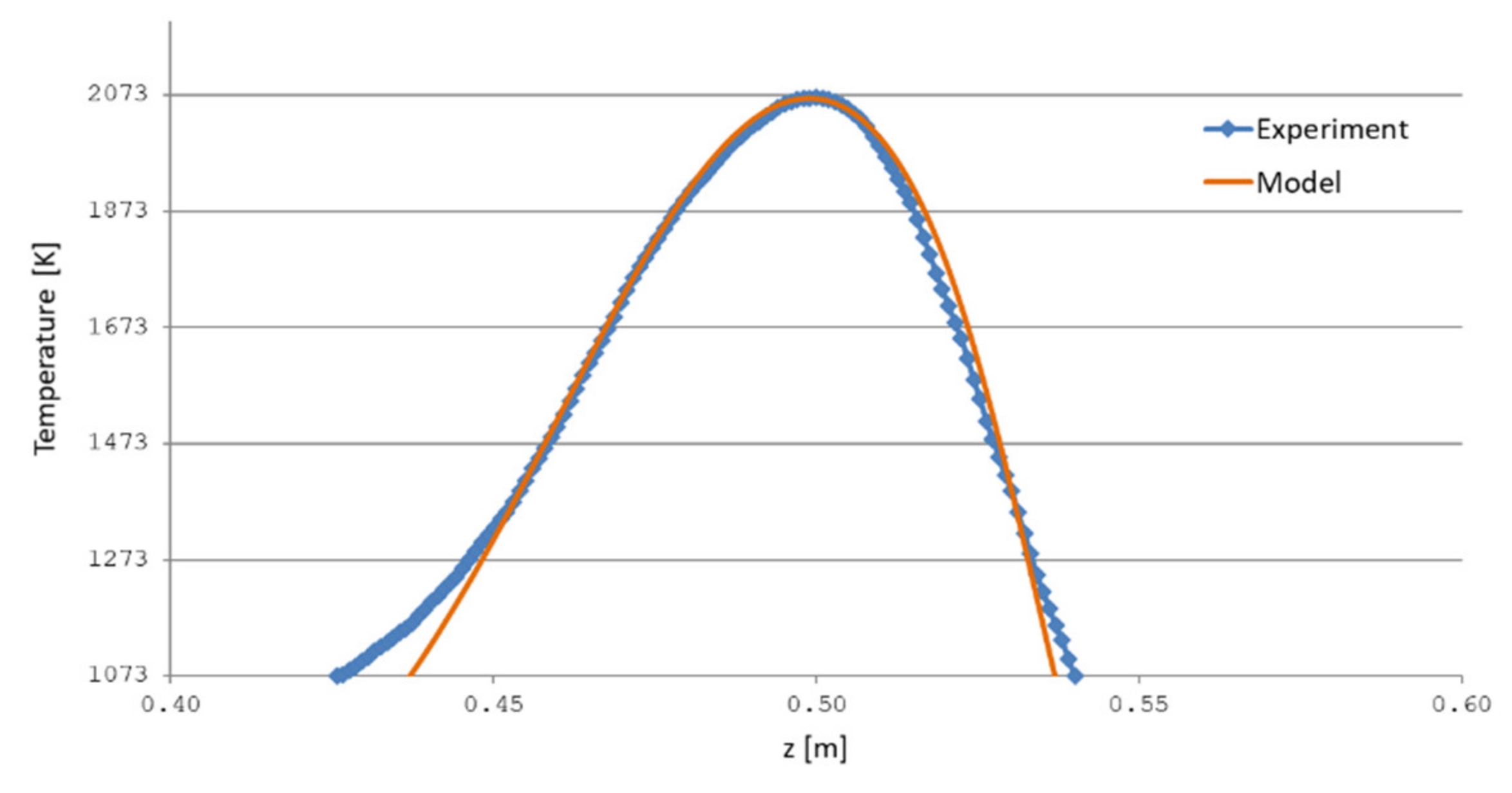
As noted earlier, to identify a moving heat source, it is necessary to determine the power function qmax, form parameter H and source moving speed. We also know that when the flow rate of the burner hydrogen changes, the shape and power of the source changes. Figure 13 presents a comparison of simulation results and experimental data.

Figure 13.
Comparison of the results of numerical simulation and experiment with a moving heat source. v(t) = 70 (mm/min); QH2 = 31.5 [l].
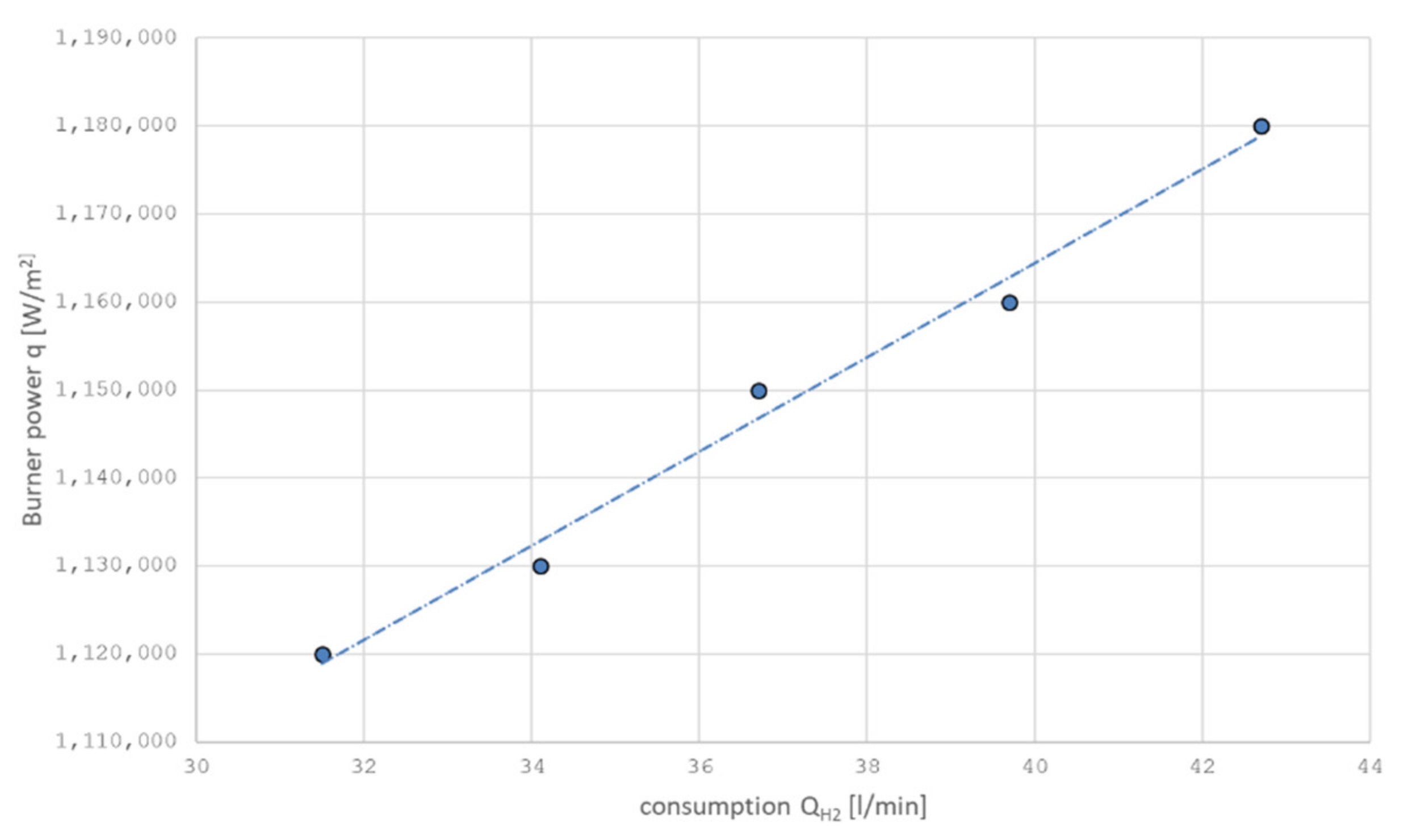
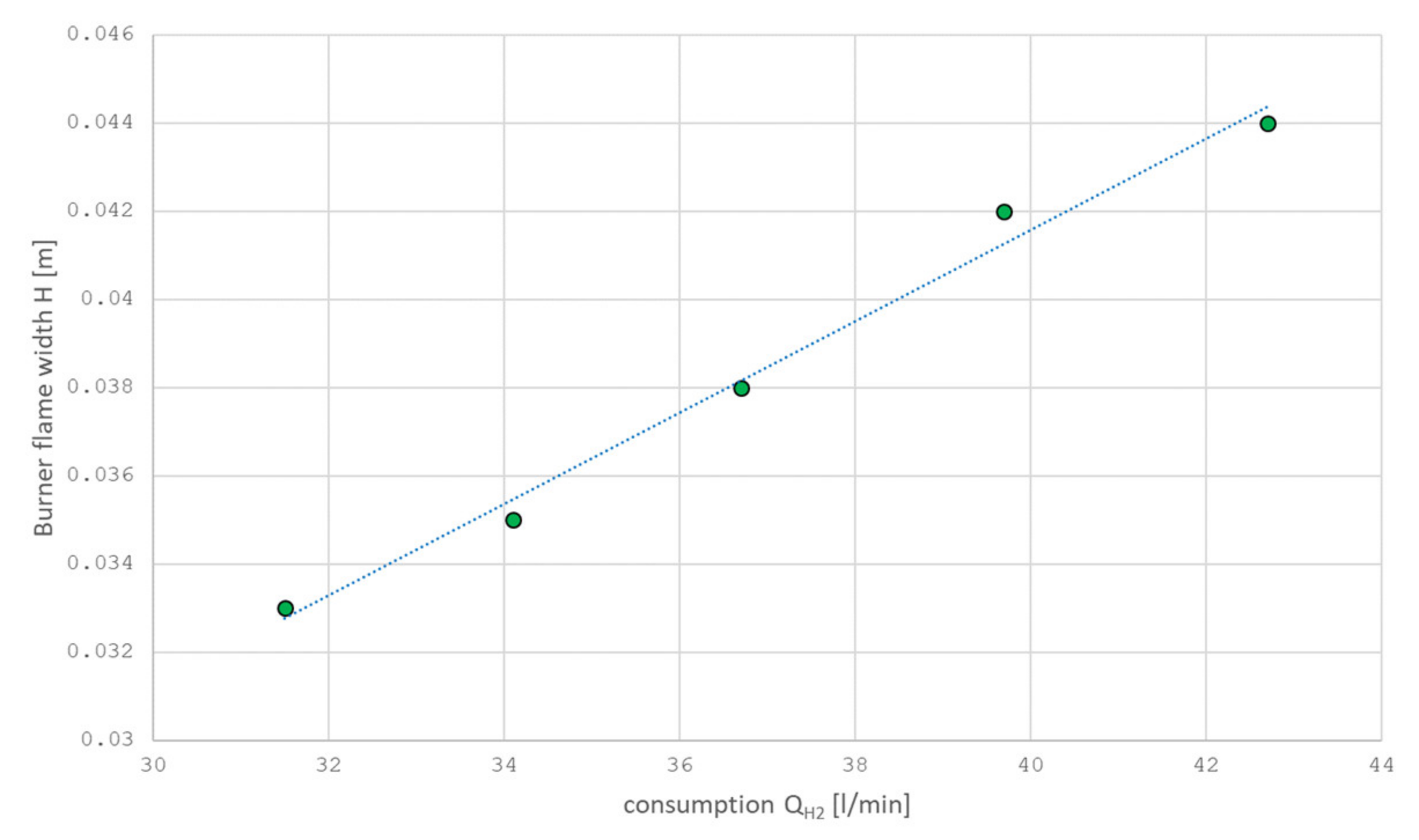
As the flow rate of the hydrogen–oxygen mixture increases, the values of the parameters will also increase qmax and H. The experiments showed that, in the researched range, the parameters qmax and H are linearly dependent on hydrogen consumption (Figure 14 and Figure 15, as well as Equations (31) and (32)).
qmax = 5354.6 × QH2 + 950,201,
H = 0.001 × QH2 + 0.0001,
qmax = 5354600 × H + 949665.54

Figure 14.
The dependence of the power qmax on the consumption QH2 with a mobile burner.

Figure 15.
The dependence of the dispersion (width) H on the consumption QH2 with a mobile burner.
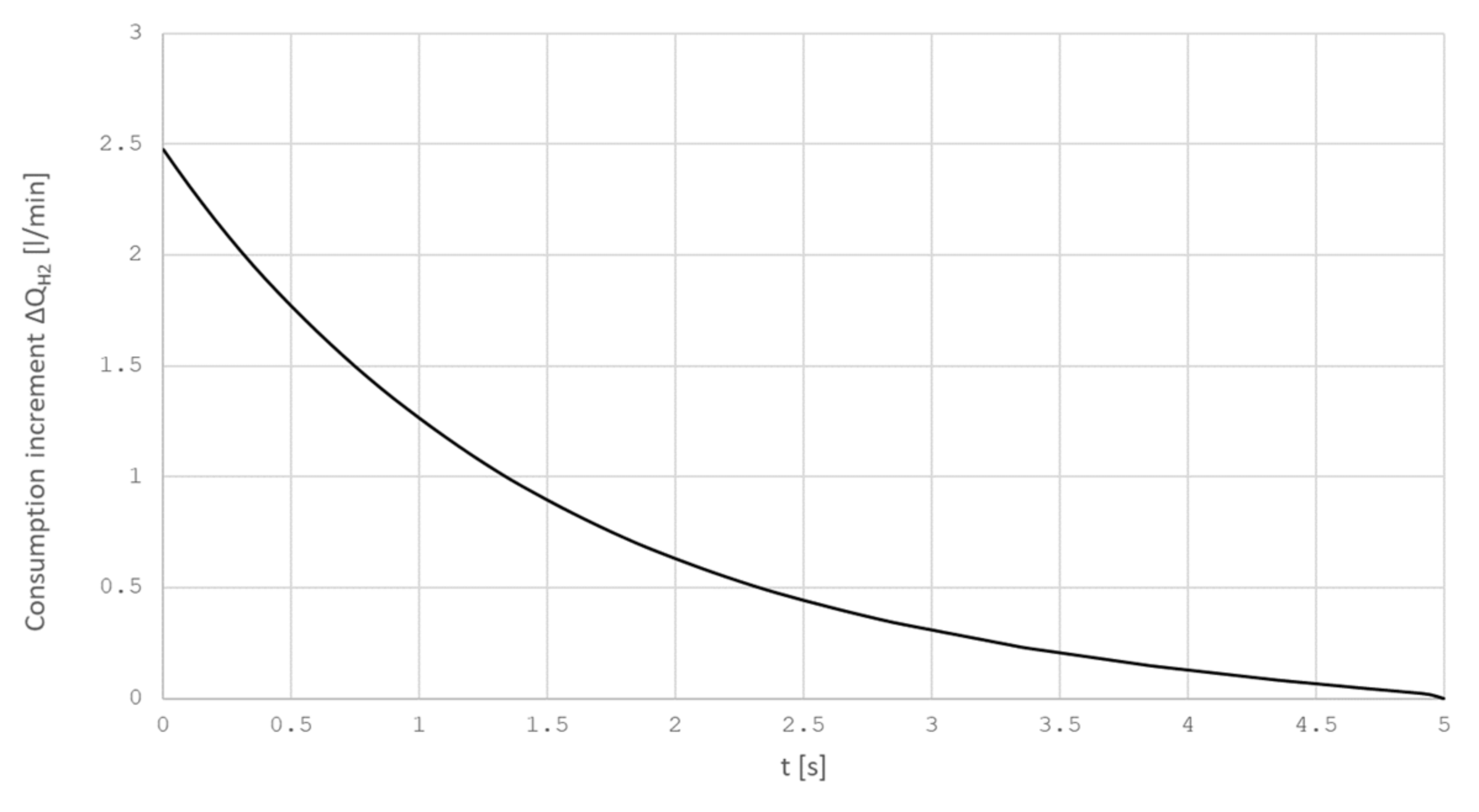
So, it is easy to obtain the dependence of qmax on dispersion (width) H. Returning to the optimal control problem, we obtain the distribution of the increment in the hydrogen flow rate from the process time (Figure 16).

Figure 16.
The consumption increment ΔQH2 from the control time τ.
We obtained a linear two-dimensional heat equation for the MCVD process. The problem of optimal stabilizing control with boundary control and boundary observation is formulated. An optimality system is obtained and an algorithm for its solution is proposed. The results of numerical studies of the temperature distribution ΔΘ and optimal control (burner power) Δuopt are presented. The distribution of the increment of hydrogen flow from the control time is obtained.
4. Optimal Control of Silica Optical Fiber Drawing
4.1. Optimal Control Problem: A Simplified Mathematical Model of Fiber Drawing
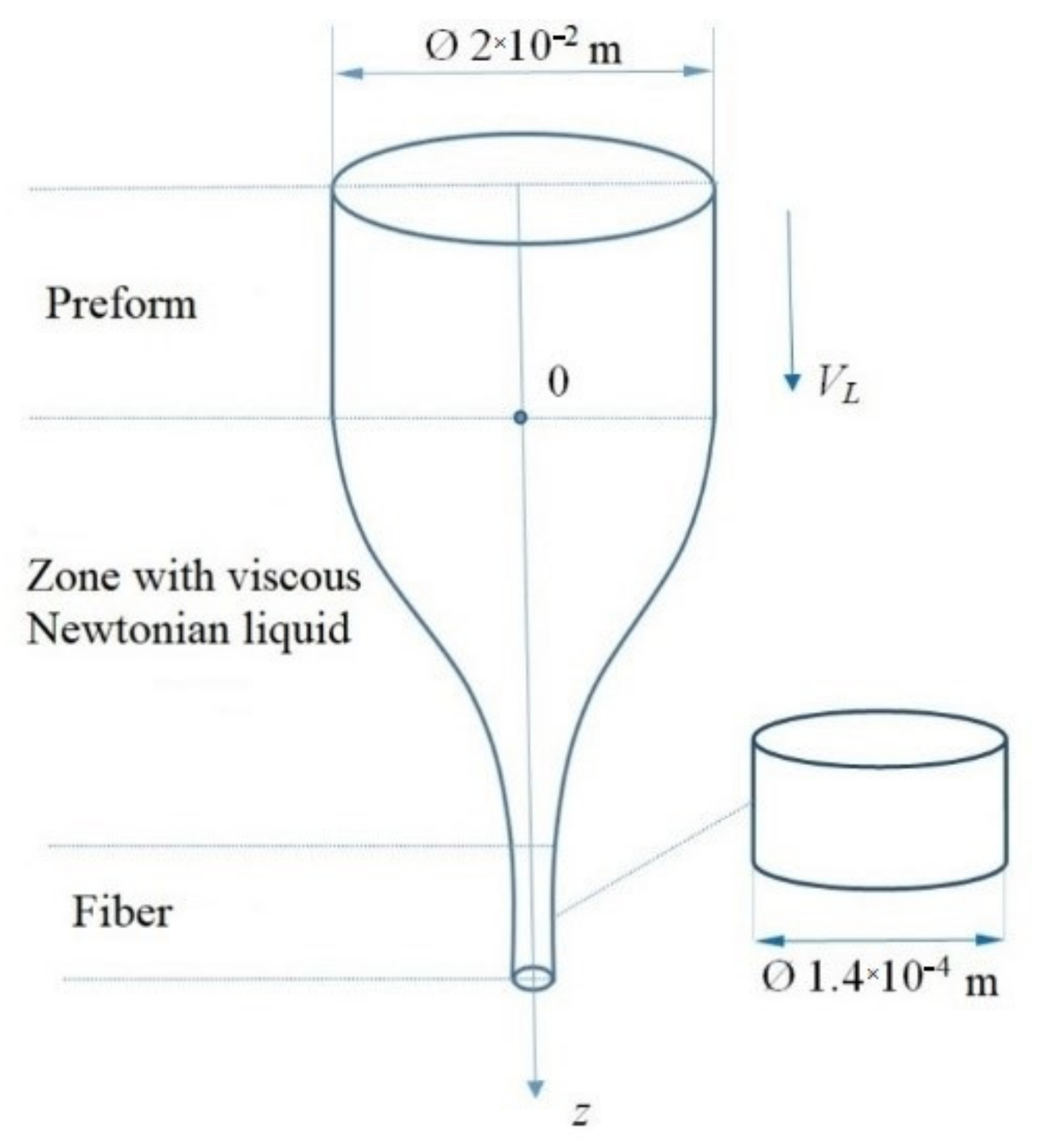
The scheme of optical fiber drawing and its main geometric characteristics are presented in Figure 17. Due to the isothermal formulation of the problem, the solution area is a zone that is filled with a viscous Newtonian liquid.

Figure 17.
Scheme of optical fiber drawing.
Let us descry a one-dimensional coordinate system (here, the spatial axis is oriented downward). The direction of is similar to the drawing direction (along the axis of symmetry). The technological drawing process can be described by the following system of partial differential equations (one-dimensional approximation):
where is the longitudinal coordinate; is time; and are the silica melt flow velocity and radius, respectively; and are the constant density and viscosity of silica melt, respectively; is solution area length; is silica preform radius; and are functions corresponding to the initial state of the system; and and are preform feed and fiber drawing velocities, respectively. Let it be that and . Let us define by the area within the segment , by Cartesian product , by piecewise-smooth boundary of , here with , , . Equations from (34) are satisfied inside the area, initial and boundary conditions from (34) are satisfied on parts of . Let us indicate the necessary spaces: is the space of functions are summed squared on ; is the space of functions from , which have a generalized first derivative belonging to .
Based on the state of system (34), let us represent the control problem. It is required to maintain the system near a state in which the deviations of the geometric characteristics of the elongated thread (fiber radius) from some optimal characteristics are minimal, provided that the fiber winding velocity is within the specified range. In this formulation of the problem under consideration, the control function will be the time function defined above. At the same time, we will observe the radius of the finished fiber that is the function is the observed parameter.
Let us call the system movement at predetermined known values of velocities and radii as programmed movement, and the control corresponding to the movement as programmed control.
According to [20,21], if some nonlinear system is linearized in the neighborhood of its stationary state, then the analysis of such a linearized system can replace the analysis of the original system. In this case, the stationary value of the fiber radius is conveniently considered as the optimal geometric characteristic.
Let us linearize the system (34) in the following assumptions:
where and are functions that correspond to programmed stationary movement; the function is a programmed control respective to the stationary mode; and are deviations of the factual movement from the programmed one; and is the deviation of the real control from the programmed one. Substituting the above relationships (35)–(37) into the system (34) and neglecting the nonlinear terms, let us obtain a linear problem in the following form:
Here, the coefficient has the following form:
The initial-boundary-value problem (38) obtained in this way describes the states that can be interpreted as deviations (disturbances) from the stationary programmed states of the original system (34).
Let us consider the functional on as follows:
where is a constant that is called the control price.
Thus, the problem (38), (40) (with boundary control and boundary observation) consists in searching for the minimum value of the functional while the control parameter takes values from the space of functions for .
The optimality system obtaining as a result of linearization is the necessary conditions for the existence of the problem (38), (39). For this case, there is a possibility to obtain the optimality system in the boundary value problem form for the parent equations and equations for the conjugate states.
The questions of optimization problem solution existence for parabolic systems with objective functional in special forms was discussed in [4]. For the existence of at least one function (optimal element) on which the functional (40) reaches its exact lower bound, it is necessary that the functional possess the properties of convexity, lower semicontinuity, and coercivity as follows
In accordance with the optimality criterion the value of the Gato differential [4] at the optimal element, equals to zero as follows:
where , is the weak differentiation operator, and is the control function variation.
It should be noted that the differential problem in formulation (38) is linear with respect to the control function . Thus, the state function of the system can be represented as a result of the action of some linear operator (note it as ) on the control function as follows:
Using the linearity property of the operator , let us obtain the following:
Let us formulate the initial-boundary-value problem (38) [22] as follows:
Let us multiply the continuity Equation (45) on a function and the movement equation on a function , integrate both equations over the domain , and find their sum. The result of the addition will be the following expression:
Let us use the Green’s formula for terms containing derivatives of functions and as follows:
Let us require that the functions and satisfy the following differential problem:
Then, considering (45) and (46), the last integral relation takes the following form:
Substituting it in (42):
It follows that
Finally, the optimality system takes the following form:
The process of solving the system (47) was conditionally divided into some stages:
- Searching for a stationary solution of the system (34) (i.e., definition of functions and );
- Determination of a function depending on stationary states;
- Searching for a solution of the optimality system (47) and finding the optimal control function (the numerical solution of the optimality system (47) was implemented using the Comsol Multiphysics modeling package);
- Result analysis.
Let us consider the process in detail.
Under stationary conditions, the solution of the system of equations can be found in an explicit analytical form as follows:
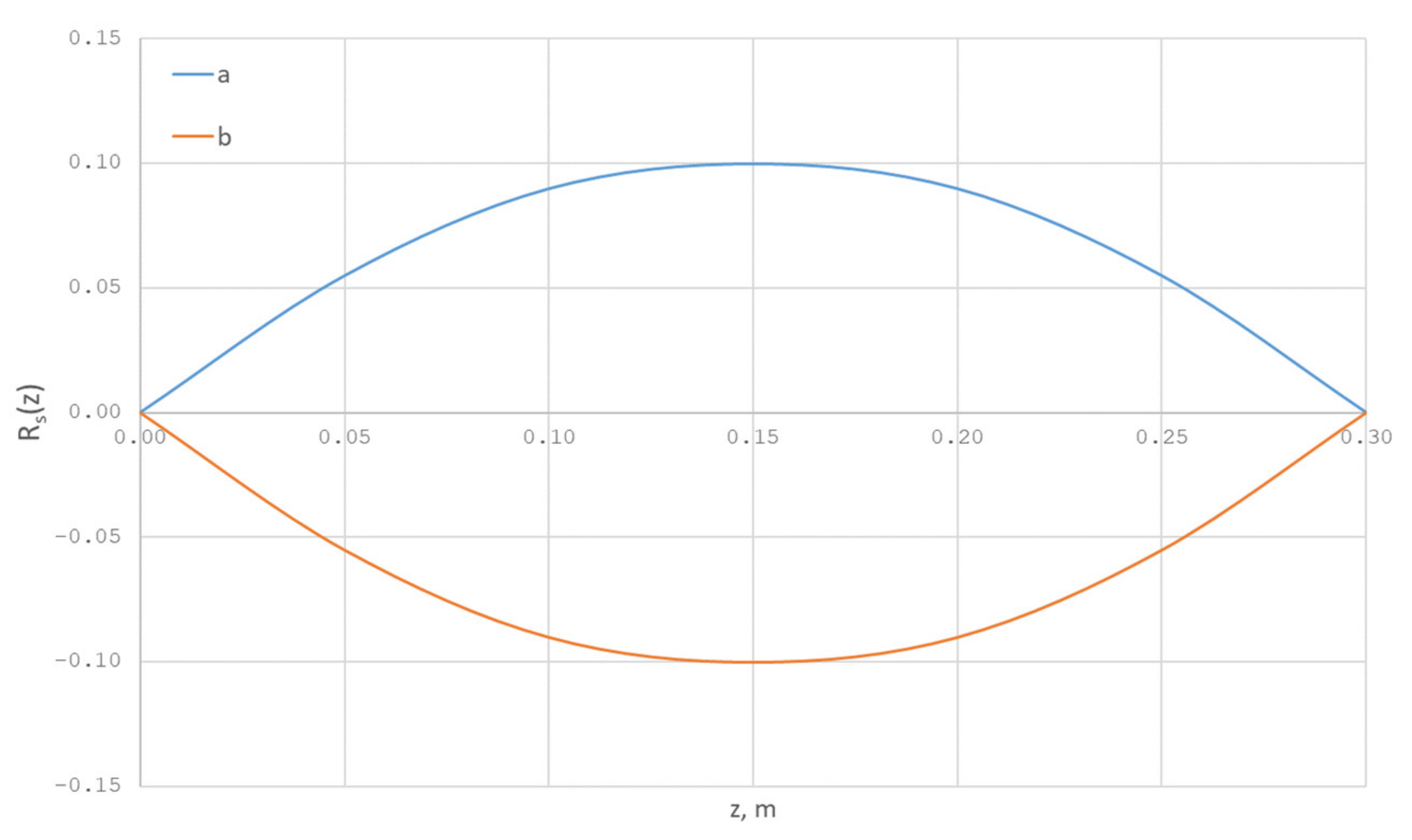
To solve the optimality system, the following values of the input parameters were used: τ = 5 s, ρ = 2200 kg/m3, µ = 10,000 Pa·s, L = 0.3 m. The function of the fiber radius deviation from its stationary state is shown in Figure 18 (line a). The deviation is specified in the form of an upward-convex function where the maximum is 10%.

Figure 18.
Deviation of the fiber radius (in fractions of the stationary solution).
Special attention is paid to the choice of the control price value . This parameter is necessary to determine in advance or based on the solutions of test problems. In this case, its value is equal to 0.5.
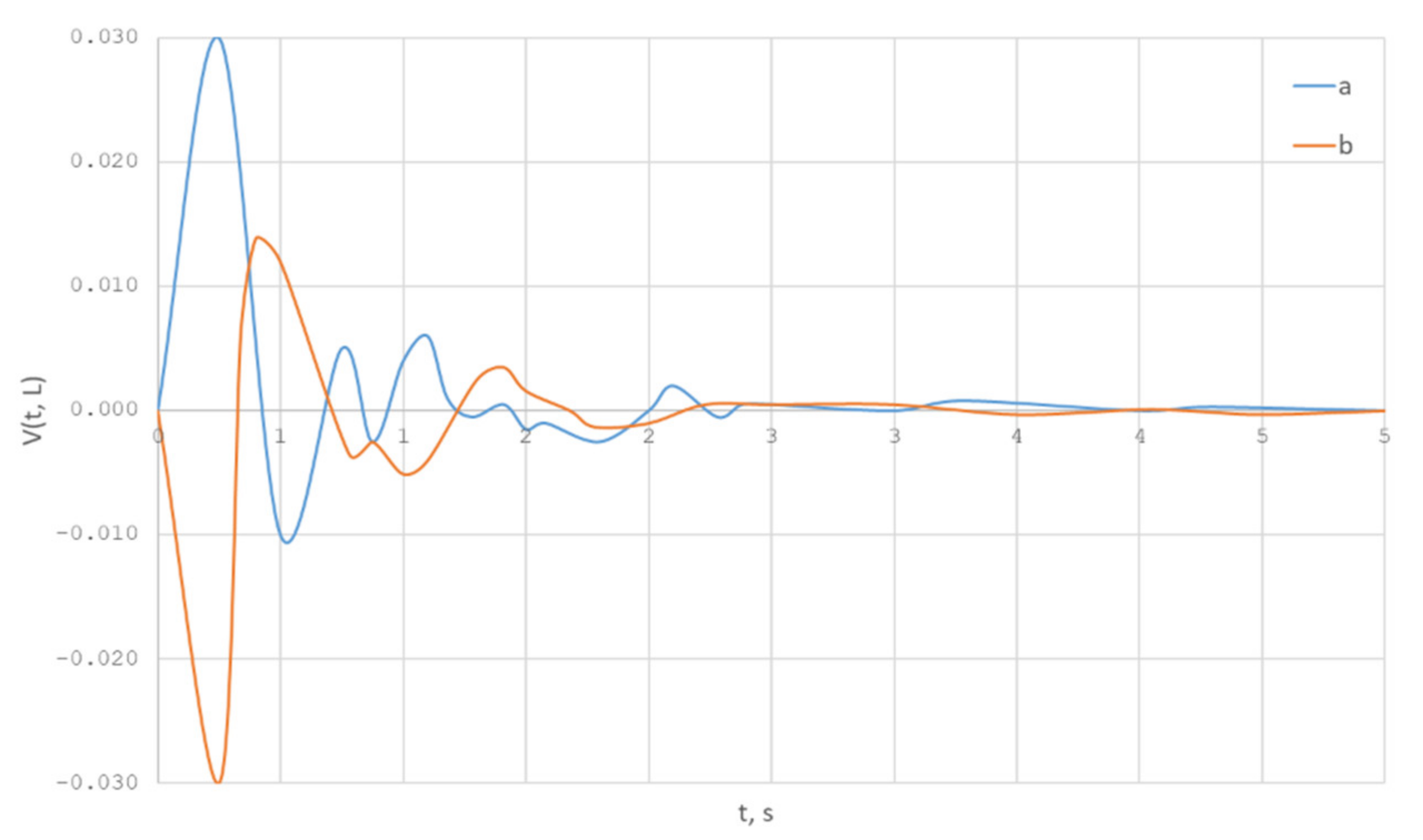
The optimal control function is shown in Figure 19.

Figure 19.
Optimal control function.
Let us solve the problem given above under the other initial condition.
Let the function be now the downward-convex function (line b in Figure 18), and the maximum of the fiber radius deviation from its stationary state is also 10%. Then, the optimal control function has the following form (line b in Figure 19).
To analyze the results, let us consider the obtained optimal control functions (lines a and b in Figure 19). As we can see, the optimal control functions are mirror symmetric with respect to each other, while the functions describing the initial state of the fiber radius are also mirror symmetric. It should be noted that the adjustment of the fiber winding speed is from −3 to +3 percent, which corresponds to the real production capabilities.
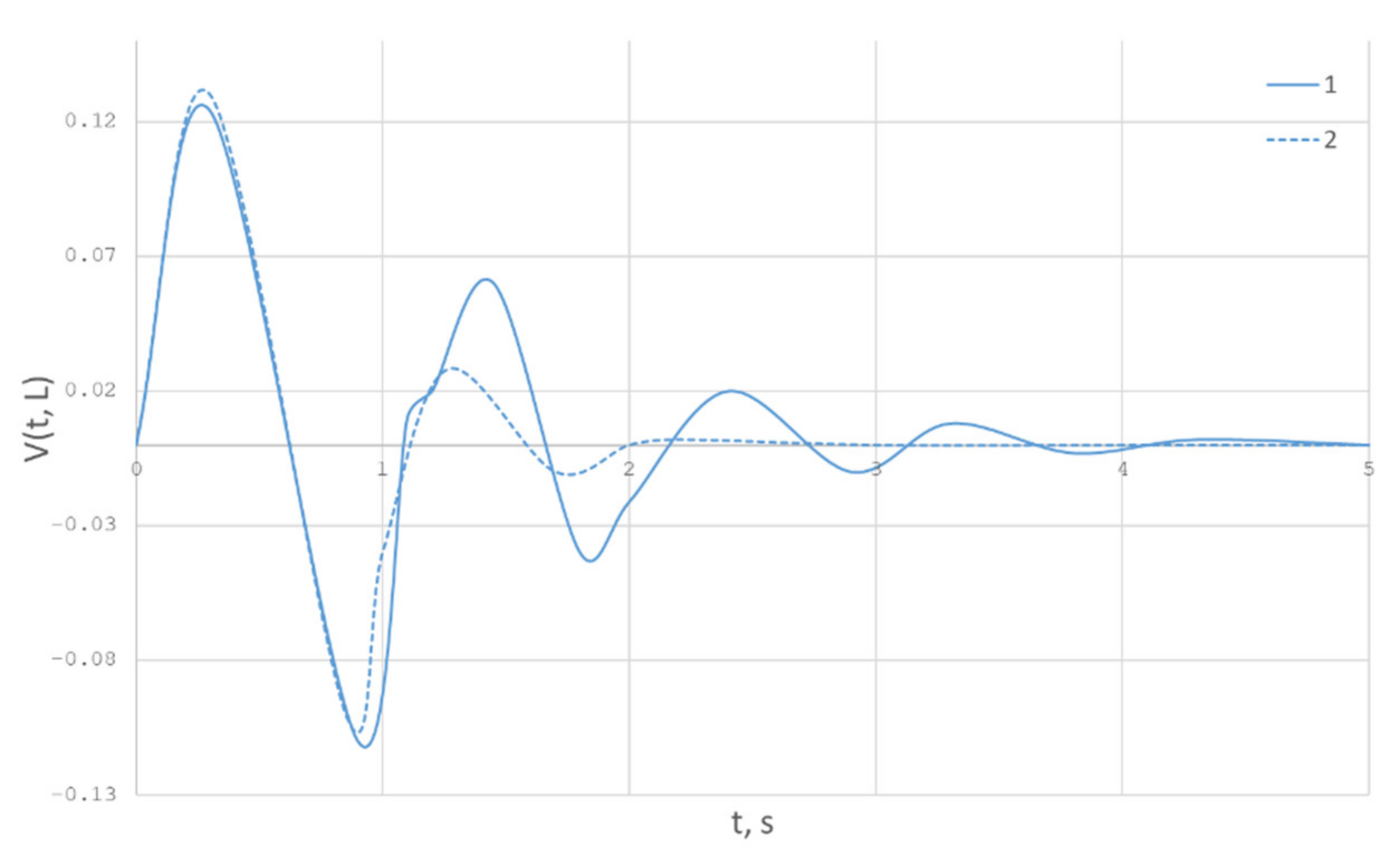
To estimate the influence of control on the resulted fiber quality, let us consider two drawing modes: Mode 1 is a non-control mode, and Mode 2 is a control mode according to the optimal state . It is clear from the Figure 20 that, in mode 2, the function of the resulted fiber radius stabilizes noticeably faster than in the mode without control. In addition, deviations in the fiber radius are smaller in mode 2.

Figure 20.
Comparison of the deviation functions of the resulted fiber radii for two drawing modes: (line 1); the optimal value of the control function (line 2).
4.2. Optimal Control Problem for the Optical Fiber Drawing in a Formulation That Takes into Account Surface Tension and Gravity Forces
Let us consider a system of partial differential equations that describes the process of drawing silica optical fibers in the following form:
For this case, the system of equations describing the perturbation of the steady-state drawing mode (isothermal case) has the following form:
where coefficients , , , and have the following forms:
Here, and are the density and viscosity of the melt, respectively, is the coefficient of surface tension, and is the gravitational acceleration. The coefficients , , , and are calculated through the functions and , which are the solutions of the system of equations for the stationary problem (34).
Let us formulate the problem of boundary control and boundary observation of a parabolic system that is supplemented by corresponding initial and boundary conditions for the disturbed movement as follows:
where the functions .
The optimal control function must be found as a function that delivers a minimum to the integral functional under the condition that parameter is small as follows:
Furthermore, using the method described in the previous problem, let us obtain the optimality system in the following form:
where are given auxiliary functions and the optimal control function .
The numerical implementation of the solution of the optimality system (52) was implemented in a similar way as described above:
- Searching for a stationary solution. These functions were found using the solution of system, which describes the stationary state of drawing process [23];
- Finding the functions , , , and , depending on stationary states;
- Solving of the optimality system (52) and finding the optimal control function ;
- Result analysis.
Let us describe the implementation process in detail.
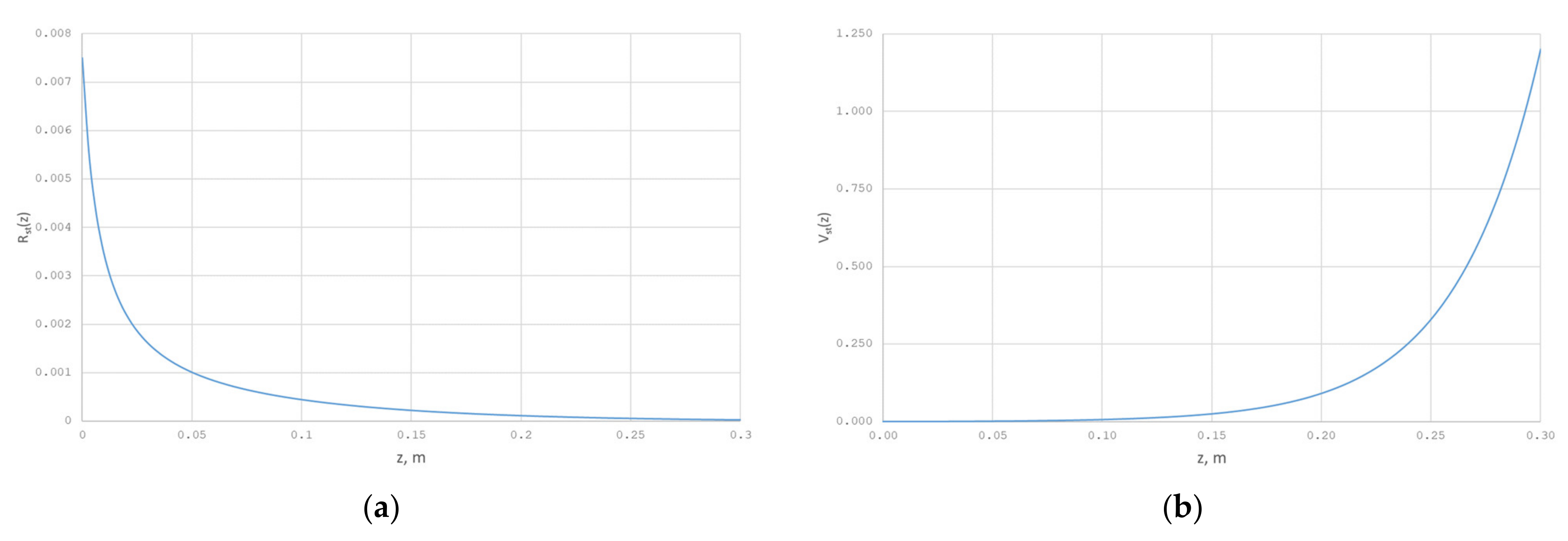
First, the stationary solutions and were found numerically (see Figure 21).

Figure 21.
(a) Radius of the silica melt flow, (b) Velocity of the silica melt flow.
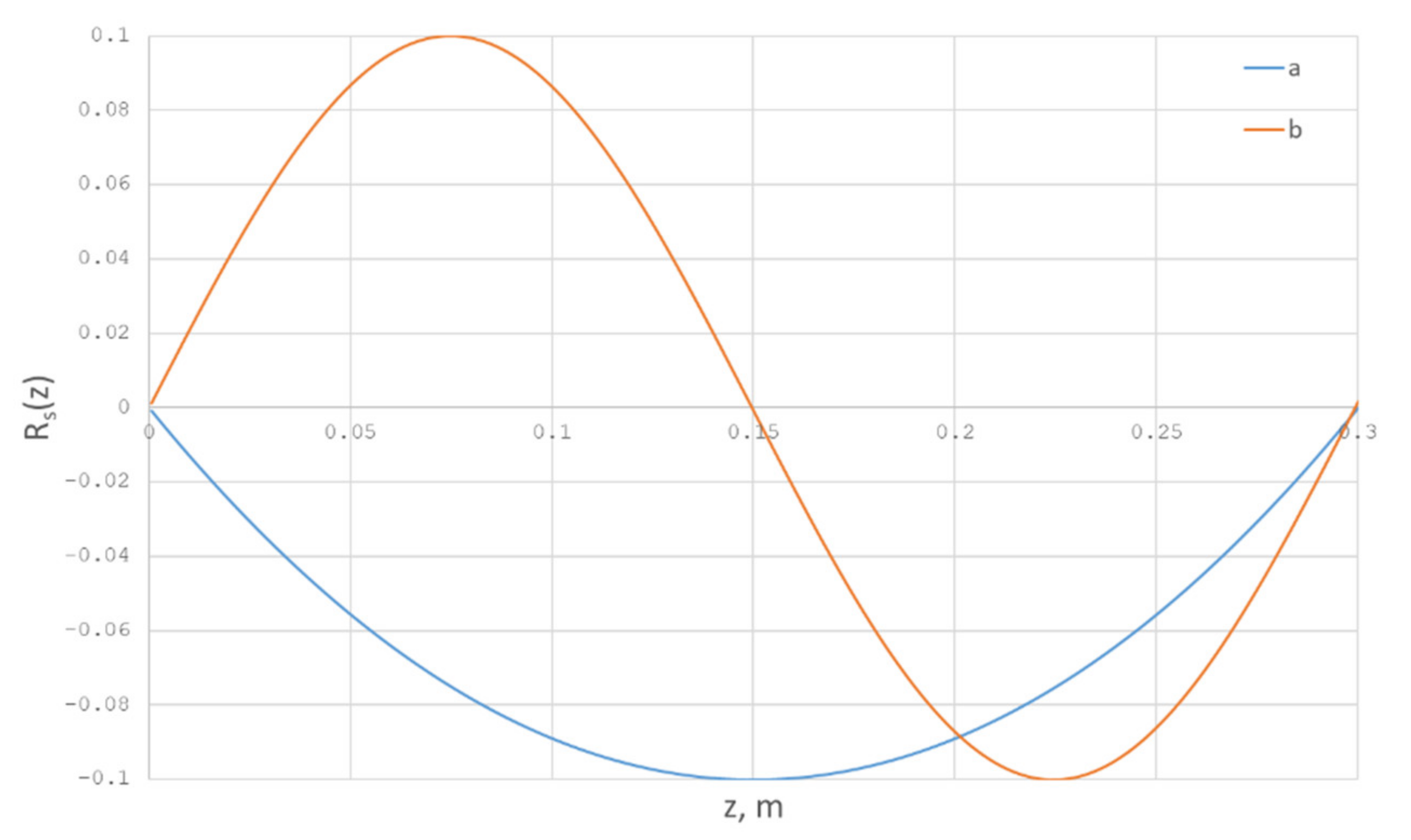
To solve the optimality system, the following values of the input parameters were used: τ = 160 s, ρ = 2200 kg/m³, µ = 10,000 Pa·s, L = 0.3 m. The function of the fiber radius deviation from its stationary state is shown in Figure 22 (line a). The deviation is specified in the form of an upward-convex function where the maximum is 10%. The obtained control function can be seen in Figure 23 (line a).

Figure 22.
Radius drawing deviation (as a fraction of the stationary solution).

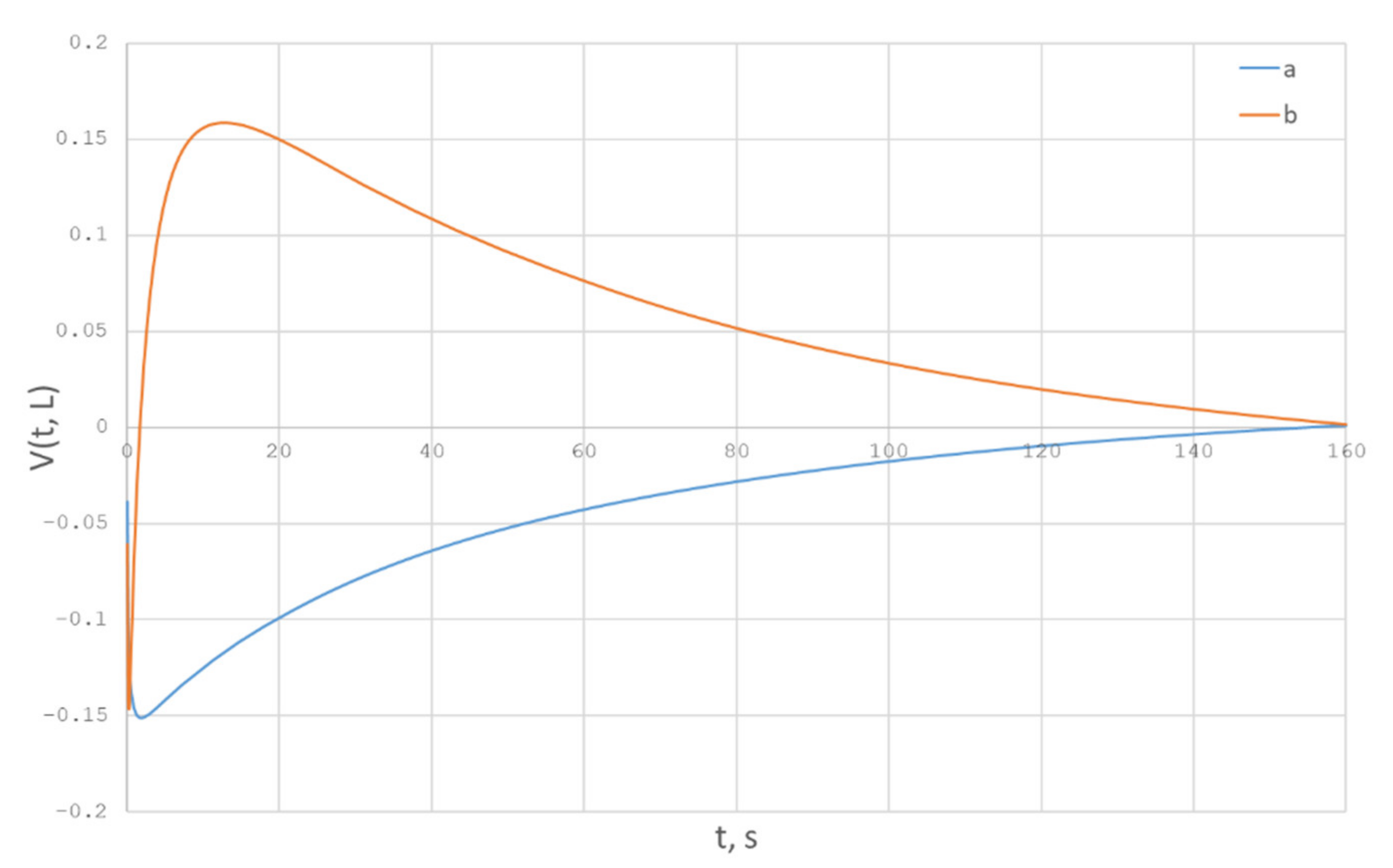
Figure 23.
Obtained control function.
Let us solve the same problem given above.
Here, the initial deviation of the fiber radius has the following form (line b in Figure 22), and the maximum of the deviation from its stationary state is also 10%. Then, having solved the optimality system (52) for the same values of the input parameters, we obtain the function in the following form (line b in Figure 23).
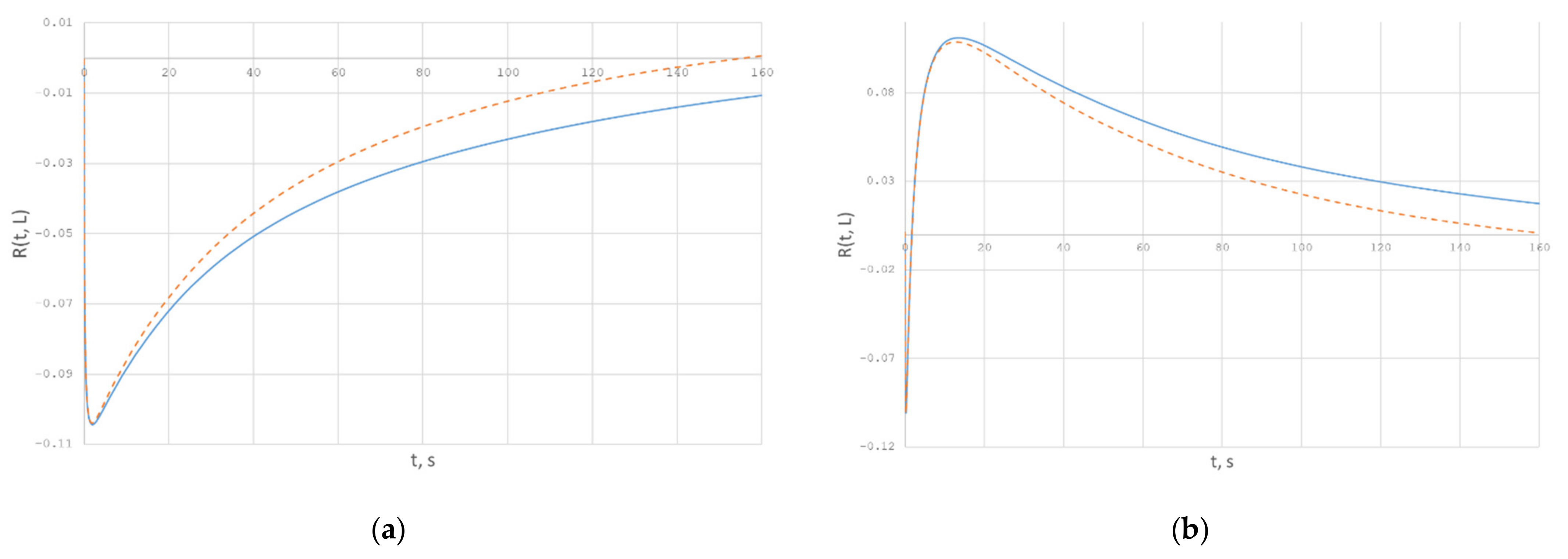
Let us analyze the results of solving the optimality system (52) with two different initial conditions for the equation of state. Note that the adjustment of the fiber winding speed is from −15 to +15 percent, which corresponds to the real production capabilities. To estimate the influence of control on the resulted fiber quality, let us consider two drawing modes: Mode 1 is a non-control mode, and mode 2 is a control mode according to the optimal state . It is clear from Figure 24 that, in mode 2 (dotted line), the function of the resulted fiber radius stabilizes noticeably faster than in the mode without control (solid line). In addition, the deviations of the fiber radius are smaller in mode 2.

Figure 24.
(a,b) Comparison of the deviation functions of the resulted fiber radii for two different drawing modes.
5. Conclusions
Overall, in this paper, two problems of optimal control of the processes of alloying of silica optical fiber preforms by the MCVD method and the silica optical fiber drawing are formulated, justified, and solved. The first problem was solved in two settings: one-dimensional and axisymmetric, and the control function is the heat flux on the outer surface of the tube. In the second problem, two mathematical models are also considered: a simplified model and a model that takes into account the forces of surface tension and gravity. Both fiber drawing problems are solved in a one-dimensional formulation, where the control function is the winding speed of the resulted fiber. For both problems, linearized mathematical models were used, for which optimality systems were obtained in a strong form, i.e., in the form of partial differential boundary value problems. Each of the fiber drawing problems is solved for two different types of initial conditions that specify the deviation of the radius relative to its stationary (programmed) state. Numerical solutions of the optimality system, including the optimal control functions, are presented.
Author Contributions
Conceptualization, V.P. and D.V.; investigation, V.P., D.V., I.G. and D.D.; methodology, V.P. and D.V.; project administration, D.V.; software, I.G. and D.D.; supervision, V.P.; validation, V.P., D.V., I.G. and D.D.; writing—original draft preparation, V.P., D.V., I.G., A.G.K. and D.D.; writing—review and editing, A.G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was carried out with the financial support of the Ministry of Science and Higher Education of the Russian Federation in the framework of the program of activities of the Perm Scientific and Educational Center “Rational Subsoil Use”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Agrell, E.; Karlsson, M.; Chraplyvy, A.R.; Richardson, D.J.; Krummrich, P.M.; Winzer, P.; Roberts, K.; Fischer, J.K.; Savory, S.J.; Eggleton, B.J.; et al. Roadmap of optical communications. J. Opt. 2016, 18, 063002. [Google Scholar] [CrossRef]
- Ferreira, M.F.S. Optical Fibers: Technology, Communications and Recent Advances; Nova Science Publishers: New York, NY, USA, 2017; ISBN 9781536109917. [Google Scholar]
- Cordeiro, C.M.B.; Ng, A.K.L.; Ebendorff-Heidepriem, H. Ultra-simplified Single-Step Fabrication of Microstructured Optical Fiber. Sci. Rep. 2020, 10, 9678. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Guo, H. A review of SLMed magnesium alloys: Processing, properties, alloying elements and postprocessing. Metals 2020, 10, 1073. [Google Scholar] [CrossRef]
- Anuszkiewicz, A.; Kasztelanic, R.; Filipkowski, A.; Stepniewski, G.; Stefaniuk, T.; Siwicki, B.; Pysz, D.; Klimczak, M.; Buczynski, R. Fused silica optical fibers with graded index nanostructured core. Sci. Rep. 2018, 8, 12329. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; An, L. Abnormal behavior of silica doped with small amounts of aluminum. Sci. Rep. 2016, 6, 6–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hehlen, M.; Epstein, R.; Patterson, W.; Sheik-Bahae, M.; Seletskiy, D. Measurement of solid-state optical refrigeration by two-band differential luminescence thermometry. J. Opt. Soc. Am. B 2009, 27, 611–618. [Google Scholar]
- Orlov, L.K.; Vdovin, V.I.; Drozdov, Y.N.; Orlov, M.L.; Ivina, N.L.; Steinman, E.A. Characterization of Interface Layers of a Solid Solution Formed During the Growth of a Carbide Layer on Silicon from Hydrogen Containing Compounds. J. Struct. Chem. 2021, 62, 630–640. [Google Scholar] [CrossRef]
- Saadi, N.S.; Hassan, L.B.; Karabacak, T. Metal oxide nanostructures by a simple hot water treatment. Sci. Rep. 2017, 7, 7158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fitt, A.D.; Furusawa, K.; Monro, T.M.; Please, C.P. Modeling the fabrication of hollow fibers: Capillary drawing. J. Light. Technol. 2001, 19, 1924–1931. [Google Scholar] [CrossRef]
- Fitt, A.D.; Furusawa, K.; Monro, T.M.; Please, C.P.; Richardson, D.J. The mathematical modelling of capillary drawing for holey fibre manufacture. J. Eng. Math. 2002, 43, 201–227. [Google Scholar] [CrossRef]
- Kostecki, R.; Ebendorff-Heidepriem, H.; Warren-Smith, S.C.; Monro, T.M. Predicting the drawing conditions for Microstructured Optical Fiber fabrication. Opt. Mater. Express 2014, 4, 29. [Google Scholar] [CrossRef] [Green Version]
- Kostecki, R.; Ebendorff-heidepriem, H.; Davis, C.; Mcadam, G.; Warren-smith, S.C.; Monro, T.M. Silica exposed-core microstructured optical fibers. Opt. Mater. Express 2012, 2, 5082–5087. [Google Scholar] [CrossRef]
- Monro, T.M.; Richardson, D.J. Holey optical fibres: Fundamental properties and device applications. Comptes Rendus Phys. 2003, 4, 175–186. [Google Scholar] [CrossRef]
- Badii, M. Periodic solutions for a class of degenerate evolution problems. Nonlinear Anal. Theory Methods Appl. 2001, 44, 499–508. [Google Scholar] [CrossRef]
- Kubyshkin, V.A.; Finyagina, V.I. Podvizhnoe Upravlenie v Sistemah s Raspredelennymi Parametrami; SINTEG: Moscow, Russia, 2005. [Google Scholar]
- Lienard, I.V.; John, H. A Heat Transfer Textbook; Phlogiston Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Rappoport, E.Y. Analiz i Sintez Sistem Avtomaticheskogo Upravleniya s Raspredelennymi Parametrami; Vysshaya Shkola: Moscow, Russia, 2005. [Google Scholar]
- Fursikov, A.V. Optimalnoe Upravlenie Raspredelennymi Sistemami. Teoriya i Prilozheniya; Nauchnaya Kniga: Moscow, Russia, 1999. [Google Scholar]
- Morgan, R. Linearization and Stability Analysis of Nonlinear Problems. Rose-Hulman Undergrad. Math. J. 2015, 16, 67–91. [Google Scholar]
- Rodríguez, R.S.; Avalos, G.G.; Gallegos, N.B.; Ayala-jaimes, G.; Garcia, A.P. SS symmetry Approximation of Linearized Systems to a Class of Nonlinear Systems Based on Dynamic Linearization. Symmetry 2021, 13, 854. [Google Scholar] [CrossRef]
- Pervadchuk, V.; Vladimirova, D.; Gordeeva, I. Optimal control of distributed systems in problems of quartz optical fiber production. In AIP Conference Proceedings; AIP Publishing LLC.: Huntington, NY, USA, 2018; p. 020036. [Google Scholar]
- Hallen, M.; Li, B.; Tanouchi, Y.; Tan, C.; West, M.; You, L. Computation of steady-state probability distributions in stochastic models of cellular networks. PLoS Comput. Biol. 2011, 7, e1002209. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).