Heat Transfer in Biological Spherical Tissues during Hyperthermia of Magnetoma
Abstract
:Simple Summary
Abstract
1. Introduction
2. Mathematical MGT Bioheat Model
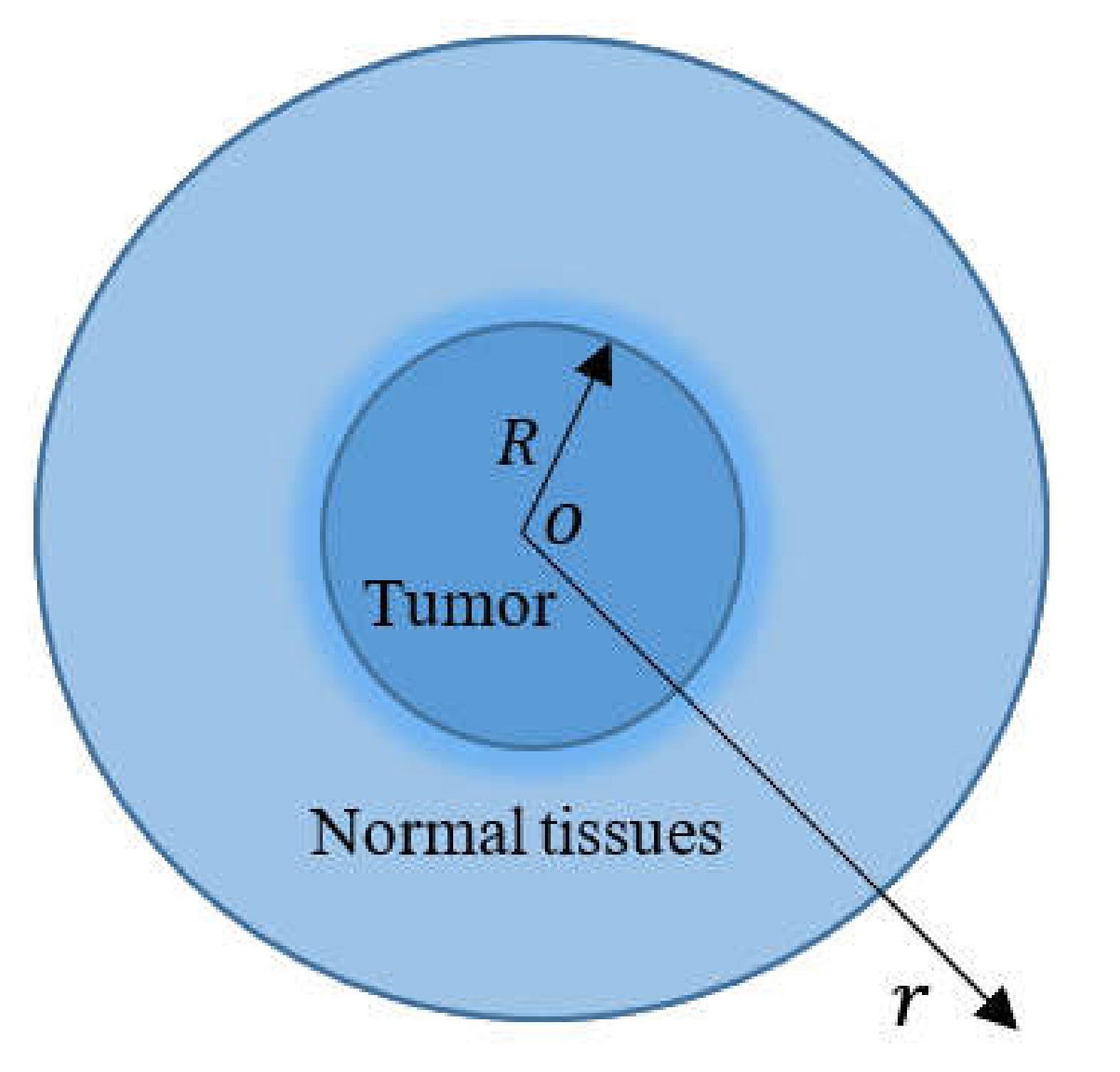
3. Formulation of the Problem
4. Solution in the Laplace Transform Space
5. Evaluation of the Thermal Damages
6. Numerical Results
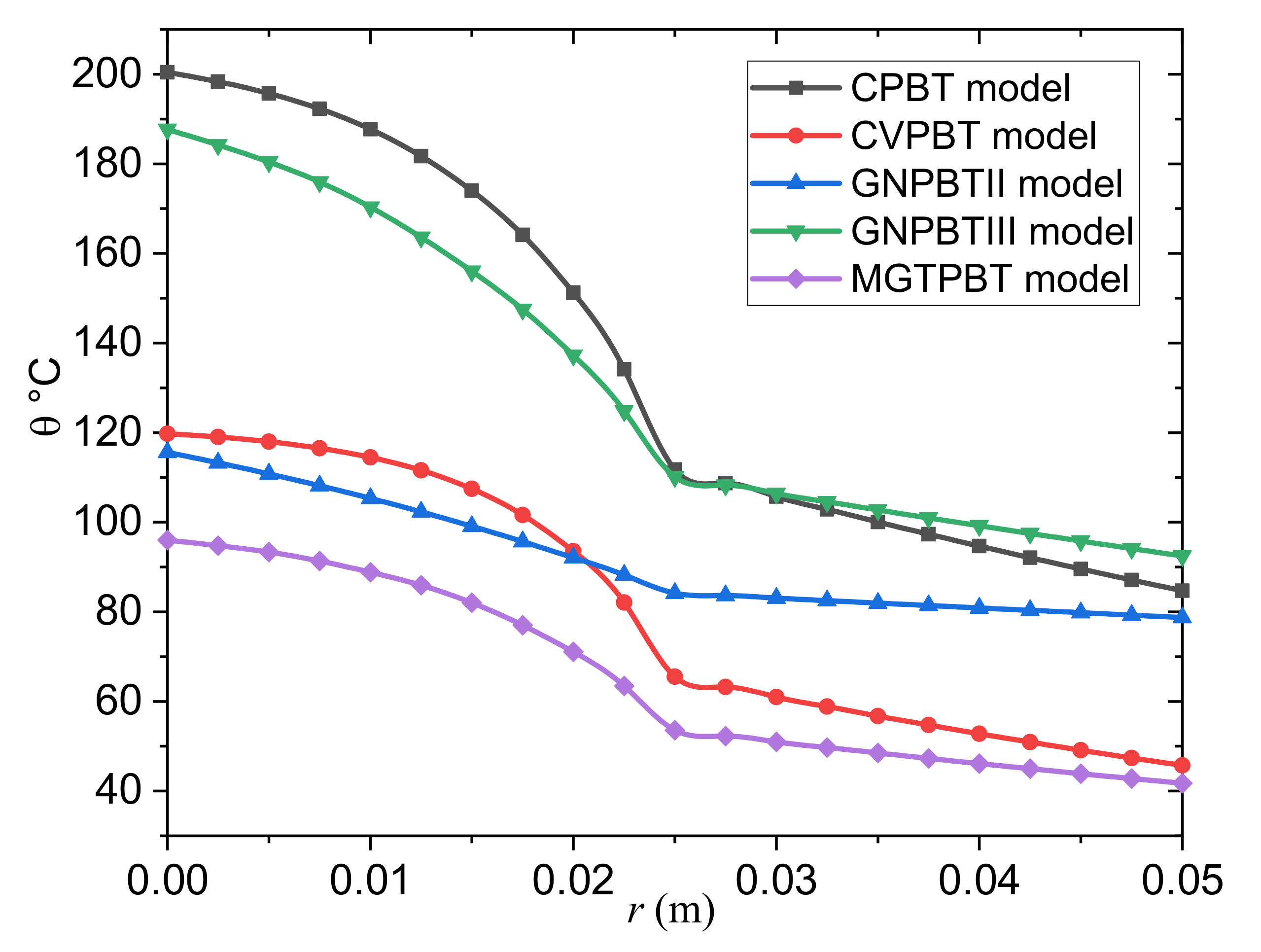
- The classical Pennes bioheat transfer (CPBT) model can be obtained when we set .
- The Cattaneo–Vernotte Pennes bioheat transfer (CVPBT) model can be obtained when we put and take .
- The Pennes bioheat transfer model based on Green and Naghdi’s theory of type II (GNPBTII) can be obtained when the terms, including and are neglected.
- The Pennes bioheat transfer model based on Green and Naghdi’s theory of type III (GNPBTIII) can be obtained when the thermal relaxation time is neglected .
- The new MGTPBT model is attained when .
- The temperature distribution in the tumor and normal tissues is greatly influenced by the thermal factors and .
- Including the relaxation coefficient, in the CVPBT and MGTPBT models may mean that the temperature decrease is slowed down.
- The predictions of the GNPBTIII and MGTPBT models are incompatible.
- The magnitude is larger in the case of the GNPBTIII model than in the case of the MGTPBT model, although the graph shows similar results for both models.
- The thermoelastic results of the GNPBTIII model differ significantly from the GNPBTII model due to energy losses in the case of the first model.
- In contrast to previous modified bioheat models, the results of the GNPBTIII model of thermoelasticity indicate convergence with the results of the conventional CPBT model, which do not fade in heat rapidly within the tumor and normal tissues, respectively.
- The profiles of the temperature differences between the MGTPBT and CVPBT models were compared. It is clear from the figure that the behavior and convergence of the results of both models are quite similar, with only slight differences in magnitude.
- The blood temperature distribution slightly differed between the MGTPBT and GNPBTII models.
- Heat wave propagation may realistically predict the temperature distribution in living tissues. The cooling function of the blood circulation keeps the tissue temperature from increasing but does not affect the speed of the thermal diffusion. According to this new hypothesis, the relaxation coefficient will become a new measure of the efficiency of the vital heat transfer in living tissues.
- Transferring thermal energy away from the interface is difficult to apply. As a result, the temperature gradually decreases. It indicates that by lowering the relaxation coefficient, the heat transfer capacity of the medium can be increased.
7. Conclusions
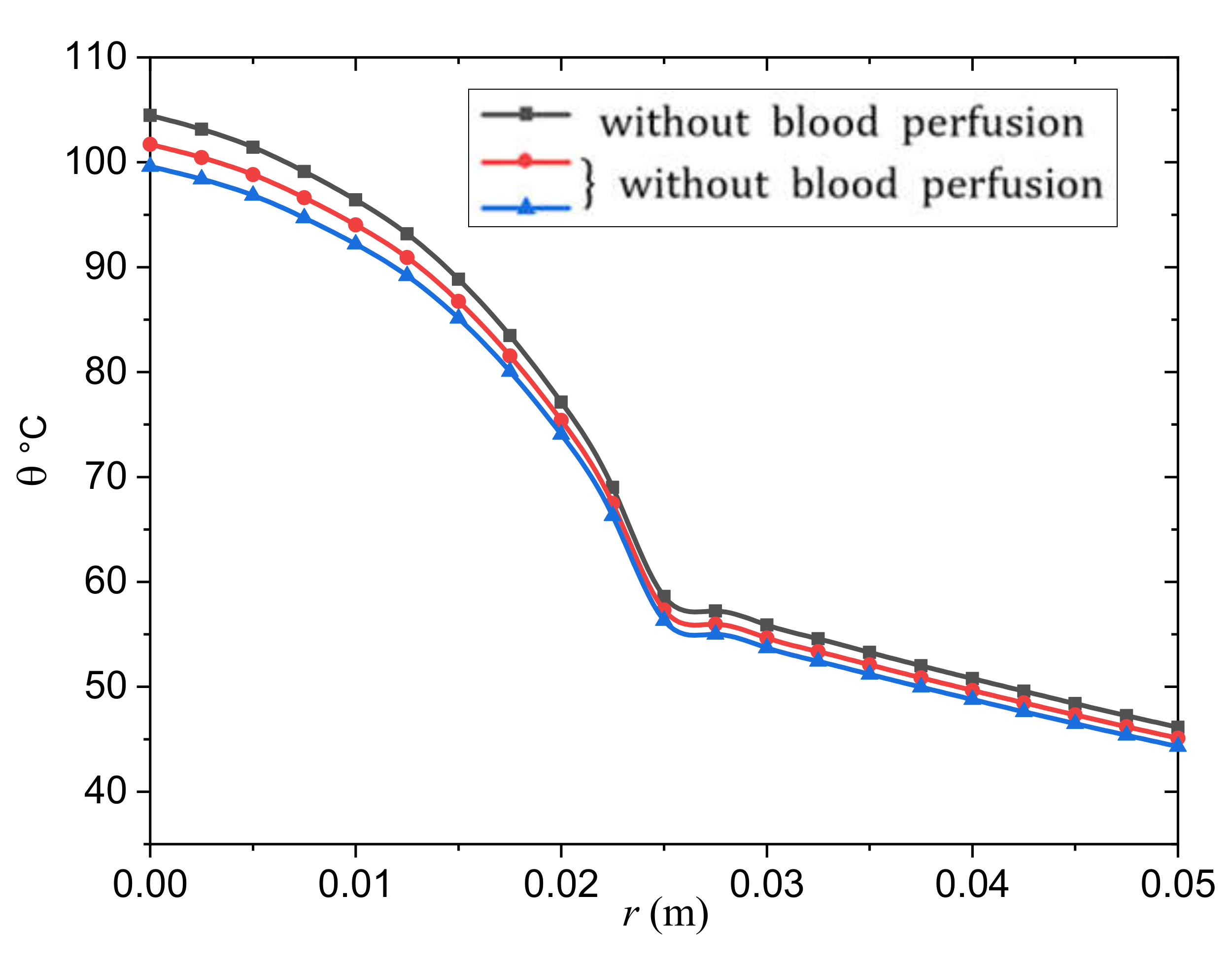
- The rate of change of blood perfusion has a significant effect on the transfer of bioheat in a tumor and normal tissue. Because the skin temperature is higher than the arterial temperature, the blood perfusion acts as a cooling agent. The perfusion rate is proportional to the amount of heat energy extracted from the blood.
- The results were influenced by the relaxation durations used and the perfusion of the blood. It is also clear that more experimental research is needed to determine the delay times more accurately.
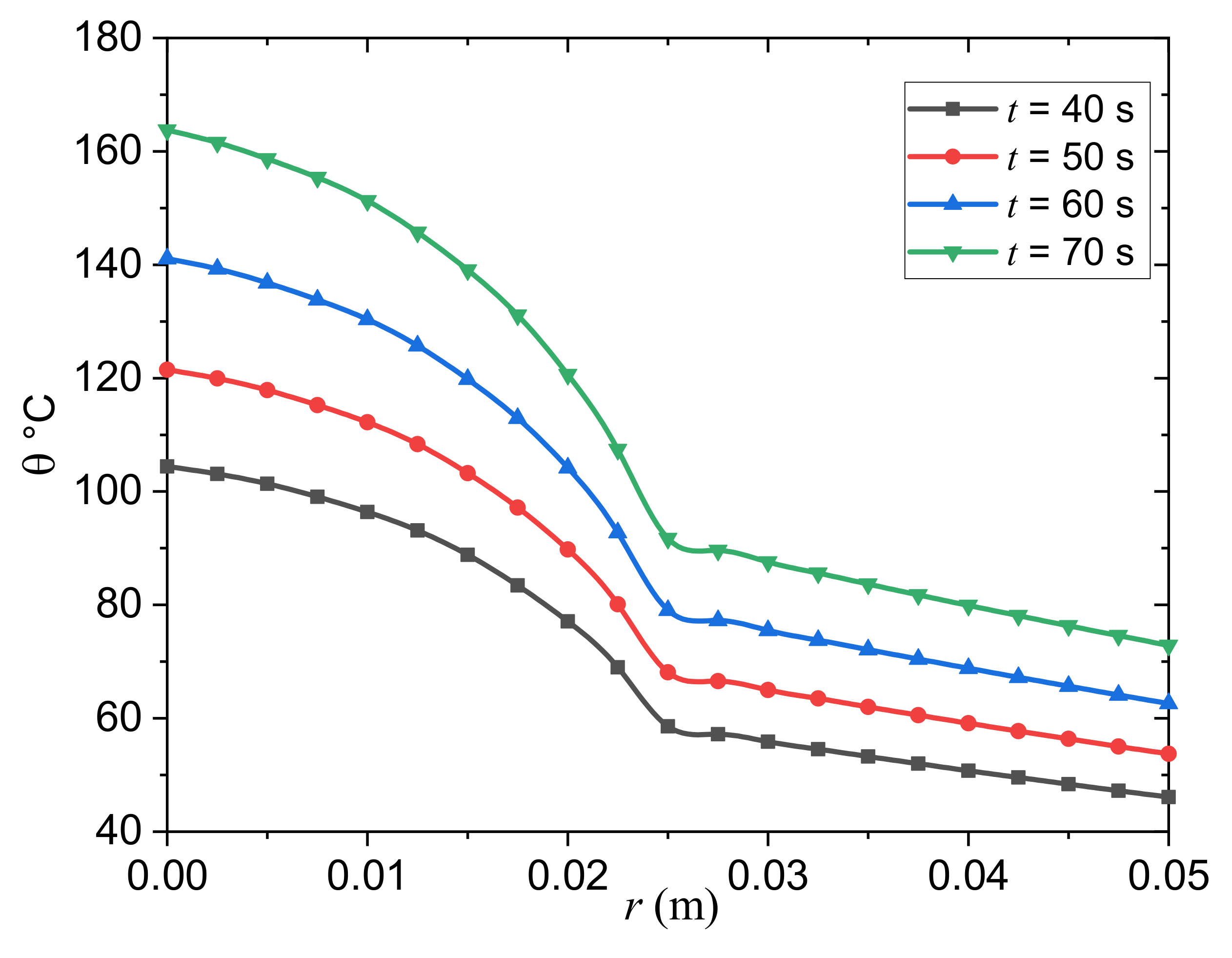
- It was found that the presence of a thermal relaxation time in the biothermal conduction equation significantly affects the temperature spread in a tumor and in normal tissue over time. As a result, having a thermal relaxation time reduces the temperature drop as well as the tissue depth.
- This MGT Pennes bioheat model adds some additional dimensions to the investigation of transient heat transfer mechanisms in biological systems.
- The propagation of thermal waves may provide a realistic prediction of the temperature distribution in living tissue.
- In the case of the MGT Pennes biothermal model, the temperature spreads with a finite speed in the tumor and the normal tissue instead of an infinite speed in the classical model.
- The relaxation parameter can be proposed as a novel measure of bioheat transfer efficiency in living tissues in the revolutionary MGT Pennes bioheat model.
- The findings reported here may be of value for the design of many biomedical and biomechanical application areas, including in healthy and diseased tissues, as well as for the development of theoretical knowledge of bioheat transfer in spherical tissue architecture.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Modeling Heat Transfer in Tumors: A Review of Thermal Therapies. Ann. Biomed. Eng. 2019, 47, 676–693. [Google Scholar] [CrossRef] [PubMed]
- Habash, R.W.; Bansal, R.; Krewski, D.; Alhafid, H.T. Thermal therapy, part 1: An introduction to thermal therapy. Crit. Rev. Biomed. Eng. 2006, 34, 459–489. [Google Scholar] [CrossRef] [PubMed]
- Dewhirst, M.W.; Samulski, T.V. Hyperthermia in the Treatment for Cancer; Upjohn: Kalamazoo, MI, USA, 1988. [Google Scholar]
- Field, S.B.; Hand, J.W. An Introduction to the Practical Aspects of Hyperthermia; Taylor & Francis: New York, NY, USA, 1990. [Google Scholar]
- Hall, E.J.; Roizin-Towle, L. Biological Effects of Heat. Cancer Res. 1984, 44, 4708s–4713s. [Google Scholar] [PubMed]
- Das, P.; Colombo, M.; Prosperi, D. Recent advances in magnetic fluid hyperthermia for cancer therapy. Colloids Surf. B Biointerfaces 2019, 174, 42–55. [Google Scholar] [CrossRef]
- Fan, W.; Yung, B.; Huang, P.; Chen, X. Nanotechnology for multimodal synergistic cancer therapy. Chem. Rev. 2017, 117, 13566–13638. [Google Scholar] [CrossRef]
- Lagendijk, J.J.W. Hyperthermia treatment planning. Phys. Med. Biol. 2000, 45, R61–R76. [Google Scholar] [CrossRef]
- Hooshmand, P.; Moradi, A.; Khezry, B. Bioheat transfer analysis of biological tissues induced by laser irradiation. Int. J. Therm. Sci. 2015, 90, 214–223. [Google Scholar] [CrossRef]
- Lin, S.M.; Li, C.Y. Analytical solutions of non-Fourier bio-heat conductions for skin subjected to pulsed laser heating. Int. J. Therm. Sci. 2016, 110, 146–158. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y.; Yang, J. Bio-heat transfer analysis based on fractional derivative and memory-dependent derivative heat conduction models. Case Stud. Therm. Eng. 2021, 27, 101211. [Google Scholar] [CrossRef]
- Gupta, P.K.; Singh, J.; Rai, K.N. A numerical study on heat transfer in tissues during hyperthermia. Math. Comput. Model. 2013, 57, 1018–1037. [Google Scholar] [CrossRef]
- Gupta, P.K.; Singh, J.; Rai, K.N.; Rai, S.K. Solution of the heat transfer problem in tissues during hyperthermia by finite difference–decomposition method. Appl. Math. Comput. 2013, 219, 6882–6892. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Weinbaum, S.; Jiji, L.M.; Lemmons, D.E. Theory and experiment for the effect of vascular microstructure on surface tissue heat transfer part I: Anatomical foundation and model conceptualization. ASME J. Biomech. Eng. 1984, 106, 321–330. [Google Scholar] [CrossRef]
- Weinbaum, S.; Jiji, L.M.; Lemmons, D.E. Theory and effect of vascular microstructure on surface tissue heat transfer part II: Model formulation and solution. ASME J. Biomech. Eng. 1984, 106, 331–341. [Google Scholar] [CrossRef]
- Sarkar, D.; Haji-Sheikh, A.; Jain, A. Temperature distribution in multi-layer skin tissue in presence of a tumor. Int. J. Heat Mass Transf. 2015, 91, 602–610. [Google Scholar] [CrossRef]
- Duck, F.A. Physical Properties of Tissue: A Comprehensive Reference Book; Academic Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Arkin, H.; Xu, L.X.; Holmes, K.R. Recent developments in modeling heat transfer in blood perfused tissues. IEEE Trans. Biomed. Eng. 1994, 41, 97–107. [Google Scholar] [CrossRef]
- Weinbaum, S.; Jiji, L.M. A new simplified bioheat equation for the effect of blood flow on local average tissue temperature. J. Biomech. Eng. 1985, 107, 131–139. [Google Scholar] [CrossRef]
- Khanafer, K.M.; Bull, J.L.; Pop, I.; Berguer, R. Influence of pulsatile blood flow and heating scheme on the temperature distribution during hyperthermia treatment. Int. J. Heat Mass Transf. 2007, 50, 4883–4890. [Google Scholar] [CrossRef]
- Khanafer, K.M.; Al Amiri, A.; Pop, I.; Bull, J.L. Flow and heat transfer in biological tissues: Application of porous media theory. In Emerging Topics in Heat and Mass Transfer in Porous, Media; Vad’ asz, P., Ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Kundu, B. Exact analysis for propagation of heat in a biological tissue subject to different surface conditions for therapeutic applications. Appl. Math. Comput. 2016, 285, 204–216. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, D.; Rai, K.N. A numerical study on dual-phase-lag model of bio-heat transfer during hyperthermia treatment. J. Therm. Biol. 2015, 49–50, 98–105. [Google Scholar] [CrossRef]
- Liu, K.-C.; Wang, Y.-N.; Chen, Y.-S. Investigation on the bio-heat transfer with the dual-phase-lag effect. Int. J. Therm. Sci. 2012, 58, 29–35. [Google Scholar] [CrossRef]
- Jaunich, M.; Raje, S.; Kim, K.; Mitra, K.; Guo, Z. Bio-heat transfer analysis during short pulse laser irradiation of tissues. Int. J. Heat Mass Transf. 2008, 51, 5511–5521. [Google Scholar] [CrossRef]
- Maamoun, W.; Badawi, M.I.; Aly, A.A.; Khedr, Y. Nanoparticles in enhancing microwave imaging and microwave Hyperthermia effect for liver cancer treatment. Rev. Adv. Mater. Sci. 2021, 60, 223–236. [Google Scholar] [CrossRef]
- Majchrzak, E.; Stryczyński, M. Dual-phase lag model of heat transfer between blood vessel and biological tissue. Math. Biosci. Eng. 2021, 18, 1573–1589. [Google Scholar] [CrossRef]
- Dutta, J.; Kundu, B. An improved analytical model for heat flow in cancerous tumours to avoid thermal injuries during hyperthermia. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2021, 235, 500–514. [Google Scholar] [CrossRef]
- Chen, K.C.; Yeh, C.S. Extended Irreversible Thermodynamics Approach to Magnetorheological Fluids. J. Non-Equilib. Thermodyn. 2001, 26, 355–372. [Google Scholar] [CrossRef]
- Versaci, M.; Palumbo, A. Magnetorheological Fluids: Qualitative comparison between a mixture model in the Extended Irreversible Thermodynamics framework and an Herschel–Bulkley experimental elastoviscoplastic model. Int. J. Non-Linear Mech. 2020, 118, 103288. [Google Scholar] [CrossRef]
- Blanc-Béguin, F.; Nabily, S.; Gieraltowski, J.; Turzo, A.; Querellou, S.; Salaun, P.Y. Cytotoxicity and GMI bio-sensor detection of maghemite nanoparticles internalized into cells. J. Magn. Magn. Mater. 2009, 321, 192–197. [Google Scholar] [CrossRef]
- Moroz, P.; Jones, S.K.; Gray, B.N. Status of hyperthermia in the treatment of advanced liver cancer. J. Surg. Oncol. 2001, 77, 259–269. [Google Scholar] [CrossRef]
- Jiang, G.; Li, W.; Rao, S.; Shi, Y.; Tang, X.; Zhu, C.; Gao, P.; Wang, Y.; Hu, S. Heat flow, depth–temperature, and assessment of the enhanced geothermal system (EGS) resource base of continental China. Environ. Earth Sci. 2016, 75, 1432. [Google Scholar] [CrossRef]
- Chen, L.; Chu, Y.; Zhang, Y.; Han, F.; Zhang, J. Analysis of Heat Transfer Characteristics of Fractured Surrounding Rock in Deep Underground Spaces. Math. Probl. Eng. 2019, 2019, 1926728. [Google Scholar] [CrossRef] [Green Version]
- Blyakhman, F.; Buznikov, N.; Sklyar, T.; Safronov, A.; Golubeva, E.; Svalov, A.; Kurlyandskaya, G. Mechanical, Electrical and Magnetic Properties of Ferrogels with Embedded Iron Oxide Nanoparticles Obtained by Laser Target Evaporation: Focus on Multifunctional Biosensor Applications. Sensors 2018, 18, 872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gmeiner, W.H.; Ghosh, S. Nanotechnology for cancer treatment. Nanotechnol. Rev. 2014, 3, 111–122. [Google Scholar] [CrossRef] [PubMed]
- Grossman, J.H.; McNeil, S.E. Nanotechnology in Cancer Medicine. Phys. Today 2012, 65, 38–42. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, S.; Roco, C.; Déléris, A.; Spoerri, P.; Cezar, C.; Weaver, J.; Vandenburgh, H.; Mooney, D. Improved magnetic regulation of delivery profiles from ferrogels. Biomaterials 2018, 161, 179–189. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–307. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K.A. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. A re-examination of the basic postulates of thermomechanics. Proc. R. Soc. Lond. A 1991, 432, 171–194. [Google Scholar]
- Green, A.E.; Naghdi, P.M. On undamped heat waves in an elastic solid. J. Therm. Stresses 1992, 15, 253–264. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. Thermoelasticity without energy dissipation. J. Elast. 1993, 31, 189–208. [Google Scholar] [CrossRef]
- Tzou, D.Y. A unified field theory for heat conduction from macro- to micro-scale. ASME J. Heat Trans. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Tzou, D. Macro-to-Micro Heat Transfer; Taylor and Francis: Washington, DC, USA, 1996. [Google Scholar]
- Tzou, D.Y. Experimental support for the Lagging behavior in heat propagation. J. Thermophys. Heat Trans. 1995, 9, 686–693. [Google Scholar] [CrossRef]
- Quintanilla, R. Moore-Gibson-Thompson thermoelasticity with two temperatures. Appl. Eng. Sci. 2020, 1, 100006. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Ahmed, I.-E.; Nasr, M.E.; Khalil, K.M.; Zakria, A.; Mohammed, F.A. Thermoelastic processes by a continuous heat source line in an infinite solid via Moore–Gibson–Thompson thermoelasticity. Materials 2020, 13, 4463. [Google Scholar] [CrossRef]
- Marin, M.; Othman, M.I.A.; Seadawy, A.R.; Carstea, C. A domain of influence in the Moore–Gibson–Thompson theory of dipolar bodies. J. Taibah Univ. Sci. 2020, 14, 653–660. [Google Scholar] [CrossRef]
- Aboueregal, A.E.; Sedighi, H.M. The effect of variable properties and rotation in a visco-thermoelastic orthotropic annular cylinder under the Moore–Gibson–Thompson heat conduction model. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1004–1020. [Google Scholar] [CrossRef]
- Fernández, J.R.; Quintanilla, R. Moore-Gibson-Thompson theory for thermoelastic dielectrics. Appl. Math. Mech. 2021, 42, 309–316. [Google Scholar] [CrossRef]
- Aboueregal, A.E. An advanced model of thermoelasticity with higher-order memory-dependent derivatives and dual time-delay factors. Waves Random Complex Media 2021, 22, 1–22. [Google Scholar] [CrossRef]
- Pellicer, M.; Quintanilla, R. On uniqueness and instability for some thermomechanical problems involving the Moore-Gibson-Thompson equation. J. Appl. Math. Phys. 2020, 71, 84. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Moustapha, M.V.; Nofal, T.A.; Rashid, S.; Ahmad, H. Generalized thermoelasticity based on higher-order memory-dependent derivative with time delay. Results Phys. 2021, 20, 103705. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Ahmad, H.; Yao, S.-W. Functionally graded piezoelectric medium exposed to a movable heat flow based on a heat equation with a memory-dependent derivative. Materials 2020, 13, 3953. [Google Scholar] [CrossRef]
- Bazarra, N.; Fernández, J.R.; Quintanilla, R. Analysis of a Moore-Gibson-Thompson thermoelastic problem. J. Comput. Appl. Math. 2021, 382, 113058. [Google Scholar] [CrossRef]
- Conti, M.; Pata, V.; Pellicer, M.; Quintanilla, R. On the analyticity of the MGT-viscoelastic plate with heat conduction. J. Differ. Equ. 2020, 269, 7862–7880. [Google Scholar] [CrossRef]
- Singh, B.; Mukhopadhyay, S. Galerkin-type solution for the Moore–Gibson–Thompson thermoelasticity theory. Acta Mech. 2021, 232, 1273–1283. [Google Scholar] [CrossRef]
- Alumutairi, L.; Yu, B.; Filka, M.; Nayfach, J.; Kim, M.-H. Mild magnetic nanoparticle hyperthermia enhances the susceptibility of Staphylococcus aureus biofilm to antibiotics. Int. J. Hyperth. 2020, 37, 66–75. [Google Scholar] [CrossRef] [Green Version]
- Hristov, J. Bio-Heat Models Revisited: Concepts, Derivations, Nondimensalization and Fractionalization Approaches. Front. Phys. 2019, 7, 189. [Google Scholar] [CrossRef] [Green Version]
- Kazemi Alamouti, A.; Habibi, M.R.; Mazidi Sharfabadi, M.; Akbari Lalimi, H. Numerical study on the effects of blood perfusion and tumor metabolism on tumor temperature for targeted hyperthermia considering a realistic geometrical model of head layers using the finite element method. SN Appl. Sci. 2021, 3, 462. [Google Scholar] [CrossRef]
- Dutta, J.; Kundu, B. Two-dimensional hybrid analytical approach for the investigation of thermal aspects in human tissue undergoing regional hyperthermia therapy. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 3951–3966. [Google Scholar] [CrossRef]
- Tucci, C.; Trujillo, M.; Berjano, E.; Iasiello, M.; Andreozzi, A.; Vanoli, G.P. Pennes’ bioheat equation vs. porous media approach in computer modeling of radiofrequency tumor ablation. Sci. Rep. 2021, 11, 5272. [Google Scholar] [CrossRef]
- Ragab, M.; Abo-Dahab, S.M.; Abouelregal, A.E.; Kilany, A.A. A Thermoelastic Piezoelectric Fixed Rod Exposed to an Axial Moving Heat Source via a Dual-Phase-Lag Model. Int. J. Complex. 2021, 2021, 221–232. [Google Scholar] [CrossRef]
- Kaminski, W. Hyperbolic heat conduction equation for materials with a nonhomogeneous inner structure. J. Heat Transf. 1990, 112, 555–560. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, Y.; Chen, J.K. Non-Fourier heat conduction effect on laser induced thermal damage in biological tissues. Numer. Heat Transf. Part A 2008, 54, 1–19. [Google Scholar] [CrossRef]
- Honig, G.; Hirdes, U. A method for the numerical inversion of Laplace transform. J. Comp. Appl. Math. 1984, 10, 113–132. [Google Scholar] [CrossRef] [Green Version]
- Moritz, A.R.; Henriques, F., Jr. Studies of thermal injury: II. The relative importance of time and surface temperature in the causation of cutaneous burns. Am. J. Pathol. 1947, 23, 695. [Google Scholar]
- Abbas, I.; Hobiny, A.; Alzahrani, F. An analytical solution of the bioheat model in a spherical tissue due to laser irradiation. Indian J. Physics 2020, 94, 1329–1334. [Google Scholar] [CrossRef]
- Dumas, A.; Barozzi, G.S. Laminar heat transfer to blood flowing in a circuar duct. Int. J. Heat Mass Transf. 2014, 27, 391–398. [Google Scholar] [CrossRef]
- Mondal, S.; Sur, A.; Kanoria, M. A graded spherical tissue under thermal therapy: The treatment of cancer cells. Waves Random Complex Media 2020, 107, 1–20. [Google Scholar] [CrossRef]
- Andrä, W.; d’ Ambly, C.; Hergt, R.; Hilger, I.; Kaiser, W. Temperature distribution as function of time around a small spherical heat source of local magnetic hyperthermia. J. Magn. Magn. Mater. 1999, 194, 197–203. [Google Scholar] [CrossRef]
- Gautheric, M. Thermopathology of breast cancer: Measurement and analysis of in vivo temperature and blood flow. Ann. N. Y. Acad. Sci. 1980, 335, 383–415. [Google Scholar] [CrossRef]
- Hu, L.; Gupta, A.; Gore, J.P.; Xu, L.X. Effect of forced convection on the skin thermal expression of breast cancer. ASME J. Heat Transf. 2004, 126, 204–211. [Google Scholar] [CrossRef]
- Maenosono, S.; Saita, S. Theoretical assessment of FePt nanoparticles as heating elements for magnetic hyperthermia. IEEE Trans. Magn. 2006, 42, 1638–1642. [Google Scholar] [CrossRef]
- Liu, K.-C.; Chen, H.-T. Analysis for the dual-phase-lag bio-heat transfer during magnetic hyperthermia treatment. Int. J. Heat Mass Transf. 2009, 52, 1185–1192. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ragab, M.; Abouelregal, A.E.; AlShaibi, H.F.; Mansouri, R.A. Heat Transfer in Biological Spherical Tissues during Hyperthermia of Magnetoma. Biology 2021, 10, 1259. https://doi.org/10.3390/biology10121259
Ragab M, Abouelregal AE, AlShaibi HF, Mansouri RA. Heat Transfer in Biological Spherical Tissues during Hyperthermia of Magnetoma. Biology. 2021; 10(12):1259. https://doi.org/10.3390/biology10121259
Chicago/Turabian StyleRagab, Mahmoud, Ahmed E. Abouelregal, Huda F. AlShaibi, and Rasha A. Mansouri. 2021. "Heat Transfer in Biological Spherical Tissues during Hyperthermia of Magnetoma" Biology 10, no. 12: 1259. https://doi.org/10.3390/biology10121259
APA StyleRagab, M., Abouelregal, A. E., AlShaibi, H. F., & Mansouri, R. A. (2021). Heat Transfer in Biological Spherical Tissues during Hyperthermia of Magnetoma. Biology, 10(12), 1259. https://doi.org/10.3390/biology10121259







