Genomic Selection for End-Use Quality and Processing Traits in Soft White Winter Wheat Breeding Program with Machine and Deep Learning Models
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Germplasm
2.2. Phenotyping
2.3. Statistical Analysis
2.4. Genotyping
2.5. Genomic Selection Models
2.5.1. Ridge Regression Best Linear Unbiased Prediction (RRBLUP)
2.5.2. Bayesian Models
2.5.3. Random Forests (RF)
- Bootstrap sampling (b = (1, …, B)) to select genotypes with replacement from the training set, and an individual plant can appear once or several time during the sampling
- Best set of features (SNPj, j = (1, …, J) were selected to minimize the mean square error (MSE) using the max feature function in the random forest regression library.
- Splitting is performed at each node of the tree using the SNPj genotype to lower the MSE.
- The above steps are repeated until a maximum depth is reached or a minimum node. The final predicted value of an individual of genotype is the average of the values from the set of trees in the forest.
2.5.4. Support Vector Machine (SVM)
2.5.5. Multilayer Perceptron (MLP)
2.5.6. Convolutional Neural Network (CNN)
2.6. Prediction Accuracy and Cross-Validation Scheme
3. Results
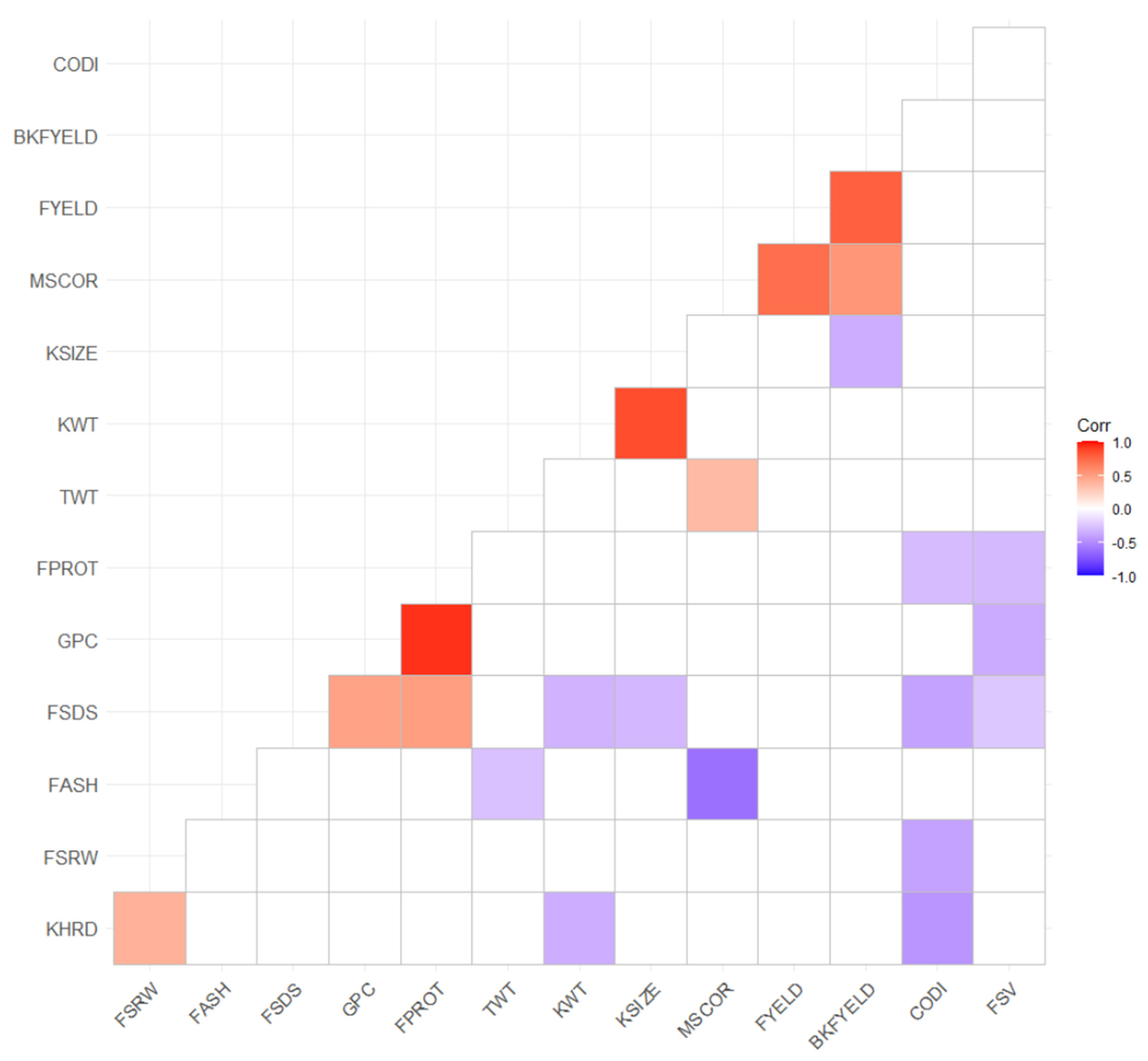
3.1. Phenotypic Data Summary
3.2. Cross-Validation Genomic Selection Accuracy and Model Comparison
3.3. Forward Predictions
3.4. Across Location Predictions
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Souza, E.J.; Guttieri, M.J.; Graybosch, R.A. Breeding wheat for improved milling and baking quality. J. Crop Prod. 2002, 5, 39–74. [Google Scholar] [CrossRef]
- Kiszonas, A.M.; Fuerst, E.P.; Morris, C.F. A comprehensive survey of soft wheat grain quality in U.S.gGermplasm. Cereal Chem. J. 2013, 90, 47–57. [Google Scholar] [CrossRef]
- Bhave, M.; Morris, C.F. Molecular genetics of puroindolines and related genes: Allelic diversity in wheat and other grasses. Plant Mol. Biol. 2008, 66, 205–219. [Google Scholar] [CrossRef] [PubMed]
- Kiszonas, A.M.; Morris, C.F. Wheat breeding for quality: A historical review. Cereal Chem. 2018, 95, 17–34. [Google Scholar] [CrossRef] [Green Version]
- Guzman, C.; Peña, R.J.; Singh, R.; Autrique, E.; Dreisigacker, S.; Crossa, J.; Rutkoski, J.; Poland, J.; Battenfield, S. Wheat quality improvement at CIMMYT and the use of genomic selection on it. Appl. Transl. Genom. 2016, 11, 3–8. [Google Scholar] [CrossRef] [Green Version]
- Morris, C.F.; Li, S.; King, G.E.; Engle, D.A.; Burns, J.W.; Ross, A.S. A comprehensive genotype and environment assessment of wheat grain ash content in oregon and washington: Analysis of variation. Cereal Chem. J. 2009, 86, 307–312. [Google Scholar] [CrossRef]
- Kiszonas, A.M.; Fuerst, E.P.; Morris, C.F. Modeling end-use quality in U.S. soft wheat germplasm. Cereal Chem. J. 2015, 92, 57–64. [Google Scholar] [CrossRef]
- Campbell, G.M.; Fang, C.; Muhamad, I.I. On predicting roller milling performance VI: Effect of kernel hardness and shape on the particle size distribution from First Break milling of wheat. Food Bioprod. Process. 2007, 85, 7–23. [Google Scholar] [CrossRef]
- Gale, K.R. Diagnostic DNA markers for quality traits in wheat. J. Cereal Sci. 2005, 41, 181–192. [Google Scholar] [CrossRef]
- Carter, A.H.; Garland-Campbell, K.; Morris, C.F.; Kidwell, K.K. Chromosomes 3B and 4D are associated with several milling and baking quality traits in a soft white spring wheat (Triticum aestivum L.) population. Theor. Appl. Genet. 2012, 124, 1079–1096. [Google Scholar] [CrossRef] [PubMed]
- Jernigan, K.L.; Godoy, J.V.; Huang, M.; Zhou, Y.; Morris, C.F.; Garland-Campbell, K.A.; Zhang, Z.; Carter, A.H. Genetic dissection of end-use quality traits in adapted soft white winter wheat. Front. Plant Sci. 2018, 9, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Chai, Y.; Zhang, X.; Lu, S.; Zhao, Z.; Wei, D.; Chen, L.; Hu, Y.G. Multi-locus GWAS of quality traits in bread wheat: Mining more candidate genes and possible regulatory network. Front. Plant Sci. 2020, 11, 1091. [Google Scholar] [CrossRef] [PubMed]
- Kristensen, P.S.; Jahoor, A.; Andersen, J.R.; Cericola, F.; Orabi, J.; Janss, L.L.; Jensen, J. Genome-wide association studies and comparison of models and cross-validation strategies for genomic prediction of quality traits in advanced winter wheat breeding lines. Front. Plant Sci. 2018, 9, 69. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crossa, J.; Pérez-Rodríguez, P.; Cuevas, J.; Montesinos-López, O.; Jarquín, D.; de los Campos, G.; Burgueño, J.; González-Camacho, J.M.; Pérez-Elizalde, S.; Beyene, Y.; et al. Genomic selection in plant breeding: Methods, models, and perspectives. Trends Plant Sci. 2017, 22, 961–975. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker Maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Battenfield, S.D.; Guzmán, C.; Chris Gaynor, R.; Singh, R.P.; Peña, R.J.; Dreisigacker, S.; Fritz, A.K.; Poland, J.A. Genomic selection for processing and end-use quality traits in the CIMMYT spring bread wheat breeding program. Plant Genome 2016, 9. [Google Scholar] [CrossRef] [Green Version]
- Juliana, P.; Poland, J.; Huerta-Espino, J.; Shrestha, S.; Crossa, J.; Crespo-Herrera, L.; Toledo, F.H.; Govindan, V.; Mondal, S.; Kumar, U.; et al. Improving grain yield, stress resilience and quality of bread wheat using large-scale genomics. Nat. Genet. 2019, 51, 1530–1539. [Google Scholar] [CrossRef]
- Sandhu, K.S.; Mihalyov, P.D.; Lewien, M.J.; Pumphrey, M.O.; Carter, A.H. Combining genomic and phenomic information for predicting grain protein content and grain yield in spring wheat. Front. Plant Sci. 2021, 12, 170. [Google Scholar] [CrossRef]
- Heffner, E.L.; Jannink, J.-L.; Sorrells, M.E. Genomic selection accuracy using multifamily prediction models in a wheat breeding program. Plant Genome 2011, 4, 65. [Google Scholar] [CrossRef] [Green Version]
- Heffner, E.L.; Jannink, J.L.; Iwata, H.; Souza, E.; Sorrells, M.E. Genomic selection accuracy for grain quality traits in biparental wheat populations. Crop Sci. 2011, 51, 2597–2606. [Google Scholar] [CrossRef] [Green Version]
- Sandhu, K.S.; Lozada, D.N.; Zhang, Z.; Pumphrey, M.O.; Carter, A.H. Deep learning for predicting complex traits in spring wheat breeding program. Front. Plant Sci. 2021, 11, 613325. [Google Scholar] [CrossRef] [PubMed]
- Chu, Z.; Yu, J. An end-to-end model for rice yield prediction using deep learning fusion. Comput. Electron. Agric. 2020, 174, 105471. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, D.; He, F.; Wang, J.; Joshi, T.; Xu, D. Phenotype prediction and genome-wide association study using deep convolutional neural network of soybean. Front. Genet. 2019, 10, 1091. [Google Scholar] [CrossRef]
- Khaki, S.; Wang, L. Crop yield prediction using deep neural networks. Front. Plant Sci. 2019, 10, 621. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Qiu, Z.; Song, J.; Li, J.; Cheng, Q.; Zhai, J.; Ma, C. A deep convolutional neural network approach for predicting phenotypes from genotypes. Planta 2018, 248, 1307–1318. [Google Scholar] [CrossRef]
- Montesinos-López, O.A.; Martín-Vallejo, J.; Crossa, J.; Gianola, D.; Hernández-Suárez, C.M.; Montesinos-López, A.; Juliana, P.; Singh, R. New deep learning genomic-based prediction model for multiple traits with binary, ordinal, and continuous phenotypes. G3 Genes Genomes Genet. 2019, 9, 1545–1556. [Google Scholar] [CrossRef] [Green Version]
- Montesinos-López, O.A.; Montesinos-López, A.; Crossa, J.; Gianola, D.; Hernández-Suárez, C.M.; Martín-Vallejo, J. Multi-trait, multi-environment deep learning modeling for genomic-enabled prediction of plant traits. G3 Genes Genomes Genet. 2018, 8, 3829–3840. [Google Scholar] [CrossRef] [Green Version]
- Aoun, M.; Carter, A.H.; Ward, B.P.; Morris, C.F. Genome-wide association mapping of the ‘super soft’ kernel texture in white winter wheat. Theor. Appl. Genet. 2021, 134, 2547–2559. [Google Scholar] [CrossRef]
- AACC. Approved Methods of Analysis. Available online: http://methods.aaccnet.org/ (accessed on 19 April 2021).
- Bates, D.; Mächler, M.; Bolker, B.M.; Walker, S.C. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67. [Google Scholar] [CrossRef]
- Sandhu, K.S.; Patil, S.S.; Pumphrey, M.O.; Carter, A.H. Multi-trait machine and deep learning models for genomic selection using spectral 1 information in a wheat breeding program. bioRxiv 2021, 2021, 439532. [Google Scholar] [CrossRef]
- Sandhu, K.S.; Mihalyov, P.D.; Lewien, M.J.; Pumphrey, M.O.; Carter, A.H. Genome-wide association studies and genomic selection for grain protein content stability in a nested association mapping population of spring wheat. bioRxiv 2021, 2021, 440064. [Google Scholar] [CrossRef]
- Cullis, B.R.; Smith, A.B.; Coombes, N.E. On the design of early generation variety trials with correlated data. J. Agric. Biol. Environ. Stat. 2006, 11, 381–393. [Google Scholar] [CrossRef]
- Poland, J.A.; Brown, P.J.; Sorrells, M.E.; Jannink, J.L. Development of high-density genetic maps for barley and wheat using a novel two-enzyme genotyping-by-sequencing approach. PLoS ONE 2012, 7. [Google Scholar] [CrossRef] [Green Version]
- Appels, R.; Eversole, K.; Feuillet, C.; Keller, B.; Rogers, J.; Stein, N.; Pozniak, C.J.; Choulet, F.; Distelfeld, A.; Poland, J.; et al. Shifting the limits in wheat research and breeding using a fully annotated reference genome. Science 2018, 361. [Google Scholar] [CrossRef] [Green Version]
- Bradbury, P.J.; Zhang, Z.; Kroon, D.E.; Casstevens, T.M.; Ramdoss, Y.; Buckler, E.S. TASSEL: Software for association mapping of complex traits in diverse samples. Bioinformatics 2007, 23, 2633–2635. [Google Scholar] [CrossRef] [PubMed]
- Endelman, J.B. Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome 2011, 4, 250–255. [Google Scholar] [CrossRef] [Green Version]
- Pérez, P.; De Los Campos, G. Genome-wide regression and prediction with the BGLR statistical package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef]
- Shah, S.H.; Angel, Y.; Houborg, R.; Ali, S.; McCabe, M.F. A random forest machine learning approach for the retrieval of leaf chlorophyll content in wheat. Remote Sens. 2019, 11, 920. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science and Business Media: Berlin, Germany, 2009. [Google Scholar]
- Gulli, A.; Pal, S. Deep Learning with Keras; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Smola, A.; Scholkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Cho, M.; Hegde, C. Reducing the search space for hyperparameter optimization using group sparsity. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing, Brighton, UK, 12–17 May 2019. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Vanderplas, J.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Haile, J.K.; N’Diaye, A.; Clarke, F.; Clarke, J.; Knox, R.; Rutkoski, J.; Bassi, F.M.; Pozniak, C.J. Genomic selection for grain yield and quality traits in durum wheat. Mol. Breed. 2018, 38, 1–18. [Google Scholar] [CrossRef]
- Lorenz, A.J. Resource allocation for maximizing prediction accuracy and genetic gain of genomic selection in plant breeding: A simulation experiment. G3 Genes Genomes Genet. 2013, 3, 481–491. [Google Scholar] [CrossRef] [Green Version]
- Michel, S.; Kummer, C.; Gallee, M.; Hellinger, J.; Ametz, C.; Akgöl, B.; Epure, D.; Löschenberger, F.; Buerstmayr, H. Improving the baking quality of bread wheat by genomic selection in early generations. Theor. Appl. Genet. 2018, 131, 477–493. [Google Scholar] [CrossRef]
- Jernigan, K.L.; Morris, C.F.; Zemetra, R.; Chen, J.; Garland-Campbell, K.; Carter, A.H. Genetic analysis of soft white wheat end-use quality traits in a club by common wheat cross. J. Cereal Sci. 2017, 76, 148–156. [Google Scholar] [CrossRef]
- Kristensen, P.S.; Jensen, J.; Andersen, J.R.; Guzmán, C.; Orabi, J.; Jahoor, A. Genomic prediction and genome-wide association studies of flour yield and alveograph quality traits using advanced winter wheat breeding material. Genes 2019, 10, 669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsai, H.Y.; Janss, L.L.; Andersen, J.R.; Orabi, J.; Jensen, J.D.; Jahoor, A.; Jensen, J. Genomic prediction and GWAS of yield, quality and disease-related traits in spring barley and winter wheat. Sci. Rep. 2020, 10, 1–15. [Google Scholar] [CrossRef]
- Hayes, B.J.; Panozzo, J.; Walker, C.K.; Choy, A.L.; Kant, S.; Wong, D.; Tibbits, J.; Daetwyler, H.D.; Rochfort, S.; Hayden, M.J.; et al. Accelerating wheat breeding for end-use quality with multi-trait genomic predictions incorporating near infrared and nuclear magnetic resonance-derived phenotypes. Theor. Appl. Genet. 2017, 130, 2505–2519. [Google Scholar] [CrossRef] [PubMed]
- Monteverde, E.; Gutierrez, L.; Blanco, P.; Pérez de Vida, F.; Rosas, J.E.; Bonnecarrère, V.; Quero, G.; McCouch, S. Integrating molecular markers and environmental covariates to interpret genotype by environment interaction in rice (Oryza sativa L.) grown in subtropical areas. G3 Genes Genomes Genet. 2019, 9, 1519–1531. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gouy, M.; Rousselle, Y.; Bastianelli, D.; Lecomte, P.; Bonnal, L.; Roques, D.; Efile, J.C.; Rocher, S.; Daugrois, J.; Toubi, L.; et al. Experimental assessment of the accuracy of genomic selection in sugarcane. Theor. Appl. Genet. 2013, 126, 2575–2586. [Google Scholar] [CrossRef] [PubMed]
- Crossa, J.; Pérez, P.; Hickey, J.; Burgueno, J.; Ornella, L.; Cerón-Rojas, J.; Zhang, X.; Dreisigacker, S.; Babu, R.; Li, Y.; et al. Genomic prediction in CIMMYT maize and wheat breeding programs. Heredity 2014, 112, 48–60. [Google Scholar] [CrossRef] [Green Version]
- Rutkoski, J.; Singh, R.P.; Huerta-Espino, J.; Bhavani, S.; Poland, J.; Jannink, J.L.; Sorrells, M.E. Efficient Use of Historical Data for Genomic Selection: A case study of stem rust resistance in wheat. Plant Genome 2015, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fiedler, J.D.; Salsman, E.; Liu, Y.; De Jiménez, M.M.; Hegstad, J.B.; Chen, B.; Manthey, F.A.; Chao, S.; Xu, S.; Elias, E.M.; et al. Genome-wide association and prediction of grain and semolina quality traits in durum wheat breeding populations. Plant Genome 2017, 10. [Google Scholar] [CrossRef] [Green Version]
- Habier, D.; Fernando, R.L.; Garrick, D.J. Genomic BLUP decoded: A look into the black box of genomic prediction. Genetics 2013, 194, 597–607. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.; Zhao, D.; Chen, X.; Zhang, Y.; Wang, J. Use of genomic selection and breeding simulation in cross prediction for improvement of yield and quality in wheat (Triticum aestivum L.). Crop J. 2018, 6, 353–365. [Google Scholar] [CrossRef]
- He, S.; Schulthess, A.W.; Mirdita, V.; Zhao, Y.; Korzun, V.; Bothe, R.; Ebmeyer, E.; Reif, J.C.; Jiang, Y. Genomic selection in a commercial winter wheat population. Theor. Appl. Genet. 2016, 129, 641–651. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.; Hayes, B.; Goddard, M. Genomic selection: A paradigm shift in animal breeding. Anim. Front. 2016, 6, 6–14. [Google Scholar] [CrossRef] [Green Version]
- Cuevas, J.; Montesinos-López, O.; Juliana, P.; Guzmán, C.; Pérez-Rodríguez, P.; González-Bucio, J.; Burgueño, J.; Montesinos-López, A.; Crossa, J. Deep Kernel for genomic and near infrared predictions in multi-environment breeding trials. G3 Genes Genomes Genet. 2019, 9, 2913–2924. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Montesinos-López, O.A.; Montesinos-López, A.; Tuberosa, R.; Maccaferri, M.; Sciara, G.; Ammar, K.; Crossa, J. Multi-trait, multi-environment genomic prediction of durum wheat with genomic best linear unbiased predictor and deep learning methods. Front. Plant Sci. 2019, 10, 1311. [Google Scholar] [CrossRef]
- Jarquín, D.; Crossa, J.; Lacaze, X.; Du Cheyron, P.; Daucourt, J.; Lorgeou, J.; Piraux, F.; Guerreiro, L.; Pérez, P.; Calus, M.; et al. A reaction norm model for genomic selection using high-dimensional genomic and environmental data. Theor. Appl. Genet. 2014, 127, 595–607. [Google Scholar] [CrossRef] [Green Version]
- Plavšin, I.; Gunjača, J.; Šatović, Z.; Šarčević, H.; Ivić, M.; Dvojković, K.; Novoselović, D. An overview of key factors affecting genomic selection for wheat quality traits. Plants 2021, 10, 745. [Google Scholar] [CrossRef] [PubMed]
- Merrick, L.F.; Carter, A.H. Comparison of genomic selection models for exploring predictive ability of complex traits in breeding programs. bioRxiv 2021, 2021, 440015. [Google Scholar] [CrossRef]
- Gianola, D.; Fernando, R.L.; Stella, A. Genomic-assisted prediction of genetic value with semiparametric procedures. Genetics 2006, 173, 1761–1776. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Montesinos-López, O.A.; Martín-Vallejo, J.; Crossa, J.; Gianola, D.; Hernández-Suárez, C.M.; Montesinos-López, A.; Juliana, P.; Singh, R. A benchmarking between deep learning, support vector machine and Bayesian threshold best linear unbiased prediction for predicting ordinal traits in plant breeding. G3 Genes Genomes Genet. 2019, 9, 601–618. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Carver, B.F.; Powers, C.; Yan, L.; Zhu, L.; Chen, C. Effectiveness of genomic selection by response to selection for winter wheat variety improvement. Plant Genome 2019, 12, 180090. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Cabrera, A.; Hoffstetter, A.; Griffey, C.; Van Sanford, D.; Costa, J.; McKendry, A.; Chao, S.; Sneller, C. Genomic selection for wheat traits and trait stability. Theor. Appl. Genet. 2016, 129, 1697–1710. [Google Scholar] [CrossRef]
- Montesinos-López, O.A.; Montesinos-López, A.; Pérez-Rodríguez, P.; Barrón-López, J.A.; Martini, J.W.R.; Fajardo-Flores, S.B.; Gaytan-Lugo, L.S.; Santana-Mancilla, P.C.; Crossa, J. A review of deep learning applications for genomic selection. BMC Genom. 2021, 22, 1–23. [Google Scholar] [CrossRef]
- Isidro, J.; Jannink, J.L.; Akdemir, D.; Poland, J.; Heslot, N.; Sorrells, M.E. Training set optimization under population structure in genomic selection. Theor. Appl. Genet. 2015, 128, 145–158. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, M.; Kollers, S.; Maasberg-Prelle, A.; Großer, J.; Schinkel, B.; Tomerius, A.; Graner, A.; Korzun, V. Prediction of malting quality traits in barley based on genome-wide marker data to assess the potential of genomic selection. Theor. Appl. Genet. 2016, 129, 203–213. [Google Scholar] [CrossRef]
- Pook, T.; Freudenthal, J.; Korte, A.; Simianer, H. Using local convolutional neural networks for genomic prediction. Front. Genet. 2020, 11, 1366. [Google Scholar] [CrossRef]
- Bellot, P.; de los Campos, G.; Pérez-Enciso, M. Can deep learning improve genomic prediction of complex human traits? Genetics 2018, 210, 809–819. [Google Scholar] [CrossRef] [Green Version]
- Montesinos-López, A.; Montesinos-López, O.A.; Gianola, D.; Crossa, J.; Hernández-Suárez, C.M. Multi-environment genomic prediction of plant traits using deep learners with dense architecture. G3 Genes Genomes Genet. 2018, 8, 3813–3828. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]




| Location | Year | Lines Screened for Quality |
|---|---|---|
| Lind | 2015 | 122 |
| 2016 | 114 | |
| 2017 | 115 | |
| 2018 | 71 | |
| 2019 | 106 | |
| Pullman | 2015 | 183 |
| 2016 | 128 | |
| 2017 | 181 | |
| 2018 | 137 | |
| 2019 | 178 | |
| Total | 1335 |
| Trait | Abbreviation | Units | Number of Genotypes | Mean | Min | Max | S.E. | H2 | h2 |
|---|---|---|---|---|---|---|---|---|---|
| Milling traits | |||||||||
| FYELD | Flour yield | percent | 666 | 69.9 | 58.0 | 75.8 | 0.09 | 0.91 | 0.75 |
| BKYELD | Break flour yield | percent | 666 | 48.1 | 33.9 | 56.6 | 0.14 | 0.93 | 0.72 |
| MSCOR | Milling score | unitless | 646 | 85.6 | 69.1 | 98.8 | 0.10 | 0.81 | 0.77 |
| Grain characteristics | |||||||||
| TWT | Test weight | Kg/hL | 666 | 61.8 | 54.6 | 65.9 | 0.06 | 0.92 | 0.66 |
| GPC | Grain protein content | percent | 666 | 10.73 | 7.2 | 14.8 | 0.05 | 0.56 | 0.50 |
| KHRD | Kernel hardness | unitless | 666 | 23.0 | −10.2 | 52.4 | 0.4 | 0.93 | 0.64 |
| KWT | Kernel weight | mg | 666 | 39.3 | 26.5 | 54.6 | 0.17 | 0.86 | 0.75 |
| KSIZE | Kernel size | mm | 666 | 2.76 | 2.3 | 3.3 | 0.005 | 0.83 | 0.77 |
| Baking parameters | |||||||||
| CODI | Cookie diameter | cm | 622 | 9.2 | 7.8 | 10.0 | 0.008 | 0.89 | 0.82 |
| Flour parameters | |||||||||
| FPROT | Flour protein | percent | 666 | 8.93 | 6.3 | 13.0 | 0.04 | 0.57 | 0.46 |
| FASH | Flour ash | percent | 646 | 0.39 | 0.21 | 0.54 | 0.001 | 0.88 | 0.73 |
| FSV | Flour swelling volume | mL/g | 665 | 19.06 | 14.0 | 26.3 | 0.05 | 0.63 | 0.59 |
| FSDS | Flour SDS sedimentation | g/mL | 666 | 10.1 | 3.5 | 18.3 | 0.09 | 0.92 | 0.85 |
| FSRW | Water solvent retention capacity | percent | 666 | 54.18 | 43.4 | 72.6 | 0.09 | 0.85 | 0.77 |
| Location | Trait | RRBLUP | BayesA | Bayes B | Bayes C | Bayes Lasso | RF | SVM | MLP | CNN |
|---|---|---|---|---|---|---|---|---|---|---|
| Pullman | FYELD | 0.71 b | 0.61 d | 0.64 c | 0.64 c | 0.63 c | 0.76 a | 0.76 a | 0.75 a | 0.74 a |
| BKYELD | 0.70 b | 0.62 d | 0.64 c | 0.64 cd | 0.64 cd | 0.75 a | 0.75 a | 0.76 a | 0.75 a | |
| MSCOR | 0.58 c | 0.52 d | 0.52 d | 0.53 d | 0.52 d | 0.60 abc | 0.60 bc | 0.63 a | 0.61 ab | |
| TWT | 0.67 c | 0.67 c | 0.66 c | 0.66 c | 0.66 c | 0.68 abc | 0.67 bc | 0.70 ab | 0.70 a | |
| GPC | 0.55 b | 0.54 bc | 0.54 bc | 0.53 c | 0.53 c | 0.59 a | 0.60 a | 0.60 a | 0.60 a | |
| KHRD | 0.71 a | 0.67 bcd | 0.67 cd | 0.68 bcd | 0.67 d | 0.70 ab | 0.69 abcd | 0.70 ab | 0.69 abc | |
| KWT | 0.76 b | 0.77 b | 0.75 b | 0.75 b | 0.75 b | 0.81 a | 0.80 a | 0.80 a | 0.75 b | |
| KSIZE | 0.77 b | 0.75 bc | 0.74 c | 0.75 bc | 0.77 b | 0.76 bc | 0.76 bc | 0.80 a | 0.81 a | |
| CODI | 0.67 bc | 0.67 bc | 0.67 c | 0.68 bc | 0.67 c | 0.69 ab | 0.69 abc | 0.69 ab | 0.71 a | |
| FPROT | 0.58 c | 0.58 c | 0.58 bc | 0.55 d | 0.55 d | 0.61 a | 0.58 c | 0.62 a | 0.60 ab | |
| FASH | 0.55 d | 0.56 cd | 0.59 ab | 0.58 ab | 0.59 ab | 0.58 abc | 0.59 a | 0.59 a | 0.59 bc | |
| FSV | 0.55 b | 0.54 b | 0.53 b | 0.53 b | 0.53 b | 0.59 a | 0.60 a | 0.60 a | 0.60 a | |
| FSDS | 0.67 de | 0.67 bcde | 0.66 e | 0.66 e | 0.67 cde | 0.69 abcd | 0.69 abc | 0.70 ab | 0.70 a | |
| FSRW | 0.58 b | 0.52 c | 0.52 c | 0.52 c | 0.52 c | 0.60 ab | 0.60 ab | 0.61 a | 0.62 a | |
| Lind | FYELD | 0.64 b | 0.55 c | 0.58 c | 0.56 c | 0.58 c | 0.68 a | 0.69 a | 0.67 ab | 0.67 a |
| BKYELD | 0.63 b | 0.55 c | 0.57 c | 0.56 c | 0.57 c | 0.67 a | 0.68 a | 0.69 a | 0.69 a | |
| MSCOR | 0.48 c | 0.49 bc | 0.53 a | 0.50 b | 0.52 a | 0.50 b | 0.52 a | 0.52 a | 0.50 ab | |
| TWT | 0.61 ab | 0.61 ab | 0.60 b | 0.61 ab | 0.60 b | 0.61 ab | 0.61 ab | 0.63 ab | 0.64 a | |
| GPC | 0.51 b | 0.51 b | 0.51 b | 0.47 b | 0.47 b | 0.54 a | 0.52 a | 0.55 a | 0.53 a | |
| KHRD | 0.58 a | 0.56 bc | 0.56 bc | 0.57 ab | 0.54 c | 0.56 bc | 0.57 abc | 0.57 abc | 0.57 abc | |
| KWT | 0.65 bc | 0.65 bc | 0.63 c | 0.63 c | 0.63 c | 0.70 a | 0.66 ab | 0.69 a | 0.63 bc | |
| KSIZE | 0.66 bc | 0.64 c | 0.62 c | 0.63 c | 0.66 bc | 0.64 c | 0.64 c | 0.69 a | 0.68 ab | |
| CODI | 0.56 b | 0.54 b | 0.54 b | 0.56 b | 0.55 b | 0.57 ab | 0.58 ab | 0.58 ab | 0.58 a | |
| FPROT | 0.48 c | 0.48 c | 0.46 d | 0.46 d | 0.46 d | 0.51 b | 0.53 ab | 0.53 ab | 0.54 a | |
| FASH | 0.51 c | 0.44 d | 0.44 d | 0.45 d | 0.44 d | 0.54 ab | 0.53 b | 0.56 a | 0.53 b | |
| FSV | 0.48 b | 0.47 bc | 0.46 c | 0.45 c | 0.46 c | 0.54 a | 0.54 a | 0.53 a | 0.53 aa | |
| FSDS | 0.59 c | 0.60 c | 0.59 c | 0.60 bc | 0.59 c | 0.62 ab | 0.63 a | 0.63 a | 0.62 ab | |
| FSRW | 0.52 b | 0.45 c | 0.45 c | 0.45 c | 0.46 c | 0.53 ab | 0.53 a | 0.54 a | 0.54 a | |
| Average | 0.61 | 0.58 | 0.58 | 0.58 | 0.58 | 0.63 | 0.63 | 0.64 | 0.63 |
| Location | Trait | RRBLUP | RF | MLP | CNN |
|---|---|---|---|---|---|
| 2019_Pullman_Lind | FYELD | 0.41 d | 0.48 b | 0.50 a | 0.46 c |
| BKYELD | 0.31 c | 0.38 b | 0.38 b | 0.40 a | |
| MSCOR | 0.27 b | 0.30 a | 0.30 a | 0.30 a | |
| TWT | 0.32 b | 0.37 a | 0.38 a | 0.38 a | |
| GPC | 0.25 c | 0.30 b | 0.31 b | 0.33 a | |
| KHRD | 0.32 c | 0.37 ab | 0.36 b | 0.38 a | |
| KWT | 0.34 b | 0.37 a | 0.36 a | 0.36 a | |
| KSIZE | 0.34 c | 0.38 b | 0.38 b | 0.40 a | |
| CODI | 0.40 c | 0.45 b | 0.46 a | 0.46 a | |
| FPROT | 0.35 c | 0.40 b | 0.40 b | 0.41 a | |
| FASH | 0.40 b | 0.41 ab | 0.41 ab | 0.42 a | |
| FSV | 0.27 c | 0.36 b | 0.39 a | 0.36 b | |
| FSDS | 0.36 c | 0.44 a | 0.43 a | 0.41 b | |
| FSRW | 0.36 c | 0.39 b | 0.41 a | 0.42 a | |
| 2019_Lind_Pullman | FYELD | 0.43 c | 0.47 b | 0.50 a | 0.49 a |
| BKYELD | 0.31 b | 0.40 a | 0.41 a | 0.40a | |
| MSCOR | 0.28 b | 0.29 b | 0.31 a | 0.31 a | |
| TWT | 0.31 c | 0.36 ab | 0.35 b | 0.37 a | |
| GPC | 0.27 b | 0.30 a | 0.28 b | 0.31 a | |
| KHRD | 0.33 b | 0.33 b | 0.38 a | 0.37 a | |
| KWT | 0.34 b | 0.37 a | 0.38 a | 0.37 a | |
| KSIZE | 0.35 b | 0.39 a | 0.40 a | 0.40 a | |
| CODI | 0.42 c | 0.44 b | 0.46 a | 0.46 a | |
| FPROT | 0.34 c | 0.42 a | 0.42 a | 0.40 b | |
| FASH | 0.41 a | 0.42 a | 0.42 a | 0.40 b | |
| FSV | 0.30 c | 0.38 b | 0.38 b | 0.42 a | |
| FSDS | 0.38 c | 0.41 a | 0.40 b | 0.40 b | |
| FSRW | 0.37 c | 0.41 b | 0.41 b | 0.43 a | |
| Average | 0.34 | 0.38 | 0.39 | 0.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandhu, K.S.; Aoun, M.; Morris, C.F.; Carter, A.H. Genomic Selection for End-Use Quality and Processing Traits in Soft White Winter Wheat Breeding Program with Machine and Deep Learning Models. Biology 2021, 10, 689. https://doi.org/10.3390/biology10070689
Sandhu KS, Aoun M, Morris CF, Carter AH. Genomic Selection for End-Use Quality and Processing Traits in Soft White Winter Wheat Breeding Program with Machine and Deep Learning Models. Biology. 2021; 10(7):689. https://doi.org/10.3390/biology10070689
Chicago/Turabian StyleSandhu, Karansher Singh, Meriem Aoun, Craig F. Morris, and Arron H. Carter. 2021. "Genomic Selection for End-Use Quality and Processing Traits in Soft White Winter Wheat Breeding Program with Machine and Deep Learning Models" Biology 10, no. 7: 689. https://doi.org/10.3390/biology10070689
APA StyleSandhu, K. S., Aoun, M., Morris, C. F., & Carter, A. H. (2021). Genomic Selection for End-Use Quality and Processing Traits in Soft White Winter Wheat Breeding Program with Machine and Deep Learning Models. Biology, 10(7), 689. https://doi.org/10.3390/biology10070689






