Numerical Optimization of an Open-Ended Coaxial Slot Applicator for the Detection and Microwave Ablation of Tumors
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation Model
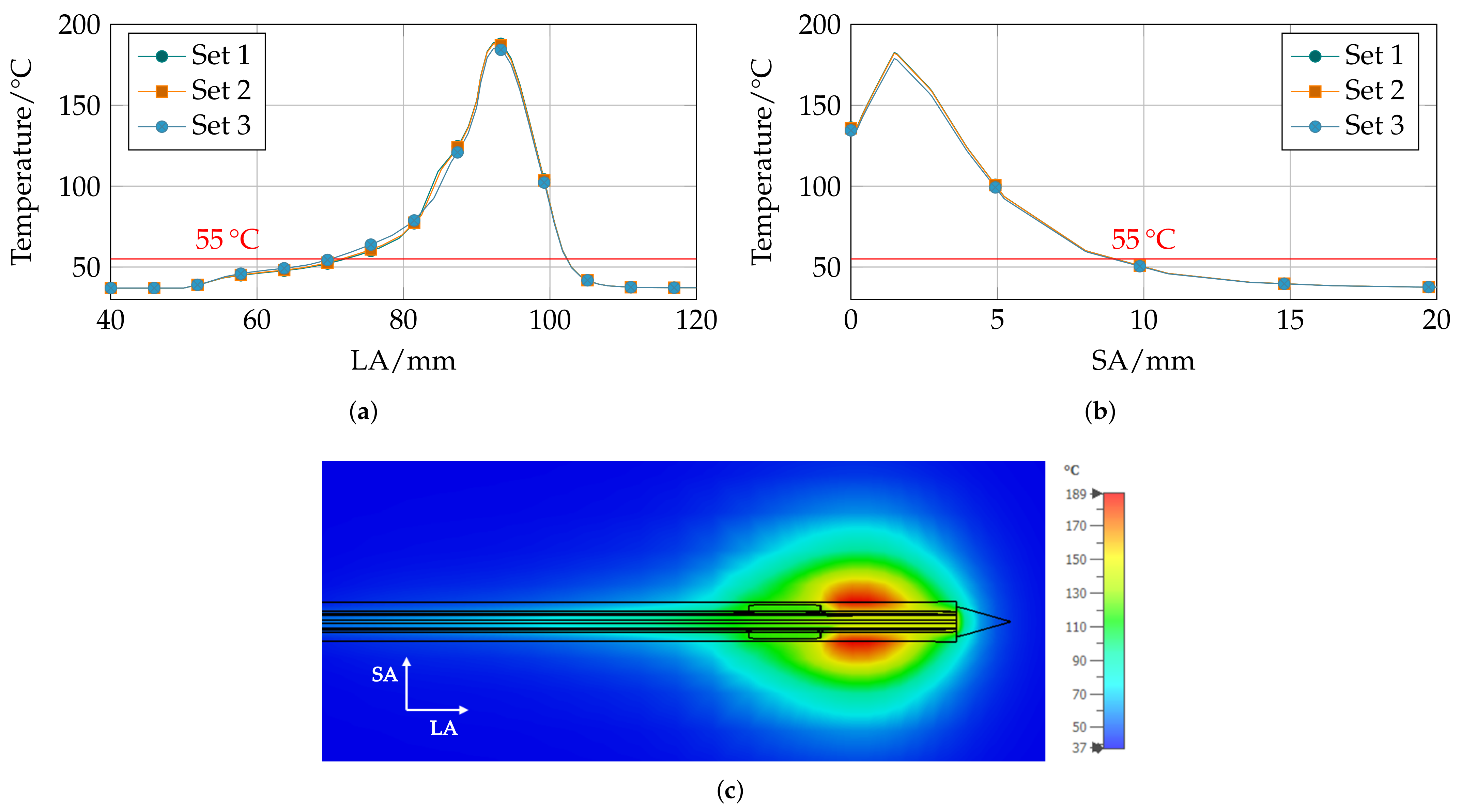
Parametric Analysis
2.2. Sensitivity Analysis
2.3. Objectives and Optimization Method
2.3.1. Applicator Efficiency
2.3.2. Volume and Sphericity of Ablation Zone
2.3.3. Multiobjective Optimization
3. Results
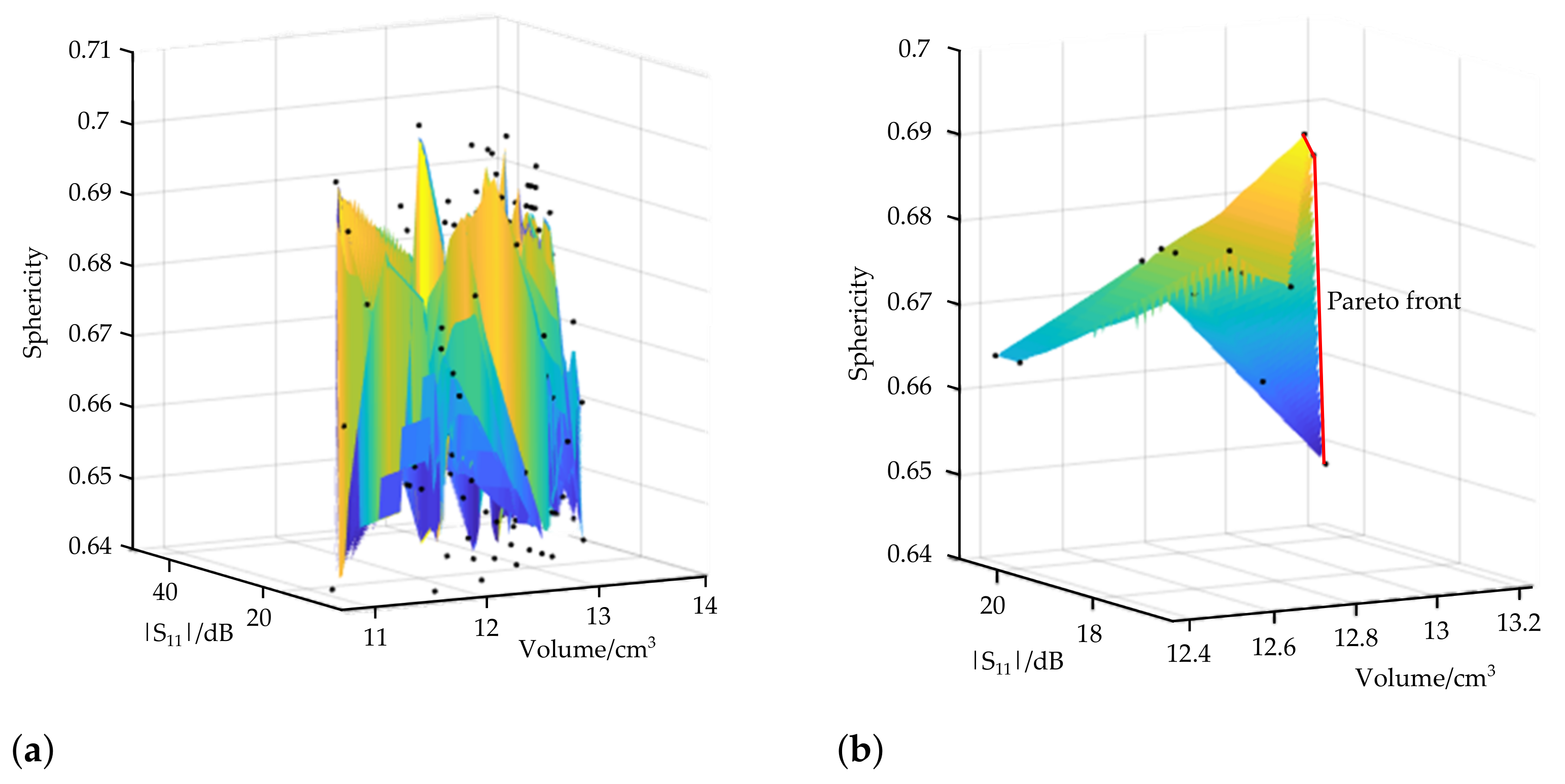
3.1. Pareto-Optimal Parameter Sets
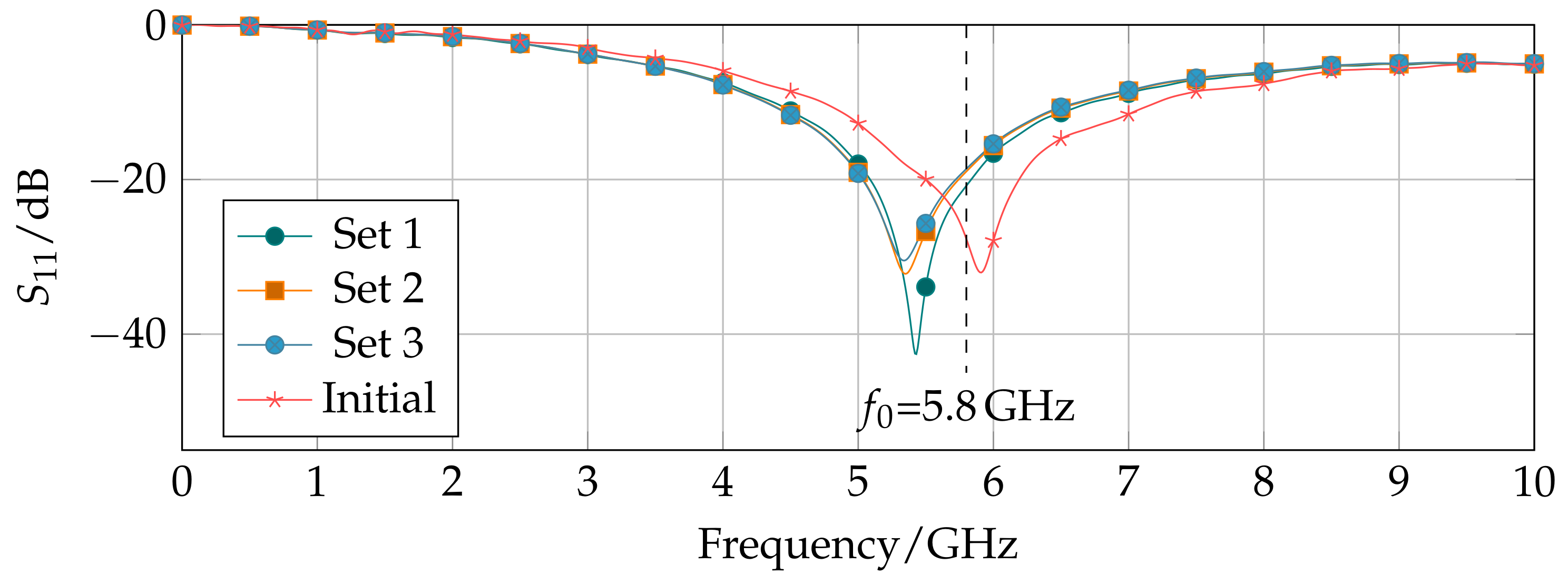
3.2. Applicator Characterization
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| RFA | Radiofrequency ablation |
| MWA | Microwave ablation |
| LITT | Laser-induced thermo-therapy |
| HIFU | High-intensity focused ultrasound |
| HCC | Hepatocellular carcinoma |
| CT | Computer tomography |
| US | Ultrasound |
| MRI | Magnetic resonance imaging |
| MWT | Microwave tomography |
| MUT | Matrial under test |
| NaCl | Sodium Chloride |
References
- Jemal, A.; Bray, F.; Center, M.M.; Ferlay, J.; Ward, E.; Forman, D. Global cancer statistics. CA A Cancer J. Clin. 2011, 61, 69–90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martin, R.C.G.; Scoggins, C.R.; McMasters, K.M. Safety and Efficacy of Microwave Ablation of Hepatic Tumors: A Prospective Review of a 5-Year Experience. Ann. Surg. Oncol. 2010, 17, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Vogl, T.J.; Nour-Eldin, N.E.A.; Hammerstingl, R.M.; Panahi, B.; Naguib, N.N.N. Microwave Ablation (MWA): Basics, Technique and Results in Primary and Metastatic Liver Neoplasms—Review Article. Rofo 2017, 189, 1055–1066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Livraghi, T.; Goldberg, S.N.; Lazzaroni, S.; Meloni, F.; Ierace, T.; Solbiati, L.; Gazelle, G.S. Hepatocellular Carcinoma: Radio-frequency Ablation of Medium and Large Lesions. Radiology 2000, 214, 761–768. [Google Scholar] [CrossRef] [PubMed]
- Lencioni, R.; Cioni, D.; Crocetti, L.; Franchini, C.; Pina, C.D.; Lera, J.; Bartolozzi, C. Early-Stage Hepatocellular Carcinoma in Patients with Cirrhosis: Long-term Results of Percutaneous Image-guided Radiofrequency Ablation. Radiology 2005, 234, 961–967. [Google Scholar] [CrossRef]
- Eichler, K.; Mack, M.G.; Straub, R.; Engelmann, K.; Zangos, S.; Woitaschek, D.; Vogl, T.J. Oligonoduläres hepatozelluläres Karzinom (HCC): MR-gesteuerte laserinduzierte Thermotherapie (LITT). Der Radiol. 2001, 41, 915–922. [Google Scholar] [CrossRef]
- Mensel, B.; Weigel, C.; Heidecke, C.D.; Stier, A.; Hosten, N. Laseninduzierte Thermotherapie (LITT) von Lebertumoren in zentraler Lokalisation: Ergebnisse und Komplikationen. Fortschr Röntgenstr 2005, 177, 1267–1275. [Google Scholar] [CrossRef]
- Kennedy, J.E. High-Intensity Focused Ultrasound in the Treatment of Solid Tumours. Nat. Rev. Cancer 2005, 5, 321–327. [Google Scholar] [CrossRef]
- Glassberg, M.B.; Ghosh, S.; Clymer, J.W.; Qadeer, R.A.; Ferko, N.C.; Sadeghirad, B.; Wright, G.W.J.; Amaral, J.F. Microwave ablation compared with radiofrequency ablation for treatment of hepatocellular carcinoma and liver metastases: A systematic review and meta-analysis. Onco Targets Ther. 2019, 12, 6407. [Google Scholar] [CrossRef] [Green Version]
- Shibata, T.; Niinobu, T.; Ogata, N.; Takami, M. Microwave Coagulation Therapy for Multiple Hepatic Metastases from Colorectal Carcinoma. Cancer 2000, 89, 276–284. [Google Scholar] [CrossRef]
- Vogl, T.J.; Riegelbauer, L.J.; Oppermann, E.; Kostantin, M.; Ackermann, H.; Trzmiel, A.; Stein, S.; Eichler, K.; Zharov, V.P.; Roy, D.; et al. Early dynamic changes in circulating tumor cells and prognostic relevance following interventional radiological treatments in patients with hepatocellular carcinoma. PLoS ONE 2021, 16, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Fallahi, H.; Prakash, P. Antenna Designs for Microwave Tissue Ablation. Crit. Rev. Biomed. Eng. 2018, 46, 495–521. [Google Scholar] [CrossRef] [PubMed]
- Lopresto, V.; Pinto, R.; Farina, L.; Cavagnaro, M. Treatment planning in microwave thermal ablation: Clinical gaps and recent research advances. Int. J. Hyperth. 2017, 33, 83–100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, M.; Scapaticci, R.; Cavagnaro, M.; Crocco, L. Towards a Microwave Imaging System for Continuous Monitoring of Liver Tumor Ablation: Design and In Silico Validation of an Experimental Setup. Diagnostics 2021, 11, 866. [Google Scholar] [CrossRef]
- Scapaticci, R.; Lopresto, V.; Pinto, R.; Cavagnaro, M.; Crocco, L. Monitoring Thermal Ablation via Microwave Tomography: An Ex Vivo Experimental Assessment. Diagnostics 2018, 8, 81. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Brace, C.L.; Converse, M.C.; Webster, J.G. Tumor Boundary Estimation Through Time-Domain Peaks Monitoring: Numerical Predictions and Experimental Results in Tissue-Mimicking Phantoms. IEEE Trans. Biomed. Eng. 2009, 56, 2634–2641. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Brace, C.L. Tissue Dielectric Measurement Using an Interstitial Dipole Antenna. IEEE Trans. Biomed. Eng. 2012, 59, 115–121. [Google Scholar] [CrossRef] [Green Version]
- Hessinger, C.; Bazrafshan, B.; Schüßler, M.; Schmidt, S.; Schuster, C.; Hübner, F.; Vogl, T.J.; Jakoby, R. A Dual-Mode Coaxial Slot Applicator for Microwave Ablation Treatment. IEEE Trans. Microw. Theory Technol. 2018, 1–10. [Google Scholar] [CrossRef]
- Prakash, P.; Deng, G.; Converse, M.C.; Webster, J.G.; Mahvi, D.M.; Ferris, M.C. Design optimization of a robust sleeve antenna for hepatic microwave ablation. Phys. Med. Biol. 2008, 53, 1057–1069. [Google Scholar] [CrossRef]
- Yang, D.; Bertram, J.M.; Converse, M.C.; ORourke, A.P.; Webster, J.G.; Hagness, S.C.; Will, J.A.; Mahvi, D.M. A Floating Sleeve Antenna Yields Localized Hepatic Microwave Ablation. IEEE Trans. Biomed. Eng. 2006, 53, 533–537. [Google Scholar] [CrossRef] [Green Version]
- Brace, C.L. Dual-slot antennas for microwave tissue heating: Parametric design analysis and experimental validation. Med. Phys. 2011, 38, 4232–4240. [Google Scholar] [CrossRef] [Green Version]
- Sawicki, J.F.; Shea, J.D.; Behdad, N.; Hagness, S.C. The impact of frequency on the performance of microwave ablation. Int. J. Hyperth. 2017, 33, 61–68. [Google Scholar] [CrossRef] [Green Version]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- O’rourke, A.P.; Lazebnik, M.; Bertram, J.M.; Converse, M.C.; Hagness, S.C.; Webster, J.G.; Mahvi, D.M. Dielectric Properties of Human Normal, Malignant and Cirrhotic Liver Tissue: In vivo and ex vivo Measurements from 0.5 to 20 GHz Using a Precision Open-Ended Coaxial Probe. Phys. Med. Biol. 2007, 52, 4707. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peyman, A.; Gabriel, C.; Grant, E. Complex permittivity of sodium chloride solutions at microwave frequencies. Bioelectromagnetics 2007, 28, 264–274. [Google Scholar] [CrossRef] [PubMed]
- Kraszewski, A.; Stuchly, M.A.; Stuchly, S.S. ANA Calibration Method for Measurements of Dielectric Properties. IEEE Trans. Instrum. Meas. 1983, 32, 385–387. [Google Scholar] [CrossRef]
- Cavagnaro, M.; Ruvio, G. Numerical Sensitivity Analysis for Dielectric Characterization of Biological Samples by Open-Ended Probe Technique. Sensors 2020, 20, 3756. [Google Scholar] [CrossRef]
- Hessinger Née Reimann, C.; Bazrafshan, B.; Hübner, F.; Schmidt, S.; Schüler, M.; Panahi, B.; Kaltenbach, B.; Polkowski, C.; Vogl, T.J.; Jakoby, R. Dielectric Contrast Between Normal and Tumor Ex-Vivo Human Liver Tissue. IEEE Access 2019, 7, 164113–164119. [Google Scholar] [CrossRef]
- Peyman, A.; Kos, B.; Djokić, M.; Trotovšek, B.; Limbaeck-Stokin, C.; Serša, G.; Miklavčič, D. Variation in dielectric properties due to pathological changes in human liver. Bioelectromagnetics 2015, 36, 603–612. [Google Scholar] [CrossRef]
- Ehrgott, M. Vilfredo Pareto and Multi-objective Optimization. In Documenta Mathematica; Deutsche Mathematiker-Vereinigung e.V.: Berlin, Germany, 2012. [Google Scholar]
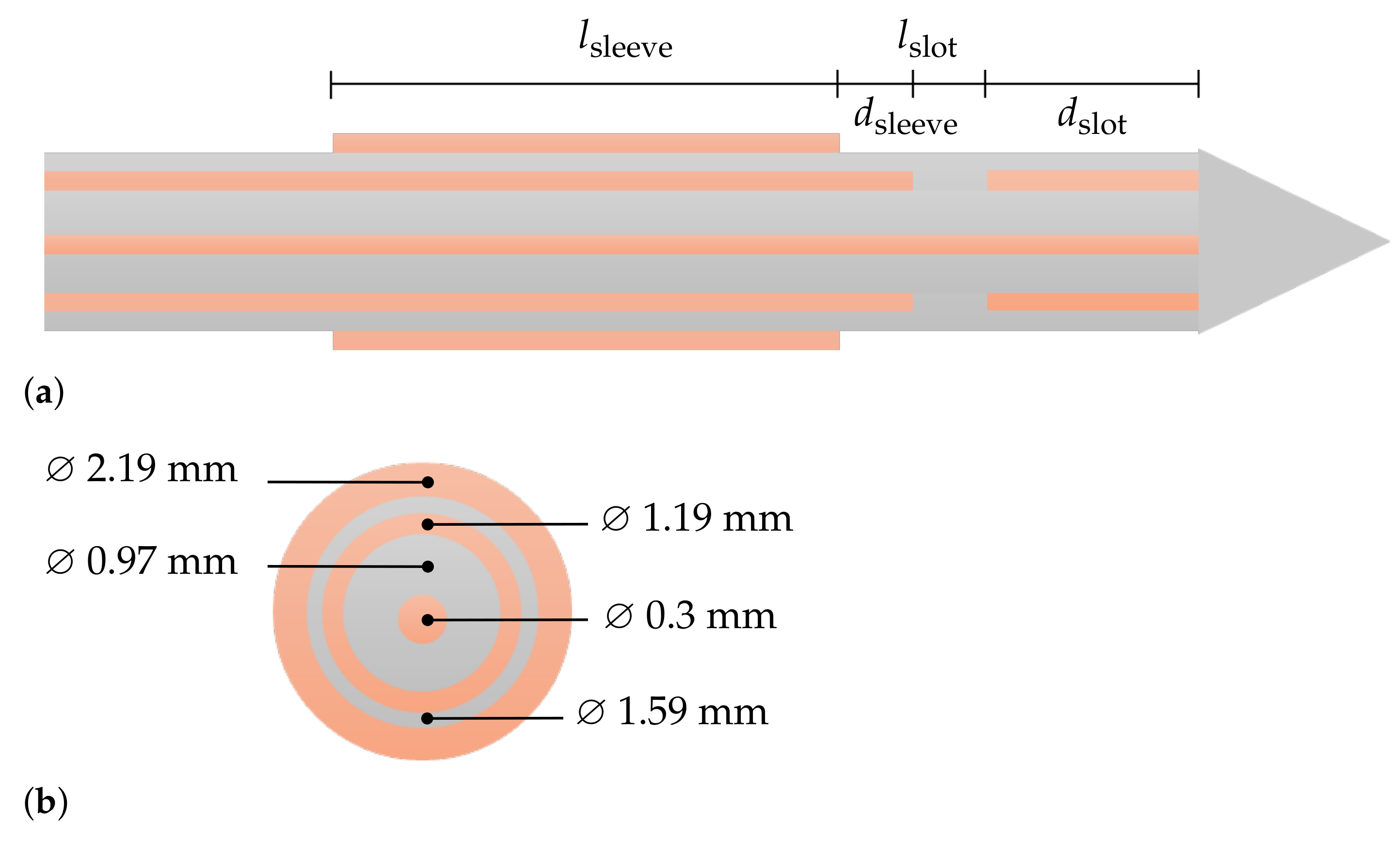
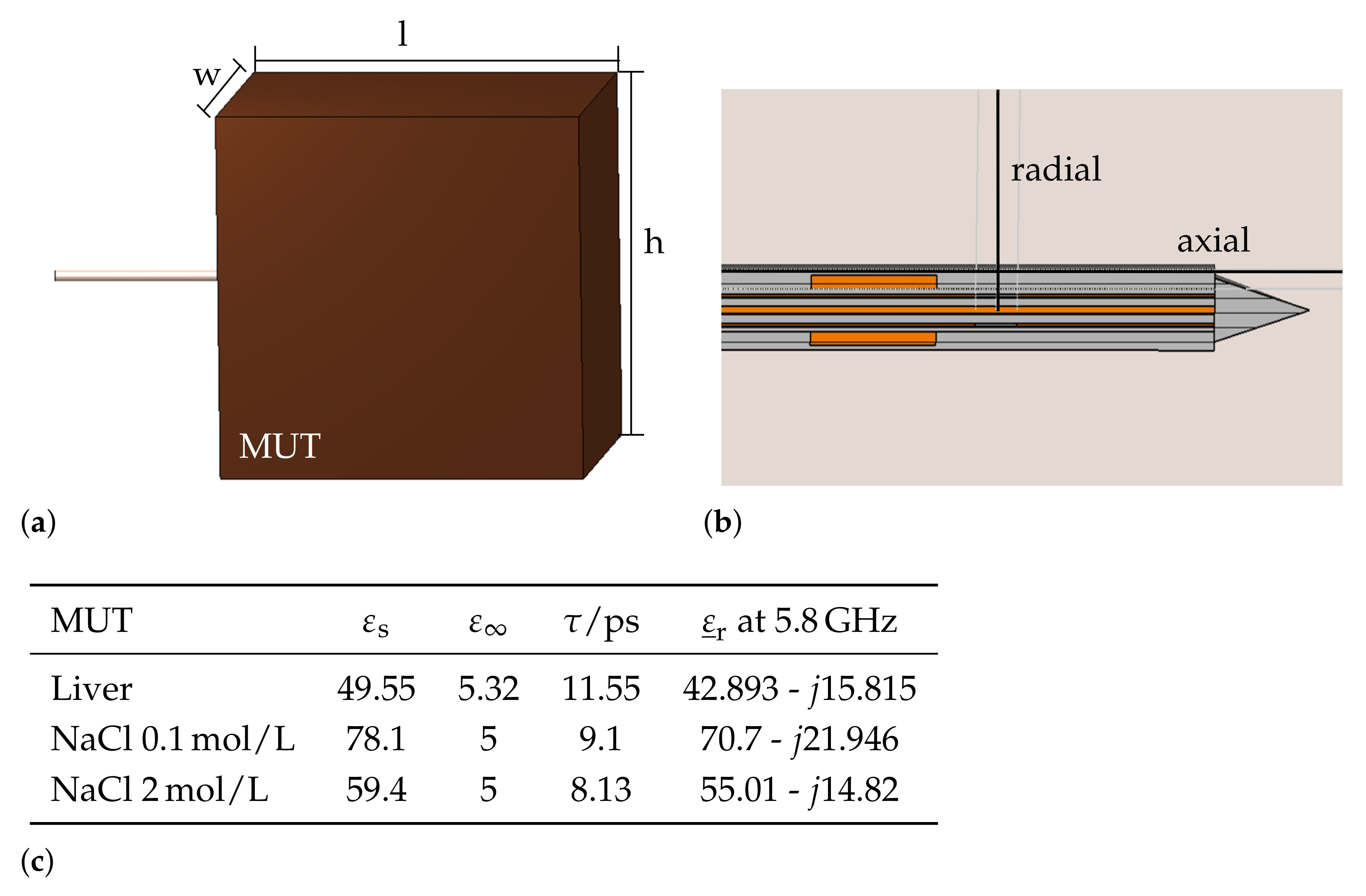

| Design Parameter | Initial Value/mm | Sweep Range | Relative Change |
|---|---|---|---|
| Length sleeve | 4.4 | 3.52, ..., 5.28 | ±20% |
| Distance sleeve | 1.1 | 0.55, ..., 1.65 | ±50% |
| Length slot | 1.4 | 1.05, ..., 1.75 | ±50% |
| Distance slot | 7.1 | 5.9, ..., 8.3 | ±18% |
| Design Parameter/mm | Objectives | Sensitivity | ||||||
|---|---|---|---|---|---|---|---|---|
| Set | /dB | V/cm3 | Sphericity | |||||
| 1 | 5.28 | 0.55 | 1.75 | 7.7 | 18.61 | 12.94 | 0.6908 | % |
| 2 | 4.84 | 0.55 | 1.75 | 7.7 | 18.97 | 13 | 0.6874 | % |
| 3 | 3.52 | 0.55 | 1.75 | 7.7 | 20.77 | 13.24 | 0.648 | % |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hessinger, C.; Schüßler, M.; Klos, S.; Kochanek, M.; Jakoby, R. Numerical Optimization of an Open-Ended Coaxial Slot Applicator for the Detection and Microwave Ablation of Tumors. Biology 2021, 10, 914. https://doi.org/10.3390/biology10090914
Hessinger C, Schüßler M, Klos S, Kochanek M, Jakoby R. Numerical Optimization of an Open-Ended Coaxial Slot Applicator for the Detection and Microwave Ablation of Tumors. Biology. 2021; 10(9):914. https://doi.org/10.3390/biology10090914
Chicago/Turabian StyleHessinger, Carolin, Martin Schüßler, Sabrina Klos, Markus Kochanek, and Rolf Jakoby. 2021. "Numerical Optimization of an Open-Ended Coaxial Slot Applicator for the Detection and Microwave Ablation of Tumors" Biology 10, no. 9: 914. https://doi.org/10.3390/biology10090914
APA StyleHessinger, C., Schüßler, M., Klos, S., Kochanek, M., & Jakoby, R. (2021). Numerical Optimization of an Open-Ended Coaxial Slot Applicator for the Detection and Microwave Ablation of Tumors. Biology, 10(9), 914. https://doi.org/10.3390/biology10090914





