How Metabolic Rate Relates to Cell Size
Abstract
:Simple Summary
Abstract
1. Introduction
2. Major Ways That Variation in Metabolic Rate May Relate to Cell Size
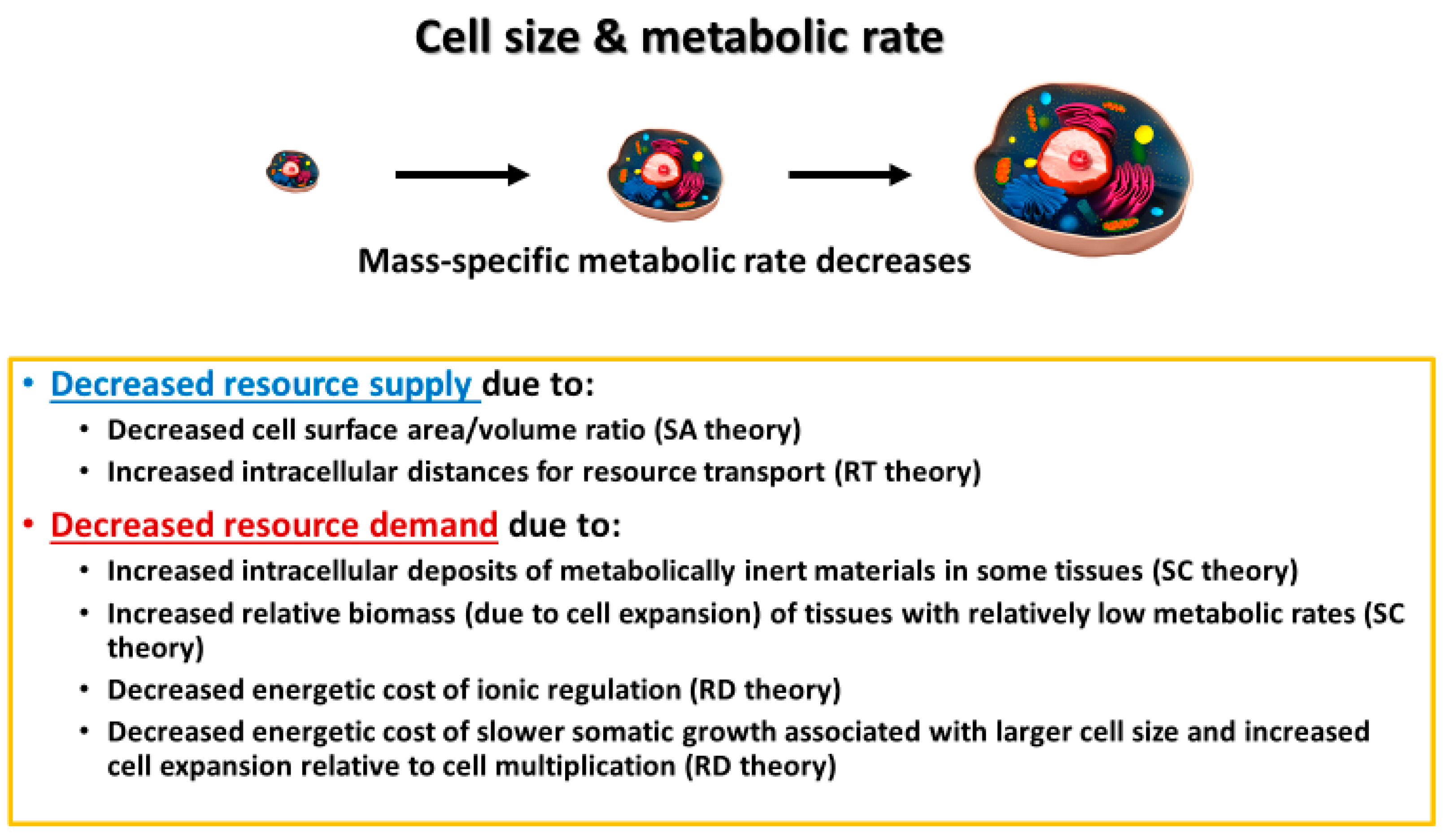
2.1. Mass-Specific or Mass-Corrected Metabolic Rate
2.1.1. Theory
2.1.2. Interspecific Patterns
2.1.3. Intraspecific Patterns
2.2. ‘Metabolic Level’ or Vertical Elevation of a Body-Mass Scaling Relationship for Metabolic Rate
2.3. Slope of a Body-Mass Scaling Relationship for Metabolic Rate
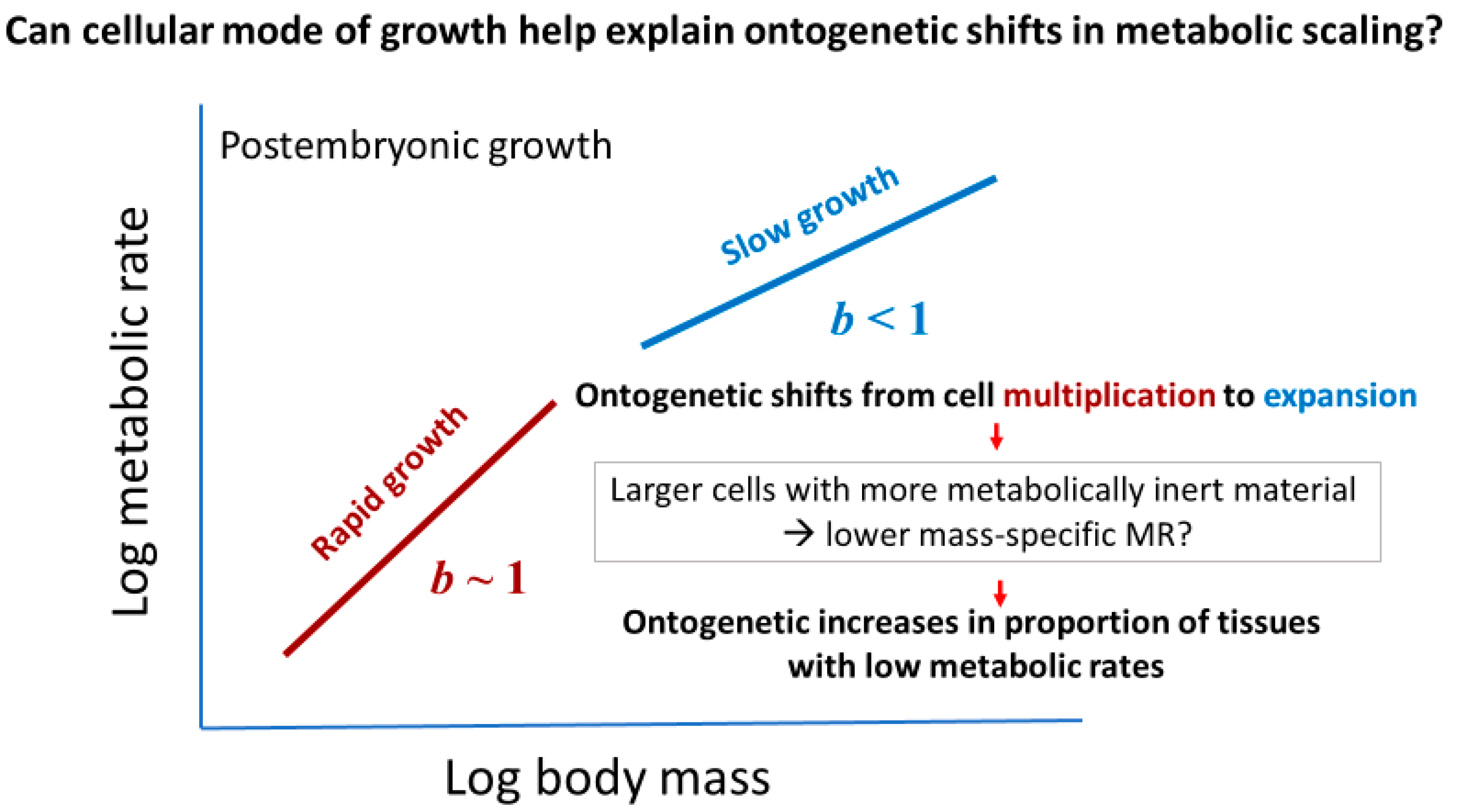
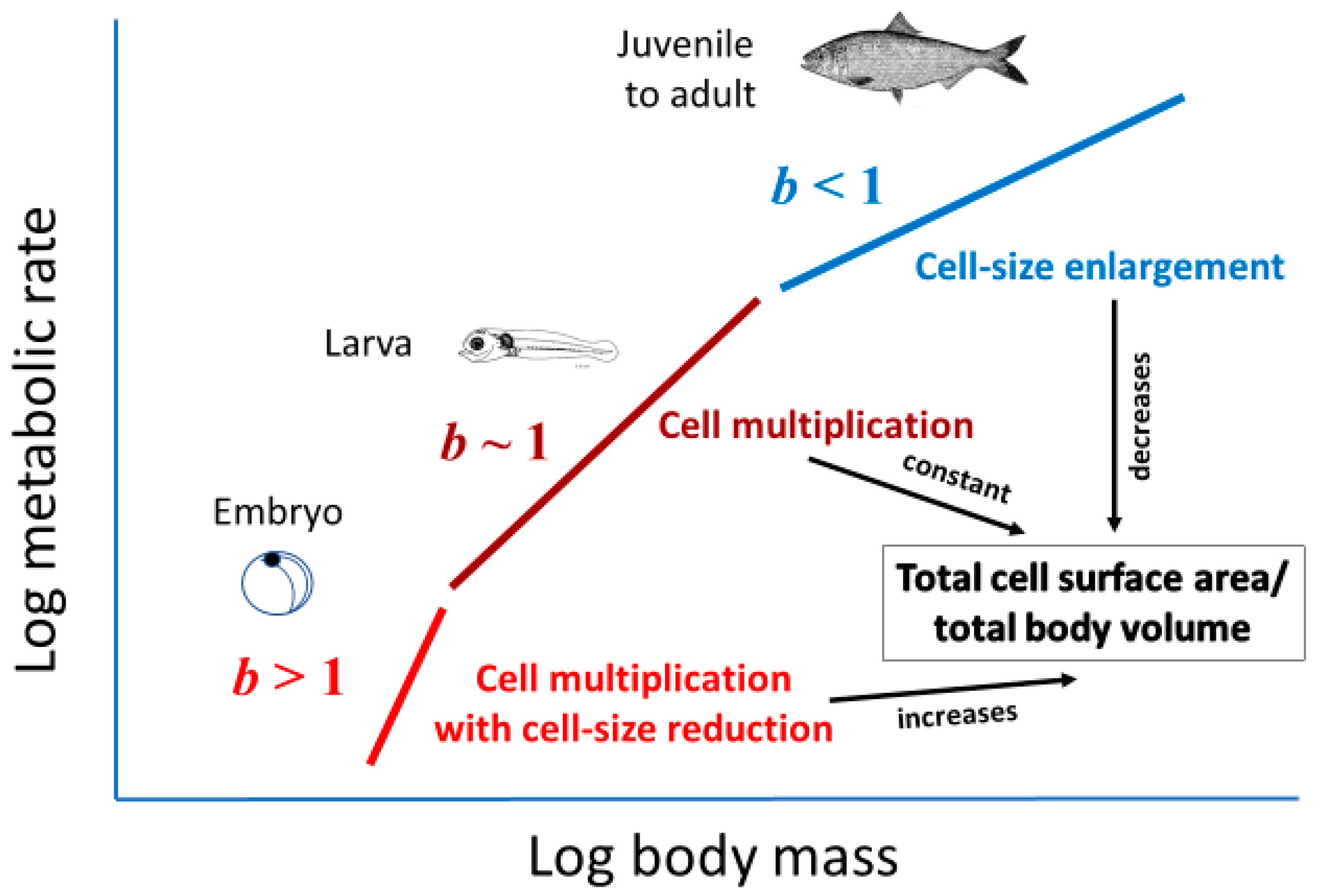
2.3.1. Effects of Cellular Mode of Growth (Cell Expansion versus Multiplication)
2.3.2. Effects of Cellular Mode of Growth (Ontogenetic Shifts in Growth Rate and Metabolic Scaling)
2.3.3. Effects of Cellular Mode of Growth (Ontogenetic Development of Larger Cells with Large Amounts of Metabolically Inert Materials)
2.3.4. Effects of Total Cellular Surface Area in Body (at Constant Metabolic Level)
2.3.5. Effects of Both Cellular and Whole-Body Surface Areas (Mediated by Variable Metabolic Level)
2.3.6. Summary of Potential Effects of Cell Size on Metabolic Scaling and Their Logical Consistency
3. Mechanisms Underlying Cell-Size Effects on Metabolic Rate and Its Scaling with Body Mass
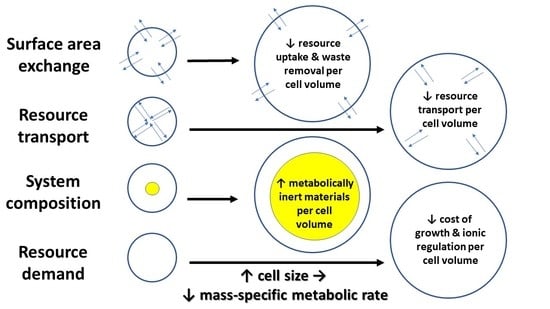
3.1. Surface Area/Volume Effects
3.2. Intracellular Resource-Transport Effects
3.3. Cell and Body Composition Effects
3.4. Effects of Resource Demand by Growth, as Mediated by the Cellular Mode of Growth
3.5. Cell-Size Variation in Time and Space
3.6. A Holistic Hierarchical View: Linking Mechanisms at the Cell, Organ, and Whole-Organism Levels
4. Effects of Biological Regulation on Metabolic Rate and Its Scaling with Body Mass
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ricklefs, R.E.; Wikelski, M. The physiology/life-history nexus. Trends Ecol. Evol. 2002, 17, 462–468. [Google Scholar] [CrossRef]
- Brown, J.H.; Gillooly, J.F.; Allen, A.P.; Savage, V.M.; West, G.B. Toward a metabolic theory of ecology. Ecology 2004, 85, 1771–1789. [Google Scholar] [CrossRef]
- Glazier, D.S. Is metabolic rate a universal ‘pacemaker’ for biological processes? Biol. Rev. 2015, 90, 377–407. [Google Scholar] [CrossRef]
- Montiglio, P.O.; Dammhahn, M.; Dubuc Messier, G.; Réale, D. The pace-of-life syndrome revisited: The role of ecological conditions and natural history on the slow-fast continuum. Behav. Ecol. Sociobiol. 2018, 72, 116. [Google Scholar] [CrossRef]
- Peters, R.H. The Ecological Implications of Body Size; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- McNab, B.K. An analysis of the factors that influence the level and scaling of mammalian BMR. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2008, 151, 5–28. [Google Scholar] [CrossRef]
- Glazier, D.S. Complications with body-size correction in comparative biology: Possible solutions and an appeal for new approaches. J. Exp. Biol. 2022, 225 (Suppl. 1), jeb243313. [Google Scholar] [CrossRef]
- Agutter, P.S.; Wheatley, D.N. Metabolic scaling: Consensus or controversy? Theor. Biol. Med. Model. 2004, 1, 13. [Google Scholar] [CrossRef] [Green Version]
- Glazier, D.S. Beyond the “3/4-power law”: Variation in the intra- and interspecific scaling of metabolic rate in animals. Biol. Rev. 2005, 80, 611–662. [Google Scholar] [CrossRef]
- Agutter, P.S.; Tuszynski, J.A. Analytic theories of metabolic scaling. J. Exp. Biol. 2011, 214, 1055–1062. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burton, T.; Killen, S.S.; Armstrong, J.D.; Metcalfe, N.B. What causes intraspecific variation in resting metabolic rate and what are its ecological consequences? Proc. R. Soc. B Biol. Sci. 2011, 278, 3465–3473. [Google Scholar] [CrossRef] [Green Version]
- Konarzewski, M.; Książek, A. Determinants of intra-specific variation in basal metabolic rate. J. Comp. Physiol. B 2013, 183, 27–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- White, C.R.; Kearney, M.R. Determinants of inter-specific variation in basal metabolic rate. J. Comp. Physiol. B 2013, 183, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Metabolic scaling in complex living systems. Systems 2014, 2, 451–540. [Google Scholar] [CrossRef] [Green Version]
- White, C.R.; Kearney, M.R. Metabolic scaling in animals: Methods, empirical results, and theoretical explanations. Compr. Physiol. 2014, 4, 231–256. [Google Scholar] [CrossRef]
- Killen, S.S.; Glazier, D.S.; Rezende, E.L.; Clark, T.D.; Atkinson, D.; Willener, A.S.; Halsey, L.G. Ecological influences and morphological correlates of resting and maximal metabolic rates across teleost fish species. Am. Nat. 2016, 187, 592–606. [Google Scholar] [CrossRef] [Green Version]
- Harrison, J.F. Do performance-safety tradeoffs cause hypometric metabolic scaling in animals? Trends Ecol. Evol. 2017, 32, 653–664. [Google Scholar] [CrossRef]
- Glazier, D.S. Rediscovering and reviving old observations and explanations of metabolic scaling in living systems. Systems 2018, 6, 4. [Google Scholar] [CrossRef] [Green Version]
- Pettersen, A.K.; Marshall, D.J.; White, C.R. Understanding variation in metabolic rate. J. Exp. Biol. 2018, 221, jeb166876. [Google Scholar] [CrossRef] [Green Version]
- Kozłowski, J.; Konarzewski, M.; Czarnoleski, M. Coevolution of body size and metabolic rate in vertebrates: A life-history perspective. Biol. Rev. 2020, 95, 1393–1417. [Google Scholar] [CrossRef]
- Pfaundler, M. Über die energetische Flächenregel. Pflüger’s Arch. Gesamte Physiol. Menschen Tiere 1921, 188, 273–280. [Google Scholar] [CrossRef] [Green Version]
- Smith, H.M. Cell size and metabolic activity in Amphibia. Biol. Bull. 1925, 48, 347–378. [Google Scholar] [CrossRef]
- Davison, J. Body weight, cell surface, and metabolic rate in anuran Amphibia. Biol. Bull. 1955, 109, 407–419. [Google Scholar] [CrossRef]
- Davison, J. An analysis of cell growth and metabolism in the crayfish (Procambrus alleni). Biol. Bull. 1956, 110, 264–273. [Google Scholar] [CrossRef]
- Szarski, H. Cell size and the concept of wasteful and frugal evolutionary strategies. J. Theor. Biol. 1983, 105, 201–209. [Google Scholar] [CrossRef]
- Vinogradov, A.E. Nucleotypic effect in homeotherms: Body-mass-corrected basal metabolic rate of mammals is related to genome size. Evolution 1995, 49, 1249–1259. [Google Scholar] [CrossRef]
- Kozłowski, J.; Konarzewski, M.; Gawelczyk, A.T. Cell size as a link between noncoding DNA and metabolic rate scaling. Proc. Natl. Acad. Sci. USA 2003, 100, 14080–14085. [Google Scholar] [CrossRef] [Green Version]
- Gregory, T.R. Genome size evolution in animals. In The Evolution of the Genome; Gregory, T.R., Ed.; Elsevier Academic Press: Burlington, MA, USA, 2005; pp. 3–87. [Google Scholar]
- Glazier, D.S. Scaling of metabolic scaling within physical limits. Systems 2014, 2, 425–450. [Google Scholar] [CrossRef] [Green Version]
- Glazier, D.S. Body-mass scaling of metabolic rate: What are the relative roles of cellular versus systemic effects? Biology 2015, 4, 187–199. [Google Scholar] [CrossRef] [Green Version]
- Chown, S.L.; Marais, E.; Terblanche, J.S.; Klok, C.J.; Lighton, J.R.B.; Blackburn, T.M. Scaling of insect metabolic rate is inconsistent with the nutrient supply network model. Funct. Ecol. 2007, 21, 282–290. [Google Scholar] [CrossRef]
- Starostová, Z.; Kubička, L.; Konarzewski, M.; Kozłowski, J.; Kratochvíl, L. Cell size but not genome size affects scaling of metabolic rate in eyelid geckos. Am. Nat. 2009, 174, E100–E105. [Google Scholar] [CrossRef]
- Maciak, S.; Janko, K.; Kotusz, J.; Choleva, L.; Boroń, A.; Juchno, D.; Kujawa, R.; Kozłowski, J.; Konarzewski, M. Standard metabolic rate (SMR) is inversely related to erythrocyte and genome size in allopolyploid fish of the Cobitis taenia hybrid complex. Funct. Ecol. 2011, 25, 1072–1078. [Google Scholar] [CrossRef]
- Huang, Q.; Zhang, Y.; Liu, S.; Wang, W.; Luo, Y. Intraspecific scaling of the resting and maximum metabolic rates of the crucian carp (Carassius auratus). PLoS ONE 2013, 8, e82837. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Huang, Q.; Liu, S.; He, D.; Wei, G.; Luo, Y. Intraspecific mass scaling of metabolic rates in grass carp (Ctenopharyngodon idellus). J. Comp. Physiol. B 2014, 184, 347–354. [Google Scholar] [CrossRef]
- Luo, Y.; He, D.; Li, G.; Xie, H.; Zhang, Y.; Huang, Q. Intraspecific metabolic scaling exponent depends on red blood cell size in fishes. J. Exp. Biol. 2015, 218, 1496–1503. [Google Scholar] [CrossRef] [Green Version]
- Takemoto, K. Heterogeneity of cells may explain allometric scaling of metabolic rate. Biosystems 2015, 130, 11–16. [Google Scholar] [CrossRef] [Green Version]
- Shestopaloff, Y.K. Metabolic allometric scaling model: Combining cellular transportation and heat dissipation constraints. J. Exp. Biol. 2016, 219, 2481–2489. [Google Scholar] [CrossRef] [Green Version]
- Hermaniuk, A.; Rybacki, M.; Taylor, J.R. Metabolic rate of diploid and triploid Edible Frog Pelophylax esculentus correlates inversely with cell size in tadpoles but not in frogs. Physiol. Biochem. Zool. 2017, 90, 230–239. [Google Scholar] [CrossRef] [PubMed]
- Czarnoleski, M.; Labecka, A.M.; Dragosz-Kluska, D.; Pis, T.; Pawlik, K.; Kapustka, F.; Kilarski, W.M.; Kozłowski, J. Concerted evolution of body mass and cell size: Similar patterns among species of birds (Galliformes) and mammals (Rodentia). Biol. Open 2018, 7, bio029603. [Google Scholar] [CrossRef] [Green Version]
- Schramm, B.W.; Labecka, A.M.; Gudowska, A.; Antoł, A.; Sikorska, A.; Szabla, N.; Bauchinger, U.; Kozlowski, J.; Czarnoleski, M. Concerted evolution of body mass, cell size and metabolic rate among carabid beetles. J. Insect Physiol. 2021, 132, 104272. [Google Scholar] [CrossRef]
- Zhu, Y.; Xiong, W.; Xu, Y.; Zhang, P.; Zhang, J.; Luo, Y. Comparison of metabolic scaling between triploid and diploid common carp. J. Comp. Physiol. B 2021, 191, 711–719. [Google Scholar] [CrossRef]
- Kestner, O. Metabolism and size of organs. J. Physiol. 1936, 87, 39P–41P. [Google Scholar]
- Oikawa, S.; Itazawa, Y. Relative growth of organs and parts of the carp, Cyprinus carpio, with special reference to the metabolism-size relationship. Copeia 1984, 1984, 800–803. [Google Scholar] [CrossRef]
- Oikawa, S.; Itazawa, Y. Tissue respiration and relative growth of parts of body of a marine teleost, porgy Pagrus major, during early life stages with special reference to the metabolism-size relationship. Comp. Biochem. Physiol. A Physiol. 1993, 105, 741–744. [Google Scholar] [CrossRef]
- Daan, S.; Masman, D.; Groenewold, A. Avian basal metabolic rates: Their association with body composition and energy expenditure in nature. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1990, 259, R333–R340. [Google Scholar] [CrossRef]
- Wang, Z.; O’Connor, T.P.; Heshka, S.; Heymsfield, S.B. The reconstruction of Kleiber’s law at the organ-tissue level. J. Nutr. 2001, 131, 2967–2970. [Google Scholar] [CrossRef] [Green Version]
- Kutschera, U.; Niklas, K.J. Organ-specific rates of cellular respiration in developing sunflower seedlings and their bearing on metabolic scaling theory. Protoplasma 2012, 249, 1049–1057. [Google Scholar] [CrossRef]
- Antoł, A.; Kozłowski, J. Scaling of organ masses in mammals and birds: Phylogenetic signal and implications for metabolic rate scaling. ZooKeys 2020, 982, 149. [Google Scholar] [CrossRef]
- Glazier, D.S. A unifying explanation for diverse metabolic scaling in animals and plants. Biol. Rev. 2010, 85, 111–138. [Google Scholar] [CrossRef]
- Killen, S.S.; Atkinson, D.; Glazier, D.S. The intraspecific scaling of metabolic rate with body mass in fishes depends on lifestyle and temperature. Ecol. Lett. 2010, 13, 184–193. [Google Scholar] [CrossRef]
- Glazier, D.S. Commentary: On the interpretation of the normalization constant in the scaling equation. Front. Ecol. Evol. 2020, 8, 90. [Google Scholar] [CrossRef] [Green Version]
- Okie, J.G. General models for the spectra of surface area scaling strategies of cells and organisms: Fractality, geometric dissimilitude, and internalization. Am. Nat. 2013, 181, 421–439. [Google Scholar] [CrossRef] [PubMed]
- Licht, L.E.; Lowcock, L.A. Genome size and metabolic rate in salamanders. Comp. Biochem. Physiol. B Comp. Biochem. 1991, 100, 83–92. [Google Scholar] [CrossRef]
- Pis, T. Resting metabolic rate and erythrocyte morphology in early development of thermoregulation in the precocial grey partridge (Perdix perdix). Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2008, 151, 211–218. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Genome size covaries more positively with propagule size than adult size: New insights into an old problem. Biology 2021, 10, 270. [Google Scholar] [CrossRef]
- Gardner, J.D.; Laurin, M.; Organ, C.L. The relationship between genome size and metabolic rate in extant vertebrates. Philos. Trans. R. Soc. Lond. B Bio. Sci. 2020, 375, 20190146. [Google Scholar] [CrossRef] [Green Version]
- Stillwell, E.J.; Benfey, T.J. Hemoglobin level, metabolic rate, opercular abduction rate and swimming efficiency in female triploid brook trout (Salvelinus fontinalis). Fish Physiol. Biochem. 1996, 15, 377–383. [Google Scholar] [CrossRef]
- Atkins, M.E.; Benfey, T.J. Effect of acclimation temperature on routine metabolic rate in triploid salmonids. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2008, 149, 157–161. [Google Scholar] [CrossRef]
- Maciak, S.; Bonda-Ostaszewska, E.; Czarnołęski, M.; Konarzewski, M.; Kozłowski, J. Mice divergently selected for high and low basal metabolic rates evolved different cell size and organ mass. J. Evol. Biol. 2014, 27, 478–487. [Google Scholar] [CrossRef] [Green Version]
- Bowden, A.J.; Andrewartha, S.J.; Elliott, N.G.; Frappell, P.B.; Clark, T.D. Negligible differences in metabolism and thermal tolerance between diploid and triploid Atlantic salmon (Salmo salar). J. Exp. Biol. 2018, 221, jeb166975. [Google Scholar] [CrossRef] [Green Version]
- Lahnsteiner, F.; Lahnsteiner, E.; Kletzl, M. Differences in metabolism of triploid and diploid Salmo trutta f. lacustris under acclimation conditions and after exposure to stress situations. Aquac. Res. 2019, 50, 2444–2459. [Google Scholar] [CrossRef]
- Hermaniuk, A.; van de Pol, I.L.; Verberk, W.C. Are acute and acclimated thermal effects on metabolic rate modulated by cell size? a comparison between diploid and triploid zebrafish larvae. J. Exp. Biol. 2021, 224, jeb.227124. [Google Scholar] [CrossRef] [PubMed]
- Ellenby, C. Oxygen consumption and cell size. A comparison of the rate of oxygen consumption of diploid and triploid prepupae of Drosophila melanogaster Meigen. J. Exp. Biol. 1953, 30, 475–491. [Google Scholar] [CrossRef]
- Kamel, S.; Marsden, J.E.; Pough, F.H. Diploid and tetraploid grey treefrogs (Hyla chrysoscelis and Hyla versicolor) have similar metabolic rates. Comp. Biochem. Physiol. A Comp. Physiol. 1985, 82, 217–220. [Google Scholar] [CrossRef]
- Licht, L.E.; Bogart, J.P. Comparative rates of oxygen consumption and water loss in diploid and polyploid salamanders (genus Ambystoma). Comp. Biochem. Physiol. A Physiol. 1990, 97, 569–572. [Google Scholar] [CrossRef]
- Scott, M.A.; Dhillon, R.S.; Schulte, P.M.; Richards, J.G. Physiology and performance of wild and domestic strains of diploid and triploid rainbow trout (Oncorhynchus mykiss) in response to environmental challenges. Can. J. Fish. Aquat. Sci. 2015, 72, 125–134. [Google Scholar] [CrossRef]
- O’Donnell, K.M.; MacRae, K.L.; Verhille, C.E.; Sacobie, C.F.D.; Benfey, T.J. Standard metabolic rate of juvenile triploid brook charr, Salvelinus fontinalis. Aquaculture 2017, 479, 85–90. [Google Scholar] [CrossRef]
- Cavalier-Smith, T. Cell volume and the evolution of eukaryotic genome size. In The Evolution of Genome Size; Cavalier-Smith, T., Ed.; Wiley: Chichester, UK, 1985; pp. 104–184. [Google Scholar]
- Xiong, W.; Zhu, Y.; Zhang, P.; Xu, Y.; Zhou, J.; Zhang, J.; Luo, Y. Effects of temperature on metabolic scaling in silver carp. J. Exp. Zool. A Ecol. Integr. Physiol. 2022, 337, 141–149. [Google Scholar] [CrossRef]
- Malerba, M.E.; Marshall, D.J. Larger cells have relatively smaller nuclei across the Tree of Life. Evol. Lett. 2021, 5, 306–314. [Google Scholar] [CrossRef]
- Glazier, D.S.; Powell, M.G.; Deptola, T.J. Body-size scaling of metabolic rate in the trilobite Eldredgeops rana. Paleobiology 2013, 39, 109–122. [Google Scholar] [CrossRef]
- Starostová, Z.; Konarzewski, M.; Kozłowski, J.; Kratochvíl, L. Ontogeny of metabolic rate and red blood cell size in eyelid geckos: Species follow different paths. PLoS ONE 2013, 8, e64715. [Google Scholar] [CrossRef] [Green Version]
- Johnston, I.A.; Kristjansson, B.K.; Paxton, C.G.; Vieira, V.L.; Macqueen, D.J.; Bell, M.A. Universal scaling rules predict evolutionary patterns of myogenesis in species with indeterminate growth. Proc. R. Soc. B Biol. Sci. 2012, 279, 2255–2261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glazier, D.S.; Butler, E.M.; Lombardi, S.A.; Deptola, T.J.; Reese, A.J.; Satterthwaite, E.V. Ecological effects on metabolic scaling: Amphipod responses to fish predators in freshwater springs. Ecol. Monogr. 2011, 81, 599–618. [Google Scholar] [CrossRef]
- Lv, X.; Xie, H.; Xia, D.; Shen, C.; Li, J.; Luo, Y. Mass scaling of the resting and maximum metabolic rates of the black carp. J. Comp. Physiol. B 2018, 188, 591–598. [Google Scholar] [CrossRef] [PubMed]
- Jackson, G.; O’Dor, R. Time, space and the ecophysiology of squid growth, life in the fast lane. Vie Milieu 2001, 51, 205–215. [Google Scholar]
- Moltschaniwskyj, N.A. Understanding the process of growth in cephalopods. Mar. Freshw. Res. 2004, 55, 379–386. [Google Scholar] [CrossRef]
- Fujita, S.; Kuranaga, E.; Nakajima, Y.I. Cell proliferation controls body size growth, tentacle morphogenesis, and regeneration in hydrozoan jellyfish Cladonema pacificum. PeerJ 2009, 7, e7579. [Google Scholar] [CrossRef] [Green Version]
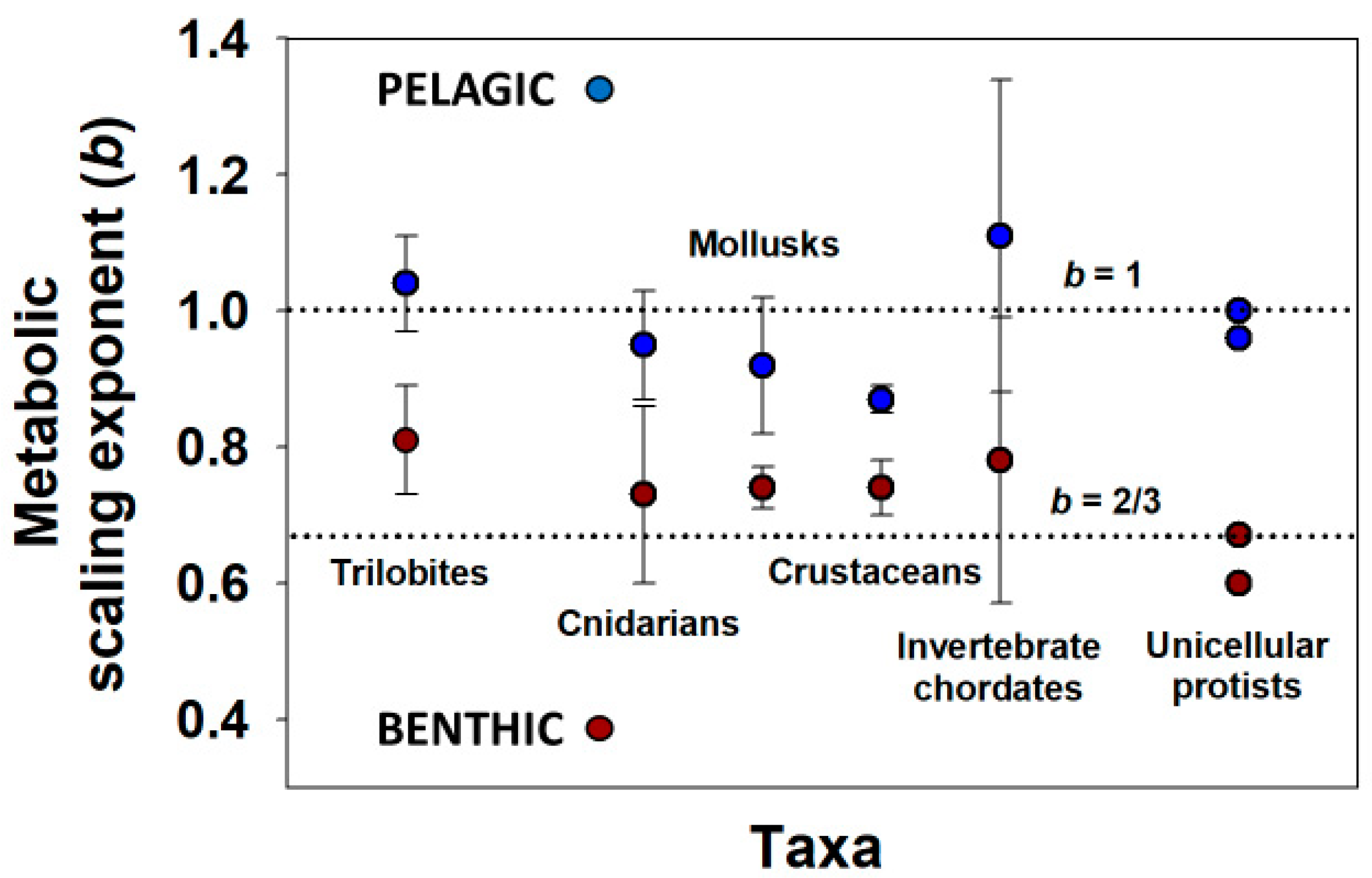
- Glazier, D.S. The 3/4-power law is not universal: Evolution of isometric, ontogenetic metabolic scaling in pelagic animals. BioScience 2006, 56, 325–332. [Google Scholar] [CrossRef] [Green Version]
- O’Farrell, P.H. How metazoans reach their full size: The natural history of bigness. In Cell Growth: Control of Cell Size; Hall, M., Raff, M., Thomas, G., Eds.; Cold Spring Harbor Laboratory Press: New York, NY, USA, 2004; pp. 1–11. [Google Scholar]
- Swire, J.; Fuchs, S.; Bundy, J.G.; Leroi, A.M. The cellular geometry of growth drives the amino acid economy of Caenorhabditis elegans. Proc. R. Soc. B Biol. Sci. 2009, 276, 2747–2754. [Google Scholar] [CrossRef] [Green Version]
- Berrill, N.J. The development of the bud in Botryllus. Biol. Bull. 1941, 80, 169–184. [Google Scholar] [CrossRef]
- Brandon, C.S.; Dudycha, J.L. Ecological constraints on sensory systems: Compound eye size in Daphnia is reduced by resource limitation. J. Comp. Physiol. A 2014, 200, 749–758. [Google Scholar] [CrossRef]
- Glazier, D.S. Separating the respiration rates of embryos and brooding females of Daphnia magna: Implications for the cost of brooding and the allometry of metabolic rate. Limnol. Oceanogr. 1991, 36, 354–361. [Google Scholar] [CrossRef]
- Glazier, D.S.; Calow, P. Energy allocation rules in Daphnia magna: Clonal and age differences in the effects of food limitation. Oecologia 1992, 90, 540–549. [Google Scholar] [CrossRef] [PubMed]
- Keskinen, E.; Takaku, Y.; Meyer-Rochow, V.B.; Hariyama, T. Postembryonic eye growth in the seashore isopod Ligia exotica (Crustacea, Isopoda). Biol. Bull. 2002, 202, 223–231. [Google Scholar] [CrossRef] [PubMed]
- Laybourn, J. Respiratory energy losses in the protozoan predator Didinium nasutum Müller (Ciliophora). Oecologia 1977, 27, 305–309. [Google Scholar] [CrossRef]
- Laybourn, J. Respiratory energy losses in Stentor coeruleus Ehrenberg (Ciliophora). Oecologia 1975, 21, 273–278. [Google Scholar] [CrossRef] [PubMed]
- Giguère, L.A.; Côté, B.; St-Pierre, J.F. Metabolic rates scale isometrically in larval fishes. Mar. Ecol. Progr. Ser. 1988, 50, 13–19. [Google Scholar] [CrossRef]
- Oikawa, S.; Itazawa, Y.; Gotoh, M. Ontogenetic change in the relationship between metabolic rate and body mass in a sea bream Pagrus major (Temminck & Schlegel). J. Fish Biol. 1991, 38, 483–496. [Google Scholar] [CrossRef]
- Kamler, E. Early Life History of Fish: An Energetics Approach; Chapman & Hall: London, UK, 1992. [Google Scholar]
- Radzinskaya, L.I.; Nikol’skaya, I.S.; Alekseeva, T.A.; Vladimirova, I.G.; Kovalenko, P.I.; Ozernyuk, N.D. Changes in the intensity of respiration during ontogenesis of some invertebrates. Russ. J. Dev. Biol. 2003, 34, 317–320. [Google Scholar] [CrossRef]
- Hulbert, A.J.; Else, P.L. Membranes and the setting of energy demand. J. Exp. Biol. 2005, 208, 1593–1599. [Google Scholar] [CrossRef] [Green Version]
- Kutschera, U.; Niklas, K.J. Ontogenetic changes in the scaling of cellular respiration with respect to size among sunflower seedlings. Plant Signal. Behav. 2011, 6, 72–76. [Google Scholar] [CrossRef] [Green Version]
- Rombough, P. The energetics of embryonic growth. Resp. Physiol. Neurobiol. 2011, 178, 22–29. [Google Scholar] [CrossRef] [PubMed]
- Gaitán-Espitia, J.D.; Bruning, A.; Mondaca, F.; Nespolo, R.F. Intraspecific variation in the metabolic scaling exponent in ectotherms: Testing the effect of latitudinal cline, ontogeny and transgenerational change in the land snail Cornu aspersum. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2013, 165, 169–177. [Google Scholar] [CrossRef] [PubMed]
- Matoo, O.B.; Julick, C.R.; Montooth, K.L. Genetic variation for ontogenetic shifts in metabolism underlies physiological homeostasis in Drosophila. Genetics 2019, 212, 537–552. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, T.M. A general biphasic bodyweight model for scaling basal metabolic rate, glomerular filtration rate, and drug clearance from birth to adulthood. AAPS J. 2022, 24, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Tadros, W.; Lipshitz, H.D. The maternal-to-zygotic transition: A play in two acts. Development 2009, 136, 3033–3042. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wesley, C.C.; Mishra, S.; Levy, D.L. Organelle size scaling over embryonic development. Wiley Interdiscip. Rev. Dev. Biol. 2020, 9, e376. [Google Scholar] [CrossRef]
- Vleck, C.M.; Hoyt, D.F.; Vleck, D. Metabolism of avian embryos: Patterns in altricial and precocial birds. Physiol. Zool. 1979, 52, 363–377. [Google Scholar] [CrossRef]
- Riisgård, H.U. No foundation of a ’3/4 power scaling law’ for respiration in biology. Ecol. Lett. 1998, 1, 71–73. [Google Scholar] [CrossRef]
- Killen, S.S.; Costa, I.; Brown, J.A.; Gamperl, A.K. Little left in the tank: Metabolic scaling in marine teleosts and its implications for aerobic scope. Proc. R. Soc. B Biol. Sci. 2007, 274, 431–438. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Niklas, K.J.; Reich, P.B.; Sun, S. Ontogenetic shift in the scaling of dark respiration with whole-plant mass in seven shrub species. Funct. Ecol. 2010, 24, 502–512. [Google Scholar] [CrossRef]
- Callier, V.; Nijhout, H.F. Supply-side constraints are insufficient to explain the ontogenetic scaling of metabolic rate in the tobacco Hornworm, Manduca sexta. PLoS ONE 2012, 7, e45455. [Google Scholar] [CrossRef] [Green Version]
- Glazier, D.S.; Hirst, A.G.; Atkinson, D. Shape shifting predicts ontogenetic changes in metabolic scaling in diverse aquatic invertebrates. Proc. R. Soc. B Biol. Sci. 2015, 282, 20142302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Czarnołęski, M.; Kozłowski, J.; Dumiot, G.; Bonnet, J.C.; Mallard, J.; Dupont-Nivet, M. Scaling of metabolism in Helix aspersa snails: Changes through ontogeny and response to selection for increased size. J. Exp. Biol. 2008, 211, 391–400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glazier, D.S.; Borrelli, J.J.; Hoffman, C.L. Effects of fish predators on the mass-related energetics of a keystone freshwater crustacean. Biology 2020, 9, 40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Norin, T. Growth and mortality as causes of variation in metabolic scaling among taxa and taxonomic levels. Integr. Comp. Biol. 2022, 62, icac038. [Google Scholar] [CrossRef]
- Arendt, J.D. Adaptive intrinsic growth rates: An integration across taxa. Quart. Rev. Biol. 1997, 72, 149–177. [Google Scholar] [CrossRef]
- Arendt, J.D. Allocation of cells to proliferation vs. differentiation and its consequences for growth and development. J. Exp. Zool. 2000, 288, 219–234. [Google Scholar] [CrossRef]
- Higgins, P.J.; Thorpe, J.E. Hyperplasia and hypertrophy in the growth of skeletal muscle in juvenile Atlantic salmon, Salmo salar L. J. Fish Biol. 1990, 37, 505–519. [Google Scholar] [CrossRef]
- Gillaspy, G.; Ben-David, H.; Gruissem, W. Fruits: A developmental perspective. Plant Cell 1993, 5, 1439. [Google Scholar] [CrossRef]
- Alami-Durante, H.; Fauconneau, B.; Rouel, M.; Escaffre, A.M.; Bergot, P. Growth and multiplication of white skeletal muscle fibres in carp larvae in relation to somatic growth rate. J. Fish Biol. 1997, 50, 1285–1302. [Google Scholar] [CrossRef]
- Beemster, G.T.; Baskin, T.I. Analysis of cell division and elongation underlying the developmental acceleration of root growth in Arabidopsis thaliana. Plant Physiol. 1998, 116, 1515–1526. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Galloway, T.F.; Kjorsvik, E.; Kryvi, H. Muscle growth and development in Atlantic cod larvae (Gadus morhua L.), related to different somatic growth rates. J. Exp. Biol. 1999, 202, 2111–2120. [Google Scholar] [CrossRef] [PubMed]
- Harada, T.; Kurahashi, W.; Yanai, M.; Wakasa, Y.; Satoh, T. Involvement of cell proliferation and cell enlargement in increasing the fruit size of Malus species. Sci. Hortic. 2005, 105, 447–456. [Google Scholar] [CrossRef]
- Zhang, C.; Tanabe, K.; Wang, S.; Tamura, F.; Yoshida, A.; Matsumoto, K. The impact of cell division and cell enlargement on the evolution of fruit size in Pyrus pyrifolia. Ann. Bot. 2006, 98, 537–543. [Google Scholar] [CrossRef]
- Johnston, L.A.; Gallant, P. Control of growth and organ size in Drosophila. Bioessays 2002, 24, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Shu, Z.; Row, S.; Deng, W.M. Endoreplication: The good, the bad, and the ugly. Trends Cell Biol. 2018, 28, 465–474. [Google Scholar] [CrossRef] [PubMed]
- Winick, M.; Noble, A. Quantitative changes in DNA, RNA, and protein during prenatal and postnatal growth in the rat. Dev. Biol. 1965, 12, 451–466. [Google Scholar] [CrossRef]
- Goss, R.J. Hypertrophy versus Hyperplasia: How much organs can grow depends on whether their functional units increase in size or in number. Science 1966, 153, 1615–1620. [Google Scholar] [CrossRef]
- Zak, R. Cell proliferation during cardiac growth. Am. J. Cardiol. 1973, 31, 211–219. [Google Scholar] [CrossRef]
- Rozovski, S.J.; Winick, M. Nutrition and cellular growth. In Nutrition: Pre- and Postnatal Development; Winick, M., Ed.; Plenum Press: New York, NY, USA, 1979; Volume 1, pp. 61–101. [Google Scholar]
- Johns, P.R. Growth of fish retinas. Am. Zool. 1981, 21, 447–458. [Google Scholar] [CrossRef] [Green Version]
- Riska, B.; Atchley, W.R.; Rutledge, J.J. A genetic analysis of targeted growth in mice. Genetics 1984, 107, 79–101. [Google Scholar] [CrossRef]
- Weatherley, A.H. Approaches to understanding fish growth. Trans. Am. Fish. Soc. 1990, 119, 662–672. [Google Scholar] [CrossRef]
- Gonzalez, N.; Vanhaeren, H.; Inzé, D. Leaf size control: Complex coordination of cell division and expansion. Trends Plant Sci. 2012, 17, 332–340. [Google Scholar] [CrossRef] [PubMed]
- Fanwoua, J.; de Visser, P.H.; Heuvelink, E.; Yin, X.; Struik, P.C.; Marcelis, L.F. A dynamic model of tomato fruit growth integrating cell division, cell growth and endoreduplication. Funct. Plant Biol. 2013, 40, 1098–1114. [Google Scholar] [CrossRef]
- Takatsuka, H.; Umeda, M. Hormonal control of cell division and elongation along differentiation trajectories in roots. J. Exp. Bot. 2014, 65, 2633–2643. [Google Scholar] [CrossRef] [Green Version]
- Mauxion, J.P.; Chevalier, C.; Gonzalez, N. Complex cellular and molecular events determining fruit size. Trends Plant Sci. 2021, 26, 1023–1038. [Google Scholar] [CrossRef]
- Granier, C.; Tardieu, F. Spatial and temporal analyses of expansion and cell cycle in sunflower leaves: A common pattern of development for all zones of a leaf and different leaves of a plant. Plant Physiol. 1998, 116, 991–1001. [Google Scholar] [CrossRef] [Green Version]
- Winick, M.; Noble, A. Cellular response in rats during malnutrition at various ages. J. Nutr. 1966, 89, 300–306. [Google Scholar] [CrossRef] [PubMed]
- Winick, M.; Noble, A. Cellular response with increased feeding in neonatal rats. J. Nutr. 1967, 91, 179–182. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riska, B.; Atchley, W.R. Genetics of growth predict patterns of brain-size evolution. Science 1985, 229, 668–671. [Google Scholar] [CrossRef]
- Atchley, W.R.; Wei, R.; Crenshaw, P. Cellular consequences in the brain and liver of age-specific selection for rate of development in mice. Genetics 2000, 155, 1347–1357. [Google Scholar] [CrossRef] [PubMed]
- Arendt, J. Ecological correlates of body size in relation to cell size and cell number: Patterns in flies, fish, fruits and foliage. Biol. Rev. 2007, 82, 241–256. [Google Scholar] [CrossRef] [PubMed]
- Sebastes_goodei_larvae_drawing.gif. Available online: https://commons.wikimedia.org/wiki/File:Sebastes_goodei_larvae_drawing.gif (accessed on 19 June 2022).
- Drawing Fish #1416367. Available online: http://clipart-library.com/clipart/piode7j6T.htm (accessed on 19 June 2022).
- Mori, S.; Yamaji, K.; Ishida, A.; Prokushkin, S.G.; Masyagina, O.V.; Hagihara, A.; Hoque, A.R.; Suwa, R.; Osawa, A.; Nishizono, T.; et al. Mixed-power scaling of whole-plant respiration from seedlings to giant trees. Proc. Natl. Acad. Sci. USA 2010, 107, 1447–1451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, D.L.; Li, T.; Zhong, Q.L.; Wang, G.X. Scaling relationship between tree respiration rates and biomass. Biol. Lett. 2010, 6, 715–717. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Ran, J.; Ji, M.; Wang, Z.; Dong, L.; Hu, W.; Deng, Y.; Hou, C.; Niklas, K.J.; Deng, J. Water content quantitatively affects metabolic rates over the course of plant ontogeny. New Phytol. 2020, 228, 1524–1534. [Google Scholar] [CrossRef] [PubMed]
- Ye, X.; Lu, L.; Jiang, M.; Jia, J.; Li, W.; Wu, H.; Liao, Y.; Li, J. Metabolic scaling: Individual versus intraspecific scaling of Nile tilapia (Oreochromis niloticus). J. Comp. Physiol. B 2021, 191, 721–729. [Google Scholar] [CrossRef]
- Calder, W.A. Size, Function and Life History; Harvard University Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Muchlinski, M.N.; Snodgrass, J.J.; Terranova, C.J. Muscle mass scaling in primates: An energetic and ecological perspective. Am. J. Primatol. 2012, 74, 395–407. [Google Scholar] [CrossRef]
- Stickland, N. Growth and development of muscle fibres in the rainbow trout (Salmo gairdneri). J. Anat. 1983, 137, 323–333. [Google Scholar] [PubMed]
- Owens, F.N.; Dubeski, P.; Hanson, C.F. Factors that alter the growth and development of ruminants. J. Anim. Sci. 1993, 71, 3138–3150. [Google Scholar] [CrossRef]
- Rehfeldt, C.; Fiedler, I.; Stickland, N.C. Number and size of muscle fibres in relation to meat production. In Muscle Development of Livestock Animals: Physiology, Genetics, and Meat Quality; Te Pas, M.F.W., Everts, M.E., Haagsman, H.P., Eds.; CABI Publishing: Wallingford, UK, 2004; pp. 1–37. [Google Scholar]
- White, R.B.; Biérinx, A.S.; Gnocchi, V.F.; Zammit, P.S. Dynamics of muscle fibre growth during postnatal mouse development. BMC Dev. Biol. 2010, 10, 21. [Google Scholar] [CrossRef] [Green Version]
- Chal, J.; Pourquié, O. Making muscle: Skeletal myogenesis in vivo and in vitro. Development 2017, 144, 2104–2122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnston, I.A. Muscle development and growth: Potential implications for flesh quality in fish. Aquaculture 1999, 177, 99–115. [Google Scholar] [CrossRef]
- Biga, P.R.; Goetz, F.W. Zebrafish and giant danio as models for muscle growth: Determinate vs. indeterminate growth as determined by morphometric analysis. Am. J. Physiol. Reg. Integr. Comp. Physiol. 2006, 291, R1327–R1337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Figueiredo, V.C. Revisiting the roles of protein synthesis during skeletal muscle hypertrophy induced by exercise. Am. J. Physiol. Reg., Integr. Comp. Physiol. 2019, 317, R709–R718. [Google Scholar] [CrossRef] [PubMed]
- Dingboom, E.G.; Weijs, W.A. The effect of growth and exercise on muscle characteristics in relation to meat quality. In Muscle Development of Livestock Animals: Physiology, Genetics and Meat Quality; te Pas, M.F.W., Everts, M.E., Haagsman, H.P., Eds.; CABI Publishing: Wallingford, UK, 2004; pp. 83–102. [Google Scholar]
- Huo, W.; Weng, K.; Gu, T.; Zhang, Y.; Zhang, Y.; Chen, G.; Xu, Q. Effect of muscle fiber characteristics on meat quality in fast-and slow-growing ducks. Poult. Sci. 2021, 100, 101264. [Google Scholar] [CrossRef]
- Cieri, R.L.; Dick, T.J.; Morris, J.S.; Clemente, C.J. Scaling of fibre area and fibre glycogen concentration in the hindlimb musculature of monitor lizards: Implications for locomotor performance with increasing body size. J. Exp. Biol. 2022, 225 (Suppl. 1), jeb243380. [Google Scholar] [CrossRef]
- Krebs, C.J.; Singleton, G.R. Indexes of condition for small mammals. Aust. J. Zool. 1993, 41, 317–323. [Google Scholar] [CrossRef] [Green Version]
- Everaert, N.; Decuypere, E.; Buyse, J. Adipose tissue and lipid metabolism. In Sturkie’s Avian Physiology, 7th ed.; Scanes, C.G., Dridi, S., Eds.; Academic Press: San Diego, CA, USA, 2022; pp. 627–640. [Google Scholar] [CrossRef]
- Hirsch, J.; Han, P.W. Cellularity of rat adipose tissue: Effects of growth, starvation, and obesity. J. Lipid Res. 1969, 10, 77–82. [Google Scholar] [CrossRef]
- Dipali, S.S.; Ferreira, C.R.; Zhou, L.T.; Pritchard, M.T.; Duncan, F.E. Histologic analysis and lipid profiling reveal reproductive age-associated changes in peri-ovarian adipose tissue. Reprod. Biol. Endocrinol. 2019, 17, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Cartenì, F.; Deslauriers, A.; Rossi, S.; Morin, H.; De Micco, V.; Mazzoleni, S.; Giannino, F. The physiological mechanisms behind the earlywood-to-latewood transition: A process-based modeling approach. Front. Plant Sci. 2018, 9, 1053. [Google Scholar] [CrossRef]
- Glazier, D.S. Effects of metabolic level on the body size scaling of metabolic rate in birds and mammals. Proc. R. Soc. B Biol. Sci. 2008, 275, 1405–1410. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glazier, D.S. Metabolic level and size scaling of rates of respiration and growth in unicellular organisms. Funct. Ecol. 2009, 23, 963–968. [Google Scholar] [CrossRef]
- Glazier, D.S. Ontogenetic body-mass scaling of resting metabolic rate covaries with species-specific metabolic level and body size in spiders and snakes. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2009, 153, 403–407. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Effects of contingency versus constraints on the body-mass scaling of metabolic rate. Challenges 2018, 9, 4. [Google Scholar] [CrossRef] [Green Version]
- Glazier, D.S. Activity alters how temperature influences intraspecific metabolic scaling: Testing the metabolic-level boundaries hypothesis. J. Comp. Physiol. B 2020, 190, 445–454. [Google Scholar] [CrossRef]
- Gavrilov, V.M.; Golubeva, T.B.; Bushuev, A.V. Evolution of metabolic scaling among the tetrapod: Effect of phylogeny, the geologic time of class formation, and uniformity of species within a class. Integr. Zool. 2021, 17. [Google Scholar] [CrossRef]
- Dao, M.H. Reassessment of the cell surface area limitation to nutrient uptake in phytoplankton. Mar. Ecol. Prog. Ser. 2013, 489, 87–92. [Google Scholar] [CrossRef] [Green Version]
- Makarieva, A.M.; Gorshkov, V.G.; Li, B.L.; Chown, S.L.; Reich, P.B.; Gavrilov, V.M. Mean mass-specific metabolic rates are strikingly similar across life’s major domains: Evidence for life’s metabolic optimum. Proc. Natl. Acad. Sci. USA 2008, 105, 16994–16999. [Google Scholar] [CrossRef] [Green Version]
- DeLong, J.P.; Okie, J.G.; Moses, M.E.; Sibly, R.M.; Brown, J.H. Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc. Natl. Acad. Sci. USA 2010, 107, 12941–12945. [Google Scholar] [CrossRef] [Green Version]
- Phillipson, J. Bioenergetic Options and Phylogeny. In Physiological Ecology: An Evolutionary Approach to Resource Use; Townsend, C.R., Calow, P., Eds.; Sinauer Associates: Sunderland, MA, USA, 1981; pp. 20–45. [Google Scholar]
- Else, P.L.; Hulbert, A.J. Mammals: An allometric study of metabolism at tissue and mitochondrial level. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1985, 248, R415–R421. [Google Scholar] [CrossRef] [PubMed]
- Porter, R.K. Allometry of mammalian cellular oxygen consumption. Cell. Mol. Life Sci. 2001, 58, 815–822. [Google Scholar] [CrossRef] [PubMed]
- Weibel, E.R.; Hoppeler, H. Exercise-induced maximal metabolic rate scales with muscle aerobic capacity. J. Exp. Biol. 2005, 208, 1635–1644. [Google Scholar] [CrossRef] [Green Version]
- Snelling, E.P.; Seymour, R.S.; Runciman, S.; Matthews, P.G.; White, C.R. Symmorphosis and the insect respiratory system: Allometric variation. J. Exp. Biol. 2011, 214, 3225–3237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weibel, E.R.; Bacigalupe, L.D.; Schmitt, B.; Hoppeler, H. Allometric scaling of maximal metabolic rate in mammals: Muscle aerobic capacity as determinant factor. Resp. Physiol. Neurobiol. 2004, 140, 115–132. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Activity affects intraspecific body-size scaling of metabolic rate in ectothermic animals. J. Comp. Physiol. B 2009, 179, 821–828. [Google Scholar] [CrossRef]
- Obroucheva, N.V. Cell elongation as an inseparable component of growth in terrestrial plants. Russ. J. Dev. Biol. 2008, 39, 13–24. [Google Scholar] [CrossRef]
- Milligan, L.P.; McBride, B. Energy costs of ion pumping by animal tissues. J. Nutr. 1985, 115, 1374–1382. [Google Scholar] [CrossRef]
- Rolfe, D.F.; Brown, G.C. Cellular energy utilization and molecular origin of standard metabolic rate in mammals. Physiol. Rev. 1997, 77, 731–758. [Google Scholar] [CrossRef] [Green Version]
- Jimenez, A.G.; Dillaman, R.M.; Kinsey, S.T. Large fibre size in skeletal muscle is metabolically advantageous. Nat. Comm. 2013, 4, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Jimenez, A.G.; Williams, J.B. Differences in muscle fiber size and associated energetic costs in phylogenetically paired tropical and temperate birds. Physiol. Biochem. Zool. 2014, 87, 752–761. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H. The origin of allometric scaling laws in biology from genomes to ecosystems: Towards a quantitative unifying theory of biological structure and organization. J. Exp. Biol. 2005, 208, 1575–1592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niklas, K.J.; Kutschera, U. Kleiber’s law: How the fire of life ignited debate, fueled theory, and neglected plants as model organisms. Plant Signal. Behav. 2015, 10, e1036216. [Google Scholar] [CrossRef] [PubMed]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Banavar, J.R.; Moses, M.E.; Brown, J.H.; Damuth, J.; Rinaldo, A.; Sibly, R.M.; Maritan, A. A general basis for quarter-power scaling in animals. Proc. Natl. Acad. Sci. USA 2010, 107, 15816–15820. [Google Scholar] [CrossRef] [Green Version]
- Hirst, A.G.; Glazier, D.S.; Atkinson, D. Body shape shifting during growth permits tests that distinguish between competing geometric theories of metabolic scaling. Ecol. Lett. 2014, 17, 1274–1281. [Google Scholar] [CrossRef] [Green Version]
- Tan, H.; Hirst, A.G.; Glazier, D.S.; Atkinson, D. Ecological pressures and the contrasting scaling of metabolism and body shape in coexisting taxa: Cephalopods versus teleost fish. Philos. Trans. R. Soc. B 2019, 374, 20180543. [Google Scholar] [CrossRef]
- Sánchez-González, J.R.; Niciez, A.G. Declining metabolic scaling parallels an ontogenetic change from elongate to deep-bodied shapes in juvenile Brown trout. Curr. Zool. 2022, 68, zoac042. [Google Scholar] [CrossRef]
- Forlenza, A.; Galbraith, H.S.; Blakeslee, C.J.; Glazier, D.S. Ontogenetic changes in body shape and scaling of metabolic rate in the American eel (Anguilla rostrata). Physiol. Biochem. Zool. 2022, 95. [Google Scholar] [CrossRef]
- Brodribb, T.J.; Jordan, G.J.; Carpenter, R.J. Unified changes in cell size permit coordinated leaf evolution. New Phytol. 2013, 199, 559–570. [Google Scholar] [CrossRef]
- John, G.P.; Scoffoni, C.; Sack, L. Allometry of cells and tissues within leaves. Am. J. Bot. 2013, 100, 1936–1948. [Google Scholar] [CrossRef] [Green Version]
- Savage, V.M.; Allen, A.P.; Brown, J.H.; Gillooly, J.F.; Herman, A.B.; Woodruff, W.H.; West, G.B. Scaling of number, size, and metabolic rate of cells with body size in mammals. Proc. Natl. Acad. Sci. USA 2007, 104, 4718–4723. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Darveau, C.-A.; Suarez, R.K.; Andrews, R.D.; Hochachka, P.W. Allometric cascade as a unifying principle of body mass effects on metabolism. Nature 2002, 417, 166–170. [Google Scholar] [CrossRef] [PubMed]
- Suarez, R.K.; Darveau, C.-A. Multi-level regulation and metabolic scaling. J. Exp. Biol. 2005, 208, 1627–1634. [Google Scholar] [CrossRef] [Green Version]
- Glazier, D.S. Resource supply and demand both affect metabolic scaling: A response to Harrison. Trends Ecol. Evol. 2018, 33, 237–238. [Google Scholar] [CrossRef]
- Plant-Cell-cl-lula-Animal-Biology-Cells-Transparent-Background-png-Clipart. Available online: https://png.is/f/plant-cell-cl-lula-animal-biology-cells-transparent-background-png-clipart/comhiclipartbipqm-201909141105.html (accessed on 19 June 2022).
- Glazier, D.S.; Gring, J.P.; Holsopple, J.R.; Gjoni, V. Temperature effects on metabolic scaling of a keystone freshwater crustacean depend on fish-predation regime. J. Exp. Biol. 2020, 223, jeb232322. [Google Scholar] [CrossRef] [PubMed]
- Gjoni, V.; Basset, A.; Glazier, D.S. Temperature and predator cues interactively affect ontogenetic metabolic scaling of aquatic amphipods. Biol. Lett. 2020, 16, 20200267. [Google Scholar] [CrossRef]
- Bennett, M.D.; Leitch, I.J. Genome size evolution in plants. In The Evolution of the Genome; Gregory, T.R., Ed.; Elsevier Academic Press: Burlington, MA, USA, 2005; pp. 89–162. [Google Scholar]
- Chan, Y.H.M.; Marshall, W.F. Scaling properties of cell and organelle size. Organogenesis 2010, 6, 88–96. [Google Scholar] [CrossRef] [Green Version]
- Levy, D.L.; Heald, R. Mechanisms of intracellular scaling. Annu. Revi. Cell Dev. Biol. 2012, 28, 113–135. [Google Scholar] [CrossRef] [Green Version]
- Reber, S.; Goehring, N.W. Intracellular scaling mechanisms. Cold Spring Harb. Perspect. Biol. 2015, 7, a019067. [Google Scholar] [CrossRef] [Green Version]
- Miettinen, T.P.; Björklund, M. Mitochondrial function and cell size: An allometric relationship. Trends Cell Biol. 2017, 27, 393–402. [Google Scholar] [CrossRef]
- Heald, R.; Gibeaux, R. Subcellular scaling: Does size matter for cell division? Curr. Opin. Cell Biol. 2018, 52, 88–95. [Google Scholar] [CrossRef] [PubMed]
- Marshall, W.F. Scaling of subcellular structures. Annu. Rev. Cell Dev. Biol. 2020, 36, 219. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Levy, D.L. Regulation of organelle size and organization during development. Semin. Cell Dev. Biol. 2022. [Google Scholar] [CrossRef]
- Kooijman, S.A.L.M. Dynamic Energy and Mass Budgets in Biological Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Maino, J.L.; Kearney, M.R.; Nisbet, R.M.; Kooijman, S.A. Reconciling theories for metabolic scaling. J. Anim. Ecol. 2014, 83, 20–29. [Google Scholar] [CrossRef] [Green Version]
- von Bertalanffy, L.; Pirozynski, W.J. Tissue respiration, growth, and basal metabolism. Biol. Bull. 1953, 105, 240–256. [Google Scholar] [CrossRef]
- Kleiber, M. The Fire of Life; Wiley: New York, NY, USA, 1961. [Google Scholar]
- Chaui-Berlinck, J.G.; Navas, C.A.; Monteiro, L.H.A.; Bicudo, J.E.P.W. Control of metabolic rate is a hidden variable in the allometric scaling of homeotherms. J. Exp. Biol. 2005, 208, 1709–1716. [Google Scholar] [CrossRef] [Green Version]
- Hill, D.J.; Han, V.K.M. Control of cellular multiplication and differentiation. In Fetal Growth; Sharp, F., Fraser, R.B., Milner, R.D.G., Eds.; Springer: London, UK, 1989; pp. 83–98. [Google Scholar]
- Neufeld, T.P.; De La Cruz, A.F.A.; Johnston, L.A.; Edgar, B.A. Coordination of growth and cell division in the Drosophila wing. Cell 1998, 93, 1183–1193. [Google Scholar] [CrossRef] [Green Version]
- Conlon, I.; Raff, M. Size control in animal development. Cell 1999, 96, 235–244. [Google Scholar] [CrossRef] [Green Version]
- Mizukami, Y.; Fischer, R.L. Plant organ size control: AINTEGUMENTA regulates growth and cell numbers during organogenesis. Proc. Natl. Acad. Sci. USA 2000, 97, 942–947. [Google Scholar] [CrossRef] [Green Version]
- Álvarez, B.; Moreno, S. Fission yeast Tor2 promotes cell growth and represses cell differentiation. J. Cell Sci. 2006, 119, 4475–4485. [Google Scholar] [CrossRef] [Green Version]
- Horvath, B.M.; Magyar, Z.; Zhang, Y.; Hamburger, A.W.; Bako, L.; Visser, R.G.; Bachem, C.W.; Bögre, L. EBP1 regulates organ size through cell growth and proliferation in plants. EMBO J. 2006, 25, 4909–4920. [Google Scholar] [CrossRef] [PubMed]
- Breuer, C.; Ishida, T.; Sugimoto, K. Developmental control of endocycles and cell growth in plants. Curr. Opin. Plant Biol. 2010, 13, 654–660. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Thompson, C.B. Metabolic regulation of cell growth and proliferation. Nat. Rev. Mol. Cell Biol. 2019, 20, 436–450. [Google Scholar] [CrossRef] [PubMed]
- Ricklefs, R.E.; Shea, R.E.; Choi, I.H. Inverse relationship between functional maturity and exponential growth rate of avian skeletal muscle: A constraint on evolutionary response. Evolution 1994, 48, 1080–1088. [Google Scholar] [CrossRef] [PubMed]
- Mueller, C.A.; Augustine, S.; Kooijman, S.A.; Kearney, M.R.; Seymour, R.S. The trade-off between maturation and growth during accelerated development in frogs. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2012, 163, 95–102. [Google Scholar] [CrossRef]
- Drummond-Barbosa, D.; Spradling, A.C. Stem cells and their progeny respond to nutritional changes during Drosophila oogenesis. Dev. Biol. 2001, 231, 265–278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Post, J.R.; Lee, J.A. Metabolic ontogeny of teleost fishes. Can. J. Fish. Aquat. Sci. 1996, 53, 910–923. [Google Scholar] [CrossRef]
- Glazier, D.S. Biological scaling analyses are more than statistical line fitting. J. Exp. Biol. 2021, 224, jeb241059. [Google Scholar] [CrossRef]
- Rubin, H. Cell aging in vivo and in vitro. Mech. Ageing Dev. 1997, 98, 1–35. [Google Scholar] [CrossRef]
- Yang, J.; Dungrawala, H.; Hua, H.; Manukyan, A.; Abraham, L.; Lane, W.; Mead, H.; Wright, J.; Schneider, B.L. Cell size and growth rate are major determinants of replicative lifespan. Cell Cycle 2011, 10, 144–155. [Google Scholar] [CrossRef] [Green Version]
- Patra, K.C.; Bardeesy, N. A cell size theory of aging. Dev. Cell 2018, 45, 665–666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zadrag-Tecza, R.; Kwolek-Mirek, M.; Alabrudzińska, M.; Skoneczna, A. Cell size influences the reproductive potential and total lifespan of the Saccharomyces cerevisiae yeast as revealed by the analysis of polyploid strains. Oxid. Med. Cell. Longev. 2018, 2018, 1898421. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neurohr, G.E.; Terry, R.L.; Lengefeld, J.; Bonney, M.; Brittingham, G.P.; Moretto, F.; Miettinen, T.P.; Vaites, L.P.; Soares, L.M.; Paulo, J.A.; et al. Excessive cell growth causes cytoplasm dilution and contributes to senescence. Cell 2019, 176, 1083–1097. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Cuyper, C.; Vanfleteren, J.R. Oxygen consumption during development and aging of the nematode Caenorhabditis elegans. Comp. Biochem. Physiol. A Physiol. 1982, 73, 283–289. [Google Scholar] [CrossRef]
- Sutcliffe, D.W. Quantitative aspects of oxygen uptake by Gammarus (Crustacea, Amphipoda): A critical review. Freshw. Biol. 1984, 14, 443–489. [Google Scholar] [CrossRef]
- Poehlman, E.T.; Goran, M.I.; Gardner, A.W.; Ades, P.A.; Arciero, P.J.; Katzman-Rooks, S.M.; Montgomery, S.M.; Toth, M.J.; Sutherland, P.T. Determinants of decline in resting metabolic rate in aging females. Am. J. Physiol. Endocrinol. Metab. 1993, 264, E450–E455. [Google Scholar] [CrossRef]
- Piers, L.S.; Soares, M.J.; McCormack, L.M.; O’Dea, K. Is there evidence for an age-related reduction in metabolic rate? J. Appl. Physiol. 1998, 85, 2196–2204. [Google Scholar] [CrossRef]
- Sukhotin, A.A.; Abele, D.; Pörtner, H.O. Growth, metabolism and lipid peroxidation in Mytilus edulis: Age and size effects. Mar. Ecol. Prog. Ser. 2002, 226, 223–234. [Google Scholar] [CrossRef]



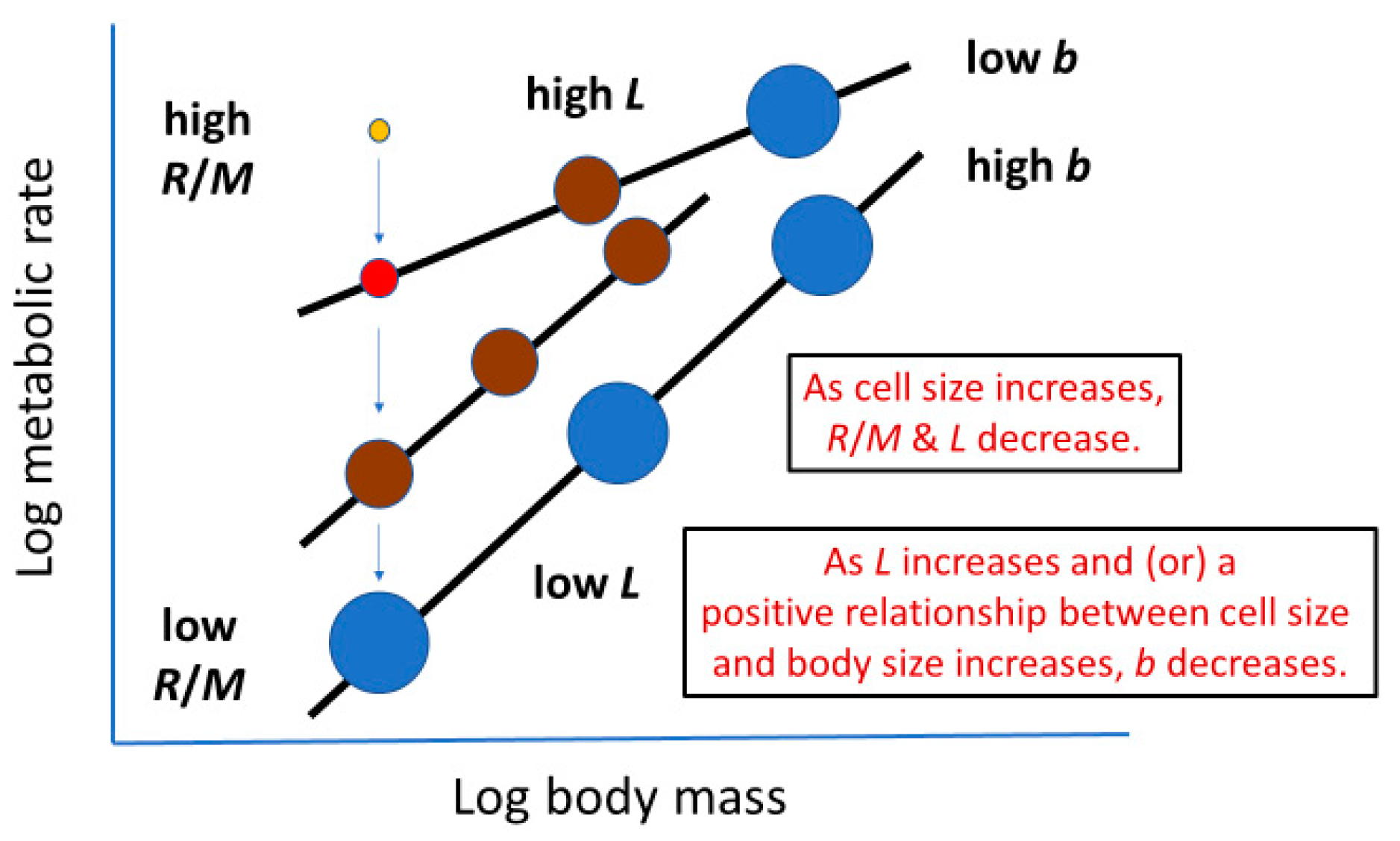
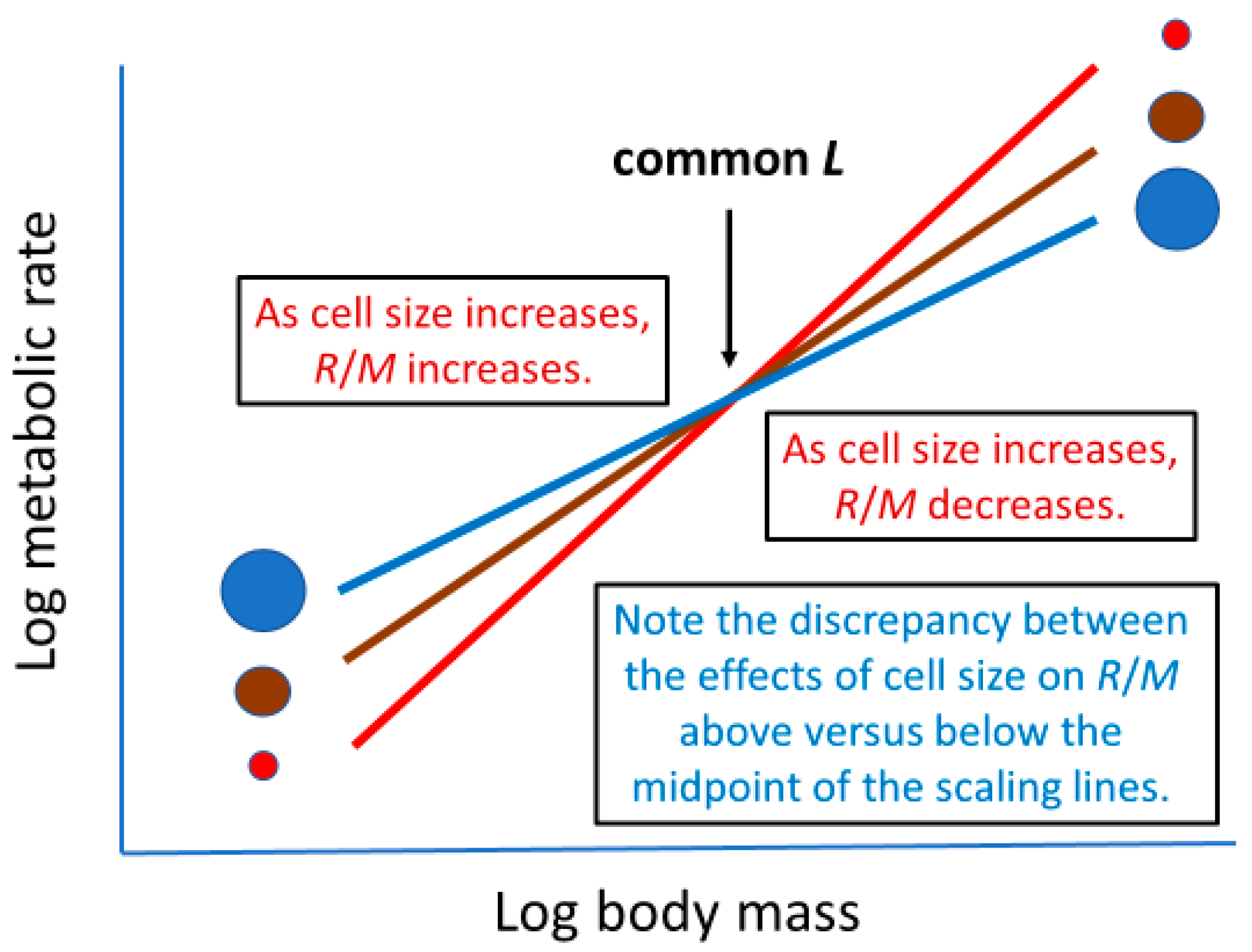
| Metabolic Effect | Possible Mode of Effect | Sources |
|---|---|---|
| Mass-specific or mass-corrected metabolic rate | Cellular SA/V geometry 1,2 | [22,23,25,26,27,28] |
| Metabolic level (L) of body-mass scaling relationship 3 | Cellular SA/V geometry 2 | [29] [present study] |
| Metabolic scaling slope (b) | Cellular mode of growth and/or changes in cell composition | [23,24,27] [present study] |
| Total cellular SA of body | [21,36] | |
| Relative influences of cellular and organismal SA vs. organismal V, as mediated by metabolic level (L) | [29,36] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glazier, D.S. How Metabolic Rate Relates to Cell Size. Biology 2022, 11, 1106. https://doi.org/10.3390/biology11081106
Glazier DS. How Metabolic Rate Relates to Cell Size. Biology. 2022; 11(8):1106. https://doi.org/10.3390/biology11081106
Chicago/Turabian StyleGlazier, Douglas S. 2022. "How Metabolic Rate Relates to Cell Size" Biology 11, no. 8: 1106. https://doi.org/10.3390/biology11081106
APA StyleGlazier, D. S. (2022). How Metabolic Rate Relates to Cell Size. Biology, 11(8), 1106. https://doi.org/10.3390/biology11081106