Cancer and Chaos and the Complex Network Model of a Multicellular Organism
Abstract
:Simple Summary
Abstract
1. Introduction
1.1. The Aims
1.2. Structure of This Article
1.3. Meanings of the Word “Chaos”
1.4. Deterministic Chaos
- Networks describing living entities are not fully random, especially in the stability aspect. This aspect is connected to notions chaos and order, because the stability is an effect of natural selection, which leaves more stable entities.
- Negative feedbacks have been incorrectly taken into account in the statistical study of their effects on post-disturbance stability, but they are commonly considered the basis of the homeostasis of living objects. Their proportion should be much greater than random [34,35]. In Kauffman’s model, this surplus over randomness does not have the most important property: it cannot go beyond the range of correct operations, but this is the main reason for the loss of stability after a random disturbance.
- Using two-valued signals, as is in Boolean networks, is too extreme of a simplification that has a significant impact on statistical conclusions, and we should consider signals beyond two-valued signals.
1.5. Main Feature of Half-Chaos
2. Free Cell without Meiosis as a Half-Chaotic System
2.1. Basic Simplifying Assumptions
2.2. Evolutionary Stability of the Half-Chaos
2.3. Regulation
2.4. Source of Variation
2.5. In-Ice-Modularity
2.6. Chaos in Term “Genome Chaos” as “Deterministic Chaos” in Module
2.7. Summary of the Description of a Free Single Cell
3. Half-Chaos in Modeling a Multicellular Animal Organism
3.1. Basic Components of the Model
3.2. Two Parts of an Individual’s Ontogenesis
3.3. The Soma Cell
3.4. Mechanisms of Loss of Control of “Correctness”
4. Model Basics and Half-Chaos Support
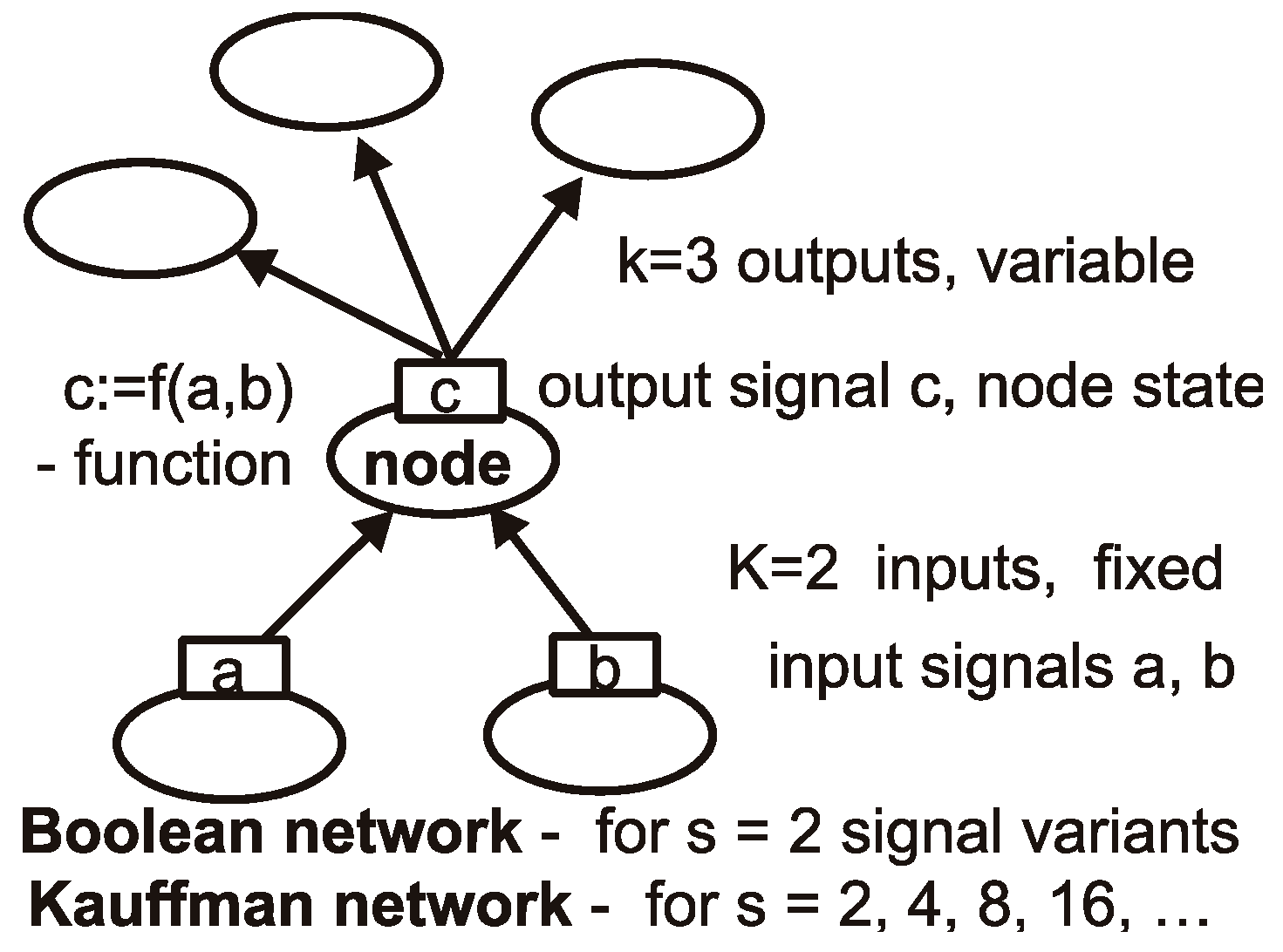
4.1. Description of Networks
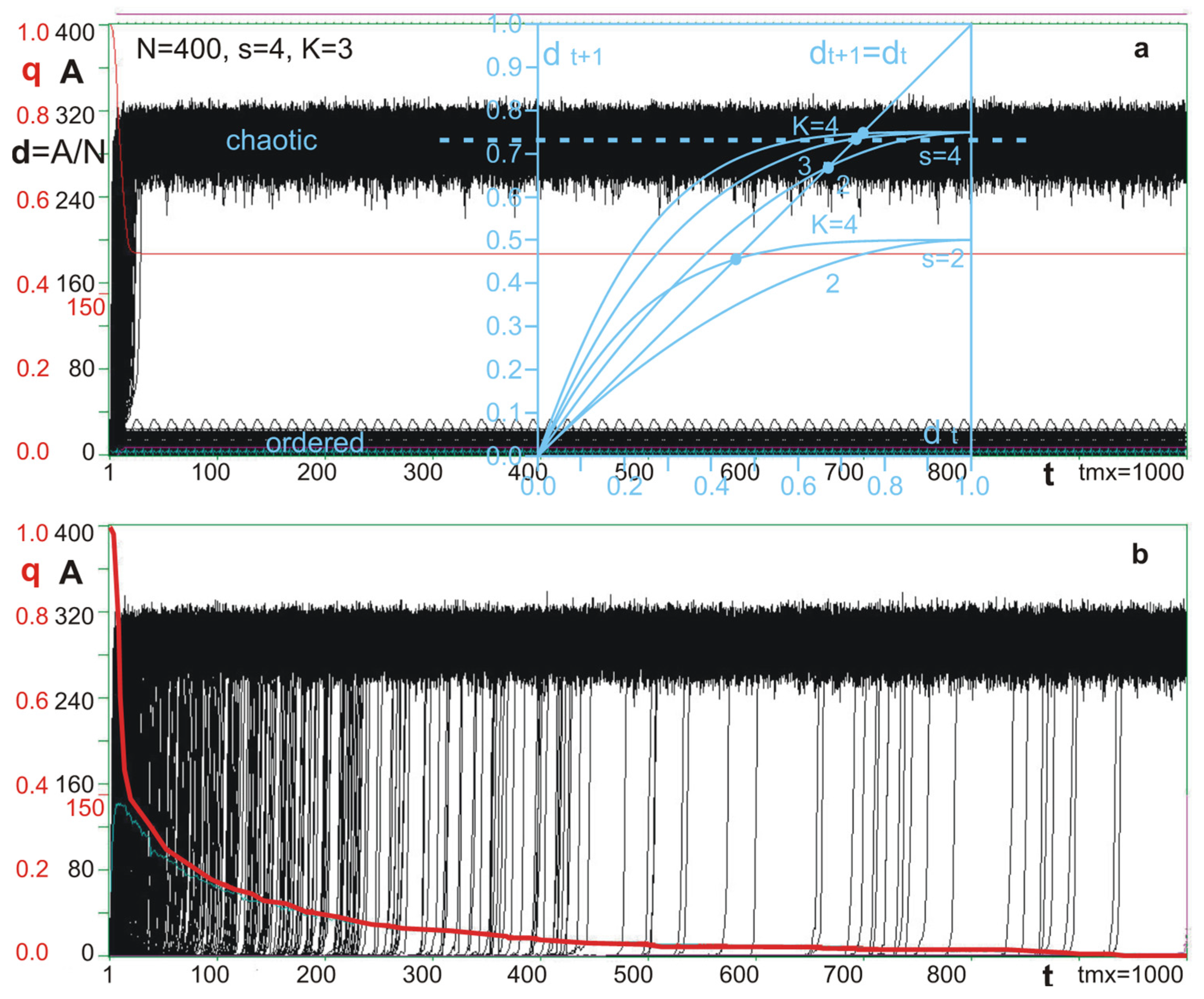
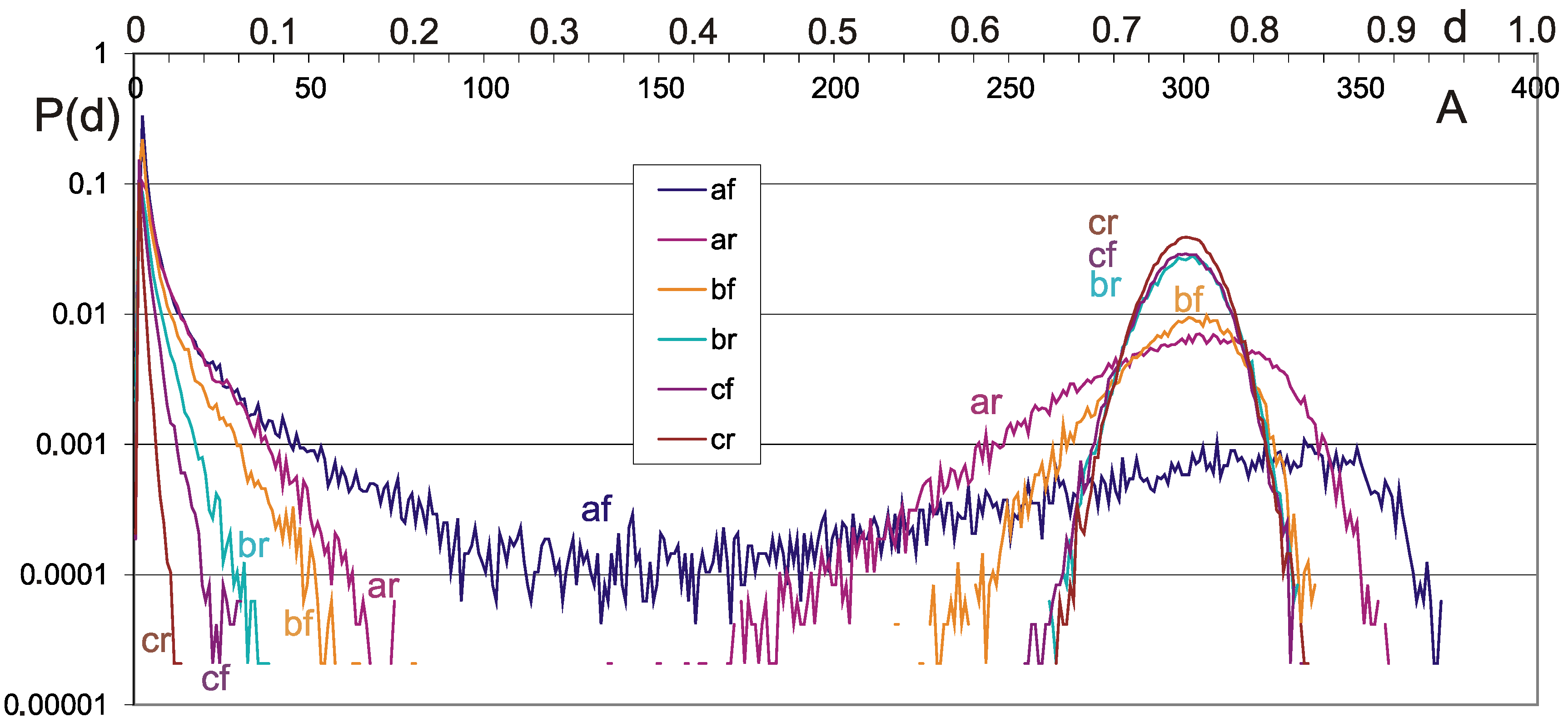
4.2. Damage Propagation
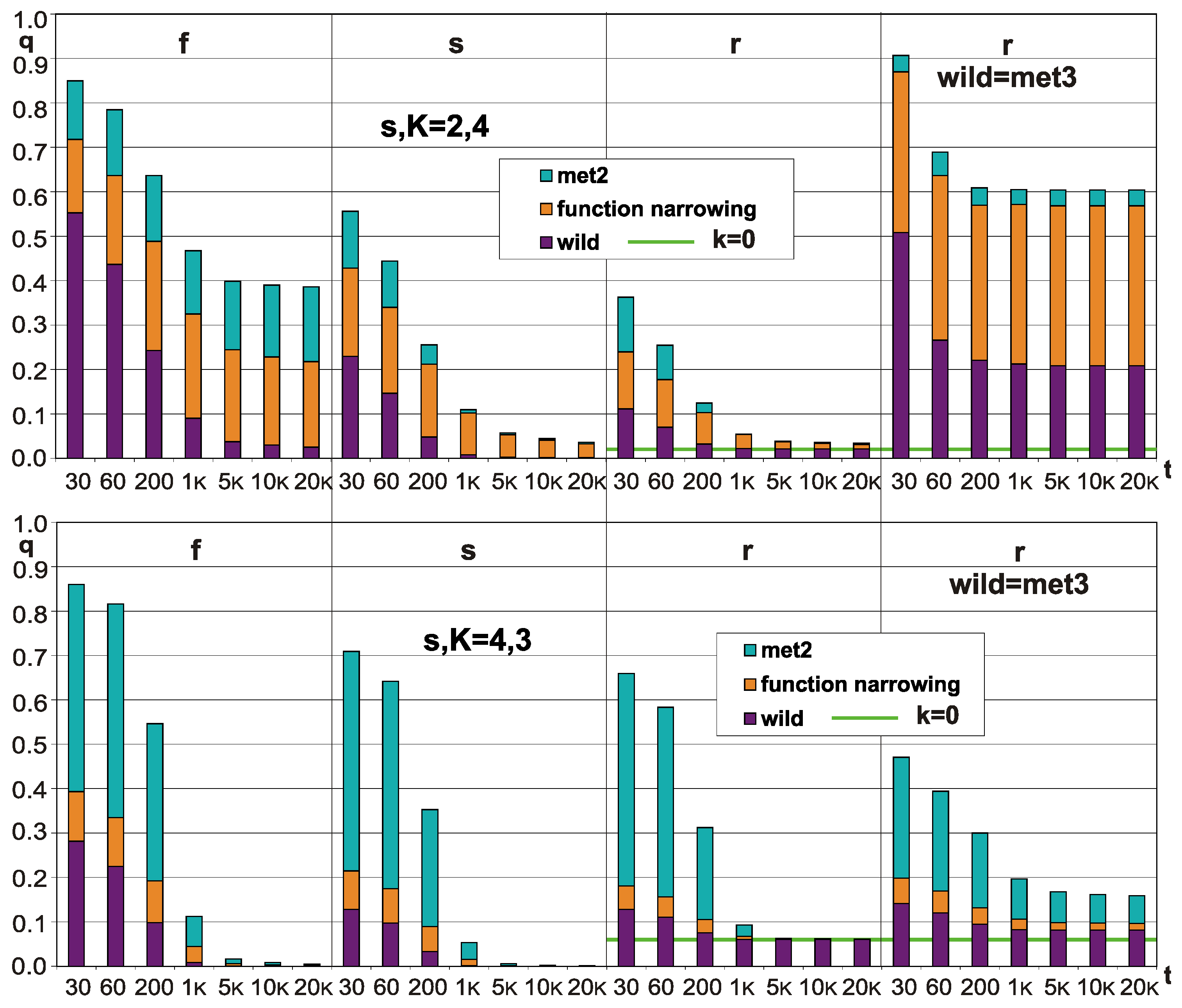
4.3. Negative Feedbacks
4.4. Modularity
4.5. Function Narrowing
5. Summary of Model Circumstances of Cancer Cell Formation
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tez, M. Cancer is an adaptation mechanism of the aged stem cell against stress. Rejuvenation Res. 2008, 11, 1059–1060. [Google Scholar] [CrossRef]
- Gecow, A. Life Is Not on the Edge of Chaos but in a Half-Chaos of Not Fully Random Systems. Definition and Simulations of the Half-Chaos in Complex Networks. In A Collection of Papers on Chaos Theory and Its Applications; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Gecow, A.; Iantovics, L.B. Semi-Adaptive Evolution with Spontaneous Modularity of Half-Chaotic Randomly Growing Autonomous and Open Networks. Symmetry 2022, 14, 92. [Google Scholar] [CrossRef]
- Erdős, P.; Rényi, A. On the evolution of random graphs. In The Structure and Dynamics of Networks; Princeton University Press: Princeton, NJ, USA, 1960; pp. 17–61. [Google Scholar]
- Barabási, A.-L.; Albert, R.; Jeong, H. Mean-field theory for scale-free random networks. Phys. A 1999, 272, 173–187. [Google Scholar] [CrossRef]
- Kauffman, S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 1969, 22, 437–467. [Google Scholar] [CrossRef]
- Kauffman, S.A. Boolean systems, adaptive automata, evolution. In Discovered Systems and Biological Organization; Series F: Computer and System Sciences; Bienenstock, E., Fogelman-Soulie, F., Weisbuch, G., Eds.; Springer: New York, NY, USA, 1986; Volume 20. [Google Scholar]
- Kauffman, S.A. Requirements for Evolvability in Complex Systems—Orderly Dynamics and Frozen Components. Physica D 1990, 42, 135–152. [Google Scholar] [CrossRef]
- Kauffman, S.A. The Origins of Order: Self-Organization and Selection in Evolution; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Liu, G.; Stevens, J.; Horne, S.; Abdallah, B.; Ye, K.; Bremer, S.; Ye, C.; Chen, D.J.; Heng, H. Genome chaos: Survival strategy during crisis. Cell Cycle 2014, 13, 528–537. [Google Scholar] [CrossRef]
- Tez, M. Genome’s Chaotic Behavior for Adaptation may explain Carcinogenesis! Suggestion from Surgical Oncologist. J. Cancer Biol. Res. 2014, 2, 1047. [Google Scholar]
- Tez, S.; Tez, M. Cancer is The Chaotic Search for Adaptation to Previously Unknown Environments. Theor. Biol. Forum 2016, 109, 149–154. [Google Scholar]
- Shapiro, J.A. How Chaotic Is Genome Chaos? Cancers 2021, 13, 1358. [Google Scholar] [CrossRef]
- Li, C.; Wendlandt, E.B.; Darbro, B.; Xu, H.; Thomas, G.S.; Tricot, G.; Chen, F.; Shaughnessy, J.D.; Zhan, F. Genetic Analysis of Multiple Myeloma Identifies Cytogenetic Alterations Implicated in Disease Complexity and Progression. Cancers 2021, 13, 517. [Google Scholar] [CrossRef]
- Russo, G.; Tramontano, A.; Iodice, I.; Chiariotti, L.; Pezone, A. Epigenome Chaos: Stochastic and Deterministic DNA Methylation Events Drive Cancer Evolution. Cancers 2021, 13, 1800. [Google Scholar] [CrossRef]
- Heng, H.H. Karyotypic Chaos, A Form of Non- Clonal Chromosome Aberrations, Plays A Key Role For Cancer Progression and Drug Resistance. FASEB: Nuclear Structure and Cancer; Vermont Academy: Saxtons River, VT, USA, 2007. [Google Scholar]
- Duesberg, P. Chromosomal chaos and cancer. Sci. Am. 2007, 296, 52–59. [Google Scholar] [CrossRef] [PubMed]
- Wright, B.E.; Longacre, A.; Reimers, J.M. Hypermutation in derepressed operons of Escherichia coli K12. Proc. Natl. Acad. Sci. USA 1999, 96, 5089–5094. [Google Scholar] [CrossRef]
- Wright, B.E. A biochemical mechanism for nonrandom mutations and evolution. J. Bacteriol. 2000, 182, 2993–3001. [Google Scholar] [CrossRef]
- Kussell, E.; Leibler, S. Phenotypic diversity, population growth, and information in fluctuating environments. Science 2005, 309, 2075–2078. [Google Scholar] [CrossRef]
- Suzuki, Y.; Lu, M.; Ben-Jacob, E.; Onuchic, J.N. Periodic, quasi-periodic and chaotic dynamics in simple gene elements with time delays. Sci. Rep. 2016, 6, 21037. [Google Scholar] [CrossRef]
- Gecow, A. Emergence of Matured Chaos During Network Growth, Place for Adaptive Evolution and More of Equally Probable Signal Variants as an Alternative to Bias p. In Chaotic Systems; Tlelo-Cuautle, E., Ed.; IntechOpen: London, UK, 2011; pp. 280–310. [Google Scholar] [CrossRef]
- Gecow, A. Life Evolves in Experimentally Confirmed ‘Half-Chaos’ of Not Fully Random Networks, but Not ‘on the Edge of Chaos’. In Proceedings of the CHAOS 2020 Proceedings, Florence, Italy, 9–12 June 2020; ISAST: Oakland, CA, USA, 2020; pp. 259–270. Available online: http://www.cmsim.org/images/CHAOS2020-Proceedings-A-Gr-1-316.pdf (accessed on 6 April 2022).
- Zayed, J.M.; Nouvel, N.; Rauwald, U.; Scherman, O.A. Chemical Complexity—Supramolecular self-assembly of synthetic and biological building blocks in water. Chem. Soc. Rev. 2010, 39, 2806–2816. [Google Scholar] [CrossRef]
- Iantovics, L.B.; Enăchescu, C.; Filip, F.G. (Eds.) Complexity in Artificial and Natural Systems; “Petru Maior” University Publishing House: Târgu Mureș, Romania, 2008; ISBN 978-973-7794-76-5. [Google Scholar]
- Iantovics, L.B.; Radoiu, D.; Marusteri, M.; Dehmer, M. (Eds.) Special Issue on Complexity in Sciences and Artificial Intelligence, BRAIN; Asociatia LUMEN: Monroe, LA, USA, 2010; ISSN 2067-3957. [Google Scholar]
- Iantovics, L.B.; Hluchý, L.; Kountchev, R. (Eds.) Special Issue on Understanding Complex Systems; Acta Universitatis Apulensis: Alba Iulia, Romania, 2011; ISSN 1582-5329. [Google Scholar]
- Gecow, A. Emergence of Growth, Complexity Threshold and Structural Tendencies during Adaptive Evolution of System; Springer: Berlin/Heidelberg, Germany, 2007; Dresden, EPNACS’2007. [Google Scholar]
- Gecow, A. Structural Tendencies—Effects of adaptive evolution of complex (chaotic) systems. Int. J. Mod. Phys. C 2008, 19, 647–664. [Google Scholar] [CrossRef]
- Gecow, A. A certain complexity threshold during growth of functioning networks. In Proceedings of the 2008 First International Conference on Complexity and Intelligence of the Artificial and Natural Complex Systems, Tirgu Mures, Romania, 8–10 November 2008; pp. 69–76. [Google Scholar]
- Gecow, A. Complexity Threshold for Functioning Directed Networks in Damage Size Distribution. arXiv 2010, arXiv:1004.3795. [Google Scholar]
- Iantovics, L.B. Agent-Based Medical Diagnosis Systems. Comput. Inform. 2008, 27, 593–625. [Google Scholar]
- Iantovics, L.B.; Rotar, C.; Niazi, M.A. MetrIntPair-A Novel Accurate Metric for the Comparison of Two Cooperative Multiagent Systems Intelligence Based on Paired Intelligence Measurements. Int. J. Intell. Syst. 2018, 33, 463–486. [Google Scholar] [CrossRef]
- Korzeniewski, B. Cybernetic formulation of the definition of life. J. Theor. Biol. 2001, 209, 275. [Google Scholar] [CrossRef] [PubMed]
- Korzeniewski, B. Confrontation of the cybernetic definition of living individual with the real word. Acta Biotheor. 2005, 53, 1–28. [Google Scholar] [CrossRef] [PubMed]
- Aldana, M.; Coppersmith, S.; Kadanoff, L.P. Boolean Dynamics with Random Couplings. In Perspectives and Problems in Nonlinear Science; Kaplan, E., Marsden, J.E., Sreenivasan, K.R., Eds.; Applied Mathematical Sciences Series; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Turnbull, L.; Hütt, M.T.; Ioannides, A.A.; Kininmonth, S.; Poeppl, R.; Tockner, K.; Bracken, L.J.; Keesstra, S.; Liu, L.; Masselink, R.; et al. Connectivity and complex systems: Learning from a multi-disciplinary perspective. Appl. Netw. Sci. 2018, 3, 11. [Google Scholar] [CrossRef]
- Hughes, T.R.; Marton, M.J.; Jones, A.R.; Roberts, C.J.; Stoughton, R.; Armour, C.D.; Bennett, H.A.; Coffey, E.; Dai, H.; He, Y.D. Functional discovery via a compendium of expression profiles. Cell 2000, 102, 109–126. [Google Scholar] [CrossRef]
- Rämö, P.; Kesseli, J.; Yli-Harja, O. Perturbation avalanches and criticality in gene regulatory networks. J. Theor. Biol. 2006, 242, 164–170. [Google Scholar] [CrossRef]
- Serra, R.; Villani, M.; Semeria, A. Genetic network models and statistical properties of gene expression data in knock-out experiments. J. Theor. Biol. 2004, 227, 149–157. [Google Scholar] [CrossRef]
- Serra, R.; Villani, M.; Graudenzi, A.; Kauffman, S.A. Why a simple model of genetic regulatory networks describes the distribution of avalanches in gene expression data. J. Theor. Biol. 2007, 246, 449–460. [Google Scholar] [CrossRef]
- Wagner, A. Estimating coarse gene network structure from large-scale gene perturbation data. Genome Res. 2002, 12, 309–315. [Google Scholar] [CrossRef]
- Shmulevich, I.; Kauffman, S.A.; Aldana, M. Eukaryotic cells are dynamically ordered or critical but not chaotic. Proc. Natl. Acad. Sci. USA 2005, 102, 13439–13444. [Google Scholar] [CrossRef]
- Gecow, A. ‘Covering’—A Specific but Important Form of Adaptive Changes. OSF Preprints, 2022; in press. [Google Scholar] [CrossRef]
- Derrida, B.; Pomeau, Y. Random Networks of Automata: A Simple Annealed Approximation. Europhys. Lett. 1986, 1, 45–49. [Google Scholar] [CrossRef]
- Derrida, B.; Weisbuch, G. Evolution of Overlaps Between Configurations in Random Boolean Networks. J. Phys. 1986, 47, 1297–1303. [Google Scholar] [CrossRef]
- Gecow, A. Report of Simulation Investigations, a Base of Statement That Life Evolves in the Half-Chaos. Available online: http://vixra.org/abs/1603.0220 (accessed on 6 April 2022).
- Gecow, A. Report of Simulation Investigations, Part II, a Growth of Half-Chaotic Autonomous Networks. Available online: http://viXra.org/abs/1711.0467 (accessed on 6 April 2022).
- Gecow, A.; Nowostawski, M. Modelling Damage Propagation in Complex Networks: Life Exists in Half-Chaos. In Complex Networks XII. CompleNet-Live 2021; Teixeira, A.S., Pacheco, D., Oliveira, M., Barbosa, H., Gonçalves, B., Menezes, R., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Gecow, A. A cybernetic model of improving and its application to the evolution and ontogenesis description. In Proceedings of the Fifth International Congress of Biomathematics, Paris, France, 11–13 September 1975. [Google Scholar]
- Gecow, A. From a “Fossil” Problem of Recapitulation Existence to Computer Simulation and Answer. in: Special issue on Biologically Inspired Computing and Computers in Biology of the journal Neural Network World 3/2005. Inst. Comput. Sci. Acad. Sci. Czech Rep. S. 2005, 15, 189–201. Available online: http://www.nnw.cz/obsahy05.html#3-2005 (accessed on 6 April 2022).
- Gecow, A. Emergence of Chaos and Complexity During System Growth. In From System Complexity to Emergent Properties; Understanding Complex Systems Series; Aziz-Alaoui, M.A., Bertelle, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 115–154. [Google Scholar]
- Gecow, A. Emergence of Growth and Structural Tendencies During Adaptive Evolution of System. In From System Complexity to Emergent Properties; Understanding Complex Systems Series; Aziz-Alaoui, M.A., Bertelle, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 211–241. [Google Scholar]
- Gecow, A.; Hoffman, A. Self-improvement in a complex cybernetic system and its implication for biology. Acta Biotheor. 1983, 32, 61–71. [Google Scholar] [CrossRef]
- Gecow, A.; Nowostawski, M.; Purvis, M.K. Structural tendencies in complex systems development and their implication for software systems. J. Univers. Comput. Sci. 2005, 11, 327–356. [Google Scholar]
- Gecow, A. More Than Two Equally Probable Variants of Signal in Kauffman Networks as an Important Overlooked Case, Negative Feedbacks Allow Life in the Chaos. arXiv 2010, arXiv:1003.1988. [Google Scholar]
- Gecow, A. Informacja Dziedziczna i jej Kanały (II Odcinek Szkicu Dedukcyjnej Teorii Życia); Filozofia i Nauka, Studia filozoficzne i interdyscyplinarne. Instytut Filozofii i Socjologii PAN 2014; Volume 2, pp. 351–380. Available online: http://filozofiainauka.ifispan.waw.pl/wp-content/uploads/2014/08/Gecow_351-380.pdf (accessed on 6 April 2022).
- Sjewiercow, A.N. Morfologiczne Prawidłowości Ewolucji; PWN Warszawa: Moskwa, Russia, 1956. [Google Scholar]
- Gecow, A. The purposeful information. On the difference between natural and artificial life. Dialogue Univers. 2008, 18, 191–206. [Google Scholar] [CrossRef]
- Gecow, A. The differences between natural and artificial life Towards a definition of life. arXiv 2010, arXiv:1012.2889. [Google Scholar]
- Kauffman, S.A. At Home in the Universe; Oxford University Press: New York, NY, USA, 1996. [Google Scholar]
- Jablonka, E.; Lamb, M.J. Epigenetic Inheritance and Evolution: The Lamarckian Dimension; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Jablonka, E.; Lamb, M.J.; Avital, E. Lamarckian’ mechanisms in Darwinian evolution. TREE 1998, 13, 206–210. [Google Scholar] [CrossRef]
- Jablonka, E.; Lamb, M.J. Evolution in Four Dimensions: Genetic, Epigenetic, Behavioral, and Symbolic Variation in the History of Life; (Revised Edition at 2014); MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Gissis, S.B. Transformations of Lamarckism: From Subtle Fluids to Molecular Biology. In The Vienna Series in Theoretical Biology; Jablonka, E., Ed.; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Uller, T.; Moczek, A.P.; Watson, R.A.; Brakefield, P.M.; Laland, K.N. Developmental bias and evolution: A regulatory network perspective. Genetics 2018, 209, 949–966. [Google Scholar] [CrossRef] [PubMed]
- Moczek, A.P. Developmental Bias in Evolution Special Issue of ‘Evolution & Development’. Evol. Dev. 2020, 22. [Google Scholar] [CrossRef]
- Gecow, A. Lamarck with Jablonka Force Shift to Extended Evolutionary Synthesis, Better at Once to Draft of Deductive Theory Philosophy of the Living Nature; IFiS PAN: Warsaw, Poland, 2015. [Google Scholar]
- Gecow, A. Lamarckian Mechanisms as Developmental Bias and Their Darwinian Base—Descriptive Versus Explanatory Biology (Full Version); OSF Preprints: Charlottesville, VA, USA, 2020. [Google Scholar] [CrossRef]
- Gecow, A. Why is the Term ′Developmental Bias′ Misleading? (Full Version); OSF Preprints: Charlottesville, VA, USA, 2020. [Google Scholar] [CrossRef]
- Tez, S.; Tez, M. Chaotic Adaptation Theory (CAT) for cancer: A Lamarckian view. Theor. Biol. Forum 2018, 111, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Heng, J.; Heng, H.H. Genome Chaos, Information Creation, and Cancer Emergence: Searching for New Frameworks on the 50th Anniversary of the “War on Cancer”. Genes 2021, 13, 101. [Google Scholar] [CrossRef] [PubMed]
- Nowostawski, M.; Epiney, L.; Purvis, M. Self-adaptation and dynamic environment experiments with evolvable virtual machines. Int. Workshop Eng. Self-Organising Appl. 2005, 3910, 46–60. [Google Scholar]
- Nowostawski, M. Artificial Evolution and the EVM Architecture. New Chall. Comput. Collect. Intell. 2009, 244, 231–242. [Google Scholar]
- Nowostawski, M.; Purvis, M. Evolution and Hypercomputing in Global Distributed Evolvable Virtual Machines Environment. Int. Workshop Eng. Self-Organising Appl. 2006, 4335, 176–191. [Google Scholar]
- Nowostawski, M.; Gecow, A. Identity Criterion for Living Objects Based on the Entanglement Measure; ICCCI 2011 (Studies in Computational Intelligence). In Semantic Methods for Knowledge Management and Communication; Katarzyniak, R., Chiu, T.-F., Hong, C.-F., Nguyen, N.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 381, pp. 159–170. [Google Scholar]
- Hanel, R.; Pöchacker, M.; Schölling, M.; Thurner, S. A Self-Organized Model for Cell-Differentiation Based on Variations of Molecular Decay Rates. PLoS ONE 2012, 7, e36679. [Google Scholar] [CrossRef]
- Villani, M.; La Rocca, L.; Kauffman, S.A.; Serra, R. Dynamical Criticality in Gene Regulatory Networks. Complexity 2018, 2018, 5980636. [Google Scholar] [CrossRef]
- Tez, M. Complex system perspective in colorectal carcinogenesis. Theor. Biol. Forum 2011, 104, 17–20. [Google Scholar]
- Albert, R.; Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Altenberg, L. Modularity in Evolution: Some Low-Level Questions. In Modularity: Understanding the Development and Evolution of Natural Complex Systems; The Vienna Series in Theoretical Biology; Callebaut, W., Rasskin-Gutman, D., Eds.; MIT Press: Cambridge, MA, USA, 2005; pp. 99–128. [Google Scholar]
- Kauffman, S.A.; Peterson, C.; Samuelsson, B.; Troein, C. Genetic networks with canalyzing Boolean rules are always stable. Proc. Natl. Acad. Sci. USA 2004, 101, 17102–17107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gecow, A.; Iantovics, L.B.; Tez, M. Cancer and Chaos and the Complex Network Model of a Multicellular Organism. Biology 2022, 11, 1317. https://doi.org/10.3390/biology11091317
Gecow A, Iantovics LB, Tez M. Cancer and Chaos and the Complex Network Model of a Multicellular Organism. Biology. 2022; 11(9):1317. https://doi.org/10.3390/biology11091317
Chicago/Turabian StyleGecow, Andrzej, Laszlo Barna Iantovics, and Mesut Tez. 2022. "Cancer and Chaos and the Complex Network Model of a Multicellular Organism" Biology 11, no. 9: 1317. https://doi.org/10.3390/biology11091317






