Synergy Management of a Complex Industrial Production System from the Perspective of Flow Structure
Abstract
1. Introduction
2. Literature Review
2.1. System Synergetics
2.2. System Flow Perspective
2.3. Complex Industrial Management
2.4. Commentary
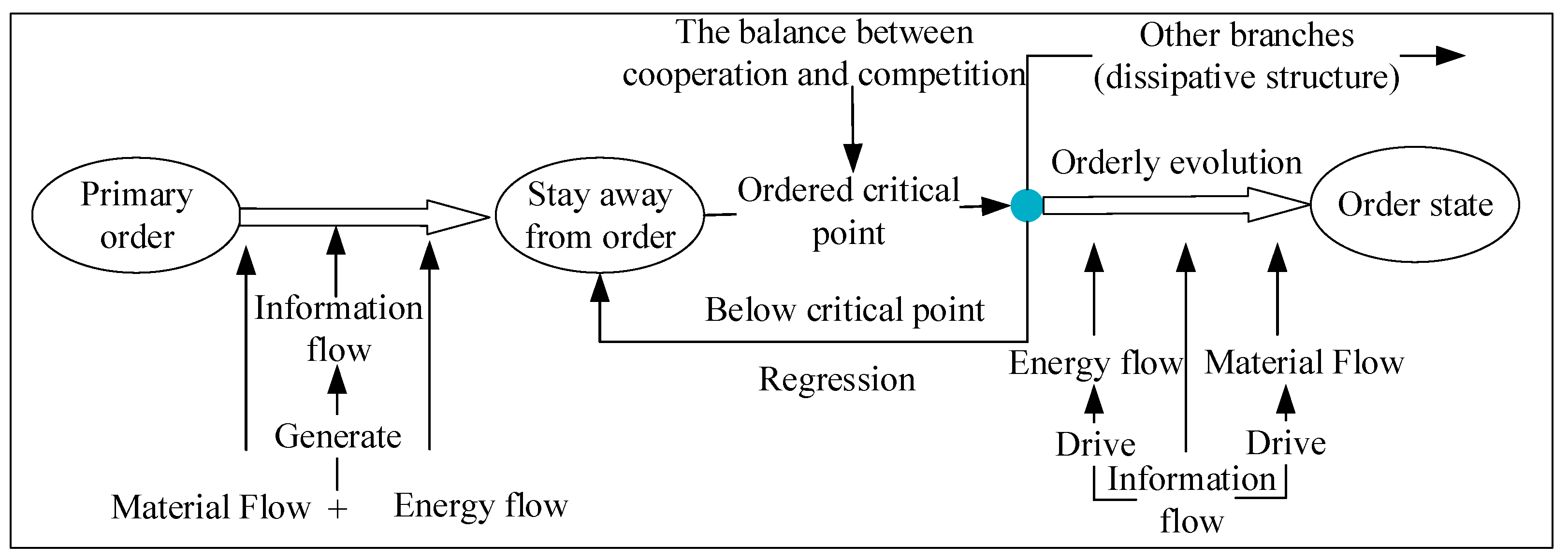
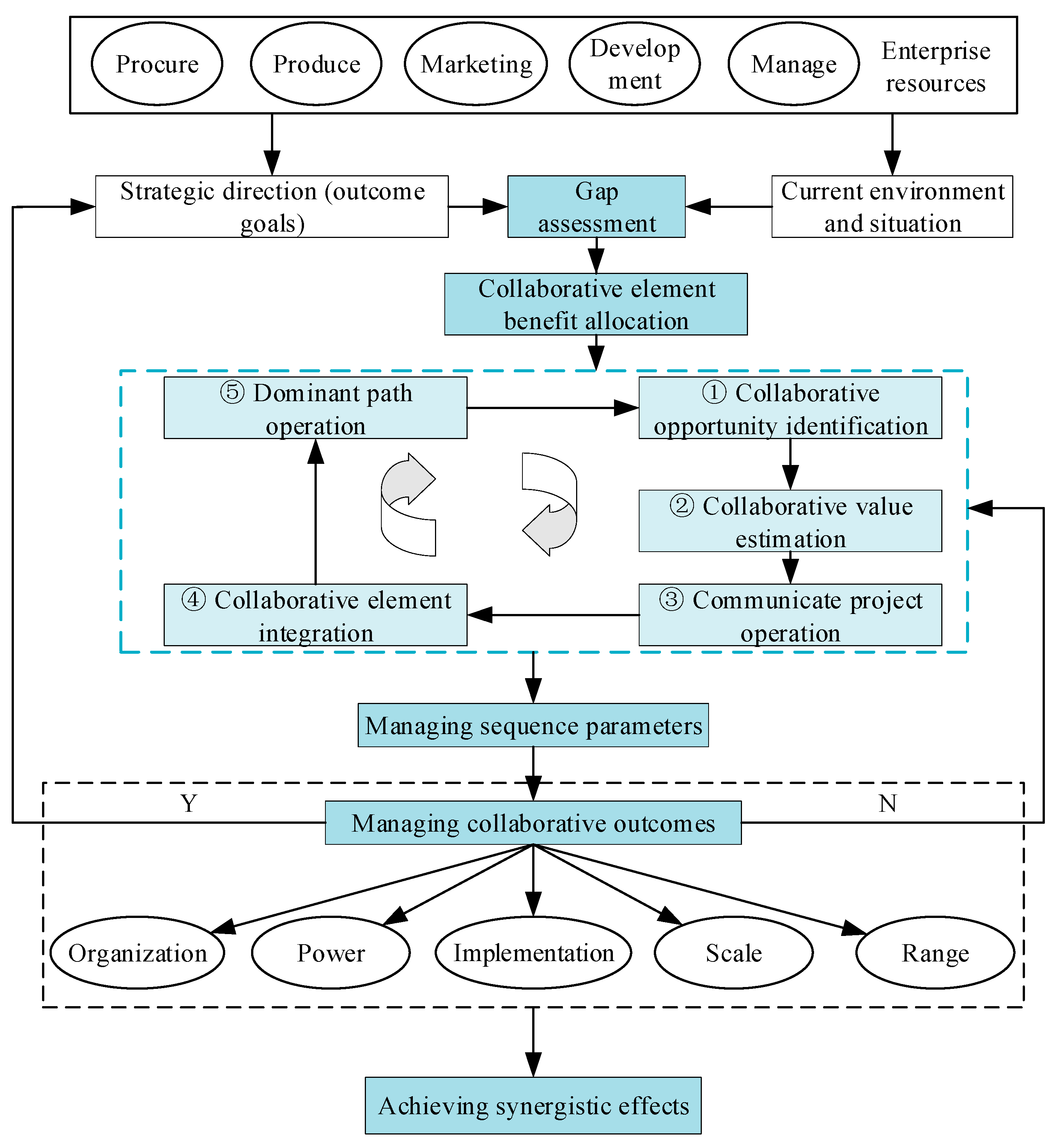
3. Construction of Flow Structure Collaborative Model for Complex Industrial Production Systems
3.1. Preparation of Flow Structure Modeling for Complex Industrial Production Systems
3.1.1. Analysis and Modeling Assumptions of Complex Industrial Production Systems
3.1.2. Determination of Order Parameters
3.2. Collaborative Evaluation Model Based on Order Parameters
3.2.1. Collaborative Evaluation Considering the Taylor Index
3.2.2. Collaborative Analysis Considering Gray Correlation
3.3. Dynamically Based Collaborative Evolution Model
3.3.1. Explanation of Coevolutionary Variables
3.3.2. Equations for the Generation Period of Collaborative Evolution
3.3.3. Equations for the Stagnant Period of Collaborative Evolution
3.3.4. Equations in the Mature Stage of Collaborative Evolution
3.4. Collaborative Disturbance Recognition Based on SOM Algorithm
4. Empirical Study on Collaborative Model of Production System Flow Structure
4.1. Overview of Empirical Case SG Enterprises
4.2. Evaluation of Collaboration Degree of Production System
4.2.1. Calculation of Collaboration Degree of SG Enterprise Production System
4.2.2. Analysis of Gray Collaborative Relationship between Subsystems
4.3. Evaluation of Collaboration Degree of SG Enterprise Production System
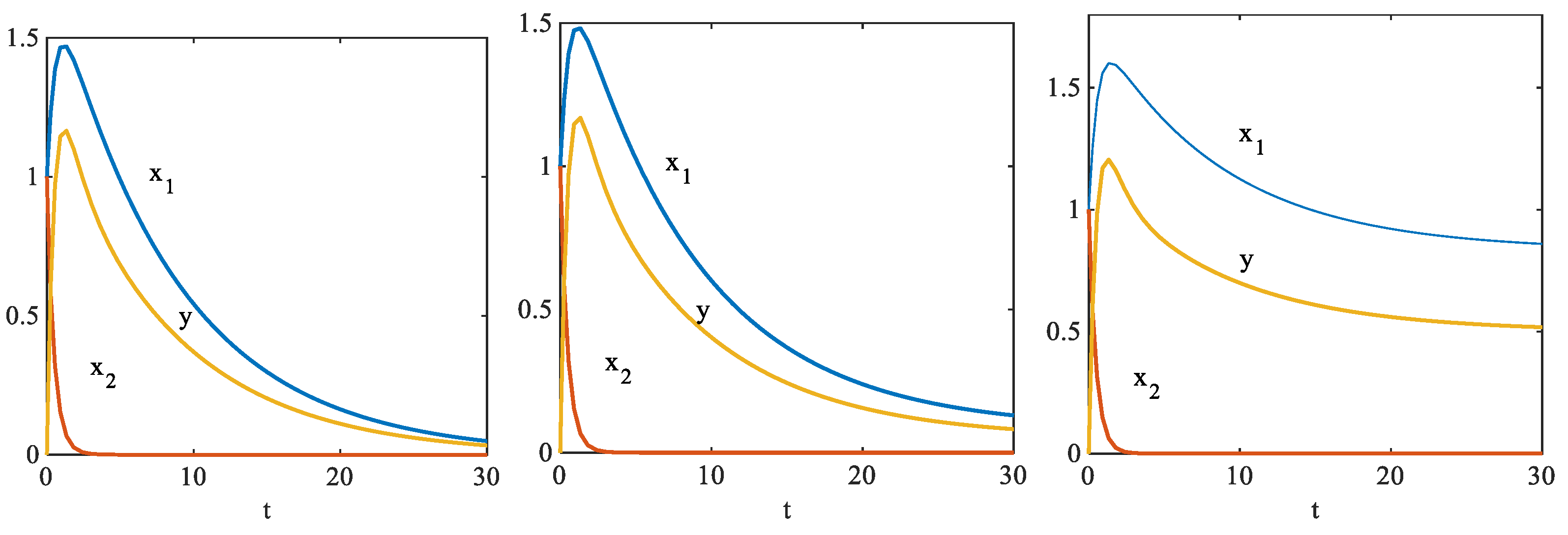
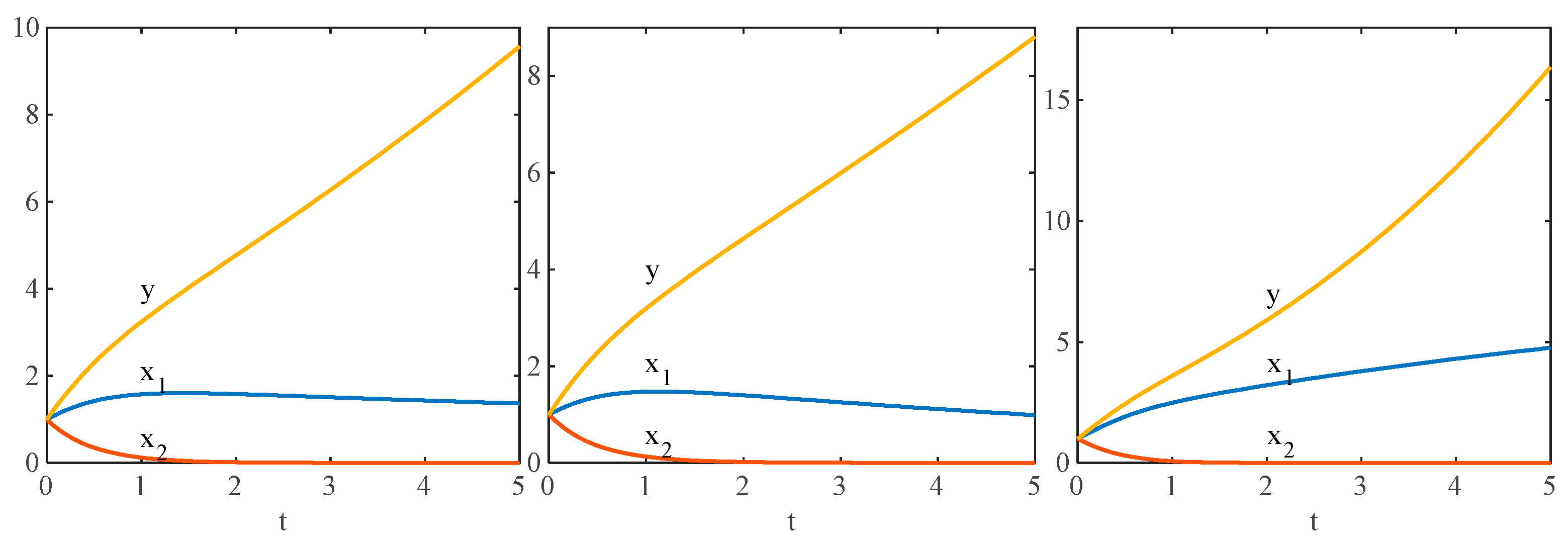
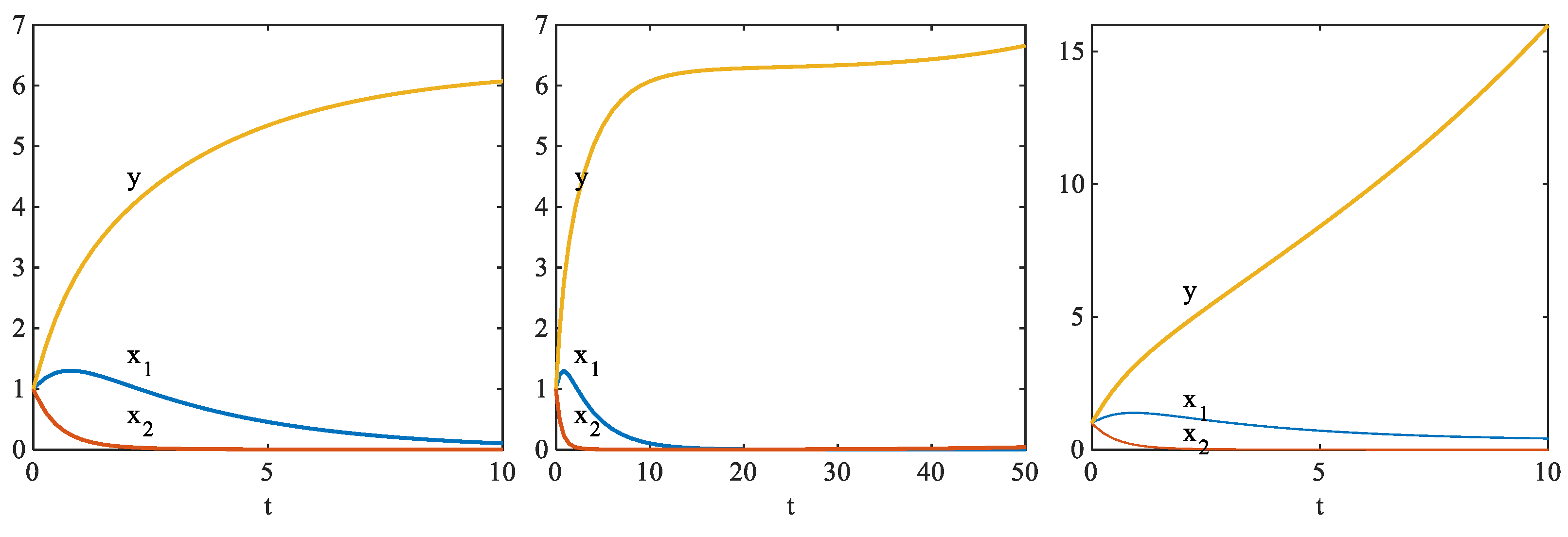
4.3.1. Collaborative Evolution Numerical Simulation
4.3.2. Analysis of Evolutionary Simulation Results
4.4. Demonstration of SOM Algorithm in SG Enterprise Production System
4.5. SG Enterprise Production System Collaboration Management Response
4.5.1. Management Mechanism Based on System Collaboration
4.5.2. Management Path Based on Collaborative Evolution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Serial Number | Parameter | Serial Number | Parameter |
|---|---|---|---|
| 1 | Return scrap rate | 75 | Failure analysis ineffective cost |
| 2 | Final scrap rate | 76 | Consumption rate of compressed gas |
| 3 | Comprehensive heat production rate | 77 | Leakage rate of compressed gas |
| 4 | Yield of finished products | 78 | Emission rate of compressed gas |
| 5 | Production reliability | 79 | Production layout safety index |
| 6 | Labor productivity | 80 | Production defect loss ratio |
| 7 | Error component rate | 81 | Energy cost loss ratio |
| 8 | Waste recycling rate | 82 | Comprehensive energy consumption per unit product |
| 9 | Qualified rate of finished products | 83 | Air pollution per unit product |
| 10 | Thermal pollution emission rate | 84 | Cost proportion of information technology construction |
| 11 | Production line downtime | 85 | Material scrap and defect data |
| 12 | Loss reduction index | 86 | Quantification of complaints and material waste |
| 13 | Device setup time | 87 | Deviation difference in material detection |
| 14 | Material balance index | 88 | Energy consumption per unit production cost |
| 15 | Special machine losses | 89 | Control index of residual energy |
| 16 | Defect decomposition index | 90 | Regulatory notice or authorization index |
| 17 | Complaint decomposition index | 91 | SOP review interval |
| 18 | Raw material consumption rate | 92 | Reporting index for major accidents |
| 19 | Rejection rate of defective products | 93 | Labor time used for rework |
| 20 | Air monitoring index | 94 | Consumption and disposal of packaging materials |
| 21 | Equipment failure loss | 95 | Manage controllable OEE ratios |
| 22 | Short stop loss | 96 | Product fragment recycling rate |
| 23 | Safety production index | 97 | Flexibility (inventory turnover days) |
| 24 | Equipment production efficiency | 98 | Production dynamic risk assessment index |
| 25 | Input–output efficiency | 99 | Environmental factory boundary noise statistical index |
| 26 | Product added scrap rate | 100 | Production process exhaust gas statistical index |
| 27 | Recovery and utilization rate of surplus energy | 101 | Energy safety isolation practice index |
| 28 | Waste heat recovery and utilization rate | 102 | Management risk progress assessment index |
| 29 | Progressiveness production equipment | 103 | Verify available material loss index |
| 30 | Wastewater recycling capacity | 104 | Water demand per unit production cost |
| 31 | Information management index | 105 | Risk assessment program coverage index |
| 32 | Reduction in production water consumption | 106 | Impact index of key control points |
| 33 | Quality index decline rate | 107 | Generation of residual heat and energy per unit product |
| 34 | Operational index (OPI) | 108 | Degree of production continuity (index) |
| 35 | OEE overall efficiency | 109 | Equipment overall efficiency (OEE) |
| 36 | Improved production line productivity | 110 | Scrap quantity/high-quality product quantity |
| 37 | Machine failure reduction rate | 111 | Reduced product value caused by obsolescence |
| 38 | Main equipment maintenance time | 112 | Number of customer complaints that generate costs |
| 39 | Key product key production | 113 | Number of customer complaints expressing dissatisfaction |
| 40 | Material specification accuracy | 114 | Basic fuel consumption of process auxiliary materials |
| 41 | Reduced use of natural gas | 115 | Volume ratio of water consumption to water intake |
| 42 | New material safety data | 116 | Utilization rate of SOP and other guidance books |
| 43 | Hazardous waste exposure index | 117 | Consumption statistics of engine oil and lubricating oil |
| 44 | Logistics stability index | 118 | Proportion of information technology cost to output value |
| 45 | Production visualization index | 119 | OEE decomposition—loss failure rate |
| 46 | Isolation index of energy | 120 | OEE decomposition—production conversion rate |
| 47 | Control index of energy | 121 | Probability of converting production indicators into actions |
| 48 | Energy shutdown index | 122 | Probability of discovering defects during regular inspections |
| 49 | Energy release index | 123 | Downtime caused by operator absence |
| 50 | Production plan completion rate | 124 | New radiation source or laser protection index |
| 51 | Unrecognized energy loss | 125 | Exhaust emissions per unit production cost |
| 52 | Water consumption per unit product | 126 | Percentage of jobs directly exposed to hazardous waste |
| 53 | Input energy per unit product | 127 | Statistics of protective devices, machinery and equipment |
| 54 | Comprehensive energy consumption per unit product | 128 | Detection rate of energy utilization tools and equipment |
| 55 | Comprehensive electricity consumption per unit product | 129 | Emission rate of solid liquid waste pollutants (sulfur) |
| 56 | Organizational structure construction level | 130 | Emission rate of gas waste pollutants (nitrogen) |
| 57 | Information system construction level | 131 | Inspection frequency of water treatment equipment and network |
| 58 | Planned downtime gap | 132 | Downtime caused by insufficient material supply |
| 59 | Hazardous waste hazard assessment index | 133 | Effective index of energy isolation device for equipment |
| 60 | Production accident impact index | 134 | Machine protection and LOTO inspection index |
| 61 | OEE breakdown maintenance rate | 135 | Proportion of full-time personnel engaged in information technology work |
| 62 | Line production gap index | 136 | Popularity of information technology related production equipment |
| 63 | Supervision improvement index | 137 | Production time statistics for no less than one rotation |
| 64 | Total loss due to quality issues | 138 | Index for incorporating new products and procedures into the process |
| 65 | Material value range stability | 139 | Speed loss caused by machine operation not reaching speed |
| 66 | Material characteristic calibration coefficient | 140 | Amount of waste generated per unit production cost |
| 67 | Measurement accuracy deviation index | 141 | Risk assessment index for three or more energy sources |
| 68 | Probability of chemical leakage | 142 | Proportion of non-recyclable waste to total waste |
| 69 | Construction of independent websites | 143 | Number of times discharge water quality is measured by external agencies/year |
| 70 | Internal network application situation | 144 | Proportion of information security investment in informatization investment |
| 71 | Product one-time qualification rate | 145 | Enterprise resource planning (ERP) application index |
| 72 | Archive data exposure level | 146 | Critical area cleaning and lubrication inspection (CIL) rate |
| 73 | Technical level evaluation index | 147 | Fire/explosion index caused by combustible or flammable materials |
| 74 | Cost of undiscovered defective products | 148 | Complexity index of the isolation system when there are more than three energy sources |
| Serial Number | Parameter | Unit | Serial Number | Parameter | Unit |
|---|---|---|---|---|---|
| 1 | Yield of finished products | % | 11 | Production defect loss ratio | % |
| 2 | Production reliability | ND | 12 | Energy cost loss ratio | % |
| 3 | Comprehensive heat production rate | % | 13 | Comprehensive energy consumption per unit product | MWh/m2 |
| 4 | Equipment production efficiency | % | 14 | Air pollution per unit product | kg/m3 |
| 5 | Wastewater recycling capacity | m3 | 15 | Cost proportion of information technology construction | % |
| 6 | Information management index | ND | 16 | Manage controllable OEE ratios | % |
| 7 | Production plan completion rate | % | 17 | Product fragment recycling rate | % |
| 8 | Unrecognized energy loss | kgce/t | 18 | Flexibility (inventory turnover days) | d |
| 9 | Water consumption per unit product | L/m3 | 19 | Equipment overall efficiency (OEE) | % |
| 10 | Product one-time qualification rate | % |
| Year | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | |||||||||||
| M1 | 0.5285 | 0.1338 | 1.0000 | 0.5165 | 0.0000 | 0.9741 | 0.3026 | 0.1649 | 0.2572 | 0.8300 | |
| M2 | 0.7693 | 0.8202 | 0.8642 | 1.0000 | 0.0000 | 0.0482 | 0.7048 | 0.8057 | 0.9552 | 0.7667 | |
| M3 | 0.0000 | 0.2683 | 0.6188 | 0.7828 | 0.6979 | 0.9253 | 0.8939 | 0.9328 | 0.8496 | 1.0000 | |
| E1 | 0.7273 | 1.0000 | 0.0000 | 0.1688 | 0.5407 | 0.0888 | 0.1802 | 0.5861 | 0.3129 | 0.3596 | |
| E2 | 0.5770 | 0.4556 | 0.0000 | 0.5164 | 0.3633 | 0.4659 | 0.3871 | 0.3936 | 0.4518 | 1.0000 | |
| E3 | 0.0000 | 0.9848 | 0.0389 | 0.1309 | 0.4597 | 0.4620 | 0.8468 | 1.0000 | 0.8810 | 0.9369 | |
| I1 | 0.6831 | 0.0000 | 0.2796 | 0.1093 | 0.4423 | 0.3555 | 0.1415 | 0.5067 | 0.7315 | 1.0000 | |
| I2 | 0.0000 | 0.0000 | 0.3855 | 0.5964 | 0.2410 | 0.6928 | 0.6024 | 0.2108 | 0.1205 | 0.0000 | |
| I3 | 0.0000 | 0.7422 | 0.6483 | 0.8021 | 0.8884 | 1.0000 | 0.5366 | 0.3592 | 0.7285 | 0.9238 | |
| Year | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | |||||||||||
| M1 | 0.1123 | 0.0284 | 0.2124 | 0.1097 | 0.0000 | 0.2069 | 0.0643 | 0.0350 | 0.0546 | 0.1763 | |
| M2 | 0.1142 | 0.1218 | 0.1283 | 0.1485 | 0.0000 | 0.0072 | 0.1047 | 0.1196 | 0.1418 | 0.1138 | |
| M3 | 0.0000 | 0.0385 | 0.0888 | 0.1123 | 0.1001 | 0.1328 | 0.1283 | 0.1338 | 0.1219 | 0.1435 | |
| E1 | 0.1835 | 0.2522 | 0.0000 | 0.0426 | 0.1364 | 0.0224 | 0.0455 | 0.1478 | 0.0789 | 0.0907 | |
| E2 | 0.1251 | 0.0988 | 0.0000 | 0.1120 | 0.0788 | 0.1010 | 0.0840 | 0.0854 | 0.0980 | 0.2169 | |
| E3 | 0.0000 | 0.1715 | 0.0068 | 0.0228 | 0.0801 | 0.0805 | 0.1475 | 0.1742 | 0.1535 | 0.1632 | |
| I1 | 0.1607 | 0.0000 | 0.0658 | 0.0257 | 0.1041 | 0.0837 | 0.0333 | 0.1192 | 0.1721 | 0.2353 | |
| I2 | 0.0000 | 0.0000 | 0.1353 | 0.2093 | 0.0846 | 0.2431 | 0.2114 | 0.0740 | 0.0423 | 0.0000 | |
| I3 | 0.0000 | 0.1120 | 0.0978 | 0.1210 | 0.1340 | 0.1508 | 0.0809 | 0.0542 | 0.1099 | 0.1394 | |
| Year | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | |||||||||||
| M1 | 0.2455 | 0.1012 | 0.3291 | 0.2420 | 0.0000 | 0.3260 | 0.1764 | 0.1174 | 0.1588 | 0.3060 | |
| M2 | 0.2478 | 0.2564 | 0.2635 | 0.2832 | 0.0000 | 0.0354 | 0.2362 | 0.2540 | 0.2770 | 0.2474 | |
| M3 | 0.0000 | 0.1254 | 0.2150 | 0.2456 | 0.2304 | 0.2681 | 0.2634 | 0.2692 | 0.2566 | 0.2786 | |
| E1 | 0.3111 | 0.3474 | 0.0000 | 0.1344 | 0.2717 | 0.0851 | 0.1405 | 0.2826 | 0.2004 | 0.2177 | |
| E2 | 0.2601 | 0.2287 | 0.0000 | 0.2452 | 0.2002 | 0.2316 | 0.2080 | 0.2101 | 0.2276 | 0.3315 | |
| E3 | 0.0000 | 0.3024 | 0.0339 | 0.0862 | 0.2022 | 0.2028 | 0.2823 | 0.3044 | 0.2876 | 0.2958 | |
| I1 | 0.2938 | 0.0000 | 0.1790 | 0.0942 | 0.2355 | 0.2076 | 0.1133 | 0.2536 | 0.3029 | 0.3405 | |
| I2 | 0.0000 | 0.0000 | 0.2706 | 0.3273 | 0.2089 | 0.3438 | 0.3285 | 0.1927 | 0.1338 | 0.0000 | |
| I3 | 0.0000 | 0.2451 | 0.2274 | 0.2555 | 0.2693 | 0.2853 | 0.2035 | 0.1580 | 0.2427 | 0.2746 | |
| Year | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | |||||||||||
| M1 | 62.0% | 49.7% | 76.7% | 61.6% | 45.5% | 75.8% | 54.9% | 50.6% | 53.5% | 71.% | |
| M2 | 96.10% | 96.53% | 96.90% | 98.04% | 89.63% | 90.04% | 95.56% | 96.41% | 97.67% | 96.08% | |
| M3 | 6.73 | 10.49 | 15.41 | 17.70 | 16.51 | 19.70 | 19.26 | 19.81 | 18.64 | 20.75 | |
| E1 | 12.00 | 10.87 | 15.01 | 14.31 | 12.77 | 14.64 | 14.27 | 12.58 | 13.72 | 13.52 | |
| E2 | 3.79% | 4.51% | 7.22% | 4.15% | 5.06% | 4.45% | 4.92% | 4.88% | 4.53% | 1.27% | |
| E3 | 200.00 | 237.96 | 201.50 | 295.15 | 282.47 | 282.39 | 232.64 | 238.54 | 266.24 | 264.08 | |
| I1 | 20.55 | 45.77 | 35.45 | 41.73 | 29.44 | 32.64 | 40.54 | 27.06 | 18.77 | 8.85 | |
| I2 | 0.20% | 0.50% | 2.50% | 3.20% | 5.10% | 3.60% | 3.90% | 5.20% | 5.50% | 5.90% | |
| I3 | 35.64% | 62.40% | 59.02% | 64.56% | 67.68% | 71.70% | 54.99% | 48.59% | 61.91% | 68.95% | |
| Relationship | E1-M1 | E1-M2 | E1-M3 | E2-M1 | E2-M2 | E2-M3 | E3-M1 | E3-M2 | E3-M3 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Year | ||||||||||
| 2013 | 0.652 | 0.691 | 0.335 | 0.734 | 0.758 | 0.532 | 0.542 | 0.568 | 0.402 | |
| 2014 | 0.956 | 0.553 | 0.583 | 0.736 | 1.000 | 0.574 | 0.698 | 0.851 | 0.458 | |
| 2015 | 0.620 | 0.701 | 0.566 | 0.597 | 0.455 | 0.422 | 0.358 | 0.565 | 0.694 | |
| 2016 | 0.843 | 0.858 | 0.994 | 0.843 | 0.836 | 0.778 | 0.644 | 0.652 | 0.737 | |
| 2017 | 0.554 | 0.947 | 0.847 | 0.572 | 0.728 | 0.800 | 0.414 | 0.595 | 0.693 | |
| 2018 | 0.599 | 0.622 | 0.716 | 0.653 | 0.919 | 0.717 | 0.687 | 0.601 | 0.841 | |
| 2019 | 0.616 | 0.795 | 0.712 | 0.733 | 0.846 | 0.886 | 1.000 | 0.820 | 0.534 | |
| 2020 | 0.713 | 0.780 | 0.488 | 0.670 | 0.872 | 0.824 | 0.726 | 0.861 | 0.523 | |
| 2021 | 0.645 | 1.000 | 0.705 | 0.808 | 0.986 | 0.815 | 0.614 | 0.918 | 0.840 | |
| 2022 | 0.586 | 0.991 | 0.501 | 0.355 | 0.407 | 0.337 | 0.690 | 0.892 | 0.577 | |
| Relationship | M1-E1 | M1-E2 | M1-E3 | M2-E1 | M2-E2 | M2-E3 | M3-E1 | M3-E2 | M3-E3 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Year | ||||||||||
| 2013 | 0.794 | 0.730 | 0.680 | 0.768 | 0.692 | 0.636 | 0.501 | 0.529 | 0.557 | |
| 2014 | 1.000 | 0.732 | 0.803 | 0.646 | 0.987 | 0.857 | 0.737 | 0.570 | 0.610 | |
| 2015 | 0.769 | 0.587 | 0.504 | 0.776 | 0.379 | 0.633 | 0.724 | 0.420 | 0.796 | |
| 2016 | 0.931 | 0.845 | 0.763 | 0.899 | 0.782 | 0.707 | 1.000 | 0.772 | 0.824 | |
| 2017 | 0.713 | 0.562 | 0.562 | 0.964 | 0.659 | 0.659 | 0.919 | 0.794 | 0.795 | |
| 2018 | 0.752 | 0.645 | 0.795 | 0.708 | 0.884 | 0.665 | 0.836 | 0.712 | 0.887 | |
| 2019 | 0.766 | 0.728 | 0.990 | 0.852 | 0.794 | 0.835 | 0.833 | 0.880 | 0.676 | |
| 2020 | 0.842 | 0.663 | 0.823 | 0.840 | 0.825 | 0.865 | 0.656 | 0.819 | 0.667 | |
| 2021 | 0.789 | 0.807 | 0.740 | 1.000 | 0.969 | 0.904 | 0.828 | 0.810 | 0.886 | |
| 2022 | 0.741 | 0.343 | 0.797 | 0.994 | 0.334 | 0.886 | 0.668 | 0.335 | 0.711 | |
| Relationship | I1-M1 | I1-M2 | I1-M3 | I2-M1 | I2-M2 | I2-M3 | I3-M1 | I3-M2 | I3-M3 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Year | ||||||||||
| 2013 | 0.608 | 0.624 | 0.666 | 0.379 | 0.384 | 0.660 | 0.349 | 0.361 | 0.556 | |
| 2014 | 0.428 | 0.509 | 0.368 | 0.472 | 0.407 | 0.563 | 0.515 | 0.901 | 0.360 | |
| 2015 | 0.872 | 0.783 | 0.693 | 0.523 | 0.690 | 0.770 | 0.453 | 0.936 | 0.827 | |
| 2016 | 0.596 | 0.600 | 0.633 | 0.905 | 0.897 | 0.837 | 0.818 | 0.833 | 0.995 | |
| 2017 | 0.715 | 0.969 | 1.000 | 0.476 | 0.565 | 0.602 | 0.379 | 0.549 | 0.643 | |
| 2018 | 0.766 | 0.810 | 0.853 | 0.751 | 1.000 | 0.826 | 0.830 | 0.476 | 1.000 | |
| 2019 | 0.550 | 0.609 | 0.761 | 0.826 | 0.955 | 0.990 | 0.998 | 0.766 | 0.492 | |
| 2020 | 0.933 | 0.849 | 0.644 | 0.500 | 0.591 | 0.740 | 0.937 | 0.549 | 0.377 | |
| 2021 | 0.674 | 0.571 | 0.510 | 0.484 | 0.549 | 0.613 | 0.617 | 0.980 | 0.739 | |
| 2022 | 0.367 | 0.421 | 0.349 | 0.577 | 0.487 | 0.624 | 0.927 | 0.618 | 0.717 | |
| Relationship | I1-E1 | I1-E2 | I1-E3 | I2-E1 | I2-E2 | I2-E3 | I3-E1 | I3-E2 | I3-E3 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Year | ||||||||||
| 2013 | 0.657 | 0.719 | 0.786 | 0.451 | 0.467 | 0.482 | 0.603 | 0.648 | 0.695 | |
| 2014 | 0.359 | 0.437 | 0.411 | 0.507 | 0.444 | 0.460 | 0.660 | 0.929 | 0.832 | |
| 2015 | 0.896 | 0.480 | 0.519 | 0.623 | 0.432 | 0.873 | 0.780 | 0.419 | 0.713 | |
| 2016 | 0.560 | 0.464 | 0.665 | 0.803 | 0.965 | 0.712 | 0.984 | 0.746 | 0.833 | |
| 2017 | 0.967 | 0.735 | 0.735 | 0.592 | 0.697 | 0.697 | 0.718 | 1.000 | 0.999 | |
| 2018 | 1.000 | 0.827 | 0.920 | 0.894 | 0.979 | 0.857 | 0.813 | 0.685 | 0.866 | |
| 2019 | 0.591 | 0.620 | 0.490 | 0.964 | 1.000 | 0.809 | 0.764 | 0.725 | 1.000 | |
| 2020 | 0.925 | 0.685 | 0.899 | 0.572 | 0.652 | 0.578 | 0.789 | 0.624 | 0.772 | |
| 2021 | 0.499 | 0.508 | 0.476 | 0.572 | 0.565 | 0.591 | 0.984 | 0.956 | 0.961 | |
| 2022 | 0.356 | 1.000 | 0.342 | 0.517 | 0.335 | 0.535 | 0.760 | 0.338 | 0.823 | |
| Relationship | M1-I1 | M1-I2 | M1-I3 | M2-I1 | M2-I2 | M2-I3 | M3-I1 | M3-I2 | M3-I3 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Year | ||||||||||
| 2013 | 0.597 | 0.341 | 0.542 | 0.613 | 0.344 | 0.554 | 0.650 | 0.590 | 0.732 | |
| 2014 | 0.421 | 0.425 | 0.701 | 0.499 | 0.364 | 0.960 | 0.360 | 0.503 | 0.550 | |
| 2015 | 0.854 | 0.470 | 0.646 | 0.770 | 0.621 | 0.978 | 0.677 | 0.690 | 0.912 | |
| 2016 | 0.585 | 0.813 | 0.909 | 0.588 | 0.810 | 0.924 | 0.618 | 0.750 | 0.998 | |
| 2017 | 0.701 | 0.428 | 0.574 | 0.955 | 0.507 | 0.730 | 0.976 | 0.538 | 0.797 | |
| 2018 | 0.751 | 0.676 | 0.915 | 0.796 | 0.905 | 0.668 | 0.833 | 0.740 | 1.000 | |
| 2019 | 0.540 | 0.743 | 1.000 | 0.598 | 0.863 | 0.884 | 0.743 | 0.889 | 0.678 | |
| 2020 | 0.913 | 0.450 | 0.971 | 0.835 | 0.531 | 0.731 | 0.629 | 0.663 | 0.568 | |
| 2021 | 0.661 | 0.435 | 0.781 | 0.560 | 0.493 | 1.000 | 0.498 | 0.548 | 0.860 | |
| 2022 | 0.361 | 0.519 | 0.966 | 0.413 | 0.436 | 0.784 | 0.340 | 0.558 | 0.846 | |
| Relationship | E1-I1 | E1-I2 | E1-I3 | E2-I1 | E2-I2 | E2-I3 | E3-I1 | E3-I2 | E3-I3 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Year | ||||||||||
| 2013 | 0.678 | 0.341 | 0.599 | 0.812 | 0.467 | 0.738 | 0.790 | 0.359 | 0.679 | |
| 2014 | 0.381 | 0.394 | 0.657 | 0.574 | 0.444 | 0.948 | 0.423 | 0.339 | 0.821 | |
| 2015 | 0.904 | 0.512 | 0.780 | 0.615 | 0.432 | 0.527 | 0.530 | 0.810 | 0.697 | |
| 2016 | 0.584 | 0.727 | 0.991 | 0.601 | 0.965 | 0.816 | 0.673 | 0.600 | 0.822 | |
| 2017 | 0.970 | 0.480 | 0.716 | 0.823 | 0.697 | 0.994 | 0.741 | 0.582 | 0.999 | |
| 2018 | 1.000 | 0.853 | 0.813 | 0.886 | 0.979 | 0.768 | 0.917 | 0.788 | 0.858 | |
| 2019 | 0.614 | 0.959 | 0.764 | 0.736 | 1.000 | 0.800 | 0.501 | 0.722 | 1.000 | |
| 2020 | 0.932 | 0.458 | 0.789 | 0.786 | 0.652 | 0.718 | 0.897 | 0.452 | 0.759 | |
| 2021 | 0.524 | 0.458 | 0.991 | 0.641 | 0.565 | 0.966 | 0.487 | 0.465 | 0.958 | |
| 2022 | 0.379 | 0.404 | 0.759 | 0.989 | 0.335 | 0.442 | 0.353 | 0.409 | 0.812 | |
| Month | January | February | March | April | May | June | July | August | |
|---|---|---|---|---|---|---|---|---|---|
| Production Line | |||||||||
| Line1 | 652,799 | 458,694 | 640,533 | 557,784 | 589,908 | 526,010 | 553,914 | 589,313 | |
| Line2 | 498,668 | 356,508 | 480,682 | 419,418 | 446,176 | 374,483 | 411,995 | 459,002 | |
| Line3 | 177,416 | 128,552 | 181,638 | 150,592 | 179,114 | 159,835 | 185,137 | 171,850 | |
| Line4 | 321,252 | 227,956 | 299,044 | 268,826 | 267,062 | 214,648 | 226,858 | 287,152 | |
| Line5 | 154,131 | 102,186 | 159,851 | 138,366 | 143,732 | 151,527 | 141,919 | 130,311 | |
| Line6 | 156,471 | 149,308 | 161,640 | 135,600 | 157,018 | 134,347 | 169,295 | 134,769 | |
| Line7 | 109,647 | 85,602 | 134,950 | 114,119 | 117,924 | 107,143 | 126,322 | 117,437 | |
| Line8 | 404,678 | 412,077 | 340,153 | 384,845 | 475,019 | 309,949 | 360,162 | 375,895 | |
| Line9 | 717,132 | 736,438 | 890,730 | 832,550 | 775,571 | 649,772 | 791,020 | 728,500 | |
| Line10 | 100,315 | 72,581 | 100,113 | 88,496 | 56,778 | 53,448 | 60,520 | 73,017 | |
| Month | January | February | March | April | May | June | July | August | |
|---|---|---|---|---|---|---|---|---|---|
| Parameter | |||||||||
| OEE | 87.1% | 83.8% | 86.9% | 86.0% | 86.2% | 84.5% | 87.2% | 88.0% | |
| OEE SR | 69.9% | 67.8% | 64.8% | 74.2% | 78.0% | 77.4% | 77.9% | 75.6% | |
| OEE SL | 72.0% | 66.5% | 72.3% | 72.7% | 72.3% | 72.2% | 73.9% | 72.3% | |
| OEE Tes | 59.5% | 67.1% | 61.1% | 71.1% | 81.9% | 86.4% | 86.0% | 81.4% | |
| Yield WS | 95.1% | 95.7% | 95.1% | 95.6% | 95.2% | 95.4% | 94.8% | 95.3% | |
| Yield KTL | 92.9% | 92.7% | 92.8% | 92.4% | 93.1% | 93.1% | 93.3% | 93.4% | |
| Yield BT3 | 96.8% | 97.8% | 97.7% | 97.7% | 97.4% | 97.1% | 97.7% | 97.1% | |
| PVT KTL | 16.3 | 16.8 | 15.6 | 16.7 | 15.7 | 17.1 | 15.6 | 18.0 | |
| PVT BT3 | 43.5 | 39.1 | 41.0 | 40.5 | 40.9 | 45.0 | 42.1 | 41.0 | |
| WS Prod | 35.0 | 26.1 | 52.5 | 35.4 | 43.8 | 26.6 | 35.9 | 59.0 | |
| KTL Prod | 108.1 | 67.3 | 73.3 | 59.8 | 111.6 | 84.0 | 77.1 | 102.9 | |
| BT3 Prod | 353.9 | 165.4 | 347.3 | 331.7 | 207.2 | 226.2 | 283.1 | 326.3 | |
| Year | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | |||||||||||
| 1 | 96.10% | 96.53% | 96.90% | 98.04% | 89.63% | 90.04% | 95.56% | 96.41% | 97.67% | 96.08% | |
| 2 | 6.73 | 10.49 | 15.41 | 17.70 | 16.51 | 19.70 | 19.26 | 19.81 | 18.64 | 20.75 | |
| 3 | 98.5% | 98.1% | 97.2% | 97.3% | 99.4% | 99.1% | 98.2% | 98.6% | 94.3% | 98.3% | |
| 4 | 89.6% | 95.5% | 91.9% | 90.4% | 89.6% | 89.7% | 97.1% | 94.9% | 86.4% | 93.1% | |
| 5 | 200.00 | 237.96 | 201.50 | 295.15 | 282.47 | 282.39 | 232.64 | 238.54 | 266.24 | 264.08 | |
| 6 | 35.64% | 62.40% | 59.02% | 64.56% | 67.68% | 71.70% | 54.99% | 48.59% | 61.91% | 68.95% | |
| 7 | 99% | 92% | 86% | 101% | 92% | 102% | 107% | 85% | 101% | 100% | |
| 8 | 887 | 493 | 311 | 396 | 305 | 293 | 234 | 271 | 189 | 211 | |
| 9 | 12.9 | 9.3 | 10.4 | 9.7 | 10.2 | 10.8 | 13.4 | 10.4 | 9.2 | 10.8 | |
| 10 | 89.6% | 95.5% | 91.9% | 90.4% | 89.6% | 89.7% | 97.1% | 94.9% | 86.4% | 93.1% | |
| 11 | 5.6% | 5.1% | 2.0% | 3.0% | 9.3% | 0.9% | 5.5% | 0.0% | 1.1% | 0.0% | |
| 12 | 1.9% | 3.7% | 3.1% | 3.5% | 0.6% | 1.8% | 0.5% | 0.3% | 0.3% | 0.2% | |
| 13 | 12.00 | 10.87 | 15.01 | 14.31 | 12.77 | 14.64 | 14.27 | 12.58 | 13.72 | 13.52 | |
| 14 | 3.79% | 4.51% | 7.22% | 4.15% | 5.06% | 4.45% | 4.92% | 4.88% | 4.53% | 1.27% | |
| 15 | 0.20% | 0.50% | 2.50% | 3.20% | 5.10% | 3.60% | 3.90% | 5.20% | 5.50% | 5.90% | |
| 16 | 36% | 62% | 59% | 65% | 68% | 72% | 55% | 49% | 71% | 62% | |
| 17 | 63.4% | 76.7% | 83.0% | 93.0% | 90.0% | 93.0% | 80.0% | 87.0% | 89.0% | 91.0% | |
| 18 | 20.55 | 45.77 | 35.45 | 41.73 | 29.44 | 32.64 | 40.54 | 27.06 | 18.77 | 8.85 | |
| 19 | 62.0% | 49.7% | 76.7% | 61.6% | 45.5% | 75.8% | 54.9% | 50.6% | 53.5% | 71.4% | |
| Index Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| Operation Sequence | |||||||||
| Process 1 | 2236.5 | 407.2 | 53.1 | 63.3% | 62.4% | 887.3 | 501 | 1932.5 | |
| Process 2 | 3172.8 | 971.1 | 920.8 | 71.2% | 59.0% | 311.4 | 59 | 2280.8 | |
| Process 3 | 3470.9 | 398.2 | 1317.5 | 85.5% | 64.6% | 189.3 | 883 | 2853.9 | |
| Process 4 | 3638.2 | 656.9 | 846.7 | 80.3% | 67.7% | 234.2 | 501 | 3365.2 | |
| Process 5 | 3854.6 | 435.7 | 793.0 | 84.1% | 71.7% | 292.8 | 166 | 2602.6 | |
| Process 6 | 2956.2 | 1185.6 | 837.8 | 65.1% | 55.0% | 396.4 | 993 | 2250.2 | |
| Process 7 | 2612.4 | 511.7 | 1981.2 | 77.0% | 48.6% | 270.7 | 669 | 1004.4 | |
| Process 8 | 3811.7 | 664.3 | 688.7 | 81.3% | 70.9% | 211.4 | 50 | 3628.7 | |
| Process 9 | 3328.2 | 428.1 | 1315.0 | 82.0% | 61.9% | 304.7 | 181 | 1673.2 | |
| Process 10 | 3706.8 | 315.5 | 1140.8 | 87.5% | 69.0% | 212.9 | 385 | 3706.8 | |
References
- Haken, H. Synergetics: Introduction and Advanced Topics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Meng, Q.; Han, W. Research on Coordination Models of Complex Systems. J. Tianjin Univ. 2000, 4, 444–446. [Google Scholar]
- Peng, B. Research on the Coevolution of Modern Logistics Industry and Advanced Manufacturing Industry. China Soft Sci. 2009, S1, 149–153. [Google Scholar]
- Zheng, D.; Li, J.; Zhang, X. Analysis of Collaborative Learning between Automobile Manufacturers and Supplier’s Supply and Demand System. China Soft Sci. 2010, 3, 152–160. [Google Scholar]
- Anbanandam, R.; Banwet, D.K.; Shankar, R. Evaluation of Supply Chain Collaboration: A Case Study of the Apparel Retail Industry in India. Int. J. Prod. Perform. Manag. 2011, 60, 82–98. [Google Scholar] [CrossRef]
- Leydesdorff, L.; Strand, O. The Swedish System of Innovation: Regional Synergies in a Knowledge-Based Economy. J. Am. Soc. Inf. Sci. Technol. 2012, 64, 1890–1902. [Google Scholar] [CrossRef]
- Wagner, T.; Boebel, F.G. Testing Synergetic Algorithms with Industrial Classification Problems. Neural Netw. 1994, 7, 1313–1321. [Google Scholar] [CrossRef]
- Schanz, M.; Pelster, A. Synergetic System Analysis for the Delay-Induced Hopf Bifurcation in the Wright Equation. SIAM J. Appl. Dyn. Syst. 2012, 2, 1056–1061. [Google Scholar] [CrossRef]
- May, G.; Barletta, I.; Stahl, B.; Taisch, M. Energy Management in Production: A Novel Method to Develop Key Performance Indicators for Improving Energy Efficiency. Appl. Energy 2015, 149, 46–61. [Google Scholar] [CrossRef]
- Hryshchuk, R.; Molodetska, K. Synergetic Control of Social Networking Services Actors’ Interactions. In Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2016; Volume 12, pp. 34–42. [Google Scholar]
- Xu, Y.L.; Yu, L.; Wang, Y.D. Analysis of Order Parameters for Co-evolution of Regional Sci-tech Innovation and Sci-tech Finance System. Sci. Technol. Manag. Res. 2017, 37, 15–20. [Google Scholar]
- Wen, X.; Zhao, X.; Jia, J. Research on System Order Parameter Identification Method Based on GPEM Main Melody Analysis. Oper. Res. Manag. 2011, 20, 168–175. [Google Scholar]
- Zheng, J.; Wu, T. Three-Dimensional Regulation Mechanism and Model Research of Circular Economy Construction System Order Parameter. Sci. Technol. Prog. Policy 2013, 30, 147–150. [Google Scholar]
- Wu, Y.; Wei, G.; He, X. Measurement and Empirical Study on Synergy Degree between High-tech Manufacturing and Factors Based on Coupling Coefficient Model. Syst. Eng. 2017, 35, 93–100. [Google Scholar]
- Wang, H.; Meng, X.; Yu, R. Research on Order Parameter Identification in Food Quality Chain Collaborative System. Syst. Eng. Theor. Pract. 2017, 37, 1741–1751. [Google Scholar]
- Wen, X.; Zhou, J. An Efficiency-Oriented System Multi-Order Parameter Identification Method. Oper. Res. Manag. 2020, 29, 183–189. [Google Scholar]
- Li, T.; Chen, W. Research on Coordinated Development of Regional Intellectual Property Management System Evolution from a Longitudinal Perspective—Measurement Based on Composite System Coordinated Development Model. Inf. Stud. 2012, 31, 99–105. [Google Scholar]
- Tang, L.; Li, J.P.; Yu, L.A.; Tan, D.H. Quantitative Evaluation Method for System Coordinated Development Based on Distance Coordinated Development Model. Syst. Eng. Theor. Pract. 2010, 30, 594–602. [Google Scholar]
- Cui, L.; Jiang, H. PLSPM-GIA Measurement Model and Its Application in the Coordinated Development of 3E Systems. Math. Stat. Manag. 2016, 35, 984–996. [Google Scholar]
- Deng, X.; Chen, M. Study on the Synergy Degree between Science and Technology Achievement Transformation System and Enterprises. Sci. Res. Manag. 2016, 37, 116–125. [Google Scholar]
- Chen, L. Research on Integrated Management Model of Engineering Project Five Elements Based on Collaborative Learning. J. Eng. Manag. 2016, 30, 101–105. [Google Scholar]
- Luo, W.; Dong, B. Research on Evaluation Model of Regional Economic and Transportation Development Synergy. J. Highw. Transp. Res. Dev. 2017, 34, 151–158. [Google Scholar]
- Li, H.; Zhang, X. Study on Regional Ecological Innovation Synergy and Its Influencing Factors. China Popul. Resour. Environ. 2016, 26, 43–51. [Google Scholar]
- Chen, W.; Yang, Z.; Li, J. Empirical Study on Synergy and Evolution of Regional Intellectual Property Management System. Stud. Sci. Sci. Manag. 2016, 37, 30–41. [Google Scholar]
- Zhang, Y.; Wang, D. Quantitative Measurement of Beijing-Tianjin-Hebei Collaborative Development Based on Composite System Synergy. Econ. Manag. Res. 2017, 38, 33–39. [Google Scholar]
- Li, J.; Fan, C.; Yuan, Q. Measurement of Collaborative Development Level of Beijing-Tianjin-Hebei Based on Distance Collaboration Model. Sci. Technol. Manag. Res. 2017, 37, 45–50. [Google Scholar]
- Lü, T.; Han, W. Chaos Control of Regional “Economy-Resource-Environment” System Based on Coordination. Syst. Eng. Theor. Pract. 2002, 3, 8–12. [Google Scholar]
- Bao, B.F.; Yu, Y.; Tao, Y. Resource Optimal Allocation in Product Customization Collaborative Manufacturing. Comput. Integr. Manuf. Syst. 2014, 20, 1807–1818. [Google Scholar]
- Fang, C. Analysis of Theoretical Basis and Regularity of Collaborative Development of Beijing-Tianjin-Hebei Urban Agglomeration. Progr. Geogr. 2017, 36, 15–24. [Google Scholar]
- Lychkina, N.N. Synergetics and Development Processes in Socio-Economic Systems: Search for Effective Modeling Constructs. Bus. Inform. 2016, 1, 66–79. [Google Scholar] [CrossRef][Green Version]
- Meynhardt, T.; Chandler, J.D.; Strathoff, P. Systemic Principles of Value Co-creation: Synergetics of Value and Service Ecosystems. J. Bus. Res. 2016, 69, 2981–2989. [Google Scholar] [CrossRef]
- Zheng, J.; Zhou, X. Evaluation of Synergy Effects in Green Supply Chain Management of Iron and Steel Enterprises. Sci. Res. Manag. 2017, 38, 563–568. [Google Scholar]
- Yang, Z.; Chen, W.; Li, J. Study on Speed Characteristics of Synergy and Evolution of China’s Intellectual Property Management System. J. Ind. Eng. Eng. Manag. 2018, 32, 171–177. [Google Scholar]
- Guo, H.; Fan, Z.; Li, J.; Wang, L.; Wu, H.; Yang, Y. Research on Co-evolution of E-commerce and Big Data Industries Considering Internal and External Factors. Oper. Res. Manag. 2019, 28, 191–199. [Google Scholar]
- Reiter, S. A system for managing job-shop production. J. Bus. 1966, 39, 371–393. [Google Scholar] [CrossRef]
- Jacobs, F.R. OPT uncovered: Many production planning and scheduling concepts and be applied with or without the software. Ind. Eng. 1984, 16, 32–41. [Google Scholar]
- Graves, S.C.; Kostreva, M.M. Overlapping operations in material requirements planning. J. Oper. Manag. 1986, 6, 283–294. [Google Scholar] [CrossRef]
- Truscott, W.G. Scheduling production activities in multi-stage batch manufacturing systems. Int. J. Prod. Res. 1985, 23, 315–328. [Google Scholar] [CrossRef]
- Potts, C.N.; Baker, K.R. Flow shop scheduling with lot streaming. Oper. Res. Lett. 1989, 8, 297–303. [Google Scholar] [CrossRef]
- Vickson, R.G. Optimal lot streaming for multiple products in a two-machine flow shop. Eur. J. Oper. Res. 1995, 85, 556–575. [Google Scholar] [CrossRef]
- Etinkaya, F.C. Unit sized transfer batch scheduling in an automated two-machine flow-line cell with one transport agent. Int. J. Adv. Manuf. Technol. 2006, 29, 178–183. [Google Scholar] [CrossRef]
- Ruth, M. Information, order and knowledge in economic and ecological systems: Implications for material and energy use. Ecol. Econ. 1995, 13, 99–114. [Google Scholar] [CrossRef]
- Sa, M. lean and green: Doing more with less. ECR J. 2003, 3, 84–91. [Google Scholar]
- Long, Y.; Huang, S.Y.; Liu, K. Basic characteristics of material flow, energy flow, and information flow in large systems. J. Huazhong Univ. Sci. Technol. 2008, 36, 87–90. [Google Scholar] [CrossRef]
- Bascur, O.A.; Hertler, C. Collaboration at the enterprise using real time data analysis: From data to action. IFAC Proc. Vol. 2009, 42, 314–319. [Google Scholar] [CrossRef]
- William, F.; Fazleena, B. Sustainable Value Stream Mapping (Sus-VSM): Methodology to visualize and assess manufacturing sustainability performance. J. Clean. Prod. 2014, 85, 8–18. [Google Scholar]
- Taulo, J.L.; Sebitosi, A.B. Material and energy flow analysis of the Malawian tea industry. Renew. Sustain. Energy Rev. 2016, 56, 1337–1350. [Google Scholar] [CrossRef]
- Suominen, O.; Mörsky, V.; Ritala, R.; Vilkko, M. Framework for optimization and scheduling of a copper production plant. In Proceedings of the 26th European Symposium on Computer Aided Process Engineering, Portorož, Slovenia, 12–15 June 2016. [Google Scholar]
- Yin, R.Y. Theory and Methods of Metallurgical Process Integration; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Zhang, H.; Luo, W. Research on lean production improvement based on EVSM and simulation technology. Ind. Eng. 2017, 20, 64–70. [Google Scholar]
- Zheng, Z.; Huang, S.; Long, J.; Gao, X. Synergistic method of material flow and energy flow in the context of intelligent manufacturing of steel. J. Eng. Sci. 2017, 39, 115–124. [Google Scholar]
- Yu, Y.X.; Yao, S.; Mao, J.S. Quantitative analysis of the coupling coefficients between energy flow, value flow, and material flow in a Chinese lead-acid battery system. Environ. Sci. Pollut. Res. 2018, 25, 34448–34459. [Google Scholar] [CrossRef]
- Li, G.; Meng, Y.; Dong, W.; Wang, T. Multi-flow modeling and analysis of information-physical-energy systems based on collaborative theory. Electr. Power Constr. 2018, 39, 1–9. [Google Scholar]
- Huang, L.; Wu, C.; Wang, B. Construction of a system safety collaborative theory model from the perspective of “flow”. China Saf. Sci. J. 2019, 29, 50–55. [Google Scholar]
- Qi, L.; Wang, K.; Zhang, F.; Zhao, X. Research on the system dynamics model of internal knowledge dissemination in enterprises. J. Manag. Sci. 2008, 21, 9–20. [Google Scholar]
- Jiang, C. Analysis of breakthrough paths for independent innovation traps of emerging Chinese enterprises. J. Manag. Sci. China 2011, 14, 36–51. [Google Scholar]
- Wang, C.; Mu, D. Simulation and optimization of manufacturing enterprise logistics operation cost based on system dynamics. Syst. Eng. Theory Pract. 2012, 32, 1241–1250. [Google Scholar]
- Love, P.; Holt, G.; Shen, L.; Li, H.; Irani, Z. Using systems dynamics to better understand change and rework in construction project management systems. Int. J. Proj. Manag. 2002, 20, 425–436. [Google Scholar] [CrossRef]
- Zhang, L.; Han, Y.; Chen, J. Bullwhip effect and cost analysis of quantity-based integrated replenishment in supplier-managed inventory. Comput. Integr. Manuf. Syst. 2007, 2, 410–416. [Google Scholar] [CrossRef]
- Lee, S.H.; Pena-Mora, F.; Park, M. Dynamic planning and control methodology for strategic and operational construction project management. Autom. Constr. 2006, 15, 84–97. [Google Scholar] [CrossRef]
- Hu, B.; Zhang, D.; Zhang, J. System dynamics modeling and simulation of enterprise lifecycle. Chin. J. Manag. Sci. 2006, 3, 142–148. [Google Scholar]
- Dai, M.; Chen, L. CSO business model and its system dynamics simulation research. Soft Sci. 2014, 28, 119–123. [Google Scholar]
- Gary, L.; Amos, N.H.C.; Tehseen, A. Towards strategic development of maintenance and its effects on production performance by using system dynamics in the automotive industry. Int. J. Prod. Econ. 2018, 200, 151–169. [Google Scholar] [CrossRef]
- Hanafi, M.; Wibisono, D.; Mangkusubroto, K.; Siallagan, M.; Badriyah, M.J.K. Designing smelter industry investment competitiveness policy in Indonesia through system dynamics model. J. Sci. Technol. Policy Manag. 2019, 10, 617–641. [Google Scholar] [CrossRef]
- Shi, D.; Wang, L. Energy revolution and its impact on economic development. Ind. Econ. Res. 2015, 2015, 1–8. [Google Scholar]
- Larson, T.; Greenwood, R. Perfect complements: Synergies between lean production and eco-sustainability initiatives. Environ. Qual. Manag. 2004, 13, 27–36. [Google Scholar] [CrossRef]
- Zhan, Y.; Tan, K.H.; Ji, G.; Chung, L.; Chiu, A.S. Green and lean sustainable development path in China: Guanxi, practices and performance. Resour. Conserv. Recycl. 2018, 128, 240–249. [Google Scholar] [CrossRef]
- Kurdve, M.; Zackrisson, M.; Wiktorsson, M.; Harlin, U. Lean and green integration into production system models—Experiences from Swedish industry. J. Clean. Prod. 2014, 85, 180–190. [Google Scholar] [CrossRef]
- Yang, R.; Long, R. Reflection on enterprise management transformation under the background of low-carbon economy. Sci. Technol. Manag. Res. 2015, 35, 235–239. [Google Scholar]
- Tetiana, H.; Karpenko, L.M.; Olesia, F.V.; Yu, S.I.; Svetlana, D. Innovative Methods of Performance Evaluation of Energy Efficiency Projects. Acad. Strateg. Manag. J. 2018, 17, 465–476. [Google Scholar]
- Jarrahi, F.; Manenti, A.; Tortorella, G.L.; Gaiardelli, P. Facing the challenges of the future through the synergetic adoption of Industry 4.0 and Lean manufacturing. Augmented knowledge: A new era of industrial systems engineering. In Proceedings of the XXIV Summer School Francesco Turco, Brescia, Italy, 11–13 September 2019; pp. 129–135. [Google Scholar]
- Javied, T.; Deutsch, M.; Frank, J. A model for integrating energy management in lean production. Procedia CIRP 2019, 84, 357–361. [Google Scholar] [CrossRef]
- Dues, C.M.; Tan, K.H.; Lim, M. Green as the new Lean: How to use Lean practices as a catalyst to greening your supply chain. J. Clean. Prod. 2013, 40, 93–100. [Google Scholar] [CrossRef]
- Lee, J.; Yuvamitra, K.; Guiberteau, K.; Kozman, T.A. Six-Sigma Approach to Energy Management Planning. Strateg. Plan. Energy Environ. 2014, 33, 23–40. [Google Scholar] [CrossRef]
- Pampanelli, A.B.; Found, P.; Bernardes, A.M. A Lean & Green Model for a production cell. J. Clean. Prod. 2014, 85, 19–30. [Google Scholar]
- Zhang, Q.; Grossmann, I.E. Enterprise-wide optimization for industrial demand side management: Fundamentals, advances, and perspectives. Chem. Eng. Res. Des. 2016, 116, 114–131. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, W.; Li, H.; He, P. CO2 emission trends of China’s primary aluminum industry: A scenario analysis using system dynamics model. Energy Policy 2017, 105, 225–235. [Google Scholar] [CrossRef]
- Hilorme, T.; Honchar, O. Model of energy saving forecasting in entrepreneurship. J. Entrep. Educ. 2020, 22, 1–8. [Google Scholar]
- Proaño, L.; Sarmiento, A.T.; Figueredo, M.; Cobo, M. Techno-economic evaluation of indirect carbonation for CO2 emissions capture in cement industry: A system dynamics approach. J. Clean. Prod. 2020, 263, 121–457. [Google Scholar] [CrossRef]
- Chang, J.H.; Chiu, H.N. A comprehensive review of lot streaming. Int. J. Prod. Res. 2005, 43, 1515–1536. [Google Scholar] [CrossRef]
- Sarin, S.C.; Kalir, A.A.; Chen, M. A single-lot, unified cost-based flow shop lot-streaming problem. Int. J. Prod. Econ. 2008, 113, 413–424. [Google Scholar] [CrossRef]
- Zeng, M. Building an integrated energy system. China Electr. Power Enterp. Manag. 2018, 10, 57–59. [Google Scholar]
- Hillman, J.; Axon, S.; Morrissey, J. Social enterprise as a potential niche innovation breakout for low carbon transition. Energy Policy 2018, 117, 445–456. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, X. Has information and communication technology reduced energy consumption in enterprises? Evidence from survey data of Chinese manufacturing firms. China Ind. Econ. 2019, 2, 155–173. [Google Scholar]
- Zhao, Y.Q. System Dynamics Modeling and Dynamic Simulation of the Iron and Steel Production Process. Computer Applications. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2012. [Google Scholar]
- Zhou, J.; Chen, J. Construction of evaluation index system for the integration of the two industrializations in manufacturing enterprises. Comput. Integr. Manuf. Syst. 2013, 19, 2251–2263. [Google Scholar]
- Miao, C.; Feng, J.; Sun, L.; Ma, L. Evolution model of enterprise capability system based on collaborative theory and self-organization theory. J. Nanjing Univ. Sci. Technol. 2013, 37, 192–198. [Google Scholar]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Chen, H.; Liu, P.; Yu, H.; Xiao, X. Diagnostics of Oil Filter Clogging Fault for Electrostatic Servo Actuator Based on Improved PCA-SOM. China Mech. Eng. 2020, 32, 799–805. [Google Scholar]
- Li, W.; Zhang, S.; He, G. Semisupervised Distance-Preserving Self-Organizing Map for Machine-Defect Detection and Classification. IEEE Trans. Instrum. Meas. 2013, 62, 869–879. [Google Scholar] [CrossRef]



| Number | Parameter | Unit |
|---|---|---|
| 1 | Yield of finished products | % |
| 2 | Production reliability | ND |
| 3 | Comprehensive heat production rate | % |
| 4 | Equipment production efficiency | % |
| 5 | Wastewater recycling capacity | m3 |
| 6 | Information management index | ND |
| 7 | Production plan completion rate | % |
| 8 | Unrecognized energy loss | kgce/t |
| 9 | Water consumption per unit product | L/m3 |
| 10 | Product one-time qualification rate | % |
| 11 | Production defect loss ratio | % |
| 12 | Energy cost loss ratio | % |
| 13 | Comprehensive energy consumption per unit product | MWh/m2 |
| 14 | Air pollution per unit product | kg/m3 |
| 15 | Cost proportion of information technology construction | % |
| 16 | Manage controllable OEE ratios | % |
| 17 | Product fragment recycling rate | % |
| 18 | Flexibility (inventory turnover days) | d |
| 19 | Equipment overall efficiency (OEE) | % |
| Number | Variable | Dynamic Significance | Realistic Meaning |
|---|---|---|---|
| 1 | Si | Subsystem (status) | Substance flow, energy flow, information flow subsystem states |
| 2 | xi | Subsystem order parameter | Key production indicators for leading system collaboration trends |
| 3 | y | Large system status | Collaborative evolution status of production systems |
| 4 | a | Status parameters | Collaborative evolution speed of production systems |
| 5 | b | Action coefficient 1 | The effect of the relationship between two subsystems on another subsystem |
| 6 | Action coefficient 2 | Feedback or reverse effect of b | |
| 7 | Trend index | The driving effect of key indicators on production collaboration | |
| 8 | Damping coefficient | Non-collaborative factors, such as production and operation obstacles | |
| 9 | Correlation coefficient | Production correlation or resource allocation contradiction between subsystems | |
| 10 | Attenuation coefficient | The degree of attenuation of key indicators on production driving effects | |
| 11 | Impact coefficient 1 | The comprehensive driving effect of key indicators on production collaboration | |
| 12 | Impact coefficient 2 | The role of subsystem competitive behavior in collaborative evolution process | |
| 13 | Random variable | Conflicts between subsystems or non-directional interference from external environments | |
| 14 | Impact coefficient 3 | The impact of cooperative behavior between subsystems on evolutionary results | |
| 15 | Impact coefficient 4 | The impact of competitive behavior between subsystems on evolutionary results | |
| 16 | Impact coefficient 5 | The impact of collaboration between subsystems on large-scale system collaboration | |
| 17 | Self-feedback coefficient | Collaborative self-organization capability of production systems | |
| 18 | Ideal evolution result | Ordered state of collaborative evolution of production systems | |
| 19 | Coevolution bias | Deviation between actual evolution stage results and ideal results |
| Subsystem Name | Code | Order Parameter Name | Unit |
|---|---|---|---|
| Material flow subsystem | M1 | Equipment overall efficiency (OEE) | % |
| M2 | Yield of finished products | % | |
| M3 | Production reliability | ND | |
| Energy flow subsystem | E1 | Comprehensive energy consumption per unit product | MWh/m2 |
| E2 | Air pollution per unit product | kg/m3 | |
| E3 | Wastewater recycling capacity | m3 | |
| Information flow subsystem | I1 | Flexibility (inventory turnover days) | D |
| I2 | Cost proportion of information technology construction | % | |
| I3 | Information management index | ND |
| Order Parameter | Code | Theil Index | Proportion to System Weight | Proportion to Subsystem Weight | Comprehensive Weight of Subsystems |
|---|---|---|---|---|---|
| Order parameter of material flow subsystem | M1 | 0.2997 | 0.1276 | 0.4599 | 0.2776 |
| M2 | 0.2016 | 0.0859 | 0.3094 | ||
| M3 | 0.1504 | 0.064 | 0.2308 | ||
| Energy flow subsystem order parameter | E1 | 0.3116 | 0.1327 | 0.4015 | 0.3305 |
| E2 | 0.1596 | 0.068 | 0.2056 | ||
| E3 | 0.305 | 0.1299 | 0.3929 | ||
| Order parameter of information flow subsystem | I1 | 0.2823 | 0.1202 | 0.3067 | 0.3919 |
| I2 | 0.4969 | 0.2116 | 0.54 | ||
| I3 | 0.1411 | 0.0601 | 0.1533 |
| System | Ordering Degree of Material Flow Subsystem | Order Degree of Energy Flow Subsystem | Ordering Degree of Information Flow Subsystem | Order Degree of Production System | Collaboration Degree of Production System | |
|---|---|---|---|---|---|---|
| Year | ||||||
| 2013 | 0.481 | 0.411 | 0.210 | 0.041 | — | |
| 2014 | 0.377 | 0.882 | 0.114 | 0.038 | −0.064 | |
| 2015 | 0.870 | 0.015 | 0.393 | 0.005 | −0.250 | |
| 2016 | 0.728 | 0.225 | 0.479 | 0.078 | −0.117 | |
| 2017 | 0.161 | 0.472 | 0.402 | 0.031 | −0.150 | |
| 2018 | 0.676 | 0.313 | 0.636 | 0.135 | −0.212 | |
| 2019 | 0.563 | 0.485 | 0.451 | 0.123 | −0.080 | |
| 2020 | 0.540 | 0.709 | 0.324 | 0.124 | −0.029 | |
| 2021 | 0.610 | 0.565 | 0.401 | 0.138 | −0.057 | |
| 2022 | 0.850 | 0.718 | 0.448 | 0.274 | 0.124 | |
| Orderliness | Ordered Level | Synergy | Collaboration Level |
|---|---|---|---|
| 0~0.1 | Unordered state | <0 | Uncooperative |
| 0.1~0.5 | Low-level order | 0~0.3 | Low-level collaboration |
| 0.5~0.7 | Intermediate order | 0.3~0.6 | Moderate synergy |
| 0.7~1.0 | Advanced order | 0.6~0.8 | Highly collaborative |
| 0.8~1.0 | Extreme synergy |
| M-E | M1 | M2 | M3 | E1 | E2 | E3 |
|---|---|---|---|---|---|---|
| M1 | 1 | 0 | 0 | 0.68 | 0.79 | 0.64 |
| M2 | 0 | 1 | 0 | 0.67 | 0.78 | 0.67 |
| M3 | 0 | 0 | 1 | 0.64 | 0.73 | 0.63 |
| E1 | 0.81 | 0.66 | 0.75 | 1 | 0 | 0 |
| E2 | 0.84 | 0.73 | 0.76 | 0 | 1 | 0 |
| E3 | 0.77 | 0.66 | 0.74 | 0 | 0 | 1 |
| I-M | I1 | I2 | I3 | M1 | M2 | M3 |
|---|---|---|---|---|---|---|
| I1 | 1 | 0 | 0 | 0.64 | 0.53 | 0.80 |
| I2 | 0 | 1 | 0 | 0.66 | 0.59 | 0.82 |
| I3 | 0 | 0 | 1 | 0.63 | 0.65 | 0.79 |
| M1 | 0.65 | 0.67 | 0.65 | 1 | 0 | 0 |
| M2 | 0.59 | 0.65 | 0.72 | 0 | 1 | 0 |
| M3 | 0.6 | 0.70 | 0.67 | 0 | 0 | 1 |
| I-E | I1 | I2 | I3 | E1 | E2 | E3 |
|---|---|---|---|---|---|---|
| I1 | 1 | 0 | 0 | 0.70 | 0.56 | 0.79 |
| I2 | 0 | 1 | 0 | 0.75 | 0.65 | 0.77 |
| I3 | 0 | 0 | 1 | 0.63 | 0.55 | 0.84 |
| E1 | 0.68 | 0.65 | 0.62 | 1 | 0 | 0 |
| E2 | 0.65 | 0.65 | 0.66 | 0 | 1 | 0 |
| E3 | 0.79 | 0.71 | 0.85 | 0 | 0 | 1 |
| Serial Number | Factors Contributing to the Variability of Production System Flow Structure | Use Actual Data | Unit |
|---|---|---|---|
| 1 | Material flow equilibrium | Material processing balance time | s |
| 2 | Accumulated dissipation of energy flow | Loss of comprehensive energy efficiency of equipment | kpcs/s |
| 3 | Information flow, generation, and operation time | Equipment, materials, and fuel input time | s |
| 4 | The synergistic efficiency of material flow and energy flow | Comprehensive efficiency of equipment technology | % |
| 5 | Collaborative efficiency of material flow, energy flow, and information flow | Comprehensive efficiency of equipment management | % |
| 6 | Production system random impact index | Unidentified equipment comprehensive loss | kpcs/s |
| 7 | Special product production flow structure impact index | Customized product quantity per process | kpcs |
| 8 | Comprehensive efficiency of production system and flow structure | Processing efficiency of each process | kpcs/d |
| Process Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Data Category | |||||||||||
| Basic data | 24 | 24 | 2 | 1 | 5 | 24 | 24 | 1 | 24 | 1 | |
| Problem data | 5 | 5 | 24 | 24 | 24 | 2 | 1 | 24 | 1 | 24 | |
| Energy Control Projects | Project Management | Collaborative Management |
|---|---|---|
| Pollution control methods | Input and emission control | Full process control |
| Energy management methods | Planning, measurement, and post control | Self-organizing management |
| Pollutant generation | No changes before and after management | Reduce after management |
| Pollutant discharge level | Next cycle reduction | Reduction within the cycle |
| Energy consumption | Increased consumption of governance processes | Reduce |
| Energy usage costs | Increase | Reduce |
| Administrative expenses | Increase | Reduce |
| Proactive implementation | Passive | Active |
| Product quality | Unchanged | Increase |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; He, Z.; Jiang, L.; Liu, Z.; Leng, X. Synergy Management of a Complex Industrial Production System from the Perspective of Flow Structure. Systems 2023, 11, 453. https://doi.org/10.3390/systems11090453
Song J, He Z, Jiang L, Liu Z, Leng X. Synergy Management of a Complex Industrial Production System from the Perspective of Flow Structure. Systems. 2023; 11(9):453. https://doi.org/10.3390/systems11090453
Chicago/Turabian StyleSong, Jiekun, Zeguo He, Lina Jiang, Zhicheng Liu, and Xueli Leng. 2023. "Synergy Management of a Complex Industrial Production System from the Perspective of Flow Structure" Systems 11, no. 9: 453. https://doi.org/10.3390/systems11090453
APA StyleSong, J., He, Z., Jiang, L., Liu, Z., & Leng, X. (2023). Synergy Management of a Complex Industrial Production System from the Perspective of Flow Structure. Systems, 11(9), 453. https://doi.org/10.3390/systems11090453








