Evaluation Research on Resilience of Coal-to-Liquids Industrial Chain and Supply Chain

Abstract

The objective of this study is to enhance the resilience of the coal-to-liquids (CTL) industrial chain and supply chain to withstand increasing shock pressures. There is an urgent need to improve the resilience of the industrial chain and supply chain. This paper identifies 21 resilience-influencing factors from 4 perspectives: absorption capacity, adaptability, recovery capacity, and self-learning capacity; it then constructs an evaluation indicator system. The Interval Type 2 Fuzzy-Decision-Making Trial and Evaluation Laboratory-Analytic Network Process (IT2F-DEMATEL-ANP) method is adopted to determine the weights of the indicator system, and a resilience evaluation is performed based on the Interval Type 2 Fuzzy-Prospect Theory-Technique for Order Preference by Similarity to an Ideal Solution (IT2F-PT-TOPSIS) method. Furthermore, in the case of the CTL industrial chain and supply chain of China Shenhua Energy Group Ningxia Coal Industry Co., Ltd. (CENC) (Ningxia, China), this study ranks the resilience level from 2018 to 2022 to identify the factors that have contributed to a reduction in resilience and to implement measures to enhance the resilience of the CTL industrial chain and supply chain. The results show that the level of the CTL industrial chain and supply chain resilience was lowest in 2020, while it was highest in 2021. Factors such as the degree of domestication of key technologies, the rationality of the CTL industry layout, and the stability of supply and demand chains are identified as significant determinants of resilience levels. This points the way to enhancing the resilience of the CTL industry and supply chain.

1. Introduction

The world is undergoing momentous changes unseen in a century. The intertwined and superimposed impacts of the energy transition, extreme climate, the COVID-19 pandemic, and other factors present a significant risk to the global energy market and geopolitical stability. These developments have resulted in a profound transformation of the global energy market. The issue of energy security and supply has assumed a heightened prominence in the context of the evolving global energy landscape [1].

Currently, the world’s energy demand is primarily dependent on non-renewable energy sources, while global energy consumption is increasing annually due to industrial development and population growth [2]. Given China’s resource endowment and the ongoing expansion of strategic crude oil reserves, it is challenging for China’s oil production to keep pace with the rapid economic growth and the rising demand for oil. Hence, the total amount of oil consumed continues to exceed domestic production. Moreover, the uneven geographical distribution of oil resources has resulted in a concentration of oil-exporting countries, with a heightened degree of dependence on high-risk countries and regions that are vulnerable to geopolitical friction. This has caused the “stranglehold” risk to the maritime lifeline, exerting considerable pressure on China’s oil imports. China is the world’s largest producer and consumer of coal, with a share of over 50% in its primary energy consumption for an extended period. This has made coal the mainstay of China’s energy consumption. Despite the reduction in the proportion of coal in the context of the green and low-carbon transition and the continued optimization of the energy structure, the current supply capacity of clean energy sources such as wind and solar energy exhibits significant volatility and intermittency [3]. This may have a negative impact on the stability, security, and economy of the energy system [4]. Therefore, China’s current trend of fossil energy-based energy consumption is unlikely to undergo a significant shift in the near future. This suggests that the growth of rigid domestic energy demand is also unlikely to change and that coal will continue to play a pivotal role in China’s energy security in the short term.

The development of the coal-to-liquids (CTL) industry in China, which utilizes the country’s abundant coal resources, is of great strategic significance in addressing the situation of “more coal but less oil”, reducing its degree of external dependence, stabilizing its petroleum supply, and enhancing its ability to guarantee the country’s energy security. CTL is an important and cleaner source of petroleum in China [5], and CTL technology has been listed as an important technology to be developed and deployed in China’s “14th Five-Year Plan”. In contrast to the conventional single fossil energy supply, CTL, a contemporary coal chemical industry, represents a transformation of coal utilization from a “fuel-based” to a “chemical-raw-material-based” approach. Nevertheless, this “transformation” has also given rise to a number of supply-related issues, including high energy consumption, unstable equipment operation, high storage and transportation costs, and intense pressure on price competition in production, transportation, storage, and sales. As a significant contributor to the refined oil market, the demand for CTL products is directly influenced by fluctuations in the capacity of traditional refining and chemical plants and changes in market demand for refined oil products, which exhibits a high degree of uncertainty [6]. The resolution of this uncertainty is regarded as one of the most critical issues facing the industrial chain and supply chain [7]. Furthermore, the CTL industry is subject to a “double linkage” with the oil and coal markets, rendering it susceptible to external risks. For instance, during periods of geopolitical conflict, the energy sector is particularly vulnerable to tensions in the supply chain and price volatility. This is because fluctuations in coal prices directly impact the production costs of CTL, while fluctuations in oil prices affect the sales and profits of CTL. This also makes the CTL industry more sensitive to price changes compared to the single coal or oil industry. Consequently, in comparison to the traditional single fossil energy industrial chain and supply chain, the loss cost of the CTL industrial chain and supply chain is higher, its vulnerability is increased, and the problem of dual-chain management is more pronounced.

The industrial chain and supply chain originates from the deep integration and development of the value chain, industrial chain, and supply chain [8], which is a new type of value network system that emphasizes “chain” processing and the value-added value chain as the center and is based on the industrial chain division of labor to form coherent production, circulation, distribution, and consumption. The continuous improvement of the resilience and competitiveness of the industrial chain and supply chain is a fundamental requirement for the security and stability of the industrial chain and supply chain, as well as an essential element in the operation of the modernized national economic system. The enhancement of the resilience of the CTL industrial chain and supply chain represents a pivotal strategy for the resolution of the CTL supply problem, and it is also a matter of common concern to academia, industry, and government. Therefore, this paper aims to address the following questions: (1) What is the connotation of CTL industrial chain and supply chain resilience? (2) What methodology can be employed to evaluate the resilience of the CTL industrial chain and supply chain from a scientific perspective? (3) What strategies can be employed to enhance the resilience of the CTL industrial chain and supply chain?

This study makes certain important contributions to the field:

(1)

First, this paper presents an accurate definition and connotation explanation of the resilience of the CTL industrial chain and supply chain. It not only applies the resilience theory to the CTL field, but also systematically defines and explains the concept of the resilience of the CTL industrial chain and supply chain, which provides a clear theoretical foundation and conceptual framework for the subsequent research.

(2)

Second, this paper proposes a set of evaluation frameworks for the resilience of the CTL industrial chain and supply chain. The framework incorporates an indicator system for factors such as rationality of CTL industrial layout, strategic CTL production capacity reserve, and construction of strategic CTL bases and determines the weights of the indicator system by using the interval type 2 fuzzy-decision-making trial and evaluation laboratory-analytic network process (IT2F-DEMATEL-ANP) method and conducts a resilience evaluation based on the interval type 2 fuzzy-prospect theory-technique for order preference by similarity to the ideal solution (IT2F-PT-TOPSIS), which can comprehensively and reasonably assess the resilience of CTL industrial chain and supply chain.

(3)

Finally, the results of the evaluation have led to the formulation of a series of strategies and suggestions designed to enhance the resilience of the CTL industrial chain and supply chain. These strategies not only consider optimization within the industry but also involve synergy with external factors such as government policies, market demand, and technological innovation. The implementation of these comprehensive measures will effectively enhance the resilience and sustainability of the CTL industrial chain and supply chain, which is of great significance in promoting energy supply security and economic stability.

The remainder of this paper is organized as follows: Section 2 presents a literature review, which introduces the security and management issues of the industrial chain and supply chain of CTL, concepts of the resilience of industrial chain and supply chain, and an evaluation of resilience. Section 3 introduces the resilience evaluation model of this paper. Section 4 applies the established evaluation model to the case to obtain the evaluation results. Section 5 presents the analysis of the results and countermeasure suggestions. Section 6 presents the conclusions obtained from this paper.

2. Literature Review

2.1. Industrial Chain and Supply Chain of CTL

CTL is a chemical process that liquefies coal into liquid fuels, such as gasoline and diesel [9]. It provides a means for countries with limited hydrocarbon resources to explore the substitution of oil with their dominant resource: coal. The process is divided into two categories: direct coal liquefaction and indirect liquefaction [10]. The distinction between the two is based on the technical route employed. In 2004, Shenhua Group constructed the world’s first and largest 1 Mt a-1 direct liquefaction plant [11]. The CTL industrial chain supply chain represents a comprehensive new value network system that deeply integrates the core elements and development of the value chain, industrial chain, and supply chains. In this system, the “chain” processing and value-added process of the value chain is the focal point, and the value added is realized through a series of chemical processing and physical transformation processes in which coal is transformed into oil products. Moreover, the system is founded upon the principles of the division of labor within the industrial chain, facilitating connections between disparate links, including coal mining, CTL production, oil distribution, and distribution until final consumption. This network structure encompasses the entirety of the product life cycle, demonstrating remarkable efficiency and responsiveness to market demand. The CTL industrial chain and supply chain encompass a multitude of pivotal interconnections. Initially, coal is transported from its point of origin through a series of intricate processes, including mining and transportation. At the processing plant, the coal undergoes a complex chemical transformation, whereby it is converted into synthesis gas at elevated temperatures and pressures. This synthesis gas is subsequently subjected to further chemical reactions, resulting in the production of liquid fuel products. Subsequently, the products are stored, transported, and distributed to various end users, including transportation, the chemical industry, the aerospace industry, and other sectors.

The concepts of security and resilience are closely intertwined. Security, in its ex-ante planning of the system life cycle, is concerned with the prevention of potential threats. Resilience, on the other hand, encompasses both ex-ante planning and ex-post recovery. In light of the increasing complexity of systems and the prevalence of environmental uncertainty, it is no longer feasible to merely avoid and control risks. The concept of resilience is concerned with the ability of a system to resist, recover from, and adapt to risks [12]. Gasser’s research involves a comprehensive resilience assessment of supply chain security performance in 140 countries and regions. The assessment extends beyond the conventional definitions of security, encompassing not only the frequency of risks but also the severity of accidents [13]. As CTL projects are still in the initial development phase, there has been relatively little attention paid to the issue of resilience of the CTL industrial chain and supply chain. Scholars have, however, devoted more attention to the issue of security management of CTL. Scholars have identified the high energy consumption of CTL projects and evaluated the economics of CTL projects in terms of water resources and carbon consumption, providing a useful reference for the resource consumption of the CTL industry [5,14]. Qi et al. [15] evaluated the economic impact of CTL projects through a direct assessment of their economic effects using multiplier analysis. Their findings indicated that CTL projects can stimulate economic output and employment. Zhou et al. [16] emphasized the optimal planning problem of CTL supply chains, developing a two-stage stochastic planning model to identify the optimal planning strategy for CTL supply chains under deterministic conditions. A review of the literature reveals that the majority of studies on the CTL industrial chain and supply chain have adopted a micro-level perspective, focusing on local issues within these chains. However, there is a paucity of research examining the macro-level aspects of the overall safety management of the CTL industrial chain and supply chain. This limitation results in inadequate risk identification and assessment of the overall risk of the CTL industrial chain and supply chain. Furthermore, it hinders a comprehensive understanding of the interdependence and potential systemic risks among the links in the industrial chain and supply chain.

In addition, scholars engaged in the study of energy have conducted a multitude of investigations into the security and management of the oil and coal industrial chain and supply chain. Sun et al. [17] identified the primary determinants of energy geopolitics from the perspective of China’s security of energy supply through the use of multi-attribute analysis, factor analysis, and other methodologies. In their examination of the threat posed by four types of geopolitical risks to China’s oil security, Gong et al. [18] concluded that the most significant manifestation of this threat is the disruption of oil in the international market. In conclusion, the majority of industrial chain and supply chain security management within the energy sector is concentrated on the research of single fossil energy sources. The security of the modern coal chemical industry, particularly the security of the CTL industrial chain and supply chain, has been relatively understudied by both academia and industry. Consequently, there is a paucity of in-depth and systematic understanding.

2.2. Resilience of the Industrial Chain and Supply Chain

2.2.1. Concept of Resilience

The word “resilience” is derived from the Latin word “resillo/resiliere”, meaning “to jump back/to bounce back” [19]. In the current global environment, characterized by high uncertainty and complexity, energy systems are exposed to a variety of risks, both internal and external. These systems exhibit resilience characteristics similar to those observed in physical systems, such as the ability to withstand shocks, absorb losses, and gradually recover from damaged states. Holling initially applied the concept of “resilience” in physics to the field of ecology [20], subsequently extending its scope to psychology [21], sociology [22], economics [23], and other fields. The research paradigm suggests that the development history of resilience can be approximately divided into three categories: engineering resilience, ecological resilience, and evolutionary resilience. The concept of engineering resilience is a fundamental aspect of physics, encompassing the capacity of structures and materials to withstand compression and recuperate from deformation when subjected to external forces [24]. Ecological resilience can be defined as the capacity of a system to absorb shocks before the equilibrium is altered [20]. Evolutionary resilience places particular emphasis on the system’s dynamic learning and innovation abilities, which necessitate the system’s continuous adaptation and adjustment, as well as its capacity to recover to a higher level of equilibrium following a perturbation. This study builds upon previous research to propose that evolutionary resilience is the most appropriate connotation of resilience for the CTL industrial chain and supply chain, which aligns more closely with the complexity and dynamics of the CTL industrial chain and supply chain system.

2.2.2. Application of Resilience in Industrial Chain and Supply Chain

The resilience of the industrial chain and supply chain is contingent upon an understanding of their vulnerability. Initial research on supply chain vulnerability was conducted by Cranfield University in the United Kingdom. Christopher and colleagues initially proposed the original framework for defining supply chain resilience. This framework defines supply chain resilience as the ability of a supply chain system to return to its original state or migrate to a new, more satisfactory state after a disruption, which includes the characteristics of flexibility, adaptability, and agility [25]. This paper defines the resilience of the CTL industrial chain and supply chain as the ability of the system to withstand external shocks, such as those caused by climate, the economy, technology, and society, as well as internal perturbations, and to adapt, recover, and update thereafter. This definition is based on the resilience framework developed by Afgan and Veziroglu [26].

The majority of existing studies on the resilience of the industrial chain and supply chain have focused on the manufacturing industry. These studies have been primarily based on operational and performance aspects of the industrial chain and supply chain [27], disruptions in these chains [28], and the integration of internal capabilities and external relationships [29]. They have also explored the factors influencing resilience in the industrial chain and supply chain and the enhancement paths from different perspectives. However, these studies tend to ignore the specific needs and characteristics of particular industries when exploring industrial chain and supply chain resilience, especially energy conversion industries such as CTL. These industries necessitate more intricate and customized resilience management strategies due to their inherent complexity, high risk, and sensitivity to changes in the external environment. Therefore, this paper presents a comprehensive evaluation of CTL industrial chain and supply chain resilience from a multi-dimensional approach, encompassing the external environment, industry, enterprise, and policy perspectives while integrating CTL industry characteristics. This integration serves as a complementary contribution to the existing literature on the CTL industrial chain and supply chain.

2.2.3. Methods for Evaluating Resilience

The core of resilience magnitude measurement is resilience evaluation. Relevant studies have primarily focused on the fields of urban resilience [30], regional resilience [31], and energy system resilience [32]. The evaluation methods employed in this field can be broadly classified into two categories: qualitative and quantitative. The former encompasses techniques such as hierarchical analysis based on gray theory [33] and TOPSIS [34], which rely on expert judgment and comparison to assess the resilience of a system. The latter is broadly divided into two categories, one of which is based on the evaluation indicator system for resilience evaluation. For instance, Cutter et al. [35] developed a conceptual framework of regional disaster resilience from the perspective of disasters that encompasses six dimensions: ecological, social, economic, institutional, infrastructural, and community competence. Indicators were established and scored under each dimension, and the total score was calculated by weighted average. However, the existing studies on resilience evaluation typically fail to consider the psychological expectations of experts. To address this limitation, this paper employs prospect theory to use positive and negative ideal solutions as reference points for experts’ decision-making. This approach considers the limited rationality of experts, enhancing the scientific and objective rigor of the evaluation method. Moreover, incorporating psychological factors into resilience evaluation offers a novel perspective. An alternative approach is to utilize the combination of an indicator system and a resilience curve. For instance, Pei et al. [36] established a framework for evaluating urban safety resilience that includes pre-disaster prevention, disaster-bearing carriers, emergencies, and emergency management. This framework was developed through a systematic analysis of the urban safety resilience curve. Nevertheless, the computational difficulties inherent to resilience evaluation, particularly when dealing with complex system dynamics and uncertainty, pose a significant challenge in the context of resilience curves. In order to address this issue, this paper employs an evaluation methodology based on the resilience indicator system. This methodology enables a more comprehensive assessment of the resilience of the system while circumventing the computational complexity associated with the integration of resilience curves.

2.3. Research Review

A review of the existing literature reveals a paucity of studies on CTL industrial chain and supply chain resilience, accompanied by a dearth of precise definitions of the term. Second, there is no established set of evaluation indicators that align with the specific characteristics of the CTL industrial chain and supply chain. Finally, with regard to evaluation methods, qualitative evaluation methods are susceptible to the subjective influence of decision-makers, while quantitative evaluation methods are challenging to implement, and a single method cannot fully reflect the authenticity and reliability of resilience evaluation results. To address the aforementioned gaps, this study focuses on three crucial aspects: (1) The resilience theory is employed to delineate the connotations of the CTL industrial chain and supply chain’s resilience. (2) In light of the characteristics of the CTL industrial chain and supply chain, innovative proposals are put forward for indicators such as the rationality of CTL industrial layout, the strategic capacity reserve of CTL, and the strategic base construction of CTL to construct a resilience evaluation indicator system that aligns with China’s energy security objectives. (3) In order to address the systematic, fuzzy, and multi-criteria nature of the evaluation problem pertaining to the resilience of the CTL industrial chain and supply chain, an evaluation model based on ANP-PT-TOPSIS under IT2F is constructed. This model is designed to evaluate the resilience of the CTL industrial chain and supply chain and to provide theoretical support for enhancing the resilience of the CTL industrial chain and supply chain.

3. Evaluation Model of the CTL Industrial Chain and Supply Chain’s Resilience

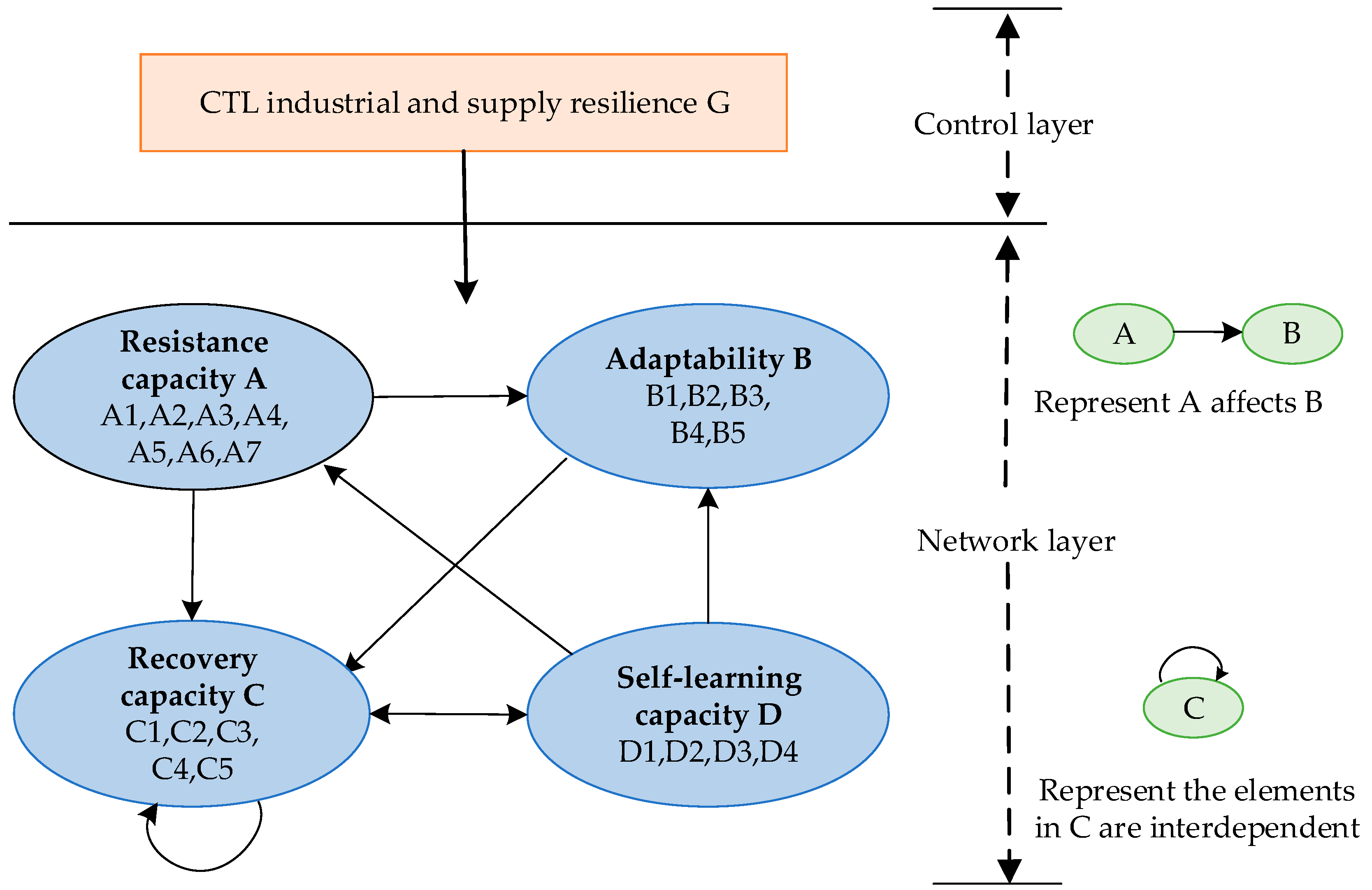
3.1. Construction of Evaluation Indicator System for CTL Industrial Chain and Supply Chain’s Resilience

In accordance with the principles of hierarchy, systematicity, and rationality that underpin the selection of evaluation indicators, this paper has identified a set of indicators with a high frequency of occurrence following a review of government documents and relevant literature. The Delphi method is used to invite experts in the CTL industry to repeatedly discuss. Based on the characteristics of the CTL industry, the resilience indicator system of the CTL industrial chain and supply chain is constructed from four dimensions, namely, environment, industry, enterprise, and government. The CTL industrial chain and supply chain resilience indicator system is constructed from the four dimensions of environment, industry, enterprise, and government. The first-level indicator is defined as the resilience of the CTL industrial chain and supply chain. The second-level indicators are divided into four indicators of absorptive capacity, adaptability, recovery capacity, and self-learning capacity. The tertiary indicators are modified to be subdivided into 21 indicators. The evaluation system is shown in Table 1.

Table 1. Evaluation system for the CTL industrial chain and supply chain’s resilience.

Second-Level Indicators	Third-Level Indicators	Indicator Definition	Reference
Absorptive capacity A	Stability of raw material source A1	The extent to which the company is able to reliably and consistently procure the raw materials required for production.	[37]
	International crude oil price A2	The profitability of CTL companies is influenced by the international crude oil price, which reflects the dynamics of supply and demand and determines the quality of production and the capacity for oil conversion.	[38]
	Revenue and profitability A3	The capacity of a company to generate net income and profits from its business activities.	[39]
	Production cost A4	The aggregate of direct and indirect costs incurred by a company in the production process.	[40]
	Degree of localization of key technologies A5	The proportion of key technologies that are independently developed and domestically produced.	[41]
	Degree of localization of key equipment A6	The share of key production equipment produced and supplied domestically.	[41]
	Capabilities of disaster defending and resistance A7	The capacity of a company to respond to and recover from natural disasters and other emergencies.	[42]
Adaptability B	Flexible production capacity B1	The capacity of the CTL industrial chain and supply chain to respond expeditiously to fluctuations in demand in response to environmental changes and uncertain events.	[43]
	CTL industry scale B2	The capacity for production and the number of companies engaged in the CTL industry.	[40]
	Safety management level B3	The level of construction, implementation, and monitoring of management systems in the company with respect to production safety.	[44]
	Equipment reliability B4	The stability and reliability of the production equipment to function properly and accomplish the production tasks as expected.	[45]
	Rationality of CTL industrial layout B5	The rationality of the geographic distribution and resource allocation of the CTL industry.	[5]
Recovery capacity C	Sustainability C1	The capacity of the CTL industrial chain and supply chain to achieve equilibrium between the disparate demands of environmental, social, and economic concerns while sustaining long-term growth.	[46]
	Stability of supply and demand chain C2	The ability of supply and demand chains to maintain stable operations against market volatility.	[47]
	CTL strategic capacity reserve C3	A reserve of CTL capacity established to respond to market or production fluctuations.	[48]
	Technical talent C4	The size and quality of the workforce with key technical knowledge and skills.	[49]
	Degree of industrial concentration C5	The degree of concentration in the distribution of companies within the industry is indicative of the concentration of competition and resource allocation within the market.	[50]
Self-learning capacity D	CTL strategic base construction D1	The level of development of the CTL industrial base built to ensure national energy security.	[5]
	Degree of industrial coupling D2	The extent to which different industries are interdependent, cooperate, and engage in synergistic development.	[51]
	Industrial innovation output value D3	The economic value and market competitiveness generated by the industry through technological innovation.	[52]
	Strength of policy support D4	The efficacy of policy concessions, financial support, and administrative services provided by the government to facilitate industrial development.	[53]

Table 1. Evaluation system for the CTL industrial chain and supply chain’s resilience.

Second-Level Indicators	Third-Level Indicators	Indicator Definition	Reference
Absorptive capacity A	Stability of raw material source A1	The extent to which the company is able to reliably and consistently procure the raw materials required for production.	[37]
	International crude oil price A2	The profitability of CTL companies is influenced by the international crude oil price, which reflects the dynamics of supply and demand and determines the quality of production and the capacity for oil conversion.	[38]
	Revenue and profitability A3	The capacity of a company to generate net income and profits from its business activities.	[39]
	Production cost A4	The aggregate of direct and indirect costs incurred by a company in the production process.	[40]
	Degree of localization of key technologies A5	The proportion of key technologies that are independently developed and domestically produced.	[41]
	Degree of localization of key equipment A6	The share of key production equipment produced and supplied domestically.	[41]
	Capabilities of disaster defending and resistance A7	The capacity of a company to respond to and recover from natural disasters and other emergencies.	[42]
Adaptability B	Flexible production capacity B1	The capacity of the CTL industrial chain and supply chain to respond expeditiously to fluctuations in demand in response to environmental changes and uncertain events.	[43]
	CTL industry scale B2	The capacity for production and the number of companies engaged in the CTL industry.	[40]
	Safety management level B3	The level of construction, implementation, and monitoring of management systems in the company with respect to production safety.	[44]
	Equipment reliability B4	The stability and reliability of the production equipment to function properly and accomplish the production tasks as expected.	[45]
	Rationality of CTL industrial layout B5	The rationality of the geographic distribution and resource allocation of the CTL industry.	[5]
Recovery capacity C	Sustainability C1	The capacity of the CTL industrial chain and supply chain to achieve equilibrium between the disparate demands of environmental, social, and economic concerns while sustaining long-term growth.	[46]
	Stability of supply and demand chain C2	The ability of supply and demand chains to maintain stable operations against market volatility.	[47]
	CTL strategic capacity reserve C3	A reserve of CTL capacity established to respond to market or production fluctuations.	[48]
	Technical talent C4	The size and quality of the workforce with key technical knowledge and skills.	[49]
	Degree of industrial concentration C5	The degree of concentration in the distribution of companies within the industry is indicative of the concentration of competition and resource allocation within the market.	[50]
Self-learning capacity D	CTL strategic base construction D1	The level of development of the CTL industrial base built to ensure national energy security.	[5]
	Degree of industrial coupling D2	The extent to which different industries are interdependent, cooperate, and engage in synergistic development.	[51]
	Industrial innovation output value D3	The economic value and market competitiveness generated by the industry through technological innovation.	[52]
	Strength of policy support D4	The efficacy of policy concessions, financial support, and administrative services provided by the government to facilitate industrial development.	[53]

(1)

The term “absorption capacity” refers to the ability of the CTL industrial chain and supply chain to withstand or absorb external shocks when perturbations occur [54], which mainly includes two parts: resisting external risks and improving self-tolerance. Hence, seven indicators are selected, including the stability of production raw material sources, the international crude oil price, revenue and profitability, production costs, the degree of localization of key technologies, the degree of localization of key equipment, and the capacities of disaster defense and resistance.

(2)

The term “adaptability” is used to describe the ability of the CTL industrial chain and supply chain as a whole to adapt to changes in the environment and to make adjustments to maintain operational performance in the face of potential risks [55]. This paper primarily concentrates on two key areas: industry and enterprise. To this end, five key indicators are selected for analysis: flexible production capacity, CTL industry scale, safety management level, equipment reliability, and rationality of CTL industrial layout.

(3)

The term “recovery capacity” is used to describe the ability of individual nodes within the CTL industrial chain and supply chain to recover from disruptive events in a timely manner [56]. This recovery process is dependent on the resilience of five key aspects: sustainability, stability of supply and demand chains, strategic reserve of CTL production capacity, technical talent, and industrial concentration.

(4)

The term “self-learning capacity” represents a new equilibrium within the CTL industrial chain and supply chain, whereby these systems are stimulated to achieve higher levels of learning and innovation in response to adversity, pressure, and environmental constraints. As a result of this stimulation, higher levels of learning are realized [52]. This paper presents four indicators designed to evaluate the self-learning capacity of the CTL industrial chain and supply chain’s resilience. The indicators include the CTL strategic base construction, the degree of industrial coupling, the industrial innovation output value, and the strength of policy support.

3.2. Interval Type 2 Fuzzy Set (IT2FS)

Each parameter and its definition are shown in

Table 2. Parameter and definition.

Syboml	Definition
$\tilde{A}$	Type 1 fuzzy set
${\mu }_{\tilde{A}}\left(x,u\right)$	Membership function
$x$	Primary variable
$J_x$	Minor variable
$\tilde{\tilde{A}}$	Interval Type 2 fuzzy set
${\tilde{A}}^u$	Upper trapezoid membership function
${\tilde{A}}^l$	Lower trapezoid membership function
$a_i^u$, $a_i^l$	Upper and lower reference points of interval type 2 fuzzy set $\tilde{\tilde{A}}$
$h_1({\tilde{A}}^u),h_2({\tilde{A}}^u)$	Denotes the membership value of the element $a_i^u$ in the upper trapezoidal membership function
$h_1({\tilde{A}}^l),h_2({\tilde{A}}^l)$	Denotes the membership value of the element $a_i^l$ in the lower trapezoidal membership function ${\tilde{A}}^u$
$d\left({\tilde{\tilde{A}}}_1,{\tilde{\tilde{A}}}_2\right)$	The distance between interval type 2 fuzzy sets ${\tilde{\tilde{A}}}_1$ and ${\tilde{\tilde{A}}}_2$
$D\left(A_i,A^{+}\right)$	The distance between indicator $A_i$ and positive ideal solution
$D\left(A_i,A^{-}\right)$	The distance between indicator $A_i$ and positive ideal solution
A	Weighted initial fuzzy matrix
$A^k$	The relation matrices given by k experts
$A_{ij}^k$	The degree of influence of indicator i on indicator j given by expert k
$X$	Normalized weighted initial fuzzy matrix
$X_{ij}$	The level of influence of indicator i on indicator j
$T$	Total relation matrix
$Defuzzified({\tilde{\tilde{A}}}_i)$	Defuzzied value of ${\tilde{\tilde{A}}}_i$
$P_S\left(s=1,2,\cdots ,m\right)$	Indicators on control layer
$C_i$	Element group on network layer
$e_{jl}\left(l=1,2,\cdots ,n_j\right)$	Elements in element group
$CI$	Consistency indicator
q	The maximum order of a matrix in the consistency test
CR	Consistency ratio
RI	Average random consistency index
${\lambda }_{\max }$	Largest eigenvalue
$w$	Eigenvector corresponding to the largest eigenvalue
$W$	Supermatrix
$F$	Weighted matrix
$\overline{W}$	Weighted supermatrix
$w_i$	Weight of attributes
$G^{+}$	The collection of positive ideal points
$g_j^{+}$	Ideal points of indicators
$G^{-}$	The collection of negative ideal points
$g_j^{-}$	Ideal points of indicators
$g_{kj}$	Evaluation value
$c_i$	Closeness coefficient
$V$	Prospect value
$w\left(p_i\right)$	Probability weight function
$v\left(\Delta x_i\right)$	$v\left(\Delta x_i\right)$ is value function, $\Delta x_i$ denotes the difference between attribute $x_i$ and the reference point
$\alpha \left(0<\alpha <1\right)$	The sensitivity of decision-makers to benefits
$\beta \left(0<\beta <1\right)$	The sensitivity of decision-makers to losses
$\chi$	The sensitivity of decision-makers to benefits
$X_{ij}$	Evaluation of the j-th indicator by the i-th expert
${\tilde{X}}_{ij}$	Semantic evaluation matrix
$r_{ij}$	Normalized semantic evaluation matrix
$Z_{ij}$	Weighted normalized semantic evaluation matrix
${\tilde{\tilde{X}}}^{+}$	Positive ideal solution of evaluation value
${\tilde{\tilde{X}}}^{-}$	Negative ideal solution of evaluation value
$R_i$	Closeness to the optimal ideal solution
$Rank$	Resilience level in a given year

.

3.2.1. Definition

Definition 1 

([57,58]). Define a type 2 fuzzy set (T2FS) $\tilde{A}$ on the domain $X$ as:

$$\tilde{A}=\left\{\left(x,u\right){\mu }_{\tilde{A}}\left(x,u\right)|\forall x\in X,\forall u\in J_x\subseteq \left[0,1\right]\right\}$$

(1)

where ${\mu }_{\tilde{A}}\left(x,u\right)$ is the membership degree function, $0\le {\mu }_{\tilde{A}}\left(x,u\right)\le 1$. $x$ denotes the main variables, $u$ denotes minor variables, and $J_x$ denotes the primary membership function of $x$. $\tilde{A}$ can also be presented:

$$\tilde{A}={\displaystyle {\int }_{x\in X}}{\displaystyle {\int }_{u\in J_x}}{\mu }_{\tilde{A}}\left(x,u\right)/\left(x,u\right)$$

(2)

Definition 2 

([57,58]). If a T2FS $\tilde{A}$ on the domain $X$ is defined to satisfy ${\mu }_{\tilde{A}}\left(x,u\right)=1$, then $\tilde{A}$ denotes an IT2FS, where

$$\tilde{A}={\displaystyle {\int }_{x\in X}}{\displaystyle {\int }_{u\in J_x}}1/\left(x,u\right)$$

(3)

Definition 3 

([57,58]). A trapezoidal IT2FS is defined as an IT2FS whose upper and lower bound affiliation functions are trapezoidal fuzzy numbers, namely

$$\tilde{\tilde{A}}=\left({\tilde{A}}^u,{\tilde{A}}^l\right)=\left[\begin{array}{c}{a}_1^u,a_2^u,a_3^u,a_4^u,h_1({\tilde{A}}^u),h_2({\tilde{A}}^u)\\ a_1^l,a_2^l,a_3^l,a_4^l,h_1({\tilde{A}}^l),h_2({\tilde{A}}^l)\end{array}\right]$$

(4)

where both ${\tilde{A}}^u$ and ${\tilde{A}}^l$ are type 1 fuzzy set, $a_1^u,a_2^u,a_3^u,a_4^u,a_1^l,a_2^l,a_3^l,a_4^l$ are the reference points of $\tilde{\tilde{A}}$, $h_1({\tilde{A}}^u),h_2({\tilde{A}}^u)$ represent the upper membership values of element reference points on the trapezoidal fuzzy function ${\tilde{A}}^u$, $h_1({\tilde{A}}^l),h_2({\tilde{A}}^l)$ represent the lower membership values of element reference points on the trapezoidal fuzzy function ${\tilde{A}}^l$.

3.2.2. The Algorithm of Trapezoidal Interval Type 2 Fuzzy Sets (IT2FSs)

Assume any two trapezoidal IT2FSs are as ${\tilde{\tilde{A}}}_2=\left({\tilde{A}}_2^u,{\tilde{A}}_2^l\right)$, ${\tilde{\tilde{A}}}_2=\left({\tilde{A}}_2^u,{\tilde{A}}_2^l\right)$, their algorithms [59] are as follows:

(1)

Additive operation

$${\tilde{\tilde{A}}}_1\oplus {\tilde{\tilde{A}}}_2=\left({\tilde{A}}_1^u,{\tilde{A}}_1^l\right)\oplus \left({\tilde{A}}_2^u,{\tilde{A}}_2^l\right)=\left\{\begin{array}{c}\begin{array}{l}{a}_{11}^u+a_{21}^u,a_{12}^u+a_{22}^u,a_{13}^u+a_{23}^u,a_{14}^u+a_{24}^u;\\ \min \left[h_1({\tilde{A}}_1^u),h_1({\tilde{A}}_2^u)\right],\min \left[h_2({\tilde{A}}_1^u),h_2({\tilde{A}}_2^u)\right]\end{array}\\ \begin{array}{l}{a}_{11}^l+a_{21}^l,a_{12}^l+a_{22}^l,a_{13}^l+a_{23}^l,a_{14}^l+a_{24}^l;\\ \min \left[h_1({\tilde{A}}_1^l),h_1({\tilde{A}}_2^l)\right],\min \left[h_2({\tilde{A}}_1^l),h_2({\tilde{A}}_2^l)\right]\end{array}\end{array}\right\}$$

(5)

(2)

Multiply operation

$${\tilde{\tilde{A}}}_1\otimes {\stackrel{⌢}{\tilde{A}}}_2=\left({\tilde{A}}_1^u,{\tilde{A}}_1^l\right)\otimes \left({\tilde{A}}_2^u,{\tilde{A}}_2^l\right)=\left\{\begin{array}{c}\begin{array}{l}{a}_{11}^u\times a_{21}^u,a_{12}^u\times a_{22}^u,a_{13}^u\times a_{23}^u,a_{14}^u\times a_{24}^u;\\ \min \left[h_1({\tilde{A}}_1^u),h_1({\tilde{A}}_2^u)\right],\min \left[h_2({\tilde{A}}_1^u),h_2({\tilde{A}}_2^u)\right]\end{array}\\ \begin{array}{l}{a}_{11}^l\times a_{21}^l,a_{12}^l\times a_{22}^l,a_{13}^l\times a_{23}^l,a_{14}^l\times a_{24}^l;\\ \min \left[h_1({\tilde{A}}_1^l),h_1({\tilde{A}}_2^l)\right],\min \left[h_2({\tilde{A}}_1^l),h_2({\tilde{A}}_2^l)\right]\end{array}\end{array}\right\}$$

(6)

(3)

Scalar multiplication

$$k{\tilde{\tilde{A}}}_1=k\left({\tilde{A}}_1^u,{\tilde{A}}_1^l\right)=\left\{\begin{array}{c}\left[k{a}_{11}^u,k{a}_{12}^u,k{a}_{13}^u,k{a}_{14}^u;h_1({\tilde{A}}_1^u),h_2({\tilde{A}}_1^u)\right],\\ \left[k{a}_{11}^l,k{a}_{12}^l,k{a}_{13}^l,k{a}_{14}^l;h_1({\tilde{A}}_1^l),h_2({\tilde{A}}_1^l)\right]\end{array}\right\}$$

(7)

(4)

Power operation

$$\sqrt[{\displaystyle \frac{1}{k}}]{{\tilde{\tilde{A}}}_1}=\left\{\begin{array}{c}\left[\sqrt[{\displaystyle \frac{1}{k}}]{a_{11}^u},\sqrt[{\displaystyle \frac{1}{k}}]{a_{12}^u},\sqrt[{\displaystyle \frac{1}{k}}]{a_{13}^u},\sqrt[{\displaystyle \frac{1}{k}}]{a_{14}^u};h_1({\tilde{A}}_1^u),h_2({\tilde{A}}_1^u)\right],\\ \left[\sqrt[{\displaystyle \frac{1}{k}}]{a_{11}^l},\sqrt[{\displaystyle \frac{1}{k}}]{a_{12}^l},\sqrt[{\displaystyle \frac{1}{k}}]{a_{13}^l},\sqrt[{\displaystyle \frac{1}{k}}]{a_{14}^l};h_1({\tilde{A}}_1^l),h_2({\tilde{A}}_1^l)\right]\end{array}\right\}$$

(8)

(5)

The distance between two trapezoidal IT2FSs [60]

$$d\left({\tilde{\tilde{A}}}_1,{\tilde{\tilde{A}}}_2\right)=\sqrt{{\displaystyle \frac{1}{12}}\left({\Delta }^u+{\Delta }^l\right)}$$

(9)

where ${\Delta }^u={\displaystyle \sum _{i=1}^4{\left(a_{1i}^u-a_{2i}^u\right)}^2}+{\displaystyle \sum _{j=1}^2{\left[h_j({\tilde{A}}_1^u)-h_j({\tilde{A}}_2^u)\right]}^2}$, ${\Delta }^l={\displaystyle \sum _{i=1}^4{\left(a_{1i}^l-a_{2i}^l\right)}^2}+{\displaystyle \sum _{j=1}^2{\left[h_j({\tilde{A}}_1^l)-h_j({\tilde{A}}_2^l)\right]}^2}$.

Then, the distance between each indicator and the positive/negative ideal solution can be obtained:

$$D\left(A_i,A^{+}\right)=\sqrt{{\displaystyle \sum _{j=1}^n{\left[d\left({\tilde{\tilde{A}}}_{ij},{\tilde{\tilde{A}}}_{j^{+}}\right)\right]}^2}},D\left(A_i,A^{-}\right)=\sqrt{{\displaystyle \sum _{j=1}^n{\left[d\left({\tilde{\tilde{A}}}_{ij},{\tilde{\tilde{A}}}_{j^{-}}\right)\right]}^2}}$$

(10)

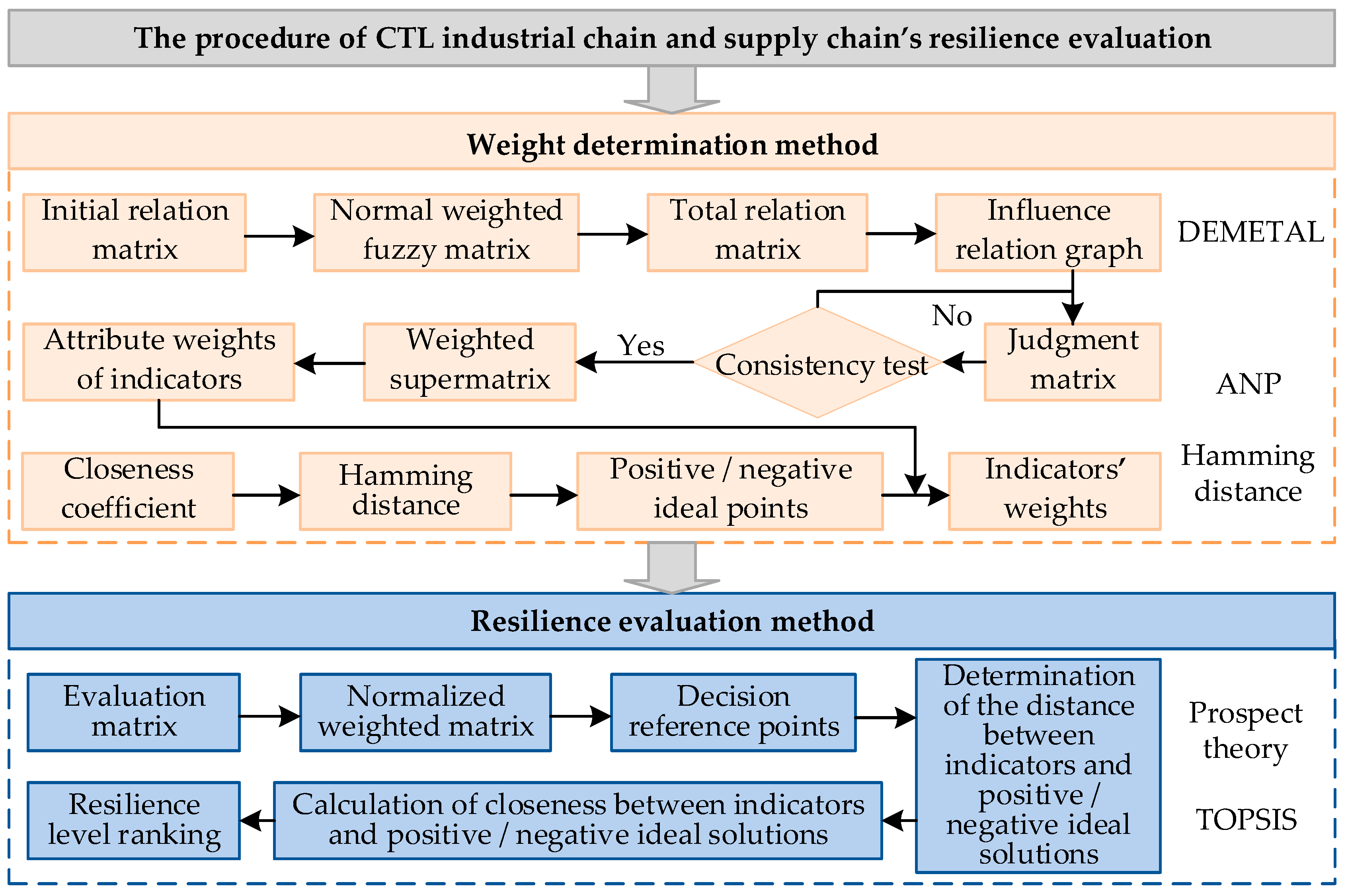
3.3. Procedure of Resilience Evaluation

Given the inherent complexity of the resilience evaluation of CTL industrial chain and supply chain and the inevitable hesitancy and uncertainty that accompany such decision-making processes [61], this study introduces IT2FS into the DEMATEL, ANP, prospect theory, and TOPSIS methods. In comparison to type 1 fuzzy sets, T2FSs are more effective in describing the uncertainty inherent to decision-making information and are therefore more suitable for multi-criteria decision-making problems. The combination of the DEMATEL and ANP methods allows for the construction of the mutual influence relationship between indicators, thereby providing a foundation for the internal and external relationship of influencing factors when constructing the ANP matrix. The combination of Prospect Theory and the TOPSIS method allows for the incorporation of psychological expectations, thereby enhancing the rationality of the resulting TOPSIS rankings. The resilience evaluation procedure is shown in Figure 1.

3.4. Determination of Indicators’ Weights Based on IT2F-DEMATEL-ANP

3.4.1. IT2F-DEMATEL Method

The IT2F-DEMATEL method represents an extension of the traditional DEMATEL approach to the context of type 2 fuzzy environments. It facilitates the transformation of linguistic variables, which are inherently inaccurate, into numerical variables. It is capable of determining the influence relationships between indicators through the establishment of a final influence matrix and the setting of a threshold. This approach avoids the potential limitations associated with the unscientific human setting of indicator influence network relationships. The specific steps are as follows:

Step 1: Determine linguistic variables. The precise numerical descriptions of the uncertain linguistic variables are selected using

Table 3. The IT2FS corresponding to linguistic variables that determine the degree of mutual influence of indicators.

Linguistic Variable	IT2FS
Very high influence (VHI)	[(0.8,0.9,0.9,1;1,1), (0.85,0.9,0.9,0.95;0.9,0.9)]
High influence (HI)	[(0.6,0.7,0.7,0.8;1,1), (0.65,0.7,0.7,0.75;0.9,0.9)]
Low influence (LI)	[(0.4,0.5,0.5,0.6;1,1), (0.45,0.5,0.5,0.55;0.9,0.9)]
Very low influence (VLI)	[(0.2,0.3,0.3,0.4;1,1), (0.25,0.3,0.3,0.35;0.9,0.9)]
No influence (NI)	[(0,0.1,0.1,0.1;1,1), (0,0.1,0.1,0.05;0.9,0.9)]

in order to transform them into specific IT2FS.

Step 2: Calculate weighted initial fuzzy matrix A. In accordance with the fuzzy relational linguistic variables, a total of k experts are selected to provide the relational matrix $A^k$, wherein the elements $A_{ij}^k$ within the matrix $A^k$ indicate the degree of influence $A_{ij}^k=\left\{\left[a_{ij1}^u,a_{ij2}^u,a_{ij3}^u,a_{ij4}^u,h_1({\tilde{A}}_{ij}^u),h_2({\tilde{A}}_{ij}^u)\right],\left[a_{ij1}^l,a_{ij2}^l,a_{ij3}^l,a_{ij4}^l,h_1({\tilde{A}}_{ij}^l),h_2({\tilde{A}}_{ij}^l)\right]\right\}$ of indicator i on indicator j as determined by expert k. The weighted initial fuzzy matrix A is then derived through the process of arithmetic averaging.

$$A={\left[A_{ij}^k\right]}_{n\times n}={\displaystyle \frac{1}{H}}{\displaystyle {\sum }_{k=1}^H{x}_{ij}^k}$$

(11)

Step 3: Calculate normalized weighted initial fuzzy matrix $X$.

$$X={\left[X_{ij}\right]}_{n\times n}=\left[\begin{array}{cccc}{X}_{11}& X_{12}& \cdots & X_{1n}\\ X_{21}& X_{22}& \cdots & X_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ X_{n1}& X_{n2}& \cdots & X_{nn}\end{array}\right]$$

(12)

$X_{ij}$ denotes the level of impact of indicator i on indicator j. When indicator i has no impact on indicator j, $X_{ij}=0$, where $X_{ij}=\left[\left(X_{ij1}^u,X_{ij2}^u,X_{ij3}^u,X_{ij4}^u,h_1({\tilde{X}}_{ij}^u),h_2({\tilde{X}}_{ij}^u)\right),\left(X_{ij1}^l,X_{ij2}^l,X_{ij3}^l,X_{ij4}^l,h_1({\tilde{X}}_{ij}^l),h_2({\tilde{X}}_{ij}^l)\right)\right]$. The weighted initial fuzzy matrix A is normalized according to Equations (13) and (14) to obtain the normalized fuzzy initial relation matrix $X$:

$$X={\displaystyle \frac{A}{S}}$$

(13)

$$X={\displaystyle \frac{A}{S}}$$

(14)

Step 4: Calculate the total relation matrix $T$. The normalized fuzzy initial relation matrix $X$ is divided into independent matrices of eight exact numbers:

$$x_k^u=\left[\begin{array}{cccc}{x}_{11k}^u& x_{12k}^u& \cdots & x_{1nk}^u\\ x_{21k}^u& x_{22k}^u& \cdots & x_{2nk}^u\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1k}^u& x_{n2k}^u& \cdots & x_{nnk}^u\end{array}\right], x_k^l=\left[\begin{array}{cccc}{x}_{11k}^l& x_{12k}^l& \cdots & x_{1nk}^l\\ x_{21k}^u& x_{22k}^l& \cdots & x_{2nk}^l\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1k}^l& x_{n2k}^l& \cdots & x_{nnk}^l\end{array}\right]$$

(15)

$$\left[t_{ijk}^u\right]=\left[x_k^u\right]\times {\left[I-X_k^u\right]}^{-1}, \left[t_{ijk}^l\right]=\left[x_k^l\right]\times {\left[I-X_k^l\right]}^{-1}$$

(16)

where $I$ is identity matrix, and the total relation matrix $T$ is

$$T={\left[t_{ij}\right]}_{n\times n}=\left(X^1+X^2+\cdots +X^k\right)=X{\left(1-X\right)}^{-1}$$

(17)

where $T_{ij}=\left[\left(T_{ij1}^u,T_{ij2}^u,T_{ij3}^u,T_{ij4}^u,h_1({\tilde{T}}_{ij}^u),h_2({\tilde{T}}_{ij}^u)\right),\left(T_{ij1}^l,T_{ij2}^l,T_{ij3}^l,T_{ij4}^l,h_1({\tilde{T}}_{ij}^l),h_2({\tilde{T}}_{ij}^l)\right)\right]$

Step 5: Draw the influence relationship diagram. The total relation matrix $T$ is defuzzified in accordance with Equation (18), and then the threshold is established through the application of the mean value method [62], which excludes correlations with minimal influence and thereby simplifies the network diagram of ANP influence relations.

$$\begin{array}{l}Defuzzified({\tilde{\tilde{A}}}_i)=\\ {\displaystyle \frac{1}{2}}\left\{\begin{array}{l}{\displaystyle \frac{1}{4}}\left[\left(a_{i4}^u-a_{1l}^u\right)+\left(h_1({\tilde{A}}_i^u)\cdot a_{i2}^u-a_{i1}^u\right)+\left(h_2({\tilde{A}}_i^u)\cdot a_{i3}^u-a_{i1}^u\right)\right]+a_{i1}^u\\ +{\displaystyle \frac{1}{4}}\left[(a_{i4}^l-a_{1l}^l)+\left(h_1({\tilde{A}}_i^l)\cdot a_{i2}^l-a_{i1}^l\right)+\left(h_2({\tilde{A}}_i^l)\cdot a_{i3}^l-a_{i1}^l\right)\right]+a_{i1}^l\end{array}\right\}\end{array}$$

(18)

3.4.2. IT2F-ANP Algorithm

In 1996, Saaty [63] proposed an analytic network process (ANP) based on the algorithm of hierarchical analysis (AHP). This process is able to reflect the mutual influence and dominance relationship between the elements of the system through the structure of the network. Furthermore, it is able to overcome the premise of AHP, which assumes that the relationship between the elements is independent of each other. In addition, CTL industrial chain and supply chain represent a complex system, comprising elements that are either directly or indirectly influenced by one another. Consequently, the ANP method is deemed an appropriate approach for assigning weights in this study. To account for the inherent fuzziness and uncertainty in the quantitative assessment of the indicators, a fuzzy set is integrated with the network analysis approach, resulting in the fuzzy analytic network process (Fuzzy-ANP). This study employs the IT2F-ANP algorithm to ascertain the weight of the indicators. The steps of the IT2F-ANP algorithm are shown below:

Step 1: Construct the ANP structure. The results of the IT2F DEMATEL calculation demonstrate the influence dominance relationship between the indicators, which can be used to construct the ANP structure of the resilience evaluation system.

Step 2: Determine linguistic variables. Experts are invited to undertake a comparative analysis of the relative importance of the indicators. Furthermore, the free and flexible linguistic variables are transformed into exact IT2FS in accordance with the specifications set forth in

Table 4. The IT2FS corresponding to linguistic variables that determine the relative importance of indicators.

Linguistic Variable	IT2FS
Absolutely strong (AS)	[(7,8,9,9;1,1), (7.2,8.2,8.8,9;0.8,0.8)]
(1/AS)	[(0.11,0.11,0.12,0.14;1,1), (0.11,0.11,0.12,0.14;0.8,0.8)]
Very strong (VS)	[(5,6,8,9;1,1), (5.2,6.2,7.8,8.8;0.8,0.8)]
(1/VS)	[(0.11,0.13,0.17,0.2;1,1), (0.11,0.13,0.16,0.19;0.8,0.8)]
Fairly strong (FS)	[(3,4,6,7;1,1), (3.2,4.2,5.8,6.8;0.8,0.8)]
(1/FS)	[(0.14,0.17,0.25,0.33;1,1), (0.15,0.17,0.24,0.31;0.8,0.8)]
Slightly strong (SS)	[(1,2,4,5;1,1), (1.2,2.2,3.8,4.8;0.8,0.8)]
(1/SS)	[(0.2,0.25,0.5,1;1,1), (0.21,0.26,0.45,0.83;0.8,0.8)]
Equal (E)	[(1,1,1,1;1,1), (1,1,1,1;1,1)]
(1/E)	[(1,1,1,1;1,1), (1,1,1,1;1,1)]

.

Step 3: Construct the judgement matrix and conduct the consistency test.

According to the ANP network model in Step 2, it can be observed that the control layer contains the indicators $P_1,P_2,\cdots ,P_m$, while the network layer contains the element groups $C_1,C_2,\cdots ,C_N$. Each element group $C_i$ comprises elements $e_{i1},e_{i2},\cdots ,e_{i{n}_i},i=1,2,\cdots ,N$. The control layer elements $P_S\left(s=1,2,\cdots ,m\right)$ are employed as the primary criteria, while the elements $e_{jl}\left(l=1,2,\cdots ,n_j\right)$ in $C_j$ serve as the secondary criteria. The elements in are analyzed in two-by-two comparisons according to the size of their influence on the linguistic variables. These elements are then transformed into the corresponding trapezoidal IT2FS, as outlined in Table 4, and a judgment matrix is constructed. To ascertain the consistency of the constructed judgment matrix, a consistency test is required:

$$CI=\left({\lambda }_{\max }-q\right)/\left(q-1\right)$$

(19)

where $Aw={\lambda }_{\max }w$, ${\lambda }_{\max }$ is the largest eigenvalue and $w$ is the eigenvector corresponding to the largest eigenvalue, q is the maximum order of a matrix.

$$CR=CI/RI$$

(20)

where CI denotes average random consistency index and CR denotes the consistency ratio. When $CR<0.1$, the fuzzy comparison judgment matrix is considered to be consistent, otherwise the expert needs to adjust his/her judgment matrix until the consistency test is satisfied.

Step 4: Calculate and construct the supermatrix. The priority vector is obtained by eigenvalue method:

$$r_{Ai}={\left({\tilde{\tilde{A}}}_{i1}\otimes {\tilde{\tilde{A}}}_{i2}\otimes \cdots \otimes {\tilde{\tilde{A}}}_{in}\right)}^{{\displaystyle \frac{1}{n}}}$$

(21)

$$w_{i{n}_i}^{(j{n}_j)}=r_{Ai}\otimes {\left(r_{A1}\oplus r_{A2}\oplus \cdots \oplus r_{An}\right)}^{-1}$$

(22)

$${\omega }_{j{n}_j}={\left[w_{i1}^{(j{n}_j)},w_{i2}^{(j{n}_j)},\cdots w_{i{n}_i}^{(j{n}_j)}\right]}^T$$

(23)

When the eigenvectors satisfy the consistency test, they are expressed in the matrix form $W_{ij}$:

$$W_{ij}=\left({\omega }_{j1},{\omega }_{j2},\cdots {\omega }_{j{n}_j}\right)$$

(24)

$$W_{ij}=\left[\begin{array}{cccc}{w}_{i1}^{(j1)}& w_{i1}^{(j2)}& \cdots & w_{i1}^{(j{n}_j)}\\ w_{i2}^{(j1)}& w_{i2}^{(j2)}& \cdots & w_{i2}^{(j{n}_j)}\\ ⋮& ⋮& \ddots & ⋮\\ w_{i{n}_i}^{(j1)}& w_{i{n}_i}^{(j2)}& \cdots & w_{i{n}_i}^{(j{n}_j)}\end{array}\right]$$

(25)

The column vector of $W_{ij}$ represents the priority vector of the importance of the elements $e_{i1},e_{i2},\cdots ,e_{i{n}_i}$ in $C_i$ relative to the elements $e_{j1},e_{j2},\cdots ,e_{j{n}_j}$ in $C_j$. If the elements in $C_j$ are not affected by the elements in $C_i$, then $W_{ij}=0$. The aforementioned steps are repeated to finally obtain the supermatrix:

$$W=\left[\begin{array}{cccc}{W}_{11}& W_{12}& \cdots & W_{1n}\\ W_{21}& W_{22}& \cdots & W_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ W_{ni}& W_{n2}& \cdots & W_{nn}\end{array}\right]$$

(26)

Step 5: Construct the weighted supermatrix. The weighted matrix F is derived by evaluating the relative importance of $C_j$ in comparison to $P_S$ as the primary criterion.

$$F=\left[\begin{array}{cccc}1& {\tilde{\tilde{A}}}_{12}& \cdots & {\tilde{\tilde{A}}}_{1n}\\ {\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\tilde{\tilde{A}}}_{12}$}\right.}& 1& \cdots & {\tilde{\tilde{A}}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\tilde{\tilde{A}}}_{1n}$}\right.}& {\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\tilde{\tilde{A}}}_{2n}$}\right.}& \cdots & 1\end{array}\right]$$

(27)

where ${\tilde{\tilde{A}}}_{ij}=\left[\begin{array}{c}{a}_{ij1}^u,a_{ij2}^u,a_{ij3}^u,a_{ij4}^u,h_1({\tilde{A}}_{ij}^u),h_2({\tilde{A}}_{ij}^u)\\ a_{ij1}^l,a_{ij2}^l,a_{ij3}^l,a_{ij4}^l,h_1({\tilde{A}}_{ij}^l),h_2({\tilde{A}}_{ij}^l)\end{array}\right]$, ${\displaystyle \frac{1}{{\tilde{\tilde{A}}}_{ij}}}=\left[\begin{array}{c}{\displaystyle \frac{1}{a_{ij1}^u}},{\displaystyle \frac{1}{a_{ij2}^u}},{\displaystyle \frac{1}{a_{ij3}^u}},{\displaystyle \frac{1}{a_{ij4}^u}},h_1({\tilde{A}}_{ij}^u),h_2({\tilde{A}}_{ij}^u)\\ {\displaystyle \frac{1}{a_{ij1}^l}},{\displaystyle \frac{1}{a_{ij2}^l}},{\displaystyle \frac{1}{a_{ij3}^l}},{\displaystyle \frac{1}{a_{ij4}^l}},h_1({\tilde{A}}_{ij}^l),h_2({\tilde{A}}_{ij}^l)\end{array}\right]$.

The weighted supermatrix can be obtained by weighing the elements in the supermatrix W:

$$\overline{W}=F\cdot W$$

(28)

where, ${\overline{W}}_{ij}={\tilde{\tilde{A}}}_{ij}\cdot W_{ij}$, $i=1,2,\cdots ,N$, $j=1,2,\cdots ,N$.

Step 6: The weighted matrix is normalized to obtain the attribute weights $w_i$ assigned by different experts to the same indicator.

In order to address the issue of subjectivity and contingency resulted from experts’ knowledge, experience, and behavioral preferences inherent in the derivation of indicator weights from ANP, this paper employs the relative entropy method based on Hamming’s distance measurement to obtain decision-makers’ weights that are subjectively and objectively integrated and weighted. The steps are as follows:

Step 7: Determine the positive and negative ideal points [64].

The positive ideal point is $G^{+}=(g_1^{+},g_2^{+},\cdots ,g_n^{+})$, while the negative one is $G^{-}=(g_1^{-},g_2^{-},\cdots ,g_n^{-})$, where $g_j^{+}=\max g_{kj}$, $g_j^{-}=\min g_{kj}$, and $g_{kj}$ denotes the evaluation value of the k-th expert to j-th indicator.

Step 8: Calculate the Hamming distance between the comprehensive evaluation values of different experts for each indicator to the positive and negative ideal points.

$$\begin{gathered} d\left(w_i,G^{+}\right)={\displaystyle \frac{1}{8}}\left[\begin{array}{l}|a_{i1}^u-a_{j1}^{u^{+}}|+|a_{i2}^u\cdot h(A_i^u)-a_{j2}^{u^{+}}\cdot h(A_j^{u^{+}})|+|a_{i3}^u\cdot h(A_i^u)-a_{j3}^{u^{+}}\cdot h(A_j^{u^{+}})|+|a_{i4}^u-a_{j4}^{u^{+}}|+\\ |a_{i1}^l-a_{j1}^{l^{+}}|+|a_{i2}^l\cdot h(A_i^l)-a_{j2}^{l^{+}}\cdot h(A_j^{l^{+}})|+|a_{i3}^l\cdot h(A_i^l)-a_{j3}^{l^{+}}\cdot h(A_j^{l^{+}})|+|a_{i4}^l-a_{j4}^{l^{+}}|\end{array}\right] \\ d\left(w_i,G^{-}\right)={\displaystyle \frac{1}{8}}\left[\begin{array}{l}|a_{i1}^u-a_{j1}^{u^{-}}|+|a_{i2}^u\cdot h(A_i^u)-a_{j2}^{u^{-}}\cdot h(A_j^{u-})|+|a_{i3}^u\cdot h(A_i^u)-a_{j3}^{u^{-}}\cdot h(A_j^{u^{-}})|+|a_{i4}^u-a_{j4}^{u^{-}}|+\\ |a_{i1}^l-a_{j1}^{l^{-}}|+|a_{i2}^l\cdot h(A_i^l)-a_{j2}^{l^{-}}\cdot h(A_j^{l^{-}})|+|a_{i3}^l\cdot h(A_i^l)-a_{j3}^{l^{-}}\cdot h(A_j^{l^{-}})|+|a_{i4}^l-a_{j4}^{l^{-}}|\end{array}\right] \end{gathered}$$

(29)

Step 9: Calculate the closeness coefficients of different experts to the same indicator.

$$c_i={\displaystyle \frac{d\left(w_i,G^{-}\right)}{d\left(w_i,G^{-}\right)+d\left(w_i,G^{+}\right)}}$$

(30)

Step 10: The weights of the same expert in the comprehensive evaluation of different indicators are derived from the calculation results of step 9, and subsequently, the weights ${\mu }_k$ of the decision-maker are determined. The decision-maker weights are multiplied with the attribute weights to obtain the expert’s objective indicator weights, namely ${\mu }_k\cdot w_i$, and finally defuzzified according to Equation (18).

3.5. Evaluation Method Based on IT2F-PT-TOPSIS

3.5.1. Prospect Theory

Given that individuals are finitely rational, the decision-makers’ behavior tends to deviate from expected utility, taking into account the decision-maker’s own psychological dependence. This aligns with the decision-preference profile outlined by prospect theory, as proposed by Kahneman and Tversky [65]. This paper introduces prospect theory, which posits that the psychological expectations of experts in making decisions are influenced by a variety of factors, including loss aversion. The prospect theory facilitates a more profound comprehension of the behavioral patterns exhibited by experts, which can assist them in evaluating risk and return in a more objective manner, thereby enabling the formulation of more rational decisions. The fundamental premise of prospect theory is the identification of decision-making reference points. In this study, positive and negative ideal points are selected as the decision-making reference points. In the context of prospect theory, the value function is represented by $v\left(\Delta x\right)$ and the probability weighting function is represented by $w\left(p\right)$, and thus prospect value is represented as

$$V={\displaystyle \sum _{i=1}^n\left[w\left(p_i\right)v\left(\Delta x_i\right)\right]}$$

(31)

where the value function $v\left(\Delta x\right)=\left\{\begin{array}{c}{\left(\Delta x_i\right)}^{\alpha },\Delta x_i\ge 0\\ -\chi {\left(-\Delta x_i\right)}^{\beta },\Delta x_i<0\end{array}\right.$ is the subjectively perceived value of the decision-maker.

$\Delta x_i$ denotes the difference between attribute $x_i$ and the reference point. $\alpha \left(0<\alpha <1\right)$ and $\beta \left(0<\beta <1\right)$ denote the sensitivity of the decision-maker to gains and losses. The smaller $\alpha$ and $\beta$ denote the more sensitive the decision-maker is to gains, and $\chi$ is the loss aversion coefficient, which controls the loss aversion of the decision-maker If $\lambda >1$, it indicates that the decision-maker is more sensitive to losses. Tversky and Kahneman demonstrated that the assignment of $\alpha =\beta =0.88$ and $\chi =2.25$ is more consistent with empirical data [66].

3.5.2. TOPSIS

The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) [67] measures the proximity of evaluation units to the “positive ideal solution” and the “negative ideal solution” by introducing the Euclidean distance, which is used to rank the relative merits of each evaluation unit. The specific steps are as follows:

Step 1: Construct the evaluation matrix. A total of q experts is invited to evaluate the resilience level under m indicators to get the semantic evaluation matrix of the u-th expert, which is converted into an IT2F number evaluation matrix $X_u={(X_{ij})}_{m\times n}$ according to

Table 5. The IT2FS corresponding to linguistic variables for evaluating the resilience level.

Linguistic Variable	IT2FS
Very poor (VP)	[(0,0,0,1;1,1), (0,0,0,0.5;0.9,0.9)]
Poor (P)	[(0,1,1,3;1,1), (0.5,1,1,2;0.9,0.9)]
Moderately poor (MP)	[(1,3,3,5;1,1), (2,3,3,4;0.9,0.9)]
Fair (F)	[(3,5,5,7;1,1), (4,5,5,6;0.9,0.9)]
Moderately good (MG)	[(5,7,7,9;1,1), (6,7,7,8;0.9,0.9)]

.

Step 2: The geometric mean is used to cluster the semantic evaluation matrices of experts.

$${\tilde{X}}_{ij}={\left[{\tilde{\tilde{X}}}^1\otimes {\tilde{\tilde{X}}}^2\otimes \cdots \otimes {\tilde{\tilde{X}}}^n\right]}^{{\displaystyle \frac{1}{n}}}$$

(32)

Step 3: Normalize ${\tilde{X}}_{ij}$.

$$r_{ij}={\displaystyle \frac{x_{ij}}{\sqrt{{\displaystyle \sum _{i=1}^n{x}_{ij}^2}}}},i=1,2,\cdots ,m;j=1,2,\cdots ,n$$

(33)

Step 4: Construct the weighted normalized matrix.

$$Z_{ij}=w_j{r}_{ij}$$

(34)

where $w_j$ is the weight of indicator $j$.

Step 5: The positive and negative ideal solutions are selected as the reference points for decision-making, and the formula is:

$$\begin{array}{l}{\tilde{\tilde{X}}}^{+}=\left({\tilde{\tilde{X}}}_1^{+},{\tilde{\tilde{X}}}_2^{+},\cdots ,{\tilde{\tilde{X}}}_n^{+}\right)\\ =\left[\max \left({\tilde{\tilde{X}}}_{11}^{+},{\tilde{\tilde{X}}}_{21}^{+},\cdots ,{\tilde{\tilde{X}}}_{m1}^{+}\right),\max \left({\tilde{\tilde{X}}}_{12}^{+},{\tilde{\tilde{X}}}_{22}^{+},\cdots ,{\tilde{\tilde{X}}}_{m2}^{+}\right),\cdots ,\max \left({\tilde{\tilde{X}}}_{1n}^{+},{\tilde{\tilde{X}}}_{2n}^{+},\cdots ,{\tilde{\tilde{X}}}_{mn}^{+}\right)\right]\\ {\tilde{\tilde{X}}}^{-}=\left({\tilde{\tilde{X}}}_1^{-},{\tilde{\tilde{X}}}_2^{-},\cdots ,{\tilde{\tilde{X}}}_n^{-}\right)\\ =\left[\max \left({\tilde{\tilde{X}}}_{11}^{-},{\tilde{\tilde{X}}}_{21}^{-},\cdots ,{\tilde{\tilde{X}}}_{m1}^{-}\right),\max \left({\tilde{\tilde{X}}}_{12}^{-},{\tilde{\tilde{X}}}_{22}^{-},\cdots ,{\tilde{\tilde{X}}}_{m2}^{-}\right),\cdots ,\max \left({\tilde{\tilde{X}}}_{1n}^{-},{\tilde{\tilde{X}}}_{2n}^{-},\cdots ,{\tilde{\tilde{X}}}_{mn}^{-}\right)\right]\end{array}$$

(35)

Step 6: Calculate the distance between each indicator and the positive and negative ideal solutions, and the formula is:

When $\Delta x_i>0$,

$$\begin{array}{l}d\left({\tilde{\tilde{A}}}_{ij},{\tilde{\tilde{A}}}_{j^{-}}\right)=\\ {\left\{{\displaystyle \frac{1}{12}}\left[{{\displaystyle \sum _{b=1}^4\left(a_{ijb}^u-a_{j^{-}b}^u\right)}}^2+{\displaystyle \sum _{b=1}^2{\left(h_b({\tilde{A}}_i^u)-h_b({\tilde{A}}^{{-}^u})\right)}^2}+{{\displaystyle \sum _{b=1}^4\left(a_{ijb}^l-a_{j^{-}b}^l\right)}}^2+{\displaystyle \sum _{b=1}^2{\left(h_b({\tilde{A}}_i^l)-h_b({\tilde{A}}^{{-}^l})\right)}^2}\right]\right\}}^{{\displaystyle \frac{\alpha }{2}}}\end{array}$$

When $\Delta x_i<0$,

$$\begin{array}{l}d\left({\tilde{\tilde{A}}}_{ij},{\tilde{\tilde{A}}}_{j^{+}}\right)=\\ \lambda {\left\{{\displaystyle \frac{1}{12}}\left[{{\displaystyle \sum _{b=1}^4\left(a_{ijb}^u-a_{j^{+}b}^u\right)}}^2+{\displaystyle \sum _{b=1}^2{\left(h_b({\tilde{A}}_i^u)-h_b({\tilde{A}}^{{+}^u})\right)}^2}+{{\displaystyle \sum _{b=1}^4\left(a_{ijb}^l-a_{j^{+}b}^l\right)}}^2+{\displaystyle \sum _{b=1}^2{\left(h_b({\tilde{A}}_i^l)-h_b({\tilde{A}}^{{+}^l})\right)}^2}\right]\right\}}^{{\displaystyle \frac{\beta }{2}}}\end{array}$$

(36)

Step 7: The TOPSIS method is applied to calculate the closeness of each metric to the optimal ideal solution with the formula:

$$R_i={\displaystyle \frac{D_i^{-}}{D_i^{-}+D_i^{+}}},i=1,2,\cdots ,m$$

(37)

If $R_i$ is larger, it signifies that the decision is more distant from the negative ideal solution and nearer to the positive ideal solution. Consequently, the decision is deemed superior or more resilient, insofar as it is more closely aligned with the positive ideal solution. Accordingly, the alternatives can be ordered and selected based on the magnitude of the $R_i$ value.

4. Case Study

As China Shenhua Energy Group Ningxia Coal Industry Co., Ltd. (CENC) is representative of China’s CTL industry, and its 4 million tons of coal indirect liquefaction demonstration project is the world’s largest CTL project in a single set, its scale, technology, and market position are indicative of the industry’s characteristics and trends. The experts involved in the scoring are more intimately acquainted with CENC’s operations, which enhances the precision and dependability of the scoring. CENC has amassed a substantial reservoir of experience in navigating challenges such as market volatility and policy shifts, which is of considerable value in evaluating the resilience of the supply chain. Therefore, it is crucial to evaluate the resilience of the CENC’s industrial chain and supply chain from 2018 to 2022. In this study, experts from the CTL industry of the CENC were invited to provide guidance. The IT2F-DETAMEL-ANP method is employed to ascertain the weights of the indicator system, and the resilience evaluation is conducted in accordance with the IT2F-PT -TOPSIS method. Furthermore, the study evaluates the resilience of the company’s industrial chain and supply chain of CTL from 2018 to 2022. It also identifies the shortcomings that affect the resilience level of its industrial chain and supply chain and proposes corresponding countermeasures and suggestions.

4.1. Calculation of Evaluation Indicators’ Weights

Respectively, project management personnel from CTL projects and four experts in the field of academic research were invited to provide their respective initial fuzzy matrices A. Taking Expert 1 as an example, according to the IT2FSs corresponding to the fuzzy language in Table 3, the resulting initial fuzzy matrix is shown in

Table 6. Initial fuzzy matrix of expert 1.

Expert 1	A	B	C	D
A	0.00	LI	LI	NI
B	NI	0.00	HI	NI
C	NI	VLI	0.00	NI
D	NI	LI	HI	0.00

.

According to the IT2FS corresponding to the fuzzy language in Table 3, the normalized fuzzy initial relation matrix is derived from Equations (11)–(14), as shown in

Table 7. Normalized fuzzy initial relation matrix.

	A	B	C	D
A	0	[(0.18,0.23,0.23,0.27;1,1), (0.20,0.23,0.23,0.25;0.9,0.9)]	[(0.20,0.24,0.24,0.29;1,1), (0.22,0.24,0.24,0.27;0.9,0.9)]	[(0.07,0.12,0.12,0.15;1,1), (0.09,0.12,0.12,0.13;0.9,0.9)]
B	[(0.09,0.14,0.14,0.17;1,1), (0.11,0.14,0.14,0.15;0.9,0.9)]	0	[(0.22,0.26,0.26,0.31;1,1), (0.24,0.26,0.26,0.28;0.9,0.9)]	[(0.07,0.12,0.12,0.15;1,1) (0.09,0.12,0.12,0.13;0.9,0.9)]
C	[(0.09,0.14,0.14,0.17;1,1), (0.11,0.14,0.14,0.15;0.9,0.9)]	[(0.13,0.17,0.17,0.22;1,1), (0.15,0.17,0.17,0.19;0.9,0.9)]	0	[(0.07,0.12,0.12,0.15;1,1), (0.09,0.12,0.12,0.13;0.9,0.9)]
D	[(0.14,0.19,0.19,0.23;1,1), (0.16,0.19,0.19,0.20;0.9,0.9)]	[(0.29,0.33,0.33,0.38;1,1), (0.31,0.33,0.33,0.36;0.9,0.9)]	[(0.31,0.35,0.35,0.40;1,1), (0.33,0.35,0.35,0.37;0.9,0.9)]	0

.

Once the total relation matrix has been derived from Equations (15)–(17), the defuzzified total relation matrix is then derived from Equation (18). The mean value of 0.3250 is selected as the threshold value, and elements smaller than this value are excluded to obtain the matrix, as illustrated in

Table 8. Total relation matrix after excluding the threshold value.

	A	B	C	D
A	0.0000	0.3977	0.4815	0.0000
B	0.0000	0.0000	0.4509	0.0000
C	0.0000	0.0000	0.3263	0.4077
D	0.4044	0.5348	0.6638	0.0000

.

In line with the results from DEMATEL, the ANP structure of the resilience evaluation system can be constructed based on the influence relations between the indicators, as shown in Figure 2.

Three leaders of the CENC’s CTL project were invited to evaluate the relative importance of the remaining indicators. As illustrated in Figure 2, the elements B1, B2, B3, B4, and B5 in element set B have an effect on the elements C1, C2, C3, C4, and C5 in element set C. The fuzzy comparison judgment matrix is now constructed according to Table 4, using C1 as the criterion and expert 1 as an example, as shown in

Table 9. Expert 1’s judgment matrix with C1 as criterion.

Expert 1	B1	B2	B3	B4	B5
B1	E	1/VS	E	E	1/SS
B2	VS	E	VS	VS	SS
B3	E	1/VS	E	E	1/FS
B4	E	1/VS	E	E	1/FS
B5	SS	1/SS	FS	FS	E

.

The consistency test is conducted in accordance with the prescribed Equations (19) and (20). Thereafter, the weighted supermatrices of the three experts are derived from Equations (21)–(28). Once normalized, the fuzzy attribute weights of different experts for a given indicator are obtained, and the fuzzy attribute weights in the context of adaptability B are presented in

Table 10. Fuzzy attribute weights in context of adaptability B.

Expert	Indicator	Fuzzy Attribute Weights
Expert 1	B1	[(0.1757,0.1706,0.1707,0.1768;1,1), (0.1742,0.1701,0.1702,0.1749;0.8,0.8)]
	B2	[(0.0847,0.0814,0.0855,0.0923;1,1), (0.0835,0.0814,0.0846,0.0906;0.8,0.8)]
	B3	[(0.2424,0.2419,0.2316,0.2196;1,1), (0.2427,0.2413,0.2333,0.2227;0.8,0.8)]
	B4	[(0.1806,0.1854,0.1898,0.1918;1,1), (0.1820,0.1860,0.1895,0.1914;0.8,0.8)]
	B5	[(0.3166,0.3207,0.3223,0.3195;1,1), (0.3176,0.3212,0.3224,0.3203;0.8,0.8)]
Expert 2	B1	[(0.0626,0.0618,0.0657,0.0712;1,1), (0.0623,0.0619,0.0649,0.0698;0.8,0.8)]
	B2	[(0.1400,0.1384,0.1408,0.1455;1,1), (0.1395,0.1383,0.1403,0.1442;0.8,0.8)]
	B3	[(0.1899,0.1895,0.1879,0.1868;1,1), (0.1899,0.1893,0.1882,0.1871;0.8,0.8)]
	B4	[(0.2523,0.2542,0.2532,0.2508;1,1), (0.2530,0.2542,0.2536,0.2515;0.8,0.8)]
	B5	[(0.3551,0.3562,0.3524,0.3457;1,1), (0.3553,0.3562,0.3530,0.3474;0.8,0.8)]
Expert 3	B1	[(0.0591,0.0582,0.0699,0.0872;1,1), (0.0586,0.0586,0.0679,0.0825;0.8,0.8)]
	B2	[(0.1034,0.1106,0.1347,0.1604;1,1), (0.1048,0.1122,0.1313,0.1537;0.8,0.8)]
	B3	[(0.1682,0.1729,0.2047,0.2414;1,1), (0.1685,0.1746,0.1999,0.2318;0.8,0.8)]
	B4	[(0.0976,0.0999,0.1175,0.1381;1,1), (0.0978,0.1008,0.1148,0.1328;0.8,0.8)]
	B5	[(0.5717,0.5583,0.4732,0.3729;1,1), (0.5704,0.5538,0.4861,0.3992;0.8,0.8)]

.

Using the relative entropy method based on the Hamming distance measurement, the objective indicator weights of the indicator system are finally obtained from Equations (29), (30), and (18), as shown in

Table 11. Objective weights of the indicator system.

Indicator	Defuzzified Weight	Normalized Weight	Objective Weight
A	0.09	0.29
A1	0.03	0.06	0.02
A2	0.04	0.09	0.03
A3	0.06	0.15	0.04
A4	0.04	0.09	0.03
A5	0.17	0.39	0.11
A6	0.05	0.11	0.03
A7	0.05	0.12	0.03
B	0.09	0.28
B1	0.03	0.10	0.03
B2	0.04	0.12	0.04
B3	0.06	0.20	0.06
B4	0.07	0.22	0.06
B5	0.11	0.36	0.10
C	0.11	0.35
C1	0.04	0.08	0.03
C2	0.19	0.40	0.14
C3	0.05	0.11	0.04
C4	0.11	0.24	0.08
C5	0.08	0.17	0.07
D	0.02	0.08
D1	0.05	0.17	0.01
D2	0.06	0.19	0.01
D3	0.07	0.23	0.02
D4	0.13	0.41	0.03

.

4.2. Calculation of CLT Industrial Chain and Supply Chain Resilience Level

A questionnaire survey was conducted with the objective of evaluating the resilience level of the CTL industrial chain and supply chain from 2018 to 2022. Three representatives of enterprise supervisors and employees with extensive working experience from the CENC’s CTL project were selected to participate in the survey. The results of the evaluation are presented in

Table 12. CTL industrial chain and supply chain resilience evaluation in 2018.

Indicator	Expert 1	Expert 2	Expert 3	Indicator	Expert 1	Expert 2	Expert 3
A1	VG	G	VG	B5	MG	F	F
A2	G	G	F	C1	G	MG	MG
A3	MG	F	F	C2	G	G	MG
A4	MG	F	MG	C3	G	MP	F
A5	VG	MG	G	C4	G	F	F
A6	VG	MG	MG	C5	F	MP	G
A7	VG	F	G	D1	F	VP	G
B1	F	MP	MP	D2	G	F	F
B2	G	F	MP	D3	MG	MG	F
B3	MG	MP	MG	D4	MG	MP	F
B4	VG	MG	MG	-	-	-	-

,

Table 13. CTL industrial chain and supply chain resilience evaluation in 2019.

Indicator	Expert 1	Expert 2	Expert 3	Indicator	Expert 1	Expert 2	Expert 3
A1	G	G	G	B5	MG	F	F
A2	G	F	F	C1	G	MG	MG
A3	F	G	F	C2	G	MG	MG
A4	G	F	F	C3	G	MP	F
A5	VG	MG	G	C4	G	F	F
A6	VG	MG	MG	C5	G	F	F
A7	VG	G	MG	D1	F	MP	F
B1	MG	F	F	D2	G	MG	F
B2	G	MP	F	D3	MG	MG	F
B3	VG	MG	MG	D4	MG	F	F
B4	VG	MG	MG	-	-	-	-

,

Table 14. CTL industrial chain and supply chain resilience evaluation in 2020.

Indicator	Expert 1	Expert 2	Expert 3	Indicator	Expert 1	Expert 2	Expert 3
A1	F	G	MG	A2	VG	MG	MG
A3	G	MG	MG	A4	F	MP	F
A5	VG	G	G	A6	VG	G	MG
A7	G	G	MG	B1	F	F	MG
B2	G	F	MP	B3	G	G	MG
B4	VG	G	MG	B5	MG	F	F
C1	G	F	MP	C2	MP	F	F
C3	G	MP	F	C4	G	F	F
C5	F	F	G	D1	MP	F	F
D2	G	MG	F	D3	MG	G	MG
D4	G	MP	MG	-	-	-	-

,

Table 15. CTL industrial chain and supply chain resilience evaluation in 2021.

Indicator	Expert 1	Expert 2	Expert 3	Indicator	Expert 1	Expert 2	Expert 3
A1	G	G	G	B5	MG	F	F
A2	VG	G	MG	C1	MG	MG	MG
A3	VG	G	G	C2	G	MG	MG
A4	F	F	MG	C3	G	MP	F
A5	VG	G	G	C4	G	F	MG
A6	VG	VG	MG	C5	G	MG	F
A7	G	VG	MG	D1	G	MP	F
B1	G	VG	MG	D2	G	MG	F
B2	G	F	F	D3	G	MG	MG
B3	G	G	MG	D4	G	MP	MG
B4	VG	G	MG	-	-	-	-

and

Table 16. CTL industrial chain and supply chain resilience evaluation in 2022.

Indicator	Expert 1	Expert 2	Expert 3	Indicator	Expert 1	Expert 2	Expert 3
A1	MG	F	F	B5	G	F	F
A2	VG	VG	MG	C1	MG	F	MP
A3	VG	VG	G	C2	MG	MG	MG
A4	F	F	MG	C3	G	F	F
A5	VG	G	G	C4	MG	G	G
A6	VG	VG	MG	C5	G	MG	G
A7	VG	G	VG	D1	G	F	F
B1	G	VG	MG	D2	G	G	G
B2	G	F	F	D3	MG	G	G
B3	G	G	G	D4	VG	G	G
B4	VG	G	MG	-	-	-	-

.

The linguistic variables are transformed into IT2FS based on Table 5. The scoring results from the experts are then aggregately weighted and normalized by Equations (32)–(34). The specific results are presented in

Table 17. Normalized and aggregately weighted scoring results from the experts (2018).

Indicator	Results
A1	[(0.1390,0.1621,0.1621,0.1679;1,1), (0.1507,0.1621,0.1621,0.1651;0.9,0.9)]
A2	[(0.1481,0.2076,0.2076,0.2491;1,1), (0.1782,0.2076,0.2076,0.2287;0.9,0.9)]
A3	[(0.1510,0.2375,0.2375,0.3232;1,1), (0.1944,0.2375,0.2375,0.2804;0.9,0.9)]
A4	[(0.1167,0.1732,0.1732,0.2291;1,1), (0.1451,0.1732,0.1732,0.2012;0.9,0.9)]
A5	[(0.7824,0.9858,0.9858,1.1102;1,1), (0.8851,0.9858,0.9858,1.0494;0.9,0.9)]
A6	[(0.1809,0.2344,0.2344,0.2772;1,1), (0.2080,0.2344,0.2344,0.2563;0.9,0.9)]
A7	[(0.1864,0.2490,0.2490,0.2885;1,1), (0.2185,0.2490,0.2490,0.2694;0.9,0.9)]
B1	[(0.0384,0.0948,0.0948,0.1490;1,1), (0.0671,0.0948,0.0948,0.1220;0.9,0.9)]
B2	[(0.0966,0.1797,0.1797,0.2468;1,1), (0.1401,0.1797,0.1797,0.2139;0.9,0.9)]
B3	[(0.0986,0.2294,0.2294,0.3506;1,1), (0.1663,0.2294,0.2294,0.2905;0.9,0.9)]
B4	[(0.3744,0.4852,0.4852,0.5738;1,1), (0.4304,0.4852,0.4852,0.5304;0.9,0.9)]
B5	[(0.3651,0.5741,0.5741,0.7812;1,1), (0.4699,0.5741,0.5741,0.6778;0.9,0.9)]
C1	[(0.1629,0.2216,0.2216,0.2714;1,1), (0.1923,0.2216,0.2216,0.2467;0.9,0.9)]
C2	[(0.8717,1.1530,1.1530,1.3450;1,1), (1.0126,1.1530,1.1530,1.2498;0.9,0.9)]
C3	[(0.1047,0.1947,0.1947,0.2675;1,1), (0.1518,0.1947,0.1947,0.2319;0.9,0.9)]
C4	[(0.3309,0.5057,0.5057,0.6555;1,1), (0.4190,0.5057,0.5057,0.5815;0.9,0.9)]
C5	[(0.1877,0.3490,0.3490,0.4795;1,1), (0.2721,0.3490,0.3490,0.4156;0.9,0.9)]
D1	[(0.0000,0.0000,0.0000,0.0348;1,1), (0.0000,0.0000,0.0000,0.0229;0.9,0.9)]
D2	[(0.0582,0.0889,0.0889,0.1152;1,1), (0.0737,0.0889,0.0889,0.1022;0.9,0.9)]
D3	[(0.0750,0.1113,0.1113,0.1472;1,1), (0.0932,0.1113,0.1113,0.1293;0.9,0.9)]
D4	[(0.0772,0.1477,0.1477,0.2130;1,1), (0.1138,0.1477,0.1477,0.1806;0.9,0.9)]

,

Table 18. Normalized and aggregately weighted scoring results from the experts (2019).

Indicator	Results
A1	[(0.1175,0.1511,0.1511,0.1679), (0.1343,0.1511,0.1511,0.1595;0.9,0.9)]
A2	[(0.1116,0.1707,0.1707,0.2212), (0.1414,0.1707,0.1707,0.1962;0.9,0.9)]
A3	[(0.1689,0.2582,0.2582,0.3347), (0.2140,0.2582,0.2582,0.2969;0.9,0.9)]
A4	[(0.1167,0.1732,0.1732,0.2291), (0.1451,0.1732,0.1732,0.2012;0.9,0.9)]
A5	[(0.7824,0.9858,0.9858,1.1102), (0.8851,0.9858,0.9858,1.0494;0.9,0.9)]
A6	[(0.1809,0.2344,0.2344,0.2772), (0.2080,0.2344,0.2344,0.2563;0.9,0.9)]
A7	[(0.2033,0.2689,0.2689,0.3137), (0.2361,0.2689,0.2689,0.2915;0.9,0.9)]
B1	[(0.0948,0.1490,0.1490,0.2028), (0.1220,0.1490,0.1490,0.1759;0.9,0.9)]
B2	[(0.0966,0.1797,0.1797,0.2468), (0.1401,0.1797,0.1797,0.2139;0.9,0.9)]
B3	[(0.3506,0.4544,0.4544,0.5373), (0.4031,0.4544,0.4544,0.4967;0.9,0.9)]
B4	[(0.3744,0.4852,0.4852,0.5738), (0.4304,0.4852,0.4852,0.5304;0.9,0.9)]
B5	[(0.3651,0.5741,0.5741,0.7812), (0.4699,0.5741,0.5741,0.6778;0.9,0.9)]
C1	[(0.1629,0.2216,0.2216,0.2714), (0.1923,0.2216,0.2216,0.2467;0.9,0.9)]
C2	[(0.7792,1.0604,1.0604,1.2986), (0.9200,1.0604,1.0604,1.1802;0.9,0.9)]
C3	[(0.1047,0.1947,0.1947,0.2675), (0.1518,0.1947,0.1947,0.2319;0.9,0.9)]
C4	[(0.4388,0.6152,0.6152,0.7383), (0.5280,0.6152,0.6152,0.6777;0.9,0.9)]
C5	[(0.2707,0.4138,0.4138,0.5364), (0.3429,0.4138,0.4138,0.4758;0.9,0.9)]
D1	[(0.0262,0.0532,0.0532,0.0790), (0.0401,0.0532,0.0532,0.0661;0.9,0.9)]
D2	[(0.0689,0.0994,0.0994,0.1253), (0.0843,0.0994,0.0994,0.1125;0.9,0.9)]
D3	[(0.0750,0.1113,0.1113,0.1472), (0.0932,0.1113,0.1113,0.1293;0.9,0.9)]
D4	[(0.1114,0.1751,0.1751,0.2383), (0.1434,0.1751,0.1751,0.2068;0.9,0.9)]

,

Table 19. Normalized and aggregately weighted scoring results from the experts (2020).

Indicator	Results
A1	[(0.0792,0.1143,0.1143,0.1440), (0.0969,0.1143,0.1143,0.1293;0.9,0.9)]
A2	[(0.1707,0.2212,0.2212,0.2615), (0.1962,0.2212,0.2212,0.2418;0.9,0.9)]
A3	[(0.2375,0.3232,0.3232,0.3958), (0.2804,0.3232,0.3232,0.3597;0.9,0.9)]
A4	[(0.0576,0.1167,0.1167,0.1732), (0.0879,0.1167,0.1167,0.1451;0.9,0.9)]
A5	[(0.8753,1.0719,1.0719,1.1499), (0.9742,1.0719,1.0719,1.1113;0.9,0.9)]
A6	[(0.2023,0.2549,0.2549,0.2871), (0.2289,0.2549,0.2549,0.2714;0.9,0.9)]
A7	[(0.2033,0.2689,0.2689,0.3137), (0.2361,0.2689,0.2689,0.2915;0.9,0.9)]
B1	[(0.0948,0.1490,0.1490,0.2028), (0.1220,0.1490,0.1490,0.1759;0.9,0.9)]
B2	[(0.0966,0.1797,0.1797,0.2468), (0.1401,0.1797,0.1797,0.2139;0.9,0.9)]
B3	[(0.3607,0.4771,0.4771,0.5565), (0.4190,0.4771,0.4771,0.5171;0.9,0.9)]
B4	[(0.4188,0.5276,0.5276,0.5943), (0.4738,0.5276,0.5276,0.5617;0.9,0.9)]
B5	[(0.3651,0.5741,0.5741,0.7812), (0.4699,0.5741,0.5741,0.6778;0.9,0.9)]
C1	[(0.0803,0.1494,0.1494,0.2052), (0.1165,0.1494,0.1494,0.1779;0.9,0.9)]
C2	[(0.2898,0.5875,0.5875,0.8717), (0.4423,0.5875,0.5875,0.7302;0.9,0.9)]
C3	[(0.1047,0.1947,0.1947,0.2675), (0.1518,0.1947,0.1947,0.2319;0.9,0.9)]
C4	[(0.3309,0.5057,0.5057,0.6555), (0.4190,0.5057,0.5057,0.5815;0.9,0.9)]
C5	[(0.2707,0.4138,0.4138,0.5364), (0.3429,0.4138,0.4138,0.4758;0.9,0.9)]
D1	[(0.0262,0.0532,0.0532,0.0790), (0.0401,0.0532,0.0532,0.0661;0.9,0.9)]
D2	[(0.0689,0.0994,0.0994,0.1253), (0.0843,0.0994,0.0994,0.1125;0.9,0.9)]
D3	[(0.0995,0.1354,0.1354,0.1658), (0.1175,0.1354,0.1354,0.1507;0.9,0.9)]
D4	[(0.1024,0.1797,0.1797,0.2399), (0.1434,0.1797,0.1797,0.2105;0.9,0.9)]

,

Table 20. Normalized and aggregately weighted scoring results from the experts (2021).

Indicator	Results
A1	[(0.1175,0.1511,0.1511,0.1679), (0.1343,0.1511,0.1511,0.1595;0.9,0.9)]
A2	[(0.1909,0.2405,0.2405,0.2709), (0.2160,0.2405,0.2405,0.2561;0.9,0.9)]
A3	[(0.3232,0.3958,0.3958,0.4246), (0.3597,0.3958,0.3958,0.4103;0.9,0.9)]
A4	[(0.1167,0.1732,0.1732,0.2291), (0.1451,0.1732,0.1732,0.2012;0.9,0.9)]
A5	[(0.8753,1.0719,1.0719,1.1499), (0.9742,1.0719,1.0719,1.1113;0.9,0.9)]
A6	[(0.2200,0.2640,0.2640,0.2871), (0.2424,0.2640,0.2640,0.2760;0.9,0.9)]
A7	[(0.2211,0.2785,0.2785,0.3137), (0.2501,0.2785,0.2785,0.2965;0.9,0.9)]
B1	[(0.1813,0.2284,0.2284,0.2572), (0.2051,0.2284,0.2284,0.2431;0.9,0.9)]
B2	[(0.1393,0.2130,0.2130,0.2761), (0.1765,0.2130,0.2130,0.2449;0.9,0.9)]
B3	[(0.3607,0.4771,0.4771,0.5565), (0.4190,0.4771,0.4771,0.5171;0.9,0.9)]
B4	[(0.4188,0.5276,0.5276,0.5943), (0.4738,0.5276,0.5276,0.5617;0.9,0.9)]
B5	[(0.3651,0.5741,0.5741,0.7812), (0.4699,0.5741,0.5741,0.6778;0.9,0.9)]
C1	[(0.1456,0.2216,0.2216,0.2714), (0.1923,0.2216,0.2216,0.2467;0.9,0.9)]
C2	[(0.7792,1.0604,1.0604,1.2986), (0.9200,1.0604,1.0604,1.1802;0.9,0.9)]
C3	[(0.1047,0.1947,0.1947,0.2675), (0.1518,0.1947,0.1947,0.2319;0.9,0.9)]
C4	[(0.3923,0.5658,0.5658,0.7128), (0.4797,0.5658,0.5658,0.6400;0.9,0.9)]
C5	[(0.3210,0.3210,0.3210,0.3210), (0.3210,0.3210,0.3210,0.3210;0.9,0.9)]
D1	[(0.0348,0.0647,0.0647,0.0889), (0.0505,0.0647,0.0647,0.0771;0.9,0.9)]
D2	[(0.0689,0.0994,0.0994,0.1253), (0.0843,0.0994,0.0994,0.1125;0.9,0.9)]
D3	[(0.0995,0.1354,0.1354,0.1658), (0.1175,0.1354,0.1354,0.1507;0.9,0.9)]
D4	[(0.1024,0.1797,0.1797,0.2399), (0.1434,0.1797,0.1797,0.2105;0.9,0.9)]

and

Table 21. Normalized and aggregately weighted scoring results from the experts (2022).

Indicator	Results
A1	[(0.0597,0.0939,0.0939,0.1278), (0.0769,0.0939,0.0939,0.1109;0.9,0.9)]
A2	[(0.2076,0.2491,0.2491,0.2709), (0.2287,0.2491,0.2491,0.2605;0.9,0.9)]
A3	[(0.3514,0.4099,0.4099,0.4246), (0.3809,0.4099,0.4099,0.4174;0.9,0.9)]
A4	[(0.0985,0.1732,0.1732,0.2291), (0.1451,0.1732,0.1732,0.2012;0.9,0.9)]
A5	[(0.8753,1.0719,1.0719,1.1499), (0.9742,1.0719,1.0719,1.1113;0.9,0.9)]
A6	[(0.2200,0.2640,0.2640,0.2871), (0.2424,0.2640,0.2640,0.2760;0.9,0.9)]
A7	[(0.2689,0.3137,0.3137,0.3249), (0.2915,0.3137,0.3137,0.3194;0.9,0.9)]
B1	[(0.1813,0.2284,0.2284,0.2572), (0.2051,0.2284,0.2284,0.2431;0.9,0.9)]
B2	[(0.1393,0.2130,0.2130,0.2761), (0.1765,0.2130,0.2130,0.2449;0.9,0.9)]
B3	[(0.4035,0.5188,0.5188,0.5764), (0.4611,0.5188,0.5188,0.5476;0.9,0.9)]
B4	[(0.4188,0.5276,0.5276,0.5943), (0.4738,0.5276,0.5276,0.5617;0.9,0.9)]
B5	[(0.4084,0.6242,0.6242,0.8091), (0.5172,0.6242,0.6242,0.7177;0.9,0.9)]
C1	[(0.0718,0.1374,0.1374,0.1981), (0.1058,0.1374,0.1374,0.1680;0.9,0.9)]
C2	[(0.6966,0.6966,0.6966,0.6966), (0.6966,0.6966,0.6966,0.6966;0.9,0.9)]
C3	[(0.1510,0.2309,0.2309,0.2992), (0.1913,0.2309,0.2309,0.2654;0.9,0.9)]
C4	[(0.5203,0.6882,0.6882,0.8028), (0.6044,0.6882,0.6882,0.7459;0.9,0.9)]
C5	[(0.4257,0.4257,0.4257,0.4257), (0.4257,0.4257,0.4257,0.4257;0.9,0.9)]
D1	[(0.0666,0.0934,0.0934,0.1120), (0.0801,0.0934,0.0934,0.1029;0.9,0.9)]
D2	[(0.1023,0.1315,0.1315,0.1461), (0.1169,0.1315,0.1315,0.1388;0.9,0.9)]
D3	[(0.1113,0.1472,0.1472,0.1718), (0.1293,0.1472,0.1472,0.1596;0.9,0.9)]
D4	[(0.2383,0.2919,0.2919,0.3131), (0.2653,0.2919,0.2919,0.3026;0.9,0.9)]

.

Based on Equations (35) and (36) the distance of each indicator from the positive and negative ideal solutions is determined. Furthermore, Equation (37) is employed to ascertain the closeness of the resilience level of the industrial chain and supply chain of CTL from 2018 to 2022 to the positive ideal solution.

Table 22. The distance of each indicator from the positive and negative ideal solution.

Years	2018		2019		2020		2021		2022
	+	−	+	−	+	−	+	−	+	−
A1	0.00	0.08	0.04	0.06	0.13	0.03	0.04	0.06	0.17	0.00
A2	0.12	0.04	0.20	0.00	0.08	0.06	0.03	0.08	0.00	0.09
A3	0.39	0.00	0.35	0.03	0.21	0.09	0.05	0.16	0.00	0.17
A4	0.00	0.07	0.00	0.07	0.15	0.00	0.00	0.07	0.02	0.06
A5	0.20	0.00	0.20	0.00	0.00	0.09	0.00	0.09	0.00	0.09
A6	0.08	0.00	0.08	0.00	0.03	0.03	0.00	0.04	0.00	0.04
A7	0.17	0.00	0.12	0.00	0.12	0.00	0.12	0.00	0.00	0.07
B1	0.31	0.00	0.20	0.06	0.20	0.06	0.00	0.14	0.00	0.14
B2	0.10	0.00	0.10	0.00	0.10	0.00	0.00	0.04	0.00	0.04
B3	0.62	0.00	0.15	0.22	0.15	0.22	0.11	0.24	0.00	0.27
B4	0.11	0.00	0.11	0.00	0.00	0.05	0.00	0.05	0.00	0.05
B5	0.12	0.00	0.12	0.00	0.12	0.00	0.12	0.00	0.00	0.06
C1	0.00	0.09	0.00	0.09	0.19	0.02	0.02	0.09	0.21	0.00
C2	0.00	0.50	0.22	0.43	1.12	0.00	0.22	0.43	0.95	0.20
C3	0.10	0.00	0.10	0.00	0.10	0.00	0.10	0.00	0.00	0.05
C4	0.41	0.00	0.19	0.11	0.41	0.00	0.29	0.07	0.00	0.18
C5	0.28	0.00	0.19	0.08	0.19	0.08	0.26	0.10	0.00	0.13
D1	0.22	0.00	0.11	0.06	0.11	0.06	0.08	0.07	0.00	0.10
D2	0.11	0.00	0.09	0.02	0.09	0.02	0.09	0.02	0.00	0.05
D3	0.10	0.00	0.10	0.00	0.04	0.03	0.04	0.03	0.00	0.04
D4	0.33	0.00	0.27	0.04	0.27	0.04	0.27	0.04	0.00	0.15
$R_i$	0.32		0.41		0.19		0.50		0.35
Rank	4		2		5		1		3

illustrates the distance of each indicator from the positive and negative ideal solutions, as well as the relative closeness. Finally, the ranking results of the resilience level of the CTL industrial chain and supply chain from 2018 to 2022 based on the closeness are obtained as follows:

$$R{\mathrm{ank}}_{21} > R{\mathrm{ank}}_{19} > R{\mathrm{ank}}_{22} > R{\mathrm{ank}}_{18} > R{\mathrm{ank}}_{20}$$

5. Results Analysis and Policy Suggestions

From the perspective of the weights assigned to the indicators by the experts, the degree of localization of key technologies, the rationality of the industrial layout of CTL, and the stability of the supply and demand chains account for relatively large weights of the indicators. This indicates that, when considering the resilience of the supply chain of the CTL industrial chain, the degree of influence of these three indicators on the level of resilience is relatively large. Specifically, the degree of localization of key technologies represents a pivotal influencing factor within the context of resistance, with the degree of technology localization directly correlated with China’s energy security. The independent mastery of CTL technology by China would render the country less vulnerable to fluctuations in the international oil market and political factors. Furthermore, it would facilitate the optimization and upgrading of other links in the relevant industrial chain and supply chain. The layout of the CTL industry is inextricably linked to the planning and layout of national energy. The rationality of the former will have a direct impact on a number of core aspects of the CTL industrial chain and supply chain, including resource supply, upstream and downstream synergistic development, industrial agglomeration, and transportation and distribution systems. Given the distinctive attributes of the CTL industry, the majority of CTL projects are situated in regions with abundant coal reserves, including Ningxia, Inner Mongolia, Shanxi, and Shaanxi. The stability of the supply and demand chain is of paramount importance for the sustained operation of the CTL industrial chain and supply chain. A stable supply and demand chain can ensure the uninterrupted provision of raw materials and facilitate the seamless sale of products. Furthermore, it can mitigate the impact of market fluctuations or unforeseen circumstances on production and economic losses.

A review of the evaluation results from previous years reveals that the resilience level of CTL industrial chain and supply chain is the lowest in 2020, the highest in 2021, and the second highest in 2019. The reasons are presented in detail:

(1)

The development of China’s CTL industrial chain and supply chain was still in its nascent stages in 2018. The stability of the political and economic environment domestically and internationally contributed to the overall stability of the industrial chain and supply chain throughout the year. Notwithstanding the numerous challenges encountered by the CTL project in 2018, including the fact that the core technology was subject to external restrictions, a shortage of talent, and deficiencies in corporate safety management, the stabilization of raw material sources and supply and demand chains, coupled with the active support of national policy, led to a remarkable development in the industrial chain and supply chain of CTL in 2018. This accomplishment not only exemplifies the capacity of the industrial chain and supply chain to adapt to alterations in the external environment but also illustrates the pivotal function of national policies in fostering industrial advancement.

(2)

In 2019, the CTL industrial chain and supply chain exhibited considerable advancement, and their resilience level demonstrated notable enhancement in comparison to 2018. This progress is primarily attributable to the robust policy support that has facilitated the standardized construction of strategic CTL bases. In this context, enterprises have implemented measures to enhance the recruitment and training of talent while simultaneously improving their safety management practices. Furthermore, the upstream and downstream synergistic effect of the industrial chain and supply chain has been reinforced, the construction of industrial supporting facilities has yielded preliminary outcomes, and the industrial coupling effect has commenced to emerge. These factors collectively contribute to the stability of the supply and demand chain, thereby significantly enhancing the flexible production capacity of enterprises. The aforementioned factors collectively indicate a notable enhancement in the resilience of CTL industrial chain and supply chain in 2019, when compared to the preceding year.

(3)

The global outbreak of the COVID-19 pandemic in 2020 had a profound impact on the CTL industrial chain and supply chain. First, there was a notable decline in energy demand due to the implementation of global epidemic prevention and control measures. Furthermore, the precipitous decline in crude oil prices had an additional detrimental impact on the market demand and profitability of CTL projects. In addition, in the context of significant and unpredictable shifts in the internal and external environments, the disaster prevention and resilience of the CTL industrial chain and supply chain have been revealed to be inadequate. The stability of the supply and demand chain has also been found to be insufficient. This deficiency results in shortcomings of the CTL industrial chain and supply chain in responding to changes in the external environment and adjusting their own strategies in a timely manner. Ultimately, these factors have collectively resulted in the lowest level of resilience observed in the CTL industrial chain and supply chain in 2020.

(4)

In 2021, with the advent of the post-epidemic era, the gradual recovery of the global economy and the rebound of energy demand have created new development opportunities for the CTL industrial chain and supply chain. In order to respond effectively to the adverse effects of the COVID-19 pandemic, the CTL industry is in urgent need of innovation and modernization to achieve its goal of sustainable development. Furthermore, synergistic collaboration with other energy sectors is of paramount importance in facilitating the transformation and green development of the entire energy industry. Such cross-field collaboration serves not only to enhance the resilience of the industrial chain and supply chain, but also represents a crucial pathway to achieving long-term, stable development. It is noteworthy that the resilience level of the CTL industrial chain and supply chain reached a peak in 2021. This provides crucial benchmarks and insights for subsequent years, indicating that the resilience and transformational capacity of the industrial chain and supply chain are pivotal in addressing global challenges.

(5)

The outbreak of the Russia-Ukraine conflict in 2022 triggered geopolitical tensions, resulting in unprecedented challenges to the management of the CTL industrial chain and supply chain. Despite some advancement in the capabilities of disaster defense and resistance, the volatility of the energy market and the sustained elevated costs of essential raw materials, such as coal, have exerted a considerable detrimental influence on the operational efficacy and profitability of the CTL industry. In addition, the rise in production costs serves to further intensify the test of sustainability in the supply chain and the equilibrium between supply and demand. Consequently, the CTL industry demonstrated a decline in resilience levels in 2022 when compared to 2021. This decline reflects the necessity to enhance the adaptability and resilience of the industrial chain and supply chain in order to effectively navigate a complex and volatile external environment.

In light of the aforementioned analysis results, the following recommendations are proposed with the aim of enhancing the resilience of the CTL industrial chain and supply chain:

(1)

It is imperative to enhance technological innovation, research, development, and localization. Although CENC’s large-scale indirect coal liquefaction system integration and complete set of clean operation technologies are generally at the international leading level, there is a need to increase the output of oleochemicals through continuous technological innovation and R&D. Furthermore, there is a necessity to improve the technological level of the CTL industry in order to cope with market changes and environmental pressures and to enhance the adaptability and competitiveness of the industry. It is recommended that investment in research and development be increased with regard to localized technologies. Furthermore, encouragement should be given to the cultivation and introduction of local technical talent, as well as to cooperation with domestic scientific research institutions. This will facilitate the acceleration of the transformation and application of technical achievements. Furthermore, cutting-edge technologies such as the Internet of Things (IoT), artificial intelligence (AI), and big data analysis should be proactively integrated into the operational framework of CTL projects to enhance the efficiency and precision of the supply chain.

(2)

It is important to strengthen the framework of risk, emergency management, and risk response capacity. In the context of an increasingly dynamic international environment and energy market, it is crucial for CTL enterprises to recognize the importance of strengthening enterprise risk management at the key nodes of low-carbon transformation. This approach can effectively mitigate the impact on the entire supply chain network in the event of a risk occurrence while also leveraging the powerful momentum of industrial chain and supply chain resilience. For instance, in the coal mining stage, it would be prudent to reinforce the identification of potential disaster-causing factors in order to prevent the insufficient provision of raw materials due to the absence of such an identification process. Similarly, in the transportation link, the deployment of 5G, IoT, and other cutting-edge technologies can be leveraged to enhance the operational resilience of the supply chain. In the synthesis stage, it is essential to enhance the monitoring of the crucial equipment and procedures involved in the CTL conversion process. Furthermore, comprehensive drills must be conducted to address potential disasters, incidents, and emergencies. In the distribution stage, financial instruments such as futures and options can be employed for the purpose of price risk management and stabilizing market expectations.

(3)

It is imperative to reinforce the interconnectivity and collaborative efforts between the involved parties and to enhance the stability of the supply and demand chain. The success of the CTL project is contingent upon the full cooperation of the upstream and downstream sectors of the CTL industrial chain. Therefore, the CENC should not only reinforce the collaboration and innovation within the CTL project but also enhance the collaboration between the CTL industry and other related industries. For instance, the formation of a cross-enterprise collaboration platform, coupled with the refinery’s economies of scale, diverse oil sources, extensive blending capabilities, robust sales channels, and other advantages, can facilitate the sharing of information and integration of resources across the coal mining, transportation, CTL conversion, and sales sectors. Furthermore, collaboration with related industries, such as energy utilization and chemical product manufacturing, can facilitate the extension of the industrial chain, global integration of the supply chain, and high-end enhancement of the value chain. It is recommended that the stability of the supply and demand chain be enhanced through the implementation of a diversified sourcing strategy, the establishment of strategic reserves, and the optimization of flexible supply chain management, thereby improving responsiveness to market fluctuations.

(4)

It is recommended that policy support be increased and the industrial layout be optimized. The stability and longevity of policies are also significant factors in enhancing resilience. The government may establish an incentive mechanism based on energy supply, which could include raising carbon quotas during carbon trading, adjusting carbon trading prices, lowering the tax rate under the carbon tax policy, and raising the carbon subsidy rate under the carbon subsidy policy. The government must assume the role of a competent supervisor and implement irregular supervision and inspection of CTL industrial chain and supply chain enterprises. This will ensure that the actual level of risk and emergency management of enterprises is monitored. In addition, it is crucial to advocate for the centralized organization of the industry in regions that are endowed with resources and have developed robust infrastructure. This approach can enhance the efficiency of resource utilization and industrial collaboration, promote rationality in industrial layout, and reinforce the resilience of the entire CTL industrial chain and supply chain.

6. Conclusions

This paper presents a comprehensive analysis of the resilience of the CTL industrial chain and supply chain from a strategic perspective, with a particular focus on energy security. It is argued that enhancing research in this domain is of paramount strategic importance for ensuring national energy security, which is elaborated as follows:

(1)

This paper presents a clear definition of the connotation of resilience of CTL industrial chain and supply chain, which is defined as the ability of the CTL industrial chain and supply chain system to withstand external shocks, such as those caused by climate, economic, technological, and societal factors, as well as internal disturbances and subsequent adaptations, recoveries, and renewals. This definition has yet to be fully explored in existing research on CTL [16]. The definition presented in this paper provides a new perspective for subsequent research.

(2)

The industrial chain and supply chain resilience evaluation framework of CTL industrial chain and supply chain, as outlined in this paper, not only encompasses the conventional elements of supply chain resilience but also introduces innovative indicators that have been overlooked in previous studies [68]. These include the rationality of the CTL industrial layout, the construction of strategic bases, and the strategic production capacity reserve. The incorporation of these indicators represents a valuable contribution to the existing evaluation of resilience within the specific context of the CTL industry, offering a more comprehensive framework for the development of the evaluation model.

(3)

By employing the TYPE 2-DEMATEL-ANP and TYPE 2-PT-TOPSIS methods to empirically analyze the resilience level of CTL industrial chain and supply chain from 2018 to 2022, this study elucidates the resilience performance and key influencing factors in different years. The majority of previous studies have employed cross-sectional data [69], whereas this paper places greater emphasis on the analysis of dynamic changes in time series data, thereby providing new insights into the long-term resilience of CTL industrial chain and supply chain. In light of the findings of the empirical analysis, this paper presents targeted policy recommendations that are closely aligned with the conclusions of this study. This approach ensures the scientific and practical relevance of the recommendations, with the aim of enhancing the overall resilience of the CTL industrial chain and supply chain.

The study not only provides a comprehensive tool for assessing the resilience of the CTL industrial chain and supply chain but also identifies specific strategies to enhance the resilience of the industry and supply chain. By implementing the policy recommendations proposed in this paper, the resilience of the CTL industry to external shocks can be enhanced, and the stability and security of the national energy supply can be ensured. The findings are of great practical significance in promoting the sustainable development of the energy industry. In addition, the research in this paper can help relevant enterprises identify and mitigate potential operational risks, optimize resource allocation, and improve the efficiency and competitiveness of the entire industrial chain. In the context of the current global energy transition and climate change challenges, these findings are of great practical significance in promoting the sustainable development of the energy industry.

To enhance the generalizability of the findings, future research could consider CTL industrial chain and supply chain in different countries and regions to explore the impact of these differences on resilience. Furthermore, the study could be extended to other types of energy supply chains, such as those involving natural gas or renewable energy, in order to validate the applicability of the models and metrics proposed in this study. Similarly, the methodology employed in this study may be equally applicable to other types of studies. Subsequent research could endeavor to apply the methodology of this study to disparate study designs and data types, with the objective of evaluating its validity and reliability. While this study has the potential for expansion, it is important to acknowledge its limitations. First, this study is constrained by data availability. Consequently, only qualitative indicators are employed to demonstrate the resilience of the CTL industrial chain and supply chain. In future studies, it would be beneficial to incorporate additional quantitative indicators to construct a more comprehensive evaluation system for the resilience indicators of the CTL industrial chain and supply chain. Secondly, the resilience of the industrial chain and supply chain is a complex system, with numerous factors influencing resilience. Consequently, the evaluation indicator system can be further refined in future research. Finally, this study employs a mixed-methods approach to investigate the resilience challenges facing the CTL industrial chain and supply chain. Future research may endeavor to refine these resilience challenges through the application of techniques such as dynamic optimal control [70], game [71], and other methods.