Dynamic Optimal Control Strategy of CCUS Technology Innovation in Coal Power Stations Under Environmental Protection Tax

Abstract

Carbon capture, utilization, and storage (CCUS) technology is an essential technology for achieving low-carbon transformation and upgrading of the coal power industry. This study applies optimal control theory to analyze the dynamic optimization of CCUS technological innovation investment in coal power stations under environmental protection tax. A dynamic control model is constructed to analyze the investment decisions of firms at system steady-state equilibrium, and numerical simulations are performed. The study shows that under both profit maximization and social welfare maximization conditions, a distinct saddle-point steady-state; the environmental protection tax affects technological innovation investment in coal power stations, which in turn affects electricity prices; the learning rate of knowledge accumulation also impacts technological innovation investment: under the social welfare maximization condition, the investment levels in technological innovation, technology, and knowledge accumulation are higher than those under profit maximization.

1. The Presentation of the Issue

As the issue of global climate change grows more pressing, curbing the release of greenhouse gases has emerged as the focus of governments and international organizations. Being a primary contributor to the greenhouse effect, atmospheric CO₂ emissions have drawn significant attention in the global transition toward sustainable, carbon-conscious economic systems [1,2,3]. The energy sector is the primary source of carbon dioxide emissions, with coal power plants being a significant part of the global energy supply, accounting for a substantial proportion of total emissions [4]. Nations heavily dependent on coal for energy generation, particularly major economies like China and India, face significant challenges in controlling their carbon footprints. Thermal power stations burning fossil fuels contribute disproportionately to atmospheric pollution in these regions, with China’s electricity sector representing a particularly substantial portion of its overall greenhouse gas output. Although the government has implemented various initiatives to advance clean energy and modernize coal-fired power plants, their carbon dioxide emissions remain substantial. Cutting these emissions is a critical global concern. In response to this challenge, CCUS technology has been developed as a potential solution.

CCUS (Carbon Capture, Utilization, and Storage) technology mitigates carbon emissions by capturing carbon generated from coal-fired power plants and either repurposing it or securely storing it [5]. This technology is crucial for achieving net-zero emissions from fossil energy and fulfilling national climate change commitments while ensuring energy security. Coal-fired power plants carry out CCUS retrofits, mainly using technologies such as chemical methods, adsorption methods, and membrane methods to separate and capture carbon dioxide in the flue gas from coal-fired boilers. Carbon dioxide regeneration, purification, and compression are achieved through pressure and temperature regulation. Efficient CO₂-enhanced oil recovery and other geological utilization technologies, as well as chemical utilization technologies such as CO₂ hydrogenation to produce methanol, are applied. CO₂ geological storage is implemented according to local conditions. Furthermore, many studies indicate that integrating CCUS technology into climate change mitigation frameworks can substantially enhance the cost-effectiveness of decarbonization efforts [6,7]. As the role of CCUS technology in carbon reduction becomes increasingly prominent, countries around the world are accelerating their investment and construction in CCUS technology. The CCUS technology in coal power stations contributes to the reliable and secure operation of the power system and can also generate electricity together with renewable energy, such as the current hotspot of biomass energy + CCUS technology. This demonstrates that CCUS technological innovation is a focus that coal power stations should pay attention to. However, CCUS technological innovation (Figure 1) also faces many challenges, including immature technology, lack of policy incentives, and regulatory frameworks [8].

Government-initiated carbon emission reduction incentive policies are an important means of promoting enterprise investment in CCUS technology innovation and implementing carbon emission reductions. Tax policies, as a market-based approach, can not only guide enterprises to directly reduce carbon dioxide emissions through price signals but also indirectly reduce carbon emission intensity by promoting technological innovation. Previous research on carbon reduction policies, such as carbon caps, carbon subsidies, and carbon trading, has mainly focused on how these policies affect emission reduction outcomes. However, few studies have linked carbon reduction policies with CCUS technology innovation.

Based on this, this paper studies the dynamic control of CCUS technology innovation in coal power plants under environmental protection tax policies. The following questions are investigated:

(1)

Does imposing an environmental protection tax effectively stimulate technological innovation in coal power stations to curb carbon emissions?

(2)

How should the environmental protection tax be adjusted to influence technological advancements in coal power stations?

(3)

How does investment in CCUS technology innovation fluctuate across different scenarios?

To answer these questions, this paper establishes a dynamic optimal control model for CCUS technology innovation under the environmental protection tax. It incorporates knowledge accumulation and considers two scenarios: profit maximization and social welfare maximization, to study how coal power stations allocate resources. This study aims to establish optimal parameters for power generation pricing, technological advancement, and knowledge development in carbon capture innovation within thermal energy facilities. The investigation further explores how ecological taxation mechanisms influence both operational strategies in fossil fuel-based electricity production and the evolution of regulatory frameworks under changing market conditions, utilizing computational modeling to assess system equilibrium states. This paper’s main contributions are as follows:

Firstly, using the method of dynamic optimal control, the evolution law of CCUS technology innovation investment in coal-fired power plants under environmental tax policies was characterized through differential equations.

Secondly, a decision-making model considering the maximization of social welfare and profit was established, and the mutual influence mechanism between environmental taxes and CCUS technological progress in coal-fired power plants was explored.

Finally, considering the impact of environmental taxes and knowledge accumulation on investment decisions, the volatility of CCUS technology investment under different scenarios was analyzed, and corresponding investment strategies were proposed.

The organization of this paper is as follows: Section 2 presents a review of the relevant literature. Section 3 develops the fundamental model. Section 4 examines the optimal conditions, steady-state equilibrium, and general solutions under both profit maximization and social welfare maximization. performs data simulations and comparative analyses between the two scenarios. Finally, Section 5 summarizes the study’s key findings. All proofs are provided in the Appendix A, Appendix B, Appendix C, Appendix D, Appendix E and Appendix F.

2. Theories and Hypotheses

2.1. CCUS Technology in Coal Power Stations

CCUS technology entails extracting carbon dioxide from industrial processes or associated energy sources, transporting it to a storage site, or purifying the captured CO₂ for reuse in new production processes to recycle it as a resource. This approach not only achieves carbon reduction but also generates economic benefits [9]. CCUS technology plays a crucial role in the net reduction of CO₂ emissions [10] and is the sole technology that allows existing coal power plants to continue functioning while significantly reducing carbon emissions.

Scholars have studied CCUS technology from multiple dimensions. Current research on CCUS technology primarily explores its business models, economic viability, technical feasibility, and related factors. Wang et al. [11] studied CCUS technology investment from the perspective of business model, and the analysis results showed that the vertical integration model is currently the most viable business approach for CCUS implementation.. technical feasibility is the key factor affecting the implementation of CCUS technology, including the maturity of the technology, compatibility, and additional energy consumption [12]. Han et al. [4] predicted the impact of CCUS investments in coal power stations in terms of economics, which provides an empirical basis for CCUS technology investment decisions. The economic benefits were also examined by comparing the cost competitiveness of coal-fired CCUS relative to renewable energy production [13]. Global analysis of CCUS project evolution reveals a clear trajectory toward clustered implementation models, with their cost optimization capabilities emerging as a critical focus area for industry participants and policymakers alike [14]. The majority of research on the technical feasibility of CCUS in coal power plants has utilized real options theory, Szolgayova [15] compared the CCS investment behavior of biomass and coal power stations, considering uncertainties in both the electricity and carbon markets, Heydari et al. [16] compared the investment behavior of CCS for biomass and coal power stations by adding coal price uncertainty extends the type of uncertainty and comparing two different abatement technologies in coal power stations using real options theory. Zhou et al. [17] considered coal price uncertainty in real options theory to examine how fluctuations in carbon pricing influence investment decisions across various low-carbon technologies, including CCS.

Currently, most CCUS technologies are still in the pilot phase and are not yet suitable for large-scale commercial applications. Some researchers suggest that existing coal power stations should be retrofitted to use biomass and CCUS technology. Compared to entirely new BECCS (Bioenergy with Carbon Capture and Storage) infrastructure, modifications based on existing equipment can reduce emissions reduction at a lower cost [18]. Numerous studies have examined the economic viability, potential for emission reduction, and broader socioeconomic effects of integrating biomass combustion with CCUS in coal power stations [19]. Different policy incentives play a significant role in shaping investors’ willingness to adopt biomass co-firing technology alongside CCUS in these facilities [20].

For a considerable period, researchers have acknowledged the advantages of CCUS technology in mitigating emissions within the power sector. They have also started evaluating its cost efficiency in coal-based electricity generation [21]. With technological advancements, an increasing number of studies have started focusing on emission reductions in existing coal power stations, emphasizing the issue of stock emissions [22]. Findings from multiple studies indicate that CCUS technologies offer a more cost-efficient approach compared to alternative emission reduction strategies, provided that the right policies and conditions are in place [22,23]. For example, mechanisms such as carbon pricing, CCUS investment subsidies, clean electricity price incentives, and direct government funding are anticipated to substantially lower the costs associated with CCUS technologies. Carbon taxation and pricing schemes play a crucial role in the decision to invest in CCUS. Zhu and Fan [24] used a real options model to simulate the impact of the carbon market and carbon capture subsidies on investment in carbon capture and storage (CCS) technologies, considering internal and external uncertainties. Power generation subsidies influence investment in CCUS technology and efforts to lower carbon emissions in coal-fired power facilities [25]. Some scholars have used the real options approach to develop an investment decision model for the integrated business model of CCUS in coal power stations, arguing that electricity price subsidies are an effective incentive policy for CCUS adoption in these facilities; the U.S. 45Q policy incentives can also effectively promote the development of CCUS technology [26]. Most of the aforementioned studies examine CCUS technology investment from the perspective of individual policies. An appropriate combination of policies is equally important. For instance, when both the carbon market and subsidy policies are in effect, power generation subsidies will influence investment in CCS technology and the reduction of carbon emissions in coal power plants.

Investment in technology is one way to reduce carbon emissions. In the case of coal power stations, CCUS is the best option for reducing emissions. According to the aforementioned research, most studies on CCUS technology investment for coal power stations employ the real options method. Only a few scholars have used game theory to study the effects of government policies to support competitive bioenergy and conventional energy supply chains in a cap-and-trade system, taking into account investments in CCUS technologies [27]. The dynamic control method is rarely used to study CCUS technology investment in coal power stations. This study uses dynamic control methods to research CCUS technology investment, filling this gap.

2.2. Environmental Tax and CCUS Technology

Pigouvian taxes are one of the main instruments of environmental policy [28]. This tax, first proposed by Pigou, compensates for the marginal social damage due to negative external factors. This mechanism addresses environmental externalities by incorporating pollution costs into market pricing, thereby optimizing resource distribution and enhancing economic productivity. Environmental taxes refer to tax credits for taxpayers investing as well as levies applied to emission-intensive sectors and hazardous substances utilization [29]. Some studies use environmental taxes to distinguish between different production technologies. For example, Yeung [30] proposed a joint dynamic game between environmental use and choice of production technology, in which industrial output produced using traditional technology is taxed. Similarly, Yeung and Petrosyan [31] proposed a dynamic game of environmental cooperation with a reduction technology, in which taxes on production with traditional technology differ from those on clean technology output.

At the corporate level, environmental policies requiring emission reductions impose costs on companies, particularly high-emission enterprises, which may weaken their global competitiveness and lead to increased costs [32]. Nevertheless, when structured effectively, such environmental policies can stimulate technological innovation and incentivize investments in emission-reduction solutions. For example, applying an emission tax on steel producers could encourage steel companies to invest in carbon capture and storage technologies, thereby reducing emission taxes [33]. Creating sustainable taxation frameworks that comprehensively account for multifaceted economic consequences represents a crucial step toward expediting the shift toward carbon neutrality. China’s Environmental Protection Tax Law, passed at the end of 2016, imposes pollution taxes (environmental taxes) on companies. Studies examining the influence of this tax on environmentally friendly investments by high-pollution enterprises have found that environmental taxes promote green investment in these companies [34]. The effectiveness of pollution control and sustainable production in resource-based industries is closely linked to the rate of environmental taxation. High pollution emissions in resource-based industries, coupled with low environmental tax rates, fail to adequately compensate for externalities, thereby hindering technological innovation [35].

The interplay between ecological fiscal policies and technological progress is mediated by the economic stimuli generated through environmental governance mechanisms. Under the assumption of complete information, pollution taxes have been confirmed to play a positive role in reducing emission costs and enhancing the development of emission-reduction technologies [36]. Additionally, even under conditions of dynamic tax rate uncertainty, environmental taxes can still incentivize innovation [37]. Nevertheless, some research challenges the effectiveness of environmental taxes in driving technological innovation [38].

The current literature inadequately addresses two critical dimensions in carbon management systems: CCUS innovation trajectories within fossil fuel-based power generation, and ecological fiscal mechanisms employing adaptive regulatory approaches. Our study develops a dynamic optimization framework analyzing these interconnected systems, where carbon pricing instruments are calibrated using emission-intensity metrics rather than aggregate pollution volumes. Through this analytical lens, we systematically investigate the strategic interplay between progressive carbon taxation schemes and capital allocation patterns in CCUS technological advancement.

Compared with other studies, the unique aspects of this research are:

(1)

It examines the impact of environmental taxes on technological innovation and how these taxes influence electricity pricing.

(2)

The learning-by-doing effect, which enhances efficiency, is introduced into technological innovation, reflected in the dynamic model of technology.

(3)

It examines and contrasts CCUS technology investments in coal power plants under both profit maximization and social welfare maximization, providing insights to support investment decision-making in the industry.

Next, the basic model of this paper will be introduced.

3. Research Design

Suppose coal-fired power plants advance CCUS technology by investing in technological advancements, with a learning-by-doing effect influencing innovation efforts—meaning that as experience $A\left(t\right)$ accumulates, investment efficiency increases. Based on relevant studies, the development of CCUS technology $d\left(t\right)$ follows the dynamic equation:

$$\dot{d}\left(t\right)=I\left(t\right)-\alpha d\left(t\right)+bA\left(t\right)$$

(1)

where $I\left(t\right)$ denotes the investment in CCUS technology innovation at a coal-fired power plant over continuous time $t\in \left(0,+\infty \right)$, $\alpha \in \left[0,1\right]$ is the CCUS technology decay rate, $b>0$ is the efficiency parameter.

Dynamic control studies often consider stem-secondary school effects, and the model in this paper introduces the accumulation of experience $\dot{A}\left(t\right)$ in the dynamic process of investment in technological innovation, according to the articles by [39,40], we express the evolution of the accumulated experience $\dot{A}\left(t\right)$ by the following forms:

$$\dot{A}\left(t\right)=\mu I\left(t\right)-\tau A\left(t\right)$$

(2)

where $\mu$ represents the learning rate associated with technological innovation investment, $\tau$ characterizes the decaying memory rate of accumulated experience.

Since Arrow [41] studied the effect of the stem-secondary school effect on costs, a large number of studies have shown that the cost of production decreases with experience so that the instantaneous cost of an investment in technological innovation can be expressed as

$$C\left(t\right)={\displaystyle \frac{\beta }{2}}{I}^2\left(t\right)-\theta A\left(t\right)$$

(3)

where $\beta >0$ is the technology innovation investment cost efficiency parameter, $\theta >0$ indicates the extent to which knowledge accumulation influences the cost of investment in technology innovation.

Referring to the demand function of Guo and Li [42], and the electricity demand function of Menanteau et al. [43], in this study, electricity demand is influenced by both electricity pricing and the CCUS technology implemented in coal power stations, with the demand function assumed as

$$D\left(t\right)=a-a_{1}p\left(t\right)+a_{2}d\left(t\right)$$

(4)

where $a>0$ is the potential market demand for electricity, $p\left(t\right)$ is the price of electricity, $a_1>0$ and $a_2>0$ are the coefficients of the impact of electricity price and CCUS technology on demand, respectively.

Taking into account that the coal power station sets its electricity selling price at $p\left(t\right)$, the unit carbon emission is $\chi \left(t\right)$, and with the improvement of CCUS technology, the unit carbon emission changes, with reference to [44], we give

$$\chi \left(t\right)=m-d\left(t\right)$$

(5)

where $m>0$ represents the carbon emissions per unit from a coal power station without CCUS technology innovation, with $m\ge d\left(t\right)$. Thus, the net emissions from coal power stations $Q\left(t\right)$ are

$$Q\left(t\right)=\left(m-d\left(t\right)\right)D\left(t\right)$$

(6)

Based on the above discussion, when the government imposes an environmental tax $\mathit{\gamma }$ on carbon emissions per unit, over continuous time $t\in \left[0,+\infty \right)$, the instantaneous profit function $\pi \left(t\right)$ is

$$\begin{array}{l}\pi \left(t\right)=\left(p\left(t\right)-c\right)D\left(t\right)-\mathit{\gamma }Q\left(t\right)-C\left(t\right)\\ \hspace{1em}\hspace{1em}=\left[p\left(t\right)-c-\mathit{\gamma }\left(m-d\left(t\right)\right)\right]\left[a-a_{1}p\left(t\right)+a_{2}d\left(t\right)\right]-{\displaystyle \frac{\beta }{2}}{I}^2\left(t\right)+\theta A\left(t\right)\end{array}$$

(7)

where $c>0$ represents a fixed marginal production cost, with $p\left(t\right)-c\ge 0$.

4. Research Results

4.1. Optimal Decision Behavior Under Profit Maximization

4.1.1. Optimality Conditions and Properties

In a continuous time framework $t\in \left[0,+\infty \right)$, the goal of coal power stations is to seek price $p\left(t\right)$ and CCUS technology innovation investments $I\left(t\right)$ to maximize their profits, ultimately seeking to maximize the present value of profit $\Pi$.

$$\begin{array}{l}\Pi =\underset{p,I}{\max }{\displaystyle {\int }_0^{+\infty }{e}^{-\rho t}}\left\{\left[p\left(t\right)-c-\mathit{\gamma }\left(m-d\left(t\right)\right)\right]\left[a-a_{1}p\left(t\right)+a_{2}d\left(t\right)\right]-{\displaystyle \frac{\beta }{2}}{I}^2\left(t\right)+\theta A\left(t\right)\right\}dt\\ s.t\left\{\begin{array}{l}\dot{d}\left(t\right)=I\left(t\right)-\alpha d\left(t\right)+bA\left(t\right)\\ \dot{A}\left(t\right)=\mu I\left(t\right)-\tau A\left(t\right)\end{array}\right.\end{array}$$

(8)

where $\rho >0$ represents the discount rate, with the initial conditions given as $d\left(0\right)=d_0$ and $A\left(0\right)=A_0$. The present value Hamiltonian function of Equation (8) is given by

$$\begin{array}{l}H=\left[p\left(t\right)-c-\mathit{\gamma }\left(m-d\left(t\right)\right)\right]\left[a-a_{1}p\left(t\right)+a_{2}d\left(t\right)\right]-{\displaystyle \frac{\beta }{2}}{I}^2\left(t\right)+\theta A\left(t\right)\\ \hspace{1em}+{\lambda }_1\left(t\right)\left[I\left(t\right)-\alpha d\left(t\right)+bA\left(t\right)\right]+{\lambda }_2\left(t\right)\left[\mu I\left(t\right)-\tau A\left(t\right)\right]\end{array}$$

(9)

where ${\lambda }_1\left(t\right)$, ${\lambda }_2\left(t\right)$ correspond to the shadow prices of the state variables $\dot{d}\left(t\right)$, $\dot{A}\left(t\right)$, respectively. By applying the Hamiltonian function from Equation (9), the derived first-order optimality conditions and co-state equations result in:

$${\displaystyle \frac{\mathsf{\partial }H}{\mathsf{\partial }p\left(t\right)}}=-2a_{1}p\left(t\right)+a+a_{1}c+a_1\mathit{\gamma }m+\left(a_2-a_1\mathit{\gamma }\right)d\left(t\right)=0$$

(10)

$${\displaystyle \frac{\mathsf{\partial }H}{\mathsf{\partial }I\left(t\right)}}=-\beta I\left(t\right)+{\lambda }_1\left(t\right)+\mu {\lambda }_2\left(t\right)=0$$

(11)

$${\dot{\lambda }}_1\left(t\right)=\rho {\lambda }_1\left(t\right)-{\displaystyle \frac{\mathsf{\partial }H}{\mathsf{\partial }d\left(t\right)}}=\left(\rho +\alpha \right){\lambda }_1\left(t\right)-a_{2}p\left(t\right)+a_{2}c+a_2\mathit{\gamma }m-2a_2\mathit{\gamma }d\left(t\right)$$

(12)

$${\dot{\lambda }}_2\left(t\right)=\rho {\lambda }_2\left(t\right)-{\displaystyle \frac{\mathsf{\partial }H}{\mathsf{\partial }A\left(t\right)}}=\left(\rho +\tau \right){\lambda }_2\left(t\right)-b{\lambda }_1\left(t\right)-\theta$$

(13)

Equation (10) yields the pricing condition for coal power stations as

$$p\left(t\right)={\displaystyle \frac{a+a_{1}c+a_1\mathit{\gamma }m+\left(a_2-a_1\mathit{\gamma }\right)d\left(t\right)}{2a_1}}$$

(14)

Equation (14) shows that the optimal tariff condition is not constant and is affected by environmental taxes and CCUS technology, Equation (14) differentiates between $\mathit{\gamma }$ and $d\left(t\right)$, respectively. ${\displaystyle \frac{\mathsf{\partial }p\left(t\right)}{\mathsf{\partial }\mathit{\gamma }}}={\displaystyle \frac{m-d\left(t\right)}{2}}\ge 0$, ${\displaystyle \frac{\mathsf{\partial }p\left(t\right)}{\mathsf{\partial }d\left(t\right)}}={\displaystyle \frac{a_2-a_1\mathit{\gamma }}{2a_1}}$. In the context of profit maximization, within a continuous time framework $t\in \left[0,+\infty \right)$, electricity prices will rise as the environmental protection tax increases. Meanwhile, the magnitude of the environmental protection tax will also determine the impact of technology on the price, when the environmental protection tax $\mathit{\gamma }>{\displaystyle \frac{a_2}{a_1}}$, the price will be reduced with the improvement of technology. when $\mathit{\gamma }<{\displaystyle \frac{a_2}{a_1}}$, the price will increase with the improvement of technology. This highlights the importance of the environmental protection tax’s dynamic value. In this study, the carbon tax is considered a constant rate. To gain deeper insights, future research should examine the effects of an environmentally adjusted tax that varies dynamically.

From Equation (14), the shadow price

$${\lambda }_1\left(t\right)={\displaystyle \frac{a_2\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]}{2a_1\left(\rho +\alpha \right)}}$$

(15)

$${\lambda }_2\left(t\right)={\displaystyle \frac{\theta +b{\lambda }_1\left(t\right)}{\rho +\tau }}$$

(16)

By applying the first-order conditions, co-state equations, and Equation (15), a dynamic equation describing the variation in CCUS technology innovation investment for coal power stations can be derived, yielding

$$\begin{array}{c}\dot{I}\left(t\right)=\rho I\left(t\right)-{\displaystyle \frac{a_2\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]}{2a_1\beta }}-{\displaystyle \frac{\mu \rho \theta }{\beta \left(\rho +\tau \right)}}\\ \hspace{1em}+{\displaystyle \frac{\alpha \left(\rho +\tau \right)-\mu b\rho }{\beta \left(\rho +\tau \right)}}\cdot {\displaystyle \frac{a_2\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]}{2a_1\left(\rho +\alpha \right)}}\end{array}$$

(17)

According to the above equation, it can be seen that CCUS technology $d\left(t\right)$, environmental protection tax $\mathit{\gamma }$, and learning rate $\mu$ have an impact on the rate of change in investment in technological innovation, the Equation (17) on, and the derivation, we can obtain Proposition 1.

Proposition 1.

There are (i)${\displaystyle \frac{\mathsf{\partial }\dot{I}\left(t\right)}{\mathsf{\partial }d\left(t\right)}}<0$; (ii) when $m>3d\left(t\right)$, ${\displaystyle \frac{\mathsf{\partial }\dot{I}\left(t\right)}{\mathsf{\partial }\mathit{\gamma }}}>0$; when $d\left(t\right)<m<3d\left(t\right)$, ${\displaystyle \frac{\mathsf{\partial }\dot{I}\left(t\right)}{\mathsf{\partial }\mathit{\gamma }}}<0$; (iii) when $a_{2}b\rho \left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]+\rho \theta \left(\rho +\alpha \right)>\left(<\right)0$, ${\displaystyle \frac{\mathsf{\partial }\dot{I}\left(t\right)}{\mathsf{\partial }\mu }}<\left(>\right)0$.

Refer to Appendix A for the proof of the proposition.

Proposition 1 shows that the instantaneous investment rate $\dot{I}\left(t\right)$ in CCUS technological innovation for coal power stations is affected by technology, the environmental tax $\mathit{\gamma }$, and the learning rate $\mu$. 1-(i) shows that the higher the CCUS technology of a coal power stations, the rate of change in its instantaneous investment in CCUS innovation decreases. 1-(ii) If $m>3d\left(t\right)$, the instantaneous investment rate in technological innovation for a coal-fired power plant increases with the increase in the environmental tax; if $d\left(t\right)<m<3d\left(t\right)$, the instantaneous investment rate in technological innovation for a coal-fired power plant decreases with the increase in the environmental tax. 1-(iii) shows that as the learning rate increases, if $a_{2}b\rho \left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]+\rho \theta \left(\rho +\alpha \right)>\left(<\right)0$, the coal power stations will decrease (boost) the instantaneous investment rate in technological innovation.

4.1.2. Steady-State Analysis

This investigation evaluates equilibrium convergence in CCUS technological advancement investments within fossil fuel-based energy systems, while assessing dynamic stability under profit optimization constraints. Through parametric analysis with $\dot{I}\left(t\right)=0$ as the equilibrium threshold, we derive optimal investment parameters for carbon capture innovation that satisfy system stabilization criteria:

$$\begin{array}{c}{I}^m\left(d\right)={\displaystyle \frac{a_2\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]}{2a_1\beta \rho }}+{\displaystyle \frac{\mu \rho \theta }{\beta \rho \left(\rho +\tau \right)}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\displaystyle \frac{\alpha \left(\rho +\tau \right)-\mu b\rho }{\beta \rho \left(\rho +\tau \right)}}\cdot {\displaystyle \frac{a_2\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]}{2a_1\rho \left(\rho +\alpha \right)}}\end{array}$$

(18)

Next, the effects of $d\left(t\right)$, $\mathit{\gamma }$ and $\mu$ on the equilibrium investment in technological innovation in coal power stations are explored, leading to Proposition 2.

Proposition 2.

Under the profit maximization condition, the (i)${\displaystyle \frac{\mathsf{\partial }{I}^m\left(d\right)}{\mathsf{\partial }d}}>0$; (ii) when $a_{2}b\rho \left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]+\rho \theta \left(\rho +\alpha \right)>\left(<\right)0$, ${\displaystyle \frac{\mathsf{\partial }{I}^m\left(d\right)}{\mathsf{\partial }\mu }}>\left(<\right)0$; (iii) when $m>3d\left(t\right)$, ${\displaystyle \frac{\mathsf{\partial }{I}^m\left(d\right)}{\mathsf{\partial }\mathit{\gamma }}}<0$; when $d\left(t\right)<m<3d\left(t\right)$, ${\displaystyle \frac{\mathsf{\partial }{I}^m\left(d\right)}{\mathsf{\partial }\mathit{\gamma }}}>0$.

See Appendix B for proofs of propositions

Proposition 2-(i) suggests that steady-state investment in technological innovation in coal power stations increases with the level of technology. As the carbon emissions of the coal-fired power plant decrease with increasing technology level, then the coal-fired power plant will further increase its technology level by increasing its investment in technological innovation. 2-(ii) shows that as the learning rate increases, if $a_{2}b\rho \left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]+\rho \theta \left(\rho +\alpha \right)>\left(<\right)0$, coal power stations will increase (decrease) the level of investment in technological innovation. 2-(iii) illustrates that if $m>3d\left(t\right)$, the steady-state investment in technological innovation of coal power stations decreases with the increase in the carbon tax; if $d\left(t\right)<m<3d\left(t\right)$, the higher the environmental protection tax is, the higher the level of CCUS technological innovation investment in coal power stations is. When the carbon emissions per unit of a coal power stations without investing in CCUS technology are in a reasonable interval, due to the environmental protection tax levied by the government, the coal-fired power plant will increase its investment in technological innovation, and reduce carbon emissions by improving its technology, which in turn reduces its cost.

Next, it is investigated whether the investment in CCUS technology innovation in coal power stations can reach a steady state. Combining equations of motion (1) (2) and control Equation (17), the following control system is obtained:

$$\left\{\begin{array}{l}\dot{I}\left(t\right)=\rho I\left(t\right)-{\displaystyle \frac{a_2\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]}{2a_1\beta }}-{\displaystyle \frac{\mu \rho \theta }{\beta \left(\rho +\tau \right)}}\\ \hspace{1em}\hspace{1em}+{\displaystyle \frac{\alpha \left(\rho +\tau \right)-\mu b\rho }{\beta \left(\rho +\tau \right)}}\cdot {\displaystyle \frac{a_2\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]}{2a_1\left(\rho +\alpha \right)}}\\ \dot{d}\left(t\right)=I\left(t\right)-\alpha d\left(t\right)+bA\left(t\right)\\ \dot{A}\left(t\right)=\mu I\left(t\right)-\tau A\left(t\right)\end{array}\right.$$

(19)

Under constant conditions $\dot{I}\left(t\right)=\dot{d}\left(t\right)=\dot{A}\left(t\right)=0$, it is possible to obtain a stable equilibrium solution of the system, which leads to Proposition 3.

Proposition 3.

Under the condition of profit maximization, the system $\left\{I^m,d^m,A^m\right\}$ possesses a steady-state equilibrium solution characterized by saddle-point stability.

The proof of the proposition is given in Appendix C.

4.2. Optimal Decision-Making Behavior Under Social Welfare Maximization

4.2.1. Optimality Conditions and Properties

The government will seek the optimal CCUS technology innovation investment to maximize social welfare. Assuming that the electricity price is still represented by Equation (14), the homeopathic consumer surplus is

$$cs\left(t\right)={\displaystyle {\int }_{p\left(t\right)}^{\frac{a+a_{2}d\left(t\right)}{a_1}}\left[a-a_{1}z+a_{2}d\left(t\right)\right]}dz={\displaystyle \frac{1}{2a_1}}{\left[a-a_{1}p\left(t\right)+a_{2}d\left(t\right)\right]}^2$$

(20)

The instantaneous social welfare function is $sw\left(t\right)=\pi \left(t\right)+cs\left(t\right)$, where is the instantaneous profit of the coal power stations. Thus, the maximization of social welfare can be tabulated as:

$$\begin{array}{l}SW=\underset{I}{\max }{\displaystyle {\int }_0^{+\infty }{e}^{-\rho t}}\left\{{\displaystyle \frac{3}{8a_1}}{\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+a_1\mathit{\gamma }\right)d\left(t\right)\right]}^2-{\displaystyle \frac{\beta }{2}}{I}^2\left(t\right)+\theta A\left(t\right)\right\}dt\\ s.t.\left\{\begin{array}{l}\dot{d}\left(t\right)=I\left(t\right)-\alpha d\left(t\right)+bA\left(t\right)\\ \dot{A}\left(t\right)=\mu I\left(t\right)-\tau A\left(t\right)\end{array}\right.\end{array}$$

(21)

The initial conditions are $d\left(0\right)=d_0$, $A\left(0\right)=A_0$.

The present value Hamiltonian function of Equation (21) is given by

$$\begin{array}{c}H={\displaystyle \frac{3}{8a_1}}{\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+a_1\mathit{\gamma }\right)d\left(t\right)\right]}^2-{\displaystyle \frac{\beta }{2}}{I}^2\left(t\right)+\theta A\left(t\right)\\ +{\omega }_1\left(t\right)\left[I\left(t\right)-\alpha d\left(t\right)+bA\left(t\right)\right]+{\omega }_2\left(t\right)\left[\mu I\left(t\right)-\tau A\left(t\right)\right]\end{array}$$

(22)

where ${\omega }_1\left(t\right)$ and ${\omega }_2\left(t\right)$ represent the shadow prices associated with the state variables $\dot{d}\left(t\right)$, $\dot{A}\left(t\right)$, respectively. The first-order necessary conditions and co-state equations derived from the Hamiltonian function (22) yield

$${\displaystyle \frac{\mathsf{\partial }H}{\mathsf{\partial }I}}=-\beta I\left(t\right)+{\omega }_1\left(t\right)+\mu {\omega }_2\left(t\right)=0$$

(23)

$$\begin{array}{l}{\dot{\omega }}_1\left(t\right)=\rho {\omega }_1\left(t\right)-{\displaystyle \frac{\mathsf{\partial }H}{\mathsf{\partial }d\left(t\right)}}\\ \hspace{1em}\hspace{1em} =\left(\rho +\alpha \right){\omega }_1\left(t\right)-{\displaystyle \frac{3\left(a_2+a_1\mathit{\gamma }\right)}{4a_1}}\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+a_1\mathit{\gamma }\right)d\left(t\right)\right]\end{array}$$

(24)

$${\dot{\omega }}_2\left(t\right)=\rho {\omega }_2\left(t\right)-{\displaystyle \frac{\mathsf{\partial }H}{\mathsf{\partial }A\left(t\right)}}=\left(\rho +\tau \right){\omega }_2\left(t\right)-b{\omega }_1\left(t\right)-\theta$$

(25)

The corresponding transversal conditions are:

$$\underset{t\to \infty }{\lim }{\omega }_1\left(t\right)d\left(t\right)e^{-\rho t}=0, \underset{t\to \infty }{\lim }{\omega }_2\left(t\right)A\left(t\right)e^{-\rho t}=0.$$

From the above equation, the shadow price is

$${\omega }_1\left(t\right)={\displaystyle \frac{3\left(a_2+a_1\mathit{\gamma }\right)}{4a_1\left(\rho +\alpha \right)}}\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+a_1\mathit{\gamma }\right)d\left(t\right)\right]$$

(26)

$${\omega }_2\left(t\right)={\displaystyle \frac{\theta +b{\omega }_1\left(t\right)}{\rho +\tau }}$$

(27)

By utilizing the first-order conditions along with the co-state equations and Equation (26), a dynamic equation for the change in investment in technological innovation in CCUS of coal power stations can be obtained

$$\begin{array}{l}\dot{I}\left(t\right)=\rho I\left(t\right)-{\displaystyle \frac{\rho \left(\rho +\tau \right)+\mu b\rho }{\beta \left(\rho +\tau \right)}}\cdot {\displaystyle \frac{3\left(a_2+a_1\mathit{\gamma }\right)}{4a_1\left(\rho +\alpha \right)}}\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+a_1\mathit{\gamma }\right)d\left(t\right)\right]\\ \hspace{1em}\hspace{1em}-{\displaystyle \frac{\mu \rho \theta }{\beta \left(\rho +\tau \right)}}\end{array}$$

(28)

Proposition 4.

Under the condition of maximizing social welfare, ${\displaystyle \frac{\mathsf{\partial }\dot{I}\left(t\right)}{\mathsf{\partial }d\left(t\right)}}<0$; when $3b\left(a_2+a_1\mathit{\gamma }\right)\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+a_1\mathit{\gamma }\right)d\left(t\right)\right]+4a_1\theta \left(\rho +\alpha \right)>\left(<\right)0$, ${\displaystyle \frac{\mathsf{\partial }\dot{I}\left(t\right)}{\mathsf{\partial }\mu }}<\left(>\right)0$; when $\left(a_2+2a_1\mathit{\gamma }\right)\left(d\left(t\right)-m\right)+a-a_{1}c+a_{2}d\left(t\right)>\left(<\right)0$, ${\displaystyle \frac{\mathsf{\partial }\dot{I}\left(t\right)}{\mathsf{\partial }\mathit{\gamma }}}<\left(>\right)0$.

See Appendix D for proofs of proposition.

Proposition 4 shows that the instantaneous rate of investment $\dot{I}\left(t\right)$ in CCUS technological innovation for coal power stations under social welfare maximization is affected by technology, environmental taxes $\mathit{\gamma }$, and the learning rate $\mu$. (i) shows that as the CCUS technology level of a coal power station increases, the rate of change in the instantaneous investment in CCUS innovation decreases. (ii) If $3b\left(a_2+a_1\mathit{\gamma }\right)\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+a_1\mathit{\gamma }\right)d\left(t\right)\right]+4a_1\theta \left(\rho +\alpha \right)>\left(<\right)0$, the instantaneous rate of investment in technological innovation of a coal power stations will increase (decrease) with the increase (decrease) in the environmental taxes (decrease); 1-(iii) shows that as the learning rate increases, if $\left(a_2+2a_1\mathit{\gamma }\right)\left(d\left(t\right)-m\right)+a-a_{1}c+a_{2}d\left(t\right)>\left(<\right)0$, the coal power stations will reduce (or increase) the immediate investment rate in technological innovation.

4.2.2. Steady-State Analysis

The local stability case, such that $\dot{I}\left(t\right)=0$, yields the steady-state investment in CCUS technological innovation for coal power stations under the condition of social welfare maximization is determined as

$$\begin{array}{l}{I}^s\left(d\right)={\displaystyle \frac{\left(\rho +\tau \right)+\mu b}{\beta \left(\rho +\tau \right)}}\cdot {\displaystyle \frac{3\left(a_2+a_1\mathit{\gamma }\right)}{4a_1\left(\rho +\alpha \right)}}\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+a_1\mathit{\gamma }\right)d\left(t\right)\right]\\ \hspace{1em}\hspace{1em} -{\displaystyle \frac{\mu \theta }{\beta \left(\rho +\tau \right)}}\end{array}$$

(29)

Similarly to the treatment of Section 4.1.2, the corresponding results are as follows, with the explanatory analysis of the propositions being consistent with the previous section and the preceding section.

Proposition 5.

Under social welfare maximization, (i)${\displaystyle \frac{\mathsf{\partial }{I}^s\left(d\right)}{\mathsf{\partial }d}}>0$; (ii) when $a_{2}b\rho \left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+3a_1\mathit{\gamma }\right)d\left(t\right)\right]+\rho \theta \left(\rho +\alpha \right)>\left(<\right)0$, ${\displaystyle \frac{\mathsf{\partial }{I}^s\left(d\right)}{\mathsf{\partial }\mu }}>\left(<\right)0$; (iii) when $3b\left(a_2+a_1\mathit{\gamma }\right)\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+a_1\mathit{\gamma }\right)d\left(t\right)\right]+4a_1\theta \left(\rho +\alpha \right)>\left(<\right)0$, ${\displaystyle \frac{\mathsf{\partial }{I}^s\left(d\right)}{\mathsf{\partial }\mathit{\gamma }}}>\left(<\right)0$.

See Appendix E for the proof of the proposition.

In terms of the next step, it is investigated whether dynamic equilibrium can be achieved by CCUS technological innovation investment in coal power stations under social welfare maximization conditions. Combining Equations (1) and (2) and control Equation (28)

$$\left\{\begin{array}{l}\dot{I}\left(t\right)=\rho I\left(t\right)-{\displaystyle \frac{\rho \left(\rho +\tau \right)+\mu b\rho }{\beta \left(\rho +\tau \right)}}\cdot {\displaystyle \frac{3\left(a_2+a_1\mathit{\gamma }\right)}{4a_1\left(\rho +\alpha \right)}}\left[a-a_{1}c-a_1\mathit{\gamma }m+\left(a_2+a_1\mathit{\gamma }\right)d\left(t\right)\right]\\ \hspace{1em}\hspace{1em}-{\displaystyle \frac{\mu \rho \theta }{\beta \left(\rho +\tau \right)}}\\ \dot{d}\left(t\right)=I\left(t\right)-\alpha d\left(t\right)+bA\left(t\right)\\ \dot{A}\left(t\right)=\mu I\left(t\right)-\tau A\left(t\right)\end{array}\right.$$

(30)

Under steady-state conditions, the system attains an equilibrium solution, which forms the basis of Proposition 6.

Proposition 6.

When social welfare maximization is considered, the system $\left\{I^s,d^s,A^s\right\}$ attains a steady-state equilibrium characterized by saddle-point stability. The proof supporting this proposition can be found in Appendix F.

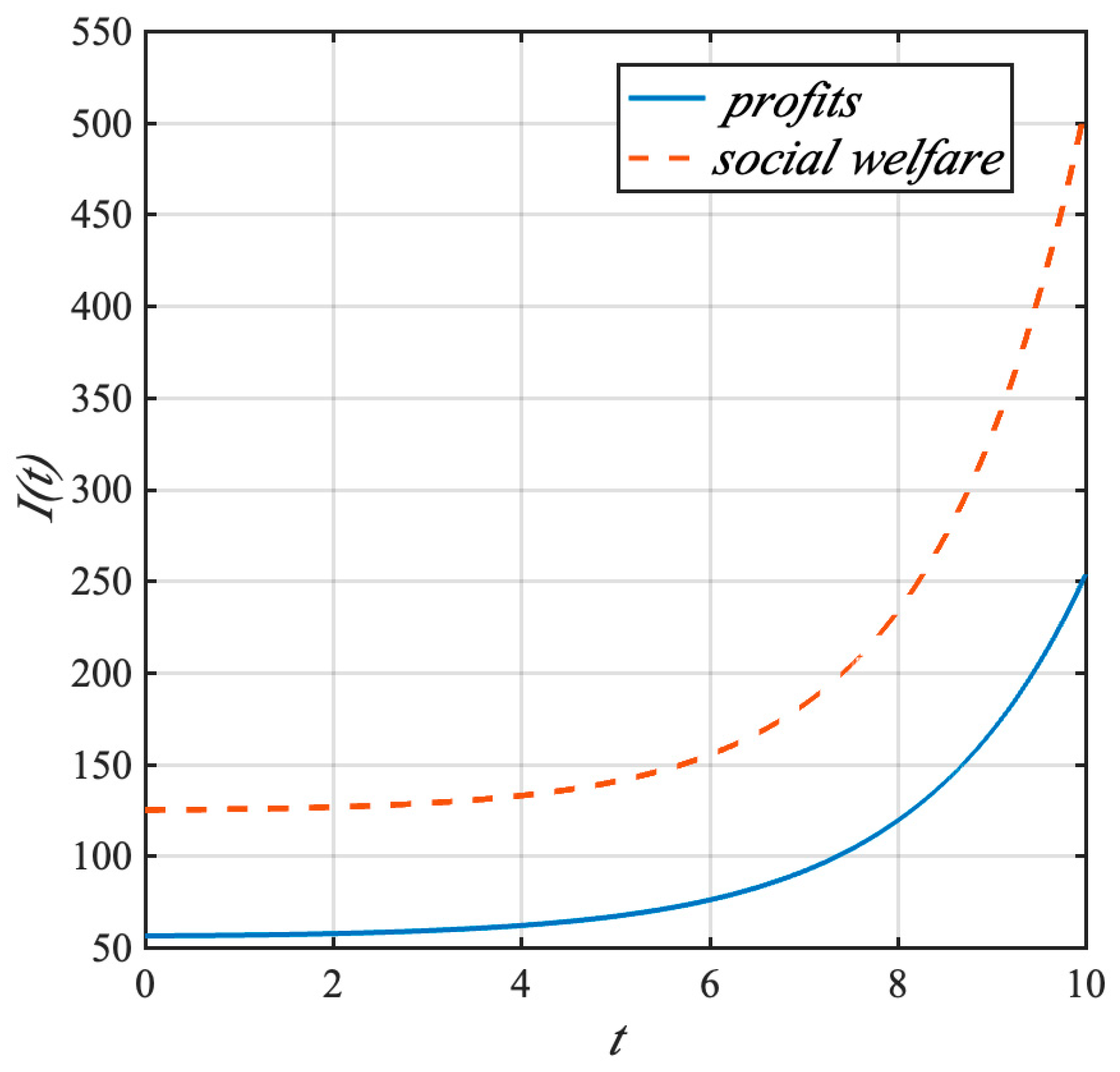
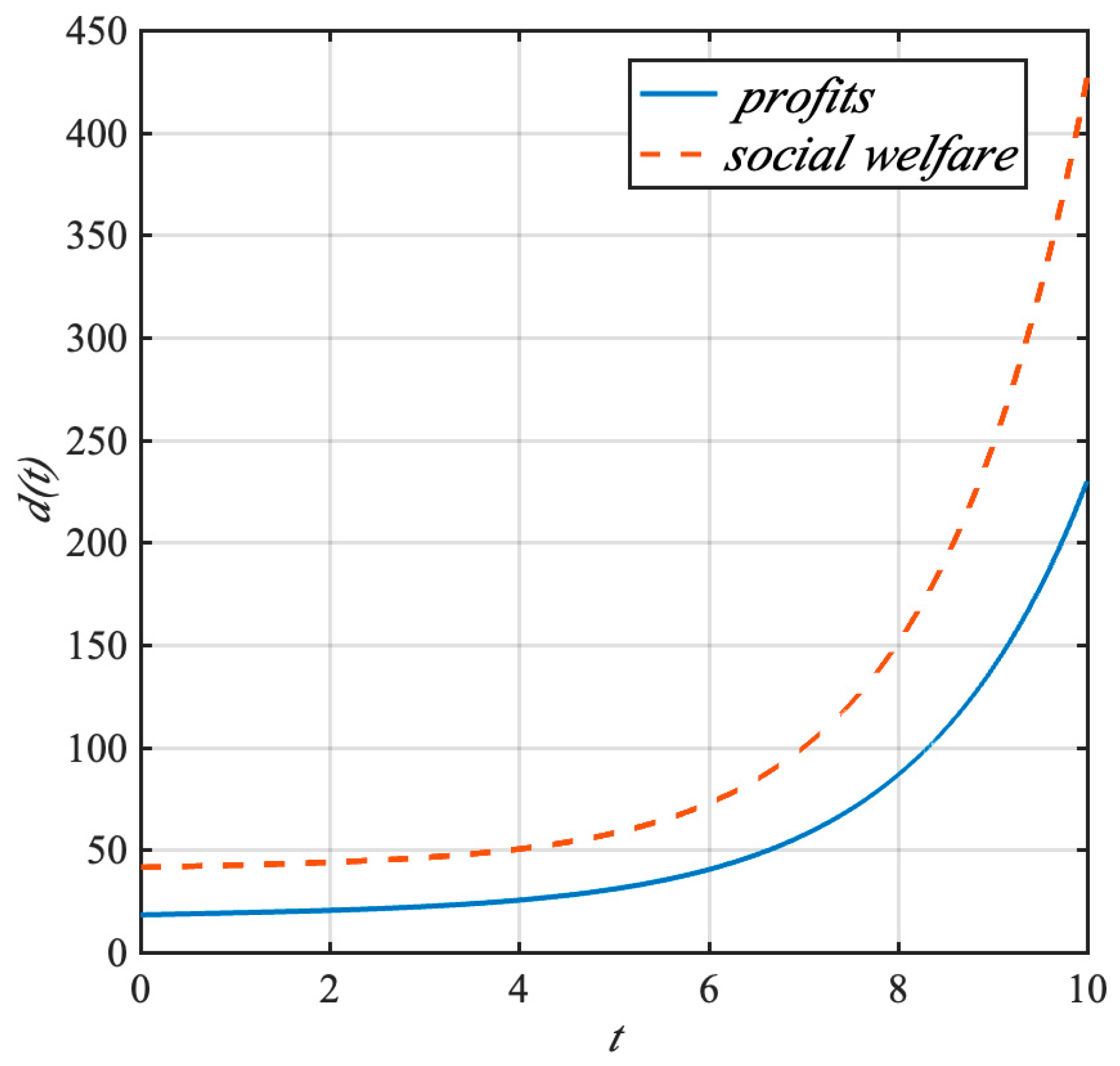
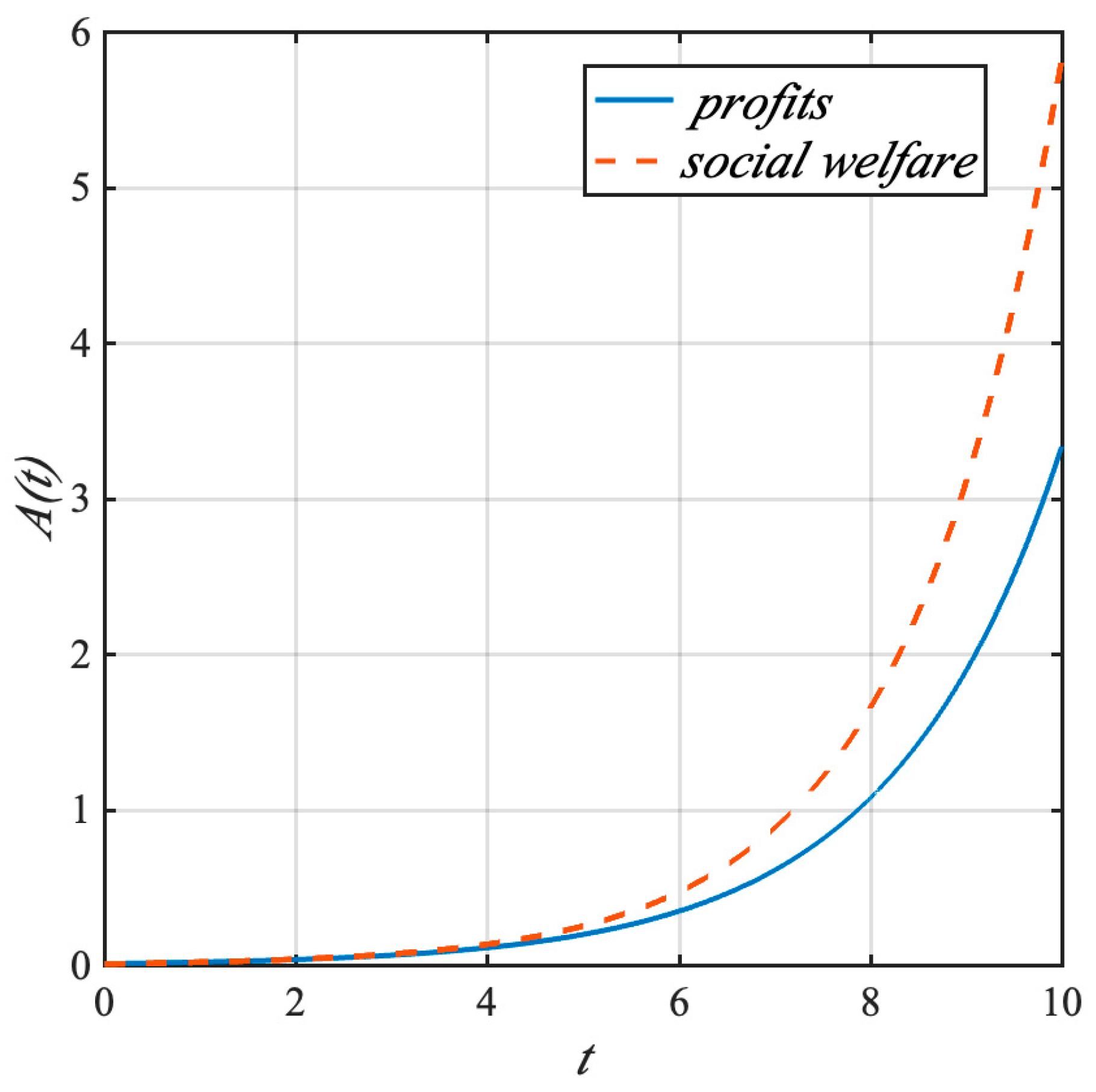
4.3. Numerical Simulation

The equilibrium solutions for technological innovation in coal-fired power plant CCUS $\left\{I^m,d^m,A^m\right\}$ and $\left\{I^s,d^s,A^s\right\}$ were obtained above, but comparing investment differences in coal power stations under profit maximization and social welfare maximization conditions remains challenging. This section analytically compares the magnitude of the equilibrium under the two scenarios and draws on the idea of numerical setting of Li & Fu, 2022 [44] (see

Table 1. Parameter values utilized for numerical computation.

$\mathit{a}$	$\mathit{b}$	$\mathit{m}$	$\mathit{c}$	$\mathit{\alpha }$	$\mathit{\rho }$	$\mathit{\tau }$	$\mathit{\mu }$	${\mathit{a}}_1$	${\mathit{a}}_2$	$\mathit{\theta }$	$\mathit{\gamma }$	$\mathit{\beta }$
10	0.01	0.65	0.18	0.37	0.30	0.03	0.01	0.55	0.20	0.12	0.10	0.40

) to give a general solution near the steady-state equilibrium under profit maximizing and social welfare-maximizing conditions of coal power stations.

The general solutions for both scenarios are obtained through a comparable method, with the solution under the profit maximization condition being determined first: $\Phi \left(t\right)={\left\{\overline{I}\left(t\right),\overline{d}\left(t\right),\overline{A}\left(t\right)\right\}}^T$. The system’s equilibrium state is given by ${\Phi }^m={\left\{I^m,d^m,A^m\right\}}^T$. The system is linear, and the general solution $\Phi \left(t\right)={\Phi }^m+{\displaystyle \sum _{\iota =1}^3{z}_{\iota }{\overrightarrow{v}}_{\iota }}{e}^{{\eta }_{\iota }t}$ can be expressed by the equilibrium solution, eigenvectors and eigenvalues, $z_{\iota }$ is constant coefficients, $\iota =1,2,3$, ${\eta }_{\iota }$ are the Jacobi matrix’s eigenvalues when the system reaches a steady-state equilibrium, and ${\overrightarrow{v}}_{\iota }={\left(v_{\iota 1},v_{\iota 2},v_{\iota 3}\right)}^T$ are the corresponding eigenvectors. Using the parameters set in Table 1, the expression of the general solution under the scenario of maximizing the profit of a coal-fired power plant can be obtained:

$$\begin{array}{l}\overline{I}\left(t\right)=55.34+0.6836e^{0.5669t}+0.2578e^{-0.6368t}-0.0069e^{-0.0301t}\\ \overline{d}\left(t\right)=18.45+0.72986e^{0.5669t}-\mathrm{0.96620.2578}{e}^{-0.6368t}+0.0091e^{-0.0301t}\\ \overline{A}\left(t\right)=0.0115e^{0.5669t}-0.0042e^{-0.6368t}\end{array}$$

Using the same approach, the general solution expression for the social welfare maximization condition can be obtained: $\tilde{\Phi }\left(t\right)={\left\{\tilde{I}\left(t\right),\tilde{d}\left(t\right),\tilde{A}\left(t\right)\right\}}^T$.

$$\begin{array}{l}\tilde{I}\left(t\right)=124+0.7070e^{0.6300t}+0.3134e^{-0.7t}-0.0075e^{-0.0301t}\\ \tilde{d}\left(t\right)=41.66+0.7071e^{0.6300t}-0.9496e^{-0.7t}+0.0075e^{-0.0301t}\\ \tilde{A}\left(t\right)=\tilde{I}\left(t\right)=0.0107e^{0.6300t}-0.0047e^{-0.7t}\end{array}$$

Based on the expressions for the general solutions, Figure 2, Figure 3 and Figure 4 are plotted. In the graphical representations, solution trajectories are differentiated by line patterns: broken lines correspond to scenarios optimizing social welfare, while continuous lines represent outcomes aligned with profit optimization objectives.

From Figure 2, it is found that investment in CCUS technological innovation $\overline{I}\left(t\right)$ and $\tilde{I}\left(t\right)$ both increase with time t for coal power stations, and that investment under profit maximization is lower than under social welfare maximization, $\overline{I}\left(t\right)<\tilde{I}\left(t\right)$. When comparing the investment levels under different scenarios, it is evident that the investment made under the profit maximization scenario is lower than that under the social welfare maximization scenario. This implies that, for coal-fired power stations, when making decisions about investing in CCUS technological innovation, the pursuit of social welfare has a more significant impact on the investment level than the pursuit of profit. From Figure 3, coal power stations CCUS technology $\overline{d}\left(t\right)$ and $\tilde{d}\left(t\right)$, which grows with time t in both scenarios, $\tilde{d}\left(t\right)>\overline{d}\left(t\right)$. This indicates that social welfare can more effectively promote CCUS technology innovation, as the growth of the technology is more pronounced in the social welfare-focused context. Figure 4 reflects the knowledge accumulation in the process of CCUS technological innovation in coal power stations $\overline{A}\left(t\right)$ and $\tilde{A}\left(t\right)$, the level of knowledge accumulation rises with time t in both the profit-maximizing condition and the social welfare-maximizing condition, and it starts to rise slowly and then rises faster, which suggests that employees become more proficient in mastering the technology and the process over time, which in turn improves efficiency. As illustrated in Figure 4, the level of knowledge accumulation under the social welfare maximization scenario consistently surpasses that observed in the profit maximization scenario, with $\tilde{A}\left(t\right)>\overline{A}\left(t\right)$.

The results of the above analysis can be summarized as conclusions.

In conclusion, the research findings highlight several key insights regarding the impact of different objectives on investment in technological innovation and knowledge accumulation in the context of CCUS in coal-fired power plants.

Firstly, it is evident that investment in technological innovation is greater under social welfare maximization than under profit maximization. When the primary goal is to maximize social welfare, coal-fired power plants are more willing to invest in CCUS technological innovation. This is because social welfare considerations take into account the broader benefits of reducing carbon emissions and mitigating climate change, which often require significant upfront investment in new technologies. In contrast, when the focus is solely on profit maximization, the investment in technological innovation tends to be lower, as companies may be more cautious about undertaking high-risk, high-cost projects that do not promise immediate financial returns.

Secondly, social welfare maximization is more effective in driving CCUS technological advancements in coal power plants. The pursuit of social welfare encourages power plants to adopt more advanced CCUS technologies, such as improved carbon capture methods, more efficient utilization processes, and safer storage solutions. These advancements not only help reduce the environmental impact of coal-fired power generation but also contribute to the long-term sustainability of the energy sector. On the other hand, profit maximization-driven investment may focus more on short-term gains and less on long-term technological development and environmental benefits.

Lastly, the level of knowledge accumulation under profit maximization is lower than that under social welfare maximization. Knowledge accumulation is crucial for the continuous improvement and innovation of CCUS technologies. When social welfare is the primary objective, there is a greater emphasis on research and development, as well as the sharing of knowledge and best practices among different stakeholders. This leads to a faster accumulation of knowledge and a more robust technological foundation for CCUS. In contrast, under profit maximization, the focus on knowledge accumulation may be limited, as companies may be more concerned with protecting their proprietary technologies and maximizing their competitive advantage, rather than collaborating and sharing knowledge for the greater good.

In summary, the research demonstrates that social welfare maximization has a more positive and comprehensive impact on investment in technological innovation and knowledge accumulation in the CCUS sector of coal-fired power plants. This suggests that policies and incentives aimed at promoting social welfare can play a crucial role in advancing the adoption and development of CCUS technologies, ultimately contributing to global efforts in combating climate change and achieving sustainable energy production.

5. Discussion of Results

Amid escalating climate challenges under global carbon neutrality objectives, decarbonization of thermal power facilities remains critical to achieving sustainable energy transitions. CCUS stands out as a key technological pathway for net-negative emissions in fossil fuel-based power generation. This investigation incorporates three novel dimensions. Firstly, strategic investment equilibrium analysis for low-carbon retrofitting through CCUS technological enhancement. Secondly, dynamic innovation mechanisms integrate knowledge spillover effects with technological learning curves. Finally, fiscal policy impacts through environmental taxation frameworks. Through rigorous system dynamics modeling, we systematically examine operational decision-making under contrasting optimization paradigms—corporate profitability versus societal welfare maximization. The main findings are summarized as follows:

(1)

The dynamic system demonstrates saddle-path stability characteristics under both profit-driven optimization and social welfare maximization frameworks, contingent upon specific operational thresholds. When $\rho <\alpha +\tau$, the equilibrium solution manifests unique saddle-path convergence properties. Stability analysis reveals that this dynamic equilibrium is highly sensitive to three critical factors: the temporal discount factor, technological obsolescence rate, and knowledge depreciation coefficient. The temporal discount factor reflects the time value of money and future benefits, which has a significant impact on the investment decisions and operating strategies of thermal power plants. A higher discount factor may lead to a greater emphasis on short-term profits, while a lower discount factor may encourage more long-term investment in CCUS technologies. The technological obsolescence rate indicates the speed at which CCUS technologies become outdated. As new and more efficient CCUS technologies emerge, the existing technologies may lose their competitiveness, which will affect the investment and operation of thermal power plants. The knowledge depreciation coefficient represents the rate at which the knowledge related to CCUS technologies becomes outdated. With the continuous development of science and technology, the knowledge and skills required for CCUS operation and maintenance may need to be updated in a timely manner. Otherwise, it will affect the performance and cost-effectiveness of CCUS systems.

(2)

The allocation of resources toward CCUS technology for coal power plants is greater under social welfare maximization compared to profit maximization. This is because, under the social welfare maximization framework, the focus is not only on the economic benefits of thermal power plants but also on the overall social and environmental benefits. Therefore, more resources will be allocated to CCUS technology to reduce carbon emissions and improve air quality, even if it may reduce the short-term profitability of thermal power plants. Government initiatives are more effective in advancing CCUS technology than the efforts of coal power plants alone. Governments can provide various forms of support, such as financial subsidies, tax incentives, and policy guidance, to encourage thermal power plants to adopt CCUS technologies. In addition, governments can also coordinate the efforts of different stakeholders, such as research institutions, equipment manufacturers, and power grid companies, to jointly promote the development and application of CCUS technologies.

(3)

Under social welfare maximization, CCUS technology innovation, knowledge accumulation, and the overall cleanliness of coal power stations exceed the levels achieved under profit-driven decision-making by coal power plants. This is because, under the social welfare maximization framework, there is a greater incentive to invest in R&D and innovation of CCUS technologies to improve their performance and reduce costs. At the same time, the accumulation of knowledge and experience in the application of CCUS technologies will also be more valued, which will promote the continuous improvement of the overall cleanliness of coal power stations.

(4)

Environmental protection tax will not only affect the investment in CCUS technological innovation of coal power stations but also affect the price of electricity. The static environmental protection tax cannot well reflect its impact, so the government should reasonably set the dynamic environmental protection tax to promote the CCUS technology innovation of coal-fired power plants. A dynamic environmental protection tax can better adapt to the changes in the cost and benefits of CCUS technologies and the market conditions of the power industry. By adjusting the tax rate in a timely manner, the government can encourage thermal power plants to continuously invest in CCUS technological innovation and improve their environmental performance.

The above conclusions indicate that investment in technological innovation at coal power stations is influenced by environmental protection taxes, knowledge accumulation, and technological advancement. To enhance their technological capabilities, coal power plants should focus on increasing the learning rate of knowledge accumulation through workforce training, internal knowledge sharing, and collaboration with external technical experts. Coal power stations should make reasonable investment decisions on technological innovation, realize the optimal allocation of technology selection and investment, achieve long-term investment results, and avoid the problem of underinvestment. For the government to strengthen the green culture propaganda, promote green consumption and green production, and form an atmosphere in which the whole society jointly supports green technological innovation, the government should also rationally design the tax aspect and increase the green low-carbon policy, expand the investment direction, and promote the development of green economy.

This research provides a basis for investment management strategies regarding CCUS technology innovation in coal power plants under environmental protection tax policies. The findings assist coal power stations in optimizing resource allocation and strengthening their competitiveness while also offering insights for government authorities to regulate their investment behavior. However, this paper focuses on the investment strategy of an individual coal-fired power plant, without addressing competitive or cooperative interactions among multiple plants. Additionally, it considers only a static environmental protection tax mechanism, which presents certain limitations, as other policy instruments—such as carbon trading and carbon subsidies—are not explored in depth. In the future, we can explore the dynamic control strategy of hybrid policy for multiple subjects, as well as with the development of digital economy, we can also study in depth the dynamic control problem of digital economy and joint emission reduction of multiple enterprises, so as to make the enterprise group carry out an effective investment strategy and realize the double maximization of economic and environmental benefits. In addition, we can also consider the externalities of technological progress, the impact of blockchain technology, and the influence of mental accounting on decision-making entities [45].