Electronic Tuning Square-Wave Generators with Improved Linearity Using Operational Transresistance Amplifier
Abstract
:1. Introduction
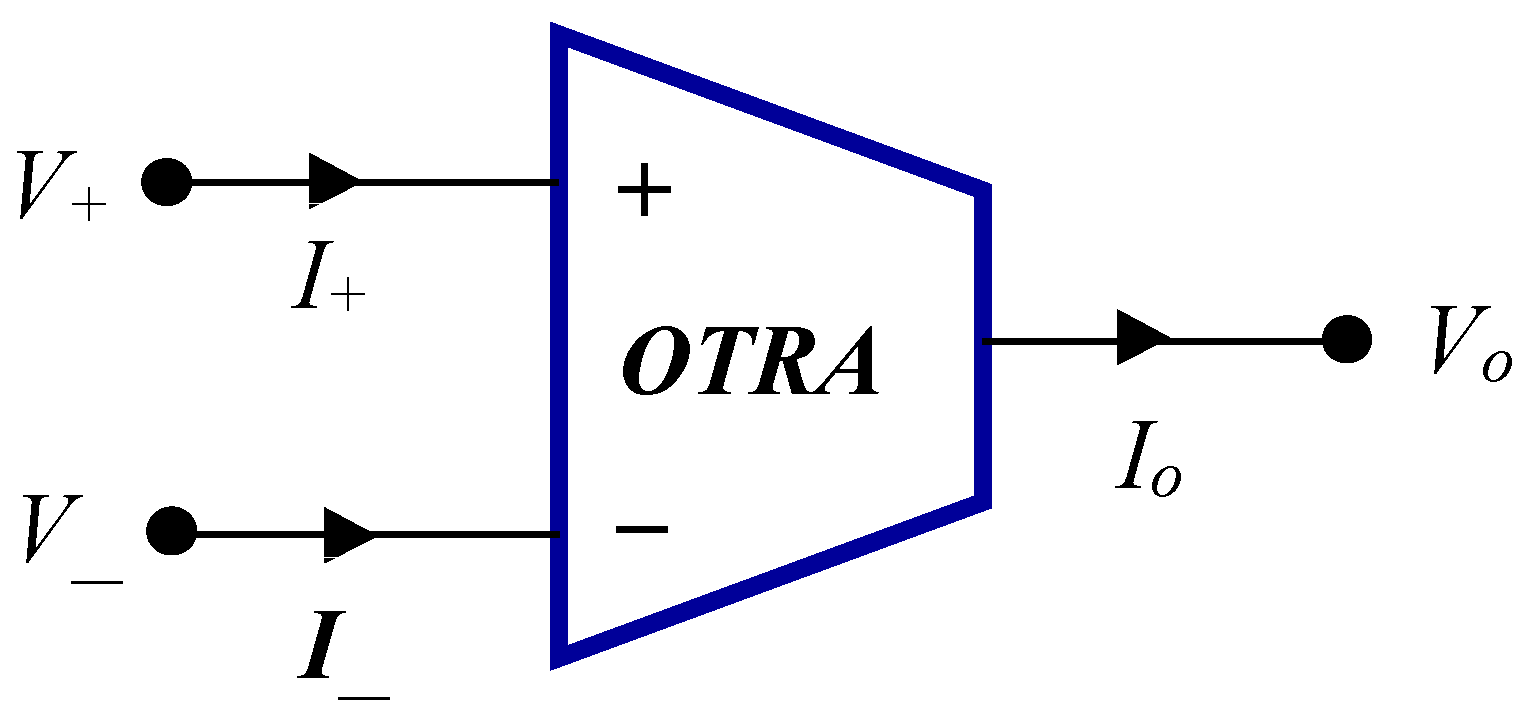
2. Circuit Description and Operation
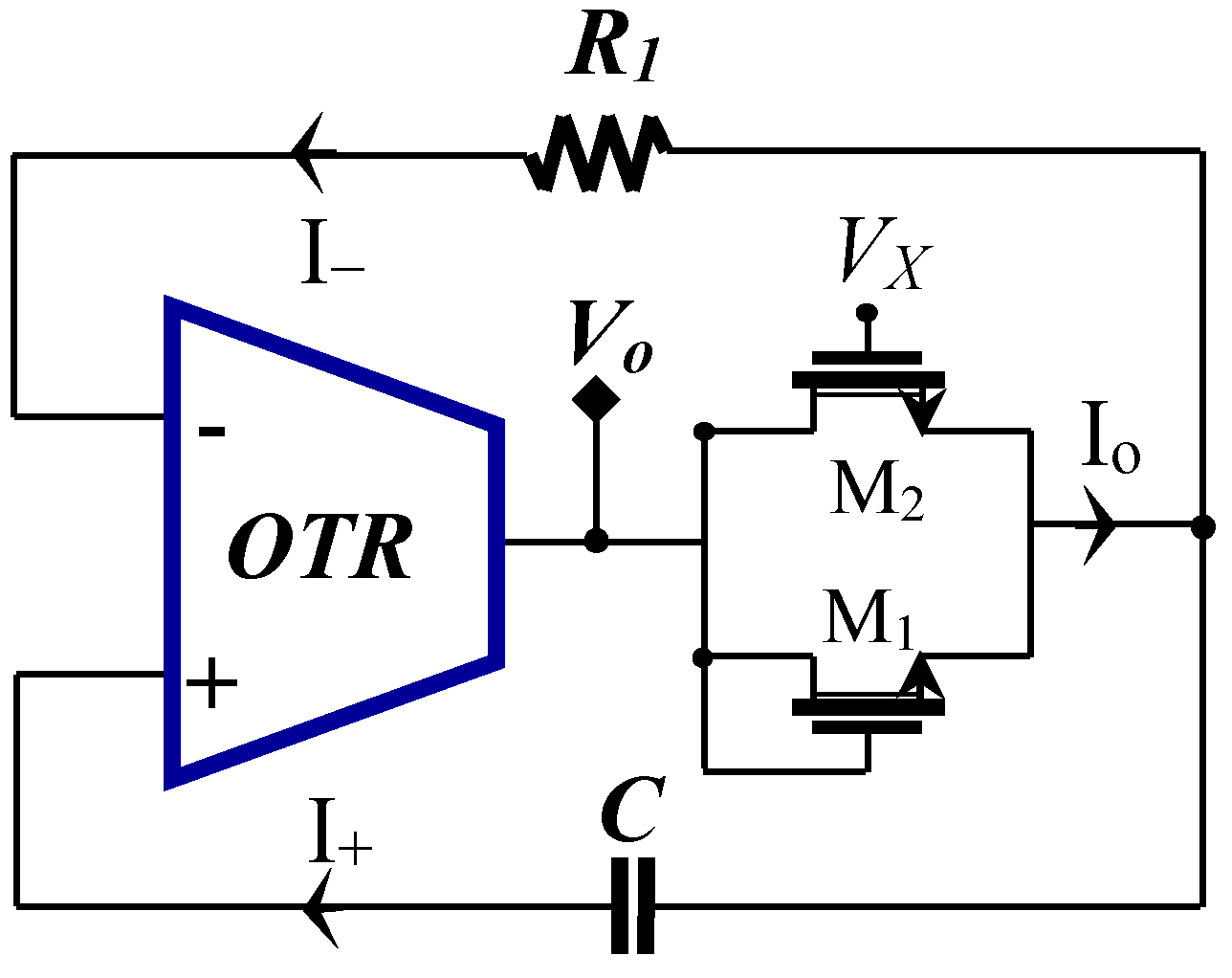
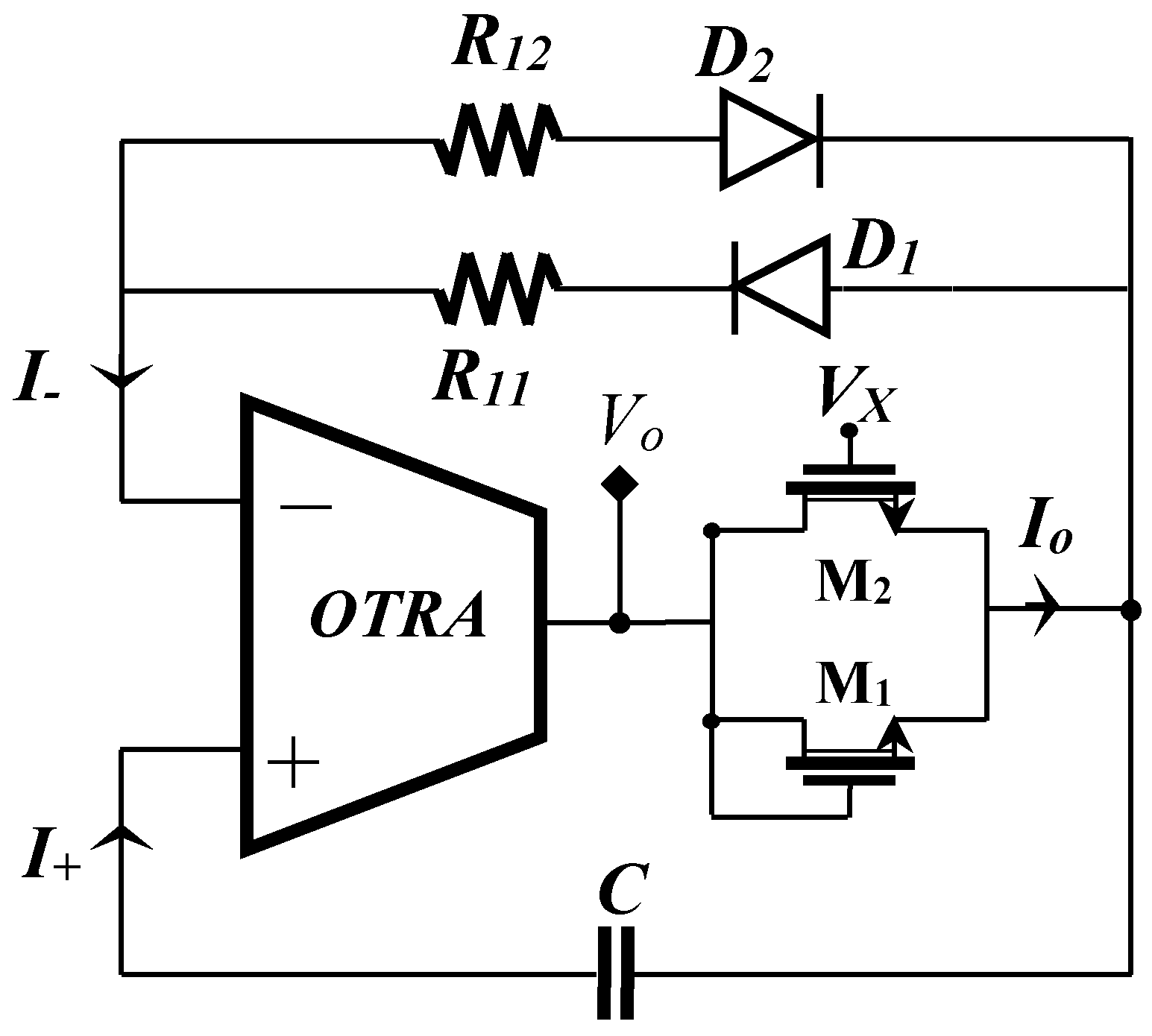
2.1. Proposed Circuit-1
2.2. Proposed Circuit-2
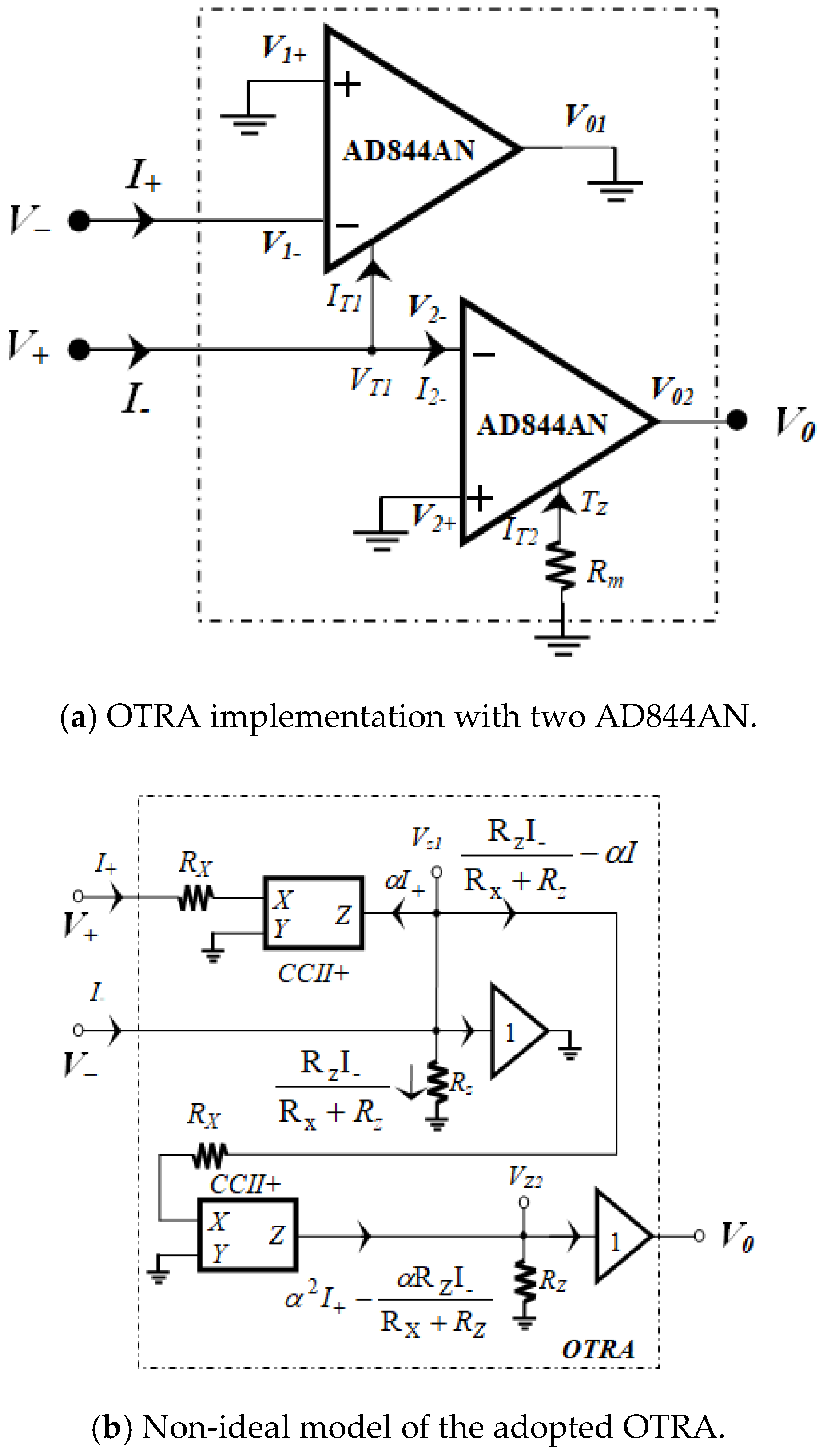
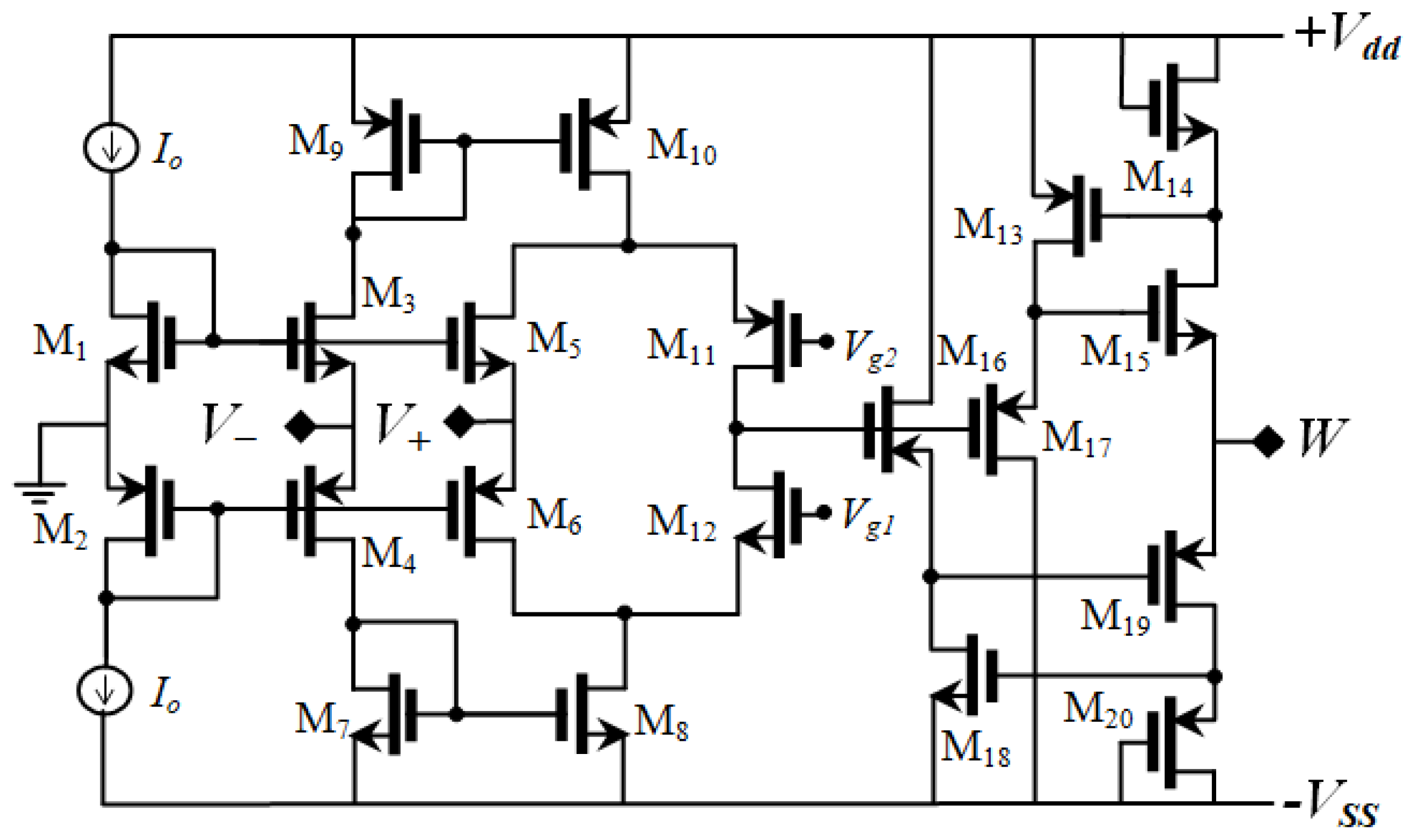
2.3. Non-Ideal Analysis
2.3.1. Non-Ideal Analysis of Proposed Circuit-1
2.3.2. Non-Ideal Analysis of Proposed Circuit-2
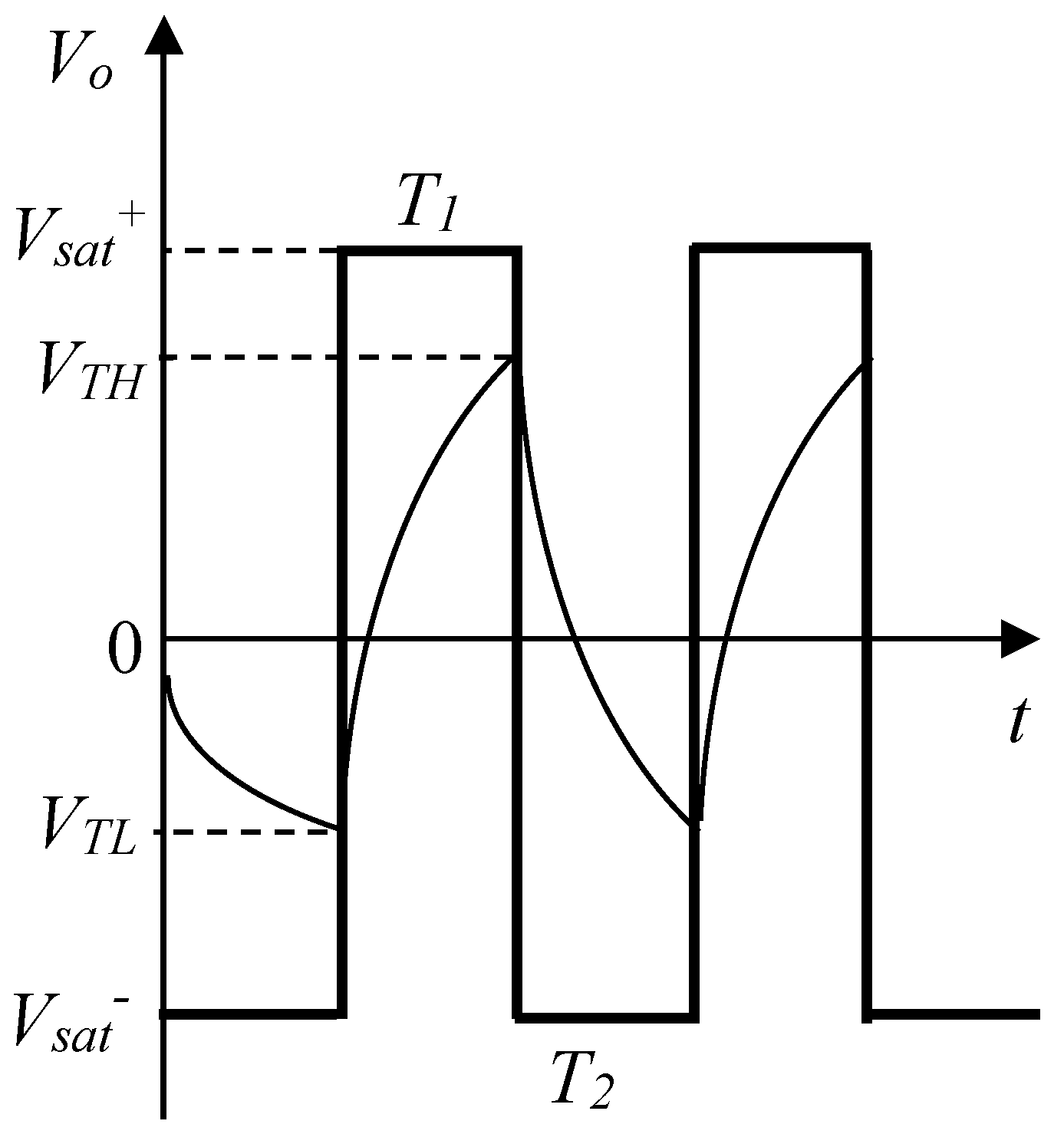
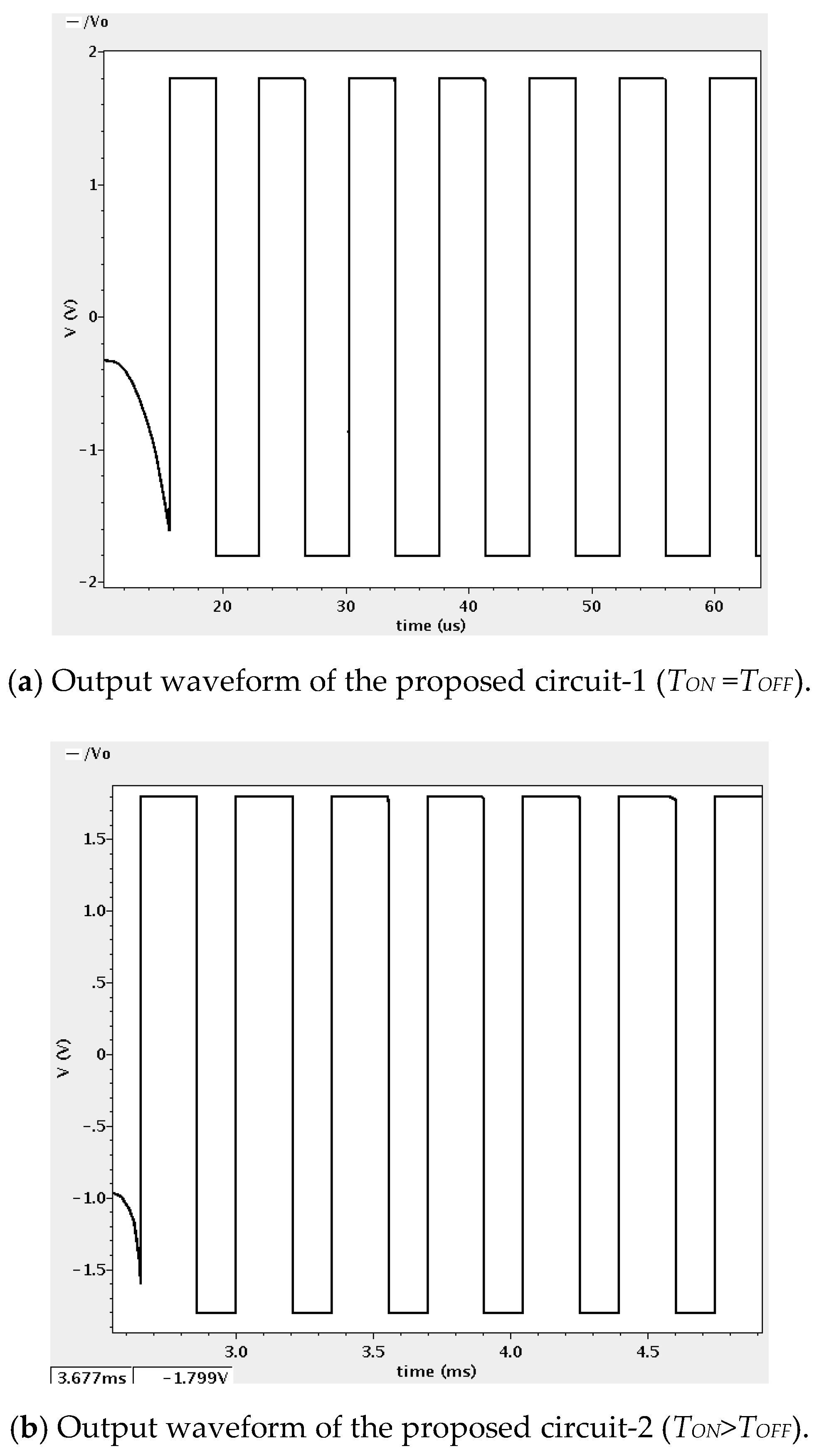
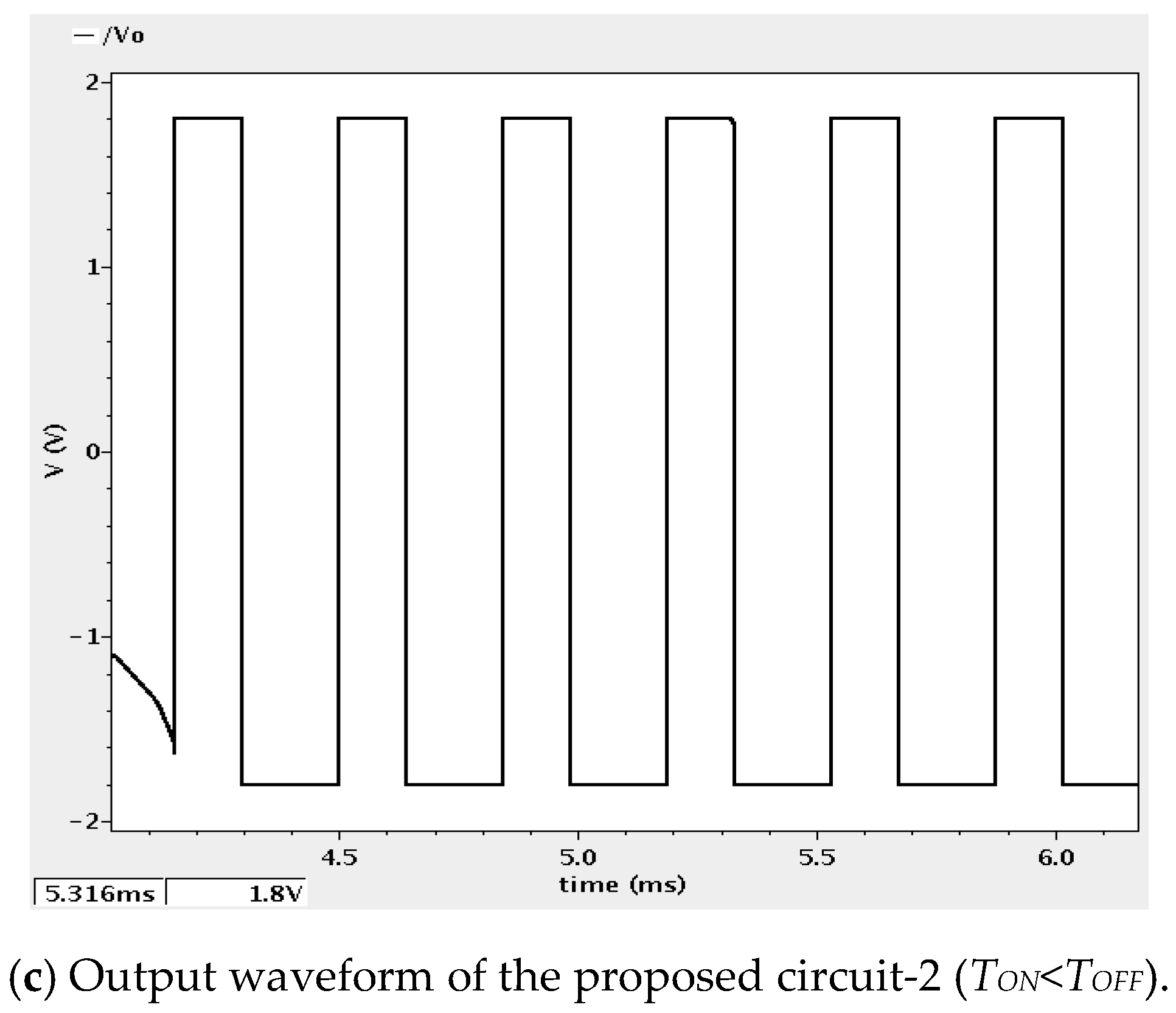
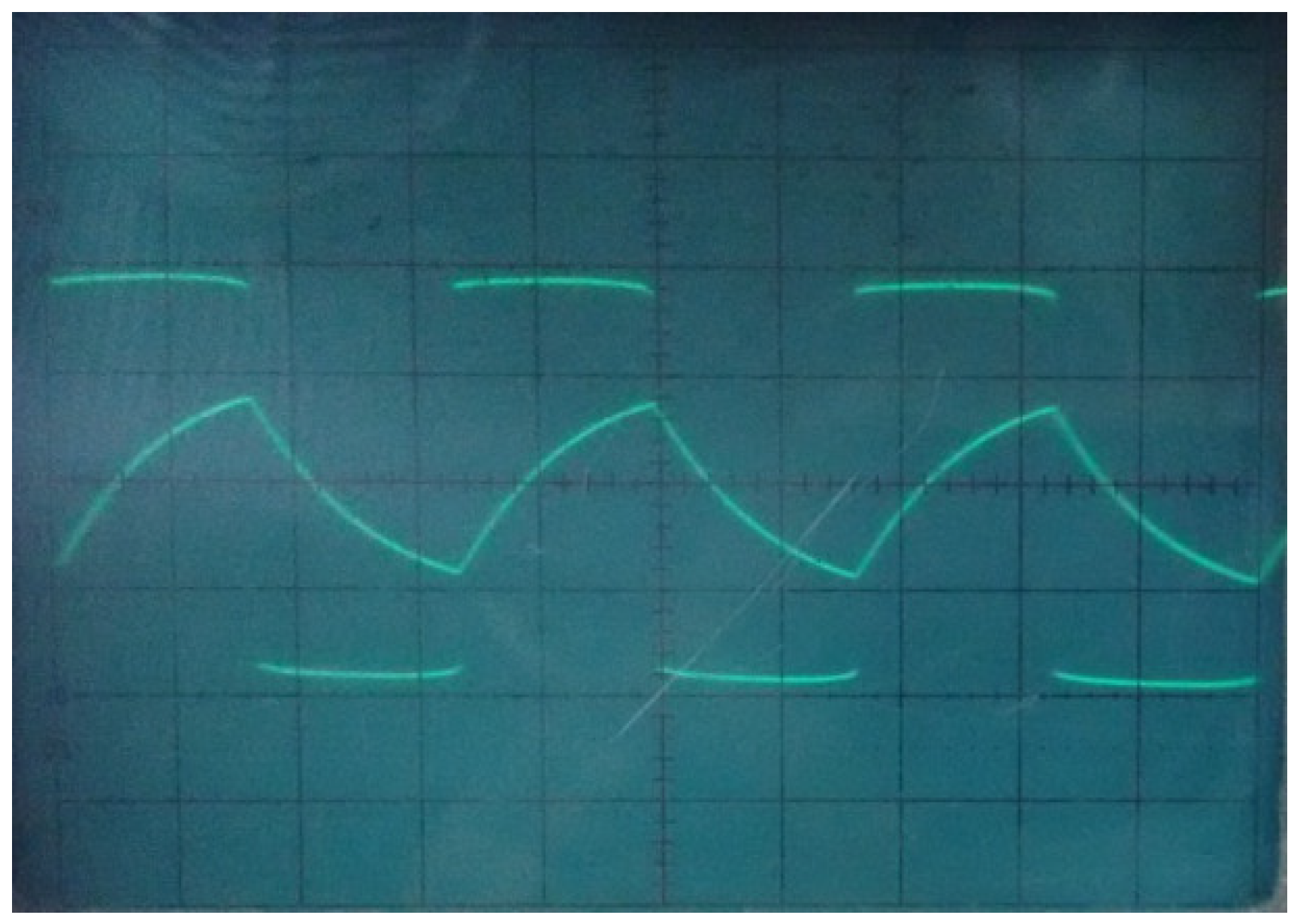
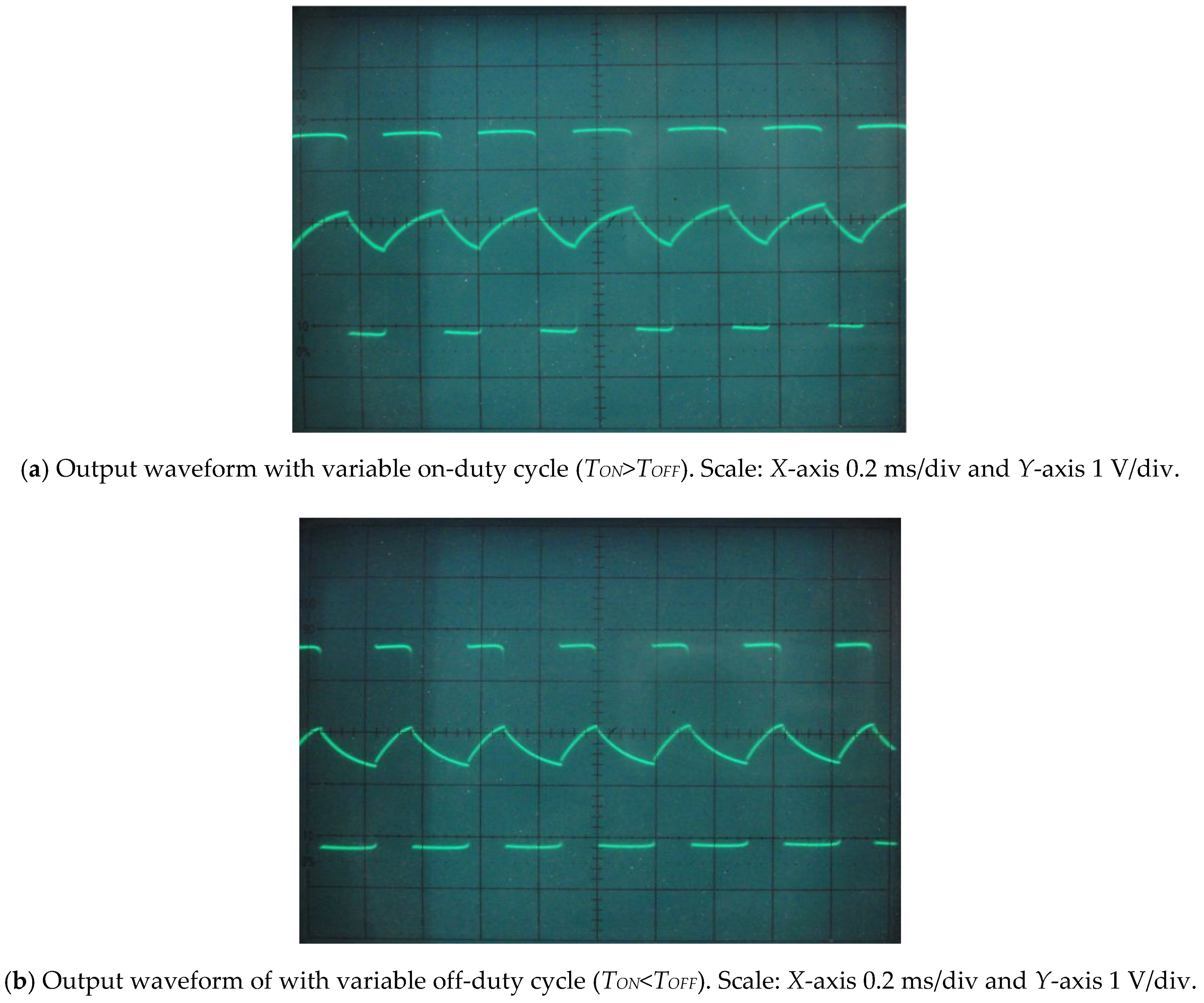
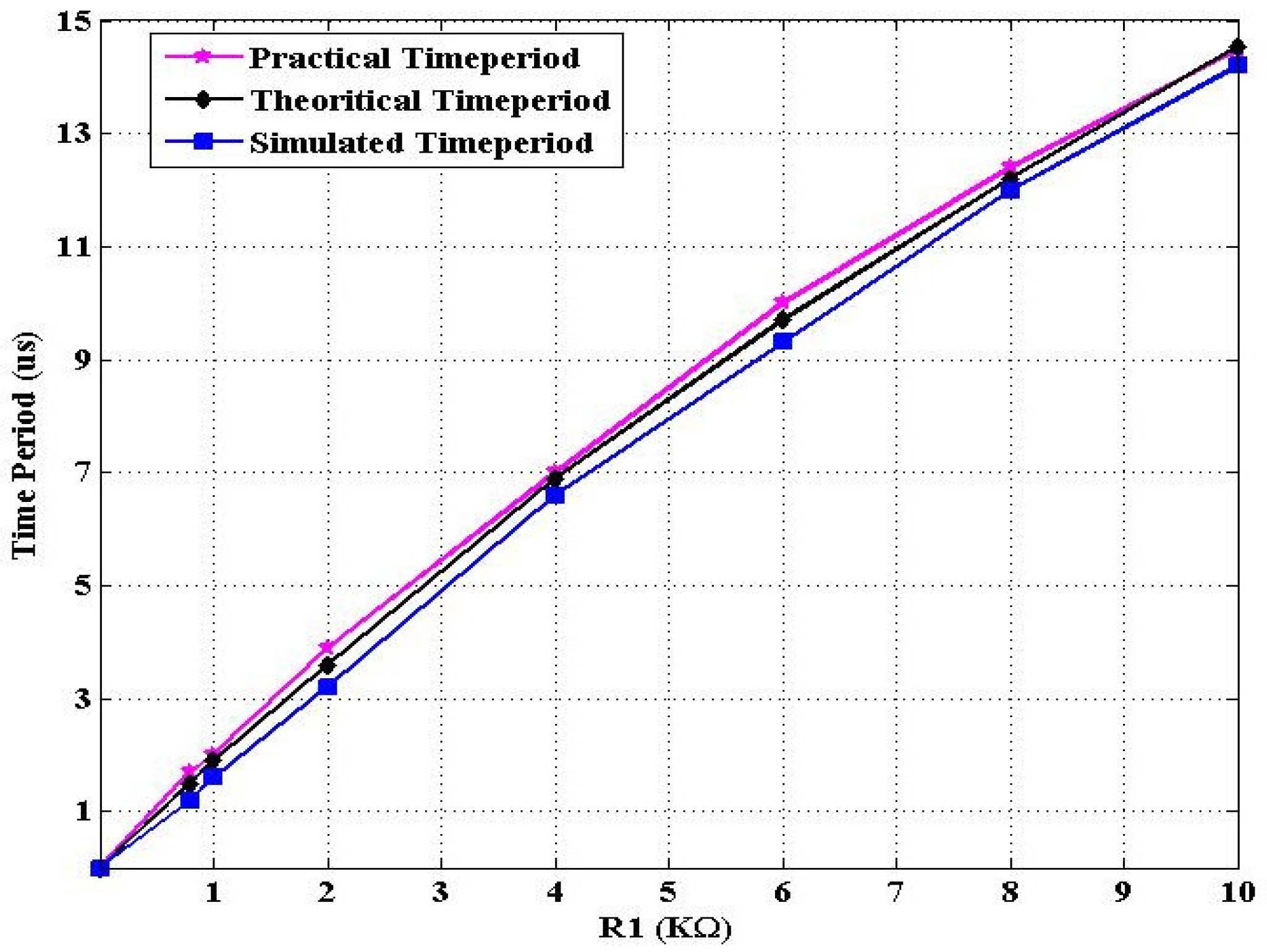
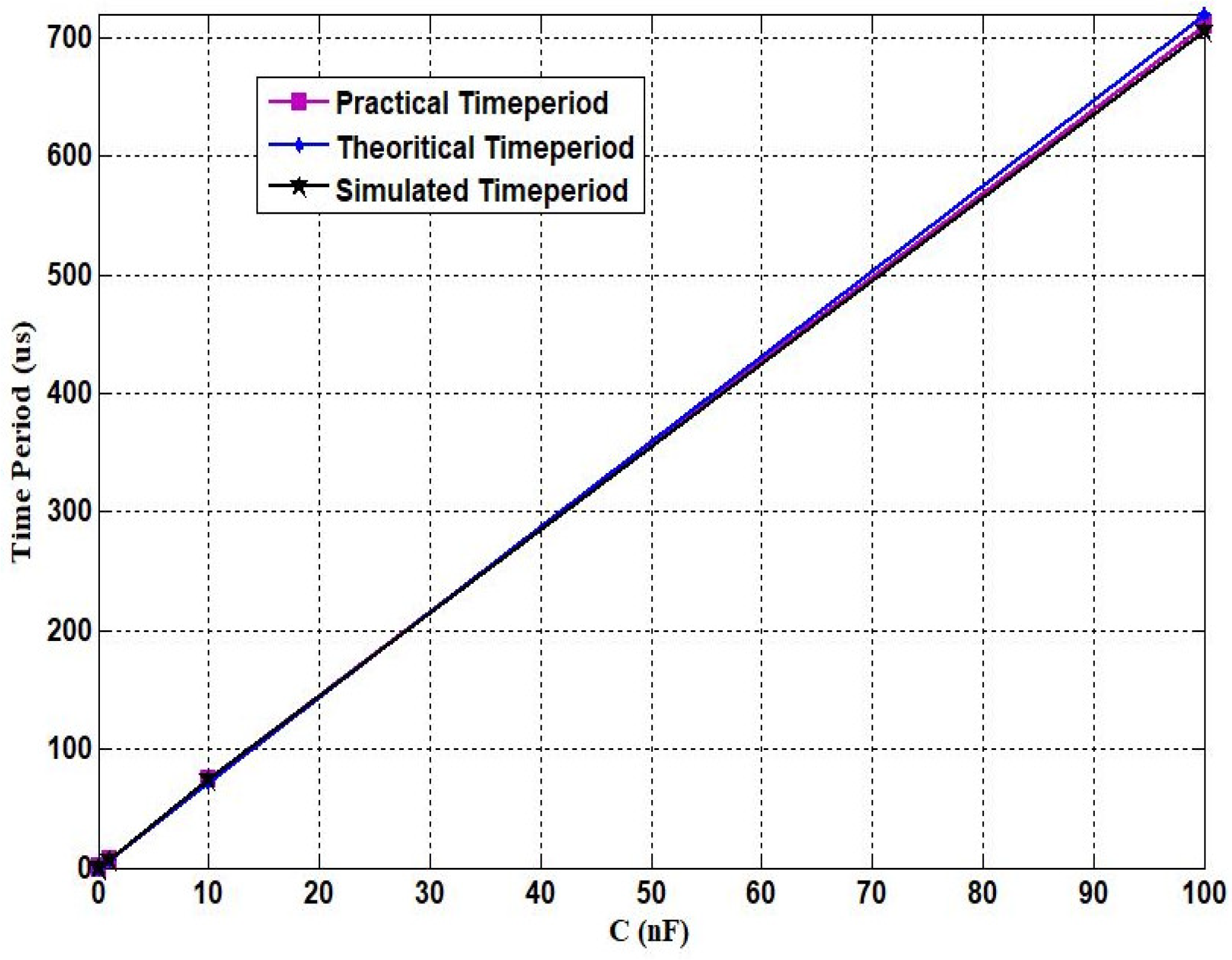
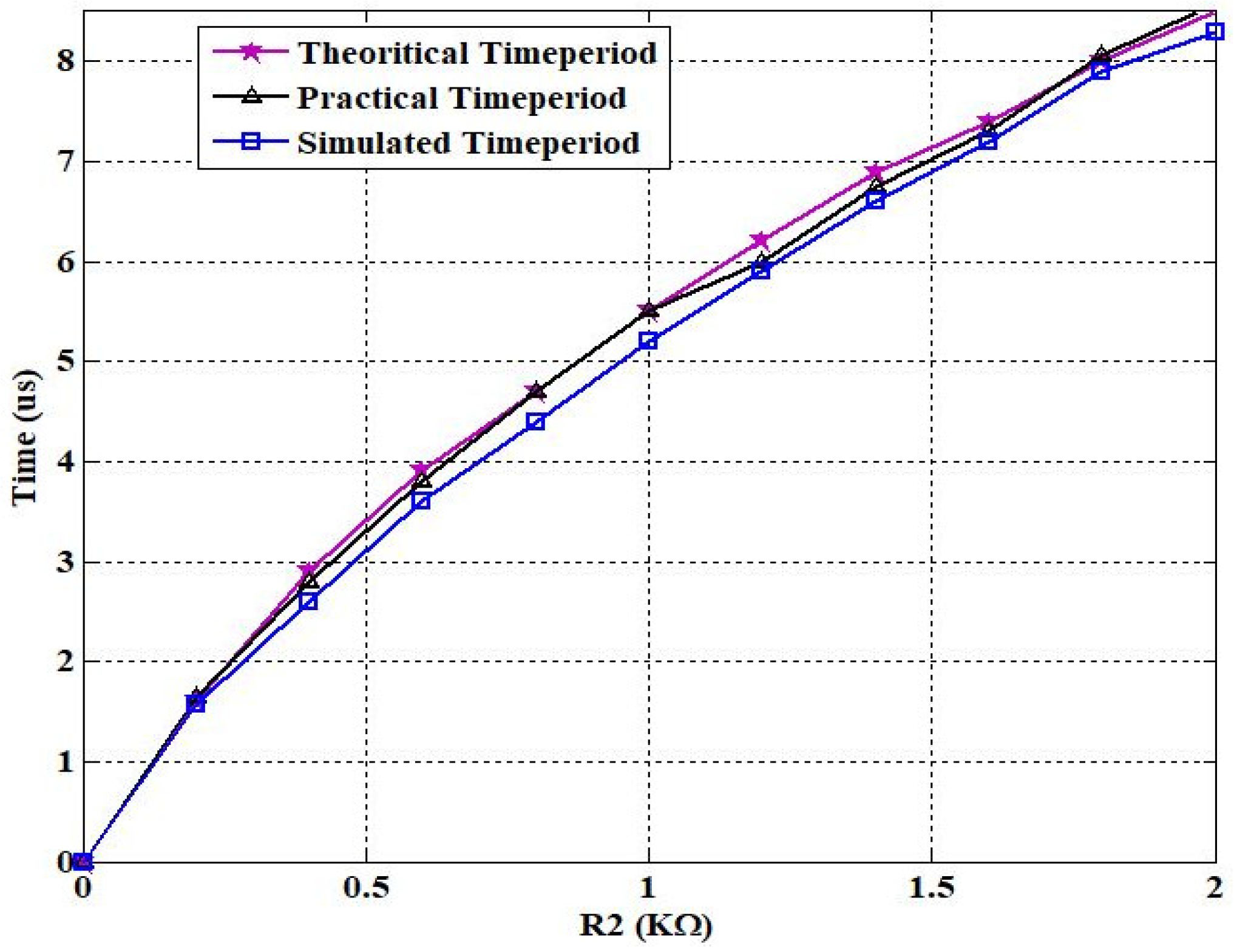
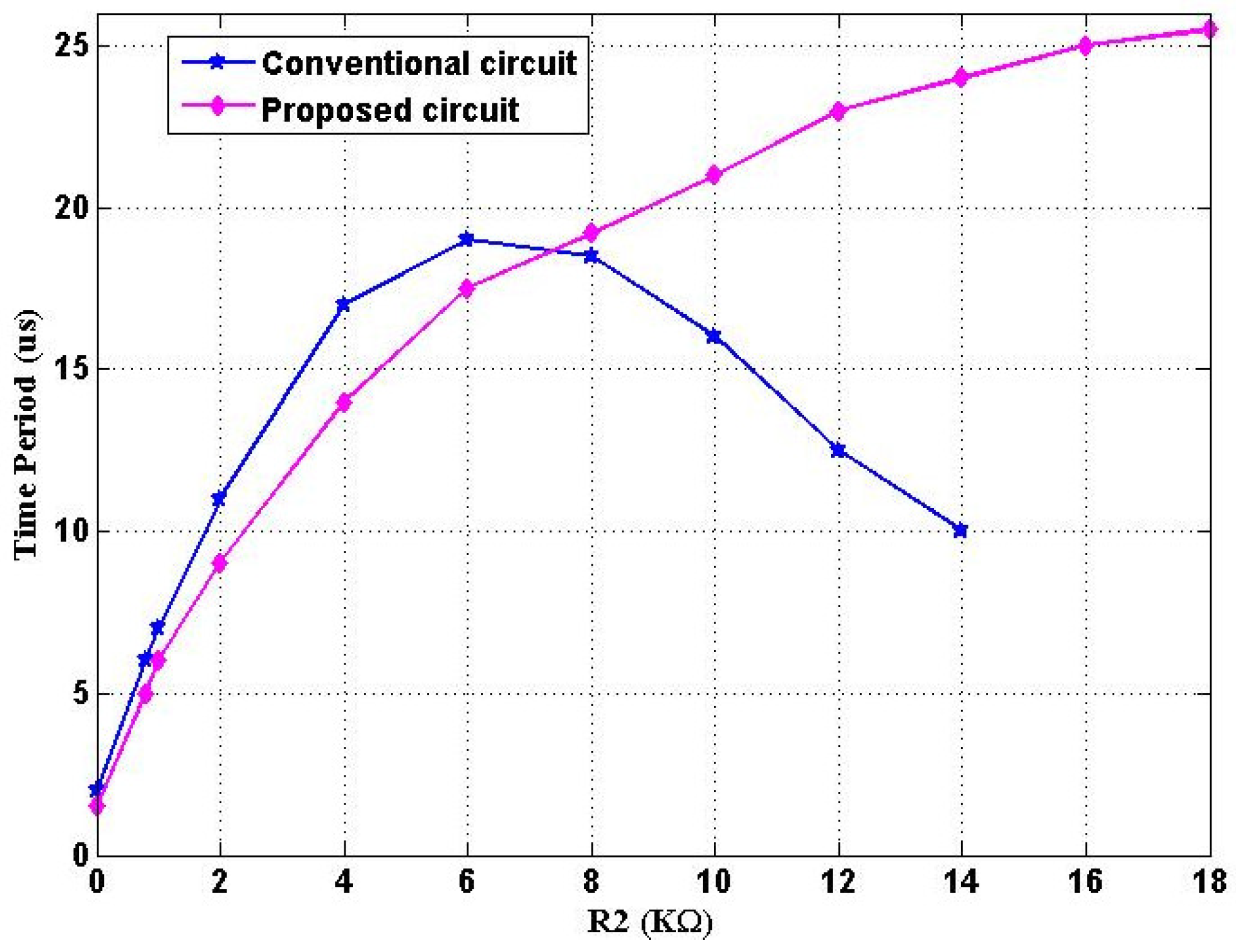
3. Simulation and Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sedra, A.S.; Smith, K.C. Microelectronic Circuits; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Sedra, A.S.; Roberts, G.W.; Gohh, F. The current conveyor: History, progress and new results. IEE Proc. Circuits Dev. Syst. 1990, 137, 78–87. [Google Scholar] [CrossRef]
- Zafar, Z.N.; Maktoomi, M.A.; Hashmi, M.S. A new adjustable square/triangular-wave generator using CCII/CCCII and OTA. In Proceedings of the 26th International Conference on Microelectronics (ICM), Doha, Qatar, 14–17 December 2014; pp. 104–107. [Google Scholar] [CrossRef]
- Kubanek, D.; Khateb, F.; Vrba, K. Current controlled square/triangular wave generator with MO-CCDVCC. In Proceedings of the International Conference on Telecommunications and Signal processing (TSP), Rome, Italy, 2–4 July 2013; pp. 444–448. [Google Scholar] [CrossRef]
- Biolek, D.; Biolkova, V. Current-Mode CDTA-based Comparators. In Proceedings of the International Conference on Electronic Devices and Systems (EDS-IMAPS2006), Brno, Czech Republic, 14 September 2006; pp. 1–5. [Google Scholar]
- Siripruchyanun, M.; Wardkein, P. A full independently adjustable, integrable simple current controlled oscillator and derivative PWM signal generator. IEICE Trans. Fund. Electron. Commun. Comp. Sci. 2003, E86-A, 3119–3126. [Google Scholar]
- Sotner, R.; Jerabek, J.; Herencsar, N.; Lahiri, A.; Petrzela, J.; Vrba, K. Practical Aspects of Operation of Simple Triangular and Square Wave Generator Employing Diamond Transistor and Controllable Amplifiers. In Proceedings of the 36th International Conference on Telecommunications and Signal Processing(TSP 2013), Rome, Italy, 2–4 July 2013; pp. 431–435. [Google Scholar] [CrossRef]
- Janecek, M.; Kubanek, D.; Vrba, K. Voltage-Controlled Square/Triangular Wave Generator with Current Conveyors and Switching Diodes. Int. J. Adv. Telecommun. Electrotech. Signals Syst. 2012, 1, 1–4. [Google Scholar] [CrossRef]
- Chien, H.-C. Voltage-controlled dual slope operation square/triangular wave generator and its application as a dual mode operation pulse width modulator employing differential voltage current conveyors. Microelectr. J. 2012, 43, 962–974. [Google Scholar] [CrossRef]
- Kumbun, J.; Siripruchyanun, M. MO-CTTA-based electronically controlled current-mode square/triangular wave generator. In Proceedings of the 1st International Conference on Technical Education (ICTE2009), Bangkok, Thailand, 21–22 January 2010; pp. 158–162. [Google Scholar]
- Srisakul, T.; Silapan, P.; Siripruchyanun, M. An electronically controlled current-mode triangular/square wave generator employing MO-CCCCTAs. In Proceedings of the 8th Int. Conf. on Electrical Engineering/Electronics, Computer, Telecommunications, and Information Technology, Khon Kaen, Thailand, 17–19 May 2011; pp. 82–85. [Google Scholar]
- Sotner, R.; Jerabek, J.; Herencsar, N. Voltage Differencing Buffered/Inverted Amplifiers and Their Applications for Signal Generation. Radioengineering 2013, 22, 490–504. [Google Scholar]
- Sotner, R.; Jerabek, J.; Herencsar, N.; Prokop, R.; Vrba, K.; Petrzela, J.; Dostal, T. Simply Adjustable Triangular and Square Wave Genrator Employing Controlled Gain Current and Differential Voltage Amplifier. In Proceedings of the 23th International Conference Radioelektronika Pardubice, Pardubice, Czech Republic, 16–17 April 2013; pp. 109–114. [Google Scholar] [CrossRef]
- Sotner, R.; Jerabek, J.; Herencsar, N.; Dostal, T.; Vrba, K. Design of Z-copy controlled-gain voltage differencing current conveyor based adjustable functional generator. Microelectron. J. 2015, 46, 143–152. [Google Scholar] [CrossRef]
- Haque, A.S.; Hossain, M.M.; Davis, W.A.; Russell, H.T., Jr.; Carter, R.L. Design of sinusoidal, triangular, and square wave generator using current feedback operational amplifier (CFOA). In Proceedings of the IEEE Proc. Region 5 Technical, Professional and Student Conference, Kansas City, MO, USA, 17–20 April 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Abuelmaatti, M.T.; Al-Shahrani, S.M. New CFOA-based triangular/square wave generator. Int. J. Electron. 1998, 84, 583–588. [Google Scholar] [CrossRef]
- Srinivasulu, A. Current conveyor based relaxation oscillator with tunable grounded resistor/capacitor. Int. J. Des. Anal. Tools Integr. Circuits Syst. 2012, 3, 1–7. [Google Scholar]
- Malik, S.; Kishore, K.; Sharma, D.; Maharana, M.; Akbar, S.A.; Islam, T. A CCII-based wide frequency range square/triangular waver generator. In Proceedings of the International Conference on Recent Trends in Information System (ReTIS), Kolkata, India, 9–11 July 2015; pp. 446–449. [Google Scholar] [CrossRef]
- Pal, D.; Srinivasulu, A.; Pal, B.B.; Demosthenous, A.; Das, B.N. Current conveyor-based square/triangular waveform generators with improved linearity. IEEE Tran. Instrum. Meas. 2009, 58, 2174–2180. [Google Scholar] [CrossRef]
- Marcellis, A.D.; Claudia, D.C.; Giuseppe, F.; Vincenzo, S. A CCII-based wide frequency range square waveform generator. Int. J. Cir. Theory. Appl. 2011, 41, 1–13. [Google Scholar] [CrossRef]
- Re Stefano, D.; Marcellis, A.D.; Ferri, G.; Stornelli, V. Low voltage integrated astable multivibrator based on a single CCII. In Proceedings of the IEEE Microelectronics and Electronic Conference Bordeaux, France, Prime, Bordeaux, France, 2–5 July 2007; pp. 177–180. [Google Scholar] [CrossRef]
- Chung, W.S.; Kim, H.; Cha, H.W.; Kim, H.J. Triangular/square-wave generator with independently controllable frequency and amplitude. IEEE Tran. Instrum. Meas. 2005, 54, 105–109. [Google Scholar] [CrossRef]
- Chen, J.; Tsao, H.W.; Chen, C. Operational transresistance amplifier using CMOS technology. Electron. Lett. 1992, 28, 2087–2088. [Google Scholar] [CrossRef]
- Salama, K.N.; Soliman, A.M. CMOS operational transresistance amplifier for analog signal processing applications. Microelectron. J. 1999, 30, 235–245. [Google Scholar] [CrossRef]
- Lo, Y.K.; Chien, H.C. Switch controllable OTRA based square/triangular waveform generator. IEEE Trans. Circuits Syst. 2007, 54, 1110–1114. [Google Scholar] [CrossRef]
- Lo, Y.K.; Chien, H.C. Single OTRA-based current-mode monostable multivibrator with two triggering modes and a reduced recovery time. IET Circuits Dev. Syst. 2007, 1, 257–261. [Google Scholar] [CrossRef]
- Lo, Y.K.; Chien, H.C.; Chiu, H.G. Switch controllable OTRA-based bistable multivibrator. IET Circuits Dev. Syst. 2008, 2, 373–382. [Google Scholar] [CrossRef]
- Hou, C.L.; Chien, H.C.; Lo, Y.K. Square wave generators employing OTRAs. IEE Proc. Circuits Dev. Syst. 2005, 152, 718–722. [Google Scholar] [CrossRef]
- Chen, J.J.; Tsao, H.W.; Liu, S.I.; Chiu, W. Parasitic-capacitance insensitive current-mode filters using operational transresistance amplifiers. IEE Proc. Circuits Dev. Syst. 2001, 142, 186–192. [Google Scholar] [CrossRef]
- Analog Devices Inc. AD844 Current Feedback Op-Amp Data Sheet; Analog Devices Inc.: Norwood, MA, USA, 1990. [Google Scholar]
- Cam, U.A. A novel single-resistance-controlled sinusoidal oscillator employing single operational transresistance amplifier. Anal. Integr. Circuits Signal Process. 2002, 32, 183–186. [Google Scholar] [CrossRef]
- Singh, A.K.; Gupta, A.; Senani, R. OTRA-basedmulti-function Inverse filter configuration. Int. J. Adv. Electr. Electron. Eng. 2017, 15, 846–856. [Google Scholar] [CrossRef]
- Bhatt, V.; Benjwal, P.; Joshi, M. OTRA based second order universal filter and it optimization like Butterworth, Chebyshev and Bessel. In Proceedings of the 2nd International Conference on Research in Intelligent and Computing in Engineering (RICE-2017), Gopeshwar, India, 24–26 March 2017; pp. 143–150. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.K.; Senani, R.; Gupta, A. OTRA, its implementations and applications: A state-of-the-art review. Anal. Integr. Circuits Signal Process. 2018, 97, 281–311. [Google Scholar] [CrossRef]
- Gurumurthy, K.; Pandey, N.; Pandey, R. OTRA based second and third order sinusoidal oscillators and their phase noise performance. AIP Conf. Proc. 2017, 1859, 020017. [Google Scholar] [CrossRef]
- Pandey, N.; Kumar, V.; Goel, A.; Gupta, A. Electronically tunable LC high pass ladder filter using OTRA. ICTACT J. Microelectron. 2017, 3, 446–451. [Google Scholar] [CrossRef]
- Nagar, B.C.; Paul, S.K. Lossless grounded FDNR simulator and its applications using OTRA. Analog Integr. Circuits Signal Process. 2017, 92, 507–517. [Google Scholar] [CrossRef]
- Shaker, P.C.; Srinivasulu, A. Four new oscillators using operational transresistance amplifier. Radio Electron. Commun. Syst. 2017, 60, 206–214. [Google Scholar] [CrossRef]
- Nagar, B.C.; Paul, S.K. Single OTRA based two quadrant analog voltage divider. Analog Integr. Circuits Signal Process. 2018, 94, 161–169. [Google Scholar] [CrossRef]
- Komanapalli, G.; Pandey, N.; Pandey, R. New Realization of third order sinusoidal oscillator using single OTRA. AEU Int. J. Electron. Commun. 2018, 93, 182–190. [Google Scholar] [CrossRef]
- Komanapalli, G.; Rajeshwari, P.; Neeta, P. New Electronically tunable low-frequency quadrature oscillator using operational transresistance amplifier. IETE J. Res. 2020, 1–9. [Google Scholar] [CrossRef]
- Kaur, G.; Ansari, A.Q.; Hashmi, M.S. Fractional order high pass filter based on operational transresistance amplifier with three fractional capacitors of different order. Adv. Electr. Electron. Eng. 2019, 17, 155–166. [Google Scholar] [CrossRef]
- Babanezhad, J.N.; Temes, G.C. A linear NMOS depletion resistor and its application in an integrated amplifier. IEEE J. Solid State Circuits 1984, 19, 932–938. [Google Scholar] [CrossRef]
- Chaturvedi, B.; Atul, K. Fully electronically tunable and easily cascadable square/triangular wave generator with duty cycle adjustment. J. Circuits Syst. Comput. 2019, 28, 1950105. [Google Scholar] [CrossRef]
- Nagalakshmi, K.; Srinivasulu, A.; Ravariu, C.; Vijay, V.; Krishna, V.V. A novel simple schmitt trigger circuit using CDTA and its application as a square-triangular waveform generator. J. Mod. Technol. Eng. 2018, 3, 205–216. [Google Scholar]


| Parameters | Op-amp | CFOA | CCII+ | CDBA | OTA | OTRA |
|---|---|---|---|---|---|---|
| Power Supply | 0.8 V | 1.8 V | 1.8 V | 1.5 V | 0.5 V | 1.8 V |
| Technology | 0.18 µm | 0.18 µm | 0.18 µm | 0.18 µm | 0.18 µm | 0.18 µm |
| Power Dissipation | 190 µW | -- | 206 µW | 194 µW | 215 µW | 210 µW |
| Open Loop Gain | 66 dB | 75 dB | 78 dB | 85 dB | 52 dB | 96 dB |
| Gain Band Width Product | 3.4 MHz | 23 MHz | -- | 100 MHz | 7.5 MHz | 152 MHz |
| Table | W (µm) | L (nm) |
|---|---|---|
| M1-M6 | 4 | 180 |
| M7-M10 | 6 | 180 |
| M11-M12 | 20 | 180 |
| M14, M20 | 2 | 180 |
| M13, M18 | 12 | 180 |
| M15 | 12 | 180 |
| M16, M19 | 4 | 180 |
| M17 | 3.3 | 180 |
| Vg1 = Vg2 = 0.8 V and I0 = 40 µA | ||
| References | No. of Active Components | No. of Passive Components | Total Components | Maximum Frequency Range | Supply Voltage |
|---|---|---|---|---|---|
| [9] | 2 DVCC | 4 (1 C & 3 R) | 6 | 860 kHz | ±10 V |
| [12] | 2 VDIBA | 3 (1 C & 2 R) | 5 | 2.8 MHz | ±5 V |
| [15] | 2 CFOA | 5 (1 C & 4 R) | 7 | 15 MHz, 1S | ±5 V |
| [16] | 1 CFOA | 4 (1 C & 3 R) | 5 | 71 kHz | -- |
| [17] | 3 CCII+ | 7 (1 C & 6 R) | 10 | 574 kHz | ±6 V |
| [19] | 2 CCII+ | 4 (1 C & 3 R) | 6 | 260 kHz | ±5 to ±15 V |
| [20] | 2 CCII+ | 6 (1 C & 5 R) | 8 | 737 kHz | ±15 V |
| [21] | 1 CCII+ | 4 (1 C & 3 R) | 5 | 2 kHz | 1.5 V, 3I.S. |
| [22] | 3 OTA | 3 (1 C & 2 R) | 6 | 16 kHz | ±5 V |
| [44] | 1 CDTA | 2 (1 C & 1 R) | 4 | 600 kHz | ±2.5 V, 1S ±9 V, 2H |
| [45] | 1DXCCTA | 2 (1 C & 1 R) | 3 | 20.6 MHz | ±1.25 V, 1S |
| [28] | 1 OTRA | 3 (1 C & 2 R) | 4 | 1.0 MHz | ±15 V |
| Proposed Figure 3 circuit | 1 OTRA | 2 (1 C & 1 R) | 3+2 NMOS Transistors | 1.5 MHz, 1S 1.2 MHz,2H | ±1.8 V, 1S ±6 V, 2H |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chandra Shaker, P.; Srinivasulu, A. Electronic Tuning Square-Wave Generators with Improved Linearity Using Operational Transresistance Amplifier. J. Low Power Electron. Appl. 2020, 10, 12. https://doi.org/10.3390/jlpea10020012
Chandra Shaker P, Srinivasulu A. Electronic Tuning Square-Wave Generators with Improved Linearity Using Operational Transresistance Amplifier. Journal of Low Power Electronics and Applications. 2020; 10(2):12. https://doi.org/10.3390/jlpea10020012
Chicago/Turabian StyleChandra Shaker, Pittala, and Avireni Srinivasulu. 2020. "Electronic Tuning Square-Wave Generators with Improved Linearity Using Operational Transresistance Amplifier" Journal of Low Power Electronics and Applications 10, no. 2: 12. https://doi.org/10.3390/jlpea10020012
APA StyleChandra Shaker, P., & Srinivasulu, A. (2020). Electronic Tuning Square-Wave Generators with Improved Linearity Using Operational Transresistance Amplifier. Journal of Low Power Electronics and Applications, 10(2), 12. https://doi.org/10.3390/jlpea10020012