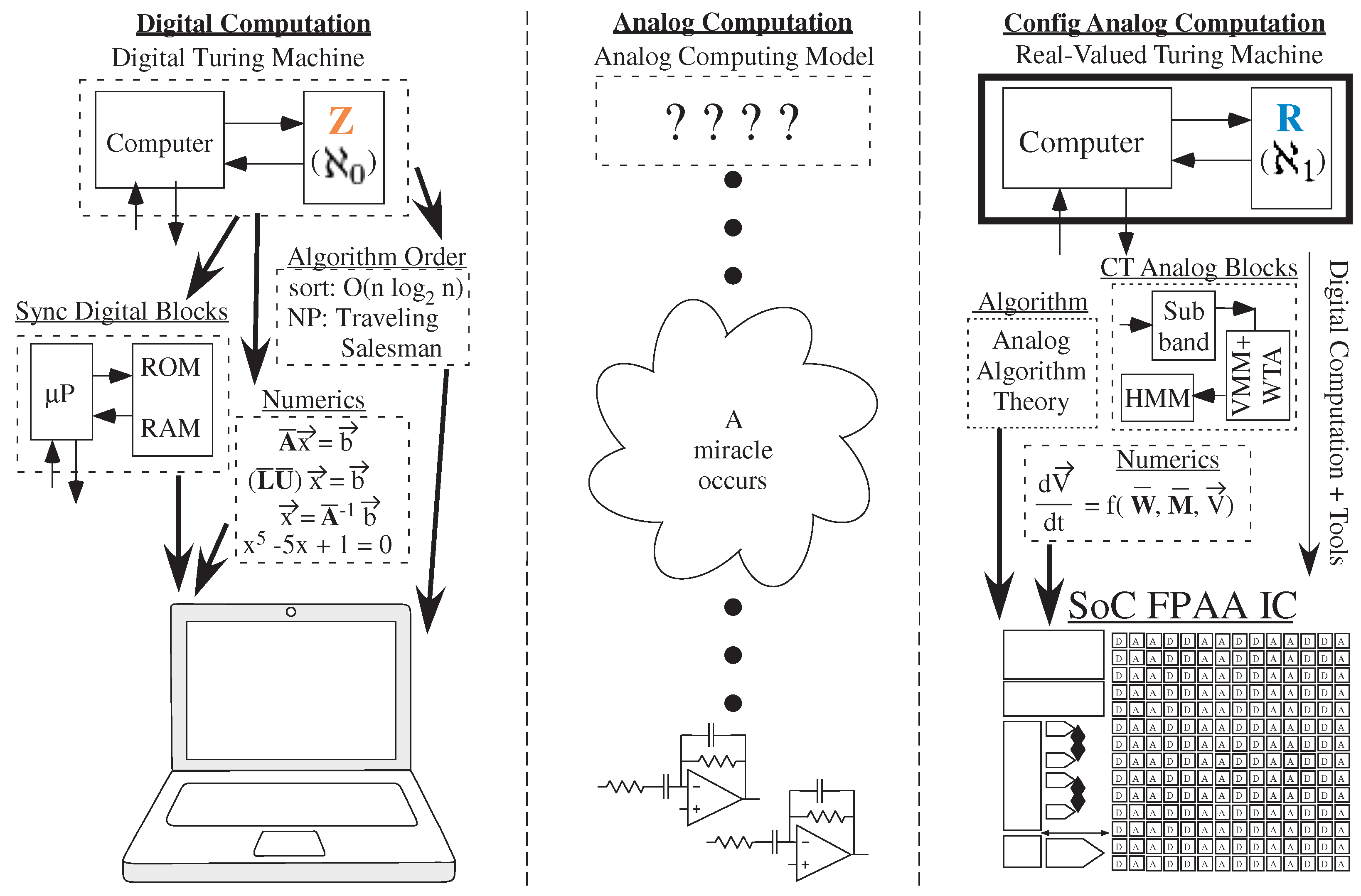
1. Introducing Physical Computing and Physical Turing Machine Modeling
The rapid progress in today’s ubiquitous programmable digital infrastructure relies as much on digital Turing machine theory [
1] as it has on Moore’s law scaling [
2,
3,
4] and VLSI [
5] in providing a framework to use these hardware capabilities. A roadmap of future directions was in place as new technologies were available. Turing Machine theory (
Figure 1) provides a core digital computation, computes over discrete, integer values, and was based upon bookkeeping businesses at the time [
6]. The mathematical framework is central to abstracting digital computations, central to computer architectures and algorithms, as well as is central to numerical computation and analysis (
Figure 1).
Not all computation operates over discrete, integer values, computational approaches that have used various physical phenomena for potentially lower power/energy and smaller area applications. Mead’s original hypothesis (1990) [
7] predicted analog processor area will decrease at least 100× in size compared to digital computation, and energy consumed will decrease at least 1000× compared to digital computation. These techniques were experimentally demonstrated through Vector-Matrix Multiplication (VMM) in custom (2004) [
8] and in configurable large-scale Field Programmable Analog Arrays (FPAA) (2012) [
9] as well as in many later systems and configurations. Following the analog computing efficiencies over digital techniques, neuromorphic computing formulated and achieved significant efficiencies over digital computing (2013) [
10]. Recently, quantum computing has advocates claiming its supremacy over digital computing, stating there exists experimental problems where quantum computing is demonstrably more capable than digital computing (2019) [
11]. Some debate these claims (e.g., [
12]). This computationally efficient quantum-computing noise generator has direct parallels to an analog noise generator and computing [
13], illustrating a relationship between these real-valued computations. Any real-valued computations will show computational efficiencies over digital ones. We define Physical Computing as computing using real-valued quantities, quantities that can be amplitude, space, or time, Physical computing includes Analog, Quantum, Neuromorphic, and Optical techniques. This work both defines and further identifies the relationships between forms of Physical Computation.
Energy efficiency, as well as other computational metrics, are often described using order notation such as O
. Typically physical computing techniques typically focus on improving the coefficient for the O
metric. As mentioned above, the coefficient for computational energy efficiency, the energy or power required per operation, decreases by typically 1000× an equivalent digital computation, while the scaling metric in O
remains unchanged. Some aspects might improve the polynomial or similar function inside of O
say by architectural improvements in the physical computing structure (e.g., [
14]). This effort affirms these improvements in energy efficiency, and builds upon these opportunities in energy efficiency by discussing the possibility to significantly change the scaling dependency characterized by O
for physical computing systems because of the different computing capabilities enabled by providing a model and framework to explore these opportunities.
For Analog computing, more carefully known as analog electronic computing and the most experimentally developed of Physical techniques, has lacked a theoretical framework and high-level computing model. Classical Analog computation is widely perceived as a bottom-up design approach practiced by a few artistic masters (
Figure 1). The goal was to formulate a problem in a few Ordinary Differential Equations (ODE), and have a circuit master design the system. Once this miracle occurs, the one particular system becomes functional [
15]. These design techniques do not scale to a wide user capability as they do for digital computation. There are no classic textbooks explaining analog system synthesis. The classical situation is less optimistic for neuromorphic, quantum, or optical computing.
Recently, analog computation has developed a framework (
Figure 1) that includes analog numerical analysis techniques [
16], analog algorithm complexity theory [
14], and analog algorithm abstraction theory [
17]. Current programmable Analog design is no longer seen as numerically inferior to digital computation [
16], or seen as too complex to have levels of abstraction like digital computation [
17], or seen to be governed by digital processor techniques where it rather now pushes the questions for both analog and digital architecture questions [
14]. Analog computation becomes relevant with the advent of programmable and configurable FPAA devices [
18,
19] and the associated design and synthesis tools [
20,
21] incorporating parts of this framework.
The recently developing analog frameworks achieve a level where one can ask realistic questions, as well as realistically propose, an analog computing model. This work proposes a Physical Turing machine as a machine operating over real-valued quantities as well as operating over real-valued sequences over real-valued timesteps. Physical computing utilizes one or more representations and internal variables encoded as real values, including amplitude, voltage, current, time, or space. This work connects all Physical computing techniques (e.g., analog, neuromorphic, optical, and quantum) through a single computing framework, enabling one, or a mixture, of these techniques as well as provides a bridge to use the results from one technique towards another technique. This Physical Computing model builds from experimental techniques and measurements as well as frameworks for their effective implementation, rather than hypothesizing unverifiable theoretical concepts.
This paper addresses Physical Computing and its associated Turing machine model addressing the capability of real-valued computation, as in physical computation, as compared with integer-valued computation, as in digital computation. The discussion starts by addressing the algorithmic complexity of real-valued and integer valued computation (
Section 2). The discussion then establishes that the physical computing substrate is real-valued even in the presence of noise (
Section 3), a necessary condition for real-valued physical computing. The discussion shows the connection and translation between quantum qubit computation and an analog system modeling that computation (
Section 4). The discussion generalizes physical computing, and the equivalence between approaches (
Section 5), finally discussing the the implications and opportunities of Physical computing (
Section 6) and summarizing this discussion (
Section 7).
2. Algorithmic Complexity of Real-Valued Computation
Physical computing techniques compute over real-valued variables (R), representations, and timescales. Analog computing can compute over continuous-valued voltage or current state variables (e.g., 1 V to 3 V) as well as computing over continuous-valued timesteps. Neuromorphic computing, which includes neuromorphic biological or electronic computing, involves similar capabilities to analog computing, at least over limited regions, as well as continuous-spatial regions at least over limited regions (e.g., dendritic cables). Optical computing also involves continuous amplitudes operating over continuous-valued timesteps with two-dimensional (2D) and three-dimensional (3D) continuous spatial dimensions. Quantum computing operates using a continuous probabilities modeling continuous-time and continuous 3D space, as well as continuous superposition mixtures of two or more states. All of these techniques compute effectively utilizing at least one real-valued dimension.
Real valued functions in multiple dimensions have the same complexity as a real-valued function in one dimension. The size of the set of all real numbers ((
R) between 0 and 1 is infinitely larger than all integers (
Z) between 0 and
∞. The size of
Z between 0 and
∞ is represented as
, and the size bf R between 0 and 1 is represented at
. Two
R dimensions can fit into a single
R dimension. Working along the diagonals of a 2D
R map, one can recount the 2D space into a single one-dimensionsal (1D) space (
Figure 2) as the same order of infinity (
). More available dimensions opens up additional implementation opportunities and resulting efficiencies, although these dimensions do not affect the system complexity.
A real-valued Physical Turing Machine models computing over
R values and timesteps, similar to a Digital Turing Machine models computing over
Z values and timesteps (
Figure 1 and
Figure 3). A Digital Turing machine computes over a
Z set of input and output alphabets with
Z internal variables and
Z size tape operating over
Z timesteps. The theoretical Turing Machine model does not require the computation follows the same approach, and yet, digital computing often resembles parts of the Turing Machine techniques. To fully model the continuous-time (CT) computation over
R values, a Physical Turing Machine Model computes over a
R set of input and output alphabets with
R internal variables and
R size tape (internal memory) operating over
R timesteps. Utilizing
Z size input and output alphabets for a Physical Computation is still modeled by the Physical Turing Machine. Physical computing operates over
(
∞ for
R) as opposed to synchronous digital computing operating over
(
∞ for
Z). Model allows directly extending known properties and theorems for
Z-valued Turing machines to these
R-valued Turing machines. Although one could consider a physical implementation specific model (e.g., [
22,
23]), it likely misses the wider computational space and becomes harder to generalize across all
R-valued computing, as well as requiring to build an entirely new theoretical infrastructure.
Deutsch began to develop an understanding of physical computing models as part of their wrestling to understand the nature of quantum computing [
24]. These discussions strengthen and generalize Deutsch’s wrestling with opportunities in quantum computing. Deutsch attempts to generalize Turing’s classical definition [
1] towards physical approaches
“Every finitely realizible physical system can be perfectly simulated by a universal model computing machine operating by finite means”
where he states a
Z-valued Turing machine cannot perfectly simulate a classical dynamical system, as well as he recognizes the impact of non-decreasing entropy (e.g., loss) impacts these computations. Deutsch only imagines
Z-valued input and output alphabets, while he opens the possibility of computing over a continuum of values, which is more concretely defined as computation over
R-values, and then moves that a quantum dynamics provides a means towards reaching these opportunities, while mostly missing this opportunity in
R-valued systems. He mathematically attempts to show non-dynamical quantum operations could be operating over a continuum, inspired by the introduction of quantum computing by Feynman [
25,
26]. A model that computes with
R-valued alphabets also simplifies to computing with
Z-valued input and output alphabets. The approach in this discussion generalizes
R-valued computation for the continuum of classical and quantum physics, heavily based in decades of physical (e.g., analog, neuromorphic) computing.
Deutsch moves to extend the Church-Turing principle to be related to a quantum physical system. This discussion also moves to effectively extend the Church-Turing principle,
“Every ‘function which would naturally be regarded as computable’ can be computed by the universal (Z-valued) Turing machine”
with the explicit restatement of the Church-Turing thesis for-
R-valued computation:
“Every finitely realizible ‘function which would naturally be regarded as computable’ can be computed by the universal (R-valued) Turing machine”
where the
Z-valued Turing machine ⊂
R-valued Turing machine. Finite means, which includes finite resources as well as finite amount of time, is essential to any practical physical computation.
Algorithmic complexity between Synchronous Digital Computation and Physical computation is the comparison between
R versus
Z Turing capabilities (
Figure 3). Algorithm complexity (
Figure 3) considers whether a particular computing structure can compute certain algorithms in Polynomial (P) time, or scales by some other function, such as exponential time (EXPTIME). One can consider the class of polynomial-time physical (P
) and digital (P
) algorithms, the class of digital NP problems (NP
) and similar class of NP problems for analog computation (NP
), as well as the class of exponential-time analog (EXPTIME
) and digital (EXPTIME
) algorithms (
Figure 3). One must consider a product of time and resources, although if one considers only polynomial resources, time complexity is sufficient. P
completely overlaps with P
as one can make digital gates from analog blocks (
Figure 3).
The open question is how does NP
and EXPTIME
overlap with P
, NP
and EXPTIME
(
Figure 3)? Does P
have any overlap with NP
or even EXPTIME
? If part of NP
P
, then a Physical computing system would solve at least one NP
application in P. Does P
extend into uncomputable spaces by digital Turing machines (e.g., halting problem)? This framework will unify previous physical computing techniques and algorithms. Hopfield’s work solving the Traveling Salesman Problem (TSP) [
27] opens one’s imagination that eventually NP
could be in solved in P
through recurrent networks modeling optimization problems minimizing energy surfaces [
27,
28,
29,
30,
31], Hava Siegelmann created a number of useful theoretical discussions for analog computing, arguing analog P
has computational capabilities beyond P
by minimizing energy surfaces (ARNN model) [
23,
32]. Multiple coupled ODEs systems have been theoretically proposed to solve NP
(e.g., 3-SAT [
33,
34]) in P
that could be implemented on a continuous-time analog platform. Quantum computing (e.g., Shor and Grover’s algorithms) has theoretically shown
is larger than
[
35,
36]. Often the Church-Turing conjecture is interpreted to mean that physical computing techniques (
Figure 3) are equivalent to a single machine processing a memory tape, which requires countable (
Z) input and output alphabets. This interpretation is far too restrictive of physical computing approaches.
A unified analog computing framework (
Figure 3) equates transformations between techniques, allowing a solution in one space could be translated to another (
Figure 4). For example, a quantum computation could be transformed to room temperature analog computation. The transformations allow all technologies to be utilized in spaces and applications where they naturally have physics advantages.
Transformations between physical computing and digital computing illustrate the differences between these computing mediums, showing significant differences between
R verses
Z computation. Transformations from
Z to
R are straight-forward, and one expects a physical system to implement computations over integer (e.g., digital) values. Transformations from
R to
Z computation require interpolations to, or numeric approximations from
R to
Z (
Figure 4). Synchronous digital simulation results of physical computation must always be approached cautiously, as digital computation is more limited than the resulting physical substrate (
Figure 4). Physical ODEs are solved in
, with
R-valued timesteps compared to
Z-valued timesteps by digital emulation. Multiple-timescale nonlinear ODEs (
Figure 4) inherently utilize
R-valued timesteps to directly handle exponentially fast moving nonlinear physical system dynamics. Analog WTA physical system uses two (or more) competitively strong nonlinearities, resulting in consistent analog solutions while creating a difficult ODEs to solve numerically (e.g., [
37]). The error of digital ODE solutions are limited as O(f
(·)) for a kth order solver (RK45 is 4th order) [
38], so high derivatives, like exponential functions destroy the accuracy and convergence of digital ODE solutions. Attempting to validate physical computing systems (e.g., systems of ODEs) through digital numerical approximations creates the unnecessary concern over having exponentially fast moving nonlinear results for a physical system that are very real for synchronous digital computation. Physical algorithms must be developed and verified only through physical hardware, and discrete simulation or analysis of physical algorithms cannot invalidate potential results.
Competing exponentially increasing and decreasing functions converge effectively using physical computing to solve the ODE functions, tasks that are extremely difficult for
Z-based computing. For example, a Winner-take-all (WTA) circuit (
Figure 5) operating with subthreshold currents utilizes competing exponential functions modeled by the transistor current-voltage relationships:
by scaling the input signals by the bias currents,
, and scaling the voltages by U
,
, and defining
,
as the gate to surface potential coupling for the MOSFET transistor, &
is the coupling of the drain voltage into the source-side surface potential (assume 0.01 for this example). I
is the current source current set by V
on the gate of M
. Transistors M3 and M4, that have the corresponding output currents of I
and I
, have their drains at the upper power supply for this example, resulting in both transistors (M3, M4) operating in saturation with subthreshold currents. The capacitors,
C, could be either parasitic or explicit capacitances; for clarity of this discussion, all capacitors are considered equal to
C. The difference between
and
results in a stiff ODE, resulting in higher sampling for stable performance in
Z-based computation, resulting in a significant computational issue (e.g., [
16]), as the I
and input currents I
, I
can be orders of magnitude different from each other.
Even beyond the significant issue of widely different timeconstants creating a stiff ODE system, these ODEs have competing exponential functions that converge in the physical system but cause tremendous stress on
Z-based simulation. To eliminate the stiff ODE computation,
resulting in
. The resulting ODE system where time is normalized by
(time becomes unitless):
assuming
for ease of the discussion. One could transform (
2) for better numerics, and yet, in generally such a transformation is not possible, so we want to illustrate computational issues with this system The dynamics for (
2) for an input step from an initial condition to
are analytically globally stable, while a numerical simulation (e.g., RK45) will not always converge to the correct steady-state, including some unstable trajectories (
Figure 5).
4. Connecting Quantum Computing and Analog Computing Applications
This section shows an example bridging quantum and analog computing in showing an analog circuit model for quantum qubit computation (
Figure 8). Quantum computing has been argued that could be performed through analog computing [
44,
45,
46], have hypothesized parallels with op-amp circuits [
47], that
Z-valued algorithms cannot fully simulate a quantum computer [
48], and an initial demonstration through a discrete bench-top analog circuit for a small quantum system (q-bits) utilizing sinusoidal input and output signals [
49,
50,
51]. Typical quantum computing tends to be performed using fixed devices, such as qubits, and assume that the computation is instantaneous, effectively reaching its steady-state rapidly in the measurement timescales. Therefore, the transformation between
Z-valued inputs to the measured outputs through these fixed-position qubits,
R-valued computation described through a Unitary matrix and nonlinear measurement operations. With increased CMOS scaling, analog integrated circuit techniques use more quantum concepts in their fundamental devices, providing another bridge between these techniques.
Quantum computing is primarily a linear computation over the probability wavefunction (
). A typical Quantum computation shows the comparisons between the two physical computations. Although a quantum computation has a single input state (e.g.,
or
), the computation involves the combination of these states (
Figure 8)
where
a,
b are complex numbers (=2 real numbers) representing the probability of each state (
). The input could also be a combination of these states (
Figure 8). The superposition of these two states effectively creates a real-valued representation between 0 and 1, a similar representation having a voltage between 0 V and 1 V.
Multiple quantum operations result in multiple layers of linear operations over complex values. Multiple linear operations can be consolidated to a single linear operation. A single qubit is performing a linear algebraic operation over complex values (
Figure 9) that is described through a unitary transformation. A network of qubit operations without measurement results in a single linear algebraic operation that is equivalent to a complex VMM operation described by a unitary matrix. A unitary linear transformation means the total output solution signal power is the same as the total input signal power. The inputs representing the input wavefunction for each initial qubit input. If the input signal power is normalized (to 1) as expected for complex probabilities, then the output signal power is a normalized (to 1) set of complex probabilities. A DFT or DCT or DST or Hadamard transform are all unitary matrix transformations over real or complex values.
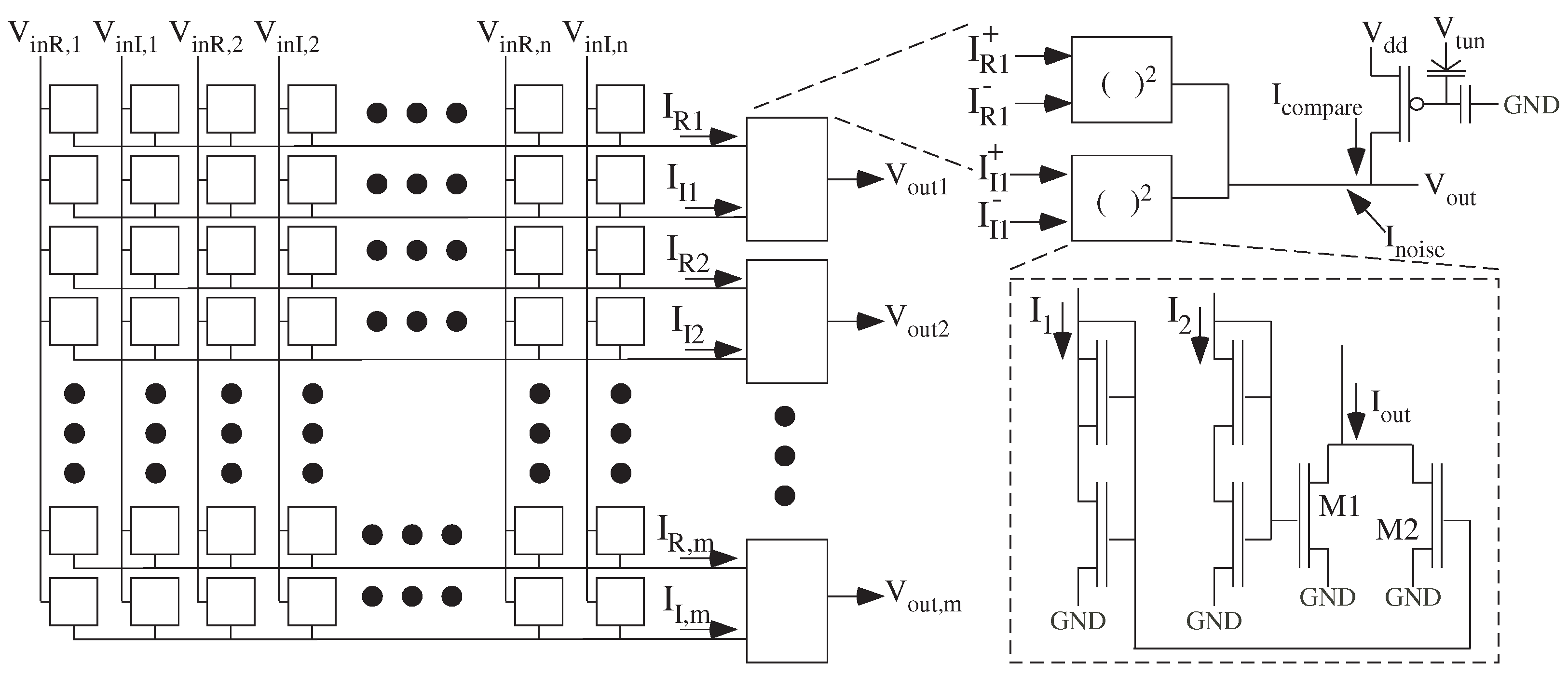
An analog VMM (e.g., [
8,
9]) using complex inputs and complex weights directly computes this formulation (
Figure 10 and
Figure 11) The rectangular-coordinate complex multiplication of a complex input (
R +
j I) and complex weight (
W +
j W) is
resulting in four real-valued multiplications (
Figure 10), but otherwise resulting in a typical VMM operation. The time-evolution of a qubit array of qubits is typically not considered as the solution is thought to happen instantaneously, often as one sees an analog computation occurs instantaneously. Even so, one can model the linear complex wavefunction dynamics (e.g., Schrodinger’s equation) of these devices converging to their steady-state solution through element time-constants (
) similarly to modeling an analog VMM converging to its linear dynamics through element time-constants (
). A time domain model could include either feedforward or feedback where the steady-state solution would still simplify to a single complex VMM operation. Using sinusoids of a single frequency with different amplitude and phase (a phasor) provides a second method of implementing the complex operations. The phasor approach computes Hilbert spaces by analog circuits [
50,
52], theoretically that can be extended to transformations with classical cochlear modeling (e.g., [
53,
54]), with no difference in overall computational capability.
Superposition is a property of all linear systems (R or Z) that allows for a number of signals or waveforms to simultaneously exist in an overlapping space. Superposition is taught from the first analog circuit analysis class. Superposition enables simultanious quantum wavefunctions or analog states including for these examples.
Quantum Measurement provides a nonlinear operation to the otherwise linear quantum operations. A measurement makes the wavefunction around that point have a certain value for the duration of the confident measurement. This nonlinearity is a comparison threshold, or a multilevel comparison threshold, with a probability directly related to the magnitude or signal power magnitude of that region’s wavefunction. Adding the square of the real and imaginary complex VMM outputs gives this signal power magnitude. The magnitude function operating around a bias current (
I), uses the differential VMM outputs signals (
Figure 10)
through translinear relationships for transistors with gate voltage changes (e.g.,
) around the bias current (
I): [
55,
56]
to create the wavefunction (
) signal power magnitude (
Figure 11).
The nonlinear measurement operation is a noisy comparison operation to an integer value (e.g., 0 or 1) based on the signal power magnitude of the local wavefunction (e.g., [
57]). The square root normalization is not required when passing through a threshold operation or a noisy threshold operation. Thresholds can be set by programming a Floating-Gate (FG) transistor at the threshold current. An analog noise generator (e.g., [
13]) before the comparison gives the probabilistic output related to the local wavefunction magnitude, as needed, beyond the comparator circuit noise. Some algorithms may not benefit from additional noise before the comparison. The probability may be represented by a dithering of the output, similar to rate-encoded values seen in integrate and fire neurons, effectively looking like a noise source. Noisy dithered outputs for Quantum computing enables Quantum systems to be efficient noise generators (e.g., [
11]), and likely was the reason the first demonstration of physical supremacy (called Quantum supremacy) for Quantum computing was a complicated noise source.
As a result of these properties, quantum computing is a form of perceptron computation over complex-valued quantities, where the input and output results are discrete elements (
Figure 9). This structure is analogous to an analog implementation (
Figure 11) of a one-layer Perceptron network with complex weights and real or complex inputs (
Figure 9). Multivalued symbol output can be abstracted where the equivalent of more outputs states is encoded into having a factor of more qubit outputs (e.g., 4 symbols → two outputs, 8 symbols → three outputs). Note that quantum entanglement is not part of these computations, as entanglement is about quantum error correction and not primary computations. Shor’s algorithm [
35] directly solved through this analog, room-temperature equivalent circuit that is similar to analog Fourier transforms (e.g., [
58]). An engineer could still choose either method for solution depending on other engineering constraints.
5. Relationships between Physical Computing Approaches
Every form of
R-valued computing has equivalents to other
R-valued techniques. These concepts build on the existence and properties of a continuous-valued environment. Optical, Neuromorphic, Quantum, and Analog computing compute over
R amplitude and
R time with various spatial forms (
Figure 12). All four physical systems described show properties of superposition within their linear operating region, allowing for a number of signals or waveforms to simultaneously exist in the same representation. Optical communication systems extensively make use of superposition to have multiple frequency or wavelength carriers communicate on the same fiber. All four physical systems may have infinite time and/or spatial responses. Optimization problems are routinely solved in analog, quantum and neuromorphic techniques, resulting from coupled ODEs or PDEs propagating energy down the established energy surfaces, either to a global minimum or local minimas. Quantum computing relaxation and annealing as in Grover’s algorithm [
36], find similar concepts within as well as analog energy relaxation techniques (e.g., [
59]) and neuromorphic L
norm minimization [
60]. A good recent review shows the different physical computing techniques for similar energy and power surface minimization [
61].
Second-Order Partial Differential Equations (PDE) provide a translatable framework between these different
R-valued computational mediums (
Figure 12) computing over
R-valued amplitude, space, and time (
Table 1). Optical computing utilizes waves, described through a second-order time and space PDE formulation of Maxwell’s equations, computing through continuous time, amplitude, and 1- to 3-dimensional space utilizing a number of spatial filters, lenses, and a variety of tunable light modulators & mirrors can modify an input optical signal. Quantum computing uses complex probability wavefunctions (
) governed through PDEs (Schrodinger’s equation) computing through continuous time, amplitude, and 1- to 3-dimensional space. Typical implementations compute multiple quantum wells, potential energy barriers, and connected states governed by these PDEs. Neuromorphic computing (e.g., [
10,
62]), including Neural Networks (e.g., [
30,
31]), uses physical computing devices, typically of an analog nature in Si or hybrid system, modeling part of a neurobiological computations (e.g., neurons) using continuous amplitude, time, with at least 1-dimensional space PDEs in neuron computation (e.g., dendritic systems) [
63]. Neurons are spatio-temporal computing elements with hundreds if not thousands of inputs, modeling voltages governed by diffusing and wave-propagating PDEs (
Figure 12). Analog neuron implementations have demonstrated hundreds of inputs (e.g., [
64]) as well as wave-propagating PDEs (e.g., [
63]). The dendritic PDEs have a significant linear operating range within the overall biological structure.
Analog computing operates in continuous-time and amplitude within a spatially coupled environment and described by multiple coupled differential equations, including coupled linear or nonlinear PDEs utilizing first and second order space and time dynamics (e.g., [
65]). The physical system is
R-value in space, but practically the parameters change in particular points with a finite granularity of parameter resolution setting, as well as output measurement capability. The PDE could be coupled transistors (e.g., resistive networks [
59]) or transistor circuits (e.g., ladder filters [
65]). Inputs, outputs and boundary conditions are set through additional analog circuitry. Analog techniques provide the mode advanced physical implementation capabilities, including programmable and reconfigurable techniques in standard CMOS processes [
18].
A bridge between computing capabilities results in a win-win silicoation (
Figure 4), where results developed from one physical system can be translated to a second physical system. Although one medium is more efficient than another for particular problems, one can transform between the two mediums through polynomial-size transformations. For example, analog, optical, quantum, and neuromorphic computing can compute VMM operations. Lenses, programmable modulators, and programmed micromirrors enable optical VMM computations. Analog and Quantum operations were discussed in the previous section. Neuromorphic operations are likely the most nonlinear of these approaches.
The paths between these systems starts by translating the core PDEs between each system (
Figure 12), although the process might be simplier when computing concepts use only a part of the physical medium’s capability (e.g.,
Section 4). An earlier example showed moving between a quantum system (qubits) and an analog computing system, one of the more challanging
R-valued translations (
Section 4). The translation between optical and quantum computing goes through their similar hyperbolic wave-propagating PDEs and similar mathematical formulations, where both heavily utilize the temporal and spatial duality between real values and Fourier transformed values. Analog techniques involve a wide range of ODE and PDE techniques that include the range of linear and nonlinear PDE systems. Analog techniques can compute the same PDEs for Maxwell’s equations as optical systems (e.g., [
65]), although with a polynomially larger complexity in many cases. Neuromorphic systems utilize parabolic PDEs (e.g., diffusion), and yet these networks can be approximate waveguiding systems by altering spatial parameters [
63] as well as through local (e.g., active channels) or active network (e.g., synfire chain [
66]) properties. The translation between analog and neuromorphic is straight-forward as most neurormophic models are built with some analog circuit modeling (e.g., [
10,
62]). The spatial steady-state solutions typically form elliptic PDE problems (Poison’s equation). Each approach has a linear region, although nonlinear operations are harder in some domains (e.g., Optical), possible in some cases (e.g., Quantum), and easy or too easy in other cases (e.g., Analog or Neuromorphic). In each case, even and odd nonlinearities are possible and a linear region are possible where some systems are more optimal in some places than others. One expects translations between other physical systems not identified, all systems computing with multiple
R-valued operations and representations.
6. Computing Opportunities for Physical Computation
After defining physical computing, describing its properties (
R versus
Z), as well as showing the transformations between these techniques, the discussion moves to considering the opportunities for physical computing. At one level, physical computing approaches often have far higher computational efficiency and lower computational area [
7,
8,
9,
18,
19], as mentioned for analog systems (1000×, 100×) at the beginning of this discussion. Neuromorphic approaches have demonstrated even greater computational efficiencies with roadmaps possible for both improved analog and neuromorphic cases [
10]. These opportunities alone are sufficient to explore these techniques, particularly in an ever energy-constrained environment. The availability of large-scale programmable and configurable analog techniques has enabled a realistic analysis of physical computing techniques.
Some examples in P
improve P
algorithms, although remain in P
(
Figure 13). Spaghetti sort [
67] solved using analog WTA networks [
14] in O(M) time rather than greater than O(Mlog M) time for physical digital implementations. Grover’s quantum computing algorithm also improved the O(·) time for the related algorithms [
36].
Sometimes these physical computing discussions involve energy relaxation down an energy surface to a minimum level; a good review of these physical computing techniques can be found elsewhere [
61]. These approaches map well to physical computing approaches, and with just the right formulation or resulting energy surface, one could have a single global minimum, resulting in an optimal solution. In general, there are local minimas that might represent good solutions, and therefore these physical computing techniques do not result in a P
solution for NP
problems (
Figure 13), although they might provide good solutions for many different cases. Analog resistive networks can create parabolic PDE with elliptical PDE steady states to create energy surfaces, energy surfaces similar to soap bubbles around fixed boundary conditions. These systems provide good solutions, but local minimas tend to limit the extent of optimality, typical of these approaches in any medium. For example, using resistive networks often achieve 96% correct for optimal path planning, but not full optimality [
59]. Very good solutions have been seen using energy surface relaxations for NP
problems (e.g., TSP) using physical techniques [
68,
69]. All well designed energy surface relaxation or related methods implemented in physical systems show similar results. These perspectives often lead individuals to believe that physical computing will not solve NP
problems (e.g., Quantum [
48]). Unless just the right surface is found and implemented, simple relaxation does not indicate whether NP
problems can be solved in P
time.
At another level, computing over
R versus
Z likely has additional benefits including addressing the relationship between NP
and EXPTIME
to P
and NP
(
Figure 13). Some examples in P
appear to be beyond P
. such as Shor’s quantum factorization algorithm [
35]. Multiple coupled ODEs systems have been proposed to solve NP problems, such at the 3-SAT problem [
33,
34,
70,
71,
72], that could be implemented on a configurable continuous-time platform [
19], although to date it has not been verified through physical computing approaches. The potential overlap of EXPTIME
(e.g., Shor Factorization) with P
and NP
gives motivation for deeper explorations. Throughout this process, synchronous digital simulation results of physical computation must always be approached cautiously, as digital computation is more limited than the resulting physical substrate (
Figure 4).
Optimal path planning is computed in a polynomial size array of neurons in polynomial time [
66], providing one approach to connect NP
and P
(
Figure 13). Physically based wave-propagation computation using neural events is proven analytically and experimentally to give an optimal solution [
66], while energy surface relaxation nearly, but not always (96% correct [
59]) reaches the optimal solution. These solutions enable an optimal solution by using wave propagation, rather than diffusive solutions falling down energy surfaces. The optimal solution is analogous to timing of optical waves through a set of barriers along the path. The first path that arrives is the winning path, typical of optical systems. Algorithm intuition sometimes arises by equating one physical solution to another physical solution. The principle of least time optimization [
61] is the closest connection to this physical optimal path planning through active propagation [
66]. This physical implementation is related to Dijkystra’s graph optimization algorithm, but with strong physical optimality results. Dijkstra’s algorithm computes an optimal path over a graph that may have been abstracted from a physical map within the timestep resolution.
Optimal path computation over a graph within the parameters set for the Dijkystra algorithm is optimal, and that particular problem is not an NP computation. Sometimes multiple paths are considered equal within the graph step timing resolution, even though one path is shorter. Continuous-time physical computation eliminates that ambiguity, only limiting the output computation to the final output readout resolution, creating a stronger definition of optimality. The class of problems for this stronger definition of optimality is unclear, requiring arbitrary smaller and smaller timesteps. The continuous variable allows for arbitrary timing resolution because the resulting computation is over continuous variables. If NP is demonstrated part of P in one physical computing platform, then it is true in all fully-capable R-valued computing platforms. It remains an open question to connect the Traveling salesman Problem (TSP) or Max cut problem to this R-valued optimal path planning. This discussion sits at a place where we have the framework to explore if NP is part of P, looking for a constructive approach based on some potential examples.
7. Summary and Discussion: Implications and Opportunities of Physical Computation
We presented a computing model for physical computing, computing over real values including analog, neuormorphic, optical, and quantum computing. These techniques build upon recent innovations in analog/mixed-signal computation as well as analog modeling, architectures and algorithms. This approach shows a potential physical computing model, enabling similar capabilities to digital computation with its deep theoretical grounding starting from Turing Machines. This paper addressed the possibility of a real-valued or analog Turing machine model, and the potential computational and algorithmic opportunities. These techniques have shown promise to increase energy efficiency, enable smaller area per computation, and potentially improve algorithm scaling. This effort describes opportunities beyond coefficient or minor polynomial scaling improvements in computational energy efficiency, but rather could significantly improve the computational energy efficiency scaling, O, resulting from fundamental algorithmic improvements from computing over R-values as compared to traditional digital computing over Z-values.
Although there is a starting theory of
R-valued computation and its
R-valued Turing Machine, and there is starting theory of
R-valued numerical analysis, architectures, and abstraction primarily coming from analog implementations, one still requires a constructive framework for engineers to design physical computing systems for an application. Although there are significant guideposts for physical computation so we no longer require a miracle to occur (
Figure 1) for such implementations, one still does not find the well-traveled paths typical of linear digital design.
A constructive framework for physical computing design requires a constructive design approach using nonlinear dynamics. Engineers are well versed in designing signal processing and control systems using linear dynamical systems and differential equations. If any part of the system is nonlinear, or perceived as nonlinear, the design effort, risk, and stress becomes almost unmanagable as there are few tools for designing nonlinear systems. Although theoretical analytical tools for nonlinear dynamics is extensive (e.g., [
73]), engineers have nearly no resources to design with nonlinear systems, resulting in another a miracle to occur gap.
As an example in analog circuits, silicon nonlinearities are tanh
, sinh
,
as well as their inverses, providing the even (x
) and odd (x
) normal forms [
73,
74]. Handling these nonlinearities requires the right current (
I) and voltage (
V) relationships. For example, the output of a VMM is a current, so a compressive odd nonlinearity following this operation would not be a tanh
(
), but could be a sinh
(
). Frameworks for solving linear equations [
75] adapted to allow for the natural nonlinearities could generate fairly general sets of coupled differential equations with even and odd nonlinearities. The analog form of L1 minimization is similar to these circuit structures [
60].
A constructive framework for physical computing design requires a constructive design approach for applying physical algorithms towards an application. Often several energy-space algorithms with the hope they will provide a a good to optimal solution for a particular application. Most of the theory for choosing these algorithms is hueristic in nature, effectively resulting from the artistry of the expert designer. Other algorithmic approaches are also possible, and yet further development in physical computing platforms is essential. For example, can neural path planning algorithm [
66] be modified to solve NP-class applications (e.g., TSP, Max-Cut, or 3-SAT)? As many transformative problems will experience chaotic dynamics in their solution (e.g., [
33,
34]), and as a result will become unfeasible to solve in PD, understanding chaotic analog dynamics, as well as implementing these dynamics in a physical system (e.g., FPAA) provides a guide for algorithm development. Because of the lack of such structures, nonlinear dynamics has hitherto not exploited these larger opportunities (e.g., [
33,
34]).
These remaining open questions of constructive frameworks for designing with nonlinear dynamics, choosing the right algorithms as well as choosing the right physical medium for a particular application, are significant challenges going forward. Furthermore, yet, now being able to define these challenges carefully within a clear framework, working through these challenges creates the opportunity of well-traveled paths through physical computing. Educating and creating a community of engineers with these new tools becomes essential towards solving and utilizing these spaces.