A New VCII Application: Sinusoidal Oscillators

Abstract

The aim of this paper is to prove that, through a canonic approach, sinusoidal oscillators based on second-generation voltage conveyor (VCII) can be implemented. The investigation demonstrates the feasibility of the design results in a pair of new canonic oscillators based on negative type VCII (VCII⁻). Interestingly, the same analysis shows that no canonic oscillator configuration can be achieved using positive type VCII (VCII⁺), since a single VCII⁺ does not present the correct port conditions to implement such a device. From this analysis, it comes about that, for 5-node networks, the two presented oscillator configurations are the only possible ones and make use of two resistors, two capacitors and a single VCII⁻. Notably, the produced sinusoidal output signal is easily available through the low output impedance Z port of VCII, removing the need for additional voltage buffer for practical use, which is one of the main limitations of the current mode (CM) approach. The presented theory is substantiated by both LTSpice simulations and measurement results using the commercially available AD844 from Analog Devices, the latter being in a close agreement with the theory. Moreover, low values of THD are given for a wide frequency range.

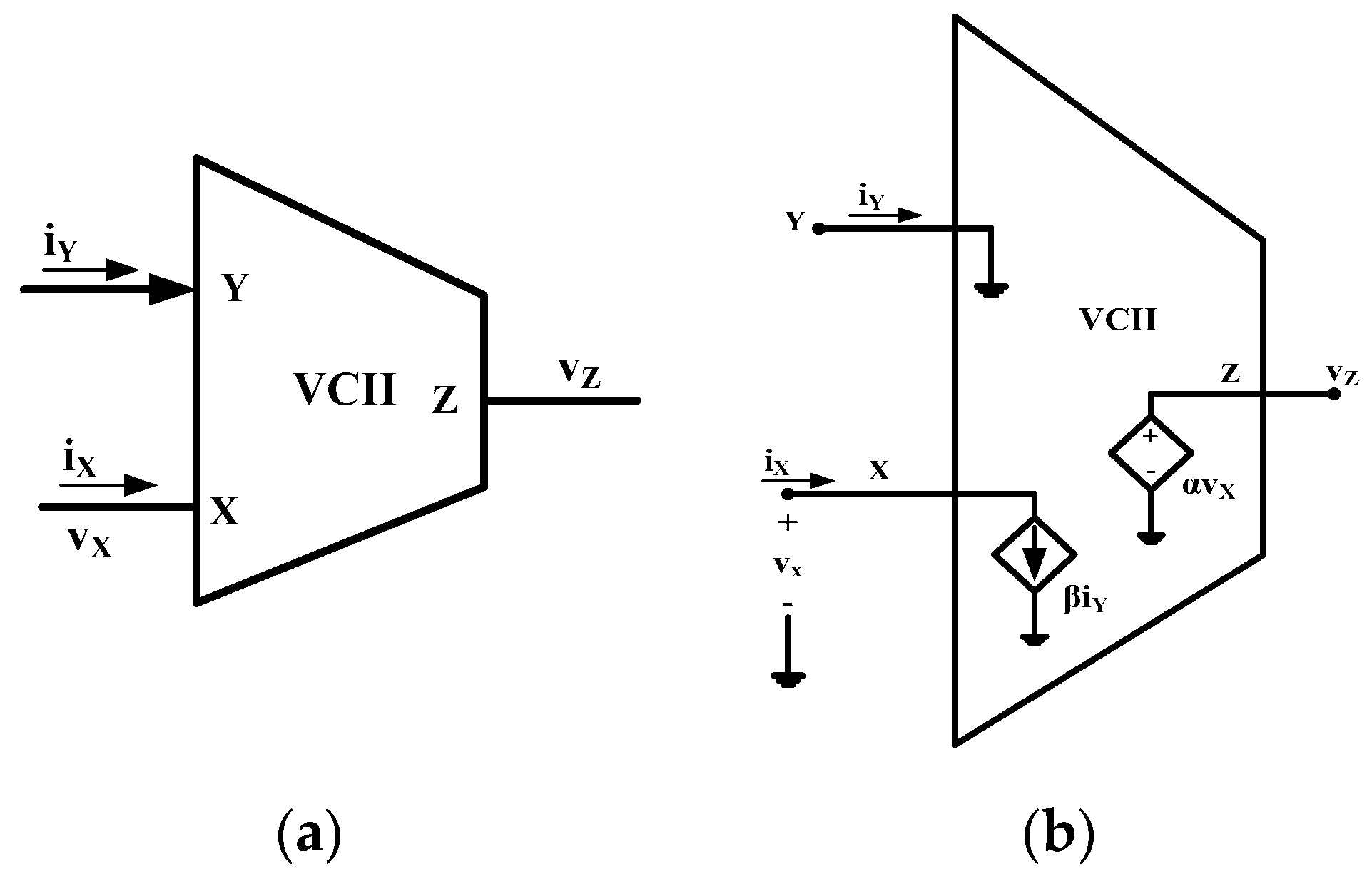
1. Introduction

There has always been an interest in designing sinusoidal oscillators due to several applications in different areas such as communication, instrumentation, biomedical, etc. [1,2,3]. Compared to LC and RLC sinusoidal oscillators, RC-active type oscillators are advantageous from the integration point of view. In the early implementations of RC-active sinusoidal oscillators, operational amplifiers (Op-Amps) were used as active elements [4,5,6]. A systematic approach was introduced in [5] to design Op-Amp-based oscillators with a single active element and the minimum number of passive elements. The design method of [5] resulted in Op-Amp-based oscillator configurations composed of one active device, two capacitors and four resistors.

However, the limited frequency performance and slew rate of Op-Amps as well as their high power consumption imposed a restriction in the application of Op-Amp-based sinusoidal oscillators. A literature survey shows that, after revealing the potential capabilities of current-mode (CM) signal processing, efforts have been made to design RC-active sinusoidal oscillators using various CM active building blocks (ABBs) [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. Undoubtedly, second-generation current conveyor (CCII) as the main ABB of CM signal processing is the most widely used one for this purpose. Different approaches were employed to realize CCII-based oscillators. For example, in [8], the Op-Amps were replaced with composite current conveyors, resulting in CM oscillators. Unfortunately, this approach did not reach a simple realization because each amplifier could only be implemented with at least two CCIIs and two resistors. The extension of the approach presented in [5] was employed in [9] to synthesize CCII-based oscillators. Although the resulting sinusoidal oscillators enjoyed a canonic structure with the minimum possible number of elements, they were still not readily cascadable, i.e., they required additional voltage buffers to be actually usable in a real-world application. Most of the other CM oscillator realizations reported in [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34] using different ABBs instead of CCIIs also suffered from a large number of active and/or passive elements.

Recently, the dual circuit of CCII, called second-generation voltage conveyor (VCII), has attracted the attention of researchers [35,36,37,38,39,40,41,42,43,44]. In particular, the recent study reported in [35,36] showed that this device helps to benefit from CM signal processing features and overcome the limitations in CCII-based circuits. Particularly, unlike CCII, there is a low-impedance voltage output port in VCII which allows it to be easily cascaded with other high-impedance processing blocks, without the need for extra voltage buffers in voltage output applications. Compared to CCII, VCII has proven superior performance in many applications [37]; up to now, this device has not been employed in the realization of sinusoidal oscillators.

However, the VCII, combining the advantages of CM processing with a voltage-mode interfacing, could provide sinusoidal oscillators operating up to higher frequency than Op-Amp-based ones. Moreover, breaking the gain-bandwidth tradeoff, it could ease decoupling oscillation frequency and oscillation condition even at the higher end of the spectrum. Among the possible implementations of VCII-based sinusoidal oscillators, those requiring the minimum number of (active and) passive components, so-called canonic, are of particular interest to minimize silicon area and power consumption. The aim of this work is only to present possible VCII-based canonic sinusoidal oscillator realizations, replicating the general approach presented in [5,9] which, as previously anticipated, has been used to synthesize Op-Amp-based and CCII-based sinusoidal oscillators. We will show that it is possible to implement sinusoidal oscillators with a minimum number of elements using a single negative type VCII (VCII⁻), two resistors and two capacitors, so demonstrating a new practical application of the VCII. The notable advantage of the proposed VCII⁻-based oscillator is that it is easily cascadable from port Z of VCII⁻, alleviating the need for any extra voltage buffer. Moreover, THD values are low also for higher frequency oscillators. However, the results of this study show that the applied approach does not reach any canonic configuration using positive type VCII (VCII⁺). The effect of non-idealities in the VCII has been considered, and the proposed approach has been tested by both simulations and measurement results.

The organization of this paper is the following: in Section 2, an introduction on the VCII as active building block as well as the basics of the general configuration of the VCII-based oscillator is introduced. Section 3 proposes, in detail, the study on the possible realizations of VCII-based oscillators, and the effects of non-idealities in VCII are considered in Section 4. Simulations and measurement results are given in Section 5. Finally, Section 6 concludes the paper.

2. General Configuration of the VCII-Based Oscillator

The symbolic representation and internal structure of VCII are shown in Figure 1. In this block, Y is a low-impedance (ideally zero) current input terminal. The current entering into Y node is transferred to X terminal which is a high-impedance (ideally infinity) current output port. The voltage produced at X terminal is transferred to Z terminal which is a low-impedance (ideally zero) voltage output terminal. The relationship between port currents and voltages are given by: $v_Z=\alpha v_X,$ $i_X=\beta i_Y$ and $v_Y=0$. In the ideal case we have α = 1 and β = ± 1. If β = 1 we are considering a VCII⁺, whereas if β = −1 we have a VCII⁻.

Using the approach presented in [5,9], the general configuration of an RC-active oscillator based on a single VCII is shown in Figure 2, where N_GC represents 4-terminal network consisting of only capacitors and conductances.

The characteristic equation (CE) of the whole system can be calculated replacing, in the circuit of Figure 2, the equivalent model of a VCII of Figure 1b and considering a fictitious input at the $Y$ node (of course, no input signal will be present in an actual oscillator circuit), as shown in Figure 3a at the building block level and Figure 3b in more detail.

The configurations in Figure 2 and Figure 3 can hence be seen as a positive feedback system for which the current transfer function (TF) is given by:

$$T_I\left(s\right)=\frac{i_{out}\left(s\right)}{i_{in}\left(s\right)}=\frac{A\left(s\right)}{1-A\left(s\right)\beta \left(s\right)}.$$

(1)

Since $A\left(s\right)=\pm 1$ and $\beta \left(s\right)=i_f\left(s\right)/i_{out}\left(s\right)$, (1) becomes:

$$T_I\left(s\right)=\frac{\pm 1}{1\mp i_f\left(s\right)/i_{out}\left(s\right)}.$$

(2)

However, since from Figure 3b $i_{out}=-i_X$ and in an oscillator circuit there is no input ($i_{in}=0$), we have $i_f=i_Y$ and the TF is given by:

$$T_I\left(s\right)=\frac{\pm 1}{1\mp i_Y\left(s\right)/i_{out}\left(s\right)}=\frac{\pm i_X\left(s\right)}{i_X\left(s\right)\pm i_Y\left(s\right)}.$$

(3)

From (3), we can derive the condition of existence (CE) as:

$$i_X\left(s\right)\pm i_Y\left(s\right)=0.$$

(4)

By assuming $v_Z=v_X$,$v_Y=0$, the transconductance functions of the passive network in Figure 2 can be expressed by a rational expression as:

$$\frac{i_X\left(s\right)}{v_Z\left(s\right)}=\frac{N_X\left(s\right)}{D\left(s\right)}$$

(5)

$$\frac{i_Y\left(s\right)}{v_Z\left(s\right)}=\frac{N_Y\left(s\right)}{D\left(s\right)}$$

(6)

where $N_X\left(s\right)$ and $N_Y\left(s\right)$ are the numerators at X and Z nodes, respectively, while $D\left(s\right)$ is a common denominator. Using (5) and (6) in (4), the CE becomes:

$$N_X\left(s\right)\pm N_Y\left(s\right)=0$$

(7)

In (7), the plus and minus signs are for VCII⁻ and VCII⁺ respectively. To ensure a pure sinusoidal oscillation, the CE in (7) should be a second-order polynomial with purely imaginary roots. This requires the network N_GC to include at least two capacitors. It has to be noted that, in Figure 2, by using a VCII⁺ rather than a VCII⁻, at least three capacitors are required to provide a phase shift to generate a positive feedback loop. Therefore, no canonic oscillator is possible using VCII⁺, and for the following, we will consider the VCII in Figure 2 as a VCII⁻. By then assuming a network with only two capacitors, Equation (7) will be in the form:

$$a{s}^2+bs+c=0.$$

(8)

In order to start the oscillation, the following commonly known criteria must be satisfied:

$$b=0$$

(9)

$$\frac{c}{a}>0$$

(10)

with $c\ne 0, a\ne 0$, so that, according to the Barkhausen criterion, purely imaginary poles for the closed-loop transfer function are obtained. The oscillation frequency is:

$${\omega }_o=\sqrt{\frac{c}{a}} .$$

(11)

3. Oscillator Circuits

In this section we analyze the possible VCII⁻-based oscillators based on the scheme of Figure 2. The passive N_GC is assumed as a general $n$-node network consisting of b possible branches between two nodes. Each node is a junction where two or more branches are connected, and each branch is an admittance connected between two nodes represented as:

$$Y_i=s{C}_i+G_i.$$

(12)

In the following, we analyze the CE to see if oscillation is possible for the particular case study of a five-node network. From this analysis we see that for a four-node network it is not possible to obtain a second-order polynomial for (7), whereas for a six-node network (or more) only non-canonic oscillators using more than the minimum number of passive components are possible.

N_GC as a Five-Node Network

In Figure 4 we assume N_GC as a five-node network. We start analyzing this network by performing KCL at node Y as reported in the following:

$$i_Y=i_3+i_6+i_7=i_3+Y_6{V}_Z+Y_7{V}_Z.$$

(13)

Since no current is flowing into Y₈ and Y₉, these admittances can be assumed as open circuit (Y₈ = Y₉ = 0). Routine analysis of Figure 4 results in i₃ as:

$$i_3=\frac{Y_3\left(Y_1+Y_2\right)}{Y_1+Y_2+Y_3+Y_4}{V}_Z.$$

(14)

Using (13)–(14), we have:

$$\frac{i_Y}{V_Z}=\frac{Y_3\left(Y_1+Y_2\right)}{Y_1+Y_2+Y_3+Y_4}+Y_6+Y_7.$$

(15)

Similar analysis for i_x results:

$$\frac{i_X}{V_Z}=-\frac{Y_2\left(Y_3+Y_4\right)}{Y_1+Y_2+Y_3+Y_4}-Y_5-Y_7$$

(16)

Using (15) and (16) in (7), the CE of the five-node network is found as:

$$-Y_2{Y}_4+Y_3{Y}_1+\left(Y_6-Y_5\right)\left(Y_1+Y_2+Y_3+Y_4\right)=0.$$

(17)

It can be noticed that CE does not depend on $Y_7,\dots ,Y_{10}$ which means that these branches can be assumed to be open circuit. For the other branches we can make different choices. If two branches have non-zero admittances, the following CEs are possible:

$$Y_1,Y_3\ne 0\to CE:Y_1{Y}_3=0$$

(18a)

$$Y_1,Y_5\ne 0\to CE:Y_1{Y}_5=0$$

(18b)

$$Y_1,Y_6\ne 0\to CE:Y_1{Y}_6=0$$

(18c)

$$Y_2,Y_4\ne 0\to CE:Y_2{Y}_4=0$$

(18d)

$$Y_2,Y_5\ne 0\to CE:Y_2{Y}_5=0$$

(18e)

$$Y_2,Y_6\ne 0\to CE:Y_2{Y}_6=0$$

(18f)

$$Y_3,Y_5\ne 0\to CE:Y_3{Y}_5=0$$

(18g)

$$Y_3,Y_6\ne 0\to CE:Y_3{Y}_6=0$$

(18h)

$$Y_4,Y_5\ne 0\to CE:Y_4{Y}_5=0$$

(18i)

$$Y_4,Y_6\ne 0\to CE:Y_4{Y}_6=0$$

(18j)

In the general case, (18) can be expressed as

$$CE: Y_a{Y}_b=0$$

(19)

By assuming Y_a = sC_a + G_a and Y_b = sC_b + G_b, (19) can be written as:

$$s^2{C}_a{C}_b+s\left[C_a{G}_b+C_b{G}_a\right]+G_a{G}_b=0$$

(20)

From (20) it is not possible to have imaginary roots. Therefore, in case of two non-zero branches, no oscillation is possible.

Finally, we investigate the possibility of achieving oscillations from (17) in the case that three branches of N_GC present non-zero admittance.

For (Y₁ = Y₅ = Y₆ = 0) or (Y₃ = Y₅ = Y₆ = 0), we have Y₂Y₄ = 0, while for (Y₂ = Y₅ = Y₆ = 0) or (Y₄ = Y₅ = Y₆ = 0), we have Y₁Y₃ = 0. In both these cases, the CE has the general form of (19).

For (Y₁ = Y₂ = Y₅ = 0), (Y₁ = Y₂ = Y₆ = 0), (Y₁ = Y₄ = Y₅ = 0), (Y₁ = Y₄ = Y₆ = 0), (Y₂ = Y₃ = Y₅ = 0), (Y₂ = Y₃ = Y₆ = 0), (Y₃ = Y₄ = Y₅ = 0), (Y₃ = Y₄ = Y₆ = 0) the CE has the following form:

$$Y_c\left(Y_a+Y_b\right)=0.$$

(21)

For (Y₁ = Y₃ = Y₆ = 0) and (Y₂ = Y₄ = Y₅ = 0), the CE is obtained as:

$$Y_a{Y}_b+Y_c\left(Y_a+Y_b\right)=0.$$

(22)

The CEs of (21) and (22) do not result in pure imaginary roots; therefore, these cases cannot give oscillator topologies.

Considering instead the cases (Y₁ = Y₂ = Y₃ = 0), (Y₁ = Y₂ = Y₄ = 0), (Y₁ = Y₃ = Y₄ = 0) and (Y₂ = Y₃ = Y₄ = 0), the CE has the following general form:

$$Y_c\left(Y_a-Y_b\right)=0 .$$

(23)

It is easy to verify that the CE in (23) cannot be associated with an oscillator topology if only two capacitors are used (we need three of them at least).

Finally, for (Y₁ = Y₃ = Y₅ = 0) and (Y₂ = Y₄ = Y₆ = 0), the CEs will be given by (24a) and (24b), respectively:

$$Y_2{Y}_4-Y_6\left(Y_2+Y_4\right)=0$$

(24a)

$$Y_1{Y}_3-Y_5\left(Y_1+Y_3\right)=0$$

(24b)

which are equations with the general form:

$$Y_a{Y}_b-Y_c\left(Y_a+Y_b\right)=0.$$

(25)

In (25), oscillation condition is related to the choice of Y_c and Y_a or Y_b as a capacitance.

In order to design an oscillator with the minimum number of components, we now have to verify the choice of the components in (25). It can be demonstrated that it is possible to have a minimum of two capacitors and at least two resistors in order to have a constant term in the constituting equation. In fact, with this choice we obtain a complete polynomial. In this case, having only three branches of the type sC + G with C ≥ 0, G ≥ 0, it is a matter of choosing an admittance between Y_a, Y_b, Y_c of the type sC + G; the two remaining admittances will be a capacitance sC, and a conductance G. Inserting all possible combinations of options into (25), two sets of CEs which show imaginary roots are obtained.

For $Y_c=s{C}_c+G_c$; $Y_a=s{C}_a; Y_b=G_b$, the CE becomes

$$-s^2{C}_a{C}_c+s\left[C_a{G}_b-C_a{G}_c-C_c{G}_b\right]-G_b{G}_c=0.$$

(26)

For $Y_c=s{C}_c+G_c$; $Y_b=s{C}_b; Y_a=G_a$, the CE becomes

$$-s^2{C}_b{C}_c+s\left[C_b{G}_a-C_c{G}_a-C_b{G}_c\right]-G_a{G}_c=0.$$

(27)

From (26) and (27), the oscillation condition (C_o) and oscillation frequency (ω₀) for the two cases are obtained respectively as:

$$C_o:\frac{G_c}{G_b}+\frac{C_c}{C_a}=1,\hspace{1em}{\omega }_0=\sqrt{\frac{G_b{G}_c}{C_a{C}_c}}$$

(28a)

$$C_o:\frac{G_c}{G_a}+\frac{C_c}{C_b}=1,\hspace{1em}{\omega }_0=\sqrt{\frac{G_a{G}_c}{C_b{C}_c}}$$

(28b)

Thus, the minimum number of elements necessary to obtain an oscillator based on the scheme of Figure 2 is four, being two of these capacitors and two resistors. Considering the two cases (Y₁ = Y₃ = Y₅ = 0) and (Y₂ = Y₄ = Y₆ = 0) and the possible choices for Y_a and Y_b, we obtain a total of four canonic oscillators, corresponding to the following CEs:

$$-s^2{C}_1{C}_5+s\left[C_1{G}_3-C_1{G}_5-C_5{G}_3\right]-G_3{G}_5=0$$

(29)

$$-s^2{C}_3{C}_5+s\left[C_3{G}_1-C_3{G}_5-C_5{G}_1\right]-G_1{G}_5=0$$

(30)

$$s^2{C}_2{C}_6+s\left[C_6{G}_4+C_2{G}_6-C_2{G}_4\right]+G_4{G}_6=0$$

(31)

$$s^2{C}_4{C}_6+s\left[C_6{G}_2+C_4{G}_6-C_4{G}_2\right]+G_2{G}_6=0$$

(32)

However, this number is reduced again to two if we consider that from each of the cases (Y₁ = Y₃ = Y₅ = 0) and (Y₂ = Y₄ = Y₆ = 0) we obtain two equal oscillators if we exchange the order of the elements which are connected in series. These two configurations are shown in Figure 5, and the corresponding transfer functions, oscillation frequencies ω₀ and oscillation conditions are reported in

Table 1. Main equations of the canonic VCII-based oscillators.

Figure 5a	Figure 5b
$T_I\left(s\right)=-\frac{s^2{C}_5{C}_3+s\left[C_5{G}_1+C_3{G}_5\right]+G_5{G}_1}{s^2{C}_5{C}_3+G_5{G}_1}$	$T_I\left(s\right)=$ $\frac{s{C}_2{G}_2}{s^2{C}_4{C}_6+G_2{G}_6}$
${\omega }_0=\sqrt{\frac{G_5{G}_1}{C_5{C}_3}}$	${\omega }_0=\sqrt{\frac{G_2{G}_6}{C_4{C}_6}}$
Co: $\frac{G_5}{G_1}+\frac{C_5}{C_3}=1$	Co: $\frac{G_6}{G_2}+\frac{C_6}{C_4}=1$

. The oscillation frequencies and oscillation conditions in (28) show a strong interdependence since they are functions of the same parameters. Since the oscillation condition requires that the sum of the ratios of the capacitances and of the conductances is constant and equal to 1, a possible strategy for frequency tuning requires varying both resistors or both capacitors, maintaining their ratio constant. For example, a ratio of 2 between C_a and C_c can be obtained by using two parallel capacitors equal to C_a to obtain C_c; all three capacitors can be varied together; thus their ratio remains constant unless there are mismatches and the effect of parasitics.

4. Analysis of Parasitic Effects: A Case Study

The only two possible canonic topologies for the VCII-based oscillator are synthesized in Figure 6, where Z_A and Z_B are a series-connected RC network and a parallel-connected RC network; we define t_A = R_AC_A and t_B = R_BC_B as the time constants associated with these networks. The two oscillator topologies shown in Figure 6 correspond to the cases:

$$\mathrm{Type} \mathrm{I}: Z_A=\frac{R_5}{1+s{R}_5{C}_5},\hspace{1em}{Z}_B=R_1+\frac{1}{s{C}_3}$$

(33a)

$$\mathrm{Type} \mathrm{II}: Z_A=R_2+\frac{1}{s{C}_4},\hspace{1em}{Z}_B=\frac{R_6}{1+s{R}_6{C}_6}.$$

(33b)

where R_i = 1/G_i. From Figure 6, the oscillation condition can be obtained as:

$$\alpha \left|\beta \right|\frac{Z_A}{Z_B}=1$$

(34)

where $\beta$ and $\alpha$ are the VCII current and voltage gains (ideally both equal to 1), and the oscillation frequency is given by:

$${\omega }_0=\frac{1}{\sqrt{{\tau }_A{\tau }_B}}.$$

(35)

The oscillation condition and the oscillation frequency are affected by the non-idealities of the VCII, i.e., finite port impedances, gain errors (a < 1, |b| < 1) and poles of the voltage and current buffers. In order to analyze the effects of these non-idealities on the oscillator behavior, a model of a real VCII has been developed and implemented (see Figure 7), able to take into account the non-idealities.

In the general case, we can model the VCII with the first-order transfer functions

$$\alpha \left(s\right)={\alpha }_0/\left(1+s{\tau }_z\right)$$

(36)

$$\beta \left(s\right)=-{\beta }_0/\left(1+s{\tau }_x\right)$$

(37)

and complex port impedances

$$Y_x\left(s\right)=G_x+s{C}_x$$

(38)

$$Z_y\left(s\right)=R_y+s{L}_y$$

(39)

$$Z_z\left(s\right)=R_z+s{L}_z.$$

(40)

In order to better understand the effects of non-idealities and to compare the performance of the two topologies in Figure 5, different cases have been considered under the hypothesis that the ideal design has been carried out starting from the oscillation condition (34). When the non-idealities of the VCII are taken into account, Equation (34) becomes

$$\alpha \left(s\right)\left|\beta \left(s\right)\right|\frac{1}{Z_B+Z_y+Z_z}\frac{1}{1/Z_A+Y_x}=1.$$

(41)

By a simple inspection of the impedances Z_A and Z_B given by (33), and of the port impedances (38)–(40), it is evident that the Type I canonic oscillator should be less affected by non-idealities. In fact, in this case Y_x can be absorbed in Z_A ($G_x$ and $C_x$ are summed to 1/$R_5$ and $C_5$, respectively), and Z_y and Z_z in Z_B: a parallel RC network is used in parallel to a port impedance modeled as an RC parallel network, and a series impedance is connected in series to port impedances modeled as RL series networks. In contrast, for the Type II canonic oscillator, a series network is connected in parallel to the parallel RC port impedance, and a parallel RC network is connected in series to LR series port impedances, thus non-ideal port impedances alter Z_A and Z_B more significantly. The Type I canonic VCII-based oscillator seems therefore more suited to a practical realization, and it has been selected for further analysis.

4.1. Resistive Port Impedances

If only the resistive parasitics G_x, R_y and R_z in (39)–(41) are considered, the oscillation condition for the Type I canonic oscillator becomes:

$$\frac{\alpha \left|\beta \right| s(R_5||R_x)C_3}{\left[1+s(R_5||R_x)C_5\right]\left[1+s(R_1+R_y+R_z)C_3\right]}=1.$$

(42)

It is evident from (42) that the effect of the port impedances is limited, since they are simply summed to the ones from the NGC network (that have to be chosen as much larger than the corresponding parasitics to make them negligible). The oscillation frequency in Table 1 is modified as follows:

$${{\omega }_0}^{\prime }=\sqrt{\frac{{G_5}^{\prime }}{C_5{C}_3{R_1}^{\prime }}}={\omega }_0·\sqrt{\frac{1+G_x/G_5}{1+G_1\left(R_y+R_z\right)}}$$

(43)

where ${R_1}^{\prime }=R_1+R_y+R_z$ and ${G_5}^{\prime }=1/{R_5}^{\prime }=G_5+G_x$, and the oscillation condition becomes

$$\frac{\alpha \left|\beta \right|}{\frac{R_1}{R_5}\left(1+\frac{R_5}{R_x}\right)\left(1+\frac{R_y+R_z}{R_1}\right)+\frac{C_5}{C_3}}=1.$$

(44)

If the parasitic capacitance $C_x$ at the X terminal is also considered, Equations (43) and (44) have to be slightly modified by considering ${G_5}^{\prime }=C_5+C_x$ instead of $C_5$. Inductances $L_y$ and $L_z$ can be neglected in several applications and have not been considered in the following. However, for the sake of completeness, we report below the expression for the oscillation frequency when inductive parasitics are also considered:

$${{\omega }_0}^{\prime }={\omega }_0·\sqrt{\frac{1+G_x/G_5}{\left(L_y+L_z\right)\left(1+G_x/G_5\right)\frac{G_5{G}_1}{C_5}+\left(1+C_x/C_5\right)\left[1+G_1\left(R_y+R_z\right)\right]}}$$

(45)

4.2. Single-Pole Transfer Functions

If the non-ideal transfer functions in (36) and (37) are also considered in addition to the terminal resistive parasitics in (38)–(40), the denominator of the oscillation condition in (34) becomes of fourth degree:

$$\frac{\alpha \left|\beta \right| s{G_5}^{\prime }{R_5}^{\prime }}{a{s}^4+b{s}^3+c{s}^2+ds+e}=1$$

(46)

Prime variables are considered for ${R_5}^{\prime },{G_5}^{\prime }$ and ${R_1}^{\prime }$ to account for parasitic resistances R_y and R_z and admittance Y_x, as in the previous subsection, and we have

$$a={R_5}^{\prime }{C_5}^{\prime }{R_1}^{\prime }{C}_3{\tau }_x{\tau }_z$$

(47a)

$$b={R_5}^{\prime }{C_5}^{\prime }{R_1}^{\prime }{C}_3·\left({\tau }_x+{\tau }_z\right)+{\tau }_x{\tau }_z·({R_5}^{\prime }{C_5}^{\prime }+{R_1}^{\prime }{C}_3)$$

(47b)

$$c={R_5}^{\prime }{C_5}^{\prime }{R_1}^{\prime }{C}_3+{\tau }_x{\tau }_z+({R_5}^{\prime }{C_5}^{\prime }+{R_1}^{\prime }{C}_3)·({\tau }_x+{\tau }_z)$$

(47c)

$$d={R_5}^{\prime }{C_5}^{\prime }+{R_1}^{\prime }{C}_3+{\tau }_x+{\tau }_z$$

(47d)

$$e=1$$

(47e)

A real value is obtained for the left-hand side, under the hypothesis of a purely imaginary denominator. By equating to zero the real part of the denominator at $\omega ={\omega }_0$, we get:

$${{{\omega }_0}^{\prime }}^2=\frac{c}{2a}\left(1-\sqrt{1-\frac{4a}{c^2}}\right)\cong \frac{c}{2a}\left(\frac{1}{2}\frac{4a}{c^2}\right)=\frac{1}{c}$$

(48)

where c is given by (47c). The approximation $\frac{4a}{c^2}$<< 1 is justified under the hypothesis that the parasitic time constants ${\tau }_x$ and ${\tau }_z$ are significantly lower than the time constants ${\tau }_A={R_5}^{\prime }{C_5}^{\prime }$ and ${\tau }_B={R_1}^{\prime }{C}_3$. Finally, the oscillation frequency ${{\omega }_0}^{\prime }$ can be expressed in terms of the ideal value ${\omega }_0$, by using the expression of coefficient c:

$${{\omega }_0}^{\prime }\cong \frac{1}{\sqrt{c}}={\omega }_0\frac{1}{\sqrt{1+\frac{{\tau }_x{\tau }_z+\left({\tau }_A+{\tau }_B\right)\left({\tau }_x+{\tau }_z\right)}{{\tau }_A{\tau }_B}}}$$

(49)

Under the simplifying assumptions ${\tau }_x$ = ${\tau }_y$ = ${\tau }_{par}$ and ${\tau }_A$ = ${\tau }_B$ = $\tau$, the relative error on the oscillation frequency $\left(1-{{\omega }_o}^{\prime }/{\omega }_o\right)$ can be readily expressed as a function of the ratio ${\tau }_{par}/\tau$, thus providing a design guideline for the bandwidth of the VCII transfer functions. The graph in Figure 8 shows that errors lower than 10% can be obtained if the time constant ratio is lower than 0.06.

5. Experimental Results

The performance of the Type I canonic oscillator of Figure 5a has been verified by both LTSpice simulations and experimental results. In particular, the approximated expression for ω₀ in (49) has been checked for different values of τ and τ_x = τ_z, and errors lower than 1% have been found.

Then, we have used the commercially available AD844 to configure a VCII⁻ as shown in Figure 9. A single VCII is realizable using two AD844 ICs, whose Spice model can be found in [45]. The situation is quite different in the case of an integrated design, where a single VCII block can be exploited to design the oscillator, as shown in the previous sections.

The circuit was supplied with a dual ±5 V voltage, achieving a total power consumption of 14 mA.

Firstly, simulation of the topology in Figure 5a has been carried out to evaluate performance in terms of robustness to parasitics, and to estimate the achievable THD. In particular, the circuit has been designed with $C_3=2C_5$ = 2 nF and $R_5=2R_1$= 15 kΩ, and an oscillation frequency f₀ = 10.6 kHz was expected.

However, AD844 parasitics can slightly change the oscillation frequency and/or cause failing of oscillation condition: in this case, starting from the nominal design, the resistance $R_1$ can be changed (to 7.3 kΩ in the present case, see the schematic in Figure 10) to allow fulfillment of oscillation condition in (41): the obtained oscillation frequency is f₀ = 10.8 kHz, as shown in Figure 11.

A model for the VCII composed of AD844 components, shown in Figure 9, has been extracted from Spice simulations according to the equations presented in Section 4. At terminal X, we have found C_x = 5.5 pF in parallel with a resistor R_x = 3 MΩ. Purely resistive input impedances have been extracted at node Y (R_y = 50 Ω) and Z (R_z = 15 Ω). Finally, a dominant pole has been found for both the transfer function $\alpha \left(s\right)$ at f = 49 MHz (corresponding to ${\tau }_x$ = 3.25 ns), and for $\beta \left(s\right)$ at f = 764 MHz (${\tau }_z$ = 208 ps).

The element values used for the different design case studies, the simulated THD and the oscillation frequency evaluated with both the LTSpice AD844 non-linear model and with the VCII linear model, including parasitics, are summarized in

Table 2. Simulation results at different frequencies.

C3 = 2C5 (nF)	R5 (kΩ)	R1 (kΩ)	f0 (Spice) (Hz)	f0 (Model) (Hz)	f0 Error (%)	THD (%)
2000	15	7.3	10.8	10.74	0.6	0.7
200	15	7.35	107.3	107.0	0.3	0.4
20	15	7.35	1.073 K	1.070 K	0.3	0.4
2	15	7.3	10.80 K	10.70 K	0.9	0.5
0.2	15	6.9	108.1 K	107.2 K	0.9	0.7
0.2	1.5	0.65	1.080 M	1.040 M	3.7	1.7

. The linear model is accurate enough to be used for circuit design, and excellent simulated performance has been achieved in terms of THD with the proposed VCII topology.

Finally, experimental verification of performance has been carried out, exploiting the test bench shown in Figure 12: for data acquisition, the Digilent Analog Discovery 2™ board was used [46]. The design of Figure 5a was implemented as the reference topology for the oscillator. Measurements were carried out in the range (10–10⁶) Hz and are reported in

Table 3. Measured results.

R1 (kΩ)	R5 (kΩ)	C3 (F)	C5 (F)	Ideal Frequency (Hz)	Measured Frequency (Hz)	Error (%)	THD (%)
15	6.8	2 µ	1 µ	11.1	10.8	−3	1.12
15	6.8	200 n	100 n	111	109	−1.9	0.94
15	6.8	20 n	10 n	1.11 k	1.08 k	−2.7	0.92
15	6	2 n	1 n	11.9 k	11.5 k	−3.3	0.47
15	6	200 p	100 p	119 k	109 k	−7.8	0.56
15	0.64	200 p	100 p	1.15 M	1.0 M	−12.9	2.24

. In agreement with simulation results, the oscillator shows a very low THD value even at 1 MHz (considering 10 harmonics). The average relative frequency error between measured and ideal values is −5.2% and is comparable with tolerances of the passive components.

An example of the output signal, both in the time and frequency domains, is reported in Figure 13a,b for a frequency of 1 MHz.

Figure 14 shows the THD and frequency error trends vs. frequency.

6. Conclusions

By means of a systematic analysis, the possibility of realizing VCII-based oscillators is studied and demonstrated. The investigation results in a pair of new canonic oscillators based on VCII⁻. However, it is shown that, using the systematic approach, no oscillator configuration is possible using VCII+. The two found oscillator configurations are the only possible ones which use only two resistors, two capacitors and a single VCII⁻. Compared to Op-Amp-based oscillators, designed using the same systematic approach which employs two capacitors and four resistors, the proposed VCII-based oscillator is preferred in terms of low number of capacitors and resistances. Another interesting feature of the found VCII-based oscillator is that the produced sinusoidal output signal is easily available through the low output impedance Z port, while the CCII-based oscillators designed using the same systematic approach requires an additional voltage buffer for practical use. Simulations and experimental results using AD844 as VCII are reported to validate the theory.

A comparison with oscillator topologies based on different ABBs, with particular attention to canonic topologies, is reported in

Table 4. Comparative table of sinusoidal oscillator topologies.

Ref.	ABB Type	ABB Number	C (Grounded)	R (Grounded)	Output Phases	Indep. wo/Co
[5]	Op-Amp	1	2 (2)	4 (2)	1	NO
[7]	OTA	3	2 (2)	--	2	YES
[9]	CCII	1	2 (2)	2 (1)	1	NO
[9]	CCII	1	2 (1)	3 (3)	1	YES
[12]	FTFN	1	2 (1)	5 (1)	1	YES
[13]	CCII	2	2 (2)	2 (1)	1	YES
[16]	CDTA	2	2 (1)	--	2	NO
[19]	OTRA	1	2 (0)	3 (1)	1	YES
[21]	CCCCTA	1	2 (2)	1 (1)	1	YES
[23]	CCIII	2	2 (2)	3 (3)	1	YES
[25]	UVC	1	2 (1)	3 (1)	1	YES
[26]	VDTA	1	2 (2)	--	2	YES
[29]	CFOA	1	3 (2)	4 (2)	1	YES
[47]	CFOA	1	2 (2)	2 (1)	1	NO
[47]	CFOA	1	2 (1)	3 (1)	1	YES
[48]	OTRA	1	2 (0)	2 (0)	1	NO
[48]	OTRA	1	2 (0)	3 (1)	1	YES
[49]	CFOA	1	3 (2)	3 (3)	1	YES
[50]	CDBA	2	2 (2)	3 (0)	2	YES
[51]	OTRA	1	3 (1)	3 (0)	1	YES
This Work	VCII	1	2 (1)	2 (1)	1	NO

Op-Amp: operational amplifier; OTA: operational transconductance amplifier; CCII: second generation current conveyor; FTFN: four terminal floating nullor; CDTA: current differencing transconductance amplifier; OTRA: operational transresistance amplifier; CCCCTA: current controlled current conveyor transconductance amplifier; CCIII: third generation current conveyor; UVC: universal voltage conveyor; VDTA: voltage dependent transconductance amplifier; CFOA: current feedback operational amplifier; CDBA: current differencing buffered amplifier; VCII: second generation voltage conveyor.

. The table reports the type of active building block (ABB) the oscillator is based on, the number of active and passive components, specifying how many of them are grounded, the availability of a quadrature output and the independence of oscillation condition from oscillation frequency that allows tuning the oscillator acting on a single component. It has to be noted that the independence from the oscillation condition on oscillation frequency often requires additional passive (and sometimes also active) components, thus resulting in non-canonic topologies. Notable exceptions are the oscillators of [21,26] that use complex ABBs with gain, whose value contributes to satisfying the oscillation condition.