Multi-Objective Resource Scheduling for IoT Systems Using Reinforcement Learning †
Abstract
1. Introduction
- The RL Markov Decision Process (MDP) must be carefully defined such that it defines the optimization problem accurately and sufficiently, and
- RL algorithms should be able to learn stable policies within reasonable computational costs using the MDP.
- ensure that the node does not violate energy neutrality in the long-term by regulating the gross node energy consumption
- proportion of the budgeted energy between different tasks.
- dynamically tradeoff between maximization of different objectives w.r.t. user-defined priorities.
- achieve all of this using much fewer computational requirements than existing methods.
- develop a suitable MDP for both SORL and MORL implementations. Furthermore, we perform comprehensive experiments to analyze how our proposed MDP overcomes the limitations of traditional definitions to achieve near-optimal solutions.
- analyze the effect that different reward incentives and environmental factors have on the learning process as well as the resultant policies.
- demonstrate that our proposed algorithms can overcome the limitation of traditional MORL methods for ENO and learn better policies at lower costs.
2. Related Work
2.1. Analytical Methods for ENO
2.2. Single Objective RL Methods for ENO
2.3. Multi-Objective Optimization Methods
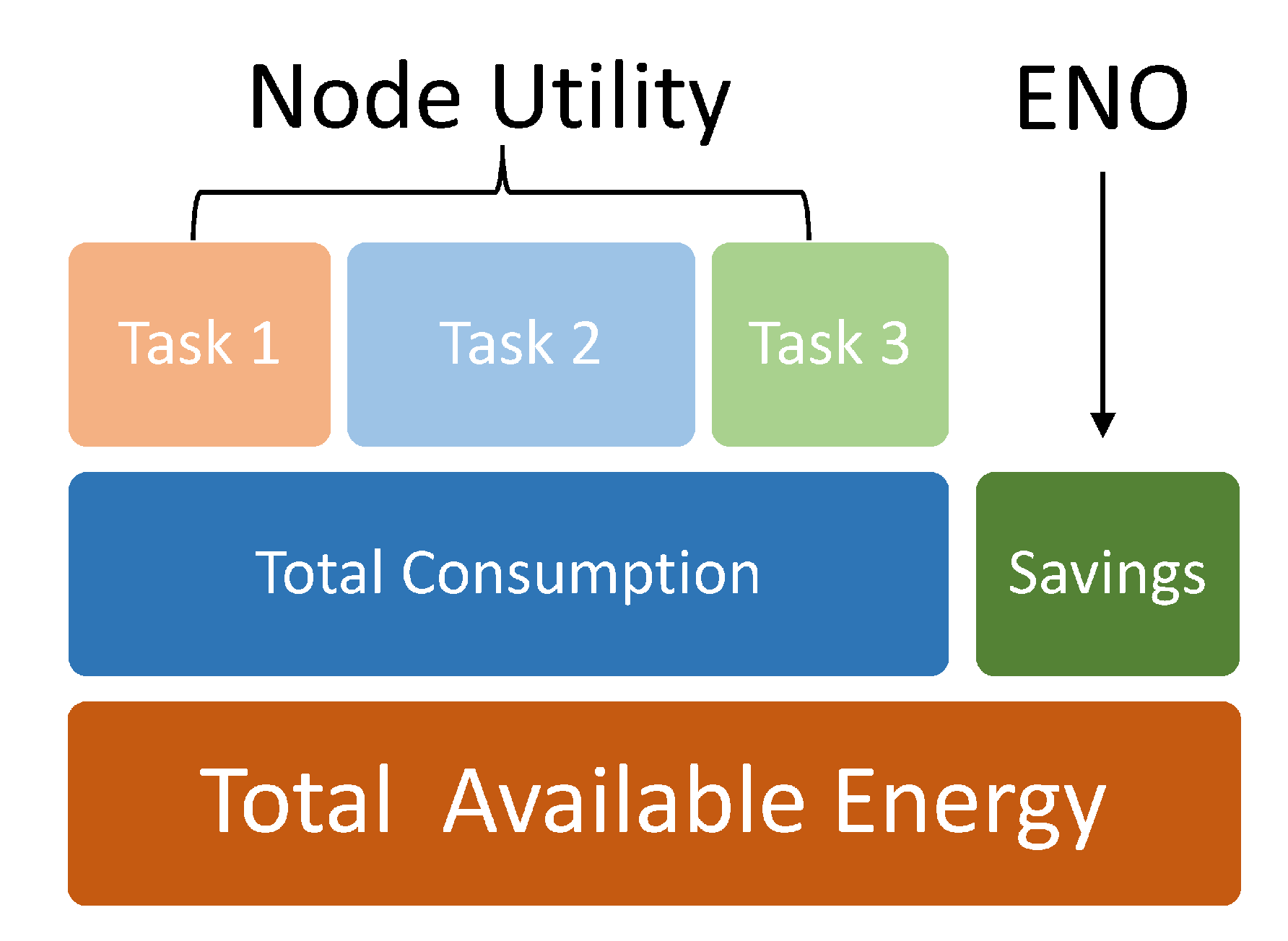
3. System Model
Energy Neutral Operation
4. Theoretical Background
4.1. Single-Objective RL
4.2. Multi-Objective RL
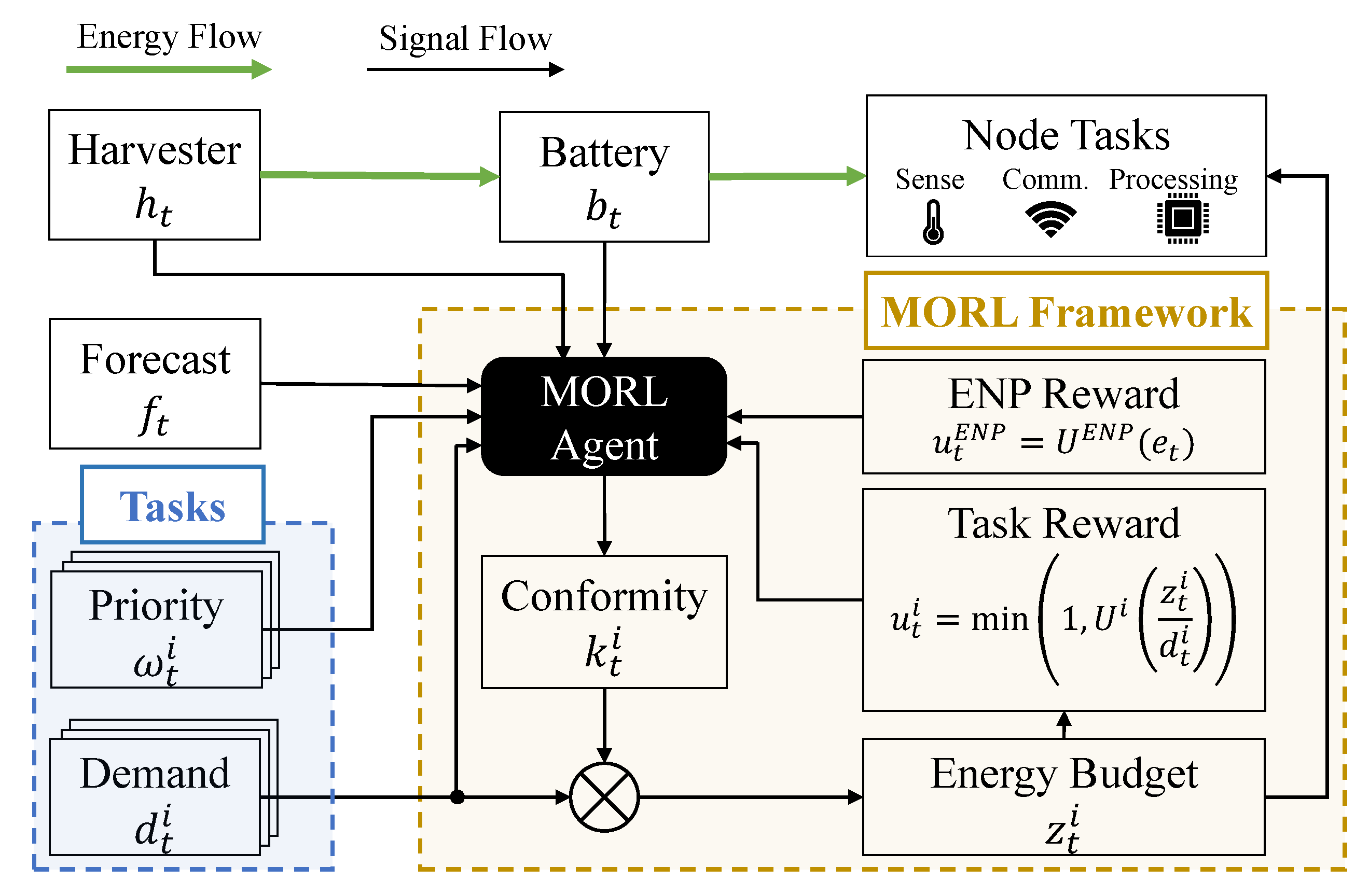
5. Proposed MORL Framework
5.1. MOMDP Formulation
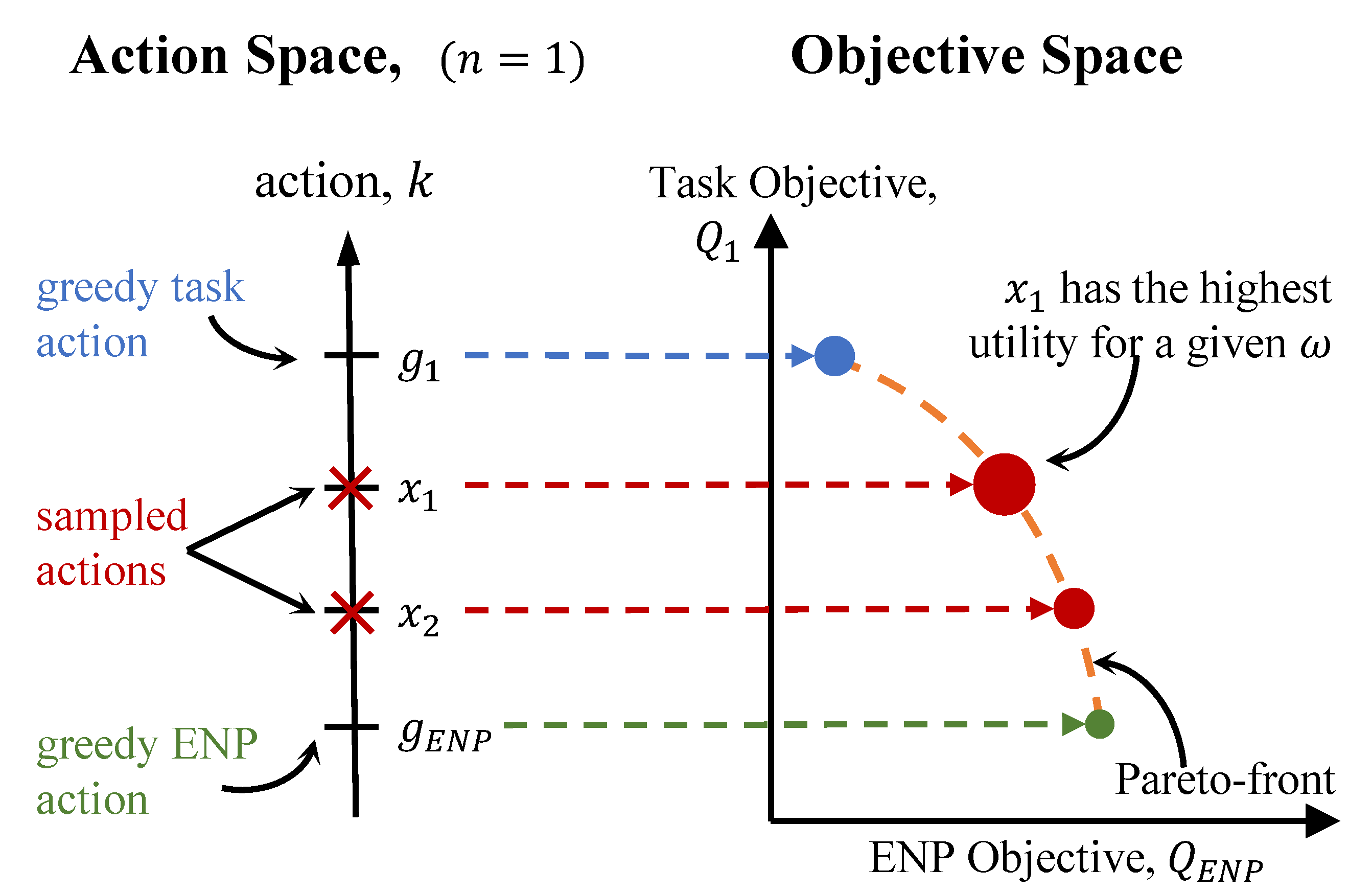
5.2. Runtime MORL
Minimizing Computation Costs
| Algorithm 1: Runtime MORL. |
 |
5.3. MORL with Off-Policy Corrections
| Algorithm 2: Off-policy MORL. |
 |
6. Evaluation Setup
6.1. Simulation Environment
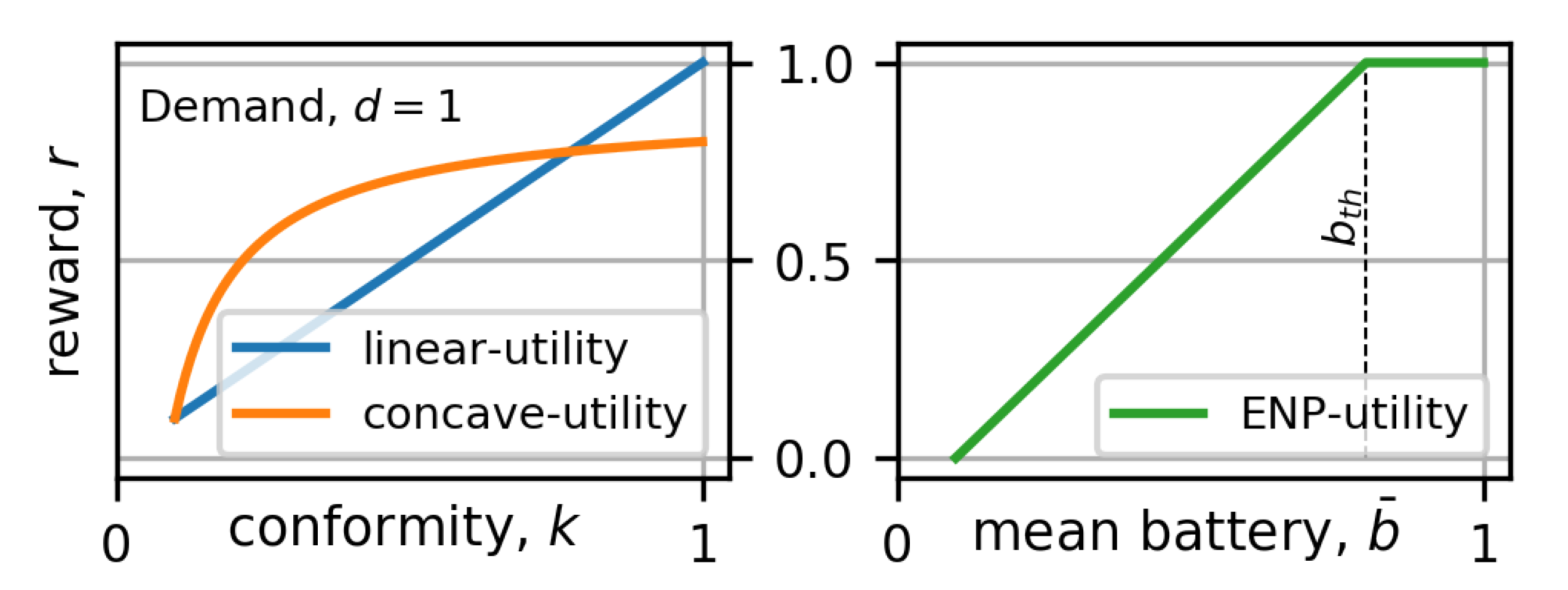
6.2. Utilities and Reward Functions
6.3. Metrics
7. Experimental Results
- Do RL agents trained using the MDP (state and action definitions) based on our proposed general MORL framework perform better than heuristic methods and traditional RL solutions when optimizing for a single objective? Specifically, do they extract higher utility at lower learning costs?
- How well does the proposed Algorithm 1 tradeoff between multiple objectives at runtime using greedy SORL agents? How does it compare to traditional scalarization methods that are optimized using non-causal information?
- Can the MORL agents trained with our proposed MOMDP learn policies to maximize the tradeoff between different objectives? What is the cost of training in such a scenario?
7.1. Single-Objective RL Policies Using Proposed MDP
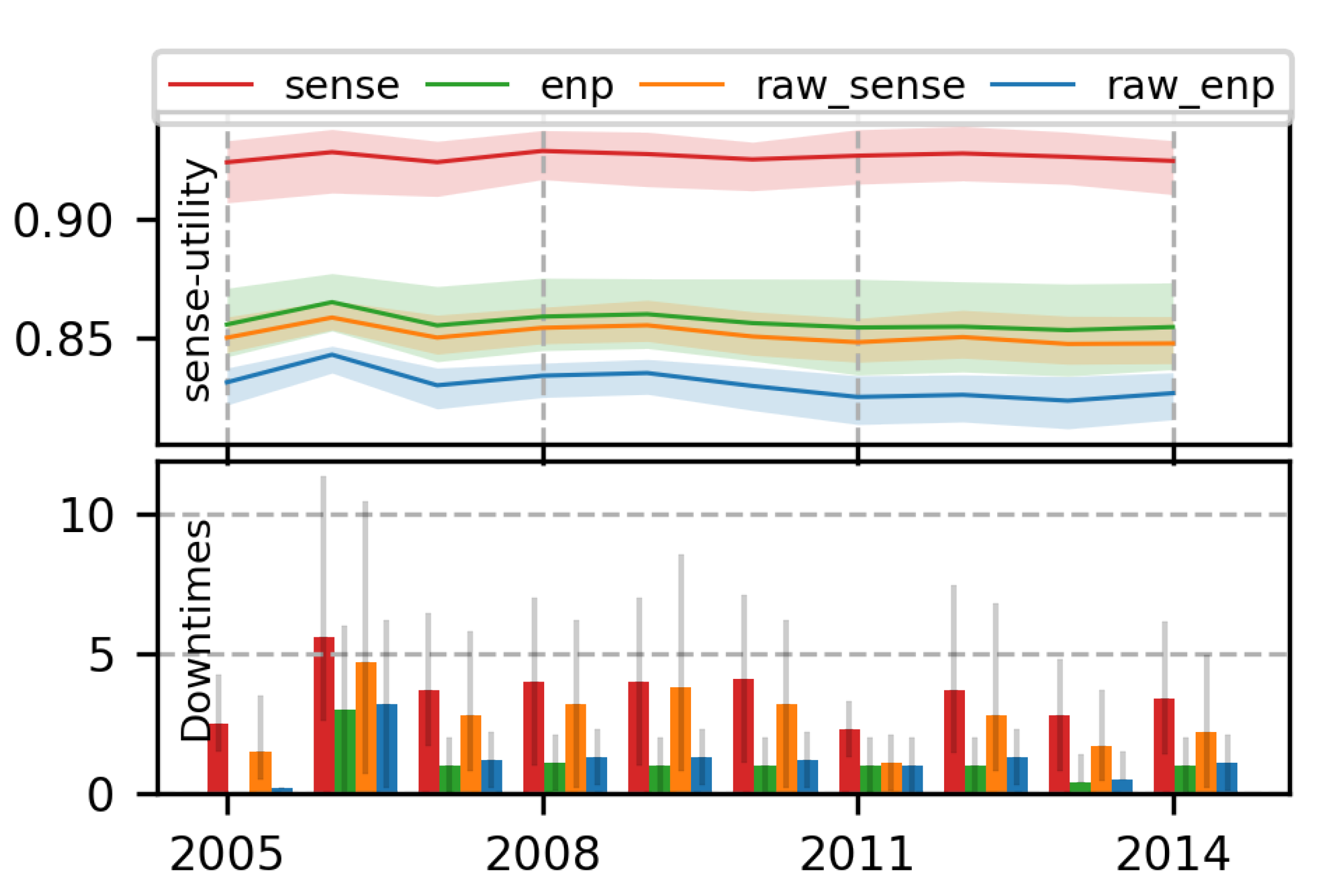
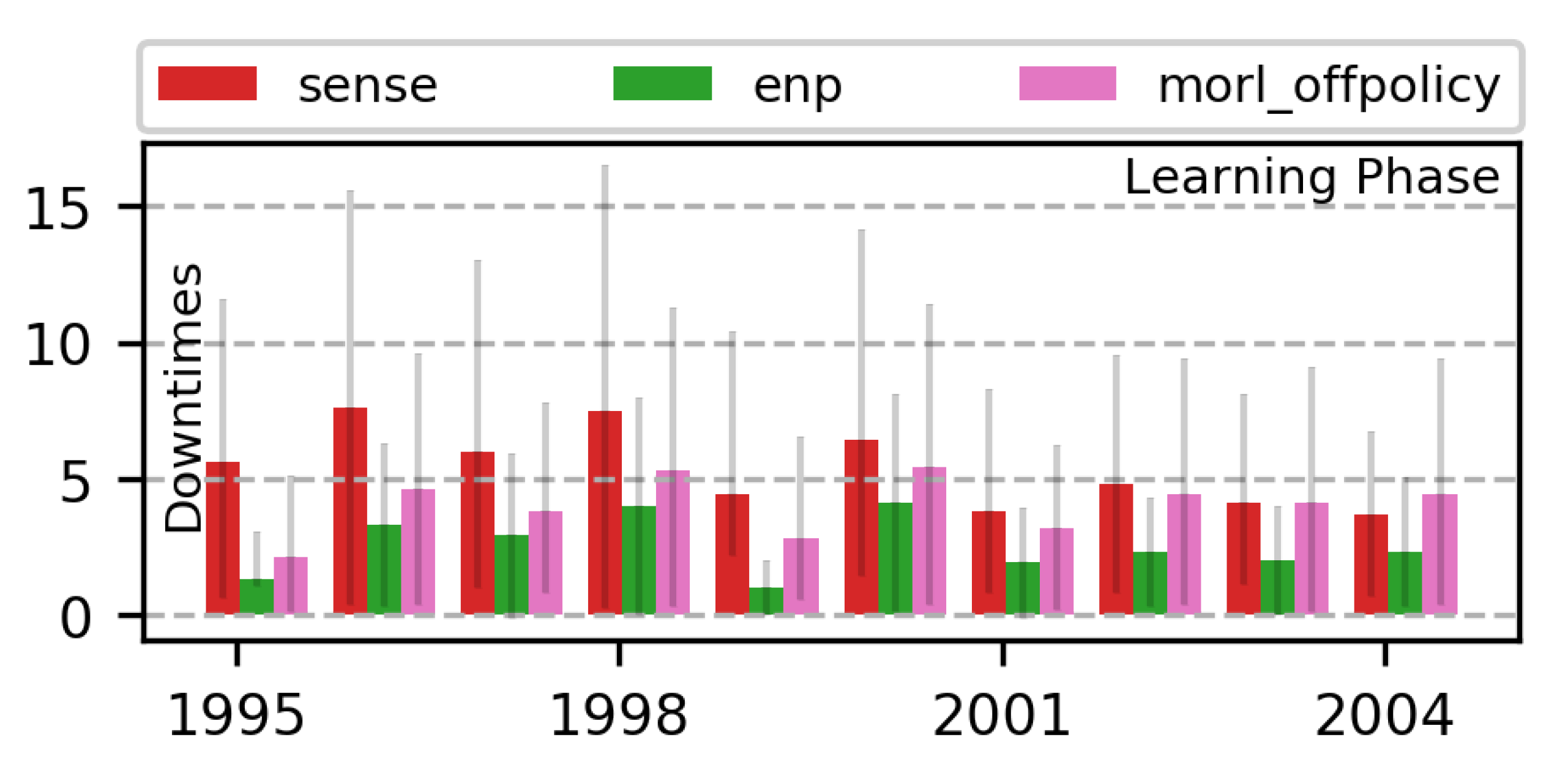
7.1.1. Comparison with Heuristic Methods
7.1.2. Adaptive Nature of RL Policies
7.1.3. Superiority of Proposed MDP Formulation
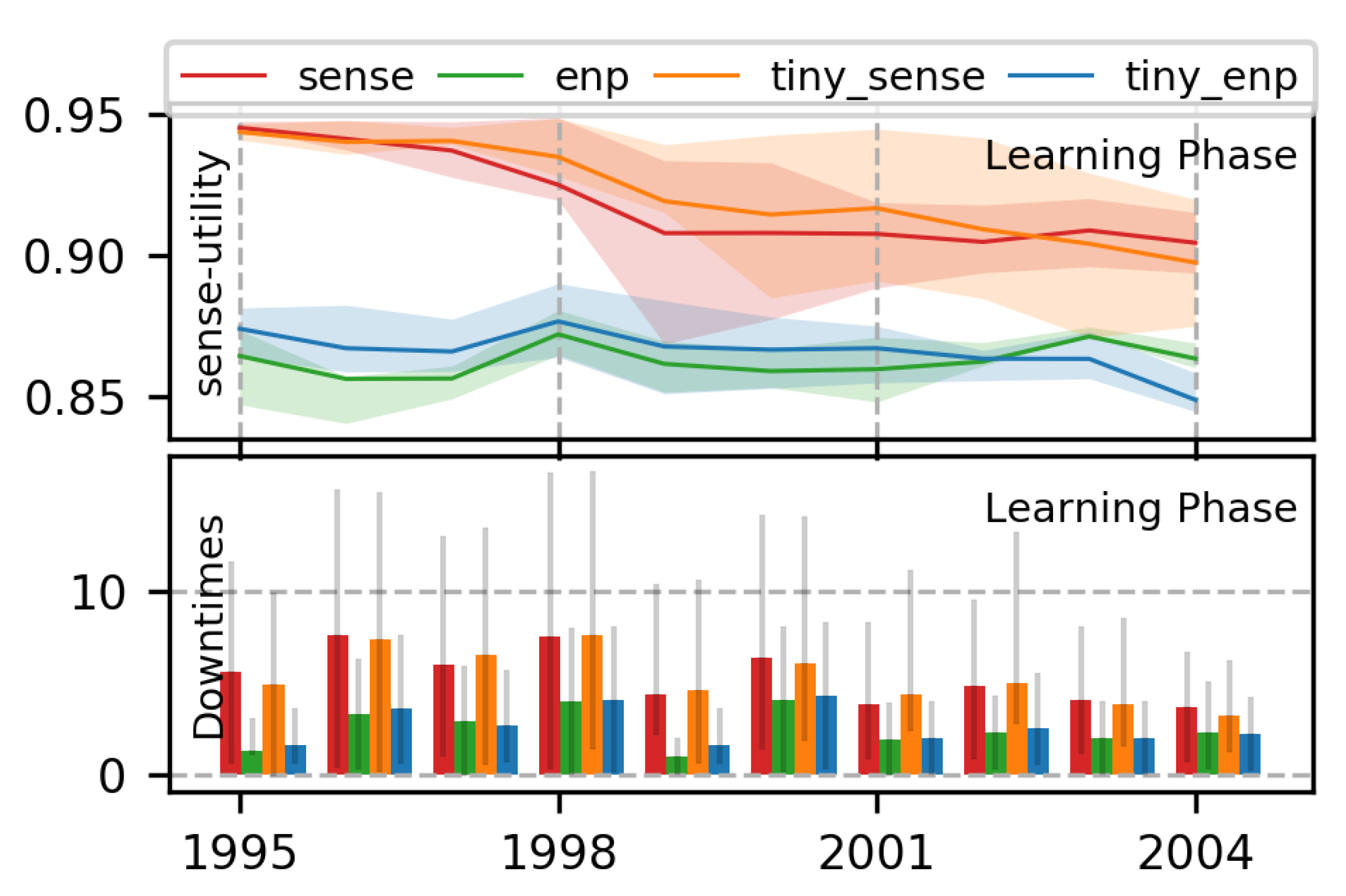
7.1.4. Effect of Size of NN
7.2. Runtime Tradeoffs
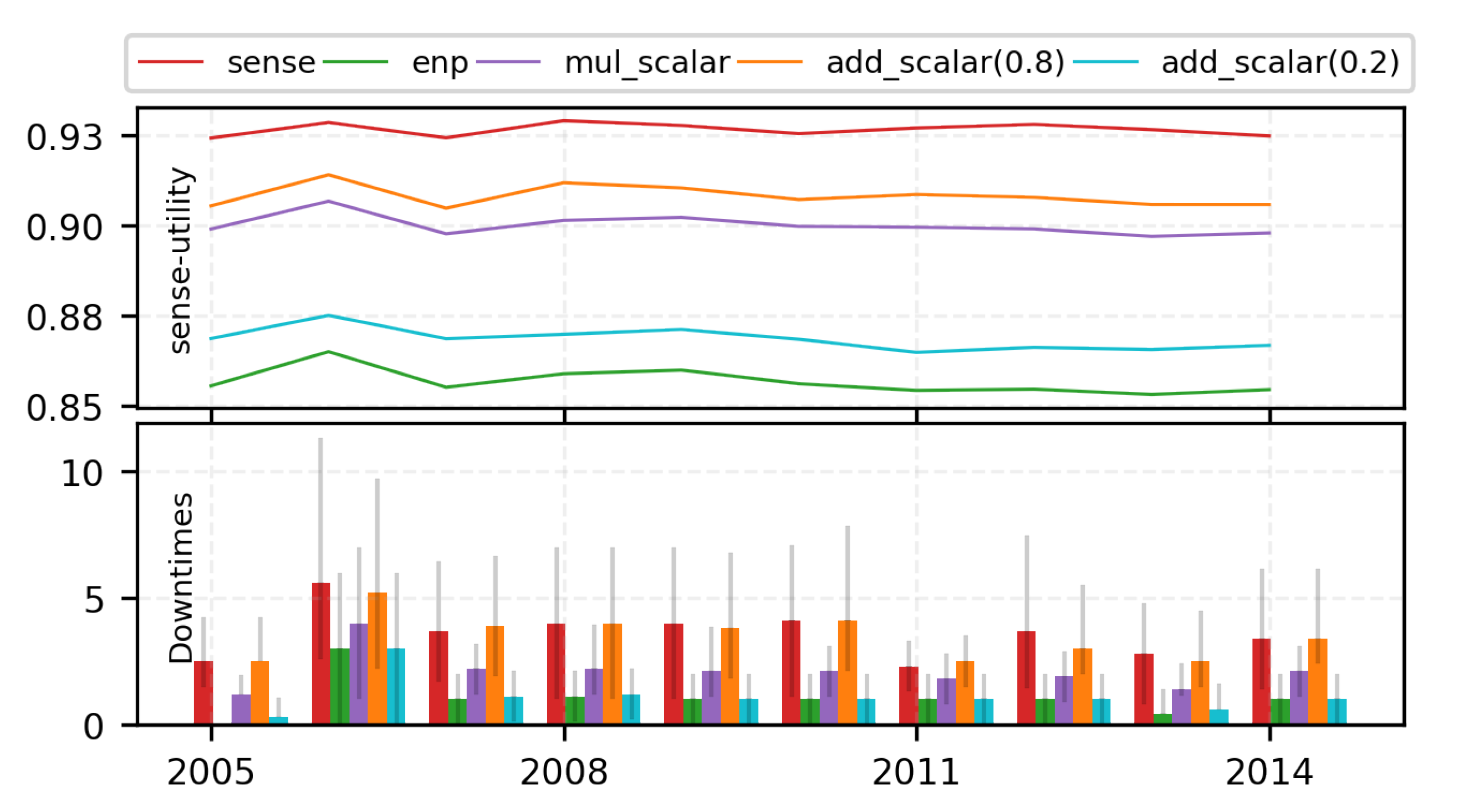
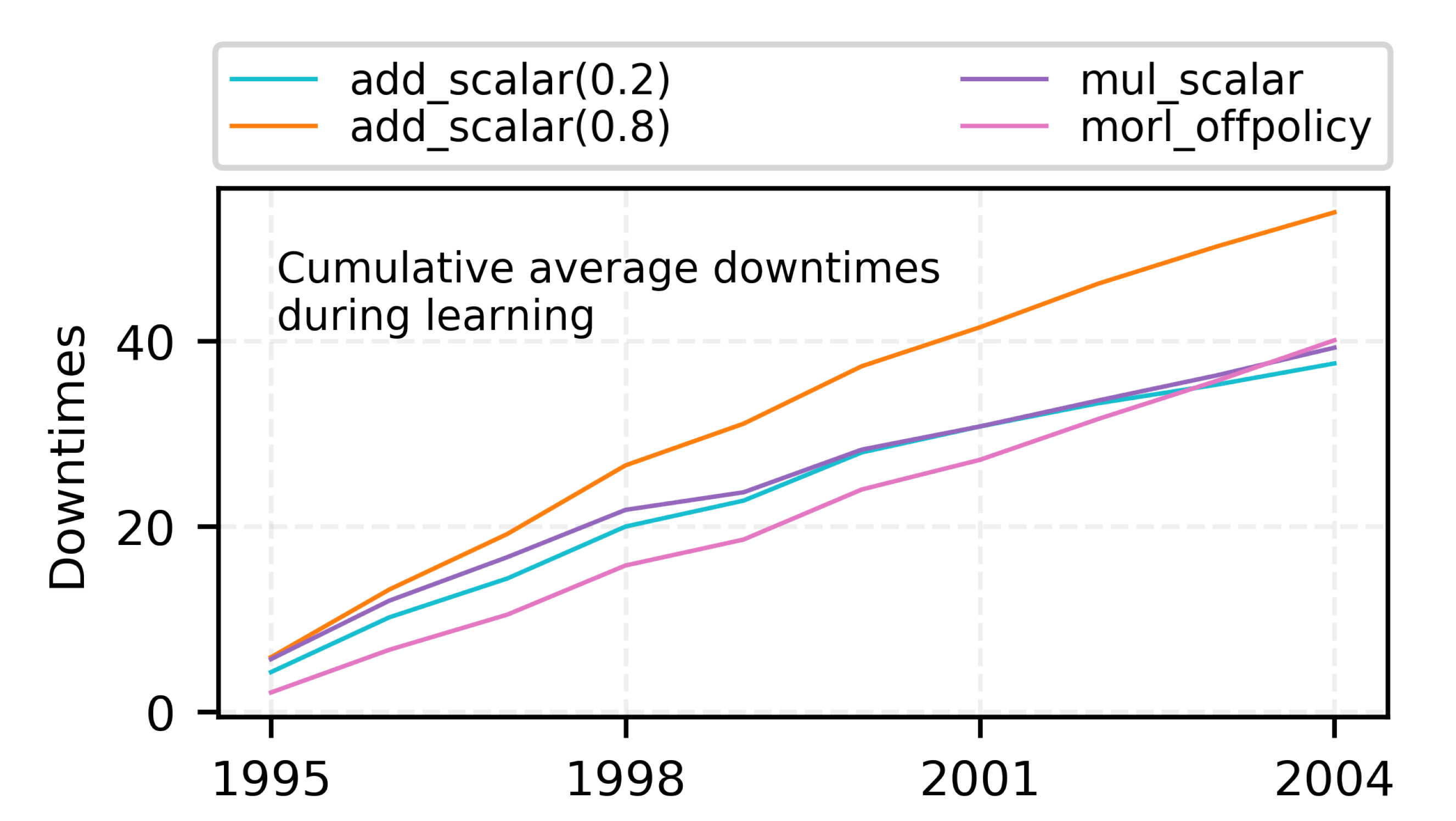
7.2.1. Limitations of Traditional Scalarization Methods
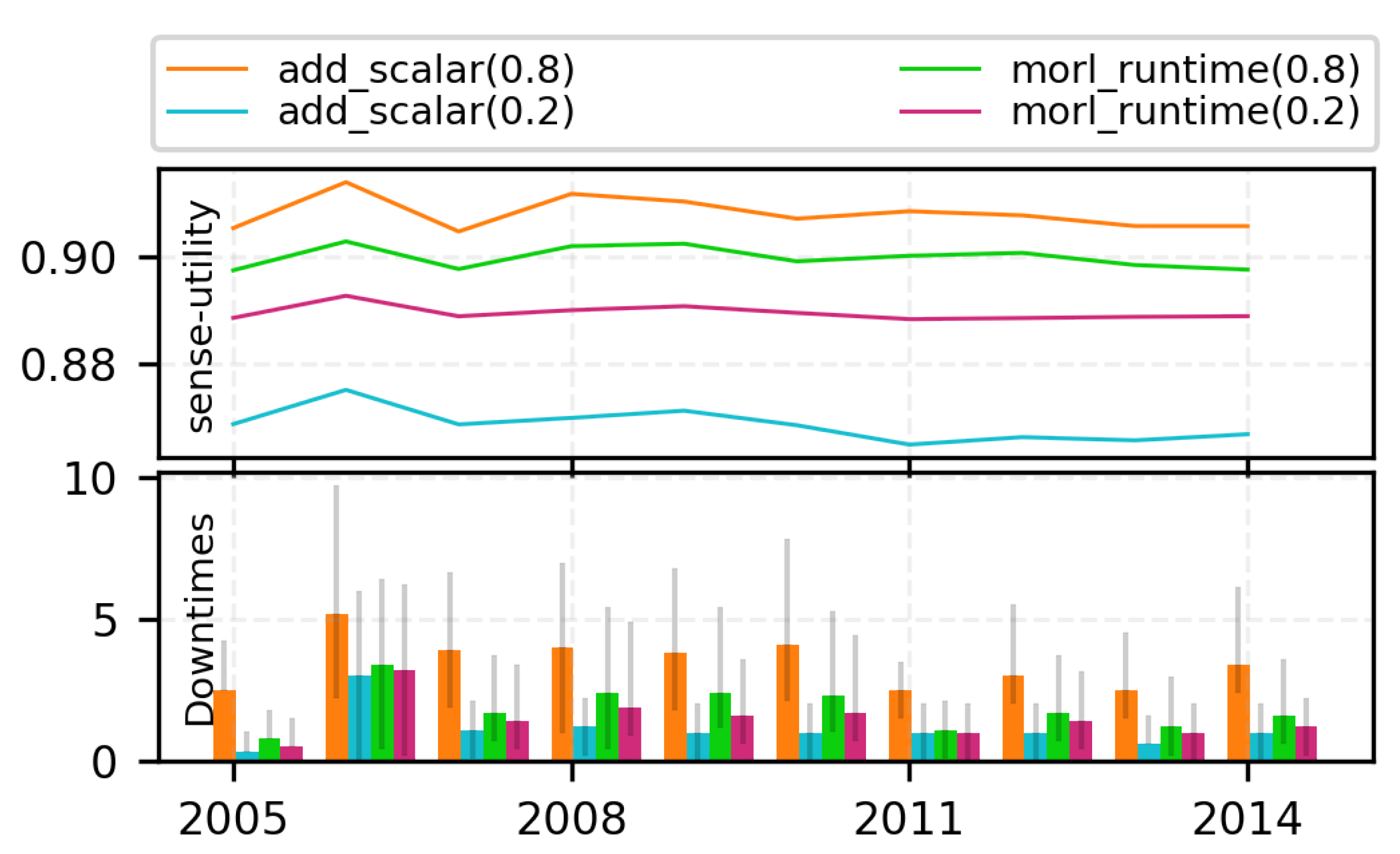
7.2.2. Trading off with Runtime MORL (Algorithm 1)
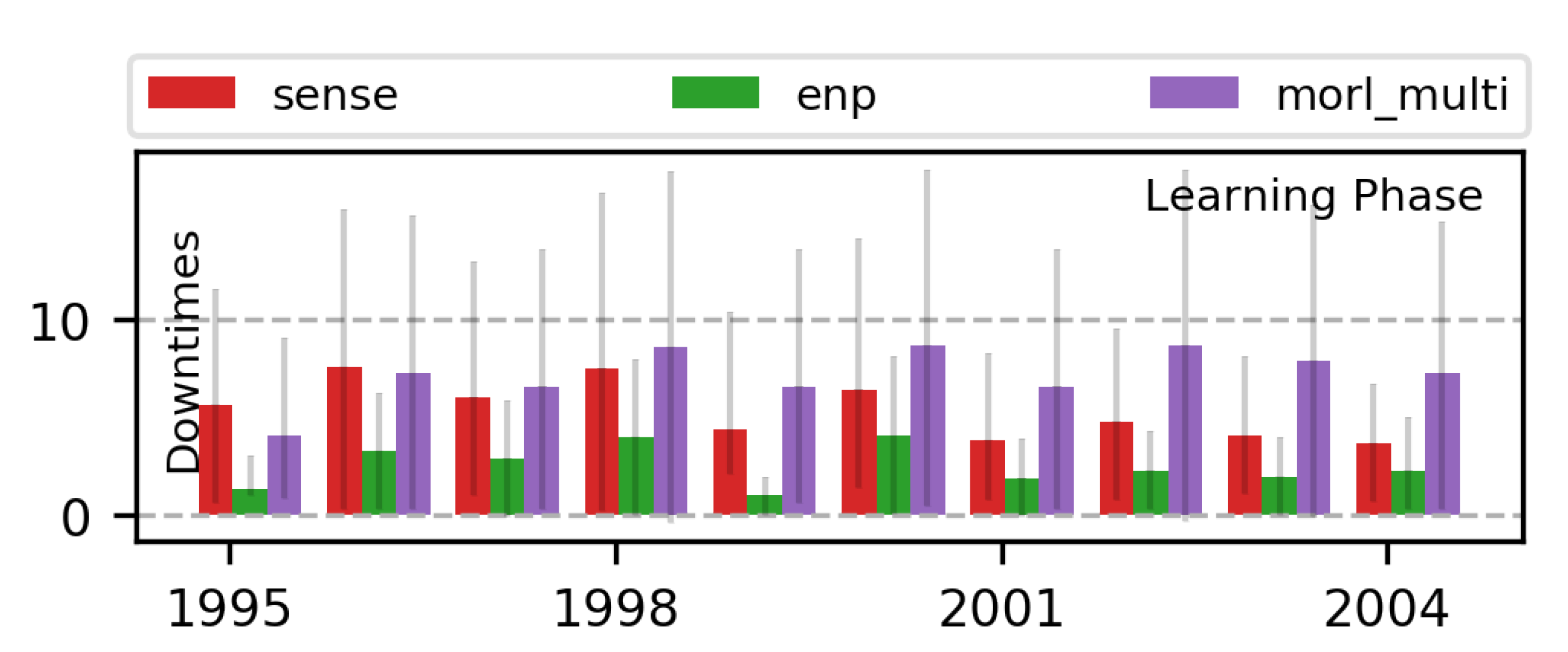
7.3. Learning Multi-Objective RL Policies for ENO
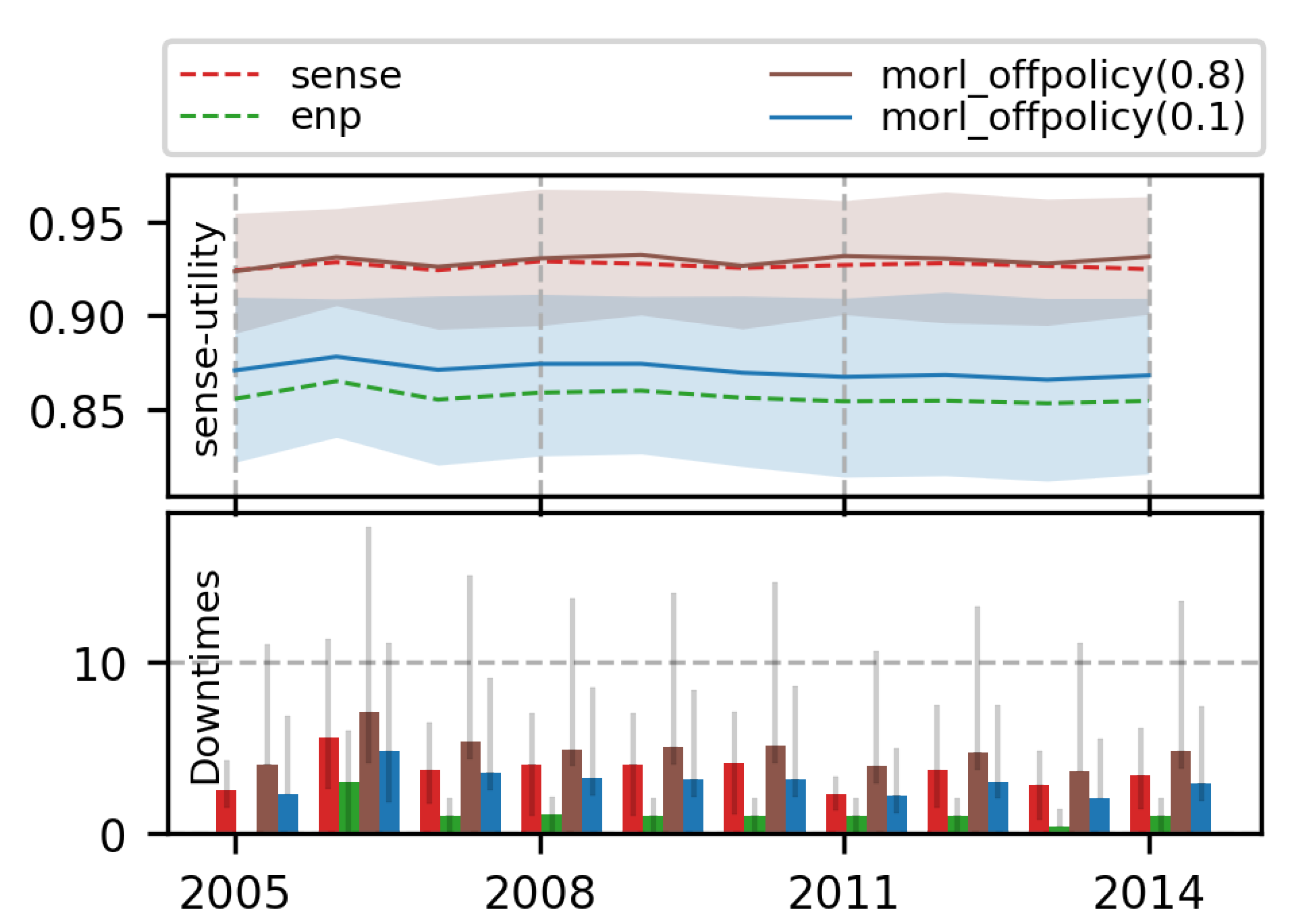
7.3.1. 2-Objective MOO with Off-Policy MORL (Algorithm 2)
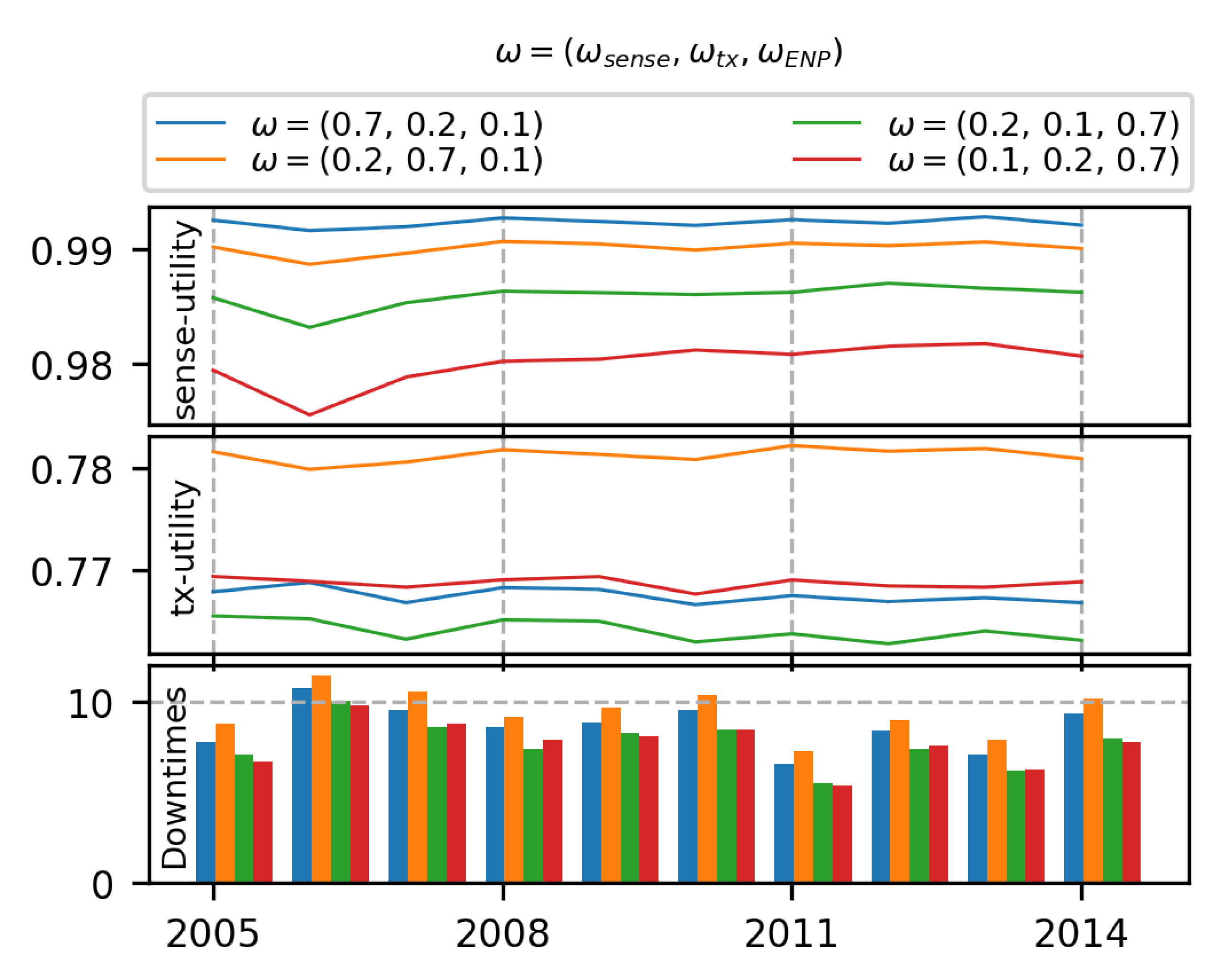
7.3.2. 3-Objective MOO with Off-Policy MORL (Algorithm 2)
8. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EHWSN | Energy Harvesting Wireless Sensor Nodes |
| IoT | Internet of Things |
| SoC | System-on-Chips |
| ENO | Energy Neutral Operation |
| ENP | Energy Neutral Performance |
| MDP | Markov Decision Process |
| RL | Reinforcement Learning |
| DL | Deep Learning |
| DRL | Deep Reinforcement Learning |
| MORL | Multi-Objective Reinforcement Learning |
| SORL | Single-Objective Reinforcement Learning |
| MOO | Multi-Objective Optimization |
| GA | Genetic Algorithms |
| JMA | Japan Meteorological Agency |
| WSN | Wireless Sensor Network |
| MC | Monte-Carlo |
| EA | Evolutionary Algorithms |
| PSO | Particle Swarm Optimization |
| QoS | Quality of Service |
References
- Ma, D.; Lan, G.; Hassan, M.; Hu, W.; Das, S.K. Sensing, Computing, and Communications for Energy Harvesting IoTs: A Survey. IEEE Commun. Surv. Tutor. 2019, 22, 1222–1250. [Google Scholar] [CrossRef]
- Nakamura, Y.; Arakawa, Y.; Kanehira, T.; Fujiwara, M.; Yasumoto, K. Senstick: Comprehensive sensing platform with an ultra tiny all-in-one sensor board for iot research. J. Sens. 2017, 2017, 6308302. [Google Scholar] [CrossRef]
- Vamplew, P.; Yearwood, J.; Dazeley, R.; Berry, A. On the limitations of scalarisation for multi-objective reinforcement learning of pareto fronts. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Auckland, New Zealand, 1–5 December 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 372–378. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Blasco, P.; Gunduz, D.; Dohler, M. A learning theoretic approach to energy harvesting communication system optimization. IEEE Trans. Wirel. Commun. 2013, 12, 1872–1882. [Google Scholar] [CrossRef]
- Ortiz, A.; Al-Shatri, H.; Li, X.; Weber, T.; Klein, A. Reinforcement learning for energy harvesting point-to-point communications. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar]
- Hsu, R.C.; Liu, C.T.; Wang, H.L. A reinforcement learning-based ToD provisioning dynamic power management for sustainable operation of energy harvesting wireless sensor node. IEEE Trans. Emerg. Top. Comput. 2014, 2, 181–191. [Google Scholar] [CrossRef]
- Shresthamali, S.; Kondo, M.; Nakamura, H. Power Management of Wireless Sensor Nodes with Coordinated Distributed Reinforcement Learning. In Proceedings of the 2019 IEEE 37th International Conference on Computer Design (ICCD), Abu Dhabi, United Arab Emirates, 17–20 November 2019; pp. 638–647. [Google Scholar]
- Shresthamali, S.; Kondo, M.; Nakamura, H. Adaptive power management in solar energy harvesting sensor node using reinforcement learning. ACM Trans. Embed. Comput. Syst. (TECS) 2017, 16, 181. [Google Scholar] [CrossRef]
- Fraternali, F.; Balaji, B.; Agarwal, Y.; Gupta, R.K. ACES–Automatic Configuration of Energy Harvesting Sensors with Reinforcement Learning. arXiv 2019, arXiv:1909.01968. [Google Scholar]
- Sawaguchi, S.; Christmann, J.F.; Lesecq, S. Highly adaptive linear actor-critic for lightweight energy-harvesting IoT applications. J. Low Power Electron. Appl. 2021, 11, 17. [Google Scholar] [CrossRef]
- Parisi, S.; Pirotta, M.; Smacchia, N.; Bascetta, L.; Restelli, M. Policy gradient approaches for multi-objective sequential decision making. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 2323–2330. [Google Scholar]
- Pirotta, M.; Parisi, S.; Restelli, M. Multi-objective reinforcement learning with continuous pareto frontier approximation. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Yang, R.; Sun, X.; Narasimhan, K. A generalized algorithm for multi-objective reinforcement learning and policy adaptation. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 14636–14647. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484. [Google Scholar] [CrossRef]
- Sudevalayam, S.; Kulkarni, P. Energy harvesting sensor nodes: Survey and implications. IEEE Commun. Surv. Tutor. 2011, 13, 443–461. [Google Scholar] [CrossRef]
- Kansal, A.; Hsu, J.; Zahedi, S.; Srivastava, M.B. Power management in energy harvesting sensor networks. ACM Trans. Embed. Comput. Syst. 2007, 6, 32. [Google Scholar] [CrossRef]
- Shresthamali, S.; Kondo, M.; Nakamura, H. Multi-objective Reinforcement Learning for Energy Harvesting Wireless Sensor Nodes. In Proceedings of the 2021 IEEE 14th International Symposium on Embedded Multicore/Many-core Systems-on-Chip (MCSoC), Singapore, 20–23 December 2021; pp. 98–105. [Google Scholar]
- Vigorito, C.M.; Ganesan, D.; Barto, A.G. Adaptive control of duty cycling in energy-harvesting wireless sensor networks. In Proceedings of the 2007 4th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, San Francisco, CA, USA, 18–21 June 2007; pp. 21–30. [Google Scholar]
- Sharma, V.; Mukherji, U.; Joseph, V.; Gupta, S. Optimal energy management policies for energy harvesting sensor nodes. IEEE Trans. Wirel. Commun. 2010, 9, 1326–1336. [Google Scholar] [CrossRef]
- Ozel, O.; Tutuncuoglu, K.; Yang, J.; Ulukus, S.; Yener, A. Transmission with energy harvesting nodes in fading wireless channels: Optimal policies. IEEE J. Sel. Areas Commun. 2011, 29, 1732–1743. [Google Scholar] [CrossRef]
- Peng, S.; Low, C. Prediction free energy neutral power management for energy harvesting wireless sensor nodes. Ad Hoc Netw. 2014, 13, 351–367. [Google Scholar] [CrossRef]
- Cionca, V.; McGibney, A.; Rea, S. MAllEC: Fast and Optimal Scheduling of Energy Consumption for Energy Harvesting Devices. IEEE Internet Things J. 2018, 5, 5132–5140. [Google Scholar] [CrossRef]
- Jia, R.; Zhang, J.; Liu, X.Y.; Liu, P.; Fu, L.; Wang, X. Optimal Rate Control for Energy-Harvesting Systems with Random Data and Energy Arrivals. ACM Trans. Sens. Netw. 2019, 15, 13. [Google Scholar] [CrossRef]
- Fu, A.; Modiano, E.; Tsitsiklis, J.N. Optimal transmission scheduling over a fading channel with energy and deadline constraints. IEEE Trans. Wirel. Commun. 2006, 5, 630–641. [Google Scholar] [CrossRef]
- Lei, L.; Kuang, Y.; Shen, X.S.; Yang, K.; Qiao, J.; Zhong, Z. Optimal reliability in energy harvesting industrial wireless sensor networks. IEEE Trans. Wirel. Commun. 2016, 15, 5399–5413. [Google Scholar] [CrossRef]
- Buchli, B.; Sutton, F.; Beutel, J.; Thiele, L. Dynamic power management for long-term energy neutral operation of solar energy harvesting systems. In Proceedings of the 12th ACM Conference on Embedded Network Sensor Systems, Memphis, TN, USA, 3–6 November 2014; pp. 31–45. [Google Scholar]
- Geissdoerfer, K.; Jurdak, R.; Kusy, B.; Zimmerling, M. Getting more out of energy-harvesting systems: Energy management under time-varying utility with PreAct. In Proceedings of the 18th International Conference on Information Processing in Sensor Networks, Montreal, QC, Canada, 16–18 April 2019; pp. 109–120. [Google Scholar]
- Mao, S.; Cheung, M.H.; Wong, V.W. Joint energy allocation for sensing and transmission in rechargeable wireless sensor networks. IEEE Trans. Veh. Technol. 2014, 63, 2862–2875. [Google Scholar] [CrossRef]
- GhasemAghaei, R.; Rahman, M.A.; Gueaieb, W.; El Saddik, A. Ant colony-based reinforcement learning algorithm for routing in wireless sensor networks. In Proceedings of the Instrumentation and Measurement Technology Conference Proceedings, IMTC 2007, Warsaw, Poland, 1–3 May 2007; pp. 1–6. [Google Scholar]
- Blasco, P.; Gündüz, D. Multi-access communications with energy harvesting: A multi-armed bandit model and the optimality of the myopic policy. IEEE J. Sel. Areas Commun. 2015, 33, 585–597. [Google Scholar] [CrossRef]
- Chan, W.H.R.; Zhang, P.; Nevat, I.; Nagarajan, S.G.; Valera, A.C.; Tan, H.X.; Gautam, N. Adaptive duty cycling in sensor networks with energy harvesting using continuous-time Markov chain and fluid models. IEEE J. Sel. Areas Commun. 2015, 33, 2687–2700. [Google Scholar] [CrossRef]
- Xiao, Y.; Han, Z.; Niyato, D.; Yuen, C. Bayesian reinforcement learning for energy harvesting communication systems with uncertainty. In Proceedings of the Communications (ICC), 2015 IEEE International Conference on, London, UK, 8–12 June 2015; pp. 5398–5403. [Google Scholar]
- Mihaylov, M.; Tuyls, K.; Nowé, A. Decentralized learning in wireless sensor networks. In Proceedings of the International Workshop on Adaptive and Learning Agents, Budapest, Hungary, 12 May 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 60–73. [Google Scholar]
- Hsu, J.; Zahedi, S.; Kansal, A.; Srivastava, M.; Raghunathan, V. Adaptive duty cycling for energy harvesting systems. In Proceedings of the 2006 ISLPED, Bavaria, Germany, 4–6 October 2006; pp. 180–185. [Google Scholar]
- OpenAI. Faulty Reward Functions in the Wild. 2020. Available online: https://openai.com/blog/faulty-reward-functions/ (accessed on 4 July 2020).
- DeepMind. Designing Agent Incentives to Avoid Reward Tampering. 2020. Available online: https://deepmindsafetyresearch.medium.com/designing-agent-incentives-to-avoid-reward-tampering-4380c1bb6cd (accessed on 4 July 2020).
- Everitt, T.; Hutter, M. Reward Tampering Problems and Solutions in Reinforcement Learning: A Causal Influence Diagram Perspective. arXiv 2019, arXiv:1908.04734. [Google Scholar] [CrossRef]
- Xu, Y.; Lee, H.G.; Tan, Y.; Wu, Y.; Chen, X.; Liang, L.; Qiao, L.; Liu, D. Tumbler: Energy Efficient Task Scheduling for Dual-Channel Solar-Powered Sensor Nodes. In Proceedings of the 56th Annual Design Automation Conference 2019 (DAC’19), Las Vegas, NV, USA, 2–6 June 2019; ACM: New York, NY, USA, 2019; pp. 172:1–172:6. [Google Scholar] [CrossRef]
- Gai, K.; Qiu, M. Optimal resource allocation using reinforcement learning for IoT content-centric services. Appl. Soft Comput. 2018, 70, 12–21. [Google Scholar] [CrossRef]
- Xu, Y.; Lee, H.G.; Chen, X.; Peng, B.; Liu, D.; Liang, L. Puppet: Energy Efficient Task Mapping For Storage-Less and Converter-Less Solar-Powered Non-Volatile Sensor Nodes. In Proceedings of the 2018 IEEE 36th International Conference on Computer Design (ICCD), Orlando, FL, USA, 7–10 October 2018; pp. 226–233. [Google Scholar]
- Dias, G.M.; Nurchis, M.; Bellalta, B. Adapting sampling interval of sensor networks using on-line reinforcement learning. In Proceedings of the 2016 IEEE 3rd World Forum on Internet of Things (WF-IoT), Reston, VA, USA, 12–14 December 2016; pp. 460–465. [Google Scholar]
- Murad, A.; Kraemer, F.A.; Bach, K.; Taylor, G. Autonomous Management of Energy-Harvesting IoT Nodes Using Deep Reinforcement Learning. arXiv 2019, arXiv:1905.04181. [Google Scholar]
- Ortiz Jimenez, A.P. Optimization and Learning Approaches for Energy Harvesting Wireless Communication Systems. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2019. [Google Scholar]
- Qiu, C.; Hu, Y.; Chen, Y.; Zeng, B. Deep deterministic policy gradient (DDPG)-based energy harvesting wireless communications. IEEE Internet Things J. 2019, 6, 8577–8588. [Google Scholar] [CrossRef]
- Kim, H.; Shin, W.; Yang, H.; Lee, N.; Lee, J. Rate Maximization with Reinforcement Learning for Time-Varying Energy Harvesting Broadcast Channels. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Big Island, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Van Huynh, N.; Hoang, D.T.; Nguyen, D.N.; Dutkiewicz, E.; Niyato, D.; Wang, P. Optimal and Low-Complexity Dynamic Spectrum Access for RF-Powered Ambient Backscatter System with Online Reinforcement Learning. IEEE Trans. Commun. 2019, 67, 5736–5752. [Google Scholar] [CrossRef]
- Long, J.; Büyüköztürk, O. Collaborative duty cycling strategies in energy harvesting sensor networks. Comput. Aided Civ. Infrastruct. Eng. 2020, 35, 534–548. [Google Scholar] [CrossRef]
- Aoudia, F.A.; Gautier, M.; Berder, O. RLMan: An energy manager based on reinforcement learning for energy harvesting wireless sensor networks. IEEE Trans. Green Commun. Netw. 2018, 2, 408–417. [Google Scholar] [CrossRef]
- Ferreira, P.V.R.; Paffenroth, R.; Wyglinski, A.M.; Hackett, T.M.; Bilén, S.G.; Reinhart, R.C.; Mortensen, D.J. Multiobjective reinforcement learning for cognitive satellite communications using deep neural network ensembles. IEEE J. Sel. Areas Commun. 2018, 36, 1030–1041. [Google Scholar] [CrossRef]
- Rioual, Y.; Le Moullec, Y.; Laurent, J.; Khan, M.I.; Diguet, J.P. Reward Function Evaluation in a Reinforcement Learning Approach for Energy Management. In Proceedings of the 2018 16th Biennial Baltic Electronics Conference (BEC), Tallinn, Estonia, 8–10 October 2018; pp. 1–4. [Google Scholar]
- Liu, C.; Xu, X.; Hu, D. Multiobjective reinforcement learning: A comprehensive overview. IEEE Trans. Syst. Man, Cybern. Syst. 2014, 45, 385–398. [Google Scholar]
- Zeng, F.; Zong, Q.; Sun, Z.; Dou, L. Self-adaptive multi-objective optimization method design based on agent reinforcement learning for elevator group control systems. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 6–9 July 2010; pp. 2577–2582. [Google Scholar]
- Ngai, D.C.K.; Yung, N.H.C. A multiple-goal reinforcement learning method for complex vehicle overtaking maneuvers. IEEE Trans. Intell. Transp. Syst. 2011, 12, 509–522. [Google Scholar] [CrossRef]
- Moffaert, K.V.; Nowé, A. Multi-Objective Reinforcement Learning using Sets of Pareto Dominating Policies. J. Mach. Learn. Res. 2014, 15, 3663–3692. [Google Scholar]
- Shelton, C.R. Importance Sampling for Reinforcement Learning with Multiple Objectives. Ph.D. Thesis, MIT, Cambridge, MA, USA, 2001. [Google Scholar]
- Li, K.; Zhang, T.; Wang, R. Deep reinforcement learning for multiobjective optimization. IEEE Trans. Cybern. 2020, 51, 3103–3114. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Yang, Z.; Merrick, K.E.; Abbass, H.A.; Jin, L. Multi-Task Deep Reinforcement Learning for Continuous Action Control. In Proceedings of the IJCAI, Melbourne, Australia, 19–25 August 2017; pp. 3301–3307. [Google Scholar]
- Li, C.; Czarnecki, K. Urban Driving with Multi-Objective Deep Reinforcement Learning. arXiv 2019, arXiv:1811.08586. [Google Scholar]
- Sharma, M.K.; Zappone, A.; Assaad, M.; Debbah, M.; Vassilaras, S. Distributed power control for large energy harvesting networks: A multi-agent deep reinforcement learning approach. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 1140–1154. [Google Scholar] [CrossRef]
- Ortiz, A.; Al-Shatri, H.; Weber, T.; Klein, A. Multi-Agent Reinforcement Learning for Energy Harvesting Two-Hop Communications with a Partially Observable State. arXiv 2017, arXiv:1702.06185. [Google Scholar] [CrossRef]
- Jia, J.; Chen, J.; Chang, G.; Tan, Z. Energy efficient coverage control in wireless sensor networks based on multi-objective genetic algorithm. Comput. Math. Appl. 2009, 57, 1756–1766. [Google Scholar] [CrossRef]
- Le Berre, M.; Hnaien, F.; Snoussi, H. Multi-objective optimization in wireless sensors networks. In Proceedings of the ICM 2011 Proceeding, Istanbul, Turkey, 13–15 April 2011; pp. 1–4. [Google Scholar]
- Marks, M. A survey of multi-objective deployment in wireless sensor networks. J. Telecommun. Inf. Technol. 2010, 3, 36–41. [Google Scholar]
- Fei, Z.; Li, B.; Yang, S.; Xing, C.; Chen, H.; Hanzo, L. A survey of multi-objective optimization in wireless sensor networks: Metrics, algorithms, and open problems. IEEE Commun. Surv. Tutor. 2016, 19, 550–586. [Google Scholar] [CrossRef]
- Iqbal, M.; Naeem, M.; Anpalagan, A.; Ahmed, A.; Azam, M. Wireless sensor network optimization: Multi-objective paradigm. Sensors 2015, 15, 17572–17620. [Google Scholar] [CrossRef]
- Konstantinidis, A.; Yang, K.; Zhang, Q. An evolutionary algorithm to a multi-objective deployment and power assignment problem in wireless sensor networks. In Proceedings of the IEEE GLOBECOM 2008—2008 IEEE Global Telecommunications Conference, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–6. [Google Scholar]
- Ahmed, M.M.; Houssein, E.H.; Hassanien, A.E.; Taha, A.; Hassanien, E. Maximizing lifetime of large-scale wireless sensor networks using multi-objective whale optimization algorithm. Telecommun. Syst. 2019, 72, 243–259. [Google Scholar] [CrossRef]
- Jia, J.; Chen, J.; Chang, G.; Wen, Y.; Song, J. Multi-objective optimization for coverage control in wireless sensor network with adjustable sensing radius. Comput. Math. Appl. 2009, 57, 1767–1775. [Google Scholar] [CrossRef]
- Giardino, M.; Schwyn, D.; Ferri, B.; Ferri, A. Low-Overhead Reinforcement Learning-Based Power Management Using 2QoSM. J. Low Power Electron. Appl. 2022, 12, 29. [Google Scholar] [CrossRef]
- Japan Meteorological Agency. Japan Meteorological Agency. 2019. Available online: https://www.jma.go.jp/jma/menu/menureport.html (accessed on 6 July 2019).
- Libelium. Waspmote-The Sensor Platform to Develop IoT Projects. Available online: https://www.libelium.com/iot-products/waspmote/ (accessed on 22 January 2021).
- Fujimoto, S.; Meger, D.; Precup, D. Off-policy deep reinforcement learning without exploration. In Proceedings of the International Conference on Machine Learning. PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 2052–2062. [Google Scholar]
- Kumar, A.; Fu, J.; Tucker, G.; Levine, S. Stabilizing off-policy q-learning via bootstrapping error reduction. arXiv 2019, arXiv:1906.00949. [Google Scholar]
- Lin, J.; Chen, W.M.; Lin, Y.; Cohn, J.; Gan, C.; Han, S. Mcunet: Tiny deep learning on iot devices. arXiv 2020, arXiv:2007.10319. [Google Scholar]
- Restuccia, F.; Melodia, T. DeepWiERL: Bringing Deep Reinforcement Learning to the Internet of Self-Adaptive Things. In Proceedings of the IEEE INFOCOM 2020—IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; pp. 844–853. [Google Scholar]

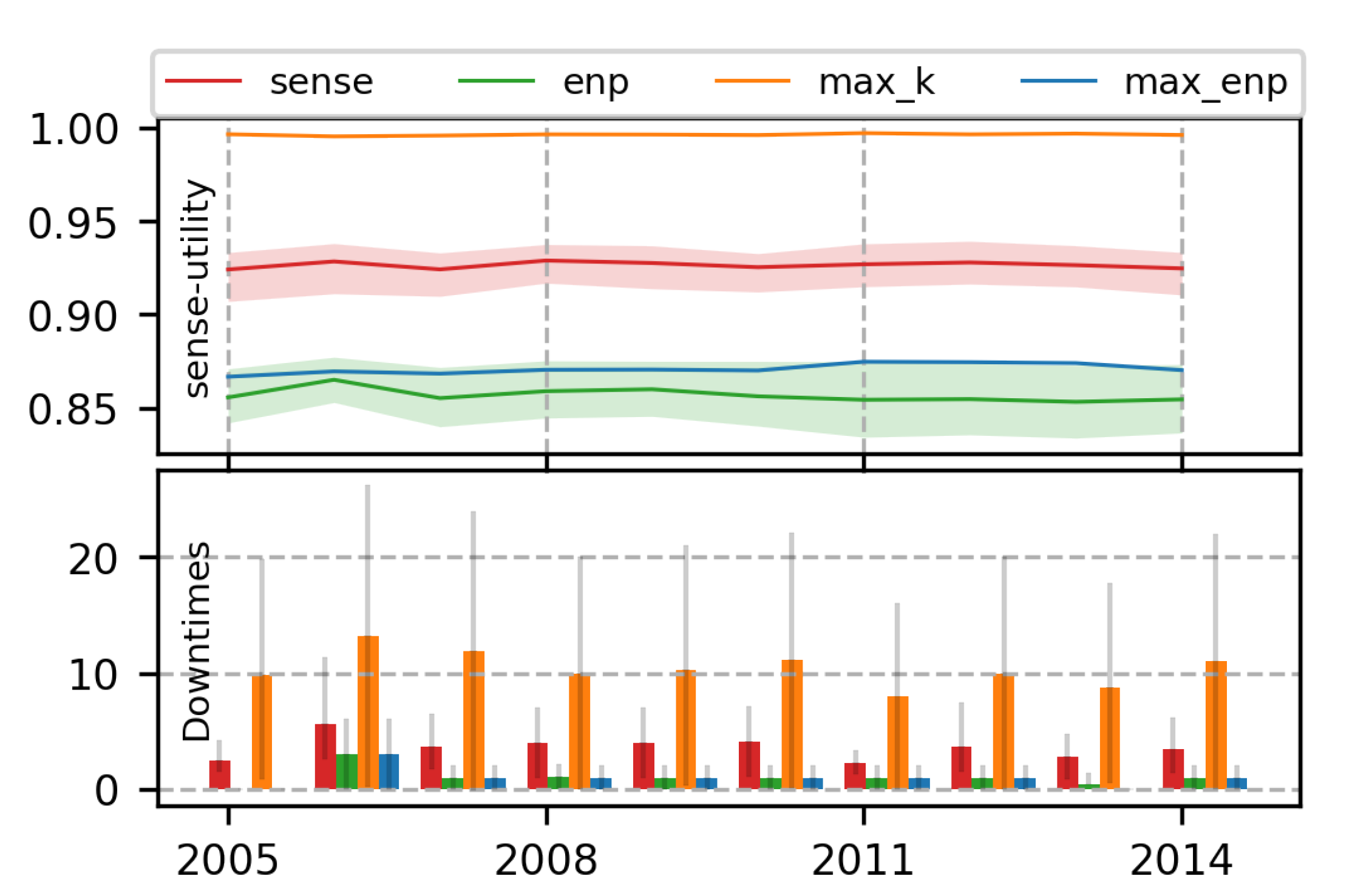
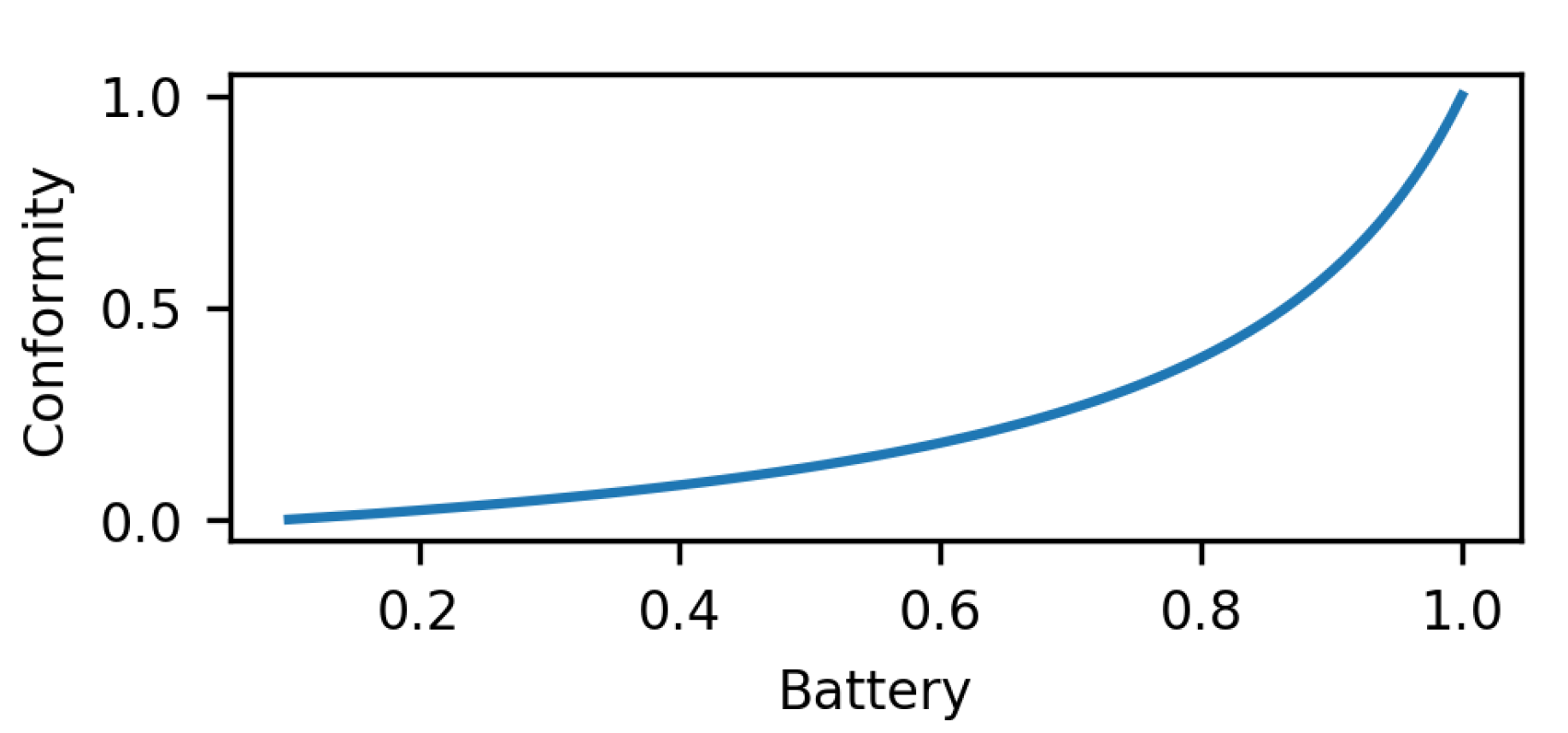
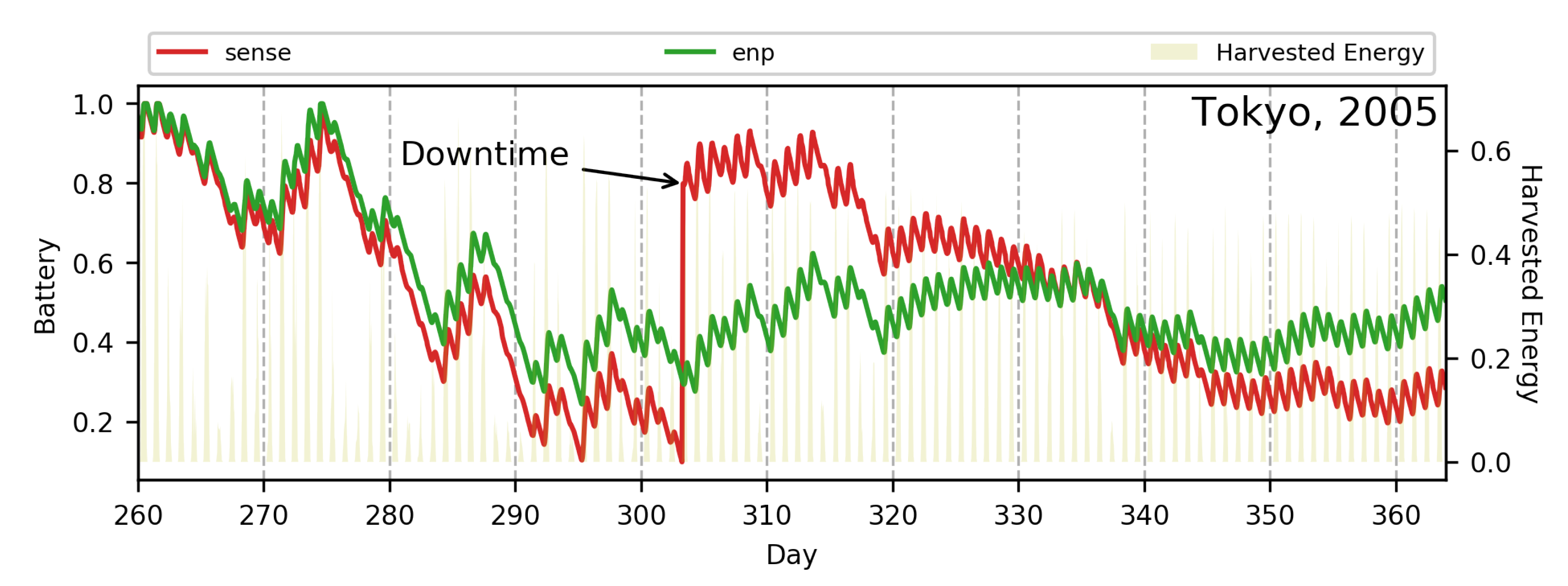
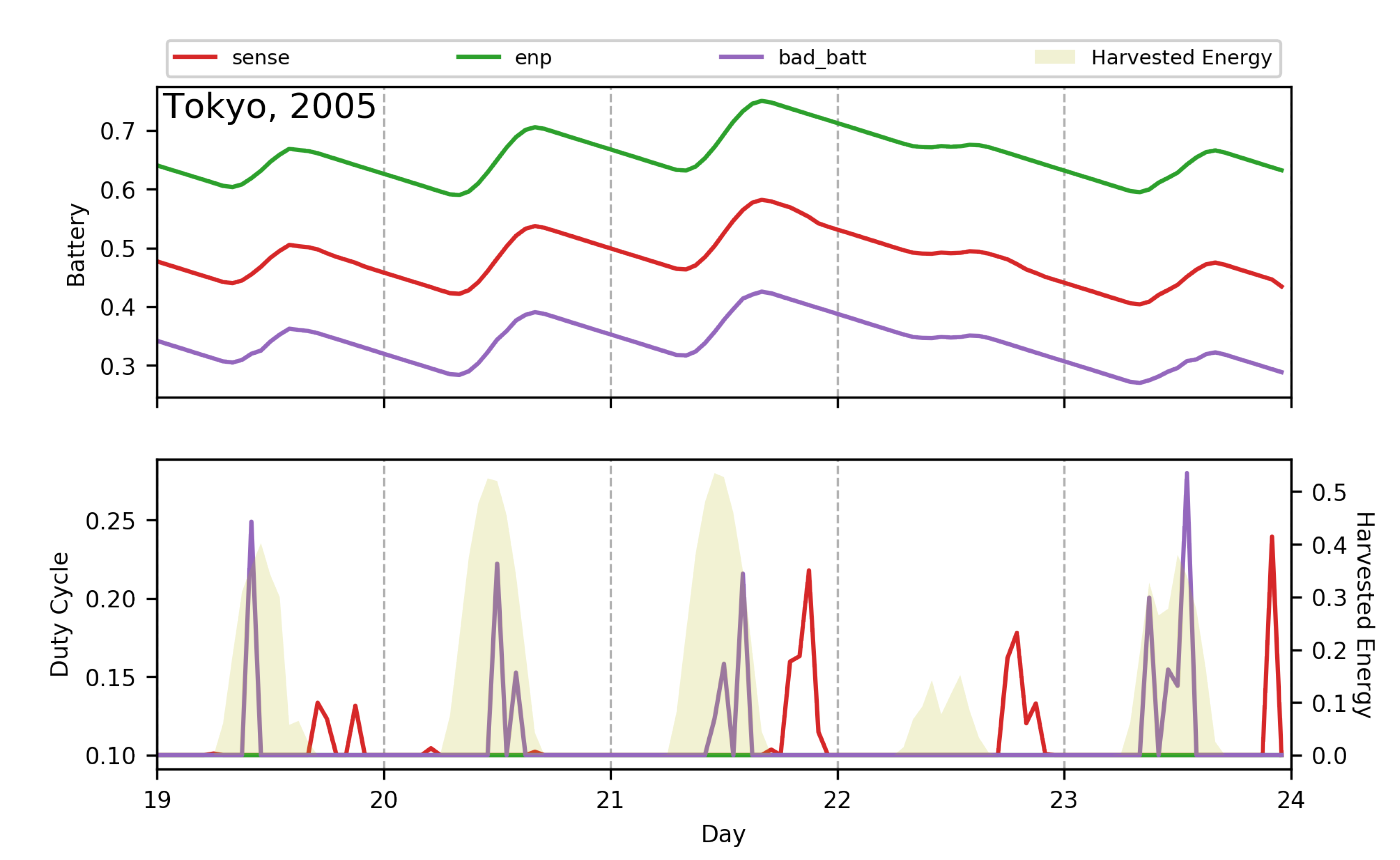
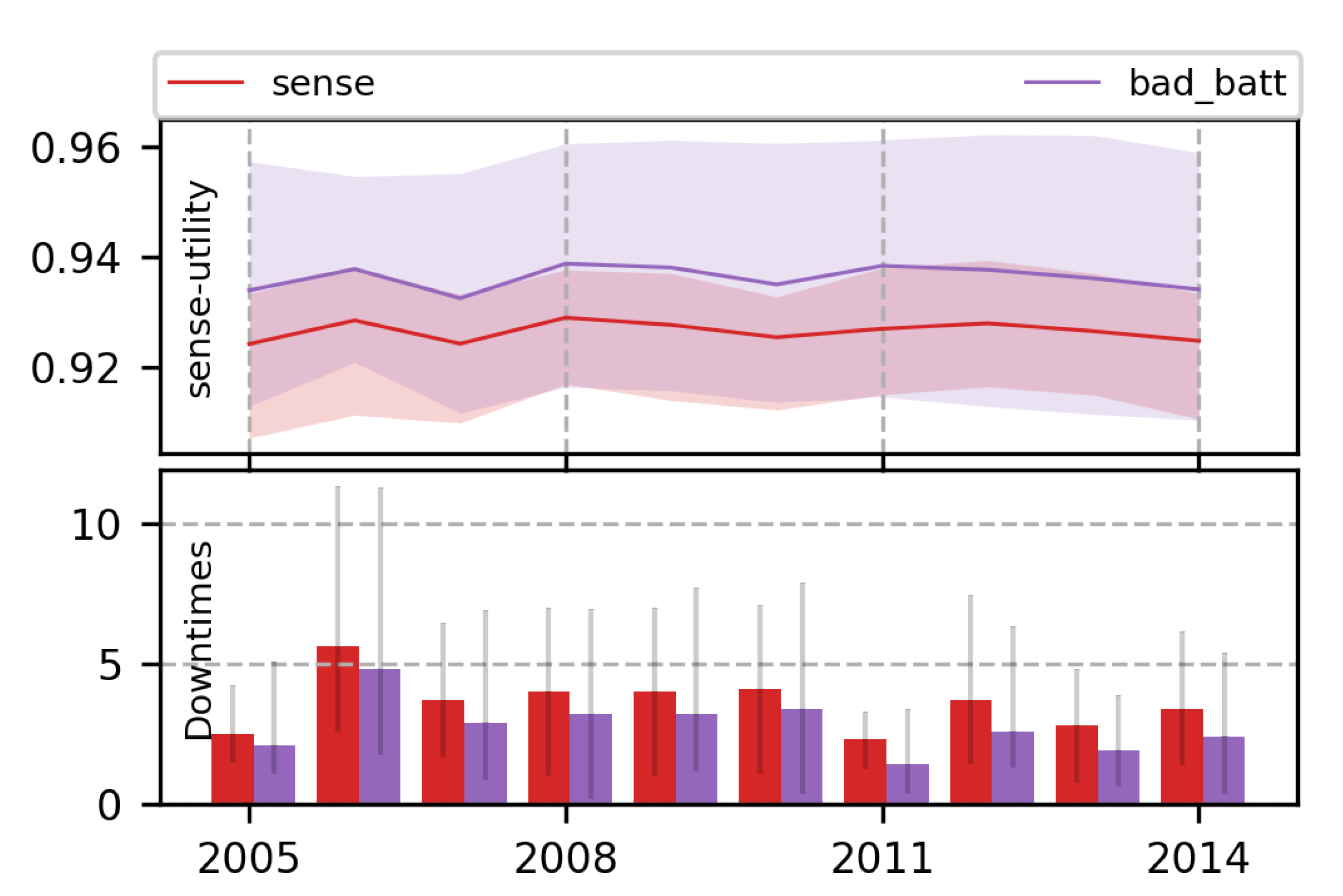
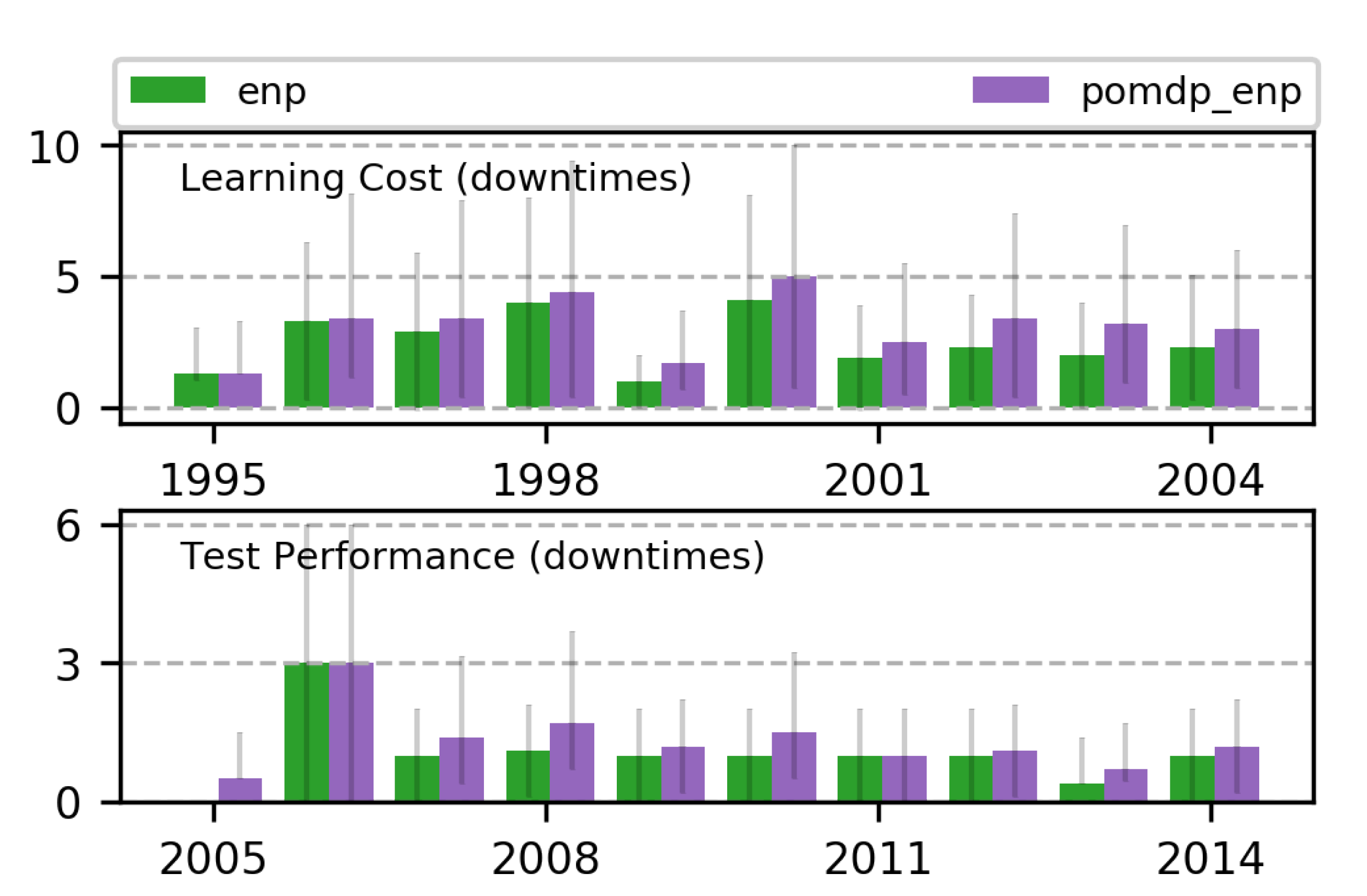
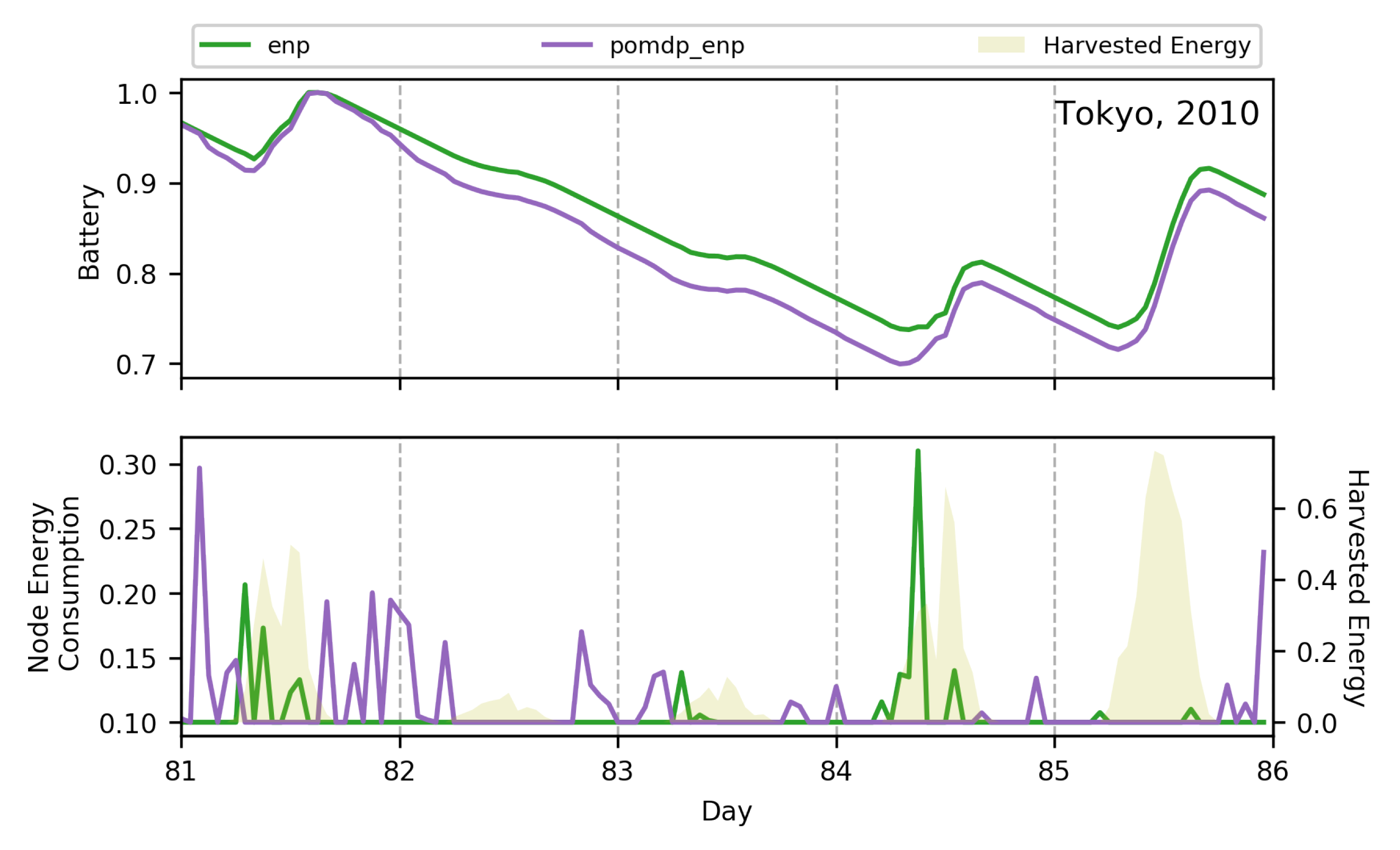
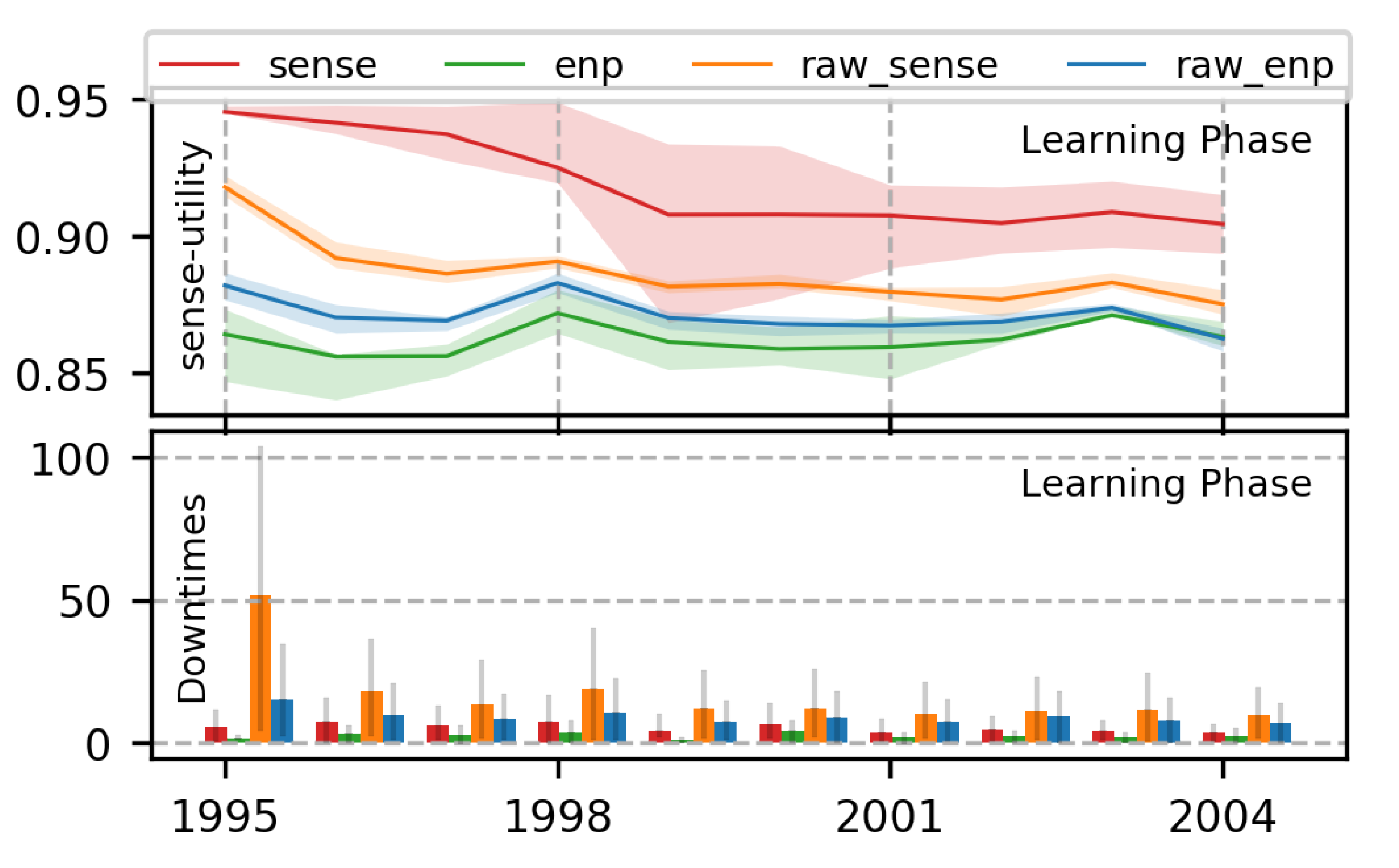

| Parameter | Maximum Value | Minimum Value |
|---|---|---|
| Battery, | of | |
| Harvester, | of | |
| EHWSN, | of | of |
| Requests, | of | of |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shresthamali, S.; Kondo, M.; Nakamura, H. Multi-Objective Resource Scheduling for IoT Systems Using Reinforcement Learning. J. Low Power Electron. Appl. 2022, 12, 53. https://doi.org/10.3390/jlpea12040053
Shresthamali S, Kondo M, Nakamura H. Multi-Objective Resource Scheduling for IoT Systems Using Reinforcement Learning. Journal of Low Power Electronics and Applications. 2022; 12(4):53. https://doi.org/10.3390/jlpea12040053
Chicago/Turabian StyleShresthamali, Shaswot, Masaaki Kondo, and Hiroshi Nakamura. 2022. "Multi-Objective Resource Scheduling for IoT Systems Using Reinforcement Learning" Journal of Low Power Electronics and Applications 12, no. 4: 53. https://doi.org/10.3390/jlpea12040053
APA StyleShresthamali, S., Kondo, M., & Nakamura, H. (2022). Multi-Objective Resource Scheduling for IoT Systems Using Reinforcement Learning. Journal of Low Power Electronics and Applications, 12(4), 53. https://doi.org/10.3390/jlpea12040053








