A Microdevice in a Submicron CMOS for Closed-Loop Deep-Brain Stimulation (CLDBS)
Abstract
:1. Introduction
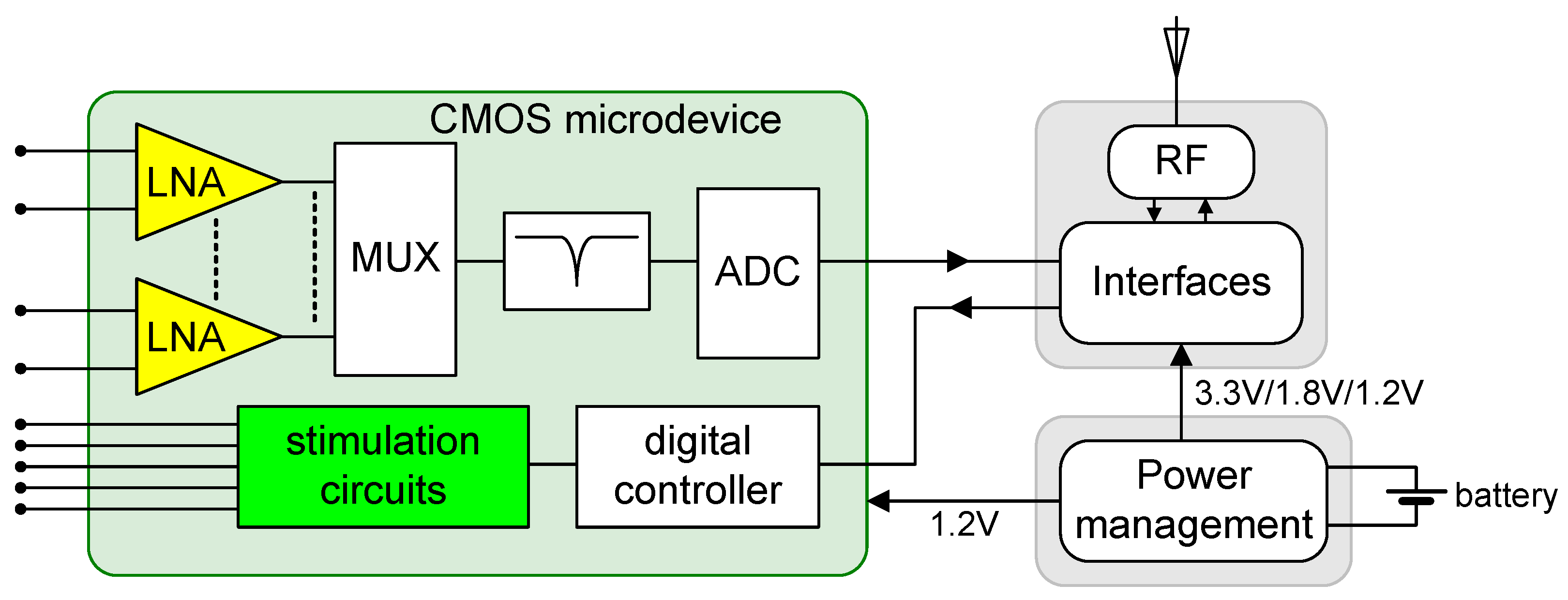
2. Design
2.1. Low-Noise Amplifier (LNA)
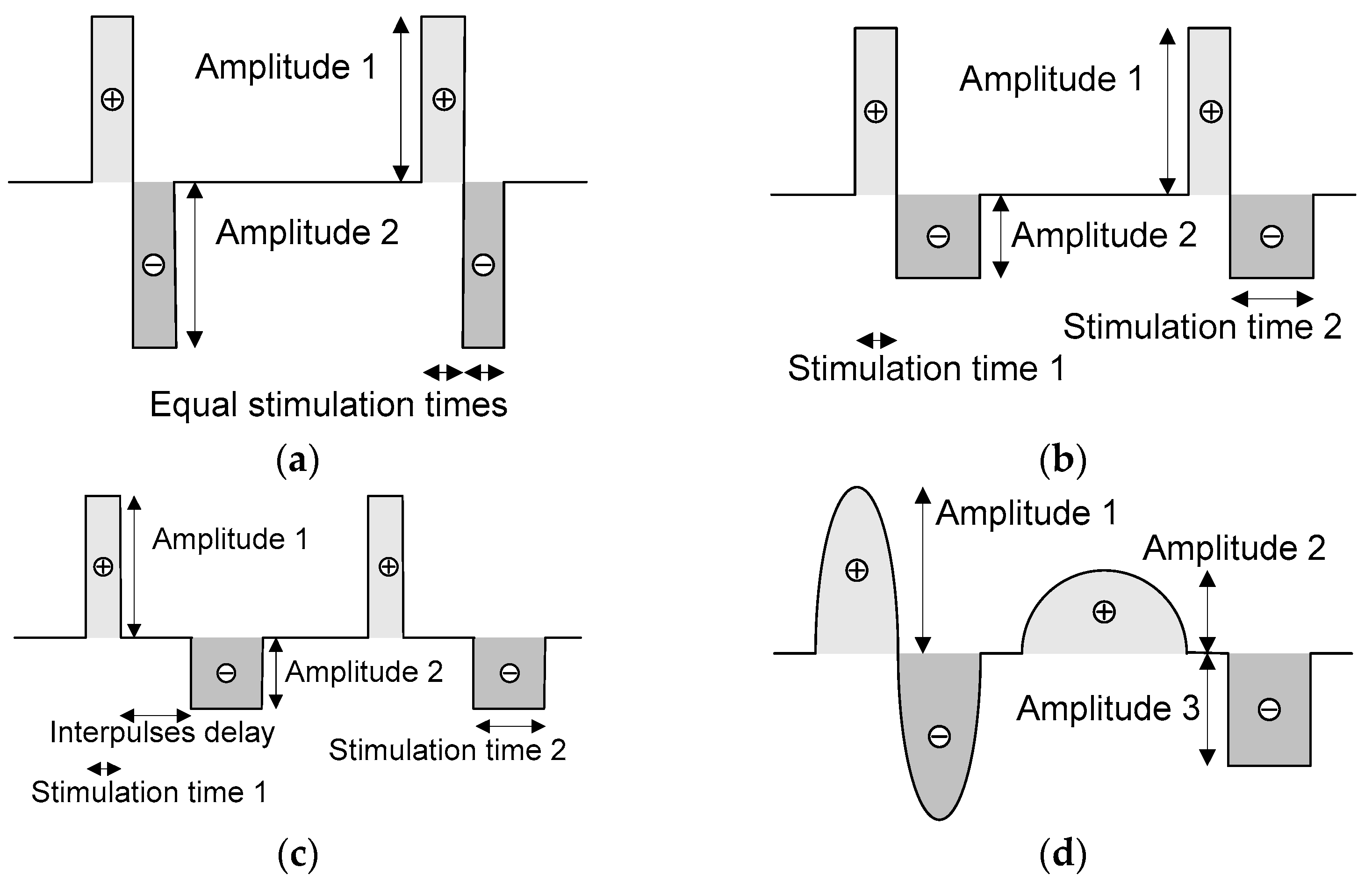
2.2. Neurostimulator
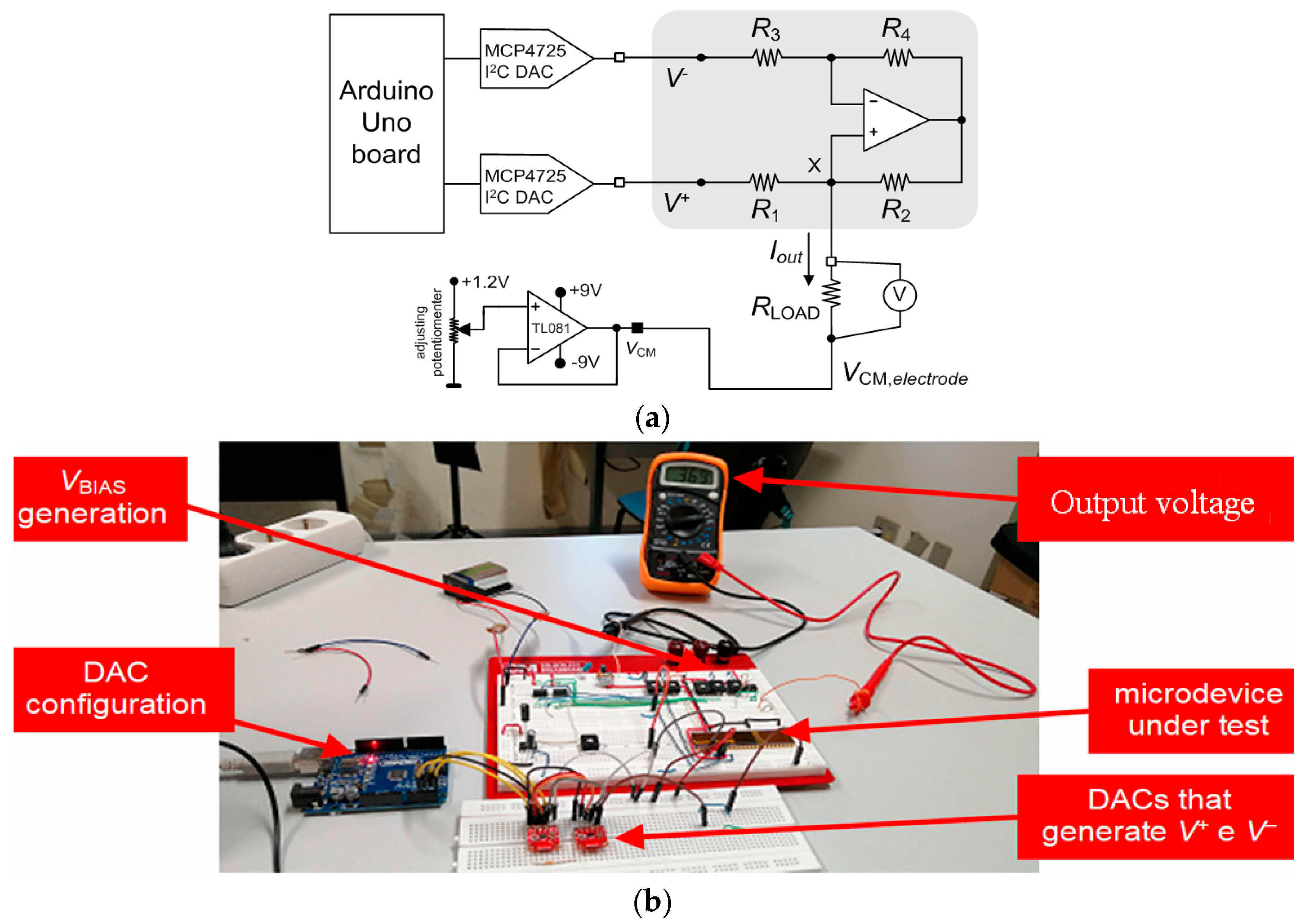
3. Experimental Results
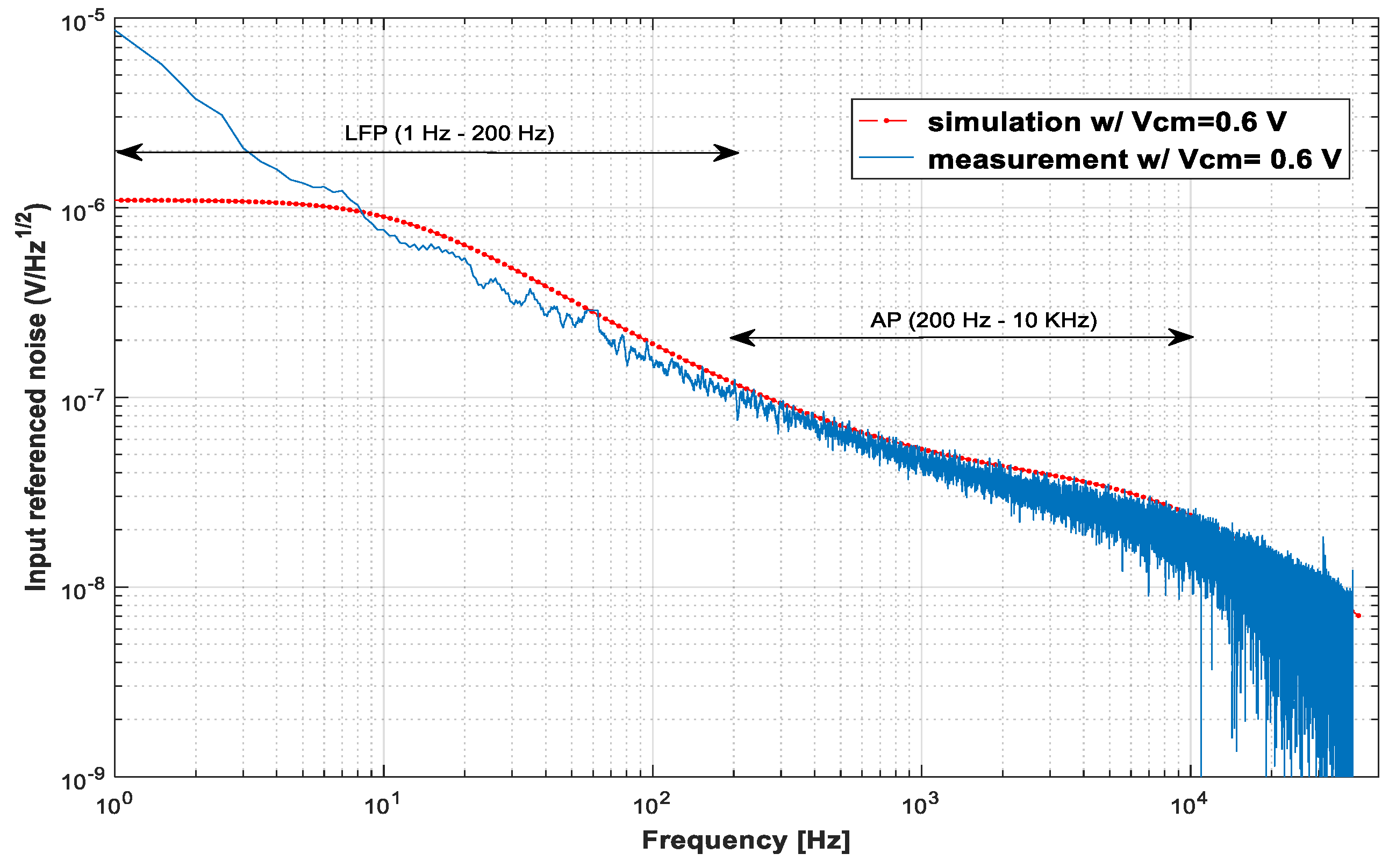
3.1. Low-Noise Amplifier (LNA)
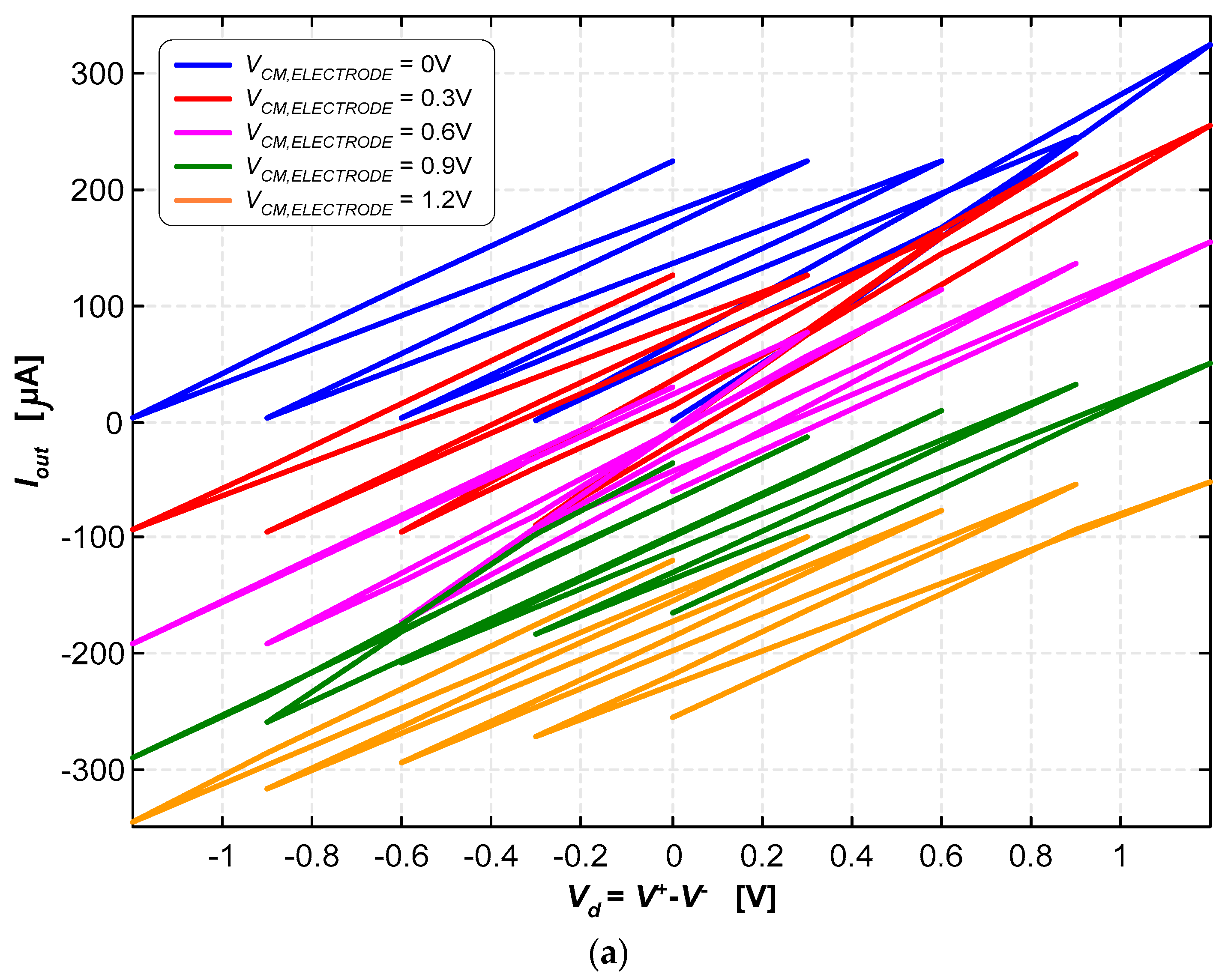
3.2. Neurostimulator Circuit


4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Appleby, B.S.; Duggan, P.S.; Regenberg, A.; Rabins, P.V. Psychiatric and neuropsychiatric adverse events associated with deep brain stimulation: A meta-analysis of ten years’ experience. Mov. Disord. 2007, 22, 1722–1728. [Google Scholar] [CrossRef] [PubMed]
- Hickey, P.; Stacy, M. Deep Brain Stimulation: A Paradigm Shifting Approach to Treat Parkinson’s Disease. Front. Neurosci. 2016, 10, 173. [Google Scholar] [CrossRef] [PubMed]
- Hoang, K.B.; Cassar, I.R.; Grill, W.M.; Turner, D.A. Biomarkers and Stimulation Algorithms for Adaptive Brain Stimulation. Front. Neurosci. 2017, 11, 303295. [Google Scholar] [CrossRef] [PubMed]
- Fins, J.J. Chapter 9: Deep Brain Stimulation: Ethical Issues in Clinical Practice and Neurosurgical Research; Neuromodulation; Academic Press: Cambridge, MA, USA, 2009; pp. 81–91. [Google Scholar]
- Faraji, B.; Rouhollahi, K.; Nezhadi, A.; Jamalpoor, Z. A Novel Closed-Loop Deep Brain Stimulation Technique for Parkinson’s Patients Rehabilitation Utilizing Machine Learning. IEEE Sens. J. 2023, 23, 2914–2921. [Google Scholar] [CrossRef]
- Parastarfeizabadi, M.; Kouzan, A.Z. A Miniature Low-Power Multi-Biomarker-Based Brain Sensor for Closed-Loop DBS. IEEE Sens. J. 2017, 17, 3109–3115. [Google Scholar] [CrossRef]
- Holleman, J.; Zhang, F.; Otis, B. Ultra-Low-Power Integrated Circuit Design for Wireless Neural Interface; Springer: New York, NY, USA, 2011. [Google Scholar]
- Chang, S.-I.; Park, S.-Y.; Yoon, E. Low-Power Low-Noise Pseudo-Open-Loop Preamplifier for Neural Interfaces. IEEE Sens. J. 2017, 17, 4843–4852. [Google Scholar] [CrossRef]
- Yang, T.; Holleman, J. An ultralow-power low-noise CMOS biopotential amplifier for neural recording. IEEE Trans. Circuits Syst. II Exp. Briefs. 2015, 62, 927–931. [Google Scholar] [CrossRef]
- Harrison, R.R.; Charles, C. A low-power low-noise CMOS for amplifier neural recording applications. IEEE J. Solid-State Circuits 2003, 38, 958–965. [Google Scholar] [CrossRef]
- Kárász, Z.; Fiáth, R.; Földesy, P.; Vázquez, A.R. Tunable Low Noise Amplifier Implementation with Low Distortion Pseudo-Resistance for in Vivo Brain Activity Measurement. IEEE Sens. J. 2013, 14, 1357–1363. [Google Scholar] [CrossRef]
- Riem, R.; Raman, J.; Borgmans, J.; Rombouts, P. A Low-Noise Instrumentation Amplifier with Built-in Anti-Aliasing for Hall Sensors. IEEE Sens. J. 2021, 21, 18932–18944. [Google Scholar] [CrossRef]
- Nordi, T.M.; Gounella, R.H.; Luppe, M.; Junior, J.N.S.; Fonoff, E.T.; Colombari, E.; Romero, M.A.; Carmo, J.P. Low-Noise Amplifier for Deep brain Stimulation (DBS). Electronics 2022, 11, 939. [Google Scholar] [CrossRef]
- Ha, S.; Kim, C.; Mercier, P.P.; Cauwenberghs, G. High-Density Integrated Electrocortical Neuronal Interface; Academic Press: London, UK, 2019. [Google Scholar]
- Wattanapanitch, W.; Fee, M.; Sarpeshkar, R. An Energy-Efficient Micropower Neural Recording Amplifier. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 136–147. [Google Scholar] [CrossRef] [PubMed]
- Kassiri, H.; Abdelhalim, K.; Genov, R. Low-distortion super-GOhm subthreshold-MOS resistors for CMOS neural amplifiers. In Proceedings of the 2013 IEEE Biomedical Circuits and Systems Conference (BioCAS), Rotterdam, The Netherlands, 31 October–2 November 2013; pp. 270–273. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm–explosion, stability, and convergence in a multimensional complex space. Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Weber, T.O.; Noije, W.A.M.V. Design of analog circuits using simulated annealing/quenching with crossovers and particle swarm optimization. In Simulating Annealing–Advances, Application and Hybridizations; Tuzuki, M.S.G., Ed.; IntechOpen: London, UK, 2012; pp. 219–244. [Google Scholar]
- Ishibe, E.I.; Soares, J.N. A CMOS bandgap reference circuit with a temperature coefficient adjustment block. In Proceedings of the 26th Symposium on Integrated Circuits and Systems Design (SBCCI), Curitiba, Brazil, 2–6 September 2013; pp. 1–6. [Google Scholar]
- Navarro, J.; Luppe, M. Performance Comparison of High-Speed Dual Modulus Prescalers Using Metaheuristic Sizing/Optimization. In Proceedings of the 33rd Symposium on Integrated Circuits and Systems Design (SBCCI), Campinas, Brazil, 24 September–28 August 2020; pp. 1–6. [Google Scholar]
- Chandrakumar, H.; Marković, D. An 80-mVpp linear-input range, 1.6-GΩ input impedance, low-power chopper amplifier for closed-loop neural recording that is tolerant to 650-mVpp common-mode interference. IEEE J. Solid-State Circuits 2017, 52, 2811–2828. [Google Scholar] [CrossRef]
- Ng, K.A.; Xu, Y.P. A multi-channel neural-recording amplifier system with 90 dB CMRR employing CMOS-inverter-based OTAs with CMFB through supply rails in 65 nm CMOS. In Proceedings of the 2015 IEEE International Solid-State Circuits Conference (ISSCC) Digest of Technical Papers, San Francisco, CA, USA, 22–26 February 2015; pp. 1–3. [Google Scholar]
- Biederman, W.; Yeager, D.J.; Narevsky, N.; Koralek, A.C.; Carmena, J.M.; Alon, E.; Rabaey, J.M. A Fully-Integrated, Miniaturized (0.125 mm2) 10.5 μW Wireless Neural Sensor. IEEE J. Solid-State Circuits 2013, 48, 960–970. [Google Scholar] [CrossRef]
- Kölbl, F.; N’Kaoua, G.; Naudet, F.; Berthier, F.; Faggiani, E.; Renaud, S.; Benazzouz, A.; Lewis, N. An Embedded Deep Brain Stimulator for Biphasic Chronic Experiments in Freely Moving Rodents. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 72–78. [Google Scholar] [CrossRef] [PubMed]
- AN-1515; A Comprehensive Study of the Howland Current Pump. Texas Instruments: Dallas, TX, USA, 26 April 2013.
- Muller, R.; Le, H.-P.; Li, W.; Ledochowitsch, P.; Gambini, S.; Bjorninen, T.; Koralek, A.; Carmena, J.M.; Maharbiz, M.M.; Alon, E.; et al. A minimally invasive 64-channel wireless µECoG implant. IEEE J. Solid-State Circuits. 2015, 50, 344–359. [Google Scholar] [CrossRef]
- Zhang, F.; Holleman, J.; Otis, B.P. Design of Ultra-Low Power Biopotential Amplifier for Biosignal Acquisition Application. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 244–355. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-J.; Park, Y.; Eom, K.; Park, S.-Y. An Area- and Energy-Efficient 16-Channel, AC-Coupled Neural Recording Analog Frontend for High-Density Multichannel Neural Recordings. Electronics 2021, 10, 1972. [Google Scholar] [CrossRef]
- Kwak, J.Y.; Park, S.-Y. Compact Continuous Time Common-Mode Feedback Circuit for Low-Power, Area-Constrained Neural Recording Amplifiers. Electronics 2021, 10, 145. [Google Scholar] [CrossRef]
- Tasneem, N.T.; Mahbub, I. A 2.53 NEF 8-bit 10 kS/s 0.5 μm CMOS Neural Recording Read-Out Circuit with High Linearity for Neuromodulation Implants. Electronics 2021, 10, 590. [Google Scholar] [CrossRef]
- Holleman, J.; Otis, B. A Sub-Microwatt Low-Noise Amplifier for Neuronal Recording. In Proceedings of the 29th Annual International Conference IEEE EMBS, Lyon, France, 23–26 August 2007; pp. 3930–3933. [Google Scholar]
- Steyaert, M.S.; Sansen, W.M. A micropower low-noise monolithic instrumentation amplifier for medical purposes. IEEE J. Solid State Circuits 1987, 22, 1163–1168. [Google Scholar] [CrossRef]
- Pinnell, R.C.; de Vasconcelos, A.P.; Cassel, J.C.; Hofmann, U.G. A miniaturized programmable Deep brain stimulator for group-housing and water maze use. Front. Neurosci. 2018, 12, 353871. [Google Scholar] [CrossRef] [PubMed]
- Ewing, S.G.; Lipski, W.J.; Grace, A.A.; Winter, C. An inexpensive charge-balanced rodent deep brain stimulation device a step-by-step guide to its procurement and construction. J. Neurosci. Methods 2013, 219, 324–330. [Google Scholar] [CrossRef]
- Kouzani, A.Z.; Abulseoud, O.A.; Tye, S.J.; Hosain, M.D.K.; Berk, M. A low power micro deep brain stimulation device for murine preclinical research. IEEE J. Transl. Eng. Health Med. 2013, 1, 1500109. [Google Scholar] [CrossRef]
- Pinnell, R.C.; Dempster, J.; Pratt, J. Miniature wireless recording and stimulation system for rodent behavioral testing. J. Neural Eng. 2015, 12, 066015. [Google Scholar] [CrossRef] [PubMed]
- Adams, S.D.; Bennet, K.E.; Tye, S.J.; Berk, M.; Kouzani, A.Z. Development of a miniature device for emerging deep brain stimulation paradigms. PLoS ONE 2019, 14, e0212554. [Google Scholar] [CrossRef] [PubMed]
- Tibara, H.; Naudeta, F.; Kölblc, F.; Ribota, B.; Faggiania, E.; N’Kaouac, G.; Renaudc, S.; Lewisc, N.; Benazzouza, A. In vivo validation of a new portable stimulator for chronic deep brain stimulation in freely moving rats. J. Neurosci. Methods 2020, 333, 108577. [Google Scholar] [CrossRef]
- Fluri, F.; Mützel, T.; Schuhmann, M.K.; Krstić, M.; Endres, H.; Volkmann, J. Development of a head-mounted wireless microstimulator for deep brain stimulation in rats. J. Neurosci. Methods 2017, 291, 249–256. [Google Scholar] [CrossRef]






| MOSFET | (W/L) |
| M1, M2 | 59 μm/0.52 μm |
| M3, M4 | 25 μm/14.9 μm |
| M5 | 48 μm/2.22 μm |
| M6 | 12.5 μm/14.9 μm |
| M7 | 12 μm/2.22 μm |
| M8n | 1.55 μm/12 μm |
| M8p | 3.1 μm/12 μm |
| M9 | 2 μm/2.22 μm |
| Mp1, Mp2 | 12 μm/0.6 μm |
| Capacitor | Total Value |
| Cc | 7.5 pF |
| C1 | 18.7 pF |
| C2 | 0.18 pF |
| MOSFET | (W/L) |
| M1, M2 | 14.8 µm/0.24 µm |
| M3, M4 | 4.68 µm/0.18 µm |
| M5 | 14.4 µm/0.36 µm |
| M6 | 18.72 µm/0.18 µm |
| M7 | 28.8 µm/0.36 µm |
| M8 | 0.51 µm/7.2 µm |
| M9 | 0.80 µm/0.36 µm |
| Capacitor | Total Value |
| Cc | 2.5 pF |
| Cx | 417.2 fF |
| Resistor | Total Value |
| R1, R2 | ≈3.52 kΩ |
| R3, R4 | ≈24.61 kΩ |
| Vin (mVpp) | VCM (V) | VCM,out (V) | Gmax (dB) | fL (Hz) | fH (kHz) |
|---|---|---|---|---|---|
| 2 | 0.5 | 0.506 | 41.1 | 6.1 | 13 |
| 0.6 | 0.63 | 41.2 | 1.5 | 11.5 | |
| 0.7 | 1.08 | 40.2 | 1.3 | 8 |
| Ref. | CMOS Process | Mid-Band Gain (dB) | Bandwidth (Hz) | Power Supply (V) | Power Consumption (μW) | Area (mm2) | IRN (μVrms) | NEF |
|---|---|---|---|---|---|---|---|---|
| This work | 65 nm | 42 | 1.5–200 200–11.5 k 1.5–11.5 k | 1.2 | 5.88 | 0.046 | 6.48 3.45 7.36 | – 2.63 5.57 |
| [21] | 40 nm | 25.7 | 200–5.0 k | 1.2 | 2.8 | N/A | 5.3 | 4.40 |
| [22] | 65 nm | 52.1 | 1.0–8.2 k | 1.0 | 2.8 | 0.042 | 4.13 | 2.93 |
| [23] | 65 nm | 46 | 1.0–10 k | 0.5 | 1.5 | 0.0039 | 6.5 | 4.34 |
| [26] | 65 nm | 30 | 300–10 k | 0.5 | 2.3 | 0.025 | 5.8 | 4.76 |
| [9] | 90 nm | 58.7 | 0.49–10.5 k | 1.0 | 2.85 | 0.137 | 3.04 | 1.93 |
| [27] | 0.13 μm | 40 | 0.05–0.5 k | 1.0 | 12.1 | 0.072 | 2.2 | 2.90 |
| [28] | 0.18 μm | 40 | 0.1–7.4 k | 1.0 | 3.44 | 0.012 | 4.27 | 3.07 |
| [29] | 0.18 μm | 40 | 0.05–7.5 k | 1.2 | 4.8 | 0.022 | 3.87 | 3.44 |
| [30] | 0.5 μm | 49.26, 60.63 | 0.5–300 270–12.9 k | 3.3 | 4.12 | 0.0144 | 3.16 | 2.53 |
| [31] | 0.5 μm | 36.1 | 0.3–4.7 k | 1.0 | 0.805 | 0.046 | 3.6 | 1.8 |
| [10] | 0.5 μm | 39.5 | 0.025–7.2 k | ±2.5 | 80 | 0.16 | 2.2 | 4.0 |
| Ref. | Current (μA) | Voltage (V) | Maximum Pulse Frequency/ Bandwidth (Hz) | Minimum Pulse Duration/ Bandwidth−1 (μs) | Charge Balance | Active Charge Balancing Method |
|---|---|---|---|---|---|---|
| This work | from −325 to +318 | 1.2 | 1.5 × 106 (BW) | 25 | Active | Continuous (Howland current pump) |
| [33] | from 20 to 2000 | 12 | 500 | 10 | Active | Switched (H-bridge) |
| [34] | from −200 to +200 | 3.6 (bat) | 185 | 90 | Active | Switched |
| [35] | from 0 to 200 | 3.2 (bat) | 130 | 90 | Passive | Switched |
| [36] | from 30 to 1000 | 3.7 (bat) | 5000 | 10 | Active | Switched |
| [37] | from −375 to +250 | 10 | 5000 | 20 | Active | Continuous (Howland current pump) |
| [38] | from 20 to 2000 | 4.8 (bat) | 300 | 40 | Active | Switched (H-bridge) |
| [39] | from 10 to 500 | 3.1 (bat) | 200 | 60 | Passive | Switched |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nordi, T.M.; Gounella, R.; Amorim, M.L.M.; Luppe, M.; Junior, J.N.S.; Afonso, J.L.; Monteiro, V.; Afonso, J.A.; Talamoni Fonoff, E.; Colombari, E.; et al. A Microdevice in a Submicron CMOS for Closed-Loop Deep-Brain Stimulation (CLDBS). J. Low Power Electron. Appl. 2024, 14, 28. https://doi.org/10.3390/jlpea14020028
Nordi TM, Gounella R, Amorim MLM, Luppe M, Junior JNS, Afonso JL, Monteiro V, Afonso JA, Talamoni Fonoff E, Colombari E, et al. A Microdevice in a Submicron CMOS for Closed-Loop Deep-Brain Stimulation (CLDBS). Journal of Low Power Electronics and Applications. 2024; 14(2):28. https://doi.org/10.3390/jlpea14020028
Chicago/Turabian StyleNordi, Tiago Matheus, Rodrigo Gounella, Marcio L. M. Amorim, Maximiliam Luppe, João Navarro Soares Junior, Joao L. Afonso, Vitor Monteiro, Jose A. Afonso, Erich Talamoni Fonoff, Eduardo Colombari, and et al. 2024. "A Microdevice in a Submicron CMOS for Closed-Loop Deep-Brain Stimulation (CLDBS)" Journal of Low Power Electronics and Applications 14, no. 2: 28. https://doi.org/10.3390/jlpea14020028
APA StyleNordi, T. M., Gounella, R., Amorim, M. L. M., Luppe, M., Junior, J. N. S., Afonso, J. L., Monteiro, V., Afonso, J. A., Talamoni Fonoff, E., Colombari, E., & Carmo, J. P. (2024). A Microdevice in a Submicron CMOS for Closed-Loop Deep-Brain Stimulation (CLDBS). Journal of Low Power Electronics and Applications, 14(2), 28. https://doi.org/10.3390/jlpea14020028











