A Power-Efficient 50 MHz-BW 76.8 dB Signal-to-Noise-and-Distortion Ratio Continuous-Time 2-2 MASH Delta-Sigma Analog-to-Digital Converter with Digital Calibration
Abstract
:1. Introduction
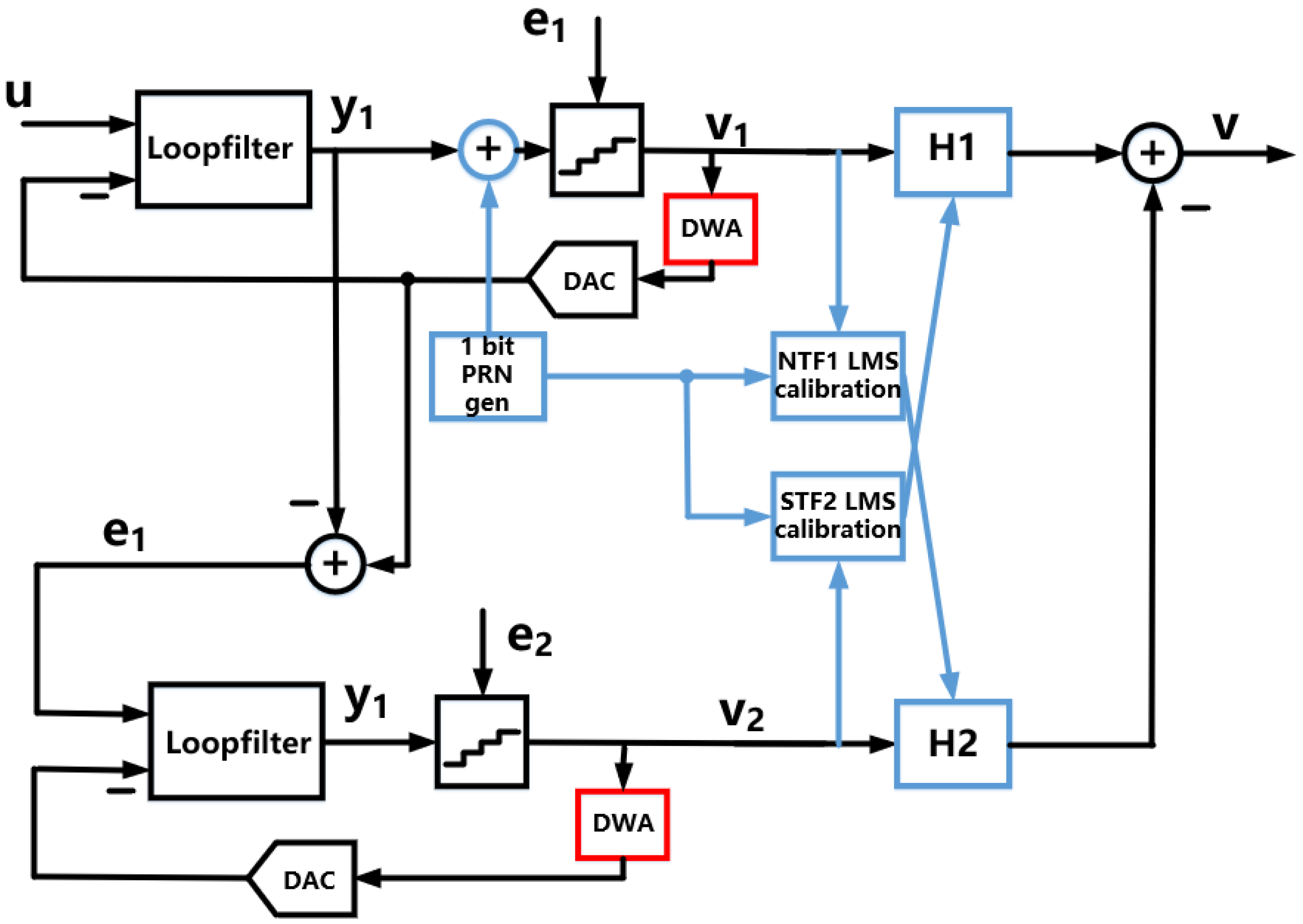
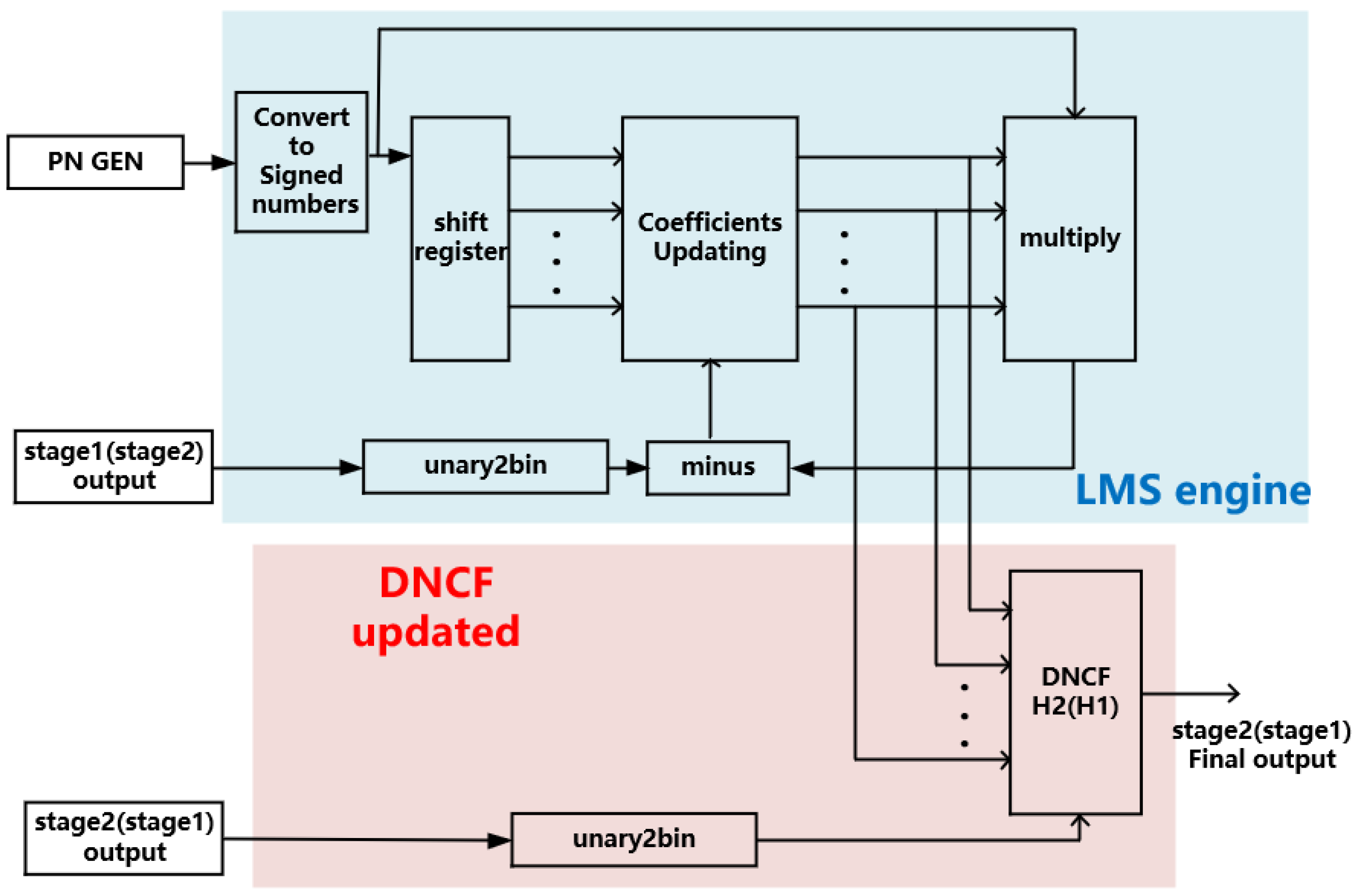
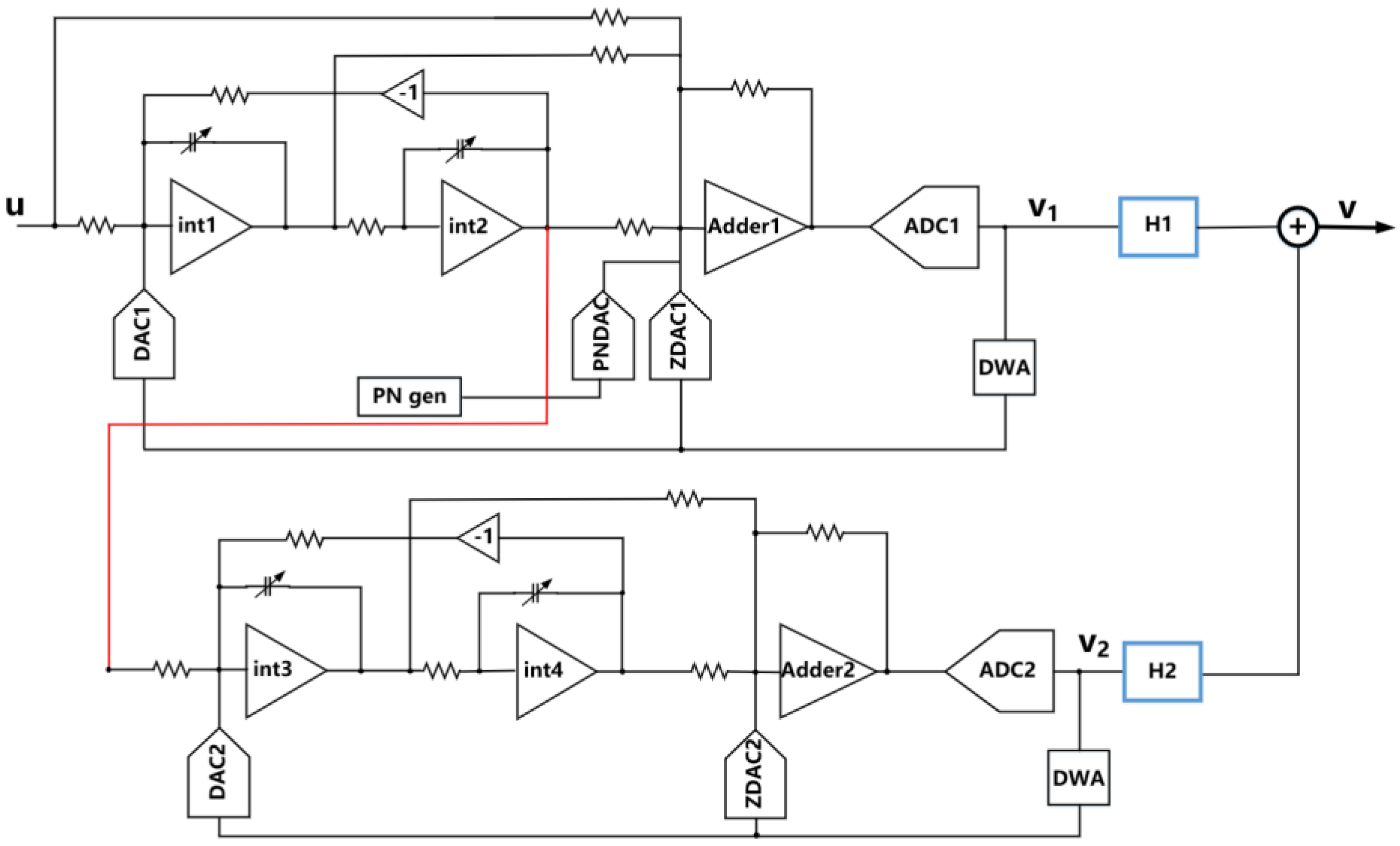
2. Proposed CT 2-2 MASH with Digital Calibration
3. Circuit Implementation
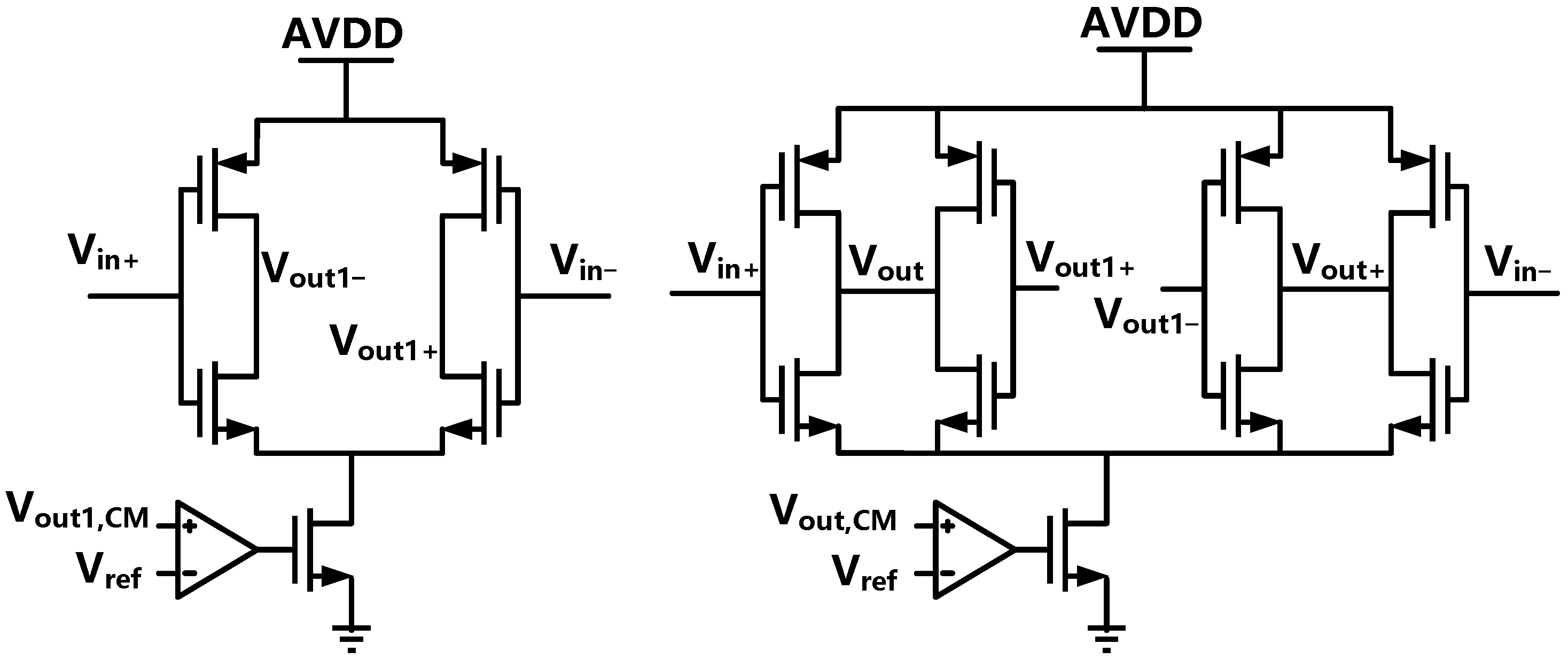
3.1. Operational Amplifier with Feedforward Compensation
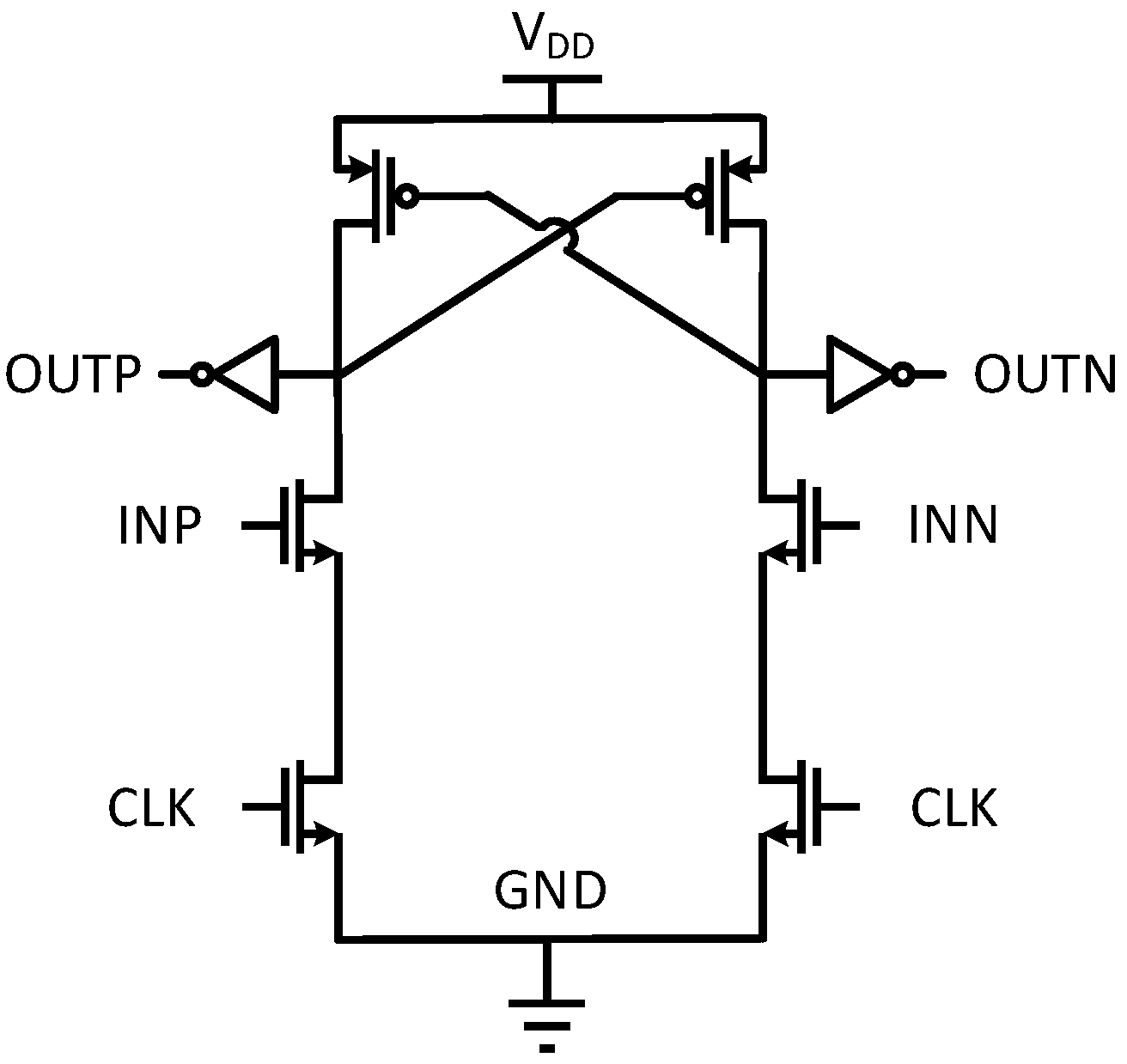
3.2. Flash Quantizer and Comparator
3.3. Current Steering DAC
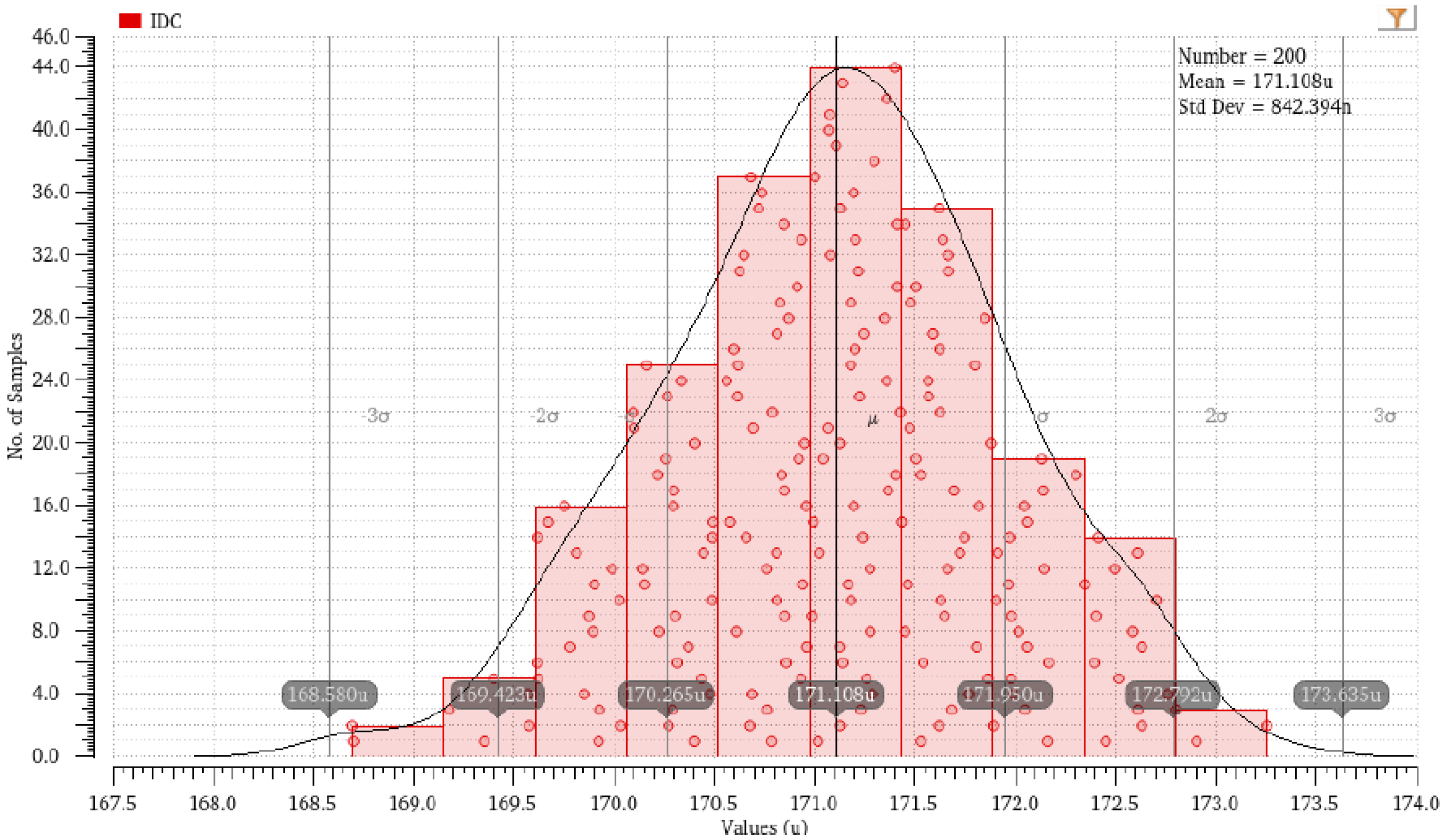
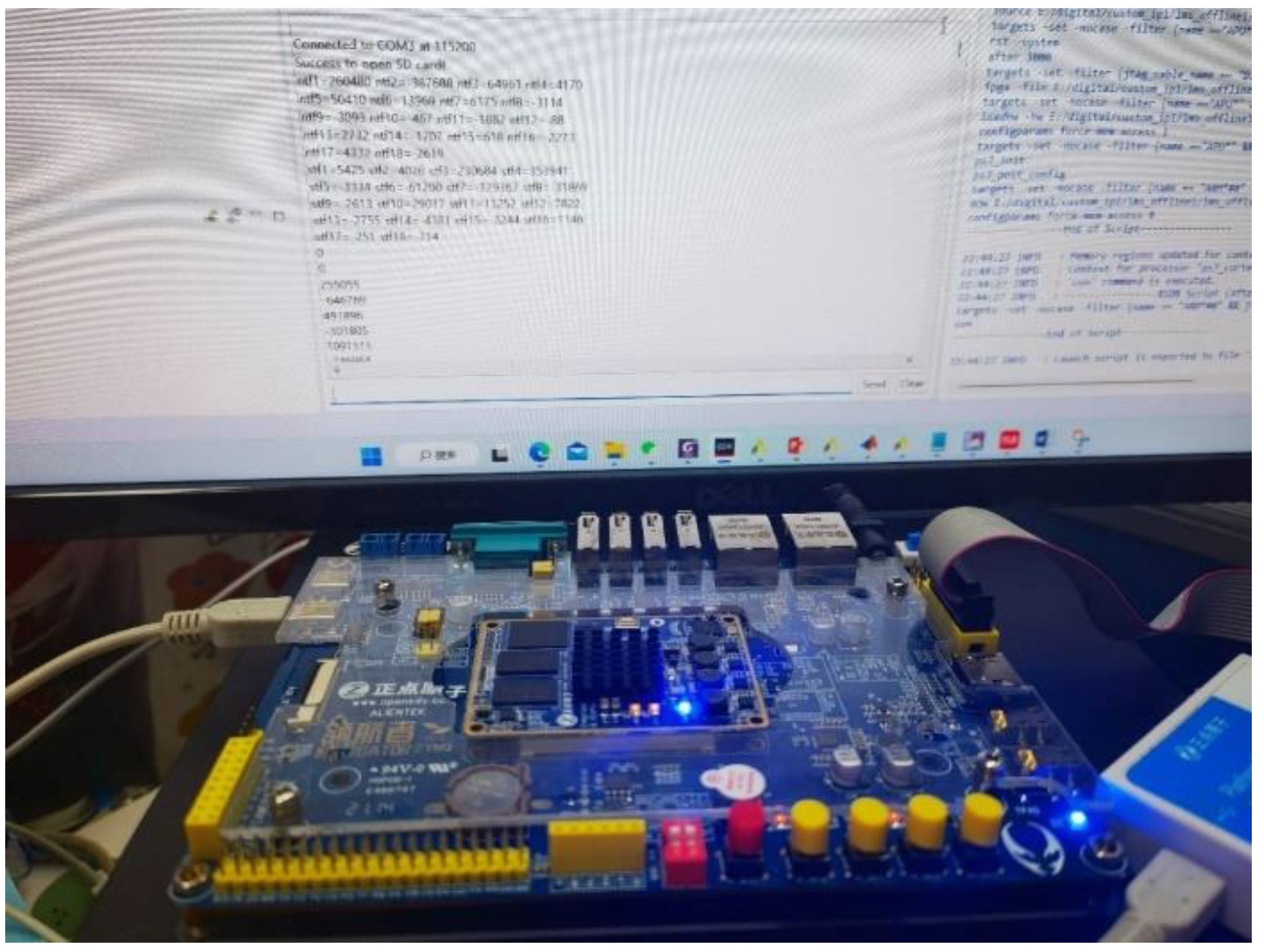
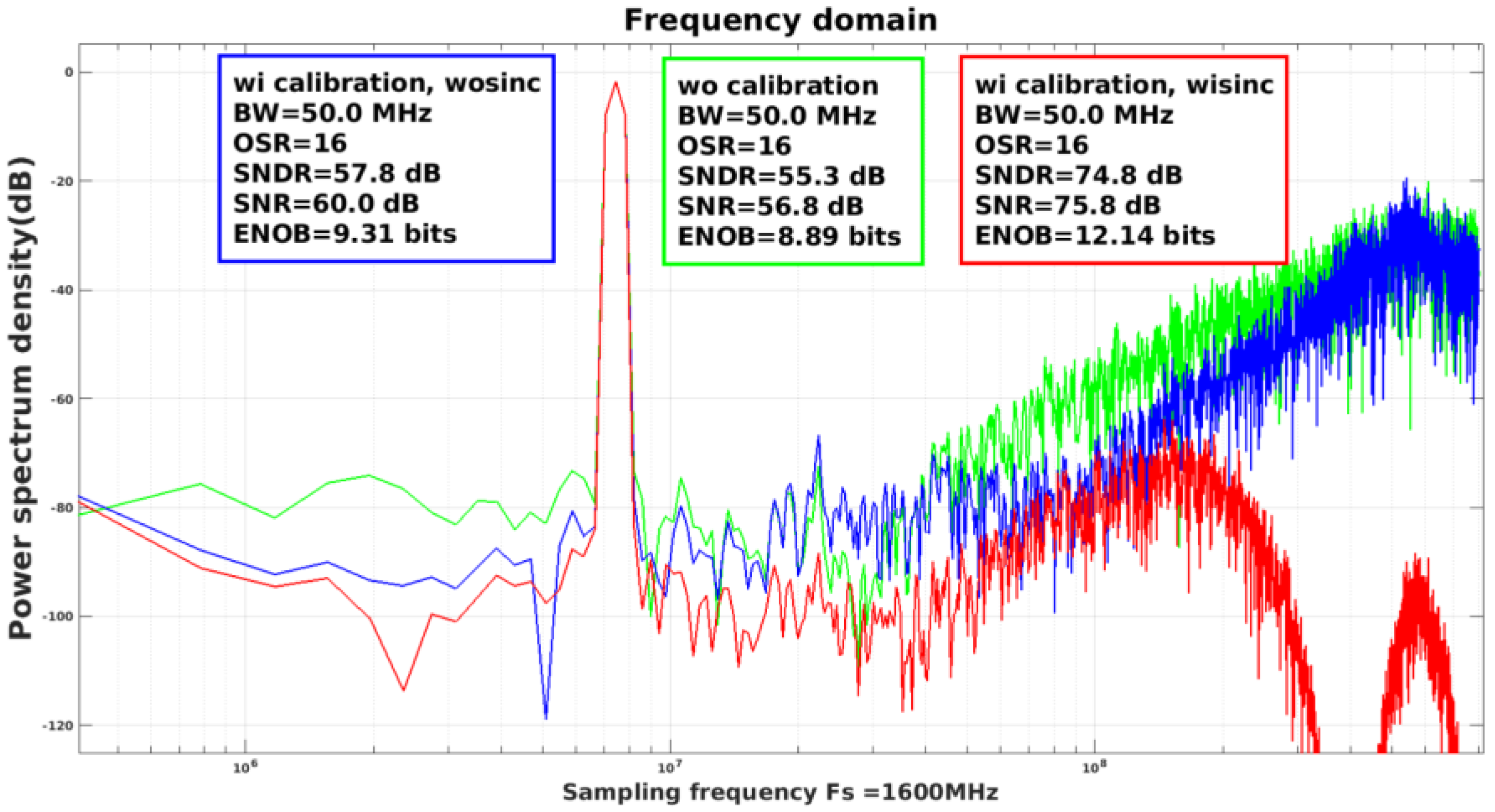
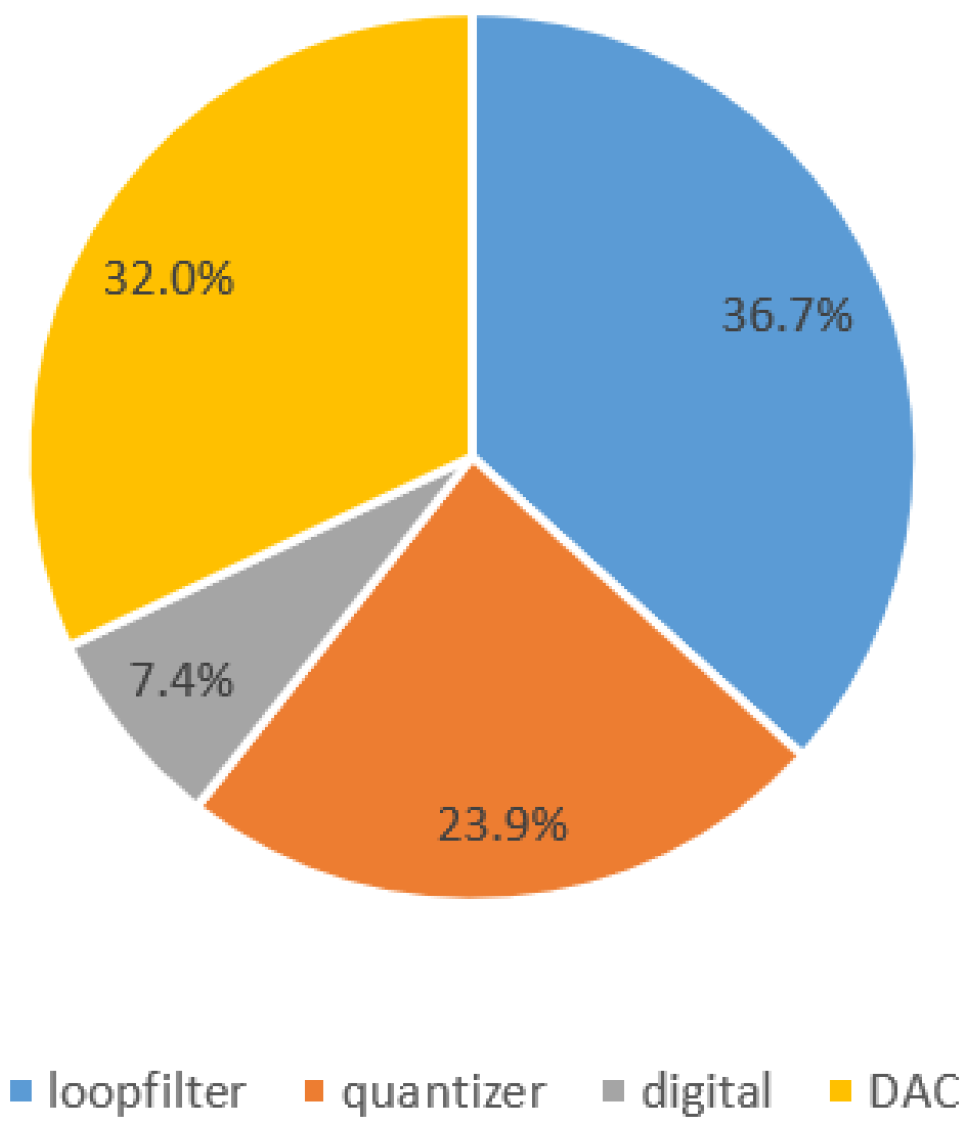
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Loeda, S.; Harrison, J.; Pourchet, F.; Adams, A. A 10/20/30/40 MHz feedforward FIR DAC continuous-time ∆Σ ADC with robust blocker performance for radio receivers. IEEE J. Solid State Circuits 2016, 51, 860–870. [Google Scholar]
- de la Rosa, J.M.; Schreier, R.; Pun, K.-P.; Pavan, S. Next-Generation Delta-Sigma Converters: Trends and Perspectives. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 484–499. [Google Scholar] [CrossRef]
- Xing, K.; Wang, W.; Zhu, Y.; Chan, C.-H.; Martins, R.P. A Single-Opamp Third Order CT ΔΣ Modulator with SAB-ELD-Merged Integrator and Three-Stage Hybrid Compensation Opamp. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 64–74. [Google Scholar] [CrossRef]
- Breems, L.J.; Bolatkale, M.; Liu, Q.; Cenci, P. High-Speed and High-Performance Continuous-Time ADCs for Automotive Re-ceivers. IEEE Open J. Solid-State Circuits Soc. 2023, 3, 174–184. [Google Scholar] [CrossRef]
- Ucar, A.; Cetin, E.; Kale, I. A Continuous-Time Delta-Sigma Modulator for RF Subsampling Receivers. IEEE Trans. Circuits Syst. II Express Briefs 2012, 59, 272–276. [Google Scholar] [CrossRef]
- Lai, W.-C. Continuous-time Sigma-Delta Modulator with RF Receiver for Wireless Respiratory Detection. In Proceedings of the 2021 IEEE International Symposium on Radio-Frequency Integration Technology (RFIT), Hualien, Taiwan, 25–27 August 2021; pp. 1–3. [Google Scholar]
- Wang, C.-Y.; Tsai, J.-H.; Su, S.-Y.; Tsai, J.-C.; Chen, J.-R.; Lou, C.-H. 20.6 An 80MHz-BW 31.9fJ/conv-step Filtering ΔΣ ADC with a Built-In DAC-Segmentation/ELD-Compensation 6b 960MS/s SAR-Quantizer in 28 nm LP for 802.11ax Applications. In Proceedings of the 2019 IEEE International Solid—State Circuits Conference—(ISSCC), San Francisco, CA, USA, 17–21 February 2019; pp. 338–340. [Google Scholar]
- Shibata, H.; Kozlov, V.; Ji, Z.; Ganesan, A.; Zhu, H.; Paterson, D.; Pavan, S. A 9-GS/s 1.125-GHz BW Oversampling Continuous-Time Pipeline ADC Achieving −164-dBFS/Hz NSD. IEEE J. Solid-State Circuits 2017, 52, 3219–3234. [Google Scholar] [CrossRef]
- Caldwell, T.; Shibata, H. High-speed oversampled continuous-time analog-to-digital converters. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1001–1004. [Google Scholar]
- Bolatkale, M.; Breems, L.J.; Rutten, R.; Makinwa, K.A.A. A 4 GHz Continuous-Time ΔΣ ADC with 70 dB DR and—74 dBFS THD in 125 MHz BW. IEEE J. Solid State Circuits 2011, 46, 2857–2868. [Google Scholar] [CrossRef]
- Park, M.; Perrott, M.H. A 78 dB SNDR 87 mW 20 MHz Bandwidth Continuous-Time ΔΣ ADC with VCO-Based Integrator and Quantizer Implemented in 0.13 μm CMOS. IEEE J. Solid State Circuits 2009, 44, 3344–3358. [Google Scholar] [CrossRef]
- Mukherjee, A.; Gandara, M.; Yang, X.; Shen, L.; Tang, X.; Hsu, C.K.; Sun, N. A 74.5-dB Dynamic Range 10-MHz BW CT-ΔΣ ADC with Distributed-Input VCO and Embedded Capacitive-π Network in 40-nm CMOS. IEEE J. Solid State Circuits 2021, 56, 476–487. [Google Scholar] [CrossRef]
- Huang, S.-J.; Egan, N.; Kesharwani, D.; Opteynde, F.; Ashburn, M. 28.3 A 125MHz-BW 71.9dB-SNDR VCO-based CT ΔΣ ADC with segmented phase-domain ELD compensation in 16nm CMOS. In Proceedings of the 2017 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 5–9 February 2017; pp. 470–471. [Google Scholar]
- Taylor, G.; Galton, I. A Mostly-Digital Variable-Rate Continuous-Time Delta-Sigma Modulator ADC. IEEE J. Solid State Circuits 2010, 45, 2634–2646. [Google Scholar] [CrossRef]
- Dong, Y.; Yang, W.; Schreier, R.; Sheikholeslami, A.; Korrapati, S. A Continuous-Time 0–3 MASH ADC Achieving 88 dB DR with 53 MHz BW in 28 nm CMOS. IEEE J. Solid State Circuits 2014, 49, 2868–2877. [Google Scholar] [CrossRef]
- Dong, Y.; Zhao, J.; Yang, W.W.; Caldwell, T.; Shibata, H.; Li, Z.; Gealow, J.C. A 72 dB-DR 465 MHz-BW Continuous-Time 1–2 MASH ADC in 28 nm CMOS. IEEE J. Solid State Circuits 2016, 51, 2917–2927. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Steensgaard, G.; Temes, C.; Wu, J.-Y. A Split 2-0 MASH with Dual Digital Error Correction. In Proceedings of the 2007 IEEE Symposium on VLSI Circuits, Kyoto, Japan, 14–16 June 2007; pp. 242–243. [Google Scholar] [CrossRef]
- Shu, Y.-S.; Kamiishi, J.; Tomioka, K.; Hamashita, K.; Song, B.-S. LMS-Based Noise Leakage Calibration of Cascaded Continuous-Time ΔΣ Modulators. IEEE J. Solid-State Circuits 2010, 45, 368–379. [Google Scholar] [CrossRef]
- Fukazawa, M.; Oshima, T.; Fujiwara, M.; Tateyama, K.; Ochi, A.; Alsubaie, R.; Matsui, T. A CT 2–2 MASH ΔΣ ADC with Multi-Rate LMS-Based Background Calibration and Input-Insensitive Quantization-Error Extraction. IEEE J. Solid State Circuits 2021, 56, 2943–2955. [Google Scholar] [CrossRef]
- Fukazawa, M.; Oshima, T.; Fujiwara, M.; Tateyama, K.; Raed, A.; Ito, M.; Matsui, T. 9.7 Background Multi-Rate LMS Calibration Circuit for 15MHz-BW 74dB-DR CT 2–2 MASH ΔΣ ADC in 28nm CMOS. In Proceedings of the 2020 IEEE International Solid-State Circuits Conference—(ISSCC), San Francisco, CA, USA, 16–20 February 2020; pp. 166–168. [Google Scholar]
- Yoon, D.-Y.; Ho, S.; Lee, H.-S. A Continuous-Time Sturdy-MASH ΔΣ Modulator in 28 nm CMOS. IEEE J. Solid State Circuits 2015, 50, 2880–2890. [Google Scholar] [CrossRef]
- Qi, L.; Jain, A.; Jiang, D.; Sin, S.-W.; Martins, R.P.; Ortmanns, M. A 76.6-dB-SNDR 50-MHz-BW 29.2-mW Multi-Bit CT Sturdy MASH with DAC Non-Linearity Tolerance. IEEE J. Solid State Circuits 2020, 55, 344–355. [Google Scholar] [CrossRef]
- Park, B.; Han, C.; Maghari, N. Correlated Dual-Loop Sturdy MASH CT ΔΣ ADC with Indirect Signal Feedforward. In Proceedings of the 2021 IEEE Asian Solid-State Circuits Conference (A-SSCC), Busan, Republic of Korea, 7–10 November 2021; pp. 1–3. [Google Scholar]
- Han, C.; Park, B.; Maghari, N. Can SMASH Smash MASH? In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Ali, A.M.; Dinc, H.; Bhoraskar, P.; Dillon, C.; Puckett, S.; Gray, B.; McShea, M. A 14 Bit 1 GS/s RF Sampling Pipelined ADC with Background Calibration. IEEE J. Solid State Circuits 2014, 49, 2857–2867. [Google Scholar] [CrossRef]
- Ho, S.; Lo, C.-L.; Ru, J.; Zhao, J. A 23 mW, 73 dB Dynamic Range, 80 MHz BW Continuous-Time Delta-Sigma Modulator in 20 nm CMOS. IEEE J. Solid State Circuits 2015, 50, 908–919. [Google Scholar] [CrossRef]
- Liu, H.; Xing, X.; Gielen, G. A 0-dB STF-Peaking 85-MHz BW 74.4-dB SNDR CT ΔΣ ADC with Unary-Approximating DAC Calibration in 28-nm CMOS. IEEE J. Solid State Circuits 2021, 56, 287–297. [Google Scholar] [CrossRef]
- Mitteregger, G.; Ebner, C.; Mechnig, S.; Blon, T.; Holuigue, C.; Romani, E. A 20-mW 640-MHz CMOS Continuous-Time ΣΔ ADC with 20-MHz Signal Bandwidth, 80-dB Dynamic Range and 12-bit ENOB. IEEE J. Solid State Circuits 2006, 41, 2641–2649. [Google Scholar] [CrossRef]
- Edward, A.; Liu, Q.; Briseno-Vidrios, C.; Kinyua, M.; Soenen, G.E.; Karsilayan, I.A. A 43-mW MASH 2-2 CT ΣΔ Modulator Attaining 74.4/75.8/76.8 dB of SNDR/SNR/DR and 50 MHz of BW in 40-nm CMOS. IEEE J. Solid State Circuits 2017, 52, 448–459. [Google Scholar] [CrossRef]
- Honarparvar, M.; de la Rosa, J.M.; Sawan, M. A 10-MHz BW 77.3-dB SNDR 640-MS/s GRO-Based CT MASH ΔΣ Modulator. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1519–1523. [Google Scholar]
- Liu, Q.; Breems, L.J.; Bajoria, S.; Bolatkale, M.; Rutten, R.; Radulov, G. A 158-mW 360-MHz BW 68-dB DR Continuous-Time 1-1-1 Filtering MASH ADC in 40-nm CMOS. IEEE J. Solid State Circuits 2022, 57, 3781–3793. [Google Scholar] [CrossRef]
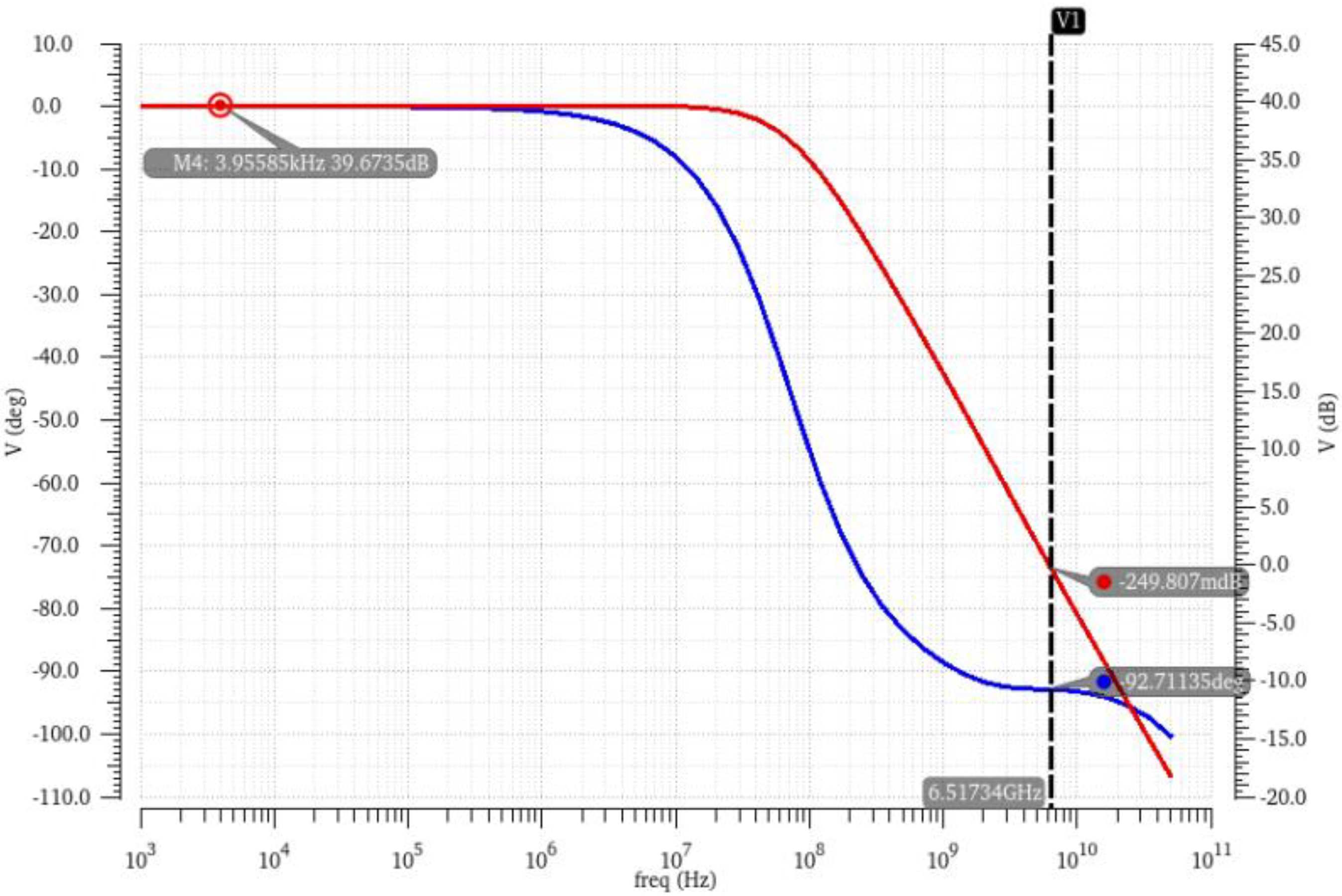
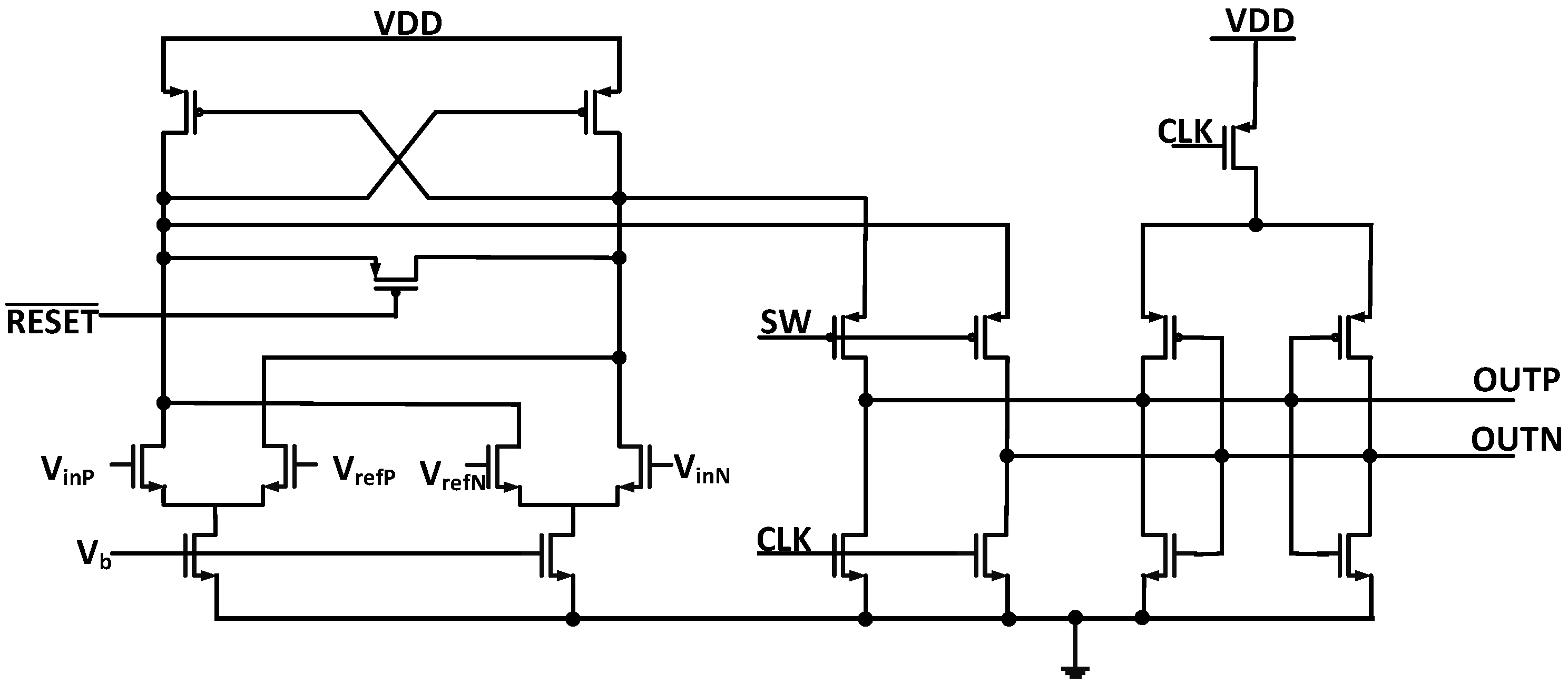
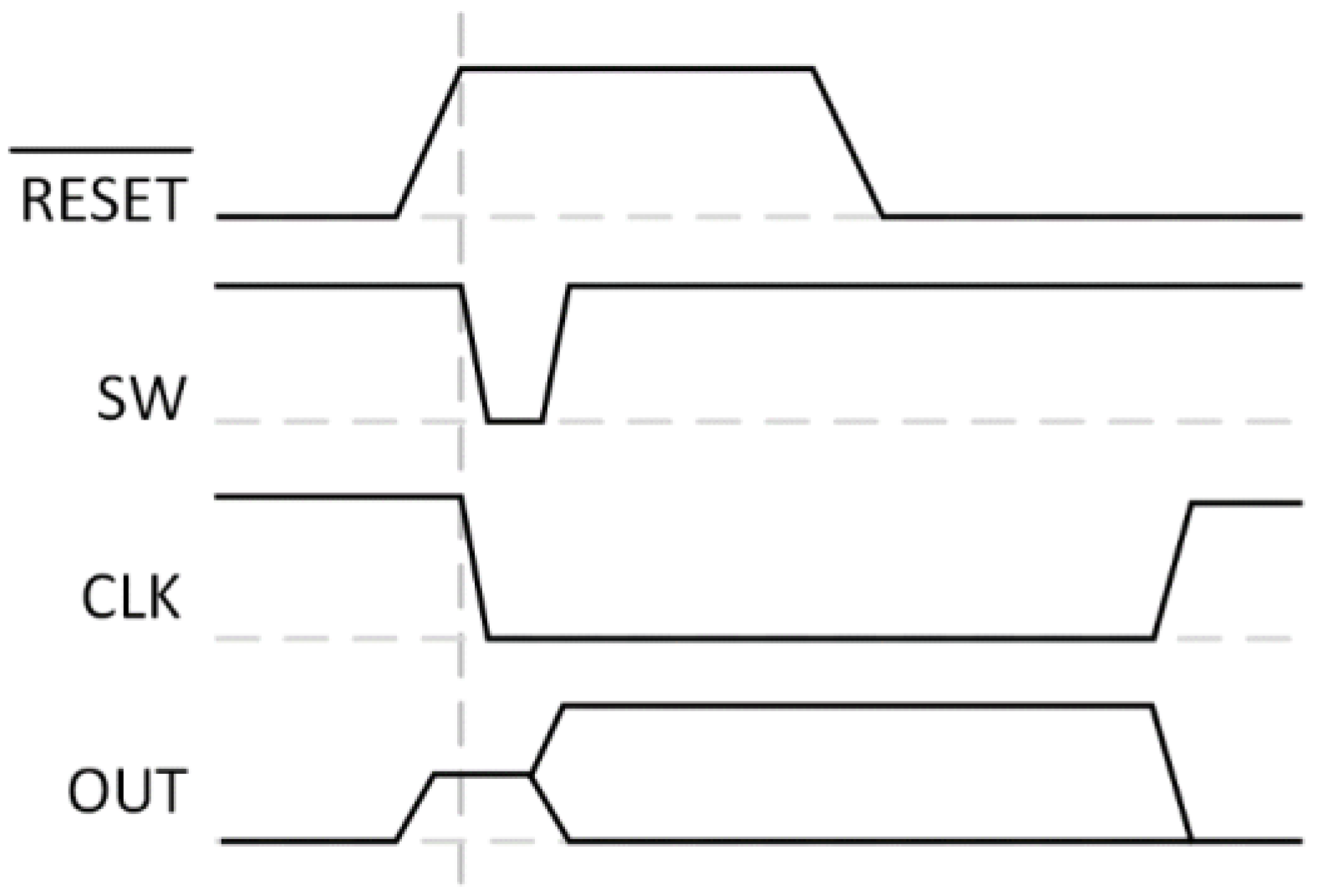
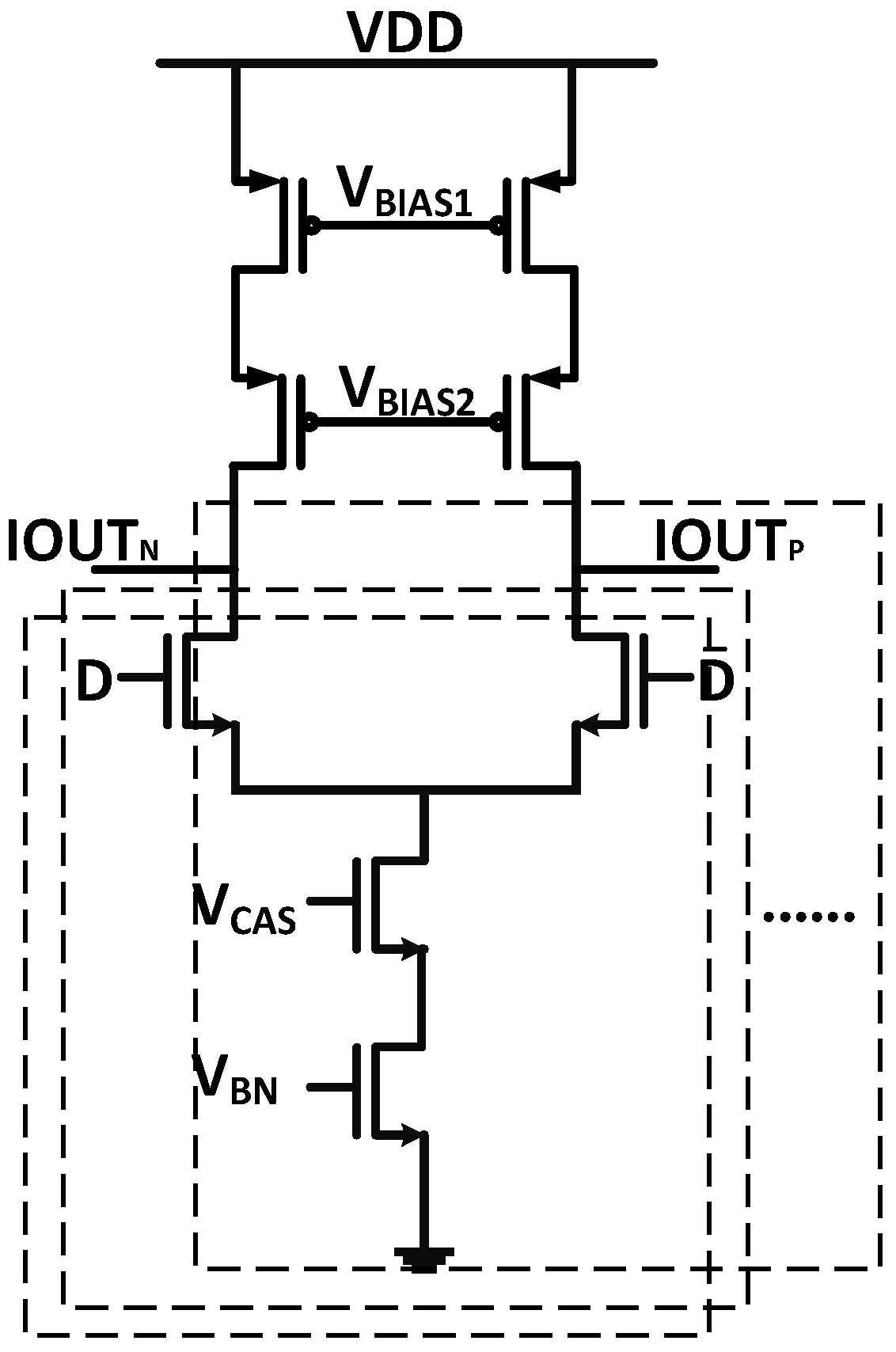

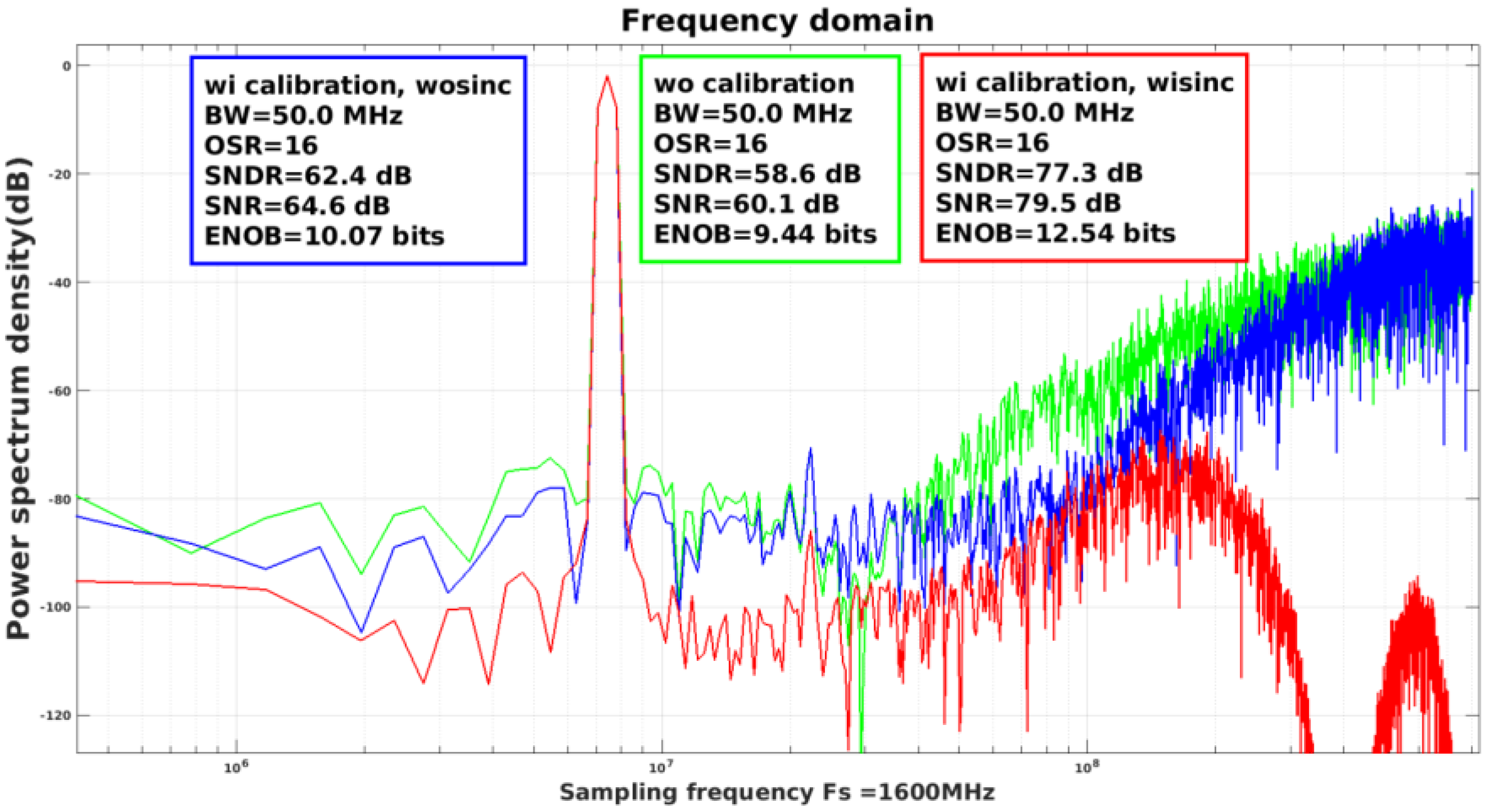
| Opamp 1-1 GBW (Hz) | Opamp 1-2 GBW (Hz) | Opamp 2-1 GBW (Hz) | Opamp 2-2 GBW (Hz) | Wo Calibration ENOB (bit) | Foreground Calibration ENOB (bit) | Background Calibration ENOB (bit) | |
|---|---|---|---|---|---|---|---|
| 1 | 60, 8 G | 60, 8 G | 60, 8 G | 60, 8 G | 14.18 | 13.90 | 14.05 |
| 2 | 40, 4.8 G | 40, 4.8 G | 40, 4.8 G | 40, 4.8 G | 12.54 | 14.33 | 13.87 |
| 3 | 34, 3.2 G | 34, 3.2 G | 34, 3.2 G | 34, 3.2 G | 11.76 | 14.08 | 13.25 |
| 4 | 30, 1.6 G | 30, 1.6 G | 30, 1.6 G | 30, 1.6 G | 10.75 | 13.50 | 12.78 |
| Characteristic | This Work |
|---|---|
| Family | Zynq-7020 |
| Device | xc7z020clg400-2 |
| Number of LUTs | 13,512/53,200 (25.4%) |
| Number of registers | 3753/106,400 (3.5%) |
| Frequency | 50 M |
| Number of sampling points required |
| This Work * | [12] | [18] | [29] | [30] | [31] | |
|---|---|---|---|---|---|---|
| Architecture | MASH 2-2 | MASH 0-3 | SMASH 3-1 | MASH 2-2 | MASH 3-1 | MASH 1-1-1 |
| Process (nm) | 40 | 28 | 28 | 40 | 65 | 40 |
| Supply (V) | 1.2/0.9 | 1.8/0.9/−1.0 | 1.2/1.5 | 1.1/1.15/2.5 | 1.0 | 1.8/1.1/1 |
| BW (Hz) | 50 M | 53 M | 50 M | 50 M | 10 M | 360 M |
| Fs (Hz) | 1.6 G | 3.2 G | 1.8 G | 1.0 G | 0.64 G | 5 G |
| SNDR (dB) | 76.8 | 71.4 | 74.9 | 74.4 | 77.3 | 65 |
| SNR (dB) | 78.3 | 83.1 | 76.8 | 75.8 | 79.8 | 65 |
| Power (mW) | 29.7 | 235 | 80.4 | 43.0 | 12 | 158 |
| FOMs (dB) ** | 169.1 | 155 | 162.8 | 165.1 | 167.8 | 159 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Shang, X.; Feng, H.; Xing, X. A Power-Efficient 50 MHz-BW 76.8 dB Signal-to-Noise-and-Distortion Ratio Continuous-Time 2-2 MASH Delta-Sigma Analog-to-Digital Converter with Digital Calibration. J. Low Power Electron. Appl. 2025, 15, 20. https://doi.org/10.3390/jlpea15020020
Li Z, Shang X, Feng H, Xing X. A Power-Efficient 50 MHz-BW 76.8 dB Signal-to-Noise-and-Distortion Ratio Continuous-Time 2-2 MASH Delta-Sigma Analog-to-Digital Converter with Digital Calibration. Journal of Low Power Electronics and Applications. 2025; 15(2):20. https://doi.org/10.3390/jlpea15020020
Chicago/Turabian StyleLi, Zhiyu, Xueqian Shang, Haigang Feng, and Xinpeng Xing. 2025. "A Power-Efficient 50 MHz-BW 76.8 dB Signal-to-Noise-and-Distortion Ratio Continuous-Time 2-2 MASH Delta-Sigma Analog-to-Digital Converter with Digital Calibration" Journal of Low Power Electronics and Applications 15, no. 2: 20. https://doi.org/10.3390/jlpea15020020
APA StyleLi, Z., Shang, X., Feng, H., & Xing, X. (2025). A Power-Efficient 50 MHz-BW 76.8 dB Signal-to-Noise-and-Distortion Ratio Continuous-Time 2-2 MASH Delta-Sigma Analog-to-Digital Converter with Digital Calibration. Journal of Low Power Electronics and Applications, 15(2), 20. https://doi.org/10.3390/jlpea15020020







