Alleviating the Communication Bottleneck in Neuromorphic Computing with Custom-Designed Spiking Neural Networks
Abstract
1. Introduction
2. Related Work
3. SNN Model
4. Storing and Communicating Information
4.1. Storing and Communicating with Values
4.2. Communicating with Time
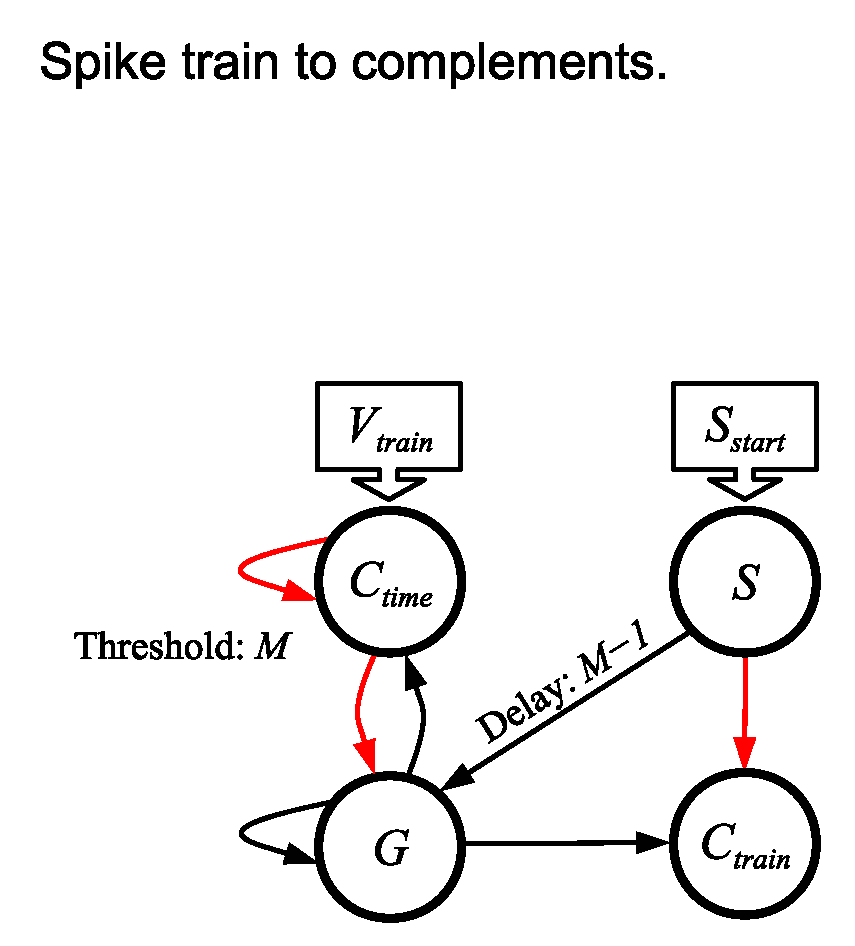
4.3. Communicating with Spike Trains
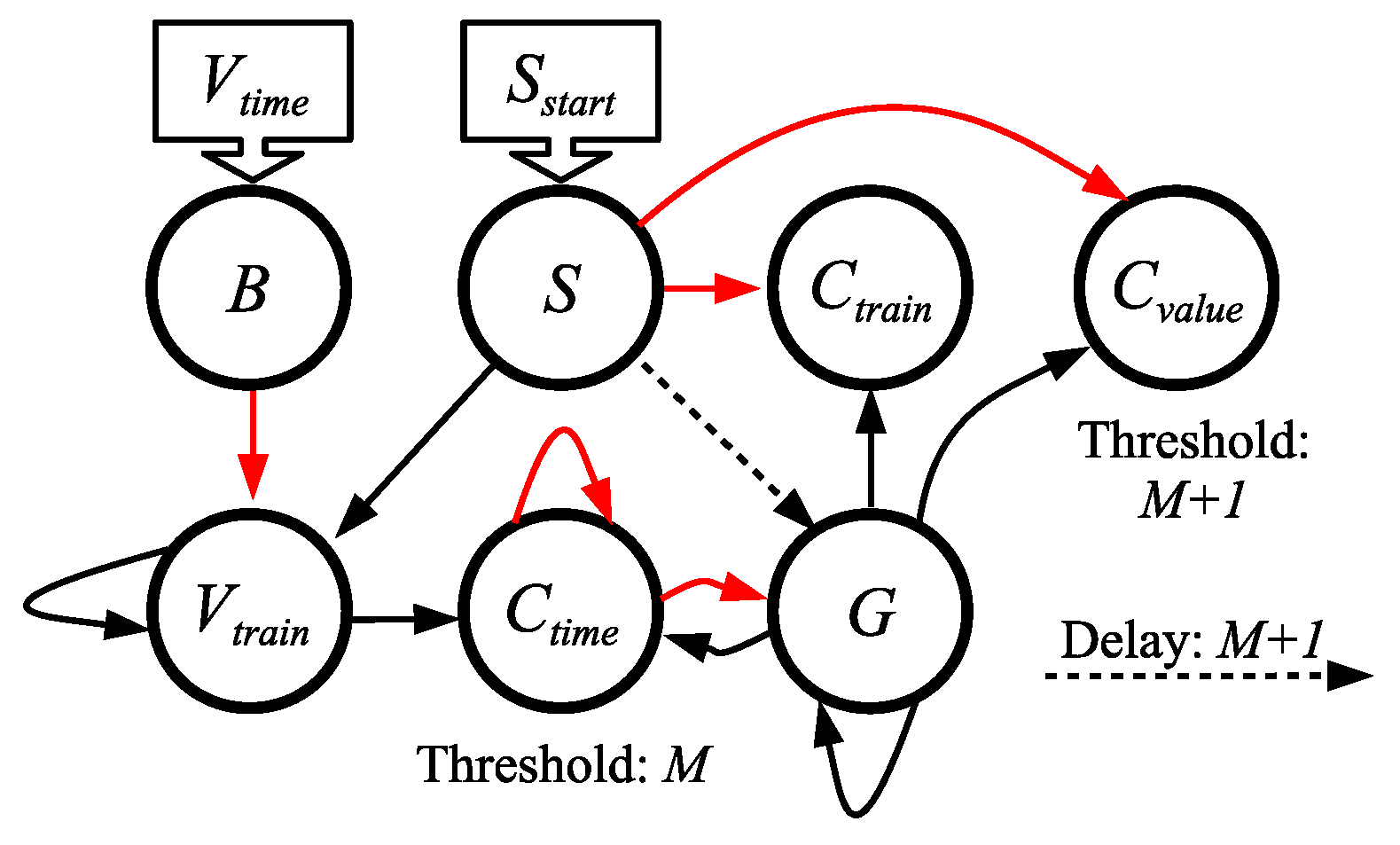
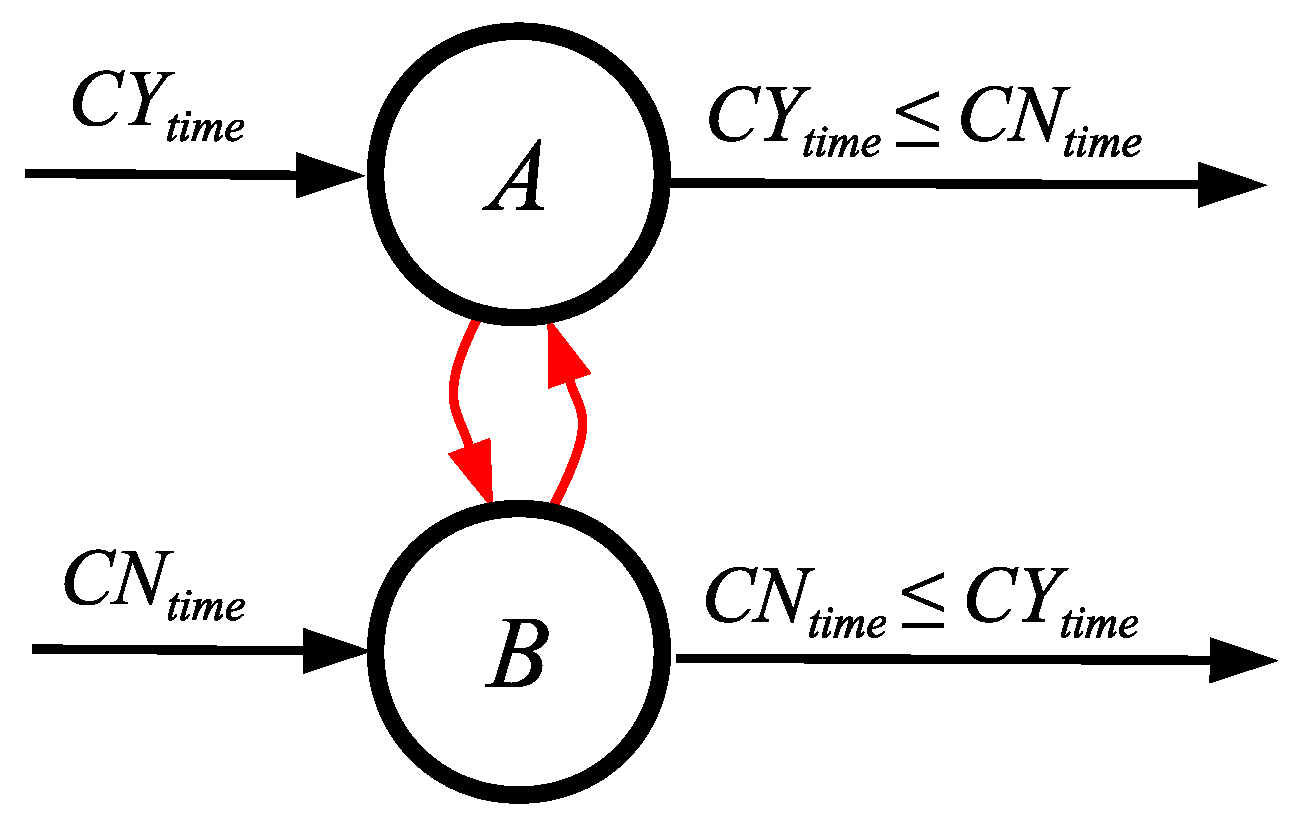
4.4. Complements and Strict Spike Trains
4.5. Summary
5. Conversion Networks
5.1.
5.2.
5.3.
- The neuron fires at timestep ().
- The neuron fires C times, once per timestep, starting at timestep 3 ().
- The neuron is guaranteed to have a potential of C after timesteps.
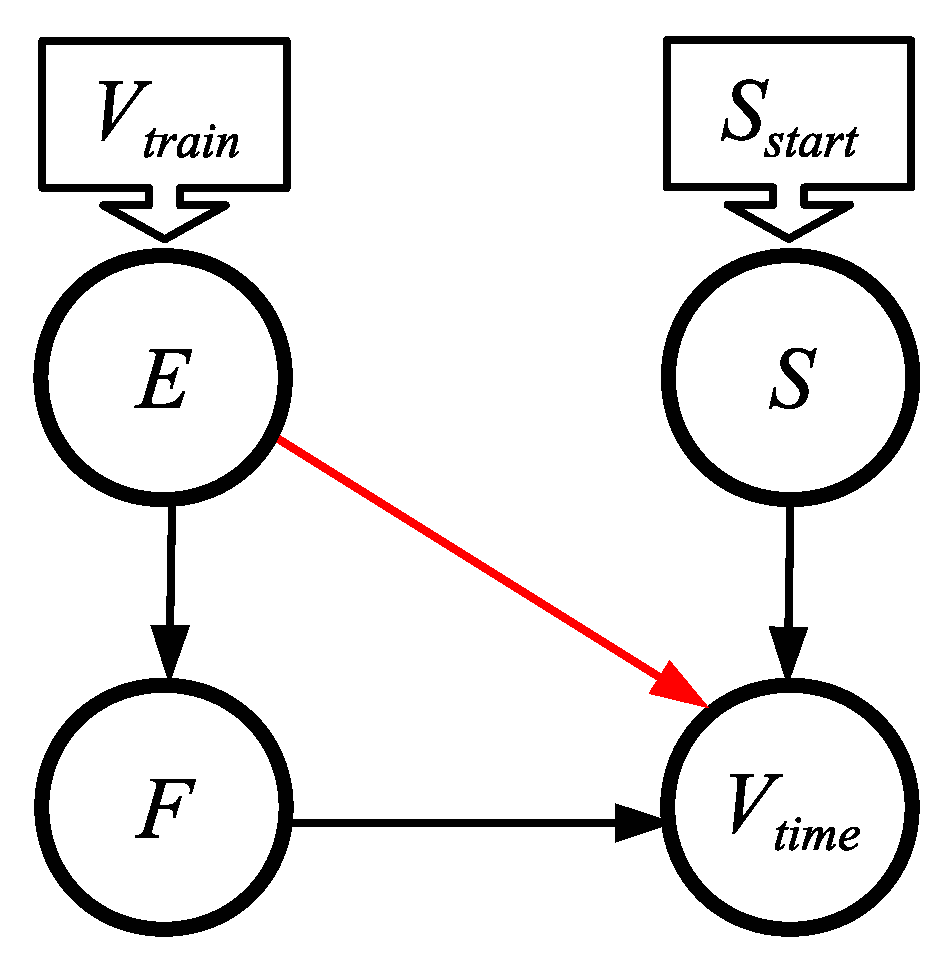
5.4.
5.5.
- The neuron fires at time . In other words, .
- The neuron fires C times, once per timestep, starting at timestep .
- The network must run for timesteps, after which point it may be reused.
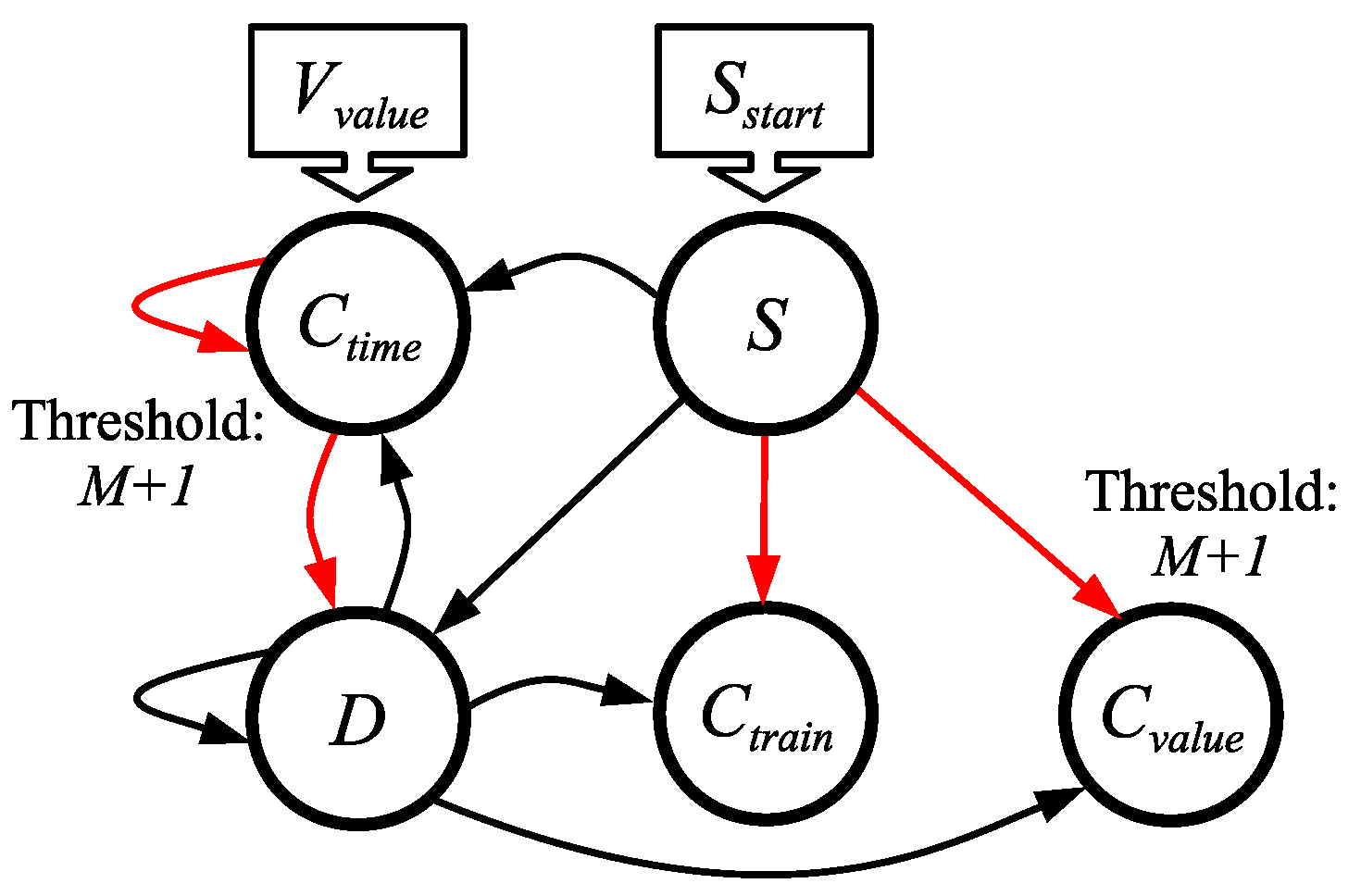
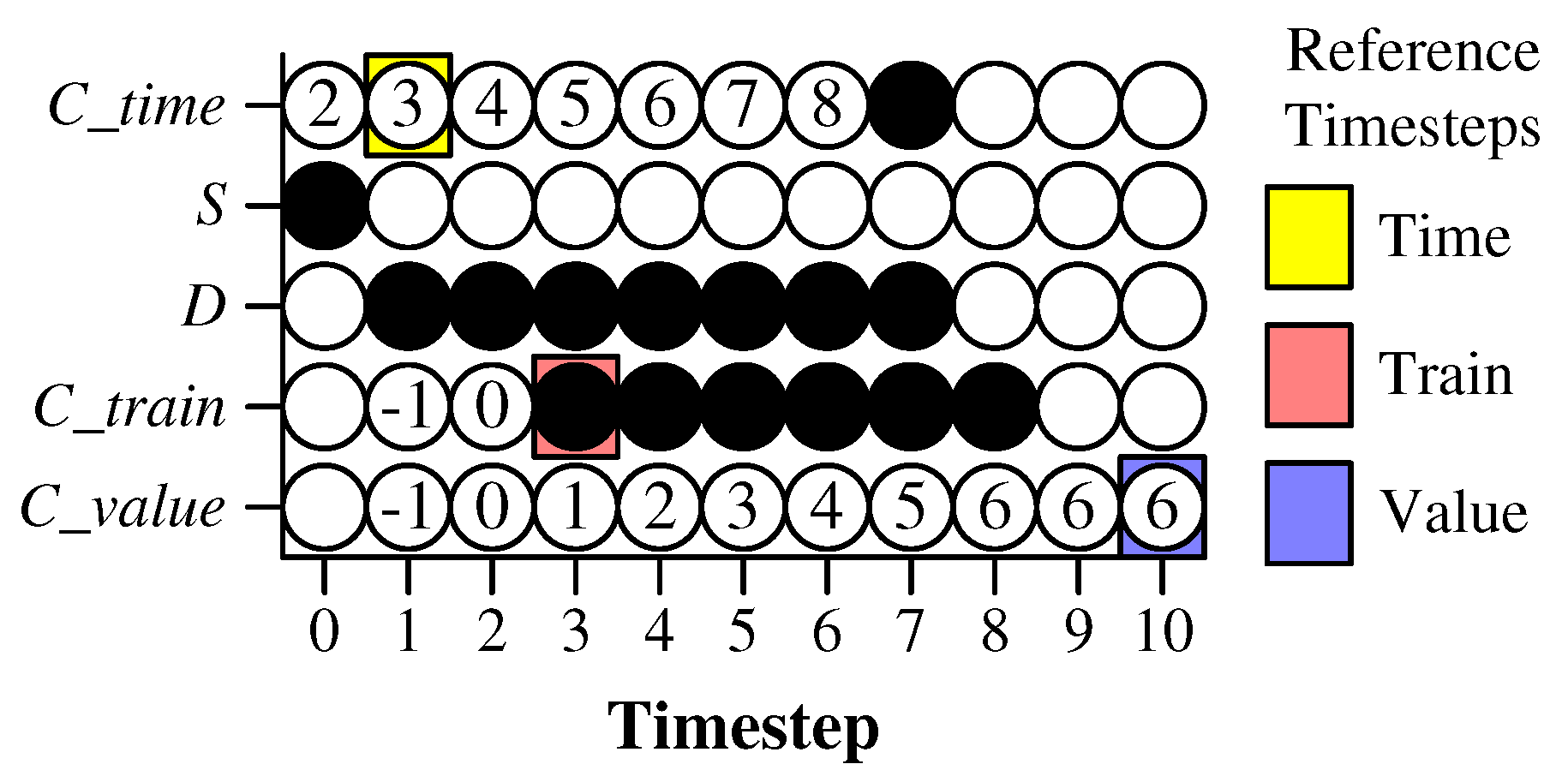
5.6.
- The value V is sent to at timestep 0.
- S is made to spike at timestep 0.
- spikes at timestep . Therefore, .
- spikes V times, one per timestep, starting at timestep .
- The network must run for timesteps.
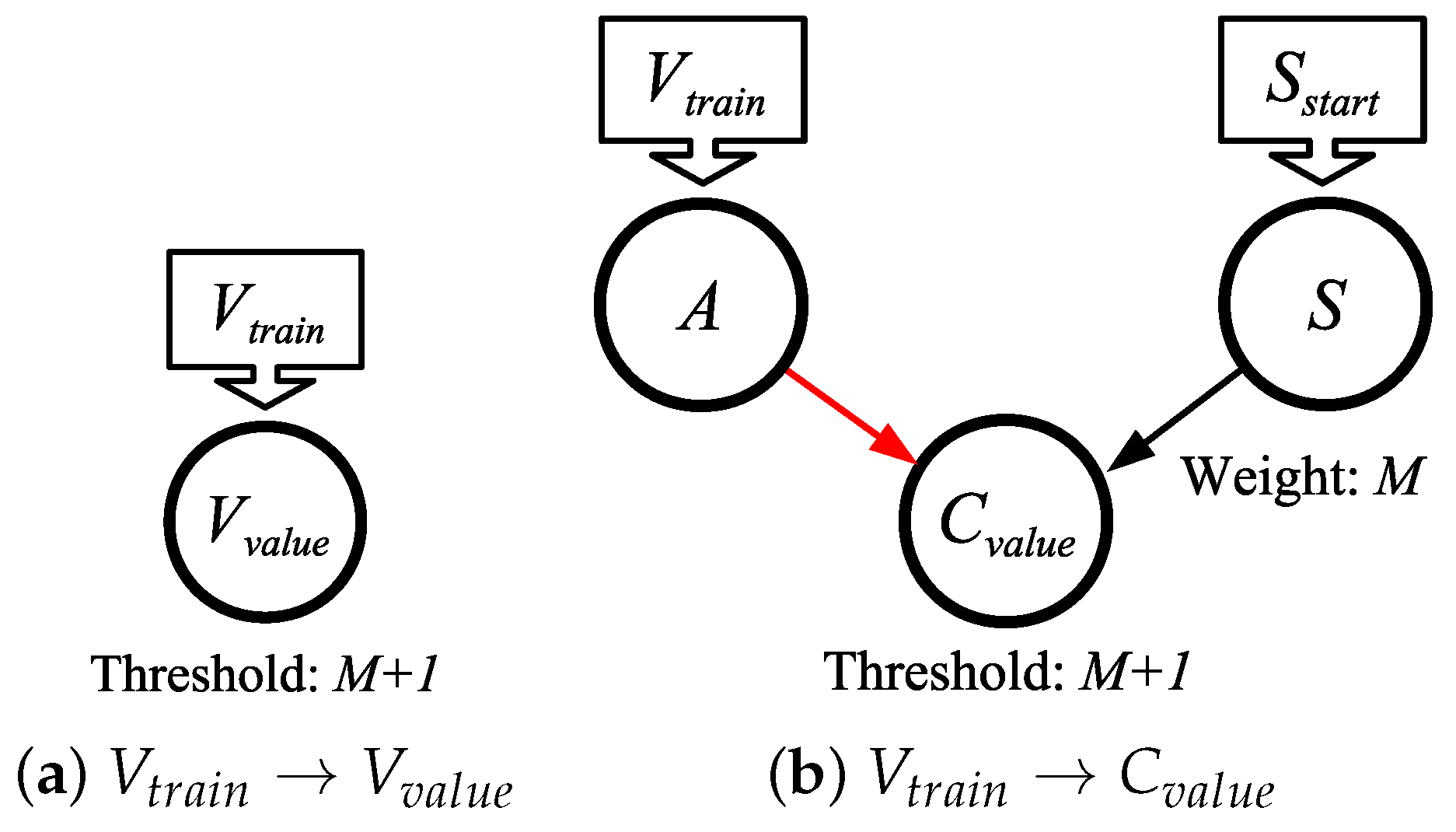
5.7.
- V is made to spike at timestep V.
- S is made to spike at timestep 0.
- spikes at timestep . Therefore, .
- spikes C times, one per timestep, starting at timestep .
- has a potential of V by timestep .
- If either or is not used, it may be deleted from the network.
- The network must run for timesteps if either or is used. Otherwise, it must run for timesteps.
5.8. Summary of Conversion Networks
- The figure that specifies the conversion.
- N: The number of neurons in the network, where neurons that are unnecessary for the conversion are deleted.
- S: The number of synapses in the network, where synapses that are unnecessary for the conversion are deleted.
- R: The reference timestep for the conversion.
- T: The number of timesteps required to perform the conversion.
6. Case Studies/Experiments
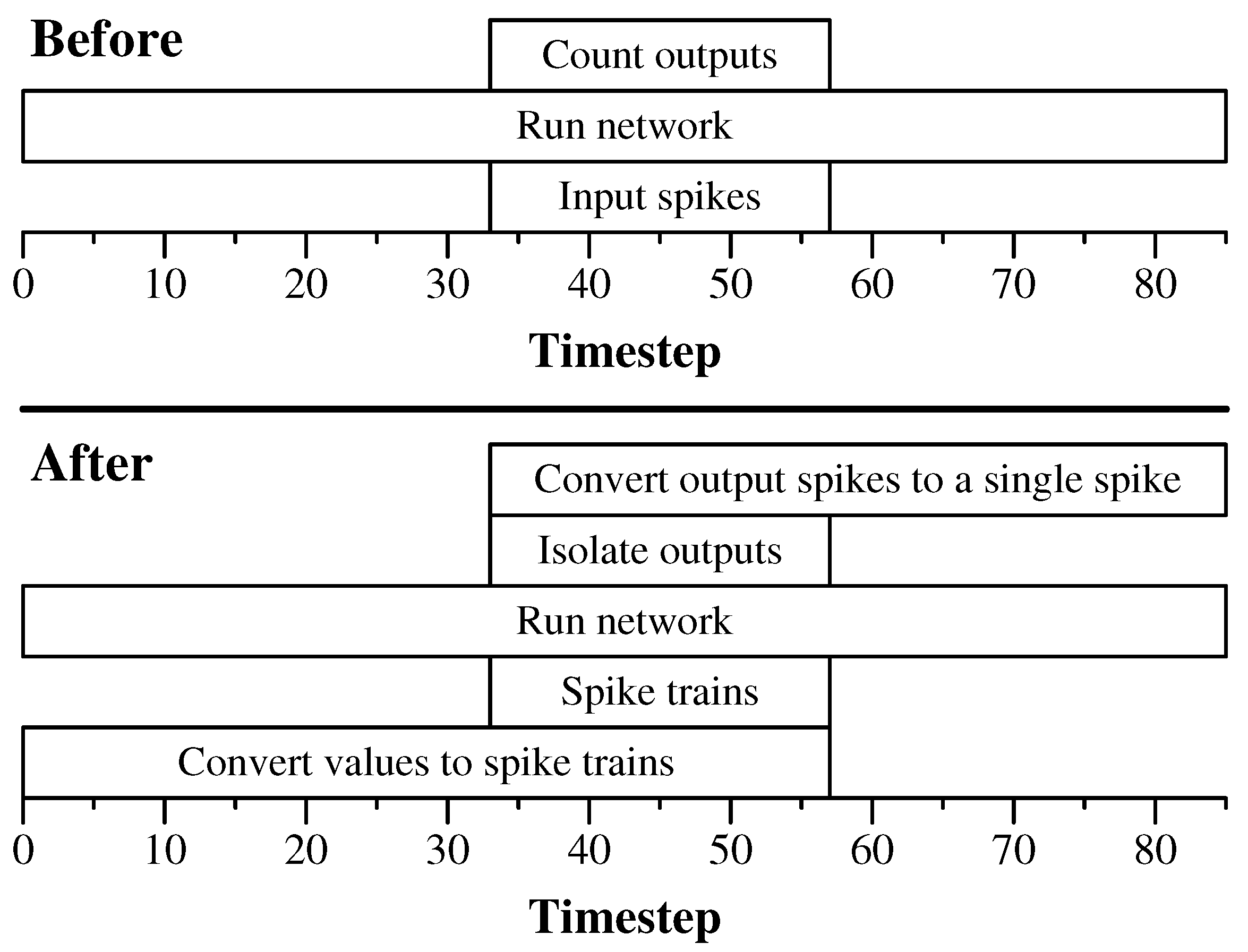
- The application has observations or features to send to the AI agent, which is implemented on an SNN that has been designed or trained specifically for the application. The application’s observations will be sent by a host.
- The host converts observations/features into spikes, using one of the three communication techniques described in Section 4 above, which are applied to specific input neurons of the SNN.
- The SNN runs for some number of timesteps, which is application-specific.
- The spiking behavior of specific output neurons is communicated to the host, which converts the spikes to actions for the application (or a classification in the case of a classification application). The communication from the SNN to the host is either by time or by spike train (lax).
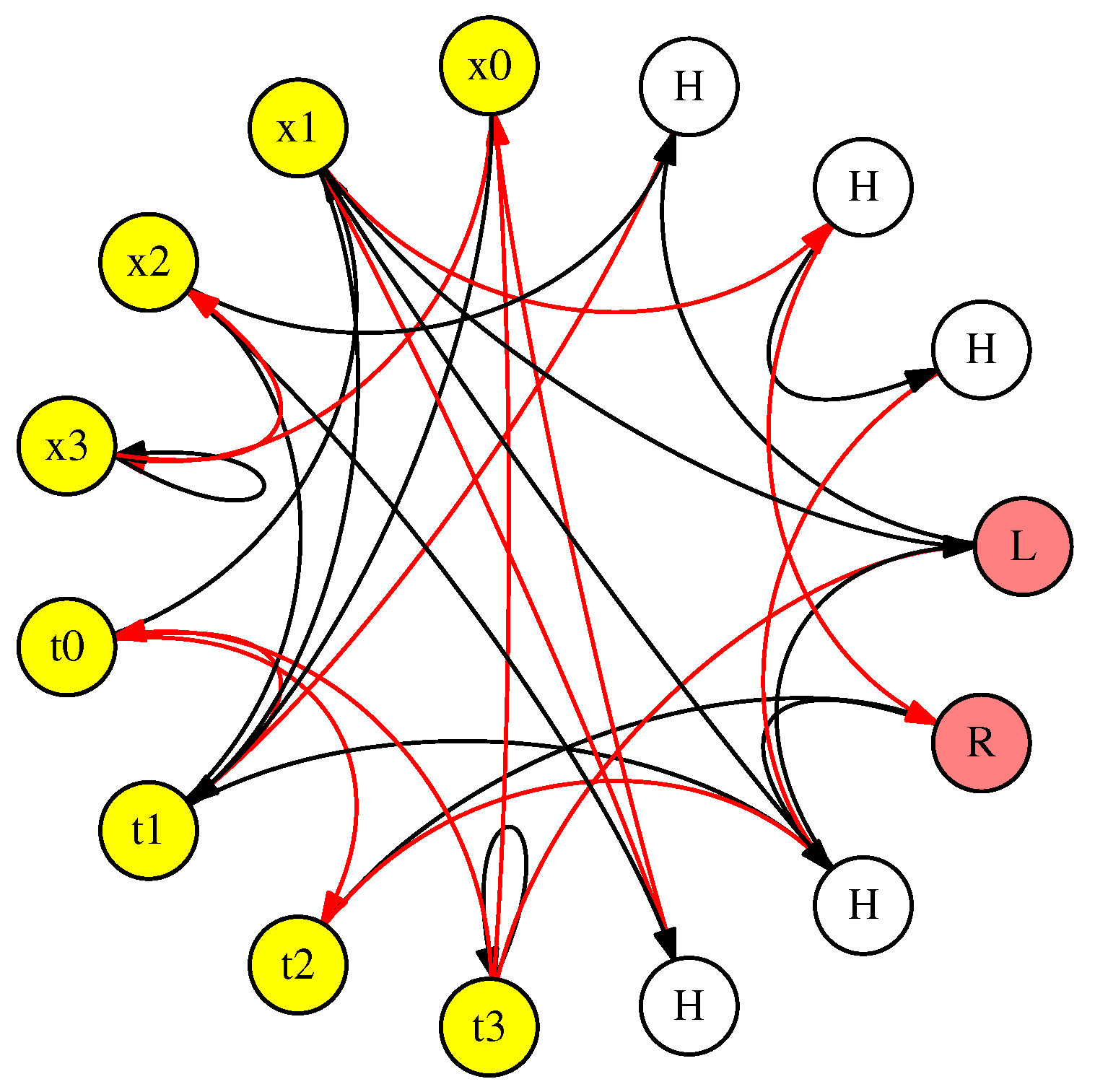
6.1. Case Study: Comparing Spike Counts
- C fires if and only if A and B both fire;
- D fires if and only if A fires, but B does not;
- E fires if and only if B fires, but A does not.
6.2. Experiment: Inference with the MAGIC Dataset
6.2.1. Training
- Value: The features are converted into values between 0 and 127 using linear interpolation, and these values are applied to the input neurons.
- Time: The features are converted into times between 0 and 47, and each feature is encoded by a single spike applied to the appropriate input neuron at the encoded timestep. We also used values between 0 and 95.
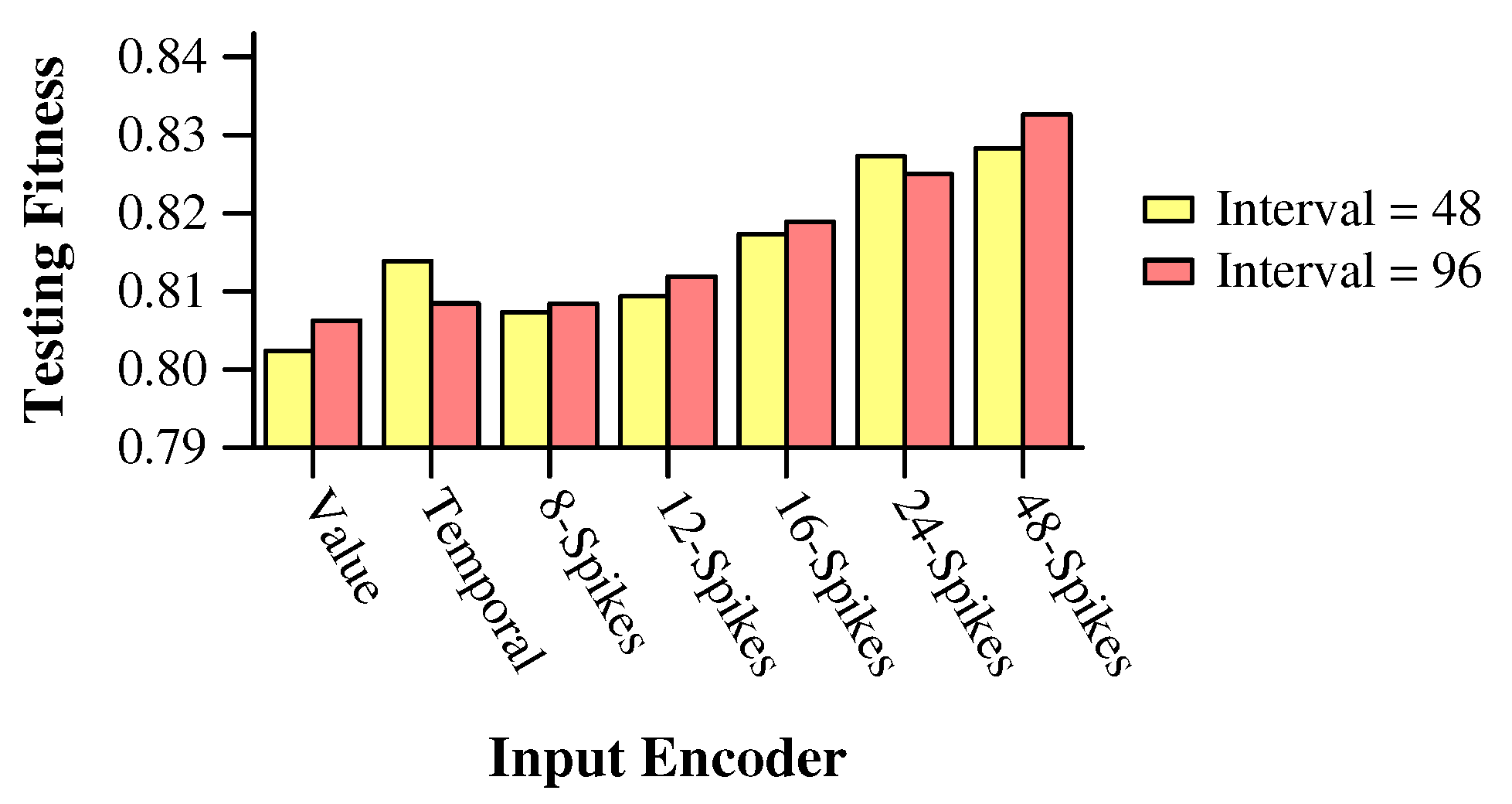
- Spike Trains: We set a maximum spike train size of 8, 12, 16, 24 or 48, and converted the features into a spike train whose size is between 1 and the maximum. We then applied the spike trains every n timesteps, where n equals 48 divided by the maximum spike train size, or 96 divided by the maximum spike train size.
6.2.2. Conversions to Improve Communication
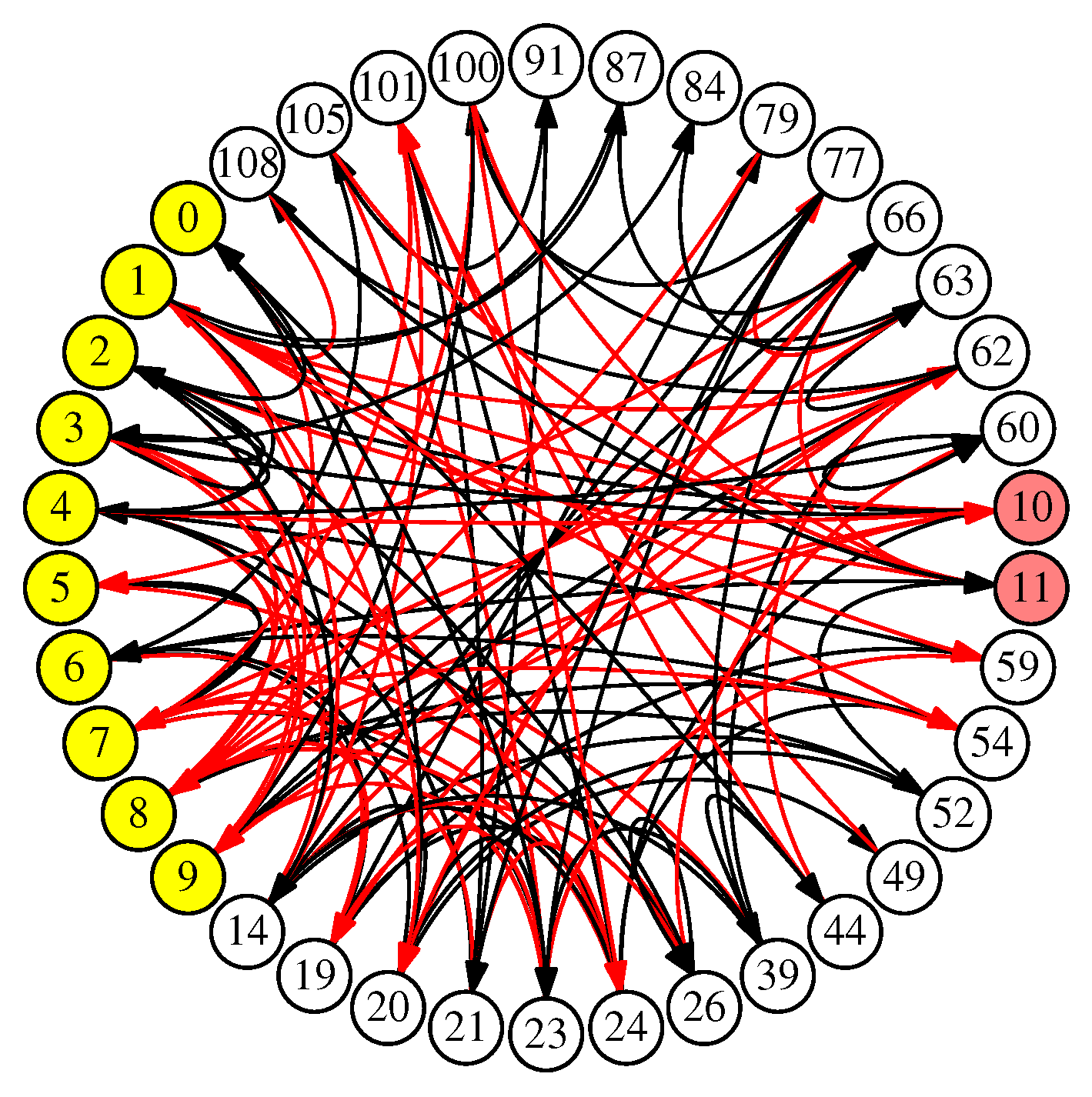
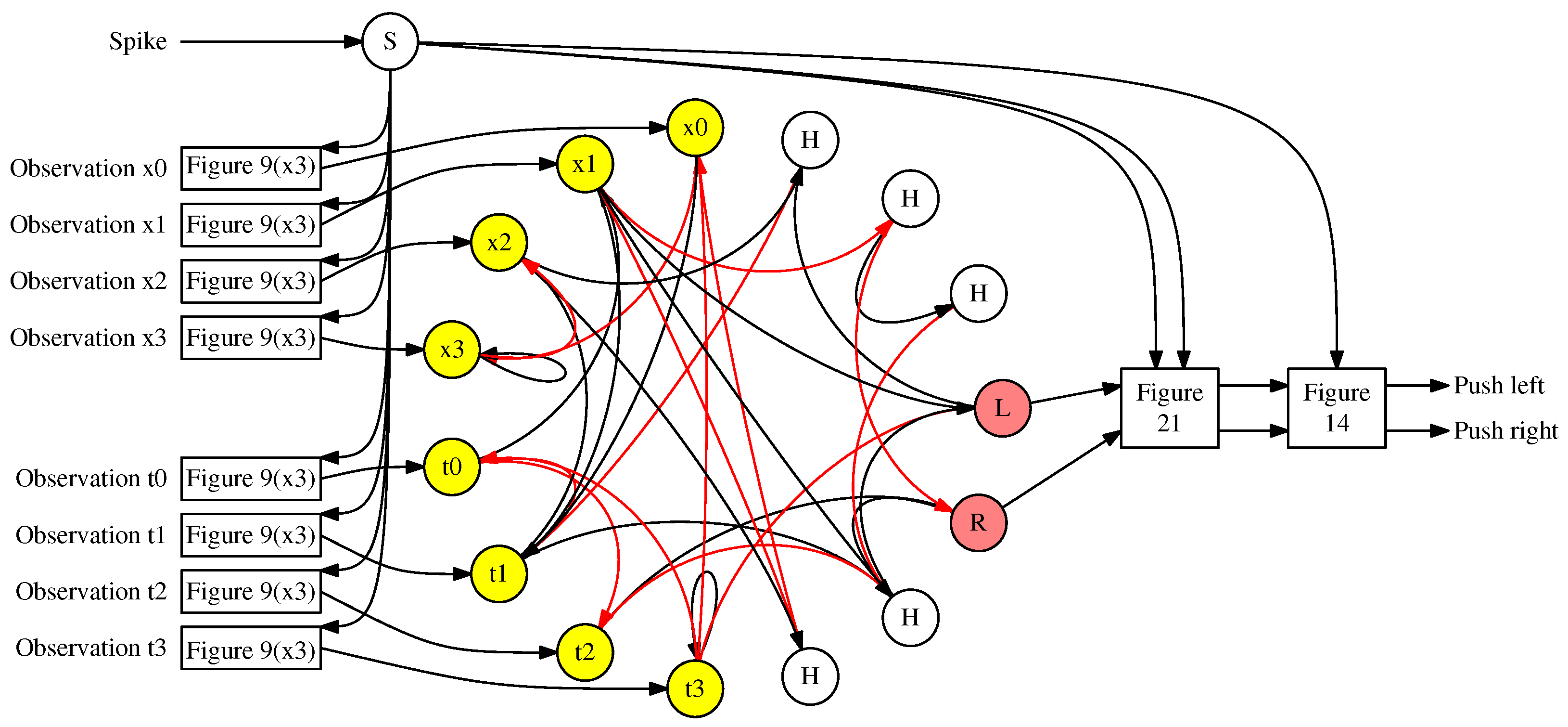
- Ten subnetworks are labeled “Figure 9(x2).” These convert the input features, that are applied to the SNN as single values, to spike trains of up to 48 spikes, applied every two timesteps. We discuss how to achieve “every two timesteps” below, but that is why the networks are labeled with “(x2).”
- The original network from Figure 16 that performs the classification on spike trains of up to 48 spikes, applied every two timesteps. As described above, this network runs for 128 timesteps, and then the spikes on its output neurons (labeled 10 and 11) are counted and compared to perform the classification.
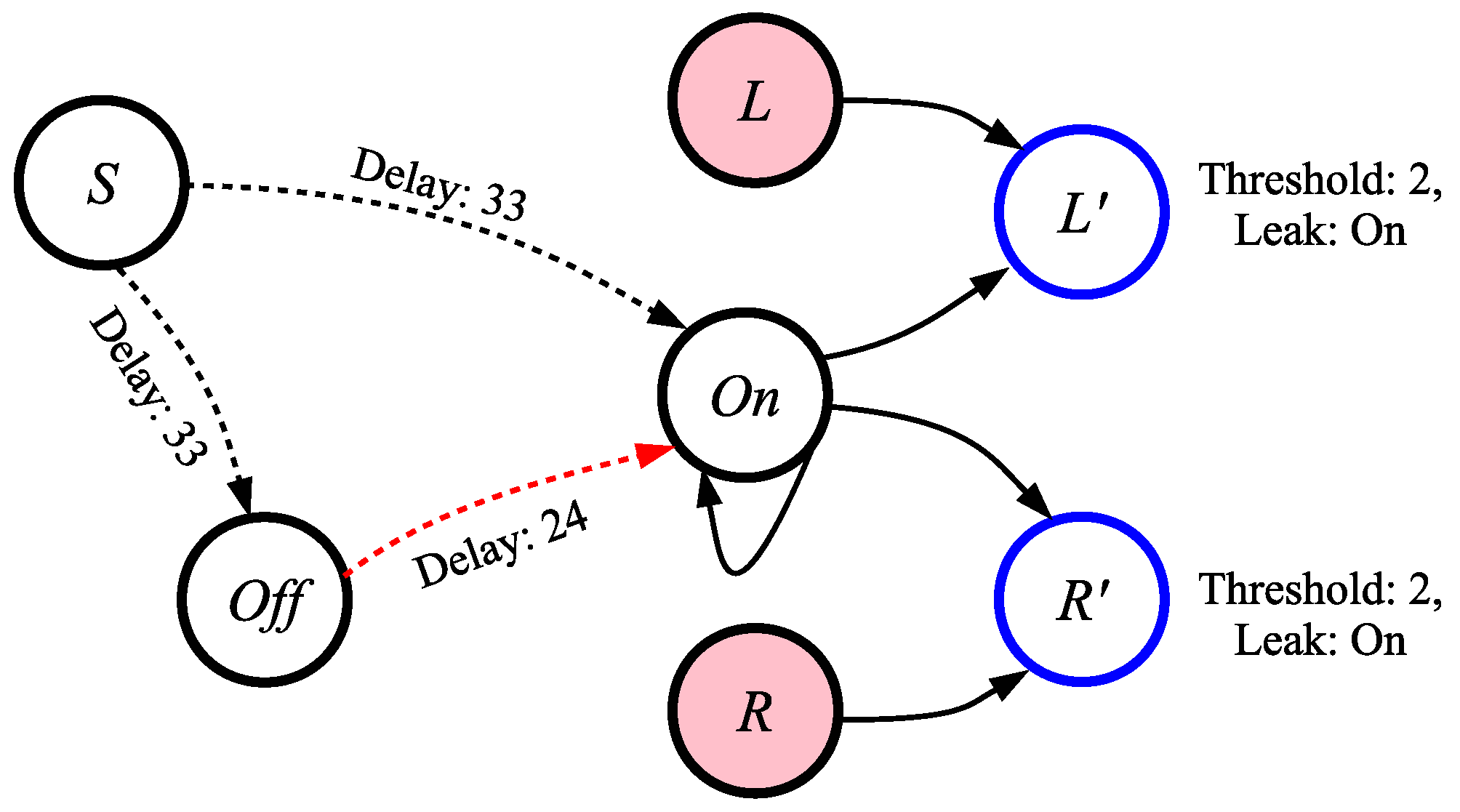
- The subnetwork labeled “Figure 14.” This network converts the output spikes from the original network into a single spike on one of two output neurons.
- The subnetwork composed of the K neuron and its synapses. The function of this subnetwork is to prevent neurons 10 and 11 from spiking when their 128 timesteps are finished, because the network needs to run extra timesteps to convert the output spikes.
6.2.3. Performance on FPGA
6.3. Experiment: The Cart–Pole Application
Performance on FPGA
7. Discussion
- Values may be stored in the network, but it requires a conversion to time or a spike train to “read” a value that is stored in the potential of a neuron.
- Spike trains communicate values from one neuron to another, but those trains must be converted into values to store them in a neuron. Spike trains are also inefficient as a mechanism to communicate with a host.
- Times communicate values from one neuron to another, but require reference times to have meaning. Like spike trains, they must be converted into values to store them in a neuron. They are efficient as a mechanism to communicate with a host because they only require one event.
- The network .
- A network to compare times and spike different output neurons as a result of differing spike times.
- A network from [18] that performs a binary AND operation to handle the specific case of two spikes arriving at the same time.
- An original network that takes spike trains as inputs and makes a binary decision based on spike counts for outputs.
- Separate networks for each input neuron.
- A subnetwork that isolates the output spikes during certain timesteps. This subnetwork was different in each experiment—the subnetwork in the MAGIC experiment disabled the output neurons when they no longer were to be counted, and the subnetwork in the Cart–Pole experiment used binary AND networks so that the outputs were only processed during the relevant timesteps.
- The network from Figure 14 that compares counts of output neurons and converts them to a single output spike.
8. Limitations
9. Online Resources
10. Conclusions
- We provided the network construction for a voting spike decoder algorithm.
- We demonstrated a classification inference speedup of 23.4× for a network running on an FPGA—all while increasing the network’s runtime and network size by 2.5×.
- We demonstrated a control inference speedup of 4.3× for the classic Cart–Pole application, which in turn makes its implementation possible in an embedded setting operating at 50 Hz.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FPGA | Field-Programmable Gate Array |
| PCIe | Peripheral Component Interconnect Express |
| RISP | Reduced Instruction Spiking Processor [7] |
| SNN | Spiking Neural Network |
| UART | Universal Asynchronous Receiver/Transmitter |
References
- Roy, K.; Jaiswal, A.; Panda, P. Towards spike-based machine intelligence with neuromorphic computing. Nature 2019, 575, 607–617. [Google Scholar] [CrossRef] [PubMed]
- Davies, M.; Wild, A.; Orchard, G.; Sandamirskaya, Y.; Fonseca Guerra, G.A.; Joshi, P.; Plank, P.; Risbud, S.R. Advancing Neuromorphic Computing With Loihi: A Survey of Results and Outlook. Proc. IEEE 2021, 109, 911–934. [Google Scholar] [CrossRef]
- Davies, M.; Srinivasa, N.; Lin, T.H.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A Neuromorphic Manycore Processor with On-Chip Learning. IEEE Micro 2018, 38, 82–99. [Google Scholar] [CrossRef]
- Akopyan, F.; Sawada, J.; Cassidy, A.; Alvarez-Icaza, R.; Arthur, J.; Merolla, P.; Imam, N.; Nakamura, Y.; Datta, P.; Nam, G.J.; et al. TrueNorth: Design and Tool Flow of a 65 mW 1 Million Neuron Programmable Neurosynaptic Chip. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2015, 34, 1537–1557. [Google Scholar] [CrossRef]
- Brainchip: Essential AI. Temporal Event-Based Neural Networks: A New Approach to Temporal Processing. 2023. Available online: https://brainchip.com/wp-content/uploads/2023/06/TENNs_Whitepaper_Final.pdf (accessed on 21 July 2025).
- Schuman, C.D.; Potok, T.E.; Patton, R.M.; Birdwell, J.D.; Dean, M.E.; Rose, G.S.; Plank, J.S. A Survey of Neuromorphic Computing and Neural Networks in Hardware. arXiv 2017, arXiv:1705.06963. [Google Scholar] [CrossRef]
- Plank, J.S.; Dent, K.E.M.; Gullett, B.; Rizzo, C.P.; Schuman, C.D. The RISP Neuroprocessor—Open Source Support for Embedded Neuromorphic Computing. In Proceedings of the IEEE International Conference on Rebooting Computing (ICRC), San Diego, CA, USA, 16–17 December 2024. [Google Scholar]
- Betzel, F.; Khatamifard, K.; Suresh, H.; Lilja, D.J.; Sartori, J.; Karpuzcu, U. Approximate communication: Techniques for reducing communication bottlenecks in large-scale parallel systems. ACM Comput. Surv. (CSUR) 2018, 51, 1–32. [Google Scholar] [CrossRef]
- Bergman, K.; Borkar, S.; Campbell, D.; Carlson, W.; Dally, W.; Denneau, M.; Franzon, P.; Harrod, W.; Hill, K.; Hiller, J.; et al. Exascale Computing Study: Technology Challenges in Achieving Exascale Systems; Tech. Rep.; Defense Advanced Research Projects Agency 804 Information Processing Techniques Office (DARPA IPTO): Arlington, VA, USA, 2008; Volume 15, p. 181. [Google Scholar]
- Amdahl, G.M. Validity of the single processor approach to achieving large scale computing capabilities. In Proceedings of the Spring Joint Computer Conference, New York, NY, USA, 18–20 April 1967; pp. 483–485. [Google Scholar] [CrossRef]
- Mysore, N.; Hota, G.; Deiss, S.R.; Pedroni, B.U.; Cauwenberghs, G. Hierarchical network connectivity and partitioning for reconfigurable large-scale neuromorphic systems. Front. Neurosci. 2022, 15, 797654. [Google Scholar] [CrossRef]
- Maheshwari, D.; Young, A.; Date, P.; Kulkarni, S.; Witherspoon, B.; Miniskar, N.R. An FPGA-Based Neuromorphic Processor with All-to-All Connectivity. In Proceedings of the IEEE International Conference on Rebooting Computing (ICRC), San Diego, CA, USA, 5–6 December 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Shrestha, S.B.; Timcheck, J.; Frady, P.; Campos-Macias, L.; Davies, M. Efficient video and audio processing with loihi 2. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 13481–13485. [Google Scholar]
- Paredes-Vallés, F.; Hagenaars, J.J.; Dupeyroux, J.; Stroobants, S.; Xu, Y.; de Croon, G.C. Fully neuromorphic vision and control for autonomous drone flight. Sci. Robot. 2024, 9, eadi0591. [Google Scholar] [CrossRef]
- Kampakis, S. Improved Izhikevich neurons for spiking neural networks. Soft Comput. 2011, 16, 943–953. [Google Scholar] [CrossRef]
- Chimmula, V.K.R.; Zhang, L.; Palliath, D.; Kumar, A. Improved Spiking Neural Networks with multiple neurons for digit recognition. In Proceedings of the 11th International Conference on Awareness Science and Technology (iCAST), Qingdao, China, 7–9 December 2020. [Google Scholar]
- Mitchell, J.P.; Schuman, C.D.; Patton, R.M.; Potok, T.E. Caspian: A Neuromorphic Development Platform. In Proceedings of the NICE: Neuro-Inspired Computational Elements Workshop, Heidelberg, Germany, 17–20 March 2020; ACM: New York, NY, USA, 2020. [Google Scholar]
- Plank, J.S.; Zheng, C.; Schuman, C.D.; Dean, C. Spiking Neuromorphic Networks for Binary Tasks. In Proceedings of the International Conference on Neuromorphic Computing Systems (ICONS), Knoxville, TN, USA, 27–29 July 2021; ACM: New York, NY, USA, 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Reeb, N.; Lopez-Randulfe, J.; Dietrich, R.; Knoll, A.C. Range and angle estimation with spiking neural resonators for FMCW radar. Neuromorphic Comput. Eng. 2025, 5, 024009. [Google Scholar] [CrossRef]
- Yanguas-Gil, A. Fast, Smart Neuromorphic Sensors based on Heterogeneous Networks and Mixed Encodings. In Proceedings of the 43rd Annual GOMACTech Conference, Miami, FL, USA, 17–20 March 2018. [Google Scholar]
- Bauer, F.; Muir, D.R.; Indiveri, G. Real-Time Ultra-Low Power ECG Anomaly Detection Using an Event-Driven Neuromorphic Processor. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 1575–1582. [Google Scholar] [CrossRef] [PubMed]
- Rizzo, C.P.; Schuman, C.D.; Plank, J.S. Neuromorphic Downsampling of Event-Based Camera Output. In Proceedings of the NICE: Neuro-Inspired Computational Elements Workshop, San Antonio, TX, USA, 11–14 April 2023; ACM: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Verzi, S.J.; Rothganger, F.; Parekh, O.J.; Quach, T.; Miner, N.E.; Vineyard, C.M.; James, C.D.; Aimone, J.B. Computing with spikes: The advantage of fine-grained timing. Neural Comput. 2018, 30, 2660–2690. [Google Scholar] [CrossRef] [PubMed]
- Severa, W.; Parekh, O.; Carlson, K.D.; James, C.D.; Aimone, J.B. Spiking network algorithms for scientific computing. In Proceedings of the IEEE International Conference on Rebooting Computing (ICRC), San Diego, CA, USA, 17–19 October 2016. [Google Scholar] [CrossRef]
- Smith, J.D.; Severa, W.; Hill, A.J.; Reeder, L.; Franke, B.; Lehoucq, R.B.; Parekh, O.D.; Aimone, J.B. Solving a steady-state PDE using spiking networks and neuromorphic hardware. In Proceedings of the International Conference on Neuromorphic Computing Systems (ICONS), Arlington, VA, USA, 30 July–2 August 2020; ACM: New York, NY, USA, 2020; pp. 1–8. [Google Scholar]
- Monaco, J.V.; Vindiola, M.M. Integer factorization with a neuromorphic sieve. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–4. [Google Scholar]
- Monaco, J.V.; Vindiola, M.M. Factoring Integers With a Brain-Inspired Computer. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 1051–1062. [Google Scholar] [CrossRef]
- Blouw, P.; Choo, X.; Hunsberger, E.; Eliasmith, C. Benchmarking Keyword Spotting Efficiency on Neuromorphic Hardware. In Proceedings of the Neuro Inspired Computational Elements (NICE), Albany, NY, USA, 26–28 March 2019; ACM: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Vogginer, B.; Rostami, A.; Jain, V.; Arfa, S.; Hantch, A.; Kappel, D.; Schafer, M.; Faltings, U.; Gonzalez, H.A.; Liu, C.; et al. Neuromorphic hardware for sustainable AI data centers. arXiv 2024, arXiv:2402.02521. [Google Scholar] [CrossRef]
- Yan, Z.; Bai, Z.; Wong, W.F. Reconsidering the energy efficiency of spiking neural networks. arXiv 2024, arXiv:2409.08290. [Google Scholar]
- Pearson, M.J.; Pipe, A.G.; Mitchinson, B.; Gurney, K.; Melhuish, C.; Gihespy, I.; Nibouche, M. Implementing spiking neural networks for real-time signal-processing and control applications: A model-validated FPGA approach. IEEE Trans. Neural Netw. 2007, 18, 1472–1487. [Google Scholar] [CrossRef]
- Cassidy, A.; Denham, S.; Kanold, P.; Andreou, A. FPGA based silicon spiking neural array. In Proceedings of the IEEE Biomedical Circuits and Systems Conference, Montreal, QC, Canada, 27–30 November 2007. [Google Scholar] [CrossRef]
- Schoenauer, T.; Atasoy, S.; Mehrtash, N.; Klar, H. NeuroPipe-Chip: A digital neuro-processor for spiking neural networks. IEEE Trans. Neural Netw. 2002, 13, 205–213. [Google Scholar] [CrossRef][Green Version]
- Schuman, C.D.; Rizzo, C.; McDonald-Carmack, J.; Skuda, N.; Plank, J.S. Evaluating Encoding and Decoding Approaches for Spiking Neuromorphic Systems. In Proceedings of the International Conference on Neuromorphic Computing Systems (ICONS), Knoxville, TN, USA, 27–29 July 2022; ACM: New York, NY, USA, 2022; pp. 1–10. [Google Scholar]
- Shrestha, S.B.; Orchard, G. SLAYER: Spike Layer Error Reassignment in Time. In Advances in Neural Information Processing Systems 31; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; pp. 1412–1421. [Google Scholar]
- Viale, A.; Marchisio, A.; Martina, M.; Masera, G.; Shafique, M. CarSNN: An Efficient Spiking Neural Network for Event-Based Autonomous Cars on the Loihi Neuromorphic Research Processor. In Proceedings of the IJCNN: The International Joint Conference on Neural Networks, Shenzhen, China, 18–20 July 2021. [Google Scholar] [CrossRef]
- Bock, R. MAGIC Gamma Telescope. UCI Machine Learning Repository; UCI: Irvine, CA, USA, 2004. [Google Scholar] [CrossRef]
- Schuman, C.D.; Mitchell, J.P.; Patton, R.M.; Potok, T.E.; Plank, J.S. Evolutionary Optimization for Neuromorphic Systems. In Proceedings of the NICE: Neuro-Inspired Computational Elements Workshop, Heidelberg, Germany, 24–26 March 2020. [Google Scholar]
- Anderson, C.W. Learning to control an inverted pendulum using neural networks. Control Syst. Mag. 1989, 9, 31–37. [Google Scholar] [CrossRef]
- Plank, J.S.; Rizzo, C.P.; White, C.A.; Schuman, C.D. The Cart-Pole Application as a Benchmark for Neuromorphic Computing. J. Low Power Electron. Appl. 2025, 15, 5. [Google Scholar] [CrossRef]
- Aimone, J.B.; Hill, A.J.; Severa, W.M.; Vineyard, C.M. Spiking Neural Streaming Binary Arithmetic. In Proceedings of the IEEE International Conference on Rebooting Computing (ICRC), Los Alamitos, CA, USA, 30 November–2 December 2021. [Google Scholar] [CrossRef]
- Wurm, A.; Seay, R.; Date, P.; Kulkarni, S.; Young, A.; Vetter, J. Arithmetic Primitives for Efficient Neuromorphic Computing. In Proceedings of the IEEE International Conference on Rebooting Computing (ICRC), San Diego, CA, USA, 5–6 December 2023. [Google Scholar] [CrossRef]
- Aimone, J.B.; Severa, W.; Vineyard, C.M. Composing neural algorithms with Fugu. In Proceedings of the International Conference on Neuromorphic Computing Systems (ICONS), Knoxville, TN, USA, 23–25 July 2019; ACM: New York, NY, USA, 2019; pp. 1–8. [Google Scholar]
- Ali, A.H.; Navardi, M.; Mohsenin, T. Energy-Aware FPGA Implementation of Spiking Neural Network with LIF Neurons. arXiv 2024, arXiv:2411.01628. [Google Scholar] [CrossRef]
- Date, P.; Gunaratne, C.; Kulkarni, S.; Patton, R.; Coletti, M.; Potok, T. SuperNeuro: A Fast and Scalable Simulator for Neuromorphic Computing. In Proceedings of the International Conference on Neuromorphic Computing Systems (ICONS), Santa Fe, NM, USA, 1–3 August 2023; ACM: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Cauwenberghs, G.; Neugebauer, C.F.; Agranat, A.J.; Yariv, A. Large Scale Optoelectronic Integration of Asynchronous Analog Neural Networks. In Proceedings of the International Neural Network Conference, Paris, France, 9–13 July 1990; Springer: Berlin/Heidelberg, Germany, 1990; pp. 551–554. [Google Scholar]
- Jacobs-Gedrim, R.B.; Agarwal, S.; Knisely, K.E.; Stevens, J.E.; van Heukelom, M.S.; Hughard, D.R.; Niroula, J.; James, C.D.; Marinella, M.J. Impact of Linearity and Write Noise of Analog Resistive Memory Devices in a Neural Algorithm Accelerator. In Proceedings of the IEEE International Conference on Rebooting Computing (ICRC 2017), Washington, DC, USA, 8–9 November 2017; pp. 160–169. [Google Scholar]
- Venker, J.S.; Vincent, L.; Dix, J. A Low-Power Analog Cell for Implementing Spiking Neural Networks in 65 nm CMOS. J. Low Power Electron. Appl. 2024, 13, 55. [Google Scholar] [CrossRef]
- Hazan, A.; Tsur, E.E. Neuromorphic Analog Implementation of Neural Engineering Framework-Inspired Spiking Neuron for High-Dimensional Representation. Front. Neurosci. 2021, 15, 627221. [Google Scholar] [CrossRef]
- Ma, G.; Yan, R.; Tang, H. Exploiting noise as a resource for computation and learning in spiking neural networks. Patterns 2023, 4, 100831. [Google Scholar] [CrossRef]
- Jiang, Y.; Lu, S.; Sengupta, A. Stochastic Spiking Neural Networks with First-to-Spike Coding. arXiv 2024, arXiv:2404.17719. [Google Scholar]
- Fonseca Guerra, G.A.; Furber, S.B. Using stochastic spiking neural networks on SpiNNaker to solve constraint satisfaction problems. Front. Neurosci. 2017, 11, 714. [Google Scholar] [CrossRef]
- Eshraghian, J.K.; Ward, M.; Neftci, E.; Wang, X.; Lenz, G.; Dwivedi, G.; Bennamoun, M.; Jeong, D.S.; Lu, W.D. Training spiking neural networks using lessons from deep learning. Proc. IEEE 2023, 111, 1016–1054. [Google Scholar] [CrossRef]
- Labs, I. Lava Software Framework. 2025. Available online: https://lava-nc.org/ (accessed on 25 March 2025).









| Technique | Can Store | Can Communicate | Maximum Timesteps | ||
|---|---|---|---|---|---|
| From Host | To Host | Neuron to Neuron | |||
| Value | Yes | Yes | No | No | 1 |
| Time | No | Yes | Yes | Yes | M |
| Spike Train | No | Yes | Yes | Yes | M |
| Original (Figure 16) | Conversions (Figure 17) | |
|---|---|---|
| Neurons | 38 | 102 |
| Synapses | 120 | 304 |
| Timesteps | 128 | 361 |
| Max input spikes | 480 | 11 |
| Max output spikes | 256 | 1 |
| Parameter/Result | Original (Figure 16) | Conversions (Figure 17) |
|---|---|---|
| Input Packets | 199.5 | 14 |
| Output Packets | 198.2 | 9 |
| Communicated Bytes | 597.3 | 37 |
| Run Time (ms) | 56.57 | 2.42 |
| Speed-Up Factor | 1 | 23.40 |
| Static Power Consumption (W) | 0.072 | 0.072 |
| Dynamic Power Consumption (W) | 0.006 | 0.019 |
| Total Power (W) | 0.078 | 0.091 |
| Original (Figure 20) | Conversions (Figure 22) | |
|---|---|---|
| Neurons | 15 | 72 |
| Synapses | 30 | 188 |
| Timesteps | 85 | 85 |
| Max input spikes | 18 | 5 |
| Max output spikes | 48 | 1 |
| Parameter/Result | Original (Figure 20) | Conversions (Figure 22) |
|---|---|---|
| Input Packets | 30.19 | 7 |
| Output Packets | 30.76 | 5 |
| Communicated Bytes | 91.14 | 12 |
| Run Time (ms) | 76.62 | 12.16 |
| Speed-Up Factor | 1 | 4.31 |
| Static Power Consumption (W) | 0.072 | 0.072 |
| Dynamic Power Consumption (W) | 0.005 | 0.021 |
| Total Power (W) | 0.077 | 0.093 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plank, J.S.; Rizzo, C.P.; Gullett, B.; Dent, K.E.M.; Schuman, C.D. Alleviating the Communication Bottleneck in Neuromorphic Computing with Custom-Designed Spiking Neural Networks. J. Low Power Electron. Appl. 2025, 15, 50. https://doi.org/10.3390/jlpea15030050
Plank JS, Rizzo CP, Gullett B, Dent KEM, Schuman CD. Alleviating the Communication Bottleneck in Neuromorphic Computing with Custom-Designed Spiking Neural Networks. Journal of Low Power Electronics and Applications. 2025; 15(3):50. https://doi.org/10.3390/jlpea15030050
Chicago/Turabian StylePlank, James S., Charles P. Rizzo, Bryson Gullett, Keegan E. M. Dent, and Catherine D. Schuman. 2025. "Alleviating the Communication Bottleneck in Neuromorphic Computing with Custom-Designed Spiking Neural Networks" Journal of Low Power Electronics and Applications 15, no. 3: 50. https://doi.org/10.3390/jlpea15030050
APA StylePlank, J. S., Rizzo, C. P., Gullett, B., Dent, K. E. M., & Schuman, C. D. (2025). Alleviating the Communication Bottleneck in Neuromorphic Computing with Custom-Designed Spiking Neural Networks. Journal of Low Power Electronics and Applications, 15(3), 50. https://doi.org/10.3390/jlpea15030050






