Multi-Threshold Dual-Spacer Dual-Rail Delay-Insensitive Logic (MTD³L): A Low Overhead Secure IC Design Methodology

Abstract

As portable devices become more ubiquitous, data security in these devices is becoming increasingly important. Traditional circuit design techniques leave otherwise secure systems vulnerable due to the characteristics of the hardware implementation, rather than weaknesses in the security algorithms. These characteristics, called side-channels, are exploitable because they can be measured and correlated with processed data, potentially giving an attacker insight into the device’s secret data. Alternative design techniques such as dual-rail asynchronous designs are capable of minimizing these potential side-channels by decoupling them from the data being processed. However, these techniques are either expensive to implement compared to standard designs or leave exploitable imbalances in the dual-rail implementation itself. Multi-Threshold Dual-Spacer Dual-Rail Delay-Insensitive Logic (MTD³L) offers security by balancing side-channels both in general and between the dual-rail signals themselves, as well as reduction in circuit overhead compared to previous secure design techniques. Results show that the Advanced Encryption Standard (AES) cores designed using MTD³L exhibit similar security to previous secure techniques with substantially less area and energy overhead.

1. Introduction

As technology advances, more and more electronic devices store secret information such as bank accounts, identification numbers, passwords, and other private data that need to be secured from unauthorized access. Although originally considered safe and secure, hardware, just as software, is prone to attacks that force the targeted system to reveal sensitive data. Cryptographic algorithms are commonly used to protect such data. However, despite the mathematical robustness of these algorithms, their physical implementations are known to be susceptible to attacks. Non-invasive attacks on such devices take advantage of side-channel information leaked from the system, instead of trying to reverse engineer it. Such side-channel information can be power, timing, electromagnetism, and any other information that might be measured from the device during computation.

Most electronic devices running cryptographic algorithms are implemented in CMOS technology, where transistors act as voltage-controlled switches. While a circuit node is switching, electrons flow across the corresponding transistors to charge/discharge its load capacitance, thereby consuming power. Due to the fact that different transistors will be turned on/off while processing different data, causing different power consumption, power-based side­channel attacks can be implemented using the IC’s transient power data. These types of power-based attacks include Differential Power Analysis (DPA) [1], and Correlation Power Analysis (CPA) [2] (which uses the Pearson product-moment correlation coefficient to guess a key). In general, these attacks acquire transient power data while the target IC performs encryption/decryption on different texts, and then use statistical algorithms to derive the key. Power-based attacks are the most powerful and prevalently implemented side-channel attacks [3], and have been successfully implemented to crack almost all cryptographic algorithms on different platforms [4,5,6,7,8,9,10,11,12]. A number of methods have been proposed for mitigating power-based attacks by decoupling transient power consumption from the data being processed. Techniques based on balancing power fluctuation include new CMOS logic gates, which go through a full charge/discharge cycle for each data processed [13,14,15,16,17,18]. Other power balancing methods include modifying the algorithm execution [19], compensating current at the power supply node [20], and using sub-threshold operation [21]. Additionally, many techniques for randomizing power data have been proposed [22,23,24,25,26,27].

The principle of timing-based attacks [28] is very similar to power-based ones except these attacks rely on timing fluctuations of the target circuit while processing different data patterns. Depending on the load capacitance and driving strength, the charge/discharge process during the switching activities at an internal circuit node will take different amounts of time to finish, which in turn causes different timing delays. Existing countermeasures include inserting dummy operations [29], using redundant representation [30], and unifying the multiplication operands [31].

Asynchronous circuits, especially dual-rail asynchronous circuits, possess unique characteristics that could help mitigate such attacks [32,33,34,35,36,37]. Dual-rail asynchronous circuits, such as NULL Convention Logic (NCL) [38], use two wires to represent one signal. The DATA­spacer alternation protocol ensures the number of switching of each signal to be independent from the input; instead, it is only determined by the number of data processed [39], making power variation significantly smaller than synchronous designs [40]. Nonetheless, switching activity remains unbalanced between the two rails of each signal, which most likely drive different capacitive loads; thus, DPA, High-Order DPA, or CPA can still succeed. Moreover, such dual­rail logic circuits are even more vulnerable to timing-based attacks due to their strong data­timing dependency.

To alleviate these issues, Dual-Spacer Dual-Rail Delay­Insensitive Logic (D³L) was developed in [41] as an extension of NCL, which was capable of mitigating both power­ and timing-based side-channel attacks. However, this increased security was gained at the cost of more than four times the area of the base synchronous circuit and almost twice the area of the NCL version. This paper details the design, implementation, and analysis of MTD³L, developed by combining the D³L paradigm with Multi-Threshold NULL Convention Logic (MTNCL) [42,43], resulting in a circuit design methodology that is just as secure as D³L, while requiring slightly more than half the area and energy compared to D³L.

The remainder of this paper is organized as follows. Section 2 presents an overview of the pertinent previous work, including NCL, MTNCL, and D³L. Section 3 details the MTD³L circuit design method. Section 4 presents AES core implementations using MTD³L, as well as versions implemented using D³L, NCL, and the standard synchronous technique. Section 5 details the simulation setups for determining resistance against side-channel attacks, and presents and analyzes the simulation results. Section 6 draws conclusions and provides direction for future work.

2. Previous Work

2.1. NULL Convention Logic (NCL)

NCL [38] is a commonly used delay-insensitive (DI) asynchronous logic design style, which utilizes a multi-rail one-hot scheme, such as dual-rail, to encode data. A dual-rail signal, D, consists of two wires or rails, D⁰ and D¹, which may assume any value from the set {DATA0, DATA1, NULL}, as depicted in Table 1. The DATA0 state corresponds to a Boolean logic 0, the DATA1 state corresponds to a Boolean logic 1, and the NULL state corresponds to the empty set (meaning that the value of D is not yet available). The two rails are mutually exclusive, such that both rails can never be asserted simultaneously; this state is defined as an illegal state.

Table 1. Dual-rail signal.

State	D0	D1
NULL	0	0
DATA0	1	0
DATA1	0	1
Illegal	1	1

Table 1. Dual-rail signal.

State	D0	D1
NULL	0	0
DATA0	1	0
DATA1	0	1
Illegal	1	1

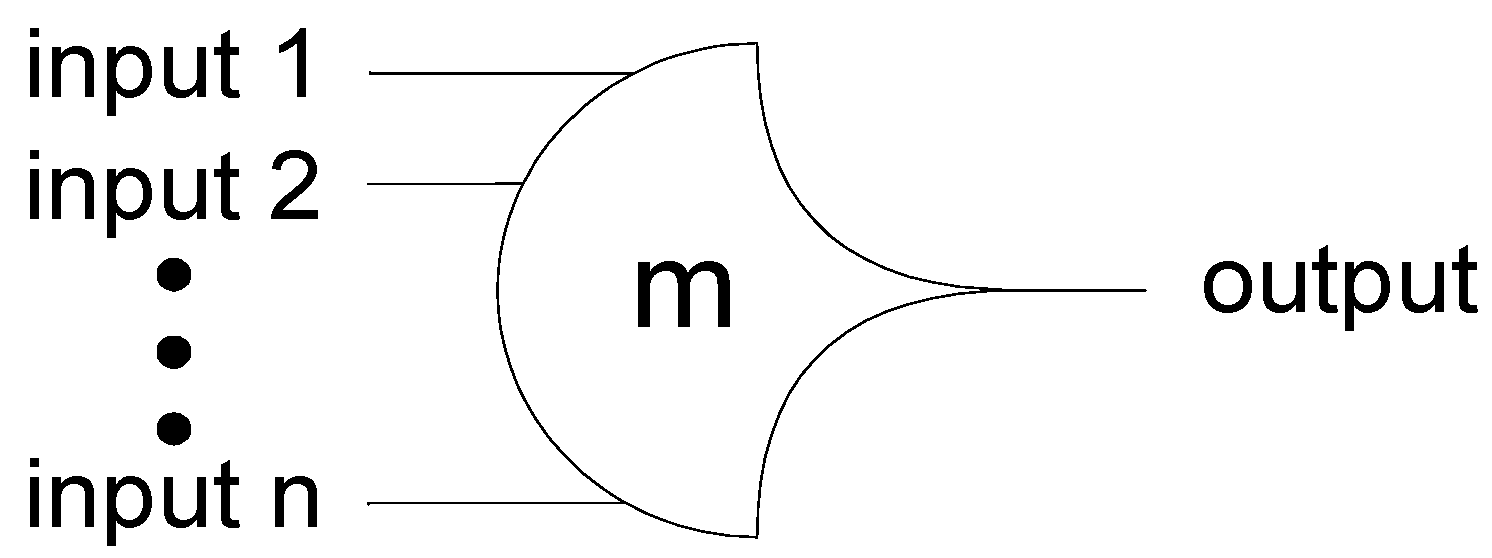
NCL circuits are comprised of 27 fundamental gates, which constitute the set of all functions consisting of four or fewer variables [43]. Since each rail of an NCL signal is considered a separate variable, a four variable function is not the same as a function of four literals, which would consist of eight variables for dual-rail logic (e.g., a literal includes both a variable and its complement, F and F’, whereas NCL rails are never complemented, such that a dual-rail NCL signal, F, consists of two variables, F¹ and F⁰, where F⁰ is equivalent to F’). The primary type of threshold gate, shown in Figure 1, is the THmn gate, where 1 ≤ m ≤ n. THmn gates have n inputs. At least m of the n inputs must be asserted before the output will become asserted. In a THmn gate, each of the n inputs is connected to the rounded portion of the gate; the output emanates from the pointed end of the gate; and the gate’s threshold value, m, is written inside of the gate.

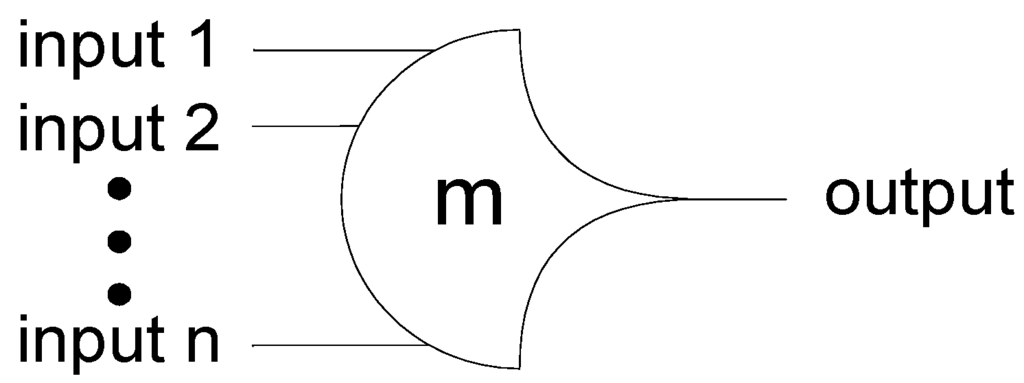
Figure 1. THmn threshold gate.

Figure 1. THmn threshold gate.

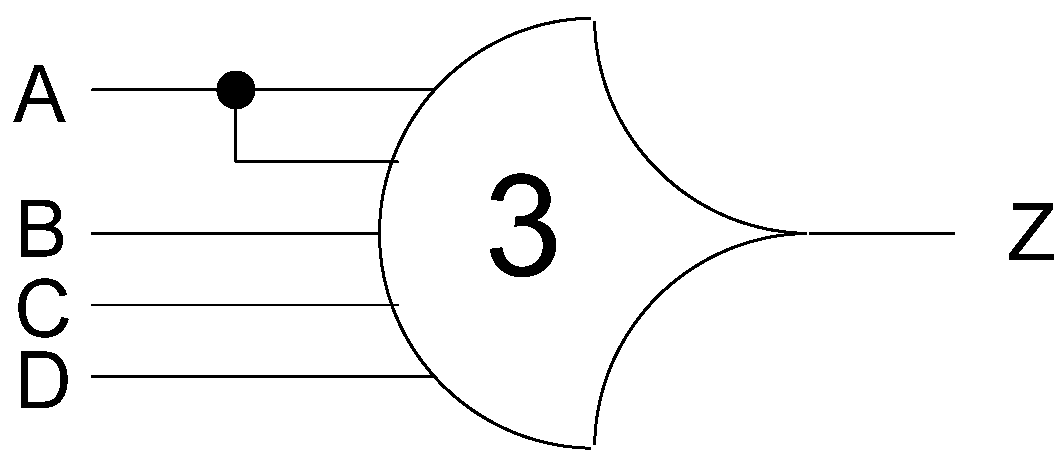
Another type of threshold gate is referred to as a weighted threshold gate, denoted as THmn w, w₁, w₂, …, w_R. Weighted threshold gates have an integer value, m ≥ w_R > 1, applied to input R. Here, 1 ≤ R < n; where n is the number of inputs; m is the gate’s threshold; and w₁, w₂, …, w_R, each >1, are the integer weights of input1, input2, …, inputR, respectively. For example, consider the TH34W2 gate, whose n = 4 inputs are labeled A, B, C, and D, shown in Figure 2. The weight of input A, W(A), is therefore 2. Since the gate’s threshold, m, is 3, this implies that in order for the output to be asserted, either inputs B, C, and D must all be asserted, or input A must be asserted along with any other input, B, C, or D.

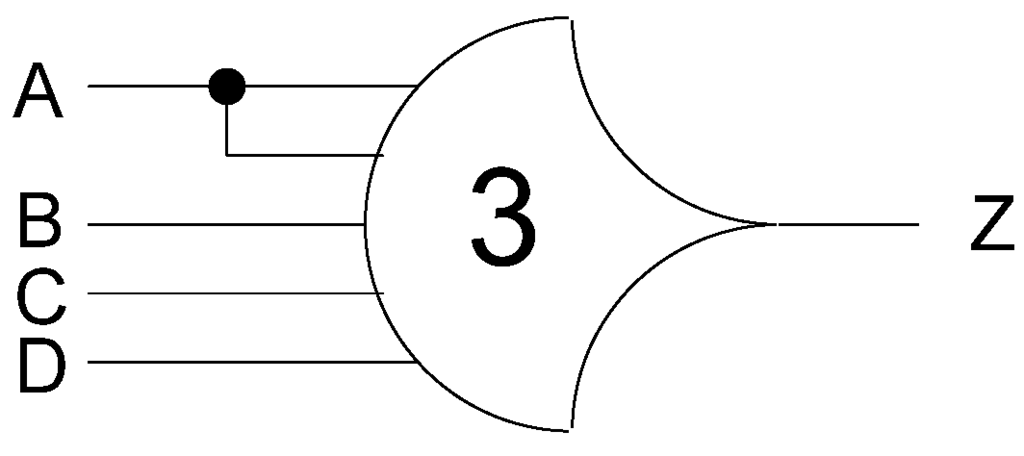
Figure 2. TH34w2 threshold gate: Z = AB + AC + AD + BCD.

Figure 2. TH34w2 threshold gate: Z = AB + AC + AD + BCD.

NCL threshold gates are designed with hysteresis state-holding capability, such that after the output is asserted, all inputs must be deasserted before the output will be deasserted. Hysteresis ensures a complete transition of inputs back to NULL before asserting the output associated with the next wavefront of input data. Therefore, a THnn gate is equivalent to an n-input C-element (i.e., when all inputs are asserted the output is asserted; the output then remains asserted until all inputs are deasserted, at which time the output becomes deasserted) [44]; and a TH1n gate is equivalent to an n-input OR gate. NCL threshold gates may also include a reset input to initialize the output. Circuit diagrams designate resettable gates by either a d or an n appearing inside the gate, along with the gate’s threshold. d denotes the gate as being reset to logic 1; n, to logic 0. These resettable gates are used in the design of DI registers.

To achieve hysteresis state-holding capability, NCL gates have both set and hold equations, where the set equation determines when the gate will become asserted and the hold equation determines when the gate will remain asserted once it has been asserted. The set equation determines the gate’s functionality as one of the 27 NCL gates [43], whereas the hold1 equation is simply all inputs ORed together. The general equation for an NCL gate with output Z is: Z = set + (Z^- × hold1), where Z^- is the previous output value and Z is the new value.

To implement an NCL gate using CMOS technology, an equation for the complement of Z is also required, which in general form is: Z’ = reset + (Z^-’ × hold0), where reset is the complement of hold1 (i.e., the complement of each input, ANDed together) and hold0 is the complement of set, such that the gate output is deasserted when all inputs are deasserted, and then remains deasserted while the gate’s set condition is false. The new output value, Z, depends on the previous output value, Z^-, which requires internal gate feedback, as shown in Figure 3, for a static implementation [43].

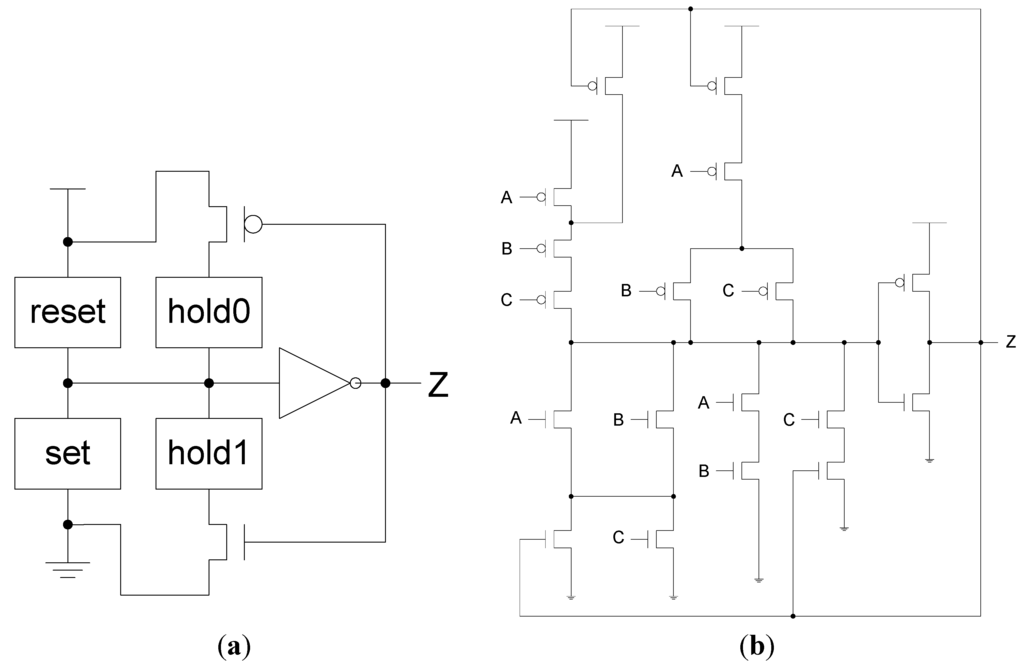
Figure 3. (a) Static NULL Convention Logic (NCL) gate structure; (b) Static NCL TH23 implementation.

Figure 3. (a) Static NULL Convention Logic (NCL) gate structure; (b) Static NCL TH23 implementation.

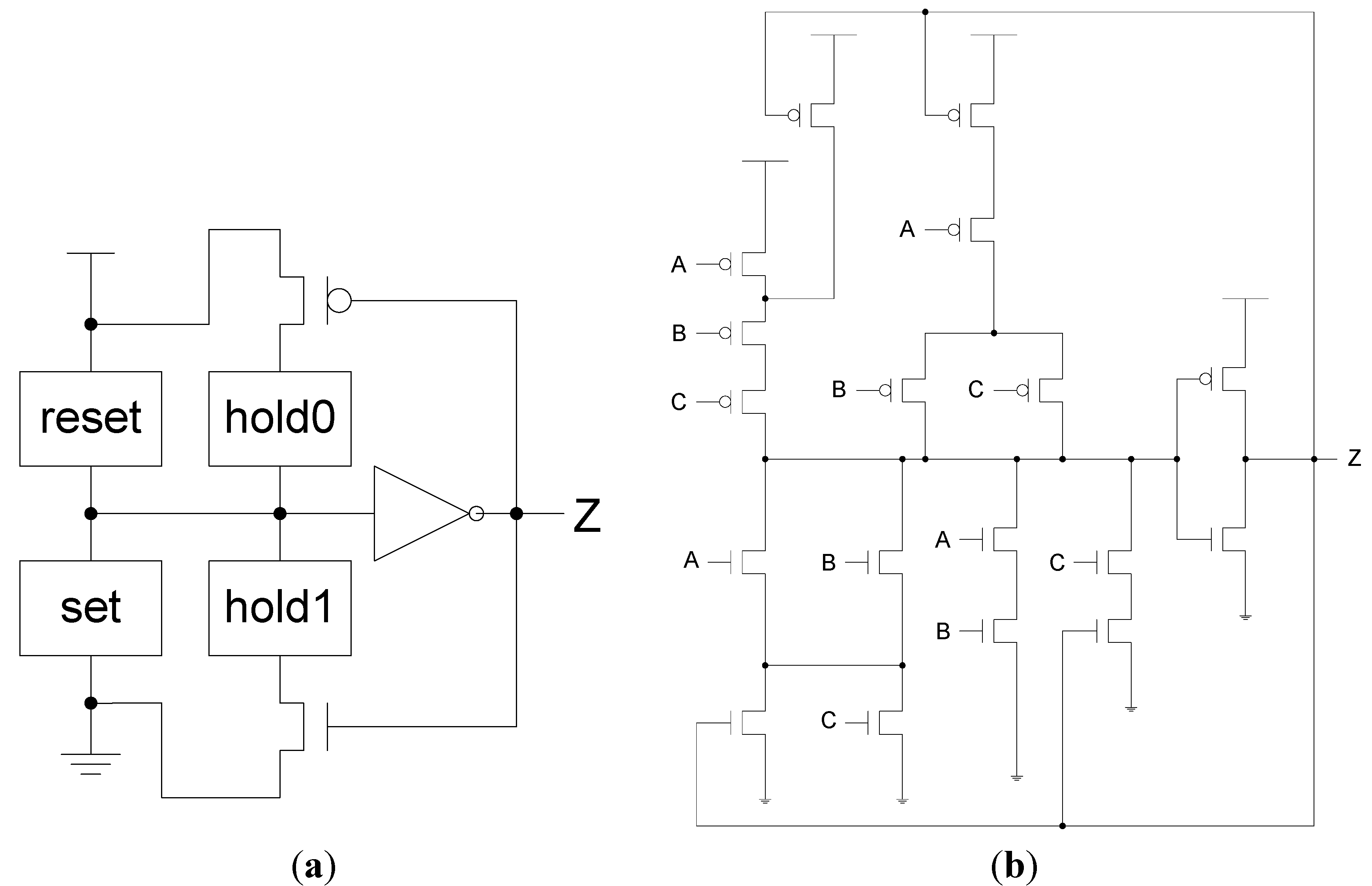
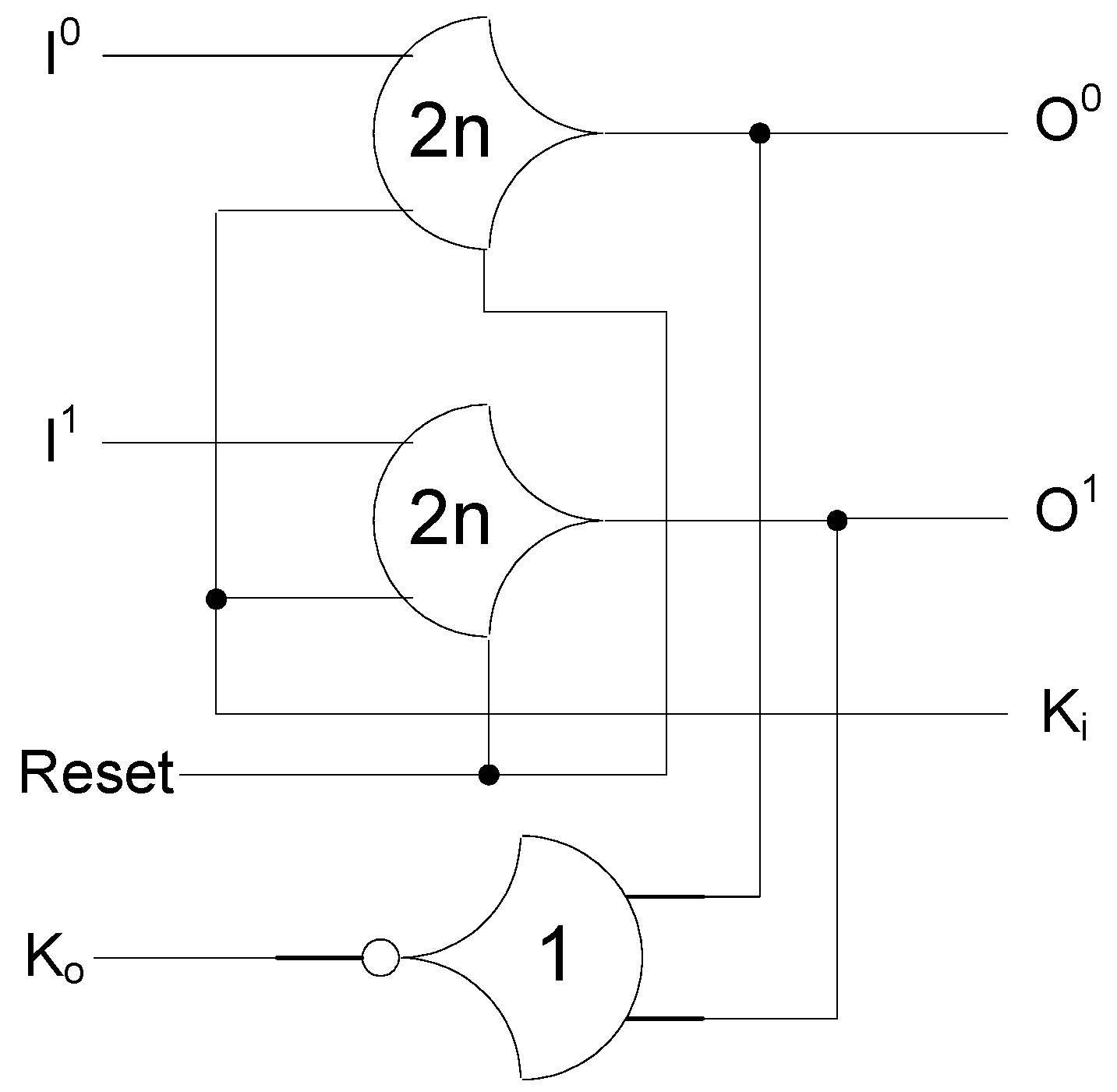
The framework for NCL systems consist of DI combinational logic sandwiched between DI registers, as shown in Figure 4, which is very similar to synchronous systems. NCL systems contain at least two DI registers, one at both the input and at the output. Two adjacent register stages interact through their request and acknowledge signals, K_i and K_o, respectively, to prevent the current DATA wavefront from overwriting the previous DATA wavefront, by ensuring that the two DATA wavefronts are always separated by a NULL wavefront. The acknowledge signals are combined in the Completion Detection circuitry [43] to produce the request signal(s) to the previous register stage. NCL registration is realized through cascaded arrangements of single-bit dual-rail registers, shown in Figure 5, which pass a DATA value at the input only when K_i is request for data (rfd) (i.e., logic 1) and likewise pass NULL only when K_i is request for null (rfn) (i.e., logic 0). They also contain a NOR gate to generate K_o, which is rfn when the register output is DATA and rfd when the register output is NULL.

Figure 4. NCL system framework: input wavefronts are controlled by local handshaking signals and Completion Detection instead of by a global clock signal. Feedback requires at least three DI registers in the feedback loop to prevent deadlock.

Figure 4. NCL system framework: input wavefronts are controlled by local handshaking signals and Completion Detection instead of by a global clock signal. Feedback requires at least three DI registers in the feedback loop to prevent deadlock.

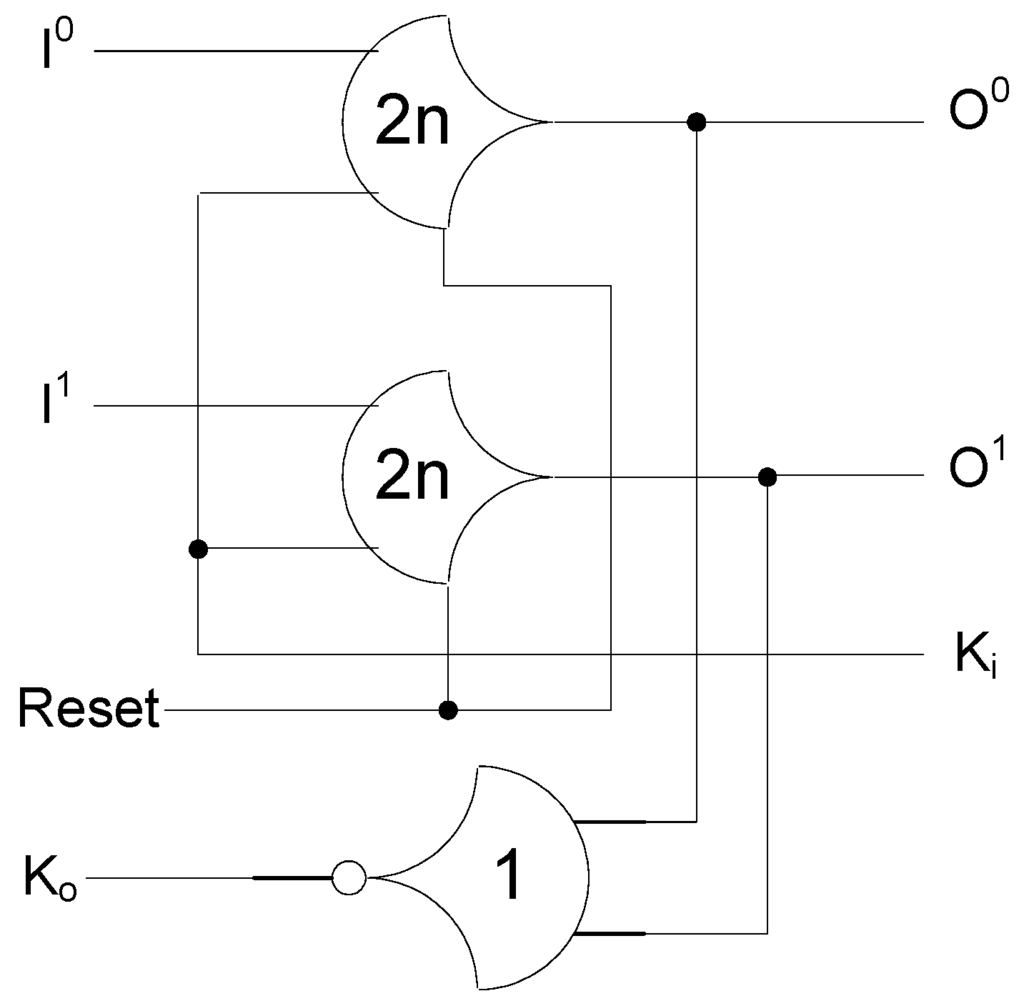
Figure 5. Single-bit dual-rail register.

Figure 5. Single-bit dual-rail register.

The NCL dual-rail encoding style decouples the relationship between the data being processed and the side-channel characteristics of the circuit, particularly power consumption, giving NCL circuits increased resistance to power related side-channel attacks over synchronous circuits. However, while the overall switching activity of a data bit may be balanced regardless of data, the individual encoding rails are not balanced, as illustrated in Figure 6. Furthermore, if the two rails are driving different capacitance, which is always the case in a large circuit, then attackers may be able to distinguish between the rails, allowing attackers to determine a relationship between the processed data and the circuit’s side-channels.

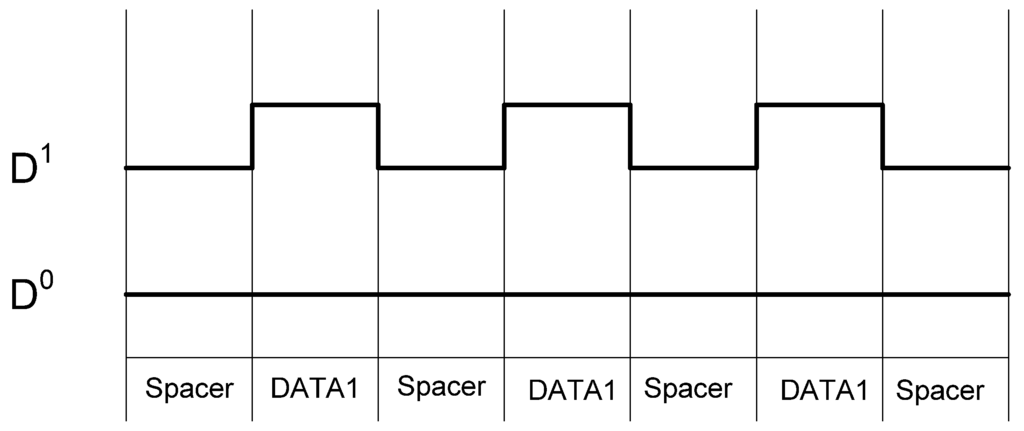
Figure 6. NCL switching activity for passing consecutive DATA1s.

Figure 6. NCL switching activity for passing consecutive DATA1s.

2.2. Multi-Threshold NULL Convention Logic (MTNCL)

MTNCL circuits utilize a sleep signal to simultaneously force all circuit elements to NULL instead of propagating a NULL input through the circuit, as described in [42]. This allows for the MTNCL gates to no longer require state-holding hysteresis logic and for the MTNCL combinational logic circuits to no longer need to be input-complete and observable, both of which significantly reduce area and power/energy, while increasing speed. The Static MTNCL (SMTNCL) gate and the Slept Early Completion and Registration Input-Incomplete (SECRII) architecture are shown in Figure 7 and Figure 8, respectively, and are both detailed in [42].

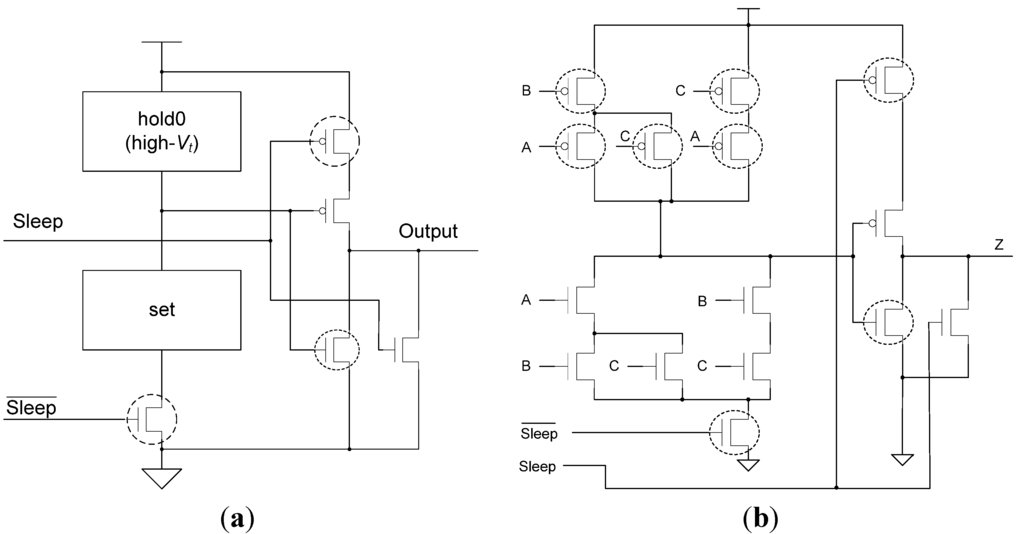
Figure 7. (a) SMTNCL gate structure; (b) SMTNCL TH23 implementation.

Figure 7. (a) SMTNCL gate structure; (b) SMTNCL TH23 implementation.

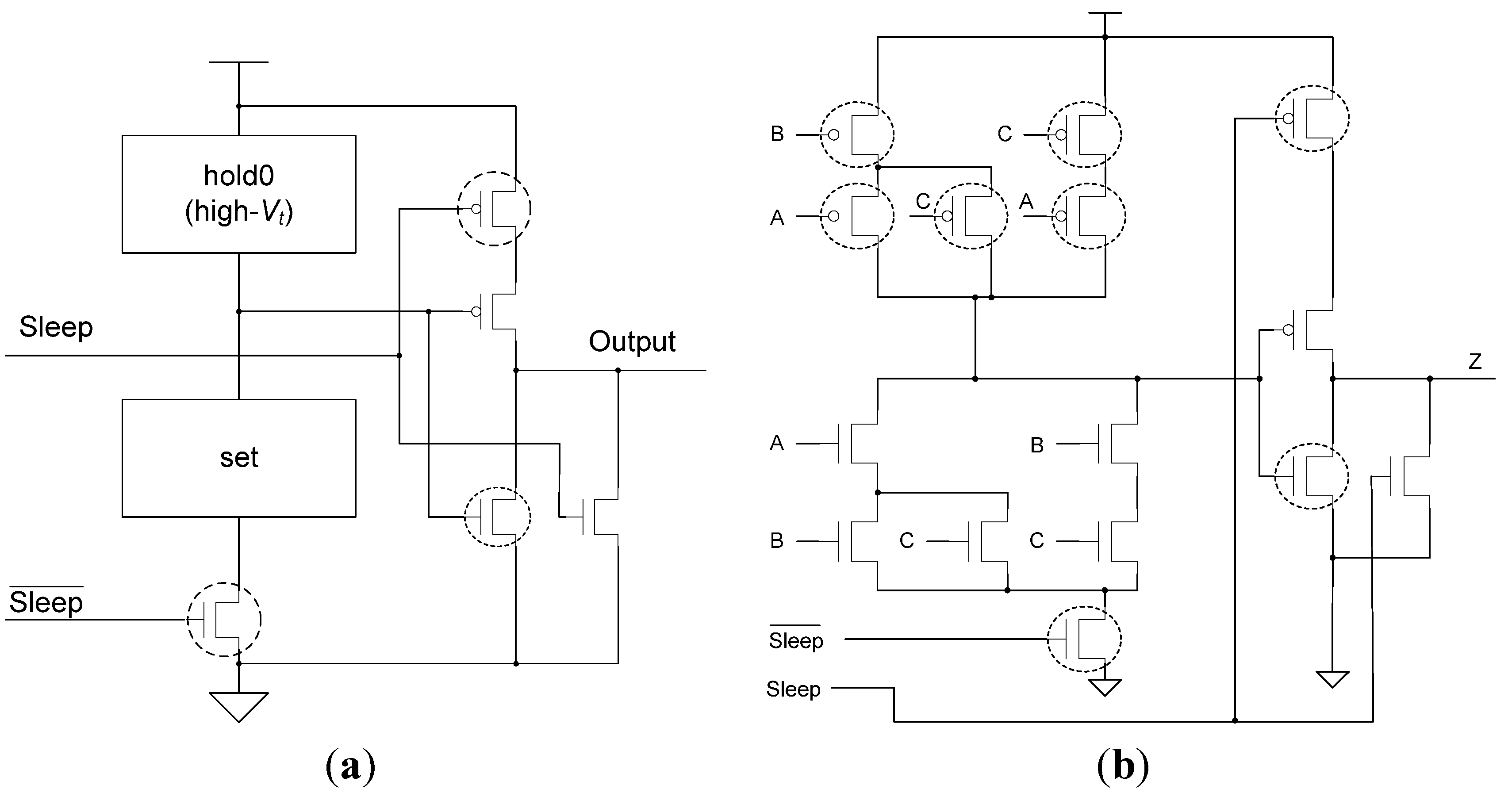
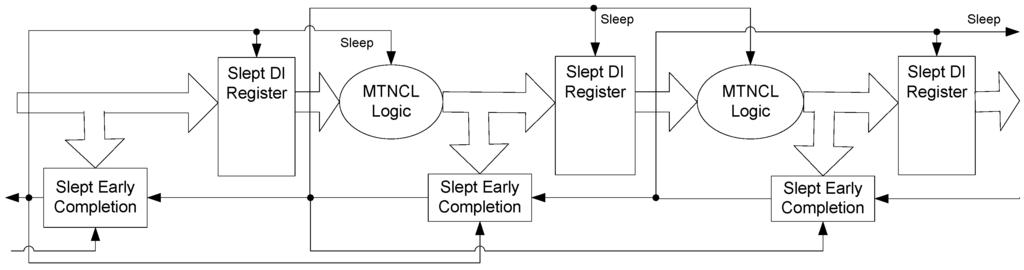
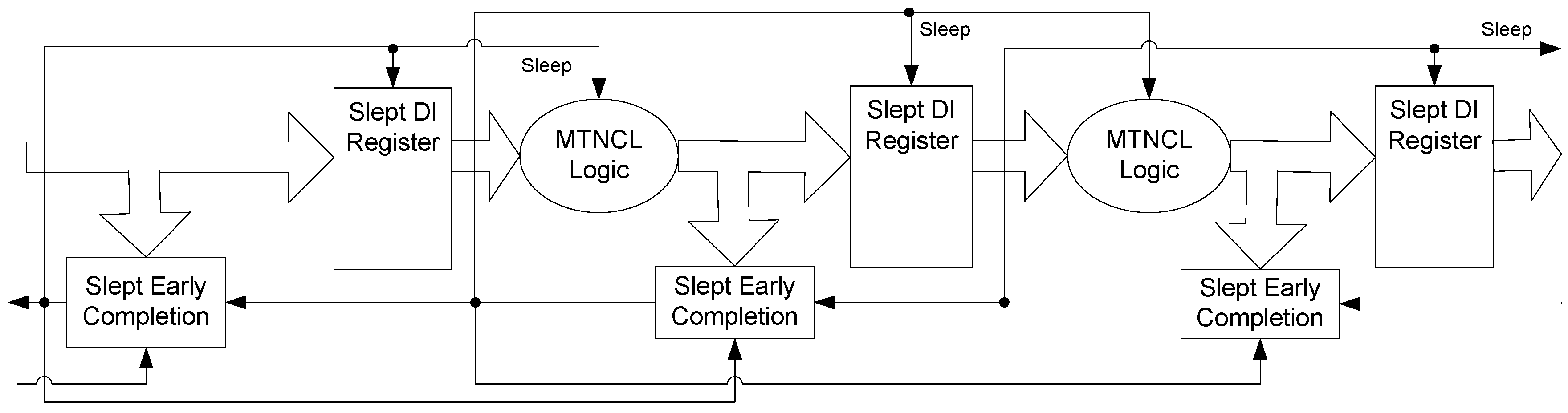
Figure 8. SECRII architecture with completion logic and registration slept.

Figure 8. SECRII architecture with completion logic and registration slept.

2.3. Dual-Spacer Dual-Rail Delay­Insensitive Logic (D³L)

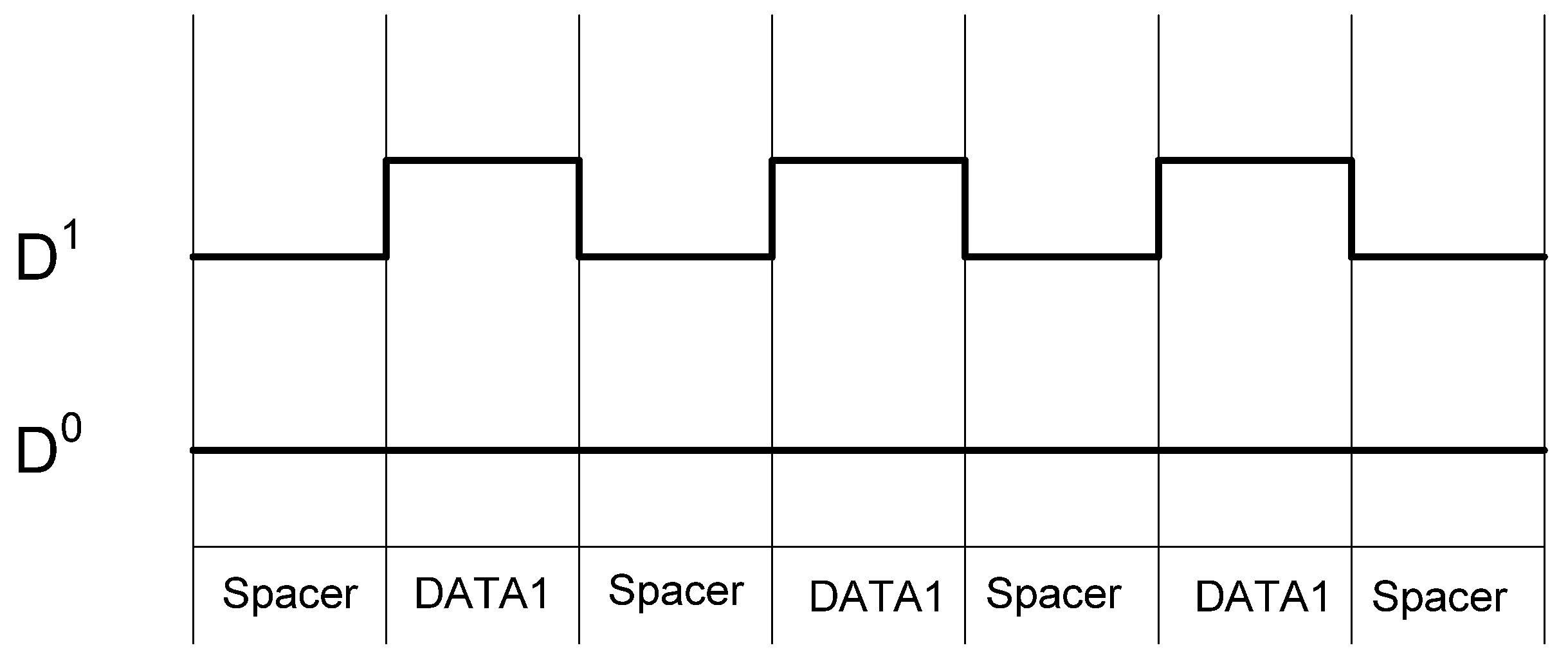
D³L is an extension of the NCL logic style that utilizes a dual-spacer protocol, as opposed to NCL’s single spacer protocol [41]. The motivation for this is the elimination of imbalanced switching activity on the two encoding wires of a data bit. By balancing this switching activity, data is further decoupled from the power consumption of the circuit, providing increased robustness against power analysis attacks.

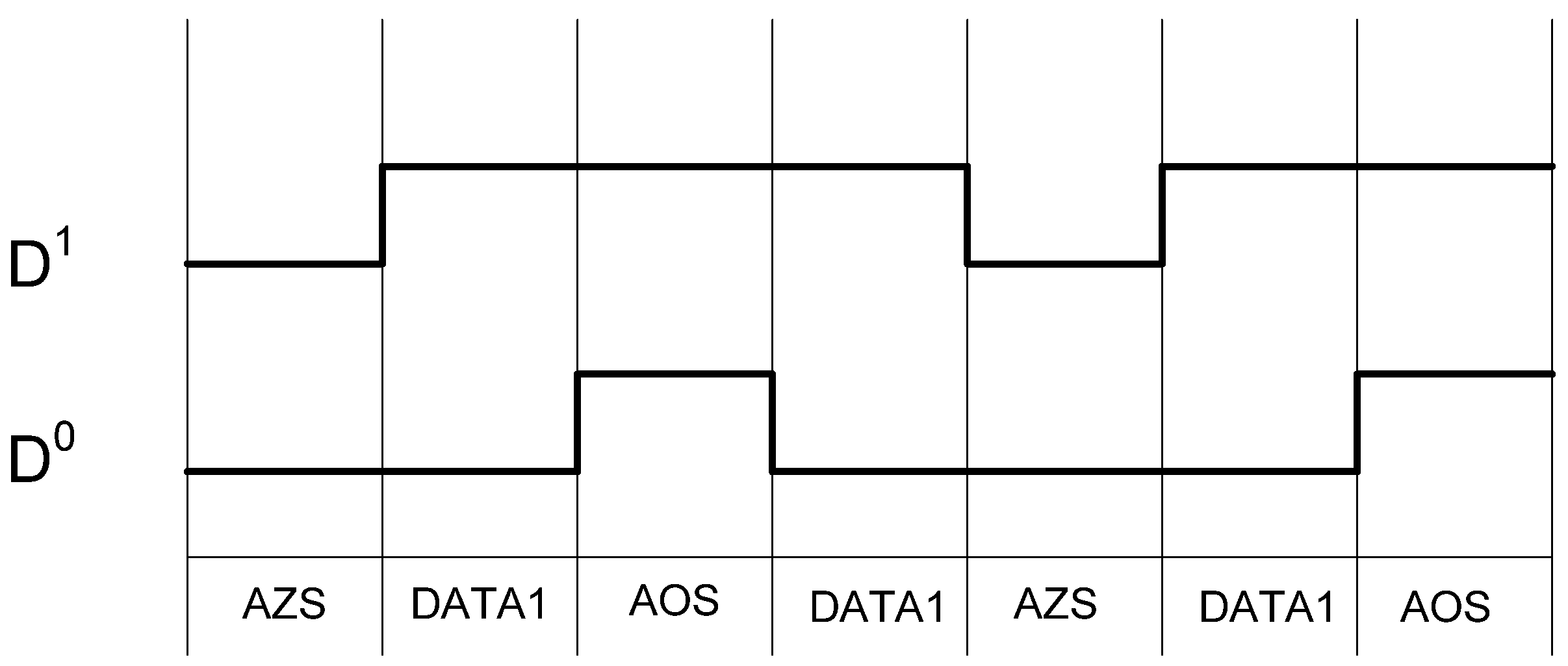
Table 2 shows the D³L encoding scheme. Like NCL, the DATA and NULL states remain the same. However, the NULL state is now called the All-Zero Spacer (AZS); and the former illegal state, where both rails are asserted, is now the All-One Spacer (AOS). The AZS and AOS are alternated between spacer cycles, implementing a dual-spacer protocol. As a result, the switching activity over a complete set of data/spacer cycles is balanced on both rails, as shown in Figure 9.

Table 2. D³L encoding scheme.

State	D0	D1
All-Zero Spacer (AZS)	0	0
Data0	1	0
Data1	0	1
All-One Spacer (AOS)	1	1

Table 2. D³L encoding scheme.

State	D0	D1
All-Zero Spacer (AZS)	0	0
Data0	1	0
Data1	0	1
All-One Spacer (AOS)	1	1

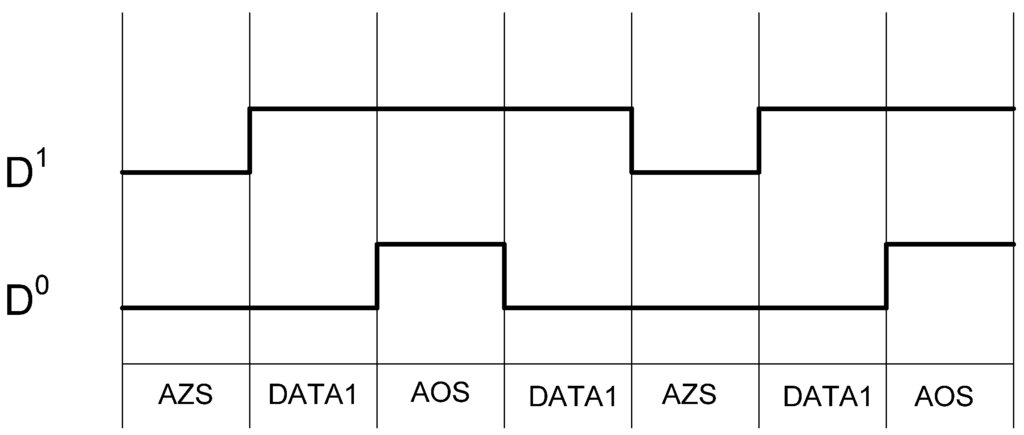
Figure 9. D³L switching activity for passing consecutive DATA1s.

Figure 9. D³L switching activity for passing consecutive DATA1s.

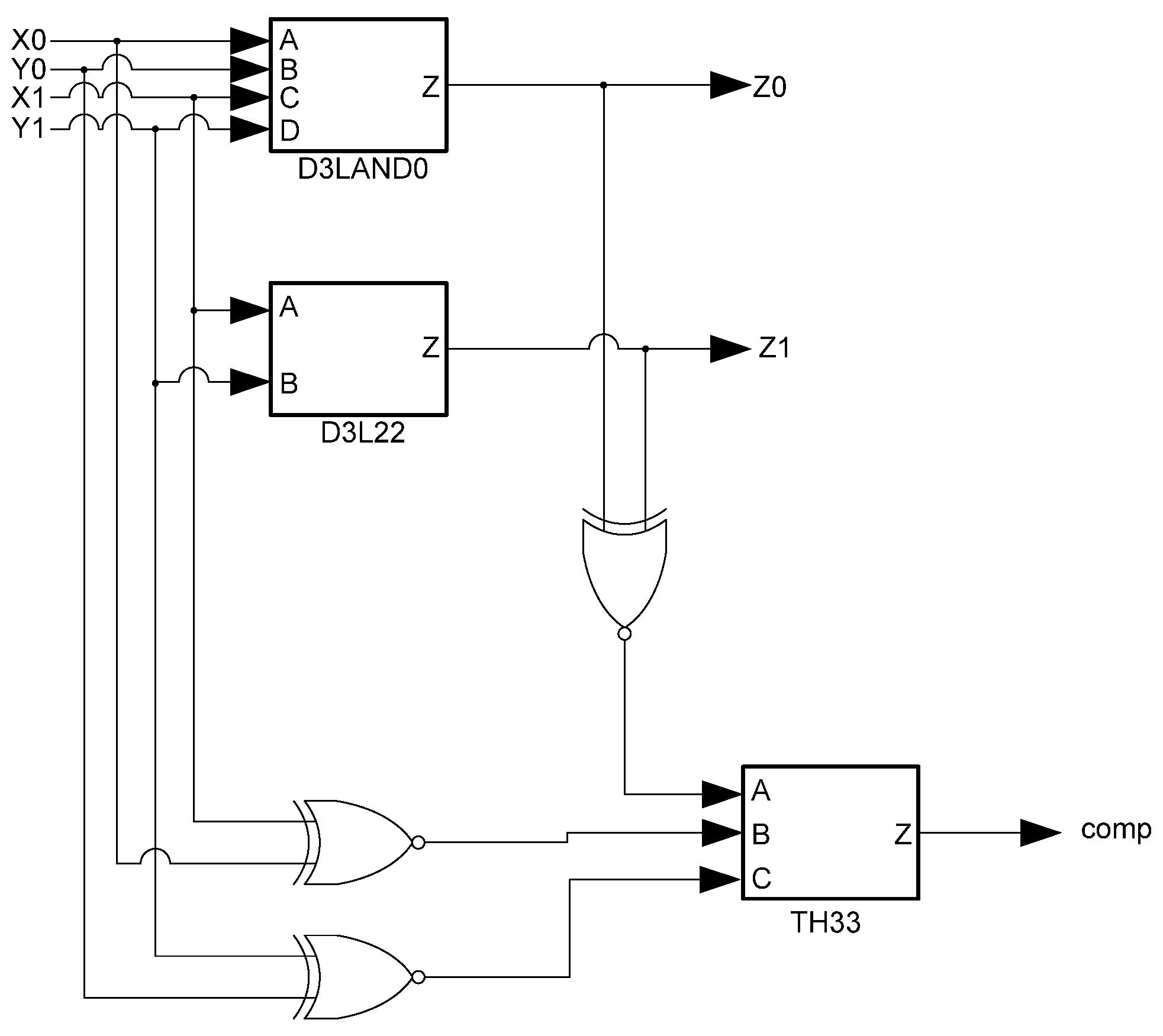
The D³L threshold gates are modified versions of the NCL threshold gates. As such, the complete set of 27 NCL functions is implemented in D³L. While NCL gates use hysteresis, D³L gates are unable to do so to accommodate the dual-spacer protocol. As such, D³L threshold gates are smaller than NCL threshold gates due to the omission of the hysteresis transistors. The removal of hysteresis, however, means that D³L gates are unable to guarantee input completeness. Instead, the NCL_X technique [45] is used to provide input-completeness. This technique adds additional logic to D³L functions that check the inputs and outputs of each function to create a completion signal. Since the spacer cycles in D³L occur when data rails are the same, an XNOR gate can be used to detect them. The outputs from these XNOR gates are input to the completion component, along with the usual handshaking signals, to ensure that the logic is ready for the next wavefront. A downside to this technique, however, is the overhead incurred by adding large amounts of XNOR and threshold gates to the design to ensure input-completeness. An input-complete D³L AND function is shown in Figure 10.

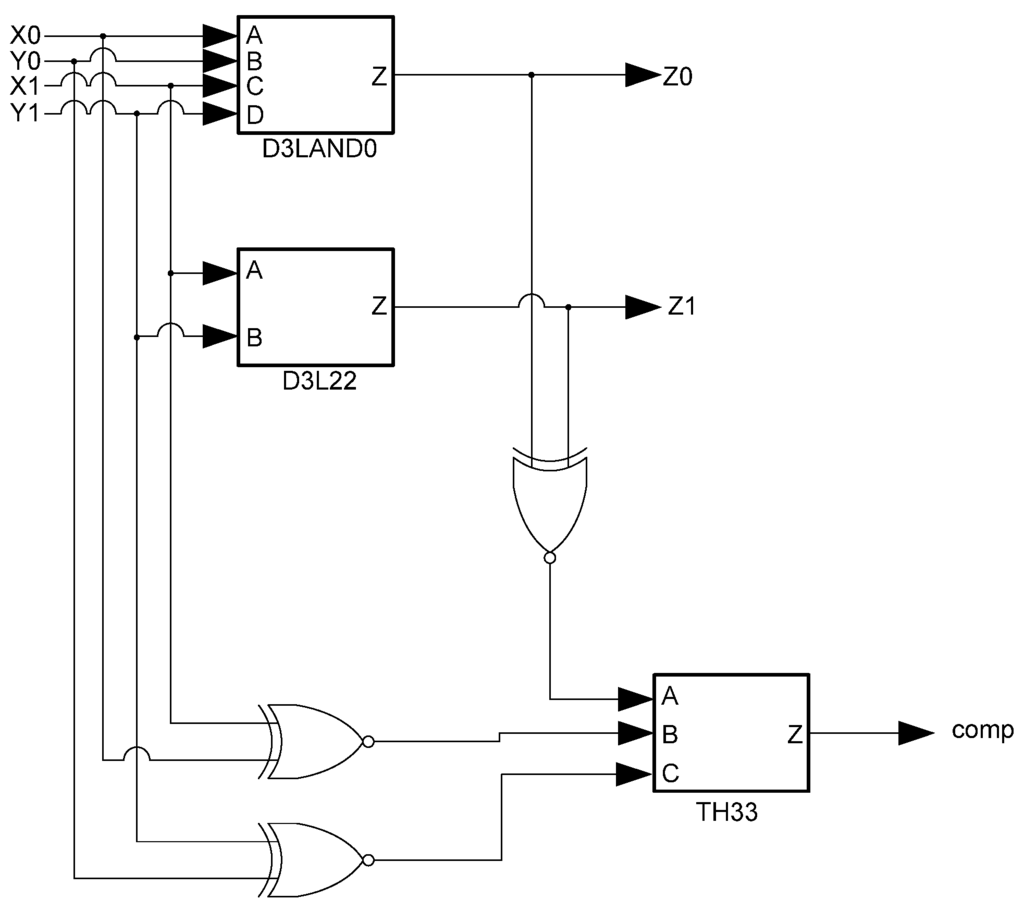
Figure 10. D³L input-complete AND function.

Figure 10. D³L input-complete AND function.

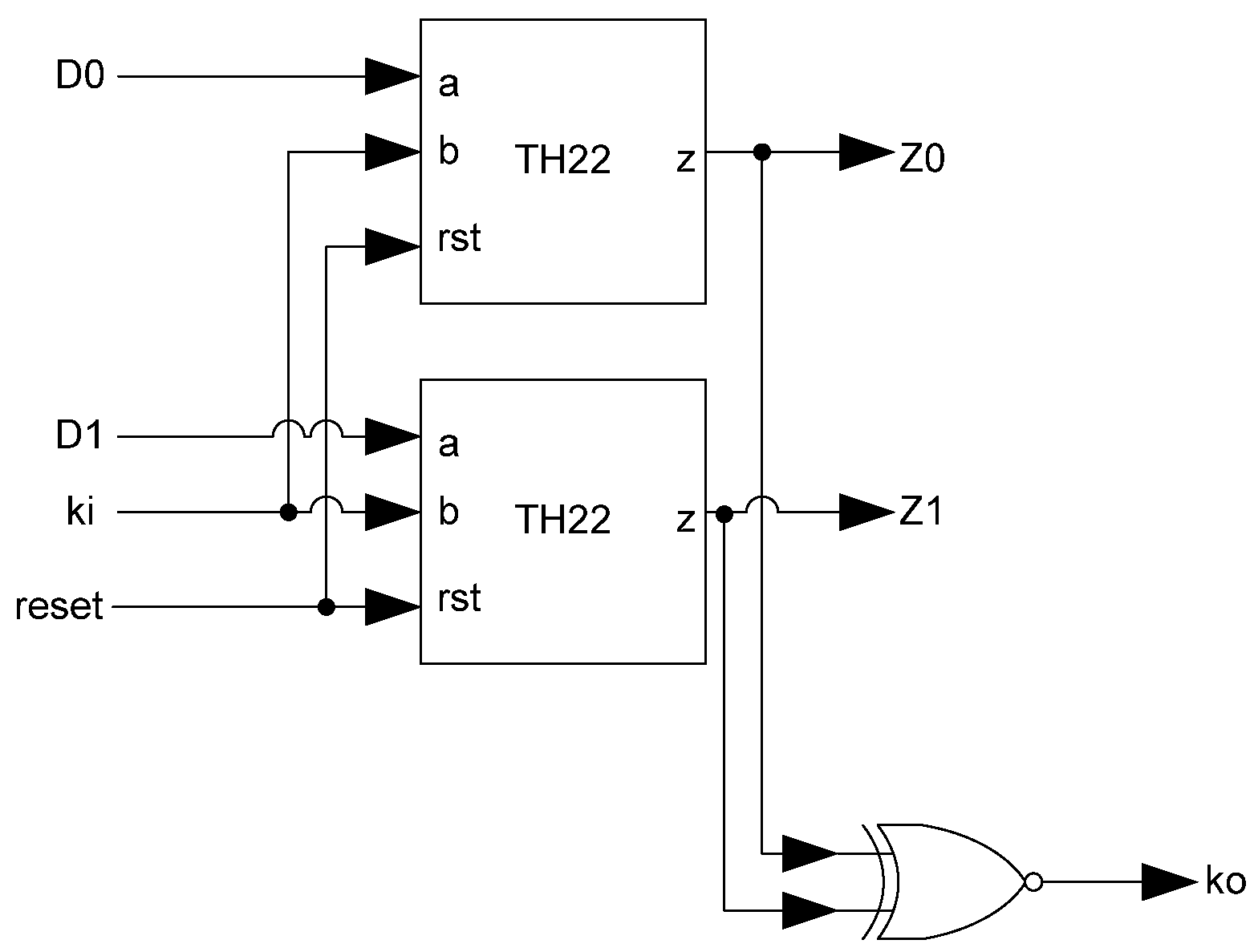
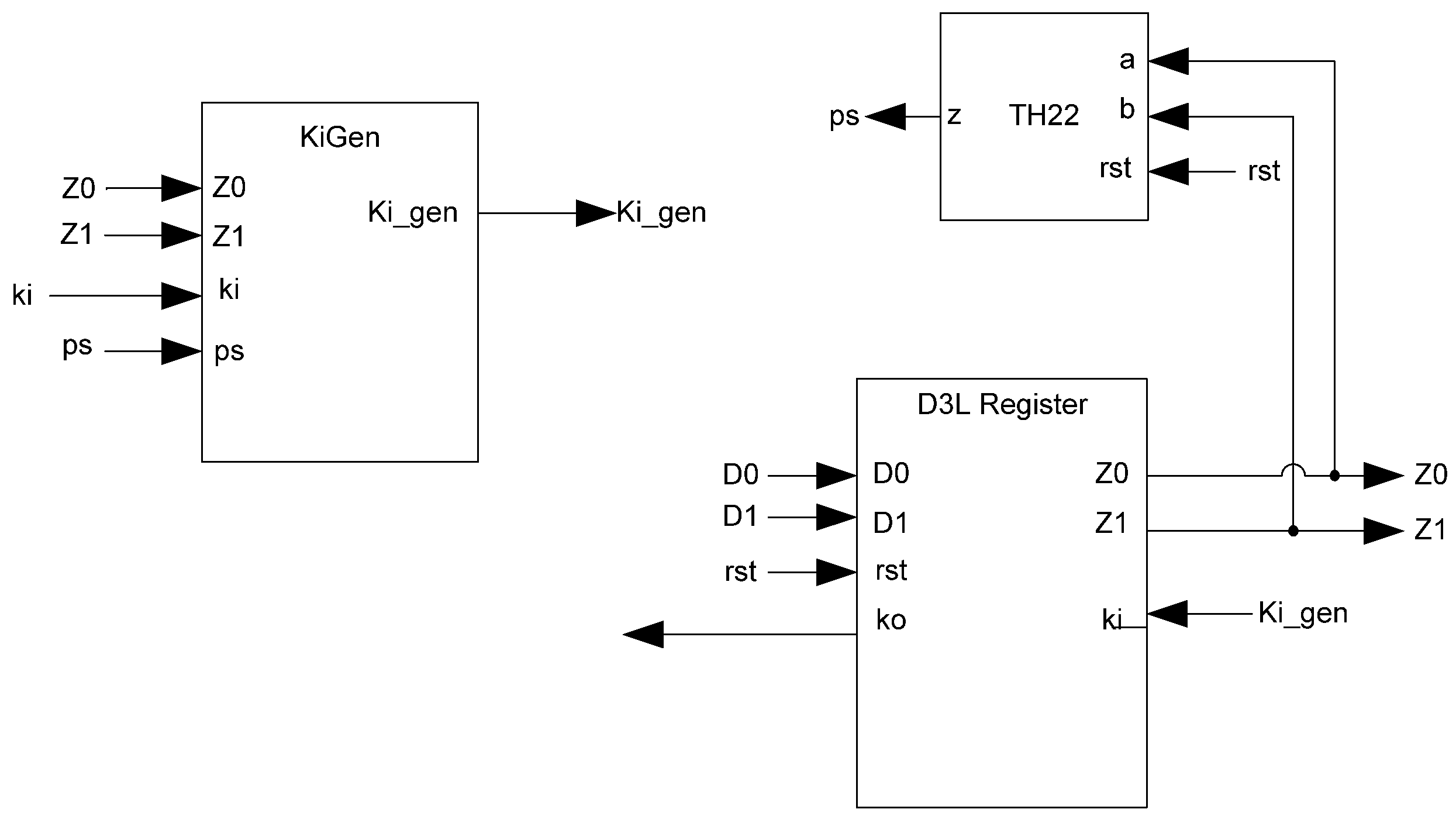
The basic D³L Register, shown in Figure 11, is a modified NCL register. It consists of two TH22 gates which are resettable to the desired value. An XNOR gate facilitates K_o generation by checking the relative values of the register’s outputs. As mentioned previously, the XNOR gate is required to detect both AZS and AOS.

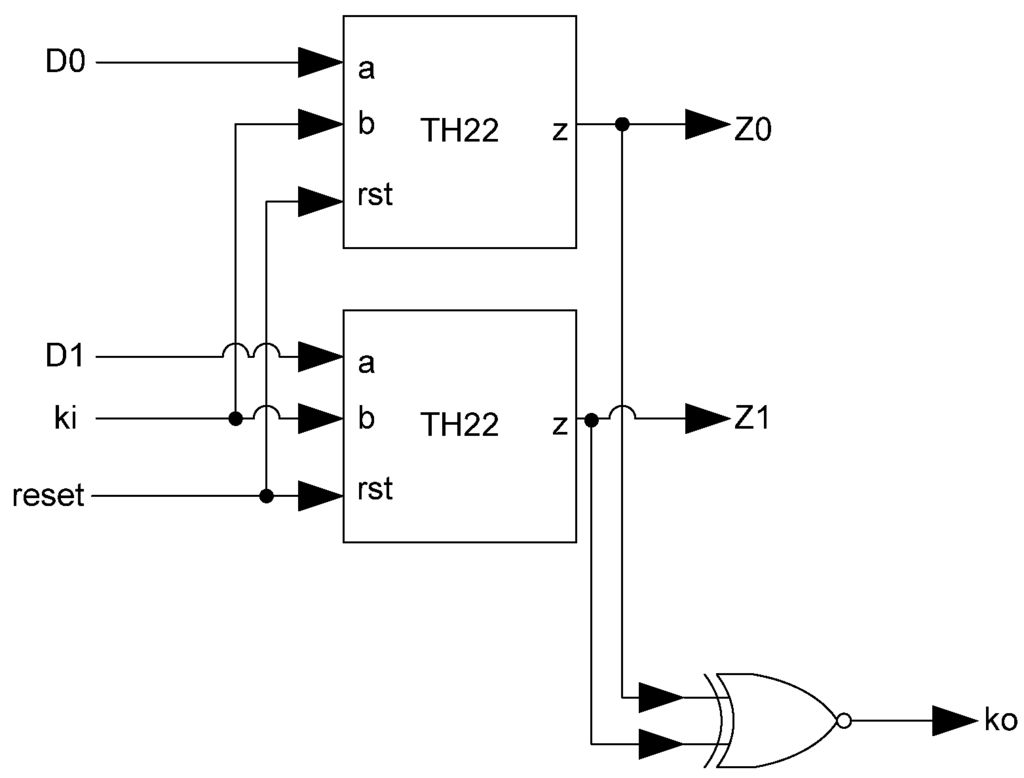
Figure 11. D³L register.

Figure 11. D³L register.

Additional logic is required to facilitate the dual-spacer protocol. NCL registers require a NULL input before they are able to accept new data. They will not recognize an all-one spacer. To fix this, extra logic capable of recognizing the all-one spacer is used to control the register’s Ki input. This Ki Generator has four inputs: the early completion Ki, ps (previous spacer), and the two dual-rail outputs of the register. The value of ps is generated by a resettable TH22 gate. This value is logic 0 for an AZS and logic 1 for an AOS. The ps gate and the register must be reset to the same value. If the register is reset to DATA then the ps gate is reset to logic 0. The Ki Generator’s output follows the Boolean equation Ki_gen = Ki ps (Z0+Z1)+ Ki ps (Z0+Z1)+ Z0 Z1 Ki+Z0 Z1 Ki resulting from the truth table shown in Table 3, yielding the transistor level implementation shown in Figure 12. If an AOS is needed then the value of Ki_gen will be changed to logic 1 allowing the register to latch it. Once the next data value arrives, Ki_gen will switch to logic 0. As a result, one of the register’s TH22 gates will have two low inputs which will change its output to logic 0, latching the data. A complete D³L register is shown in Figure 13.

Table 3. Ki Generator (KiGen) truth table.

Row	Z0	Z1	Ki	ps	Ki_gen
1	0	0	0	0	0
2	0	0	0	1	0
3	0	0	1	0	1
4	0	0	1	1	1
5	0	1	0	0	1
6	0	1	0	1	0
7	0	1	1	0	0
8	0	1	1	1	1
9	1	0	0	0	1
10	1	0	0	1	0
11	1	0	1	0	0
12	1	0	1	1	1
13	1	1	0	0	1
14	1	1	0	1	1
15	1	1	1	0	0
16	1	1	1	1	0

Table 3. Ki Generator (KiGen) truth table.

Row	Z0	Z1	Ki	ps	Ki_gen
1	0	0	0	0	0
2	0	0	0	1	0
3	0	0	1	0	1
4	0	0	1	1	1
5	0	1	0	0	1
6	0	1	0	1	0
7	0	1	1	0	0
8	0	1	1	1	1
9	1	0	0	0	1
10	1	0	0	1	0
11	1	0	1	0	0
12	1	0	1	1	1
13	1	1	0	0	1
14	1	1	0	1	1
15	1	1	1	0	0
16	1	1	1	1	0

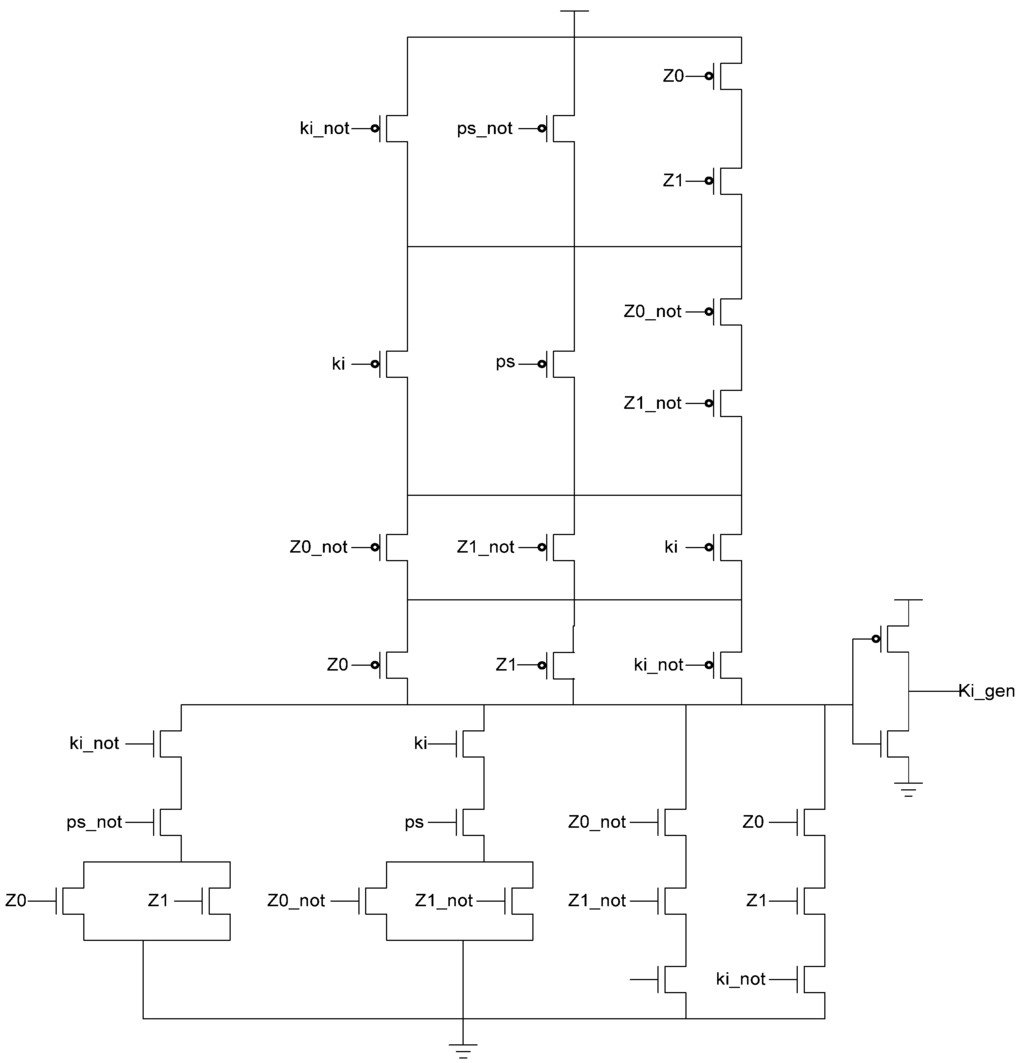
Figure 12. KiGen transistor diagram.

Figure 12. KiGen transistor diagram.

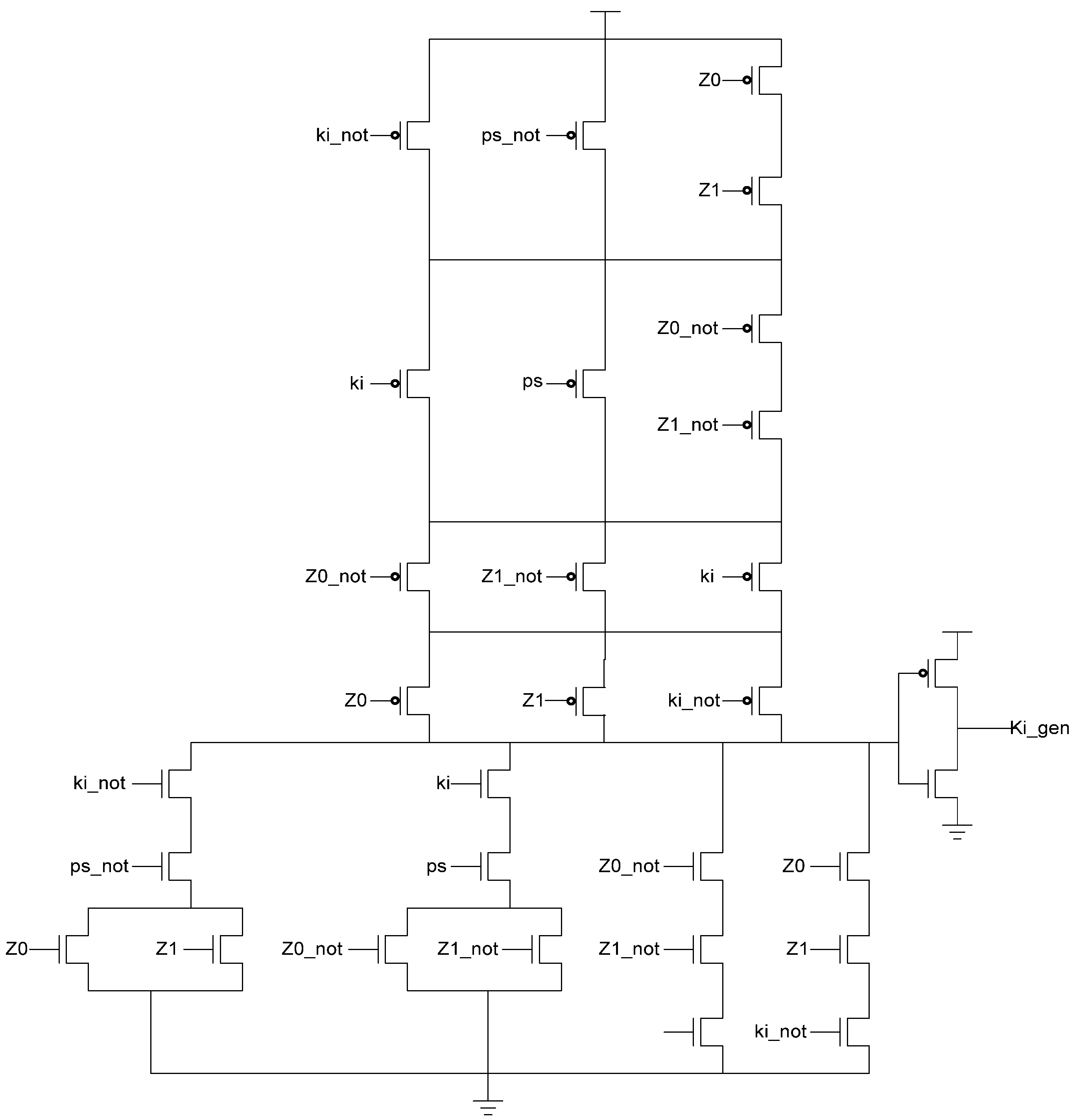
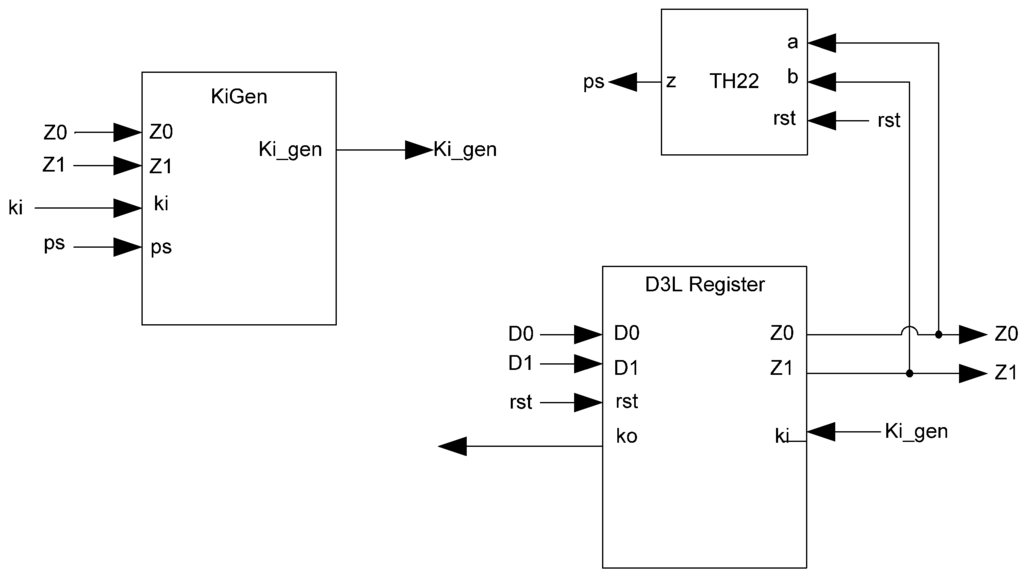
Figure 13. Complete D³L register.

Figure 13. Complete D³L register.

While the D³L register is capable of handling the dual-spacer protocol, it is insufficient to implement ring register configurations. This is because a basic D³L register is incapable of generating alternating spacers. Instead, the same spacer would pass through the ring twice causing deadlock. To solve this, a D³L filter register is required for generating alternating spacers, which consists of a basic D³L register with a spacer filter operating on the register’s inputs. The spacer filter monitors the dual-rail input, the previous spacer, and the K_o from the register to ensure that spacers are alternated as they pass through. In a typical ring register configuration, the first two registers would be normal D³L registers reset to NULL and a filter register reset to DATA0 or DATA1. When the filter register receives an AZS or AOS it outputs the alternate spacer. This ensures that the same spacer does not pass through the ring twice. Figure 14 shows the D³L filter register diagram, while Figure 15 shows the transistor level schematic of the spacer filter, whose outputs are based on the following equations:

D0_filter = D0 D1+Ko ps D0+Ko ps D0+Ko ps D1+Ko ps D1

D1_filter = D0 D1+Ko ps D1+Ko ps D1+Ko ps D0+Ko ps D0

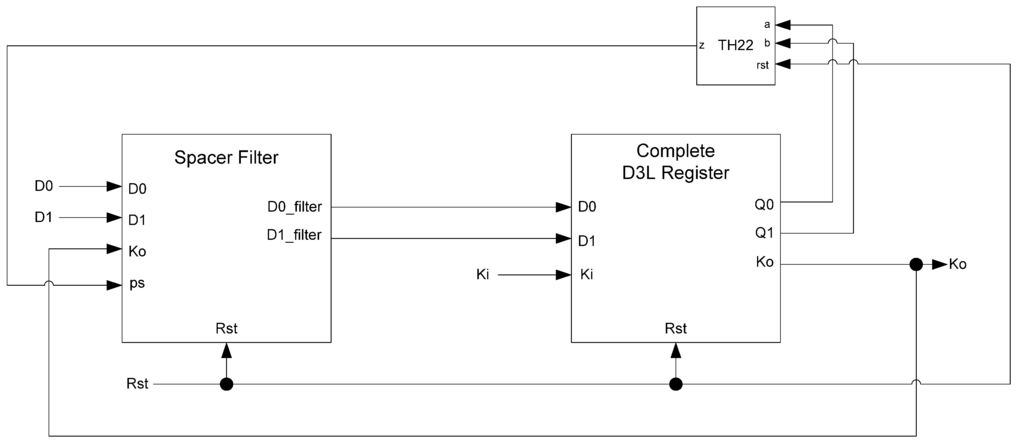
Figure 14. D³L filter register.

Figure 14. D³L filter register.

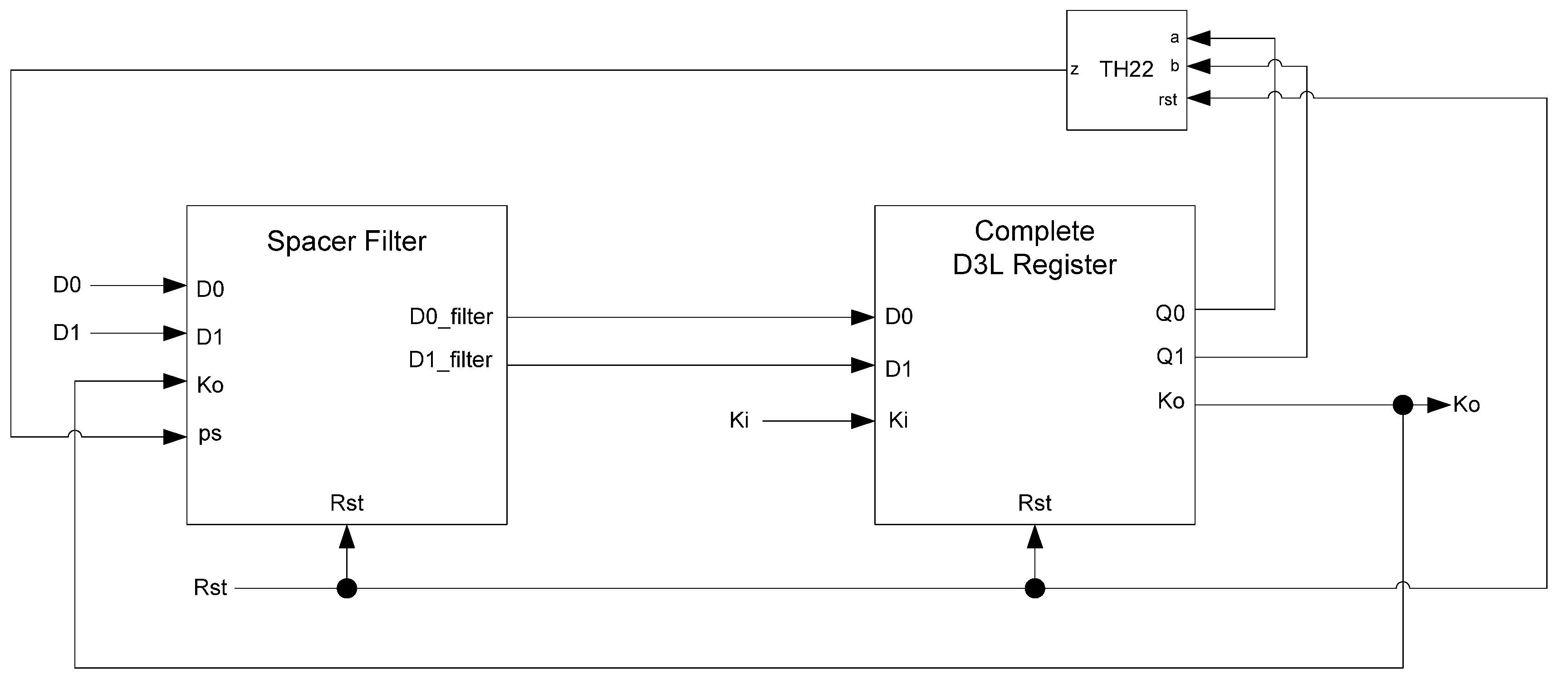
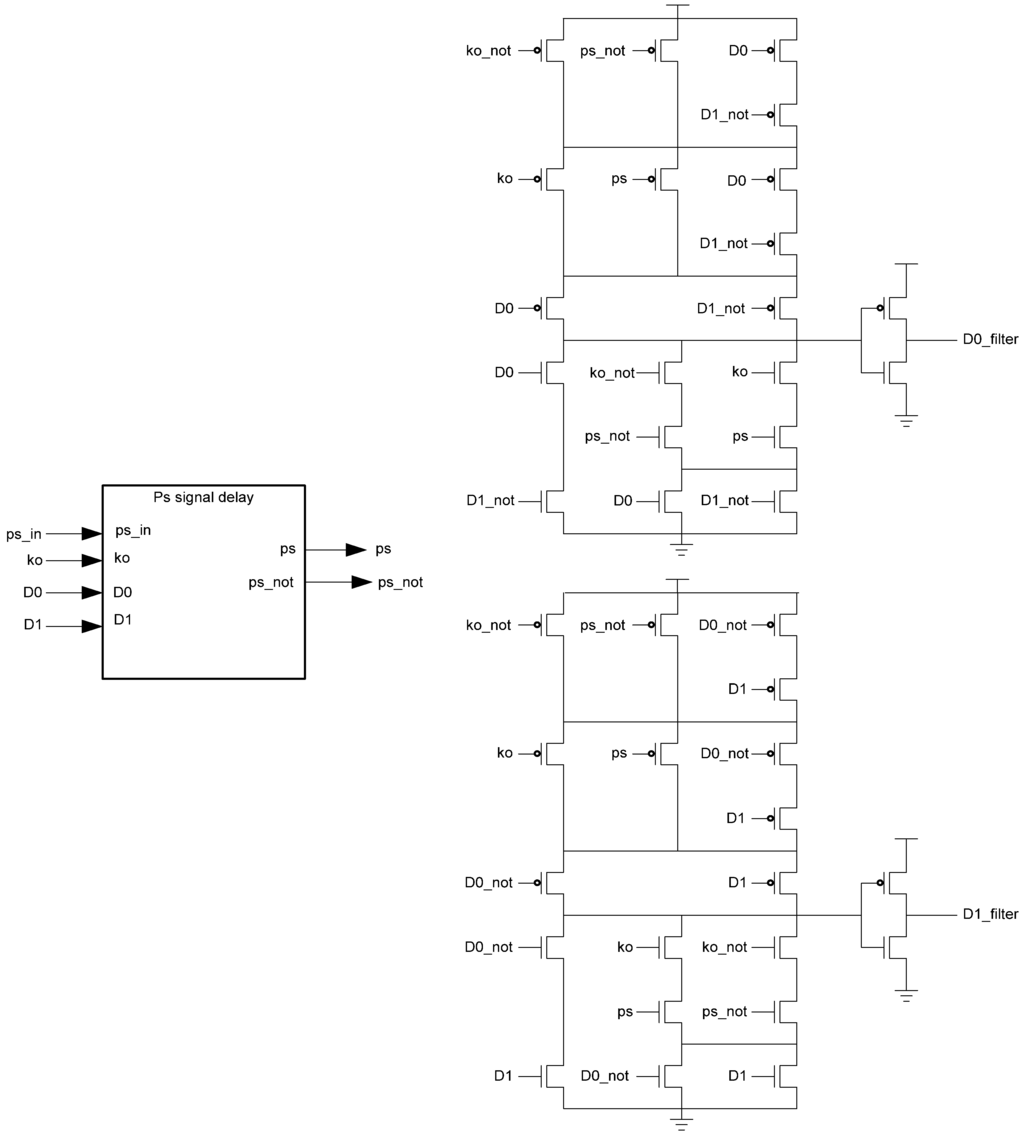
Figure 15. Spacer filter transistor level diagram.

Figure 15. Spacer filter transistor level diagram.

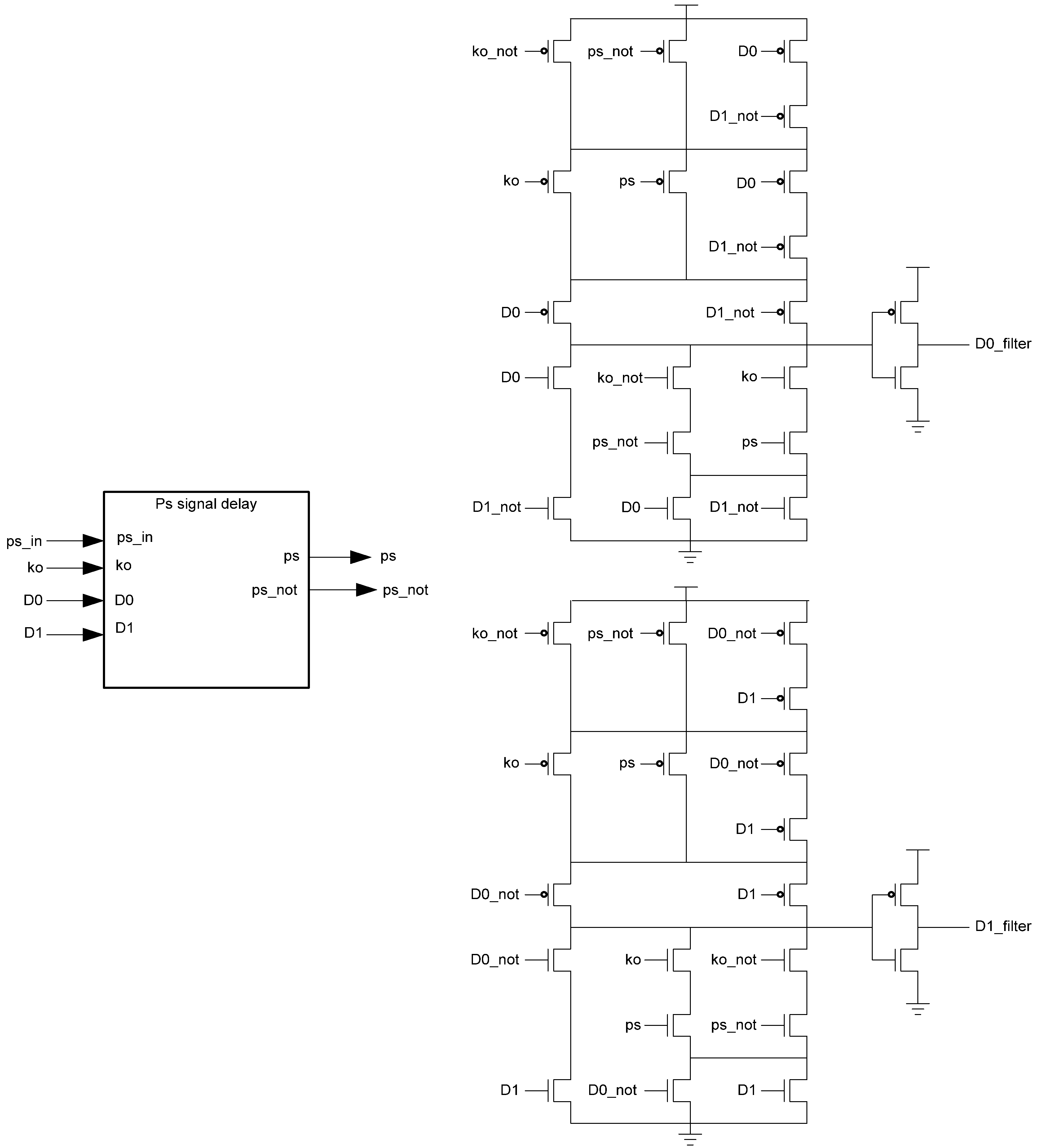
The PS signal delay component used in the spacer filter, shown in Figure 16, prevents ps from changing unless the register’s K_o is logic 1, i.e., requesting DATA. This ensures that the value of ps is only changed once the register receives the spacer.

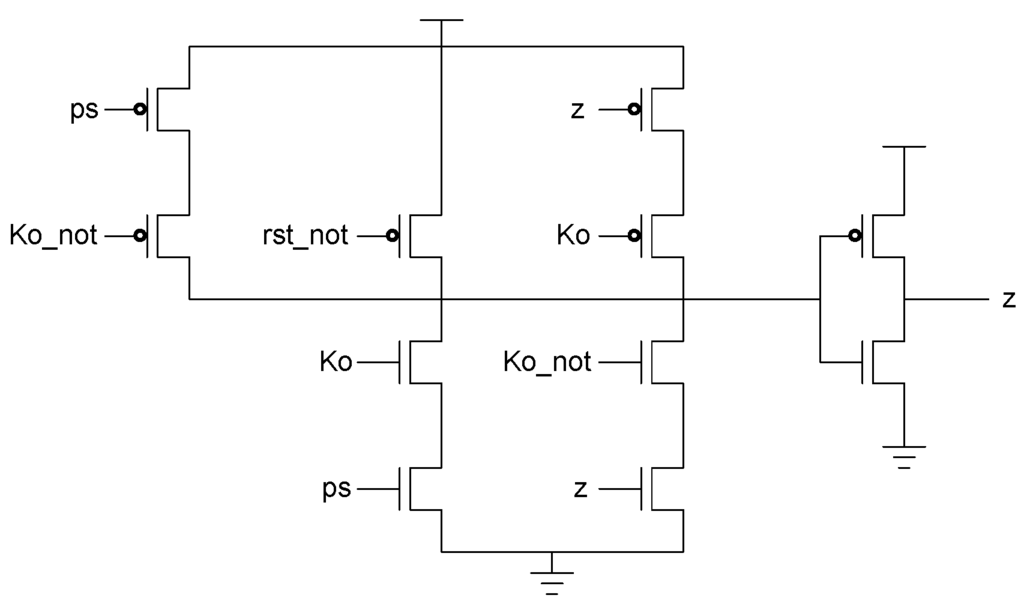
Figure 16. PS signal delay component.

Figure 16. PS signal delay component.

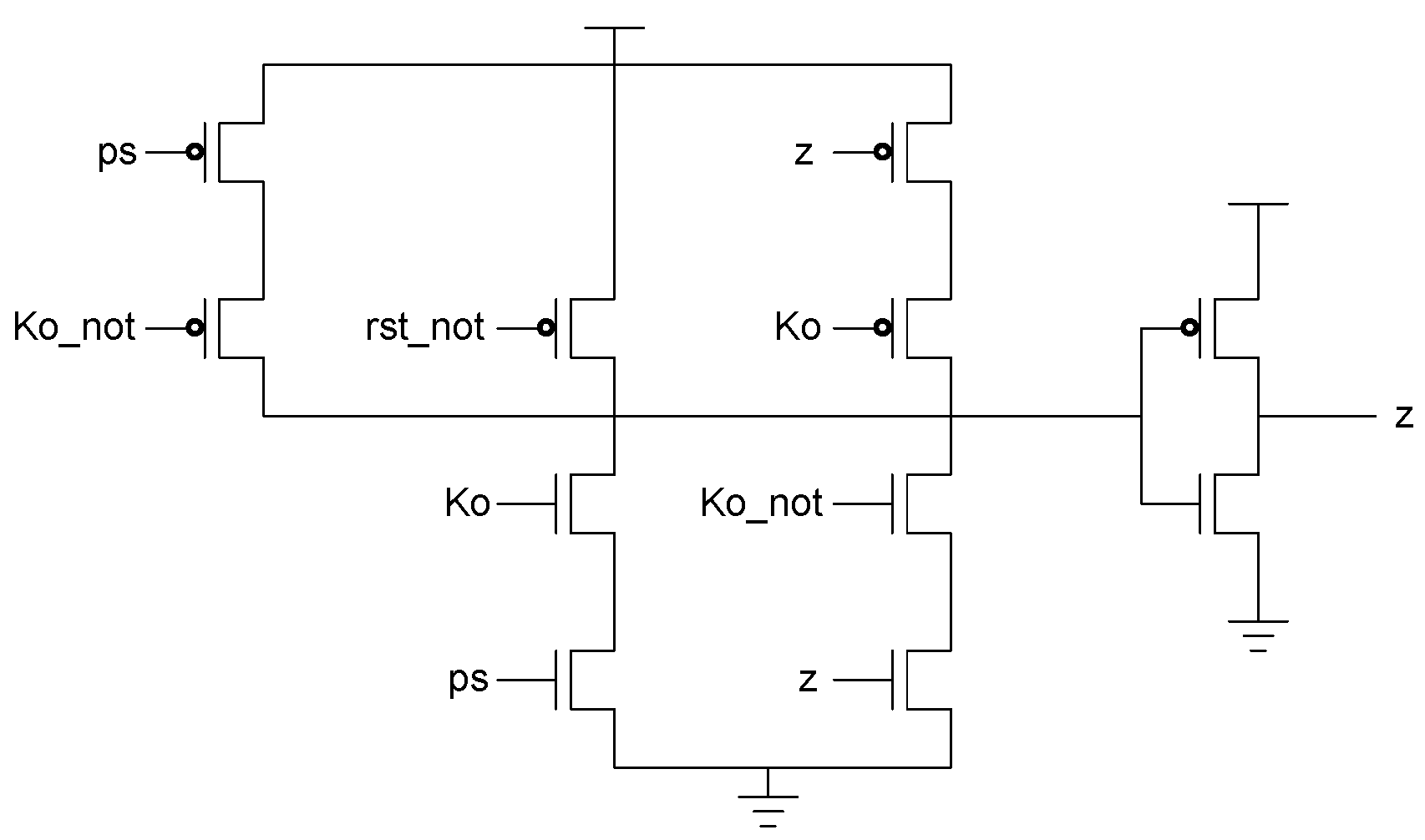
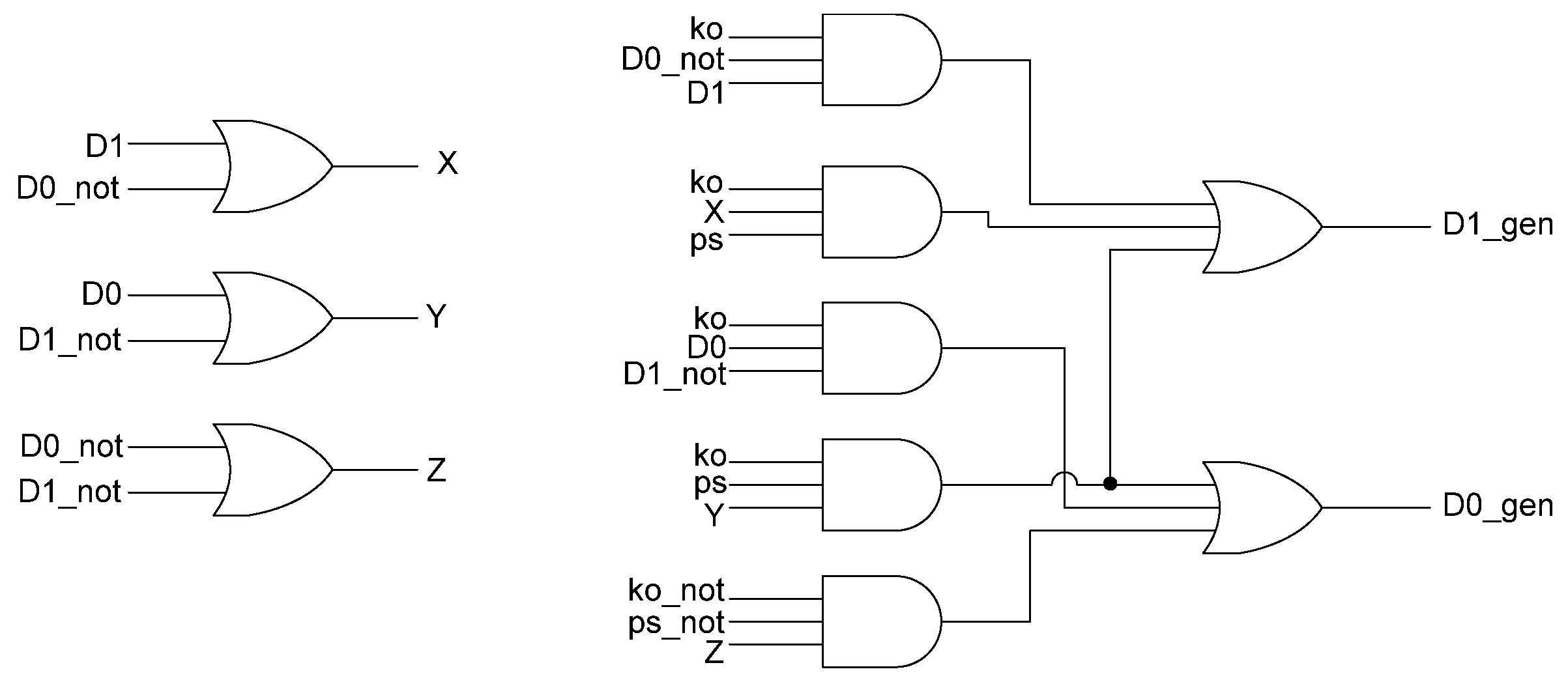
In situations where a component needs many cycles to output data but does not have input provided for each cycle, the component will not be able to receive the spacers it needs as input. Instead, a spacer generator register is used to generate these spacers for the component. A spacer generator register is a basic D³L register with a spacer generator sitting between it and its inputs. The spacer generator keeps track of the previous spacer and generates the alternate spacer when requested regardless of the dual-rail input it receives. For example, if the previous spacer was an AZS and the register requests a spacer, the spacer generator will generate an AOS. The next time a spacer is requested, it generates an AZS. Figure 17 shows the D³L spacer generator register; and Figure 18 shows the circuit diagram for the spacer generator component. The outputs of the spacer generator are given by the following equations:

D0_gen = Ko ps (D0+D1)+ Ko ps (D0+D1)+ Ko D0 D1

D1_gen = Ko ps (D0+D1)+ Ko ps (D0+D1)+ Ko D0 D1

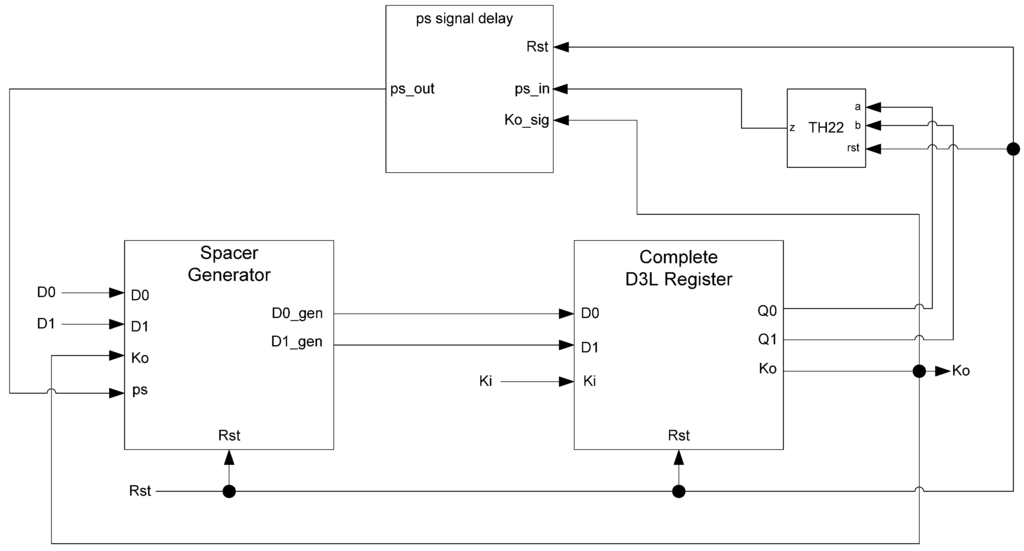
Figure 17. D³L spacer generator register.

Figure 17. D³L spacer generator register.

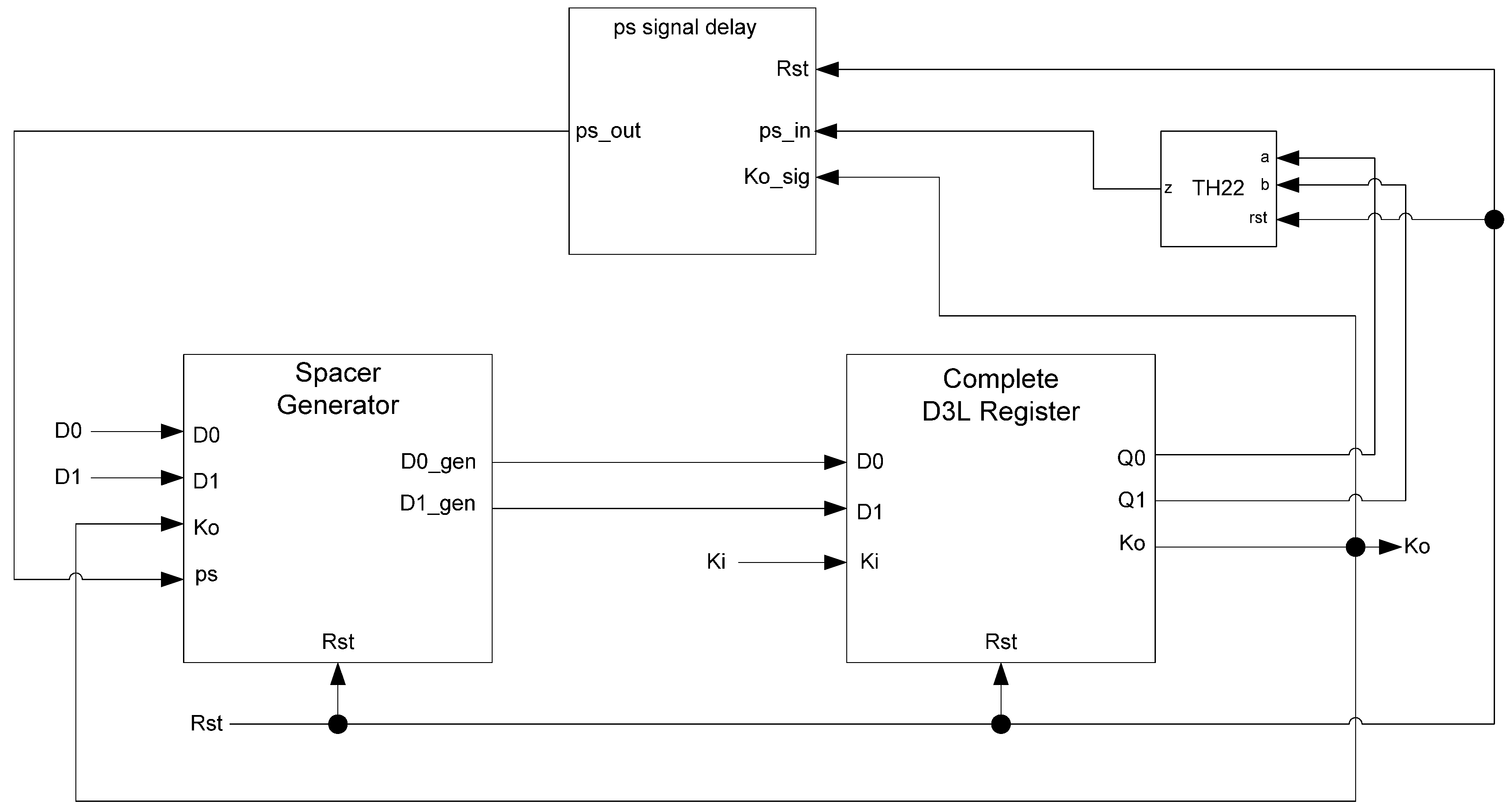
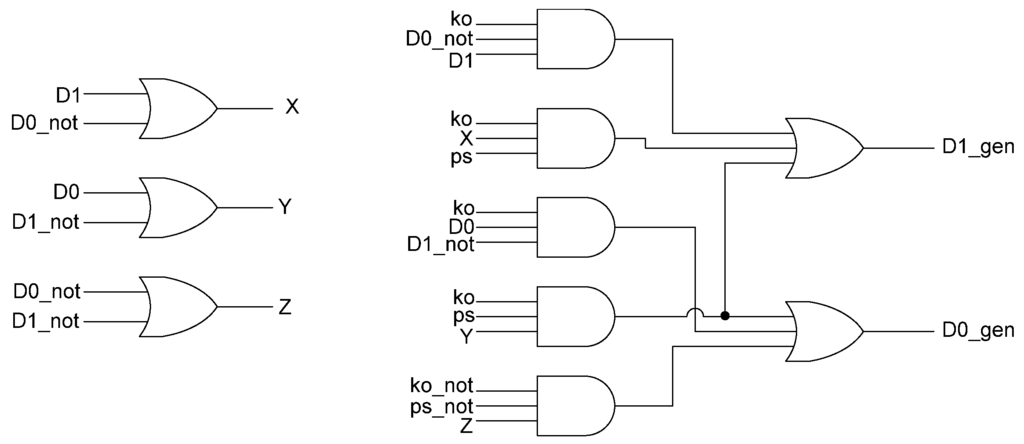
Figure 18. Spacer generator circuit diagram.

Figure 18. Spacer generator circuit diagram.

3. Multi-Threshold Dual-Spacer Dual-Rail Delay-Insensitive Logic (MTD³L)

3.1. Motivation

Although the D³L scheme successfully implements the dual-spacer protocol, it suffers from high overhead compared to equivalent NCL designs. This overhead comes from two sources. The first is the required NCL-X style completion logic in the form of several XNOR gates attached to each logic function. The second is the more complex registration. To eliminate the first source of overhead, the MTNCL technique can be combined with D³L, to form the new secure hardware paradigm presented in this paper, MTD³L.

Because D³L gates do not use hysteresis, an external source is required for input completion detection. Rather than using XNOR and threshold gates, the early completion technique used in MTNCL can be utilized to ensure that requests for a spacer will only be generated when all circuit inputs are that spacer and the following stage is requesting a spacer. At this point, the combinational logic can be slept to the proper value, ensuring input-completeness. Thus, the need for extra completion checking logic is eliminated.

3.2. MTD³L Gates

The addition of sleep logic to a D³L gate is simple. No modification to the D³L logic is required because it already matches the form of the modified NCL gates used in the MTNCL technique—a hold0 block and a set block. The only modification required is the addition of the sleep transistors. The sleep-to-0 transistors can be used in the same way as in SMTNCL. These transistors are responsible for the AZS transition. A similar set of transistors can be used for the AOS transition.

The sleep transistors are controlled by a pair of sleep signals, sleep-to-0 (s0) and sleep-to-1 (s1), and their complements, as shown in Table 4. These signals should not be asserted at the same time. Instead, if either of the inputs is asserted, the circuit will be slept to the appropriate value. Figure 19 shows the MTD³L gate design. When s0 is asserted, the circuit is slept to the all-zero state. In this case, the NMOS transistor parallel to the output inverter is turned on, the NMOS transistor gating the main circuit to ground is turned off, and the PMOS transistor gating the output circuit to V_DD is turned off. Additionally, since s1 is off, the NMOS transistor controlled by ns1 is turned on, completing the path from the output to ground, forcing the output to logic 0. The PMOS transistor controlled by s1 is also turned on, allowing the main circuit to pass an output of 1 to the output inverter, preventing glitches from occurring when s0 is later asserted. When this happens, the output inverter will have logic 1 on its input, so it will continue to output logic 0 until new data has arrived. Similarly, when s1 is asserted, the circuit is slept to the AOS. The path to V_DD for the main circuit is turned off while the path to ground remains on, allowing a 0 to eventually reach the output inverter. The output inverter’s path to ground is cut off and a direct path to V_DD is formed, forcing the output to be logic 1. When the sleep-to-1 state ends, the output inverter will have logic 0 on its input so the output will remain at logic 1, preventing a glitch. If neither sleep signal is asserted, the circuit operates as it would normally. All four power- and ground-gating transistors are turned on, allowing normal access to power and ground for the circuit and output inverter. The two parallel output transistors are turned off, so the output is only controlled by the output inverter. If both sleep signals happen to be asserted at once, the four power- and ground-gating transistors will be turned off, leaving the circuit in a floating state; however, this will never occur in a properly operating circuit.

Table 4. MTD³L sleep signals.

s0	s1	Output
0	0	Normal
0	1	All-One Spacer
1	0	All-Zero Spacer
1	1	Invalid

Table 4. MTD³L sleep signals.

s0	s1	Output
0	0	Normal
0	1	All-One Spacer
1	0	All-Zero Spacer
1	1	Invalid

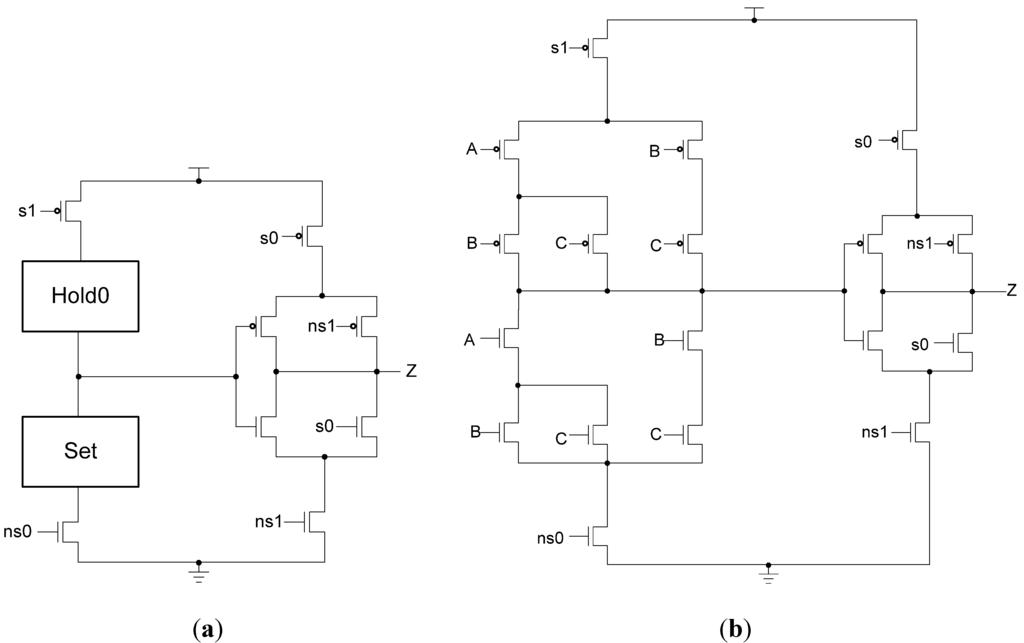
Figure 19. (a) MTD³L version 1 gate structure; (b) MTD³L23 version 1 implementation.

Figure 19. (a) MTD³L version 1 gate structure; (b) MTD³L23 version 1 implementation.

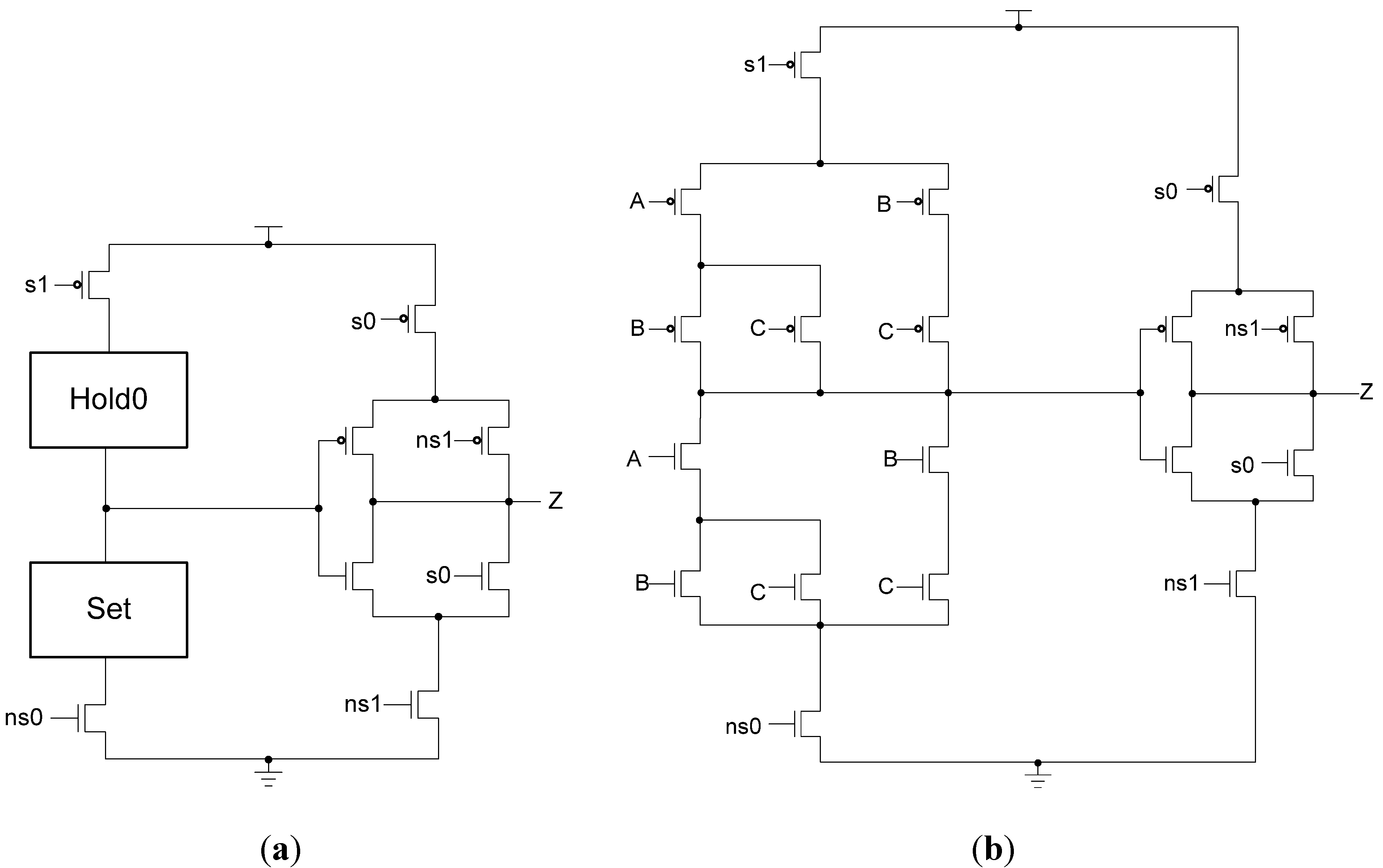
One of the drawbacks of the version 1 design is the potential for very large fanouts on the sleep signals. If the design is coarsely pipelined or the combinational logic happens to be very large, a single set of sleep signals may have to drive thousands of gates, requiring these signals to be heavily buffered. Not only must s0 and s1 be buffered but their complements will require buffering as well. To mitigate this issue and reduce the number of inputs to these gates in general, a modified design may be used to eliminate the need for the complemented sleep signals, as shown in Figure 20. This design removes the power- and ground-gating transistors from the main circuit, leaving only the four transistors on the output inverter. These four transistors are controlled by s0 and the complement of s1, allowing for the removal of s0’s complement and s1 itself. Thus, only two signals must be buffered instead of four. The drawback to this technique is that the main circuit is directly exposed to power and ground, eliminating the ability to gate the circuit with high-V_t transistors.

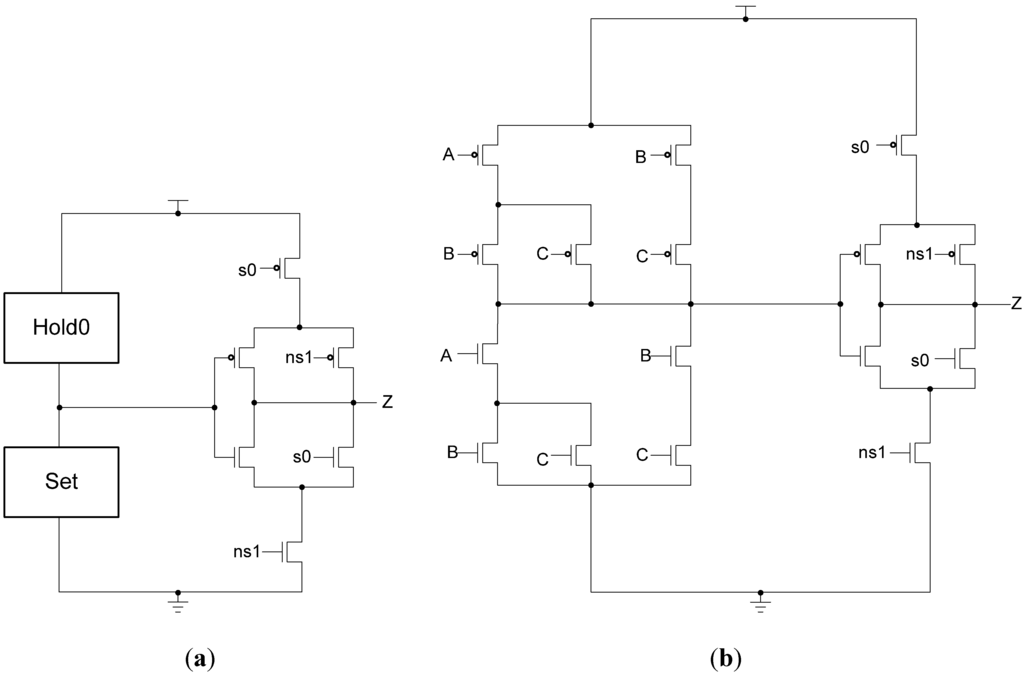
Figure 20. (a) MTD³L version 2 gate structure; (b) MTD³L23 version 2 implementation.

Figure 20. (a) MTD³L version 2 gate structure; (b) MTD³L23 version 2 implementation.

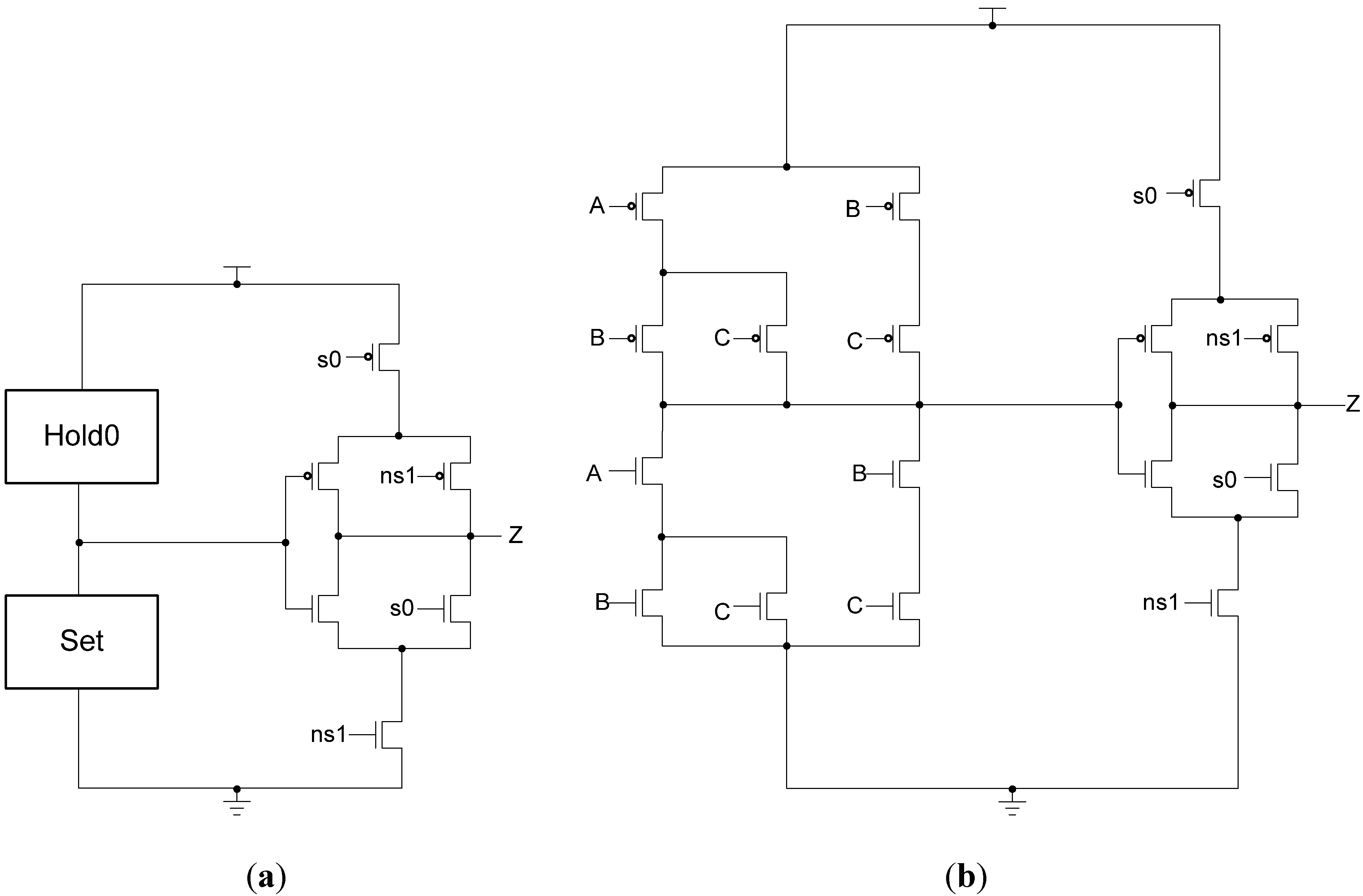
3.3. MTD³L Registration

The basic MTD³L register, shown in Figure 21, is a modified NCL register. It consists of two TH22 gates which are resettable to the desired value. An XNOR gate facilitates early completion by checking the relative values of the register’s inputs. If both input rails have the same value then the register has received a spacer and will request data. If the values are different, then DATA has been received so the register will request the next spacer.

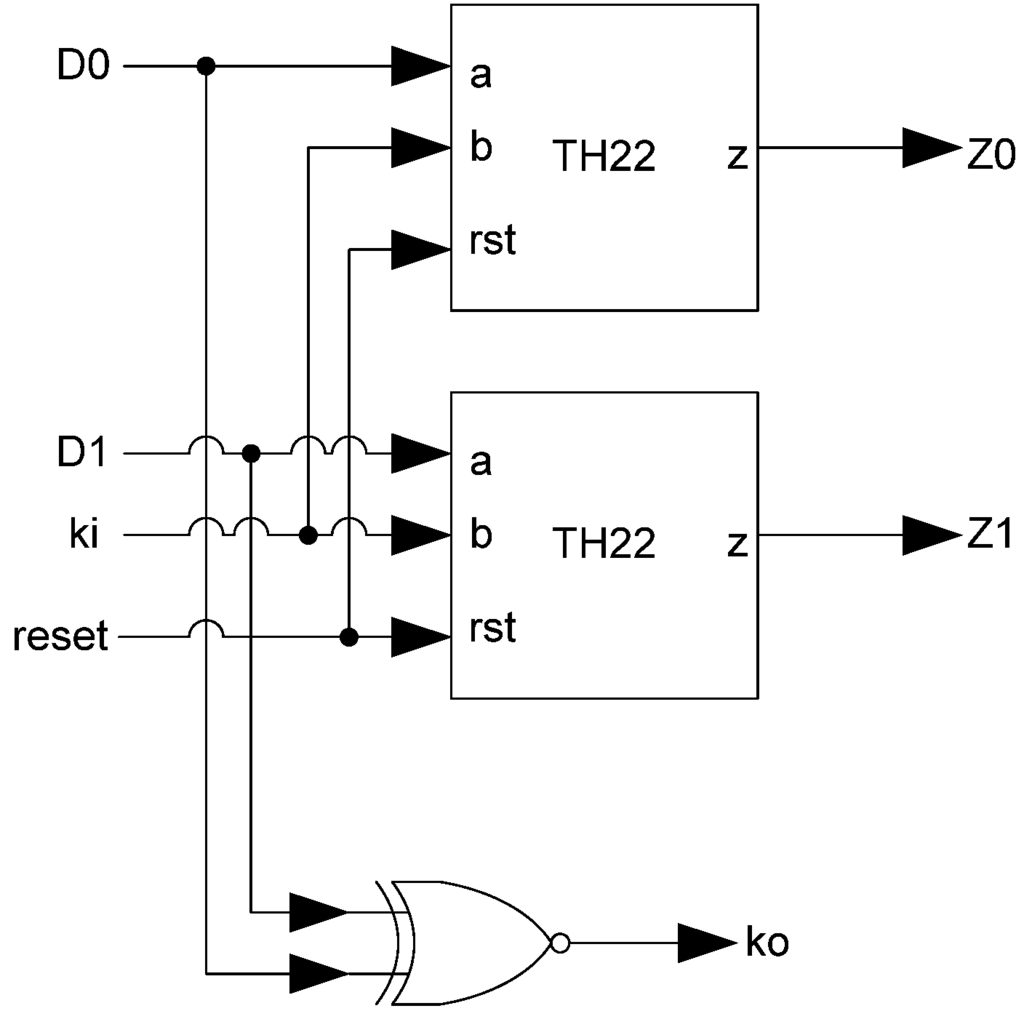
Figure 21. MTD³L register.

Figure 21. MTD³L register.

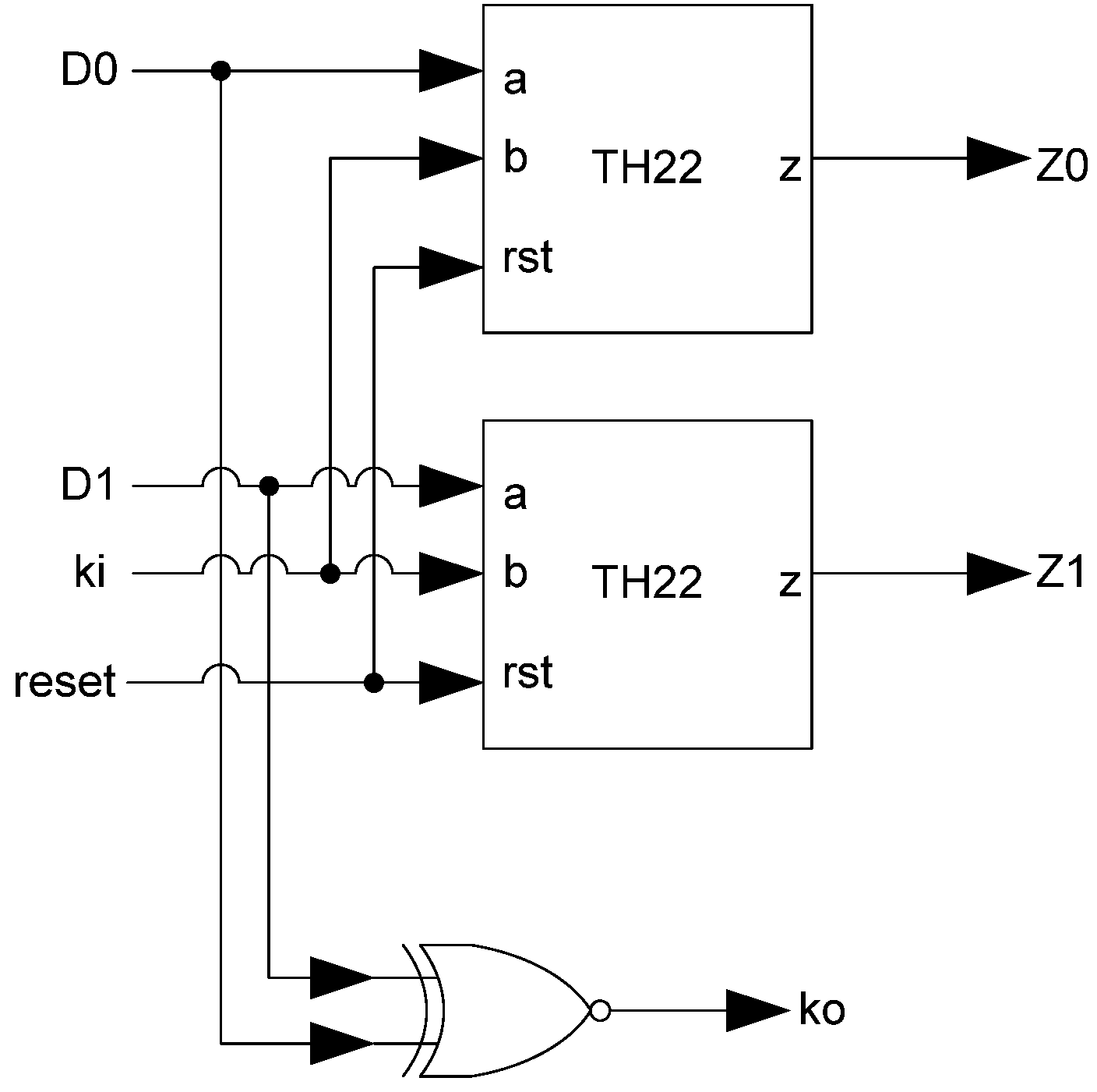
Additional logic is required to facilitate the dual-spacer protocol and early completion checking. The early completion component consists of resettable TH22 gates whose inputs are the register’s K_o and the next stage’s inverted K_o. The reset state of the early completion component is logic 1 if the register’s reset state is NULL and logic 0 if the register’s reset state is DATA. In order to ensure input-completeness, the early completion K_o is inverted before being passed back as the register’s K_i input. This prevents a partial spacer wavefront from passing through the register by ensuring that all of the register’s inputs are an AOS or AZS before the spacer wavefront is allowed to pass through the register. In order to facilitate the dual-spacer protocol, the same Ki Generator used in D³L registration, shown in Figure 12, is used for MTD³L.

If the register needs to supply sleep signals then sleep signal logic is used here as well, as shown in Figure 22. This logic generates two sleep signals, s0 and s1. The values of the sleep signals are shown in Table 5. If the register’s K_i is 0 then a spacer is being requested. To determine which spacer is being requested, Ki_gen’s value is used. If Ki_gen is logic 0 then an AZS is being requested; if it is logic 1 then an AOS is being requested. To avoid incorrect sleep states, a buffer is used as a delay element to ensure that the change in Ki_gen’s value is evaluated first. For example, if the desired change was from the no sleep state of row 2 to the sleep-to-1 state of row 3, then both Ki_gen and K_i will switch. If K_i switches first, a sleep-to-0 will be issued erroneously. However, if Ki_gen switches first then the no sleep state will be maintained until K_i changes as well, resulting in the correct sleep-to-1 state.

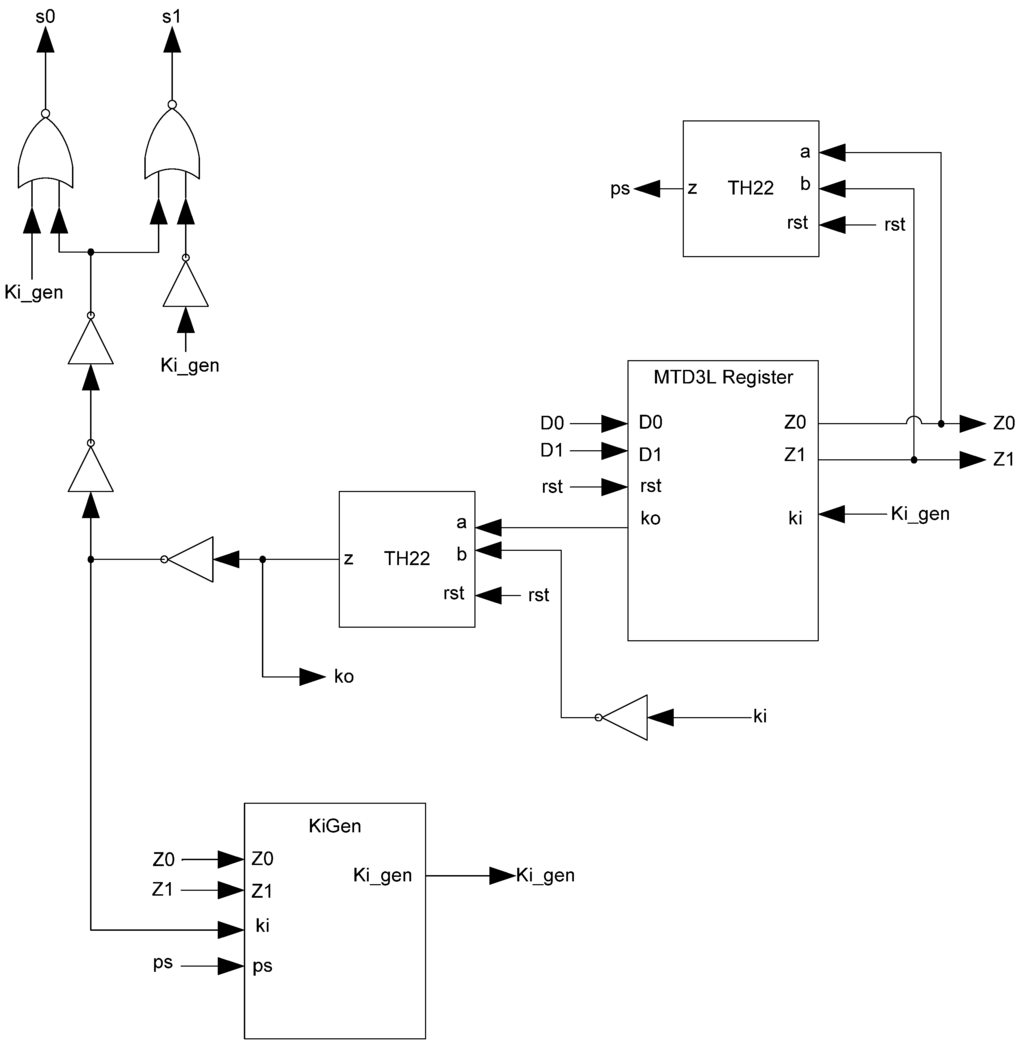
Figure 22. Complete MTD³L register.

Figure 22. Complete MTD³L register.

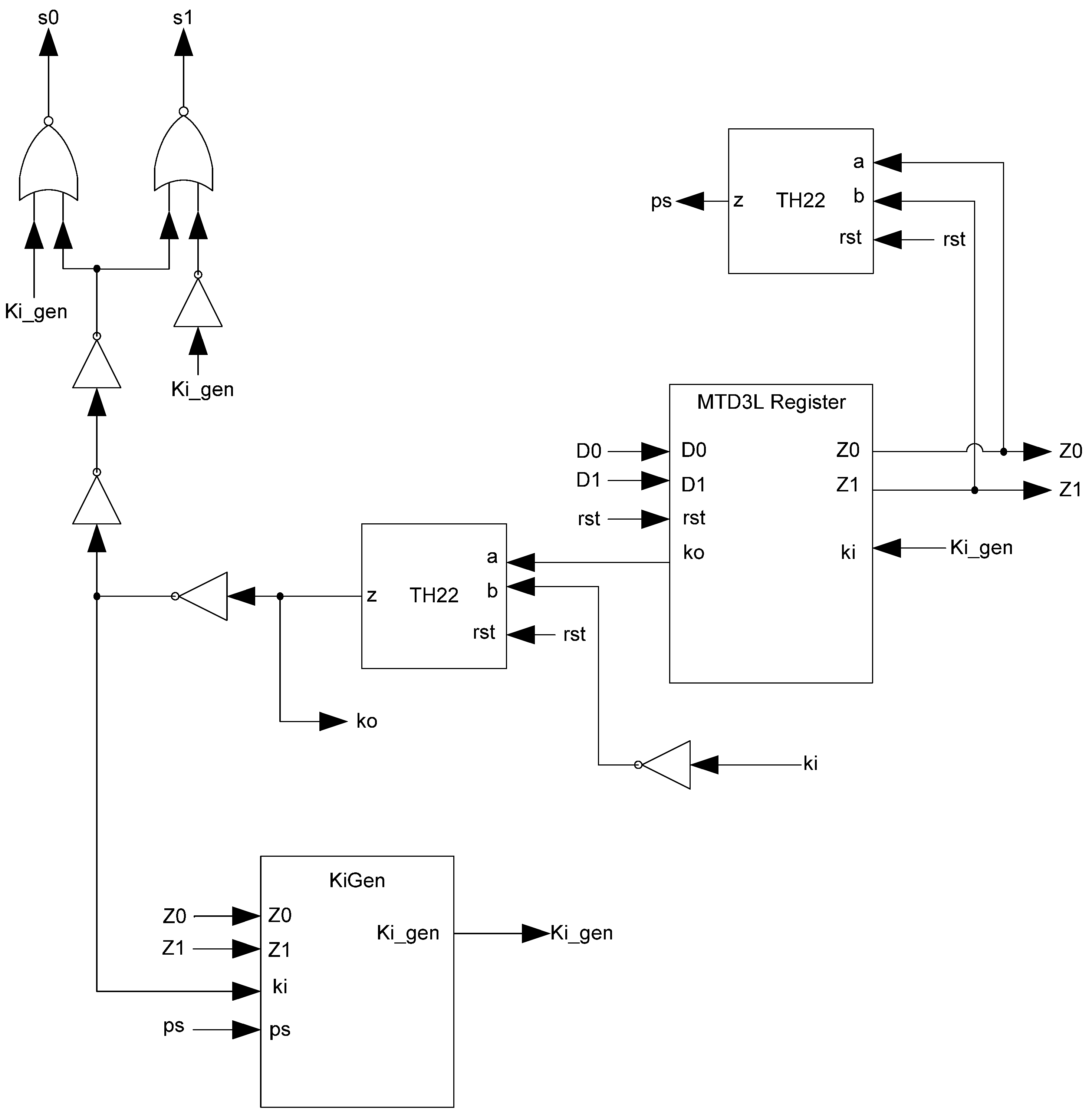
Table 5. MTD³L sleep signal switching sequence.

Ki_gen	Ki	s0	s1
0	0	1	0
0	1	0	0
1	0	0	1
1	1	0	0

Table 5. MTD³L sleep signal switching sequence.

Ki_gen	Ki	s0	s1
0	0	1	0
0	1	0	0
1	0	0	1
1	1	0	0

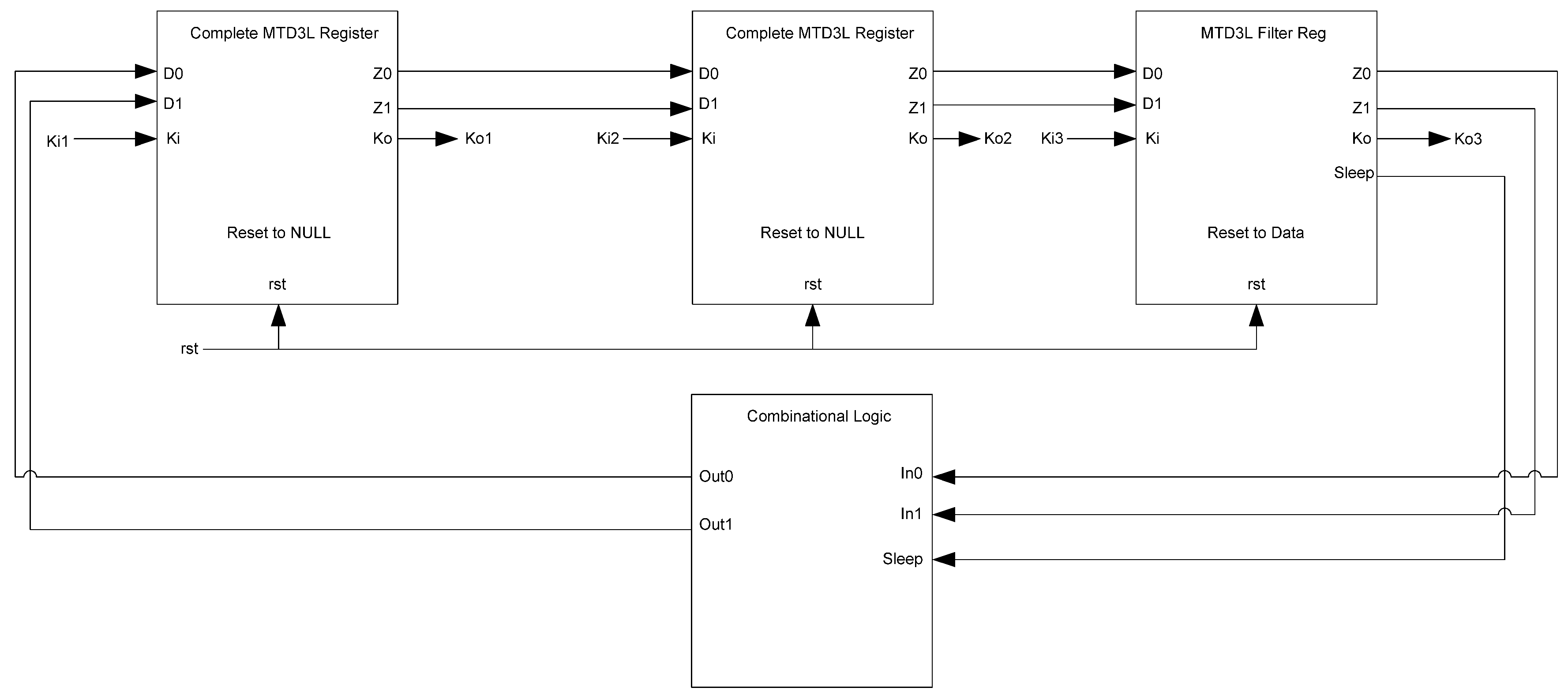
MTD³L spacer filter and spacer generator registers, shown in Figure 23 and Figure 24, respectively, are used in the same manner as they are used in D³L circuits. The filter register is used as the final register in a register ring, shown in Figure 25. It is reset to DATA and filters the spacer that passes through the ring, alternating it so that the dual-spacer protocol is enforced. The spacer generator generates the appropriate spacer as needed regardless of the values of its inputs. Typically, these registers are the ones that generate sleep signals as they are usually the registers that are facing combinational logic as shown in Figure 25. The actual spacer filter and spacer generator components are unmodified from their D³L counterparts, shown in Figure 15 and Figure 18, respectively.

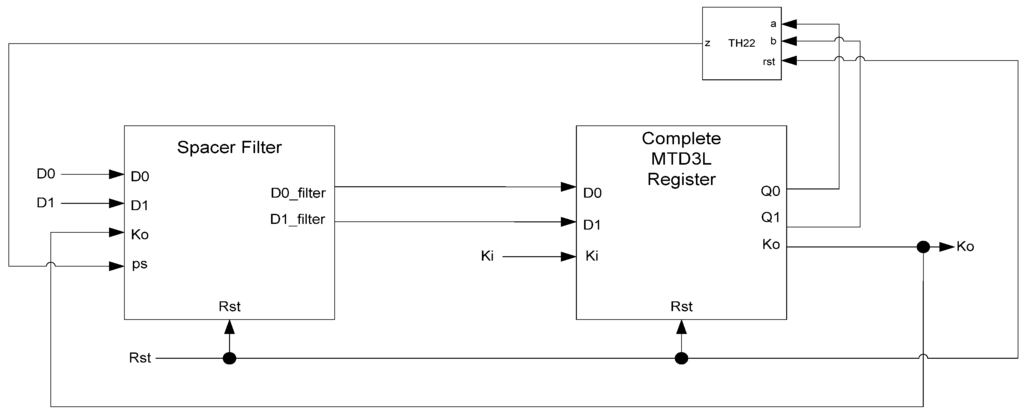
Figure 23. MTD³L spacer filter register.

Figure 23. MTD³L spacer filter register.

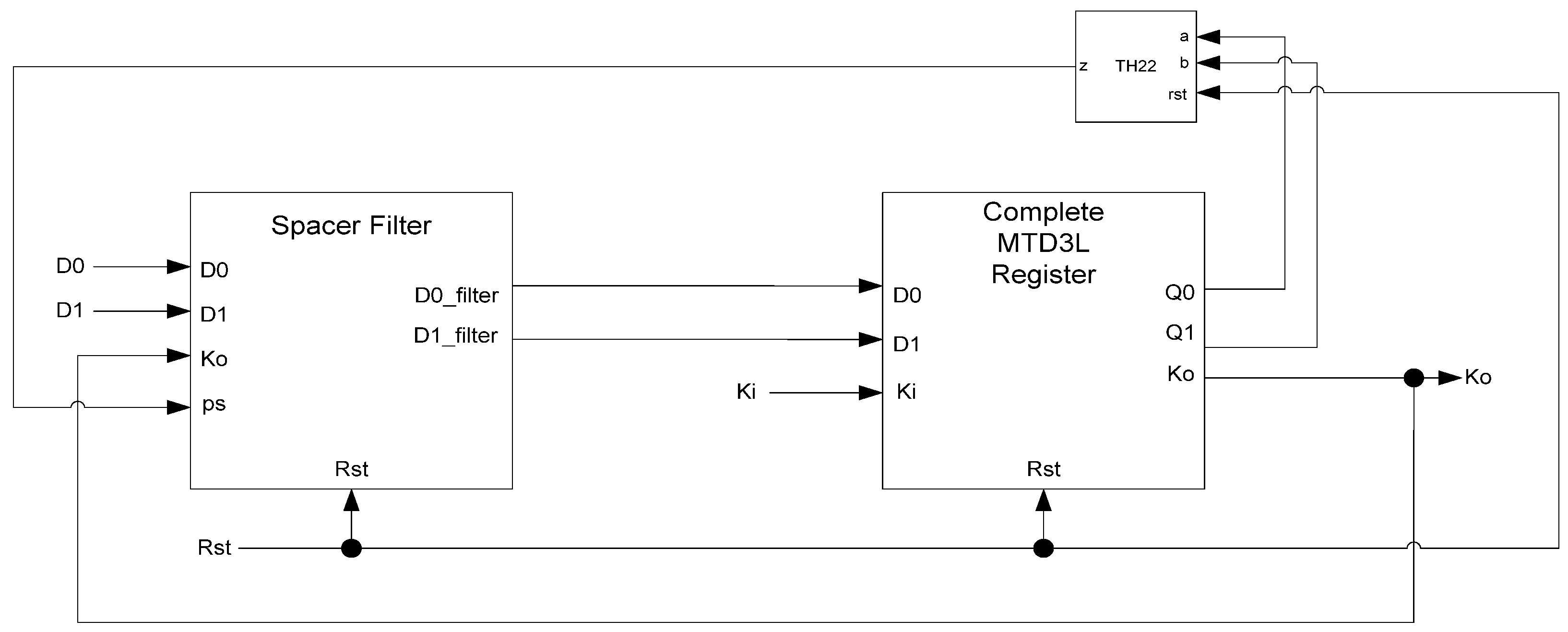
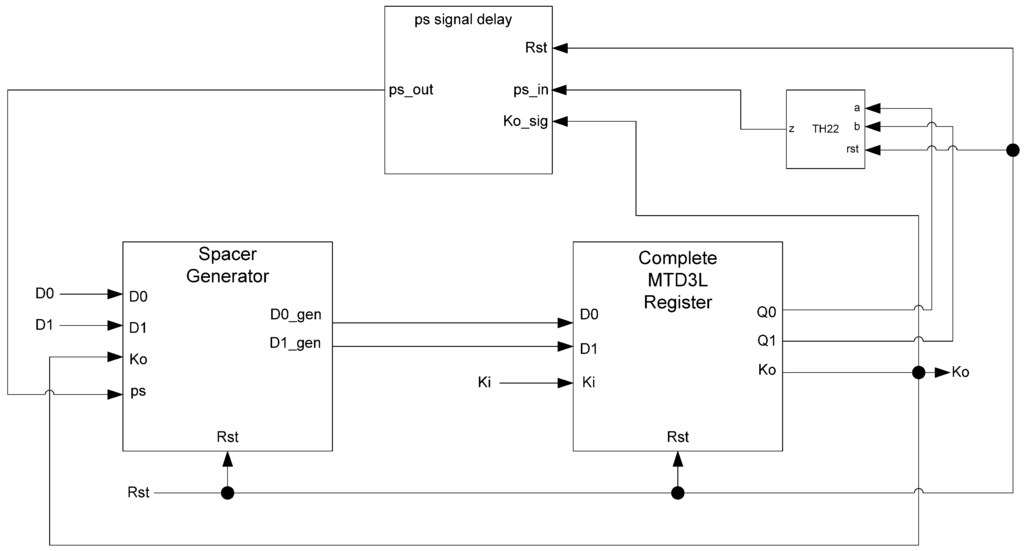
Figure 24. MTD³L spacer generator register.

Figure 24. MTD³L spacer generator register.

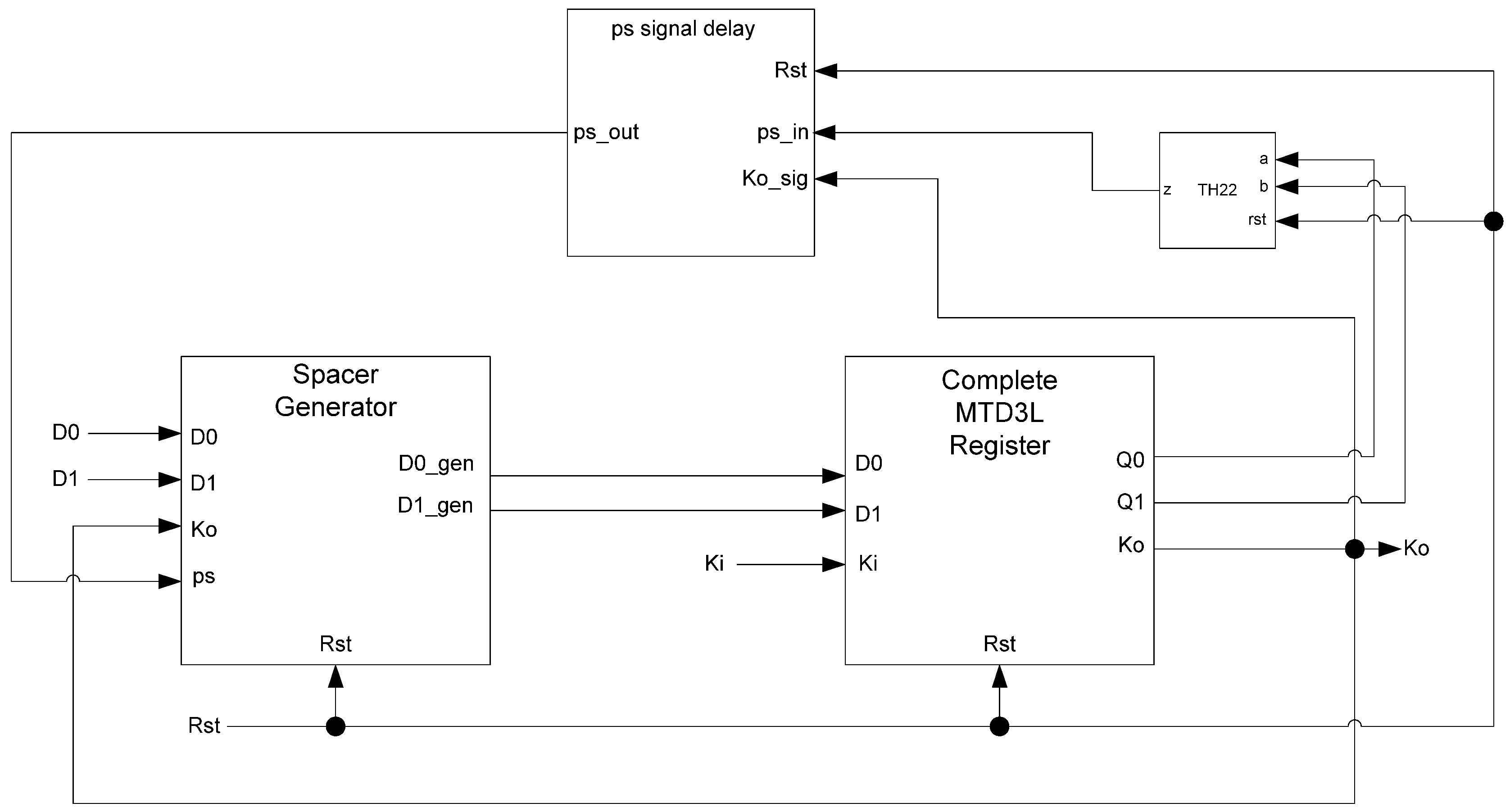
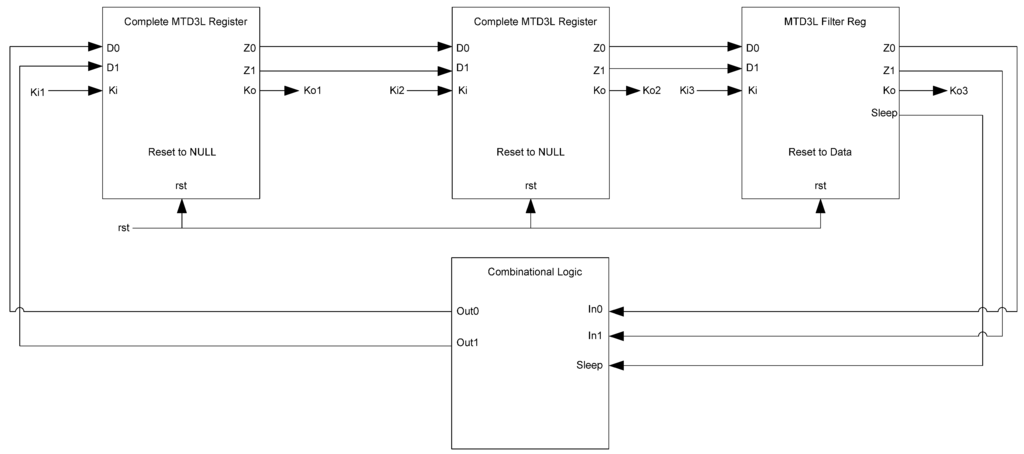
Figure 25. MTD³L ring register.

Figure 25. MTD³L ring register.

4. AES Core Implementations

4.1. MTD³L Implementation

The implementation of the 128-bit AES core [46] in each design follows the same architecture. The AES transform and key expansion functions are computed in parallel. A Control block synchronizes the two functions and ensures that the correct sub-key is sent to the Transform block at the correct time. From outside, this circuit behaves as a register in terms of handshaking, so it can be easily placed into an asynchronous system. The AES core accepts an input and produces an output with one external DATA/spacer cycle. However, the AES circuit actually produces several internal DATA/spacer cycles for processing each plaintext, which are hidden from the outside. Each round of the AES algorithm consists of one of these internal cycles.

As shown in Figure 26, each design consists of five blocks: the FirstRound block, the Control block, the AESTransform block, the KeyExpansion block, and the LastRound block. The FirstRound block is a set of input registers that latch in new data and provide it to the AESTransform and KeyExpansion blocks. The AESTransform block performs the ciphertext calculation for each round of the algorithm. The KeyExpansion block calculates the subkey used in the AESTransform block. The Control block creates the control signals as well as generating the RCon constant which is used in the KeyExpansion block. The LastRound block performs the final round of calculations and also has a set of output registers to hold the final ciphertext.

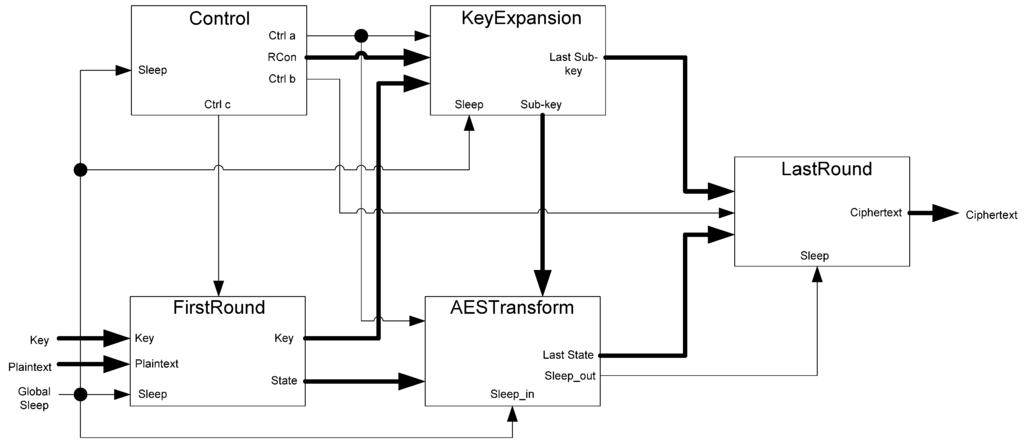
Figure 26. Advanced Encryption Standard (AES) top level diagram.

Figure 26. Advanced Encryption Standard (AES) top level diagram.

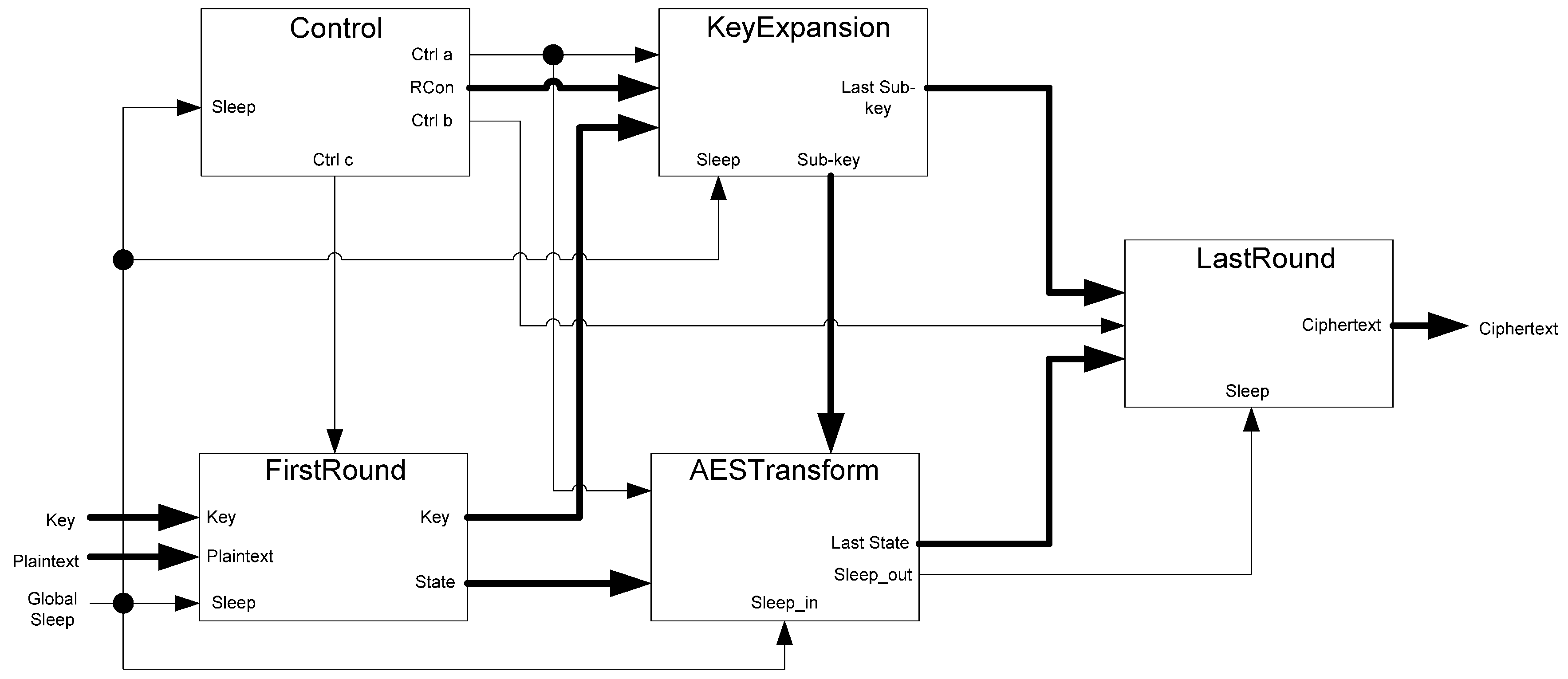
The communication between blocks, shown in Figure 27, consists of three handshaking signals: Ki1, Ki2, and Ki3. These signals are generated by a set of threshold gates in the top level circuit. The inputs of these threshold gates are the K_O values from registers throughout the design. The AESTransform, KeyExpansion, and Control blocks all have a three-ring register to save processed data. Each ring register’s K_o is used as inputs to the top-level handshaking. Additionally, an extra K_O from the registers in the FirstRound and LastRound blocks is used as well. The resulting Ki1, Ki2, and Ki3 signals are used as the K_i inputs to the ring-registers mentioned previously.

Figure 27. Top level handshaking diagram.

Figure 27. Top level handshaking diagram.

The sleep signal generation mechanism consists of two types of sleep signals: a global sleep and local sleeps. The global sleep, which is a circuit input, is meant to sleep the entire circuit between encryption stages, ensuring that everything is reset properly. This sleep is only asserted after the ciphertext is latched out and external handshaking is requesting a spacer cycle. The internal sleep signals are generated locally within each block by the ring-registers. These sleeps are asserted between calculation stages. The LastRound block, lacking registration between it and the previous AESTransform block, uses the local sleep signals generated by the AESTransform block.

The FirstRound block, shown in Figure 28, consists of a set of 128-bit registers for both the input plaintext and input keys. These are regular, non-slept generating registers. The K_i to these registers is the master K_i input for the circuit. The K_os are used to generate a reset signal for the rest of the blocks, preparing them for a fresh encryption process. This reset signal also acts as the circuit’s K_o output. The data outputs of these registers go to a set of spacer-generator registers. These registers use the Ki1 signal as their K_i, synchronizing these registers with the first stage of the ring-registers throughout the design. Their K_os are not used. Next, an AddRound block calculates the initial addition of the plaintext and key, passing this data to the AESTransform block. The initial key is also passed to the AESTransform and KeyExpansion blocks. The sleep signals for the AddRound block are generated by the data processing spacer-generator register.

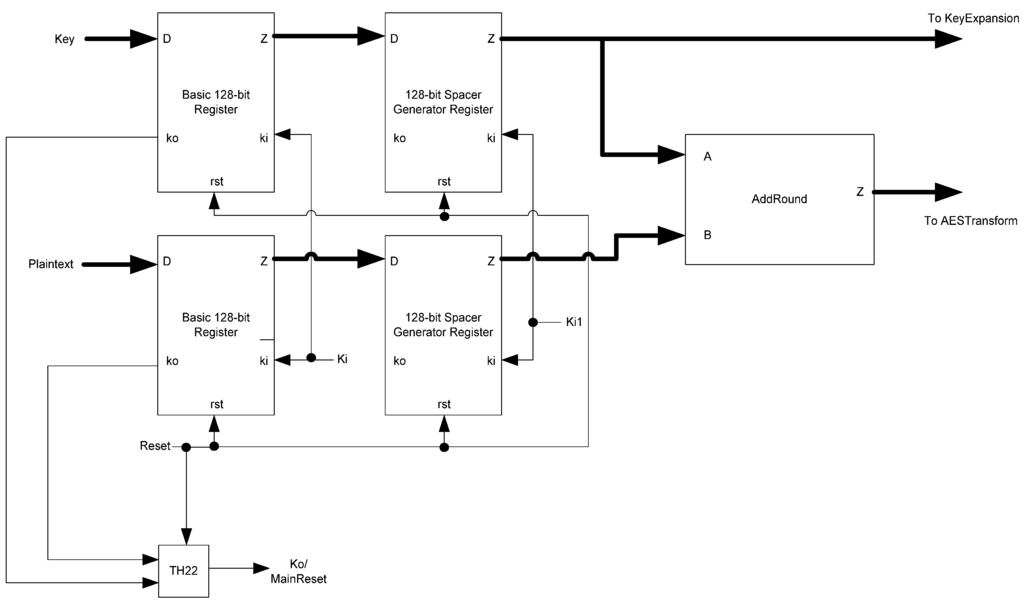
Figure 28. FirstRound block diagram.

Figure 28. FirstRound block diagram.

The AES Transform block, shown in Figure 29, handles the primary calculation of the ciphertext. It consists of the main AES components: AddRound, SubByte, MixColumns, and Shiftrows. A three-ring register is used to save data between each round of calculation. To control whether the input data is taken from the FirstRound or from the circuit feedback loop, a 2-to-1 multiplexer is used. The control signal of the multiplexer is supplied by the Control block. The output of the multiplexer serves as both the output of the circuit and the feedback loop to the first register in the ring. The first and second registers are normal registers while the third is a filter register. This filter register generates the sleep signals to be used by this block as well as the subsequent LastRound block.

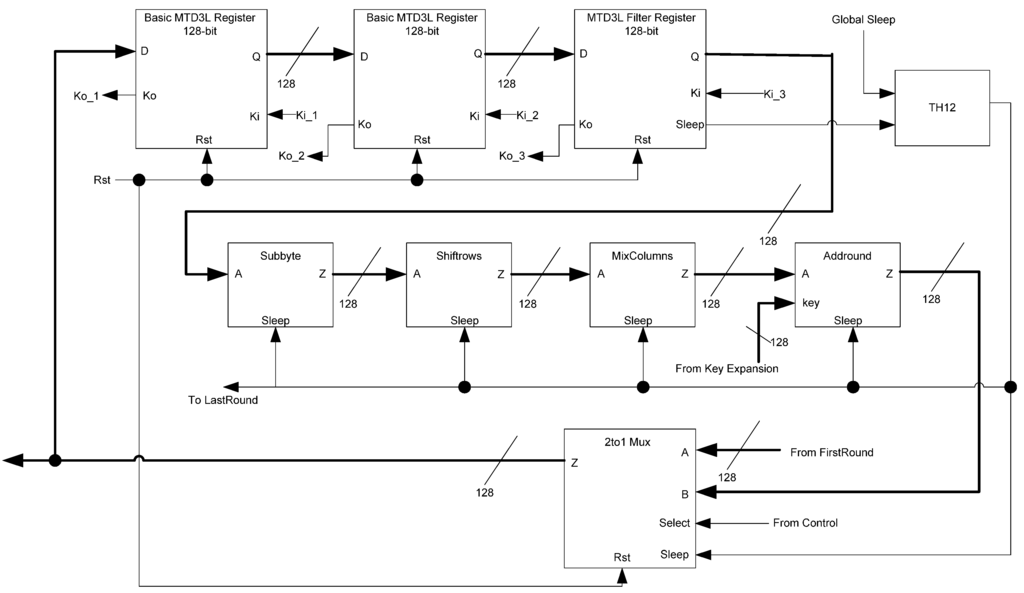
Figure 29. AES transform block diagram.

Figure 29. AES transform block diagram.

The KeyExpansion block, shown in Figure 30, is very similar to the AES Transform block. It consists of the KeyExpansion logic, a three-ring register, and a 2-to-1 multiplexer. The register and multiplexer act in the same manner as they do in the AES Transform block. The sleep signals for the KeyExpansion logic are generated by the third register in the ring, which is a filter register. The KeyExpansion logic takes the 128-bit key and transforms it into a new subkey, which is sent to the AES Transform and LastRound blocks.

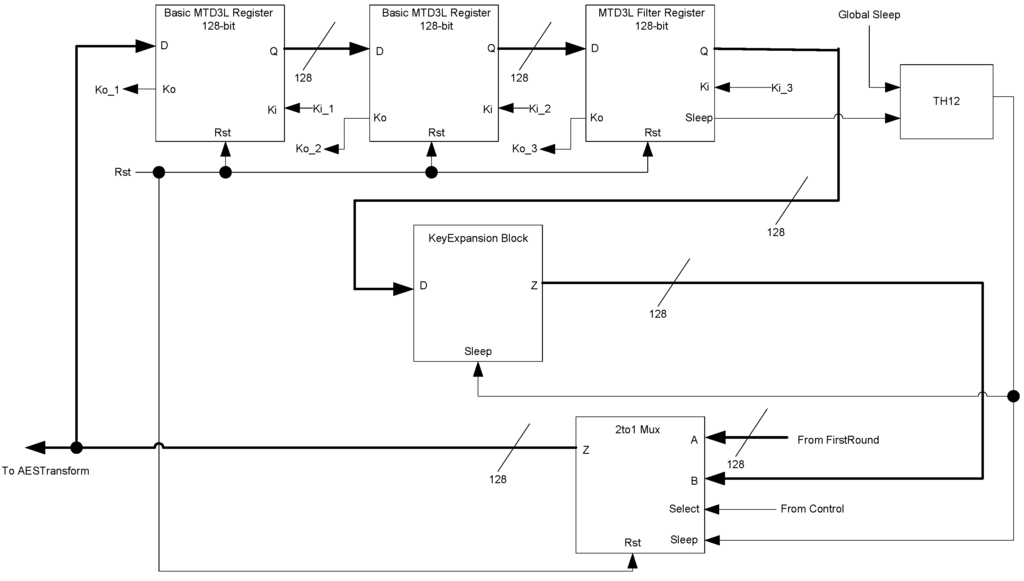
Figure 30. KeyExpansion block diagram.

Figure 30. KeyExpansion block diagram.

The Control block, shown in Figure 31, synchronizes all other blocks to ensure proper operation. It generates the control signals for the multiplexers throughout the design, the RCon constant used in the KeyExpansion calculations, and the control signal that activates the LastRound block. The LastRound block will only latch data to the output register when this signal is received. The input to the Control block is the reset signal generated by the K_o of the FirstRound block. This signal resets the Control block’s state, preparing it for a new encryption set.

The Control block is a state machine consisting of four components: a 5-bit three-ring register, the control signal logic, the increment logic, and the LastRound logic. The ring-register saves the state of the Control block. The filter register in this ring also generates the sleep signals for the block. The control signal logic generates the RCon signal and the multiplexer control signals. The increment logic is a counter, keeping count of the number of encryption rounds executed. When the counter reaches the round limit, the stop signal is activated.

The initial state of the Control block needs to be an AZS. However, the filter register in the ring-register is reset to data. Thus, extra logic is required to generate the initial AZS. A set of TH22n gates is used to do this. Each TH22n gate is tied to one of the signals, which is connected to both inputs of the gate. At reset, each of these gates will output a zero, giving the required spacer. Once the reset is finished, these gates will act as C-elements. Since each gate has the same signal on both inputs, its output will follow the value of the input.

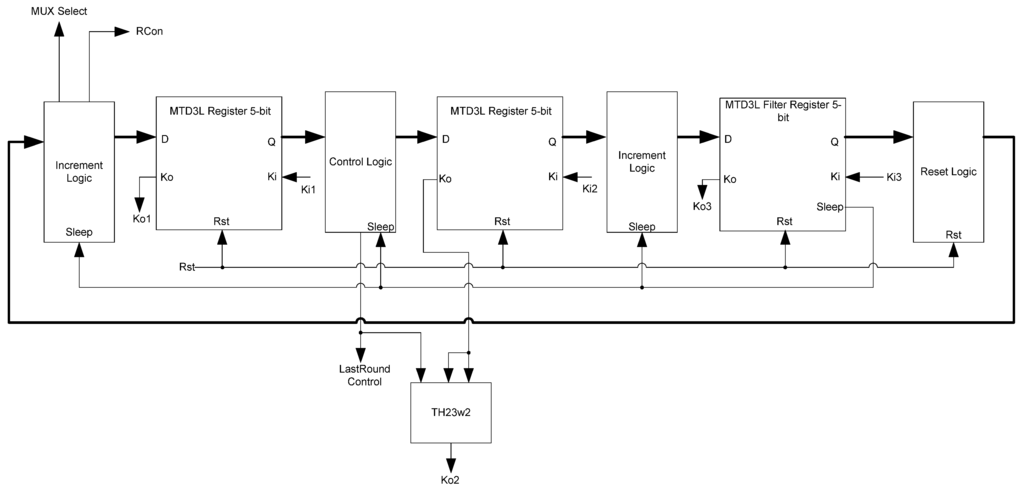
Figure 31. Control block diagram.

Figure 31. Control block diagram.

The LastRound block, shown in Figure 32, consists of the final SubByte, Shiftrows, and AddRound operations on the ciphertext as well as the final output register. The MixColumns block is not used in the final round. The inputs to this block are the last transformed ciphertext from the AESTransform block and the final subkey from the KeyExpansion block. The sleep signals are the same ones generated in the AESTransform block. The register will only latch data once the stop signal is received from the Control block, which acts as the K_i to the register. This final register is a filter register, ensuring that the output from the AES circuit is capable of generating the correct spacer and sleep signals for the following circuit block.

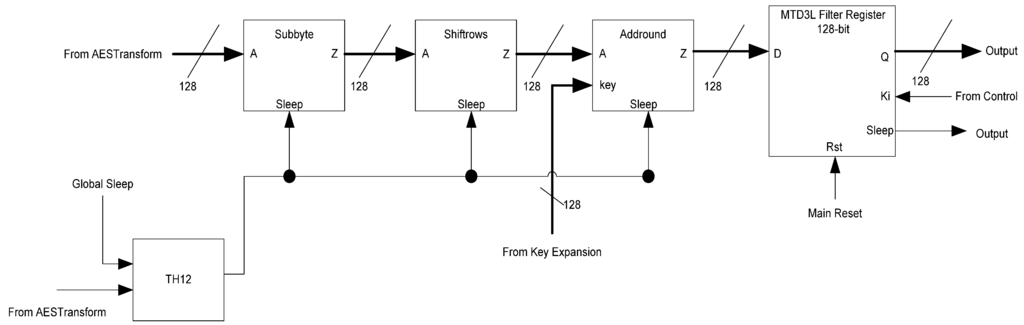
Figure 32. LastRound block diagram.

Figure 32. LastRound block diagram.

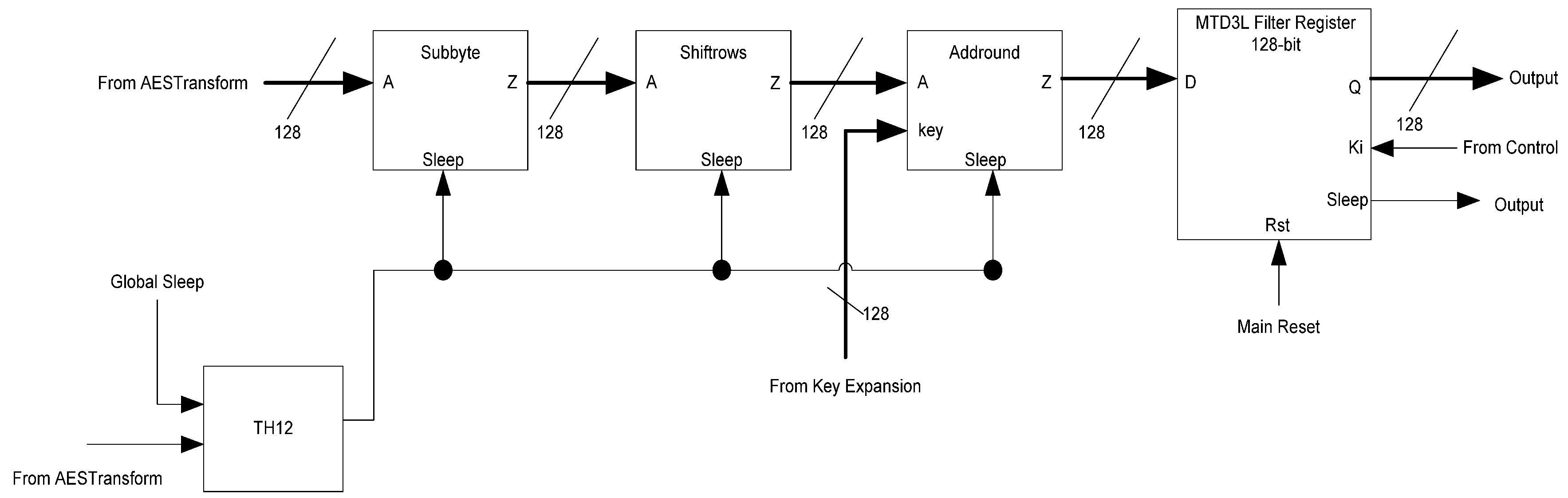
4.2. AES Implementation using D³L

The D³L implementation is very similar to the MTD³L implementation. The same five blocks are used and their configurations are essentially the same. There are two primary differences between the two designs. First, since the D³L design lacks sleep signals, a global reset is used to reset the spacer-generator registers in the FirstRound between encryptions. This reset is required for the circuit to reset properly. The second major difference is the usage of completion signals. Each combinational block has a completion signal which is used to ensure input-completeness. The completion signals (ccheck) of the FirstRound and LastRound blocks are added to the Ki1 calculation. In the AES Transform block, the Ko1 output consists of the combination of the K_o from the first register as well as the ccheck signals from the multiplexer and AES logic. This is also done in the KeyExpansion and Control blocks. The ccheck signals themselves are generated with completion checking logic inside each combinational logic block.

4.3. AES Implementation using NCL

Being extensions of the NCL style, the D³L and MTD³L designs are very similar to the NCL design as well. Additionally, the NCL design served as the base of the D³L design, which was created by taking the original NCL design and replacing the gates and signals. Because of this, the structure of the blocks themselves and the combinational logic are very similar. The primary differences in the designs are found in registration, spacer generation, and input-completeness logic. Figure 33 shows the NCL AES Transform block.

NCL threshold gate logic supports input-completeness by design, so there is no need for extra input-completeness logic. Additionally, only a single register type is needed, which can be reset to the desired values. Finally, the FirstRound block, shown in Figure 34, only needs to generate NULL spacers when needed, so the spacer-generator registers are replaced with NULL generators.

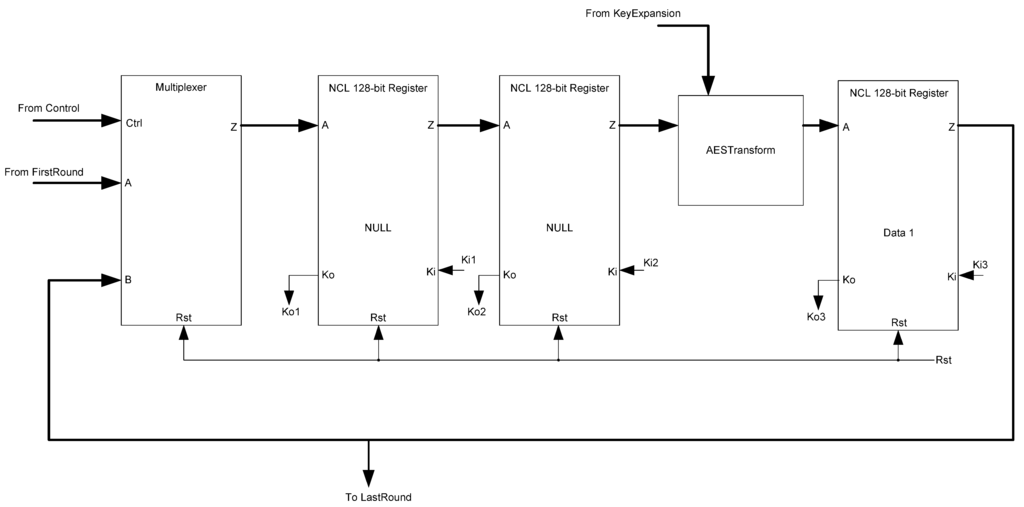
Figure 33. NCL AES Transform block diagram.

Figure 33. NCL AES Transform block diagram.

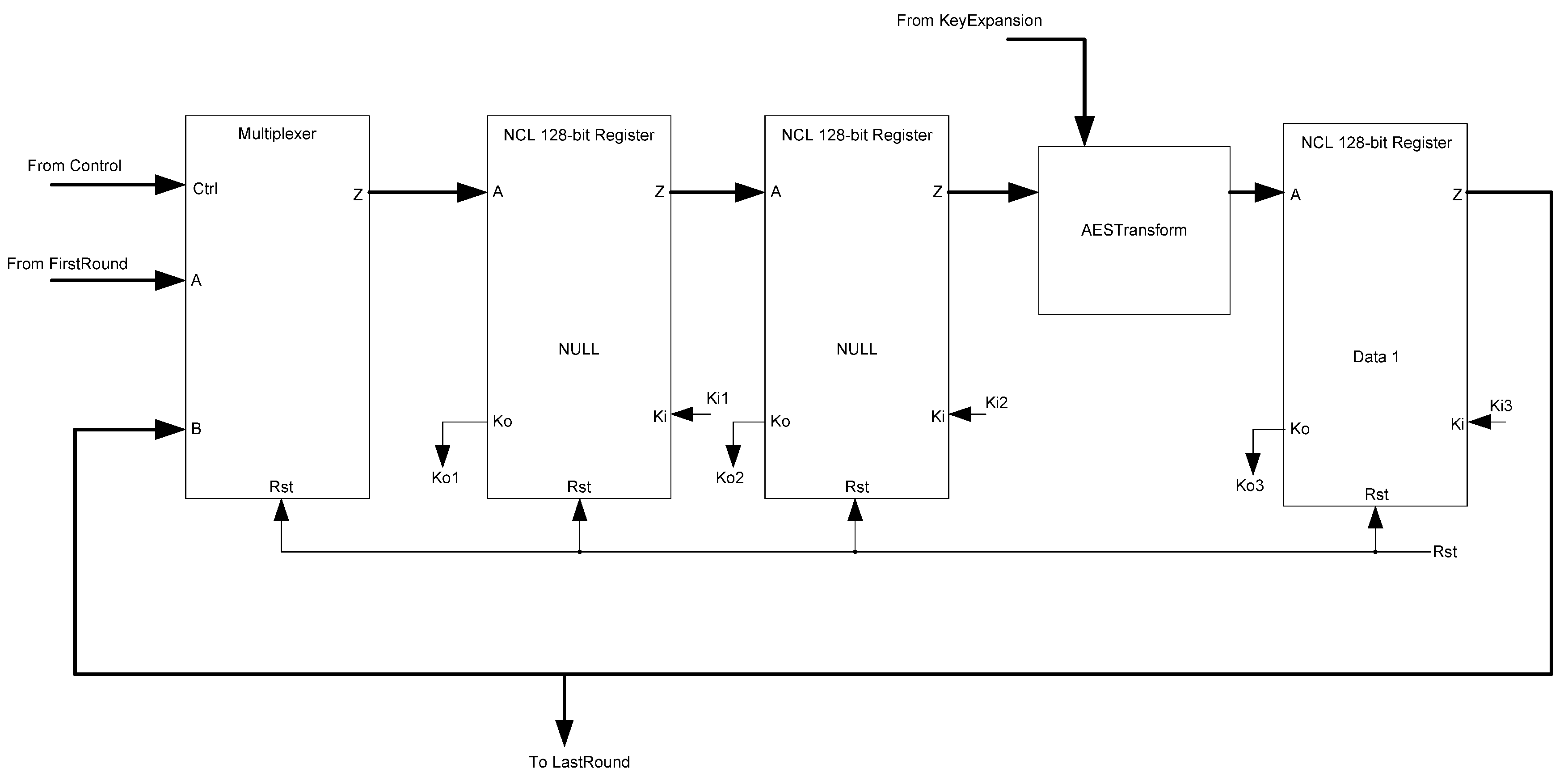
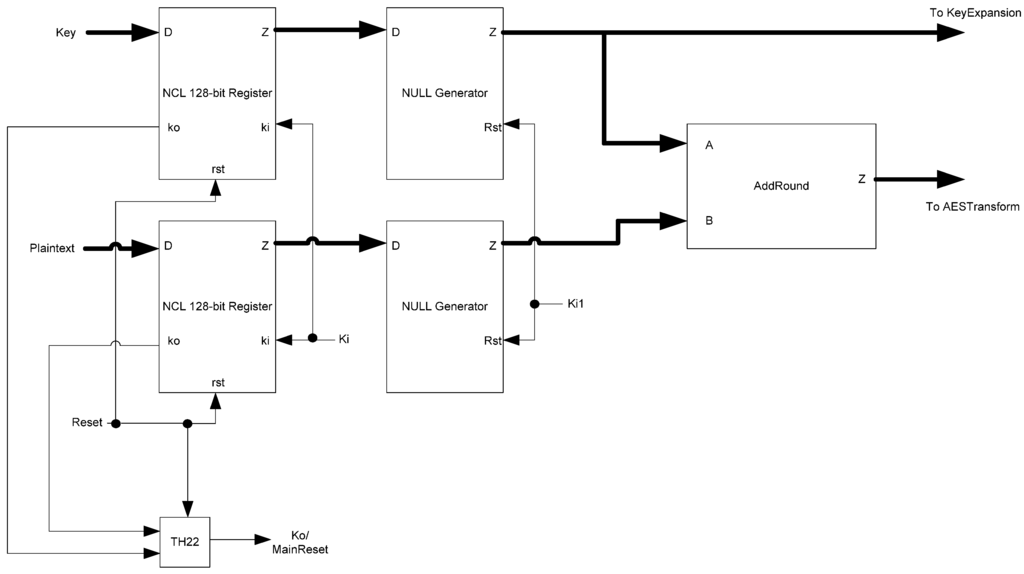
Figure 34. NCL FirstRound block diagram.

Figure 34. NCL FirstRound block diagram.

4.4. AES Implementation using Synchronous Logic

The asynchronous designs are all based off the synchronous design, which was created first. Because of this, there are several similarities between the synchronous and asynchronous designs. The synchronous design, like the other designs, consists of five logic blocks. The FirstRound block is replaced with a single AddRound block. The initial register stage is instead found in the KeyExpansion and AES Transform blocks. Registers are found in the AESTransform, KeyExpansion, and Control blocks, much like the other designs. The LastRound block contains the output register which is activated with a stop signal generated by the Control block. Two designs can be used, a single clock design and a double clock design. The single clock design was used in the power and timing simulations since it is faster. The double clock design isolates the SubByte block of the AES Transform circuit in facilitating the implementation of the CPA attack. Figure 35 shows the synchronous AES Transform block.

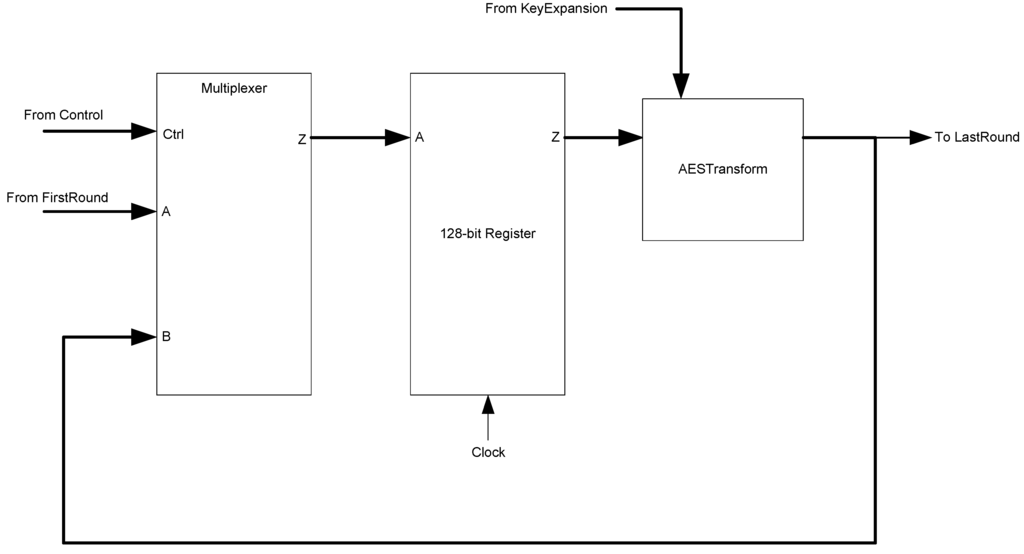
Figure 35. Synchronous AES Transform block diagram.

Figure 35. Synchronous AES Transform block diagram.

4.5. Delay Element Design

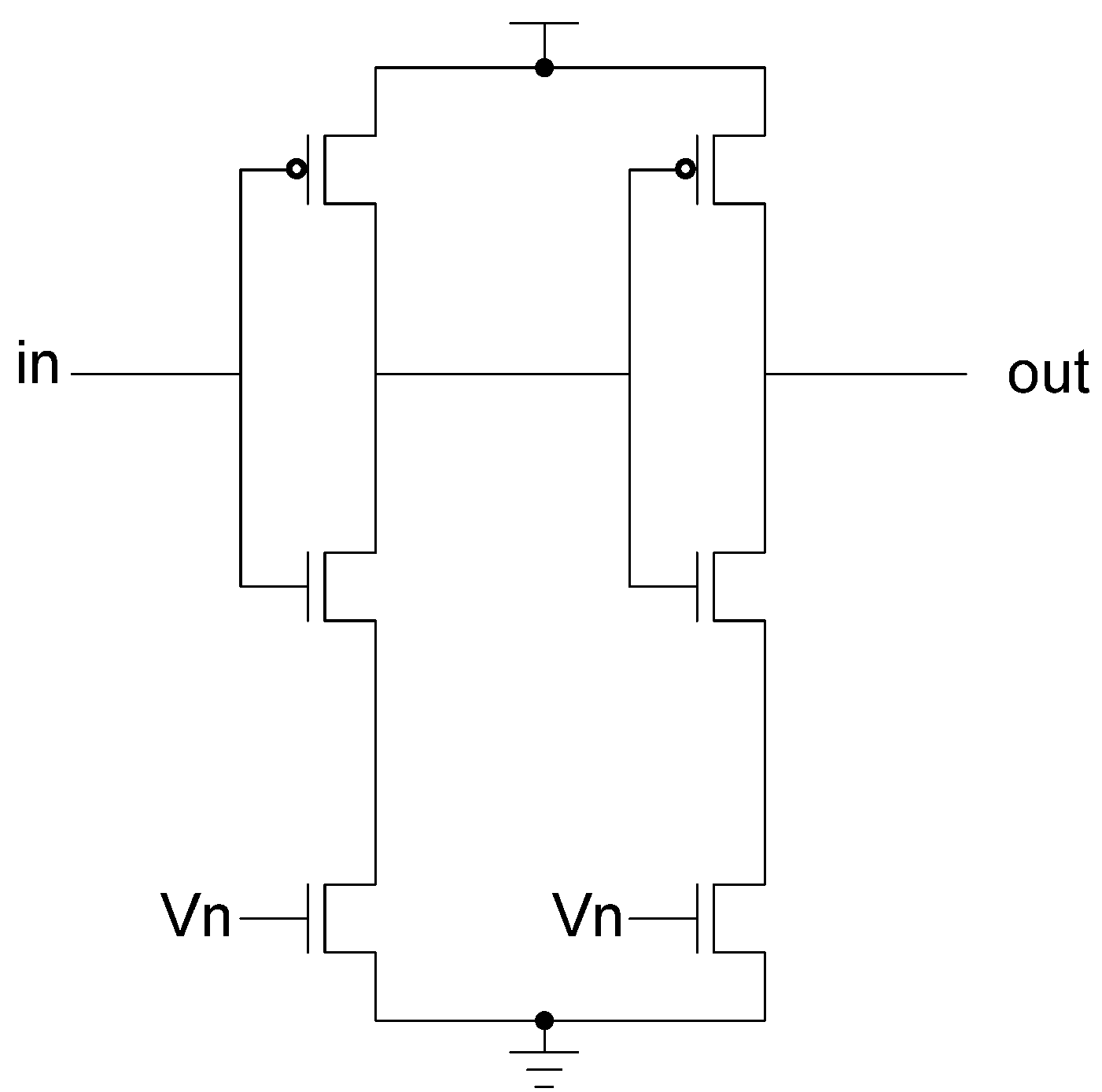
In the D³L and MTD³L designs, a delay element was designed to help mask the relationship between the circuit delay and the data being processed. The designed delay element is a buffer chain appended to the output of the targeted Sbox that can either operate at a high speed or a low speed. The inverters that make up this chain are n-volt controlled. A second NMOS transistor is added to the pull-down network of the inverter. An example buffer is shown in Figure 36. This transistor is controlled by an external voltage. To operate at high speed, the voltage given is the same as the designated supply voltage. To operate at a slow speed, the voltage is reduced as much as possible without deforming the inverter’s output.

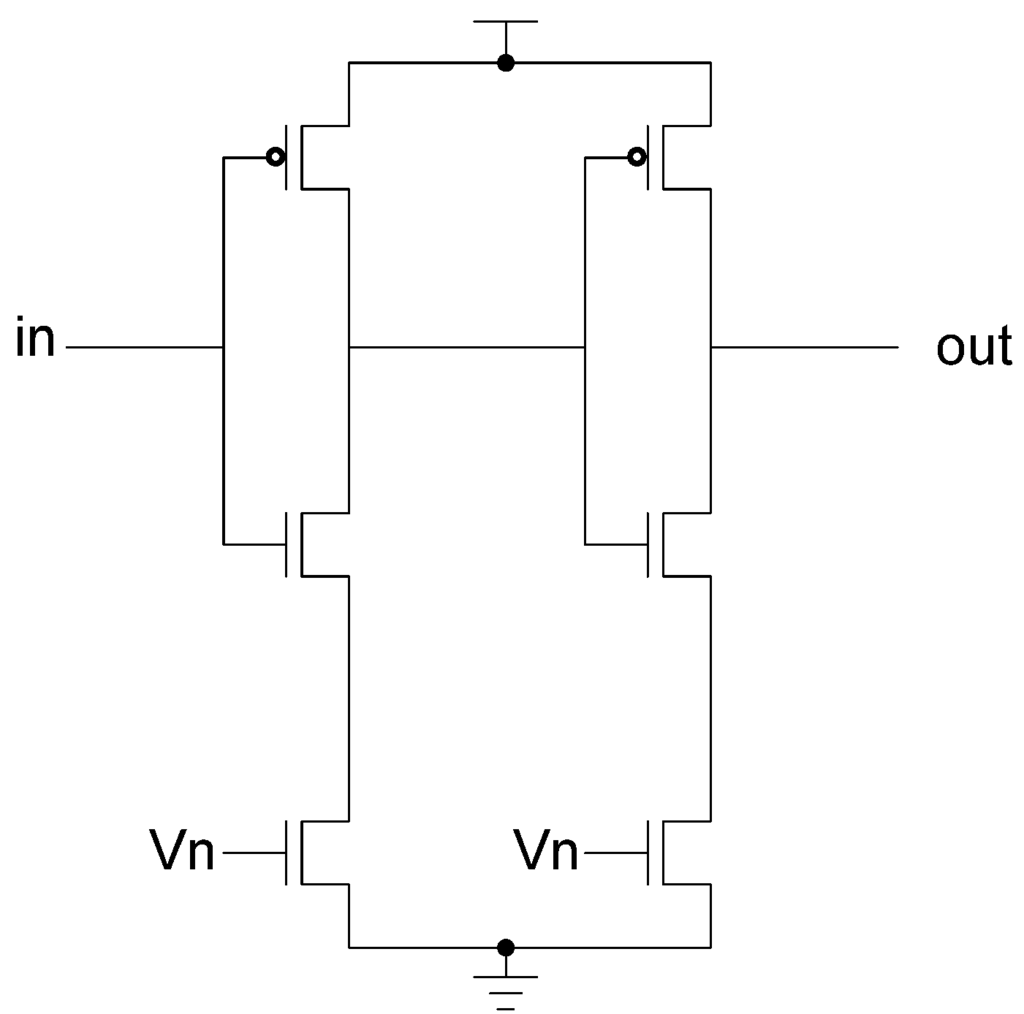
Figure 36. N-Volt controlled buffer.

Figure 36. N-Volt controlled buffer.

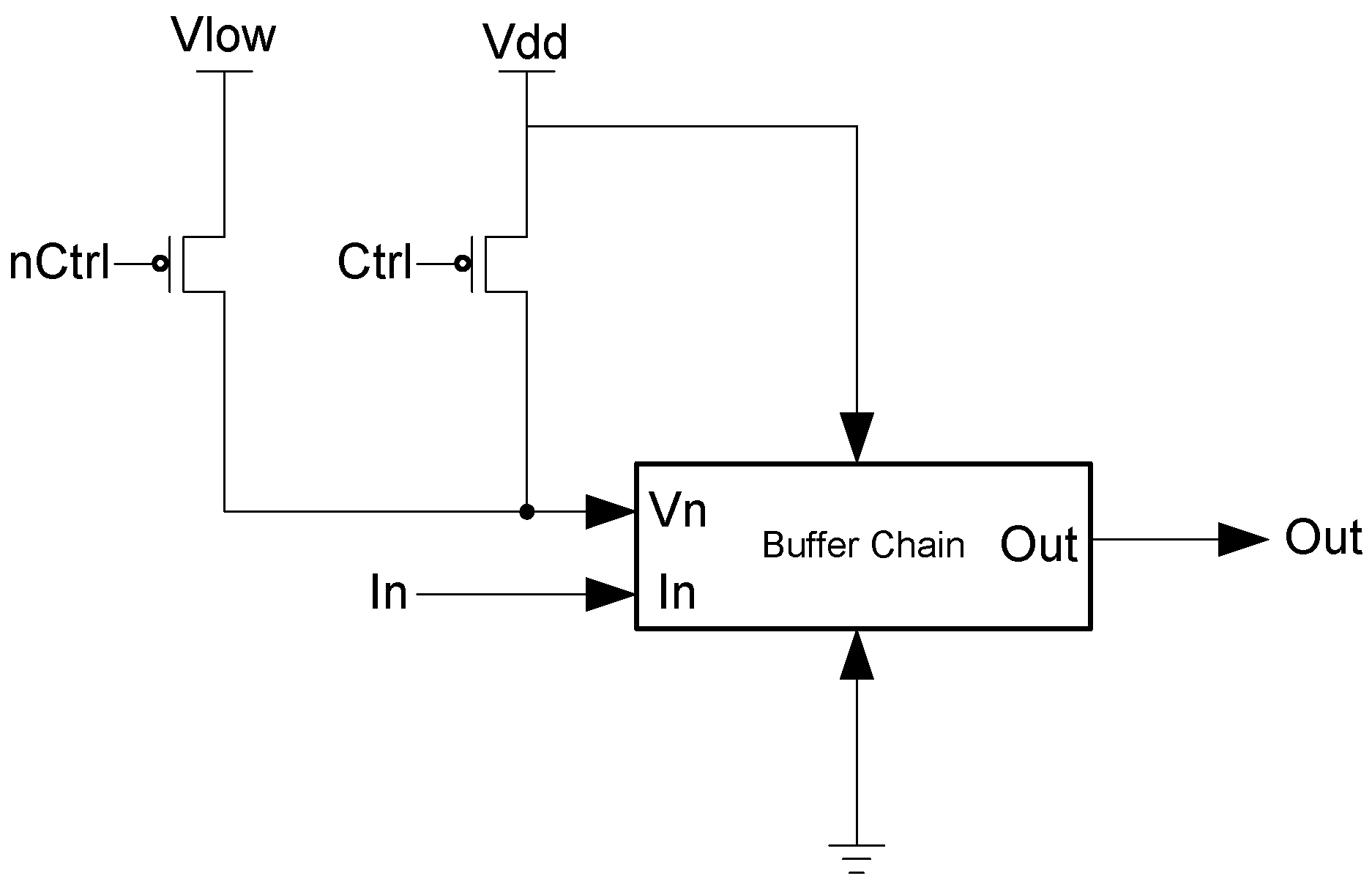
To apply different voltages levels to these inverters, a control signal is generated externally. The method of generating this control signal is not important so long as the result is sufficiently random. This control signal is used to control a pair of PMOS transistors. The source of these transistors is either a high voltage source or a low voltage source. Depending on the value of the control signal, only one of these transistors will be turned on at a time, which will supply its voltage to the delay inverters. Figure 37 shows the control logic.

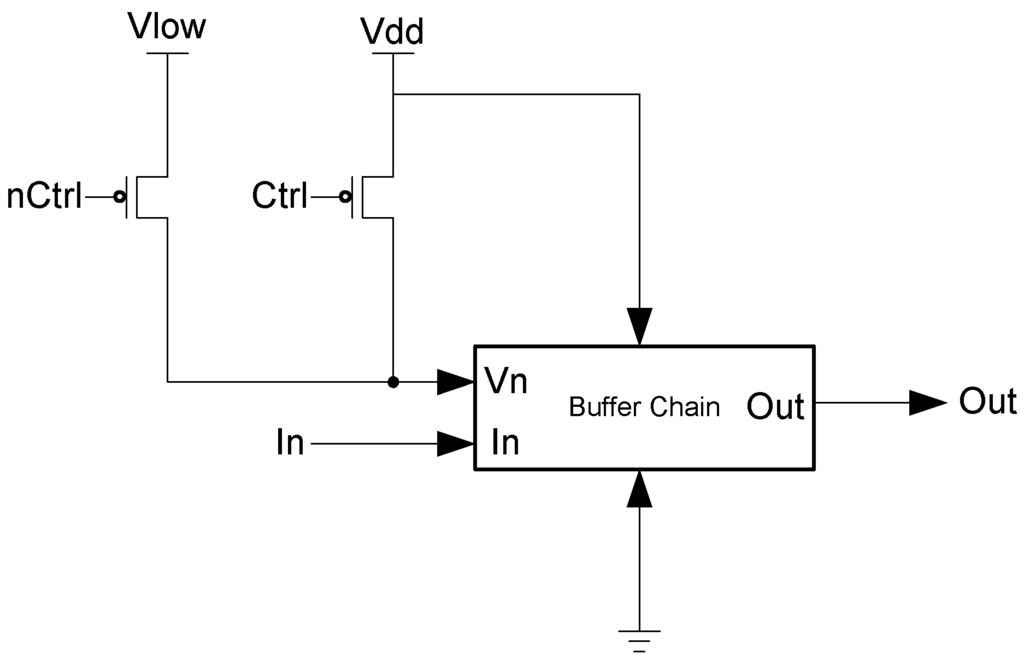
Figure 37. Buffer chain with voltage control.

Figure 37. Buffer chain with voltage control.

5. Results and Analysis

5.1. Simulation Environment and Data Collection

Each AES design presented in Section 4 was implemented at the transistor level using Cadence and the IBM 8RF-DM 130 nm process to evaluate and compare energy consumption, speed, area, and side-channel attack resistance. The full AES designs were used for the collection of energy, speed, and area data. All simulations were done using the Cadence UltraSim simulator. Each design was simulated using the input key 0x2b7e151628aed2a6abf7158809cf4f3c.

Because a complete evaluation of the D³L and MTD³L designs requires two spacer cycles, each simulation covered two complete encryptions. For the synchronous design, the simulation begins with the circuit in its reset state. Next, the key and plaintext are given and the circuit operation continues until the ciphertext is received. On the next clock cycle, a second plaintext is entered and the second encryption cycle completes. The energy and speed of the design is calculated from the reset state until the time of completion for the second encryption. The synchronous design is controlled using vector files. The NCL, D³L, and MTD³L designs, being asynchronous, are more difficult to simulate using vector files, due to the difficulties in anticipating when the handshaking signals should be changed. Thus, the asynchronous designs are simulated using controllers defined with VerilogA, which monitors the outputs of the design and makes adjustments to the design’s inputs accordingly. The NCL simulation begins in a NULL state. The first plaintext is passed followed by another NULL state. Once this cycle completes, a second plaintext is given followed by the third NULL state. The energy and speed data is calculated from the initial state through the end of the second DATA-NULL pair. The D³L and MTD³L simulations are similar, following the pattern of AZS-DATA-AOS-DATA-AZS.

The circuit area for each design was determined by laying out each design and measuring its dimensions. First, the cell layouts were completed using the Virtuoso tool in Cadence. The full designs were placed and routed according to their respective Verilog netlists using Synopsys Astro. From there, the designs’ area could be measured. The speed of each design was simply the time it took for two encryptions to be completed and any extra time needed until a third encryption is ready to begin. The synchronous design was tested to determine its maximum clock speed. The energy consumption of each design was determined by measuring the charge of each design of the duration of the simulation period and multiplying this by the supply voltage, which was the same for each design.

5.2. Simulation Results

As shown in Table 6, the synchronous design is the fastest. The NCL design is the slowest; and the MTD³L and D³L designs are in the middle. The D³L design uses the most energy followed by the MTD³L design and the NCL design. As explained in Section 2, the D³L design suffers from significant overhead problems, which can be seen in these results, particularly with respect to energy consumption. The purpose of the MTD³L design was to reduce this overhead to more reasonable levels. In this respect, the MTD³L design has a 36% reduction in energy consumption over the D³L design. However, the MTD³L design still uses nearly 300X more energy than the synchronous design, so while some overhead reduction was achieved, more efforts are needed in order to bring the MTD³L design down to desired overhead levels.

Table 6. Speed and energy comparison.

Design	Delay (ns)	Delay overhead vs. Synchronous design	Energy (nJ)	Energy overhead vs. Synchronous design
Synchronous	153	0X	1.356	0X
NCL	462	302X	2.208	163X
D3L	325	212X	6.012	443X
MTD3L	330	216X	3.84	283X

Table 6. Speed and energy comparison.

Design	Delay (ns)	Delay overhead vs. Synchronous design	Energy (nJ)	Energy overhead vs. Synchronous design
Synchronous	153	0X	1.356	0X
NCL	462	302X	2.208	163X
D3L	325	212X	6.012	443X
MTD3L	330	216X	3.84	283X

Table 7 presents the area of each design after cell placement in Synopsys Astro. The MTD³L design sees significant overhead reduction compared to the D³L design. This can be attributed to the removal of the NCL_X style completion logic. With this overhead reduction, the MTD³L design is comparable to the NCL design in area.

Table 7. Area comparison.

Design	Width (µm)	Height (µm)	Total Area (mm2)
Synchronous	1227	1223	1.50
NCL	1812	1809	3.28
D3L	2503	2503	6.27
MTD3L	1835	1838	3.37

Table 7. Area comparison.

Design	Width (µm)	Height (µm)	Total Area (mm2)
Synchronous	1227	1223	1.50
NCL	1812	1809	3.28
D3L	2503	2503	6.27
MTD3L	1835	1838	3.37

The overhead of the D³L design came from two sources. The first was the NCL_X completion checking. The second was from increased registration overhead caused by the need of handling two spacers. The MTD³L design solves the first problem but does not solve the second. The reduction in MTD³L energy consumption can be attributed to the reduced completion checking overhead due to the use of early completion instead of NCL_X style checking. However, the MTD³L design still uses the same registration scheme that the D³L design uses, so this overhead remains.

Table 8 shows a comparison of the energy consumption of different components of the NCL and MTD³L designs. The energy cost of the MTD³L registration is roughly 700% greater than that of the NCL design. The combinational logic and buffering of both designs is about the same, showing that the overhead cost comes almost exclusively from the registration. Table 9 shows the differences in transistor count and average leakage of the registration for both designs, showing that the MTD³L version requires many more transistors. This is due to the logic required to implement the dual-spacer protocol, such as the Ki Generator and the Spacer Filter. These components contribute significantly to the design overhead.

Table 8. Energy comparison.

Component	NCL design energy (nJ)	MTD3L design energy (nJ)
Registration	0.252	1.836
Logic	1.512	1.26
Buffering	0.444	0.744
Total	2.208	3.84

Table 8. Energy comparison.

Component	NCL design energy (nJ)	MTD3L design energy (nJ)
Registration	0.252	1.836
Logic	1.512	1.26
Buffering	0.444	0.744
Total	2.208	3.84

Table 9. Registration comparison.

Design	Transistor count	Average leakage (µA)
NCL	49140	2
MTD3L	242364	180

Table 9. Registration comparison.

Design	Transistor count	Average leakage (µA)
NCL	49140	2
MTD3L	242364	180

5.3. Side-Channel Attack Implementation

Because of the long simulation times required for the full designs, data collection for the power and timing attacks were performed with sub-circuits of each design. This is because each of these attacks requires many different simulation samples (256 samples in this case) to be successful. This number of simulations with the full designs would be impractical. The sub-circuits consist of the initial Addround and Subbyte stage of each design. This is because the Subbyte operation is the major vulnerable point to side-channel attacks. The attacks themselves focus on only one S-box of the Subbyte block, brute forcing all 256 plaintext input combinations of that S-box and attempting to extract one byte of the cipher key. It is assumed that if one byte of the key can be extracted then the other 15 bytes can be obtained as well.

While UltraSim in Cadence was used for the full simulations, it was found that Synopsys Nanosim could perform simulations in less time. Because so many simulation samples were required for the side-channel attacks, Nanosim was used to collect this information rather than Ultrasim. The simulation setup is similar but different for each design. For example, the synchronous design requires a clock and registers while the asynchronous designs do not. Test vectors for each design were generated. These vectors all use the same key as shown in Section 5.1. The plaintexts cover every combination of inputs for the first byte. All following bytes were kept at 0x00. Thus, the plaintexts followed the form 0xff000000000000000000000000000000. This setup helps reduce noise by attempting to isolate the attacked S-box. To help Nanosim keep track of a particular node, a small 1 ohm resistor was placed in series between the attacked S-box and its power supply.

The synchronous design consists of the Addround block and the Subbyte block with the Subbyte block being isolated by a pair of registers, as shown in Figure 38. Initially, the registers are reset to 0. Next, the key and plaintext are input to the Addround block. On the first clock edge, Addround’s output is clocked into the Subbyte block via the first register. Once the Subbyte block computes the output, the result is latched onto the second register. The second clock edge is the critical point. At this moment, the switching activity of the attacked S-box may be observed according to the changes in the second register.

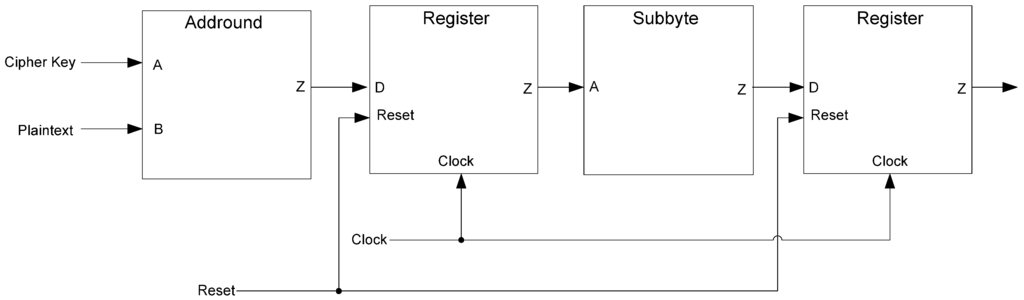
Figure 38. Synchronous side-channel attack implementation.

Figure 38. Synchronous side-channel attack implementation.

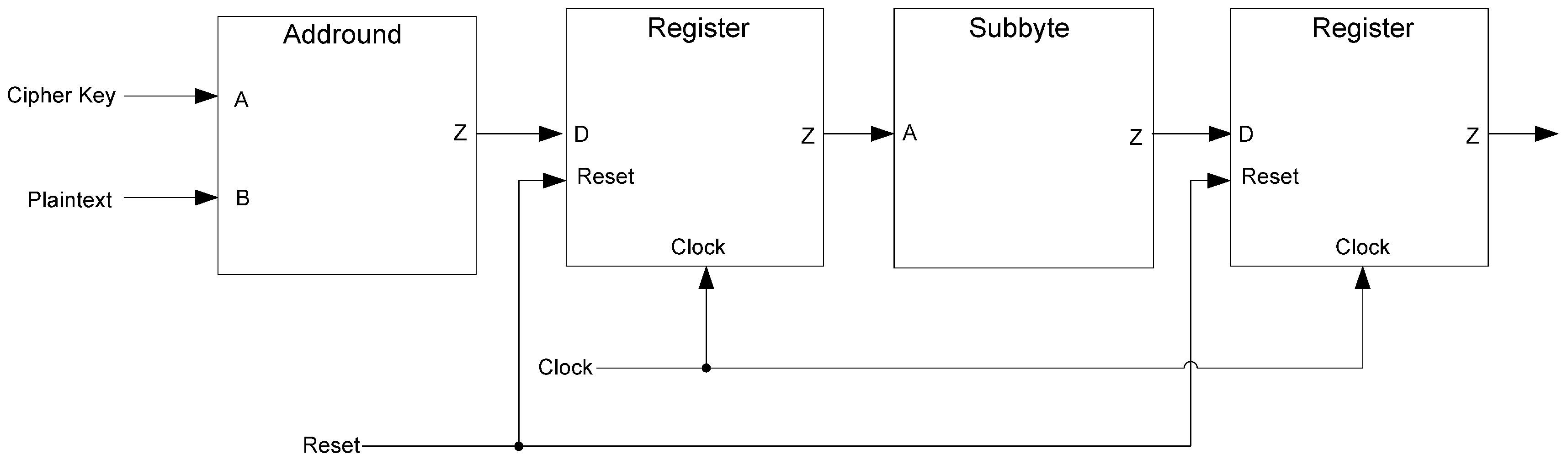
As shown in Figure 39, the NCL design consists of only the Addround and Subbyte blocks. It begins the simulation in a NULL state. Next, the key and plaintext are given as DATA. After the computation is complete, a NULL wave front is input. Thus, the NCL simulation follows a NULL-DATA-NULL pattern. For the timing attack, the simulation output is divided into two sets. The first set consists of the NULL to DATA transition. The second consists of the DATA to NULL transition. Both sets have any leading and trailing zeros removed to help align and simply the data for the timing attack.

The D³L and MTD³L designs also consist only of Addround and Subbyte blocks. Like the NCL simulation, these designs begin at the AZS. The plaintext and key are input as DATA. Once the circuit is finished, an AOS is given next. The same plaintext and key are input as DATA a second time. Once the second computation is complete, another AZS is given. Thus, these designs follow a complete dual-spacer pattern of AZS-DATA-AOS-DATA-AZS. The same data is given twice to help simplify the power and timing attacks. These data sets are divided into four groups for the timing attack. The first is the transition from the AZS to DATA. The second is the transition from DATA to the AOS. The third is from the AOS to DATA. The last is from DATA to the AZS. Each set has leading and trailing zeros removed much like the NCL data.

Figure 39. NCL, D³L, and MTD³L side-channel attack implementation.

Figure 39. NCL, D³L, and MTD³L side-channel attack implementation.

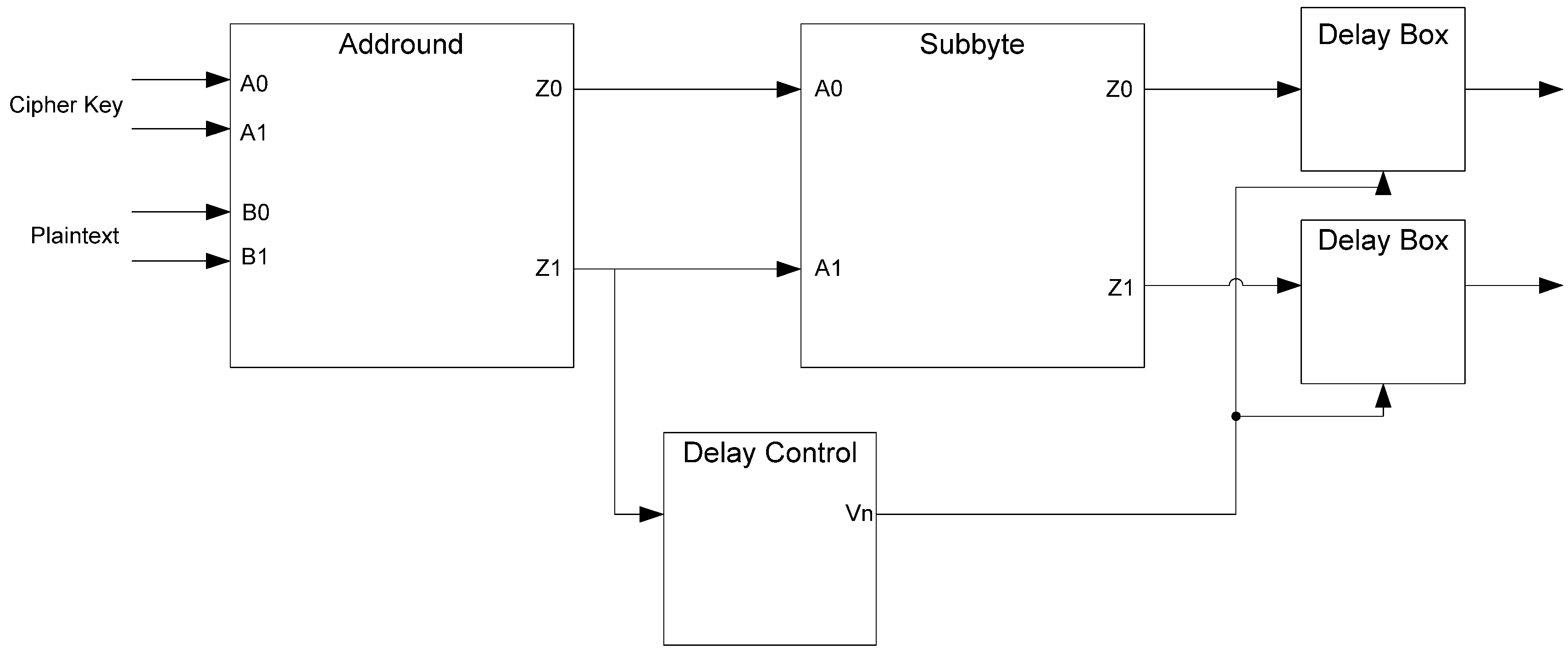
The D³L and MTD³L designs were also tested with the random delay elements, presented in Section 4, inserted into the targeted S-box, as shown in Figure 40. These delay elements are attached to each of the outputs of the target S-box. They are controlled by a signal generated by the bitwise XOR of the outputs of the Addround Z1 rail. The simulation setup is otherwise the same as the previous D³L and MTD³L simulations.

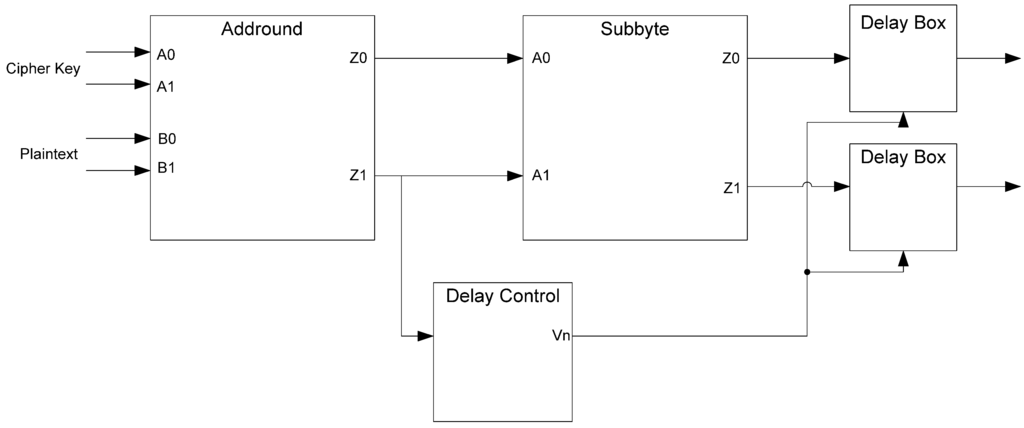
Figure 40. D³L and MTD³L delayed side-channel attack implementation.

Figure 40. D³L and MTD³L delayed side-channel attack implementation.

The power and timing attacks were carried out with a Java program. The program takes the simulation data and a statistical model of the design as input. The format of the simulation data depends on the type of attack being done. For the synchronous design, the only attack was a power analysis attack. The simulation input was in the form of a set of values of the current drawn by the power supply at a given time. The statistical model was the calculated Hamming distance given the key guess and the given plaintext. The NCL design was attacked using an energy based model. The simulation data began as a set of current values, similar to the synchronous data. This data was summed over the duration of the simulation period resulting in a single value representing the energy used in the simulation. The D³L and MTD³L designs were also attacked with an energy based model. In addition to this attack, the D³L and MTD³L designs were also attacked with a timing model. Similar to the energy attack, the power data was converted to a single time value by measuring the number of time steps where the circuit was drawing power. It is assumed that the circuit only draws significant current while it is calculating the ciphertext. The total number of discrete time steps above this threshold represent the time it took to complete the operation. Because the asynchronous designs are designed to balance switching activity independently of the data given, the Hamming distance model used for the synchronous attack is not sufficient for the asynchronous attacks. Instead, the expected energy and timing of these designs was estimated by counting the expected number of transistor switches for a given input combination. It is assumed that the energy and time delay of the circuit for a given set of inputs is directly proportional to the number of transistors that switch as a result of those inputs. The energy attacks were carried out over the complete simulation data. The timing attacks were carried out over the partitioned data.

5.4. Side-Channel Attack Results

Table 10 shows the results of the power- and energy-based attacks. The highest correlation out of the set of key guesses is shown for each design as if the highest correlation guess was generated by the correct key value. For the timing attacks against the asynchronous designs, which were each partitioned into several parts, only the part that resulted in the highest correlation is given. For example, the MTD³L timing attack had the highest result for the first data to AOS transition, so only that result is given. All other MTD³L transitions resulted in lower correlations. The synchronous attack was successful while the NCL, D³L and MTD³L attacks were not. The synchronous design, having no defense against power analysis, resulted in the highest correlation coefficient. This means that the key guess for this design has the most confidence. The NCL, D³L, and MTD³L designs each resulted in a lower coefficient and failure to guess the correct key. The D³L and MTD³L coefficients were very similar. This is expected because the changes from the D³L design to the MTD³L design should not have impacted the MTD³L design’s side-channel defenses. The NCL coefficient was unexpectedly the lowest, in disagreement with the results from [41], where the key was correctly guessed for the NCL circuit implemented using the IBM 0.5 μm process. This could be due to a number of reasons, such as a weakness in the statistical model, lack of resolution in the simulation data, or the unbalanced load effect in NCL being somewhat amplified in the large non-digital 0.5 μm process.

Table 10. Power/energy attack results.

Design	Attack type	Correlation coefficient	Correct key guess success/failure
Synchronous	Power	0.872	Success
NCL	Energy	0.207	Failure
D3L	Energy	0.376	Failure
MTD3L	Energy	0.353	Failure

Table 10. Power/energy attack results.

Design	Attack type	Correlation coefficient	Correct key guess success/failure
Synchronous	Power	0.872	Success
NCL	Energy	0.207	Failure
D3L	Energy	0.376	Failure
MTD3L	Energy	0.353	Failure

Table 11 shows the results of the time based attacks. The synchronous design was not attacked in this way, since it is already known to be susceptible, while the NCL design, also known to be susceptible, was attacked to show that the attack algorithm being used for the asynchronous designs could correctly guess the key. Since the energy attack on the NCL circuit in [41] was successful, adding random delay elements to protect it from timing attacks was moot, so this was not done. For the D³L and MTD³L circuits, only a minimal number of random delay elements were added to reduce the correlation coefficient, since reducing area without compromising susceptibility is the main objective. None of the attacks against the D³L or MTD³L designs were successful; the correlations for these designs were very similar and quite low, showing weak correlation between the statistical models and the actual behavior of the designs. Adding random delay elements is not necessary to further protect the D³L and MTD³L circuits against timing attacks, since this had minimal impact on reducing their correlation coefficients. Again, the MTD³L design performed very similarly to the D³L design. These results as well as the results given in Section 5.2 show that the MTD³L design offers similar security to the D³L design while having much less overhead with regard to area and power consumption.

Table 11. Timing attack results.

Design	Correlation coefficient	Correct key guess success/failure
NCL	0.400	Success
D3L	0.337	Failure
MTD3L	0.366	Failure
Delayed D3L	0.326	Failure
Delayed MTD3L	0.367	Failure

Table 11. Timing attack results.

Design	Correlation coefficient	Correct key guess success/failure
NCL	0.400	Success
D3L	0.337	Failure
MTD3L	0.366	Failure
Delayed D3L	0.326	Failure
Delayed MTD3L	0.367	Failure

6. Conclusions and Future Work

This paper develops MTD³L, an enhancement to the D³L technique presented in [41], by combining D³L with MTNCL. Because the D³L technique suffered significant overhead with respect to area and power consumption, a method of reducing overhead to make D³L more reasonable was necessary. The resulting MTD³L method shows significant reductions in power consumption and area overhead, and demonstrated the same strength as the D³L technique against power and timing analysis attacks. The end result is that the MTD³L technique is a substantial improvement over the original D³L technique, and is applicable for designs where security is much more important than power consumption or area, since MTD³L still has significant overhead compared to the original synchronous design. Hence, more work is required to reduce the overhead even further.

The majority of the overhead is from the increased complexity of the registration stage. This complexity was also present in the original D³L technique. The overhead required to implement the dual-spacer protocol, particularly in the filter registers, makes D³L and MTD³L registers much larger and consume much more power than NCL or synchronous registers. Therefore, course-grained pipelines will have much less overhead than fine-grained ones. Future work includes investigations of possible ways to reduce this registration overhead, bringing the MTD³L implementation cost closer to that of the NCL design.

Note that although complete layouts of the circuits were done, including place and route, all simulations were performed on the transistor-level circuits. This was because post-parasitic extraction simulations consumed all of the server memory and caused the system to crash. Since both power and timing attacks are strongly correlated to circuit parasitics, the authors have been actively applying for funding to fabricate these circuits so that hardware measurements can be made.