Reconfigurable Analog Preprocessing for Efficient Asynchronous Analog-to-Digital Conversion
Abstract
:1. Introduction
2. Asynchronous Quantization
3. System Overview
3.1. Reconfigurable Analog Mixed-Signal Platform
3.2. Asynchronous Data Converter Design
3.2.1. Successive-Approximation Register
3.2.2. Comparator
3.2.3. Time-to-Digital Converter
4. Asynchronous Sampling Implementation
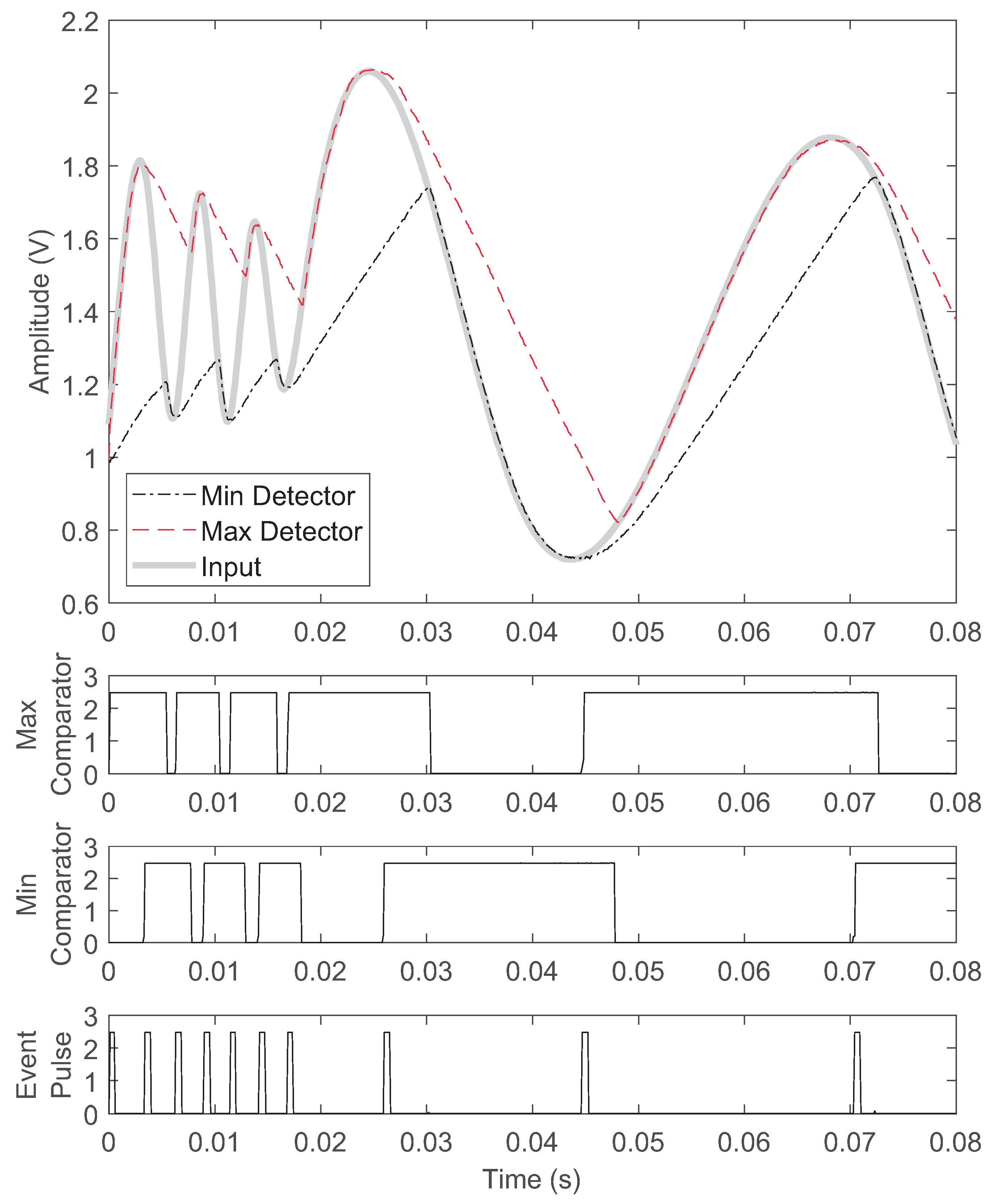
4.1. Extrema Sampling
4.2. RAMP Triggering Implementation
5. System Implementation and Example Applications
5.1. Power Consumption
5.2. Voice Recording
5.3. Electromyography
5.4. Electrocardiogram
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rumberg, B.; Graham, D.; Clites, S.; Kelly, B.; Navidi, M.; Dilello, A.; Kulathumani, V. RAMP: Accelerating wireless sensor hardware design with a reconfigurable analog/mixed-signal platform. In Proceedings of the ACM/IEEE Conference on Information Processing in Sensor Networks, Seattle, WA, USA, 13–16 April 2015; pp. 47–58. [Google Scholar]
- Kelly, B.M.; Graham, D.W. An asynchronous ADC with reconfigurable analog pre-processing. In Proceedings of the IEEE International Symposium on Circuits and Systems, Montreal, QC, Canada, 22–25 May 2016; pp. 1062–1065. [Google Scholar]
- Kinget, P.R. Scaling analog circuits into deep nanoscale CMOS: Obstacles and ways to overcome them. In Proceedings of the IEEE Custom Integrated Circuits Conference, San Jose, CA, USA, 28–30 September 2015; pp. 1–8. [Google Scholar]
- Walden, R.H. Analog-to-digital converter survey and analysis. IEEE J. Sel. Areas Commun. 1999, 17, 539–550. [Google Scholar] [CrossRef] [Green Version]
- Texas Instruments. MSP430F15x, MSP430F16x, MSP430F161x Mixed Signal Microcontroller; Texas Instruments: Dallas, TX, USA, 2002. [Google Scholar]
- Kozmin, K.; Johansson, J.; Delsing, J. Level-Crossing ADC Performance Evaluation Toward Ultrasound Application. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 1708–1719. [Google Scholar] [CrossRef]
- Martínez-Nuevo, P.; Patil, S.; Tsividis, Y. Derivative Level-Crossing Sampling. IEEE Trans. Circuits Syst. II Exp. Briefs 2015, 62, 11–15. [Google Scholar] [CrossRef]
- Trakimas, M.; Sonkusale, S. An Adaptive Resolution Asynchronous ADC Architecture for Data Compression in Energy Constrained Sensing Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 921–934. [Google Scholar] [CrossRef]
- Greitans, M.; Shavelis, R.; Fesquet, L.; Beyrouthy, T. Combined peak and level-crossing sampling scheme. In Proceedings of the International Conference on Sampling Theory and Applications, Singapore, 2–6 May 2011. [Google Scholar]
- Mark, J.; Todd, T. A Nonuniform Sampling Approach to Data Compression. IEEE Trans. Commun. 1981, 29, 24–32. [Google Scholar] [CrossRef]
- Rumberg, B.; Graham, D.W.; Kulathumani, V.; Fernandez, R. Hibernets: Energy-Efficient Sensor Networks Using Analog Signal Processing. IEEE Trans. Emerg. Sel. Top. Circuits Syst. 2011, 1, 321–334. [Google Scholar] [CrossRef]
- Kelly, B.M.; Rumberg, B.; Graham, D.W.; Kulathumani, V. Reconfigurable analog signal processing for wireless sensor networks. In Proceedings of the IEEE International Midwest Symposium on Circuits and Systems, Columbus, OH, USA, 4–7 August 2013; pp. 221–224. [Google Scholar]
- Sarpeshkar, R. Analog versus digital: Extrapolating from electronics to neurobiology. Neural Comput. 1998, 10, 1601–1638. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.K.F.; Gulak, P.G. A CMOS field-programmable analog array. IEEE J. Solid-State Circuits 1991, 26, 1860–1867. [Google Scholar] [CrossRef]
- Mackensen, E.; Muller, C. Implementation of Reconfigurable Micro-Sensor Interfaces Utilizing FPAAs. In Proceedings of the SENSORS, Irvine, CA, USA, 30 October–3 November 2005; pp. 1064–1067. [Google Scholar]
- George, S.; Kim, S.; Shah, S.; Hasler, J.; Collins, M.; Adil, F.; Wunderlich, R.; Nease, S.; Ramakrishnan, S. A Programmable and Configurable Mixed-Mode FPAA SoC. IEEE Trans. Very Large Scale Integr. Syst. 2016, 24, 2253–2261. [Google Scholar] [CrossRef]
- Rumberg, B.; Graham, D.W. A floating-gate memory cell for continuous-time programming. In Proceedings of the IEEE International Midwest Symposium on Circuits and Systems, Boise, ID, USA, 5–8 August 2012; pp. 214–217. [Google Scholar]
- Jonsson, B. An empirical approach to finding energy efficient ADC architectures. In Proceedings of the International Workshop on ADC Modelling, Testing and Data Converter Analysis and Design, and IEEE ADC Forum, Orvieto, Italy, 30 June–1 July 2011; pp. 1–6. [Google Scholar]
- Schinkel, D.; Mensink, E.; Klumperink, E.; van Tuijl, E.; Nauta, B. A Double-Tail Latch-Type Voltage Sense Amplifier with 18ps Setup+Hold Time. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 11–15 Febuary 2007; pp. 314–605. [Google Scholar]
- Adil, F.; Serrano, G.; Hasler, P. Offset removal using floating-gate circuits for mixed-signal systems. In Proceedings of the Southwest Symposium on Mixed-Signal Design, Las Vegas, NV, USA, 25–25 Febuary 2003; pp. 190–195. [Google Scholar]
- Roberts, G.; Ali-Bakhshian, M. A Brief Introduction to Time-to-Digital and Digital-to-Time Converters. IEEE Trans. Circuits Syst. II Exp. Briefs 2010, 57, 153–157. [Google Scholar] [CrossRef]
- Kelly, B.; Rumberg, B.; Graham, D. An ultra-low-power analog memory system with an adaptive sampling rate. In Proceedings of the IEEE International Midwest Symposium on Circuits and Systems, Boise, ID, USA, 5–8 August 2012; pp. 302–305. [Google Scholar]
- Farin, G. Curves and Surfaces for CAGD: A Practical Guide; Morgan Kaufmann: Burlington, MA, USA, 2001. [Google Scholar]
- DeLuca, C.J. The Use of Surface Electromyography in Biomechanics. J. Appl. Biomech. 1997, 13, 135–163. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Yoo, H.; van Hoof, C. Bio-Medical CMOS ICs; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Ieong, C.I.; Mak, P.I.; Lam, C.P.; Dong, C.; Vai, M.I.; Mak, P.U.; Pun, S.H.; Wan, F.; Martins, R.P. A 0.83 μW QRS Detection Processor Using Quadratic Spline Wavelet Transform for Wireless ECG Acquisition in 0.35 μm CMOS. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 586–595. [Google Scholar] [CrossRef] [PubMed]
- Abdallah, R.A.; Shanbhag, N.R. A 14.5 fJ/cycle/k-gate, 0.33 V ECG processor in 45nm CMOS using statistical error compensation. In Proceedings of the IEEE Custom Integrated Circuits Conference, San Jose, CA, USA, 9–12 September 2012; pp. 1–4. [Google Scholar]
- Wang, H.M.; Lai, Y.L.; Hou, M.C.; Lin, S.H.; Yen, B.S.; Huang, Y.C.; Chou, L.C.; Hsu, S.Y.; Huang, S.C.; Jan, M.Y. A ±6ms-accuracy, 0.68 mm2 and 2.21 μW QRS detection ASIC. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 1372–1375. [Google Scholar]
- Zhang, X.; Lian, Y. A 300 mV 220 nW Event-Driven ADC With Real-Time QRS Detection for Wearable ECG Sensors. IEEE Trans. Biomed. Circuits Syst. 2014, 8, 834–843. [Google Scholar] [CrossRef] [PubMed]














| Extrema Sampling Ramp Implementation | 4.95 W |
| SAR ADC Static Power Consumption | 14.75 nW |
| SAR ADC Energy/Conversion | 47.4 nJ |
| SAR ADC Resolution | 10 bits |
| TDC Power Consumption | 1.01 W @ 1.15 kHz |
| TDC Resolution | 10 bits |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kelly, B.M.; DiLello, A.T.; Graham, D.W. Reconfigurable Analog Preprocessing for Efficient Asynchronous Analog-to-Digital Conversion. J. Low Power Electron. Appl. 2019, 9, 25. https://doi.org/10.3390/jlpea9030025
Kelly BM, DiLello AT, Graham DW. Reconfigurable Analog Preprocessing for Efficient Asynchronous Analog-to-Digital Conversion. Journal of Low Power Electronics and Applications. 2019; 9(3):25. https://doi.org/10.3390/jlpea9030025
Chicago/Turabian StyleKelly, Brandon M., Alexander T. DiLello, and David W. Graham. 2019. "Reconfigurable Analog Preprocessing for Efficient Asynchronous Analog-to-Digital Conversion" Journal of Low Power Electronics and Applications 9, no. 3: 25. https://doi.org/10.3390/jlpea9030025
APA StyleKelly, B. M., DiLello, A. T., & Graham, D. W. (2019). Reconfigurable Analog Preprocessing for Efficient Asynchronous Analog-to-Digital Conversion. Journal of Low Power Electronics and Applications, 9(3), 25. https://doi.org/10.3390/jlpea9030025






