Context-Aware and Occlusion Handling Mechanism for Online Visual Object Tracking
Abstract
:1. Introduction
1.1. Related Work
1.2. Our Contributions
1.3. Paper Outline
2. The Principle of Spatio-Temporal Context and Correlation Filter Tracking
2.1. STC Based Tracking
2.1.1. Confidence Map
2.1.2. Context Prior Model
2.1.3. Learning Spatial Context Model
2.1.4. Model Update
2.2. Correlation Filter Tracking
3. Proposed Solution
3.1. Context-Aware Tracking Framework
3.2. Kalman Filter-Based Motion Estimation Model
3.2.1. Kalman Filter Prediction
3.2.2. Kalman Filter Correction
3.3. Occlusion Detection
3.4. Adaptive Learning Rate
| Algorithm 1: Proposed Tracker at time step t |
| Input: Image Sequence of n Frames. Position of Target at First Frame. Output: Target Position for each frame in Image Sequence. for frame 1 to n frames.
|
4. Experiments
4.1. Evaluation Criteria
4.2. Dataset
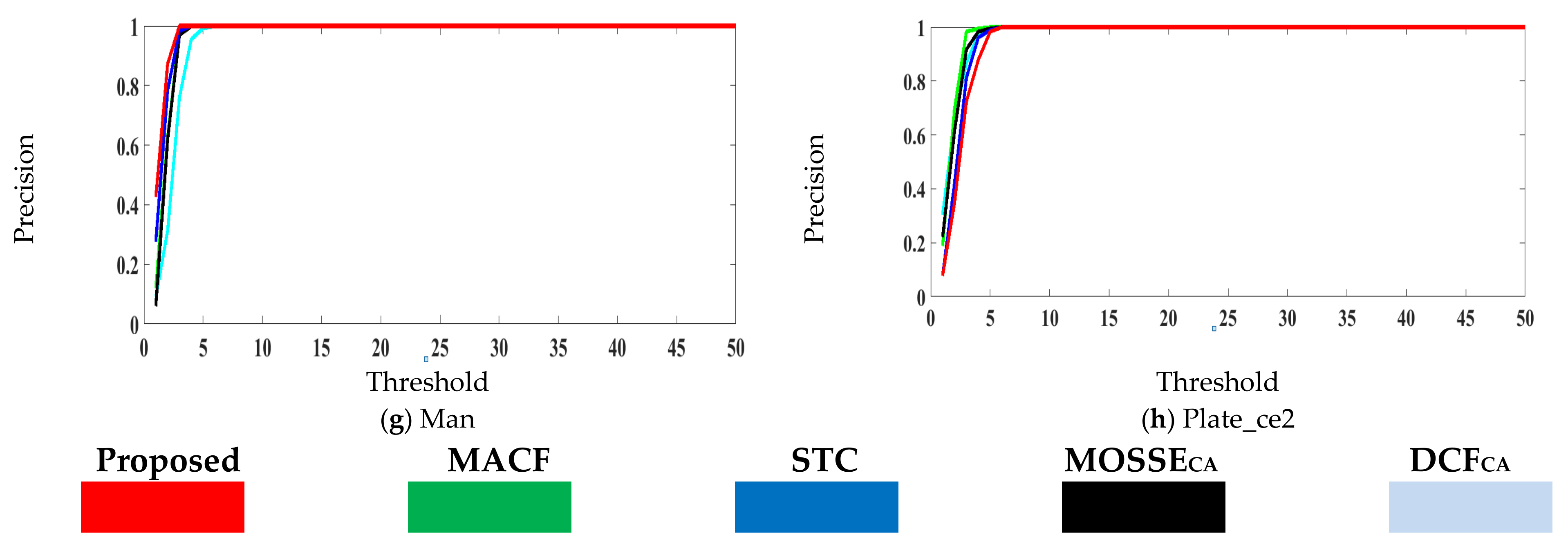
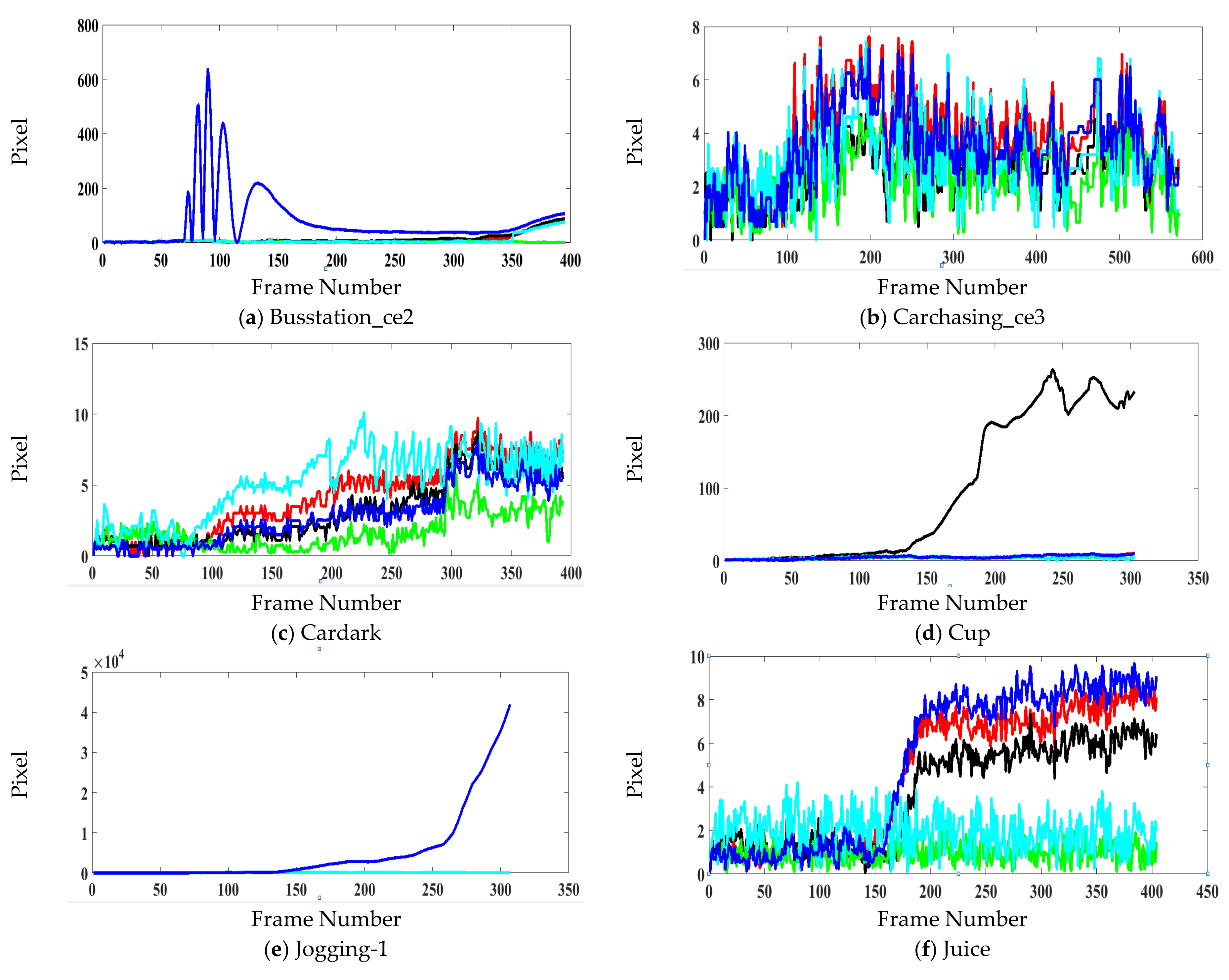
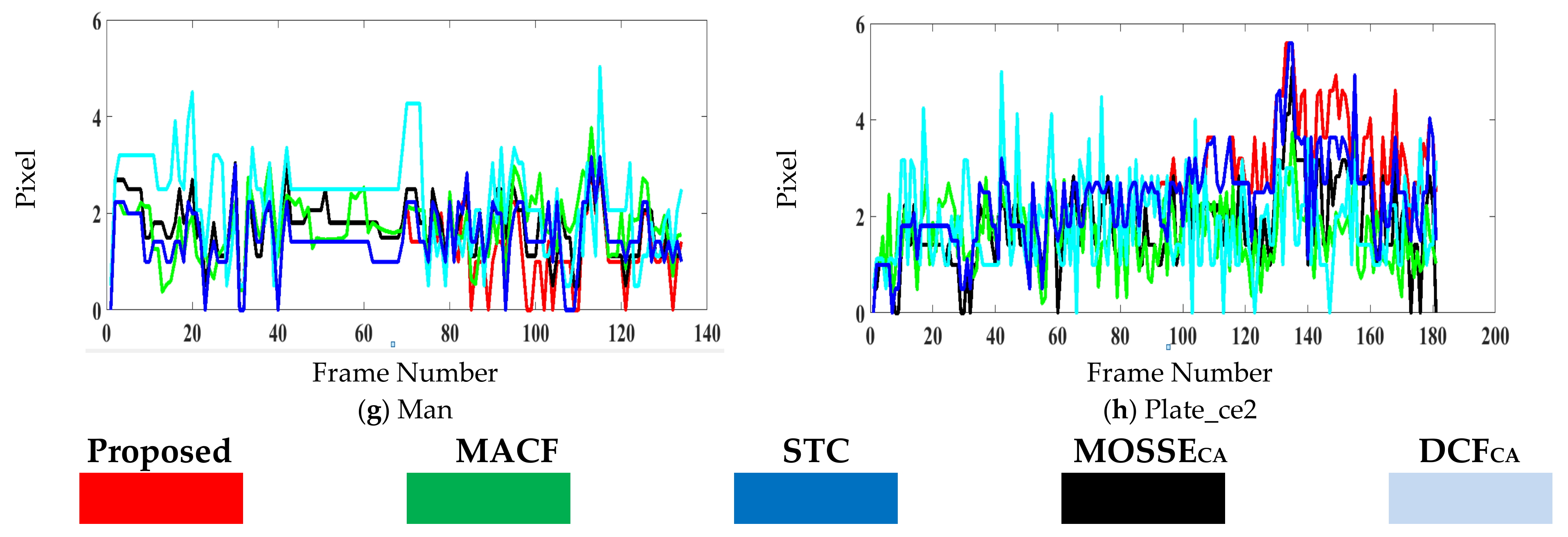
5. Performance Analysis
6. Experimental Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, S.; Wang, X. Real-time dynamic gesture recognition and hand servo tracking using PTZ camera. Multimed. Tools Appl. 2019, 78, 27403–27424. [Google Scholar] [CrossRef]
- Santhosh, P.K.; Kaarthick, B. An Automated Player Detection and Tracking in Basketball Game. Comput. Mater. Contin. 2019, 58, 625–639. [Google Scholar]
- Oh, S.H.; Javed, S.; Jung, S.K. Foreground Object Detection and Tracking for Visual Surveillance System: A Hybrid Approach. In Proceedings of the 11th International Conference on Frontiers of Information Technology, Islamabad, Pakistan, 16–18 December 2013; pp. 13–18. [Google Scholar]
- Zhou, W.; Wu, C.; Yu, X.; Gao, Y.; Du, W. Automatic fovea center localization in retinal images using saliency-guided object discovery and feature extraction. J. Med. Imaging Health Inform. 2017, 7, 1070–1077. [Google Scholar] [CrossRef]
- Kuramoto, A.; Aldibaja, M.A.; Yanase, R.; Kameyama, J.; Yoneda, K.; Suganuma, N. Mono-Camera based 3D Object Tracking Strategy for Autonomous Vehicles. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 459–464. [Google Scholar]
- Muresan, M.P.; Giosan, I.; Nedevschi, S. Stabilization and Validation of 3D Object Position Using Multimodal Sensor Fusion and Semantic Segmentation. Sensors 2020, 20, 1110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kazimierski, W. Proposal of neural approach to maritime radar and automatic identification system tracks association. IET Radar Sonar Navig. 2017, 1, 729–735. [Google Scholar] [CrossRef]
- Stateczny, A. Neural manoeuvre detection of the tracked target in ARPA systems. IFAC Proc. Vol. 2002, 34, 209–214. [Google Scholar] [CrossRef]
- Kazimierski, W.; Zaniewicz, G.; Stateczny, A. Verification of multiple model neural tracking filter with ship’s radar. In Proceedings of the 13th International Radar Symposium (IRS), Warsaw, Poland, 23–25 May 2012; pp. 549–553. [Google Scholar]
- Ali, A.; Jalil, A.; Niu, J.; Zhao, X.; Rathore, S.; Ahmed, J.; Iftikhar, M.A. Visual object tracking—Classical and contemporary approaches. Front. Comput. Sci. 2016, 10, 167–188. [Google Scholar] [CrossRef]
- Fiaz, M.; Mahmood, A.; Javed, S.; Jung, S.K. Handcrafted and deep trackers: Recent visual object tracking approaches and trends. ACM Comput. Surv. (CSUR) 2019, 52, 1–44. [Google Scholar] [CrossRef]
- Fiaz, M.; Javed, S.; Mahmood, A.; Jung, S.K.M. Comparative Study of ECO and CFNet Trackers in Noisy Environment. arXiv 2018, arXiv:1801.09360. [Google Scholar]
- Biresaw, T.A.; Cavallaro, A.; Regazzoni, C.S. Tracker-Level Fusion for Robust Bayesian Visual Tracking. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 776–789. [Google Scholar] [CrossRef]
- Sun, X.; Yao, H.; Zhang, S.; Li, D. Non-Rigid Object Contour Tracking via a Novel Supervised Level Set Model. IEEE Trans. Image Process. 2015, 24, 3386–3399. [Google Scholar]
- Jang, S.I.; Choi, K.; Toh, K.A.; Teoh, A.B.J.; Kim, J. Object tracking based on an online learning network with total error rate minimization. Pattern Recognit. 2015, 48, 126–139. [Google Scholar] [CrossRef]
- Zhang, Z.; Peng, H. Deeper and wider siamese networks for real time visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 4591–4600. [Google Scholar]
- Rahman, M.M.; Ahmed, M.R.; Laishram, L.; Kim, S.H.; Jung, S.K. Siamese High-Level Feature Refine Network for Visual Object Tracking. Electronics 2020, 9, 1918. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, X.; Sun, J.; Wang, J.; Li, K. Dual model learning combined with multiple feature selection for accurate visual tracking. IEEE Access 2019, 7, 43956–43969. [Google Scholar] [CrossRef]
- Dai, K.; Wang, D.; Lu, H.; Sun, C.; Li, J. Visual tracking via adaptive spatially regularized correlation filters. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 4670–4679. [Google Scholar]
- Javed, S.; Zhang, X.; Seneviratne, L.; Dias, J.; Werghi, N. Deep Bidirectional Correlation Filters for Visual Object Tracking. In Proceedings of the IEEE 23rd International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 6–9 July 2020; pp. 1–8. [Google Scholar]
- Zhang, K.; Zhang, L.; Liu, Q.; Zhang, D.; Yang, M.H. Fast visual tracking via dense spatio-temporal context learning. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–7 September 2014; pp. 127–141. [Google Scholar]
- Tian, J.; Zhou, Y. Real-time patch-based tracking with occlusion handling. In Proceedings of the International Conference on Neural Information Processing, Kuching, Malaysia, 3–6 November 2014; pp. 210–217. [Google Scholar]
- Panqiao, C.; Mengzhao, Y. STC Tracking Algorithm Based on Kalman Filter. In Proceedings of the 4th International Conference on Machinery, Materials and Computing Technology, Hangzhou, China, 23–24 January 2016; pp. 1916–1920. [Google Scholar]
- Munir, F.; Minhas, F.; Jalil, A.; Jeon, M. Real time eye tracking using Kalman extended spatio-temporal context learning. In Proceedings of the Second International Workshop on Pattern Recognition, Singapore, 1–3 May 2017; p. 104431. [Google Scholar]
- Cui, Z.; Yang, J.; Jiang, S.; Li, J.; Gu, Y. Robust spatio-temporal context for infrared target tracking. Infrared Phys. Technol. 2018, 91, 263–277. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, S.; Zhou, D.; Zhang, Y. An improved target tracking algorithm based on spatio-temporal context under occlusions. Multidim. Syst. Sign Process. 2020, 31, 329–344. [Google Scholar] [CrossRef]
- Yang, H.; Wang, J.; Miao, Y.; Yang, Y.; Zhao, Z.; Wang, Z.; Sun, Q.; Wu, D.O. Combining Spatio-Temporal Context and Kalman Filtering for Visual Tracking. Mathematics 2019, 7, 1059. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Yang, Y.; Zhou, W.; Shi, L.; Li, D. Motion-Aware Correlation Filters for Online Visual Tracking. Sensors 2018, 18, 3937. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Rathod, V.; Votel, R.; Huang, J. RetinaTrack: Online Single Stage Joint Detection and Tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 14656–14666. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-speed tracking with kernelized correlation filters. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 583–596. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, J.; Ali, A.; Khan, A. Stabilized Active Camera Tracking System. J. Real-Time Image Process. 2016, 11, 315–324. [Google Scholar] [CrossRef]
- Ma, C.; Yang, X.; Zhang, C.; Yang, M.H. Long-term correlation tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5388–5396. [Google Scholar]
- Masood, H.; Rehman, S.; Khan, A.; Riaz, F.; Hassan, A.; Abbas, M. Approximate Proximal Gradient-Based Correlation Filter for Target Tracking in Videos: A Unified Approach. Arab. J. Sci. Eng. 2019, 44, 9363–9380. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, X.; Yang, C.; Jiang, A.; Yan, B. Multi-channel features spatio-temporal context learning for visual tracking. IEEE Access 2017, 5, 12856–12864. [Google Scholar] [CrossRef] [Green Version]
- Khan, B.; Ali, A.; Jalil, A.; Mehmood, K.; Murad, M.; Awan, H. AFAM-PEC: Adaptive Failure Avoidance Tracking Mechanism Using Prediction-Estimation Collaboration. IEEE Access 2020, 8, 149077–149092. [Google Scholar] [CrossRef]
- Ali, A.; Jalil, A.; Ahmed, J.; Iftikhar, M.A.; Hussain, M. Correlation, Kalman filter and adaptive fast mean shift based heuristic approach for robust visual tracking. Signal Image Video Process. 2015, 9, 1567–1585. [Google Scholar] [CrossRef]
- Mueller, M.; Smith, N.; Ghanem, B. Context-Aware Correlation Filter Tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1387–1395. [Google Scholar]
- Qi, F.; Hao, Z.; Lu, Z. Spatio-Temporal Context Tracking Algorithm Based on Correlation Filtering. J. Phys. Conf. Ser. 2019, 1213, 1–7. [Google Scholar]
- Zhang, Y.; Wang, L.; Qin, J. Adaptive spatio-temporal context learning for visual tracking. Imaging Sci. J. 2019, 67, 136–147. [Google Scholar] [CrossRef]
- Shin, J.; Kim, H.; Kim, D.; Paik, J. Fast and Robust Object Tracking Using Tracking Failure Detection in Kernelized Correlation Filter. Appl. Sci. 2020, 10, 713. [Google Scholar] [CrossRef] [Green Version]
- Zekavat, R.; Buehrer, R.M. An Introduction to Kalman Filtering Implementation for Localization and Tracking Applications. In Handbook of Position Location: Theory, Practice, and Advances, 2nd ed.; Wiley Online Library: Hoboken, NJ, USA, 2018; pp. 143–195. [Google Scholar]
- Liang, P.; Blasch, E.; Ling, H. Encoding color information for visual tracking: Algorithms and benchmark. IEEE Trans. Image Process. 2015, 24, 5630–5644. [Google Scholar] [CrossRef]
- Wu, Y.; Lim, J.; Yang, M.H. Online object tracking: A benchmark. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2411–2418. [Google Scholar]
- Wu, Y.; Lim, J.; Yang, M.H. Object tracking benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1834–1848. [Google Scholar] [CrossRef] [Green Version]




| Sequence | Proposed | STC | MACF | MOSSECA | DCFCA |
|---|---|---|---|---|---|
| Busstation_ce2 | 0.878 | 0.194 | 1 | 0.820 | 0.886 |
| Carchasing_ce3 | 1 | 1 | 1 | 1 | 1 |
| Cardark | 1 | 1 | 1 | 1 | 1 |
| Cup | 1 | 1 | 1 | 0.452 | 1 |
| Jogging-1 | 0.996 | 0.228 | 0.231 | 0.231 | 0.231 |
| Juice | 1 | 1 | 1 | 1 | 1 |
| Man | 1 | 1 | 1 | 1 | 1 |
| Plate_ce2 | 1 | 1 | 1 | 1 | 1 |
| Mean Precision | 0.984 | 0.803 | 0.904 | 0.813 | 0.890 |
| Sequence | Proposed | STC | MACF | MOSSECA | DCFCA |
|---|---|---|---|---|---|
| Busstation_ce2 | 10.86 | 78.25 | 3.58 | 14.50 | 9.71 |
| Carchasing_ce3 | 3.90 | 3.55 | 2.39 | 2.61 | 3.05 |
| Cardark | 4.09 | 2.83 | 1.67 | 3.15 | 5.11 |
| Cup | 4.63 | 4.84 | 3.11 | 95.87 | 3.85 |
| Jogging-1 | 8.40 | 5010 | 94.93 | 115.98 | 89.44 |
| Juice | 4.63 | 5.08 | 0.91 | 3.71 | 1.92 |
| Man | 1.32 | 1.49 | 1.73 | 1.72 | 2.23 |
| Plate_ce2 | 2.58 | 2.34 | 1.62 | 1.77 | 1.83 |
| Mean Error | 5.05 | 638.55 | 13.74 | 29.91 | 14.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehmood, K.; Jalil, A.; Ali, A.; Khan, B.; Murad, M.; Khan, W.U.; He, Y. Context-Aware and Occlusion Handling Mechanism for Online Visual Object Tracking. Electronics 2021, 10, 43. https://doi.org/10.3390/electronics10010043
Mehmood K, Jalil A, Ali A, Khan B, Murad M, Khan WU, He Y. Context-Aware and Occlusion Handling Mechanism for Online Visual Object Tracking. Electronics. 2021; 10(1):43. https://doi.org/10.3390/electronics10010043
Chicago/Turabian StyleMehmood, Khizer, Abdul Jalil, Ahmad Ali, Baber Khan, Maria Murad, Wasim Ullah Khan, and Yigang He. 2021. "Context-Aware and Occlusion Handling Mechanism for Online Visual Object Tracking" Electronics 10, no. 1: 43. https://doi.org/10.3390/electronics10010043
APA StyleMehmood, K., Jalil, A., Ali, A., Khan, B., Murad, M., Khan, W. U., & He, Y. (2021). Context-Aware and Occlusion Handling Mechanism for Online Visual Object Tracking. Electronics, 10(1), 43. https://doi.org/10.3390/electronics10010043







