Analytical Current–Voltage Modeling and Analysis of the MFIS Gate-All-Around Transistor Featuring Negative-Capacitance
Abstract
:1. Introduction
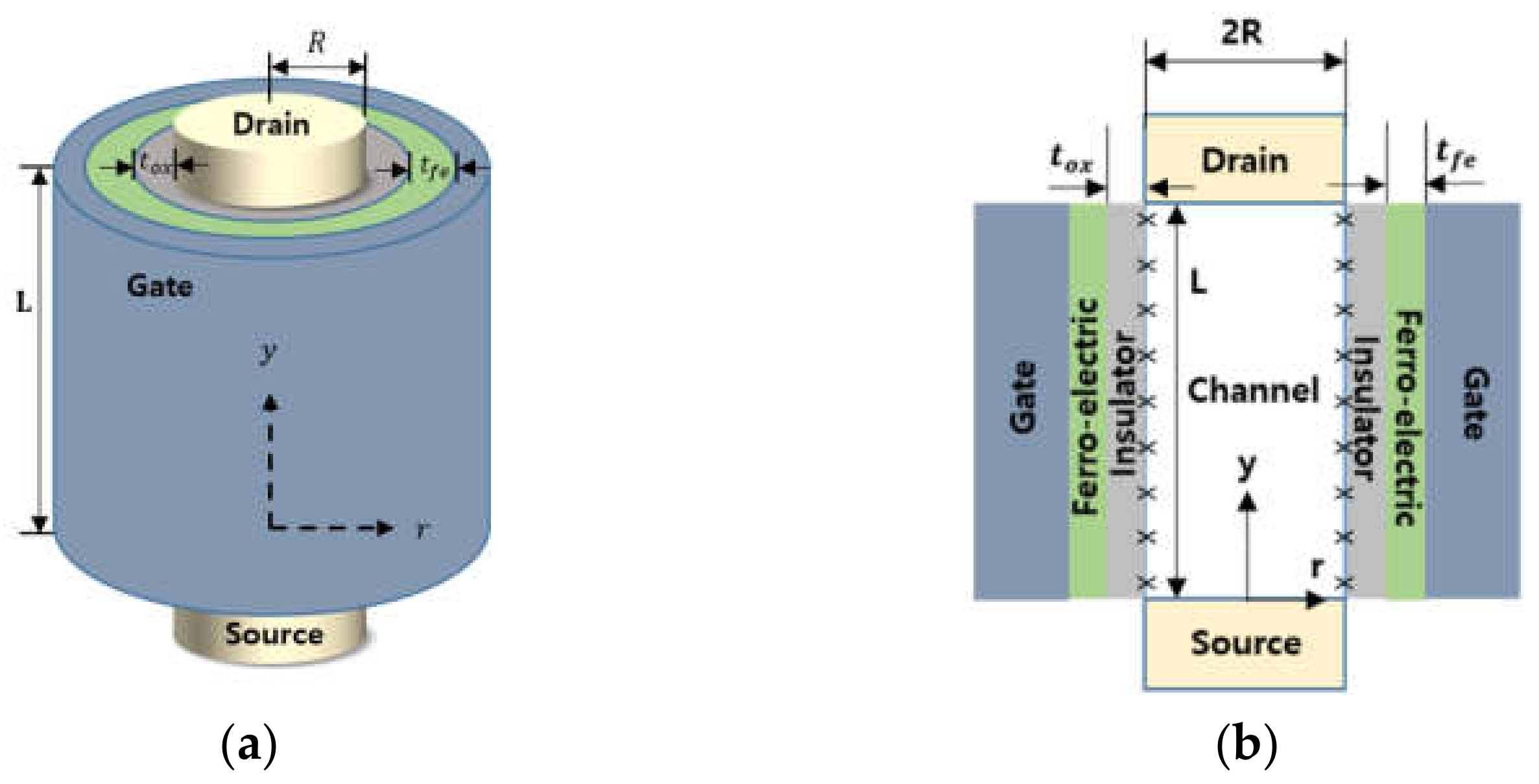
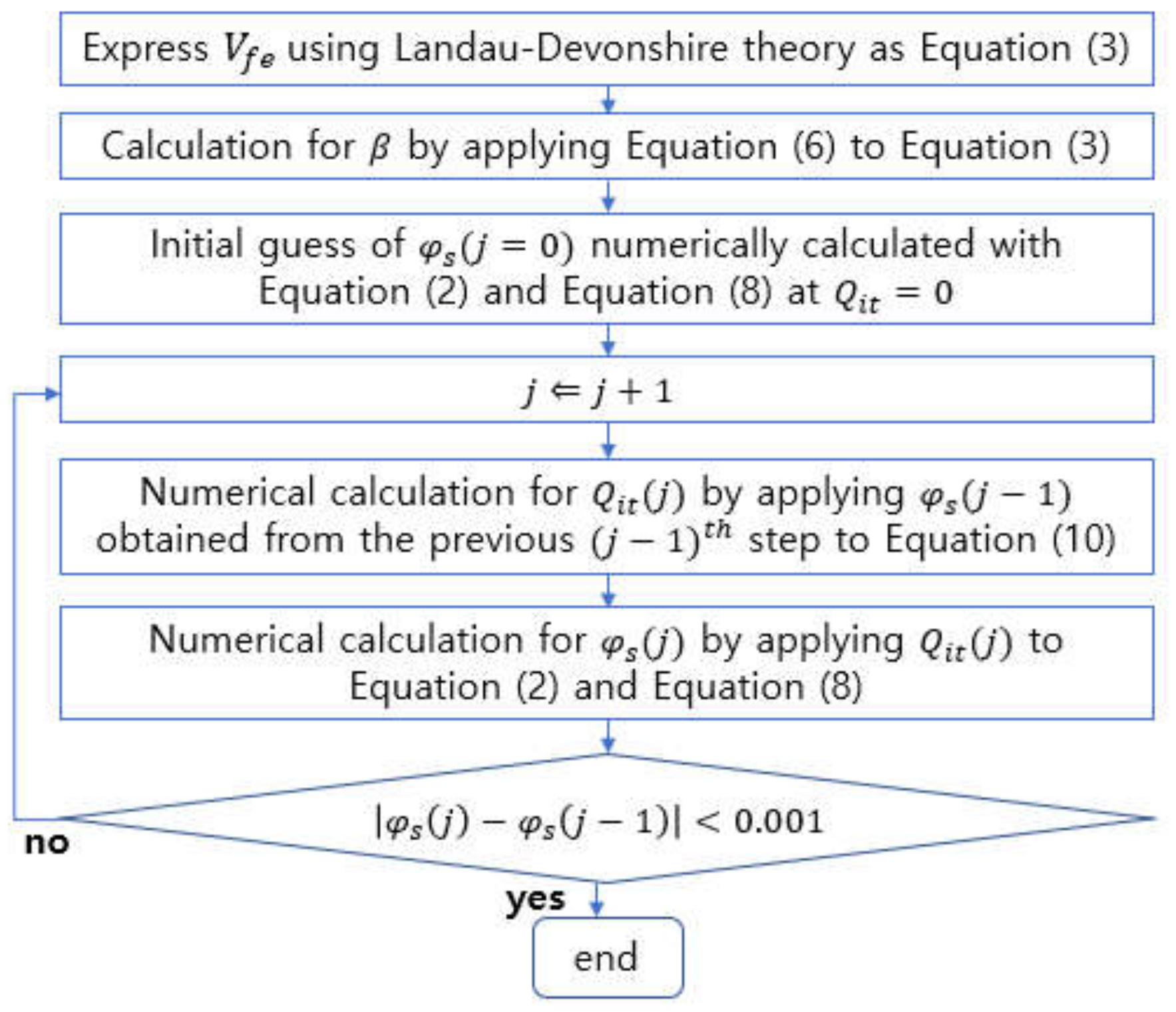
2. Method of Calculating Surface Potential of NC-GAA FET
3. Analytical Drain Current Model for NC-GAA FET
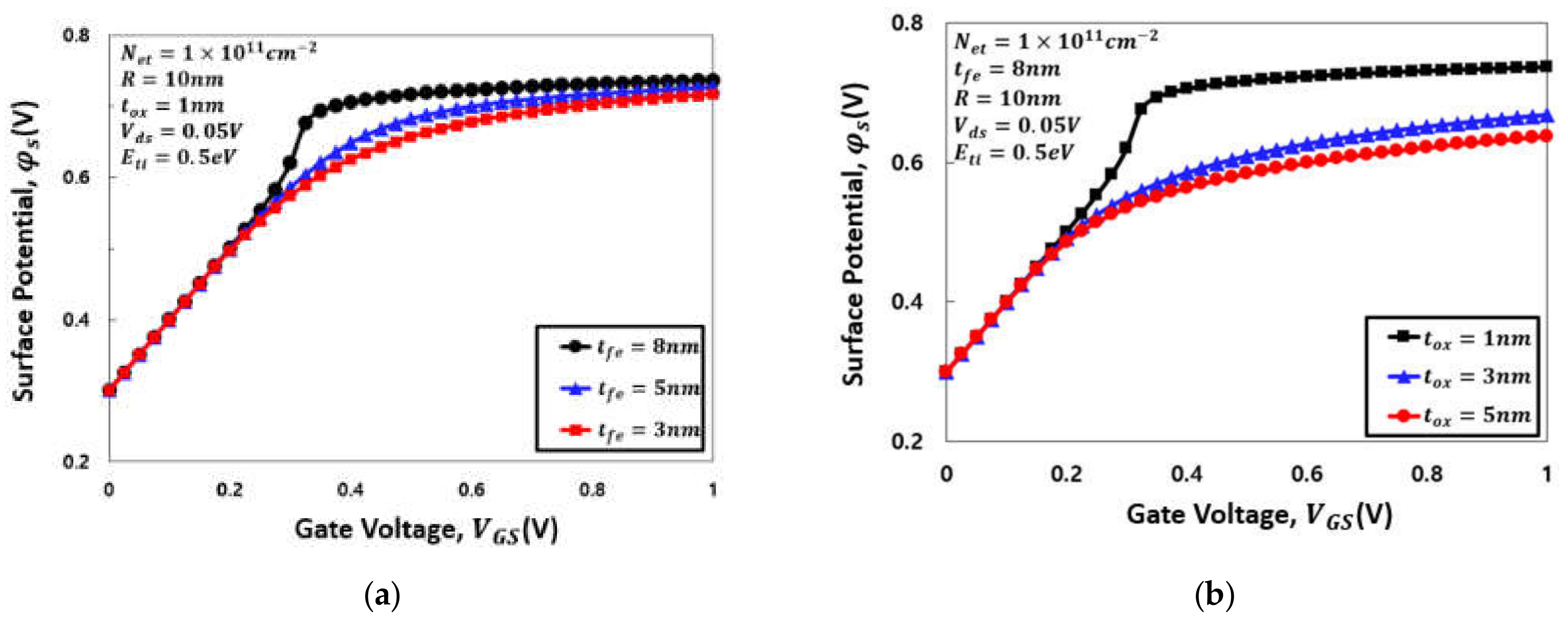
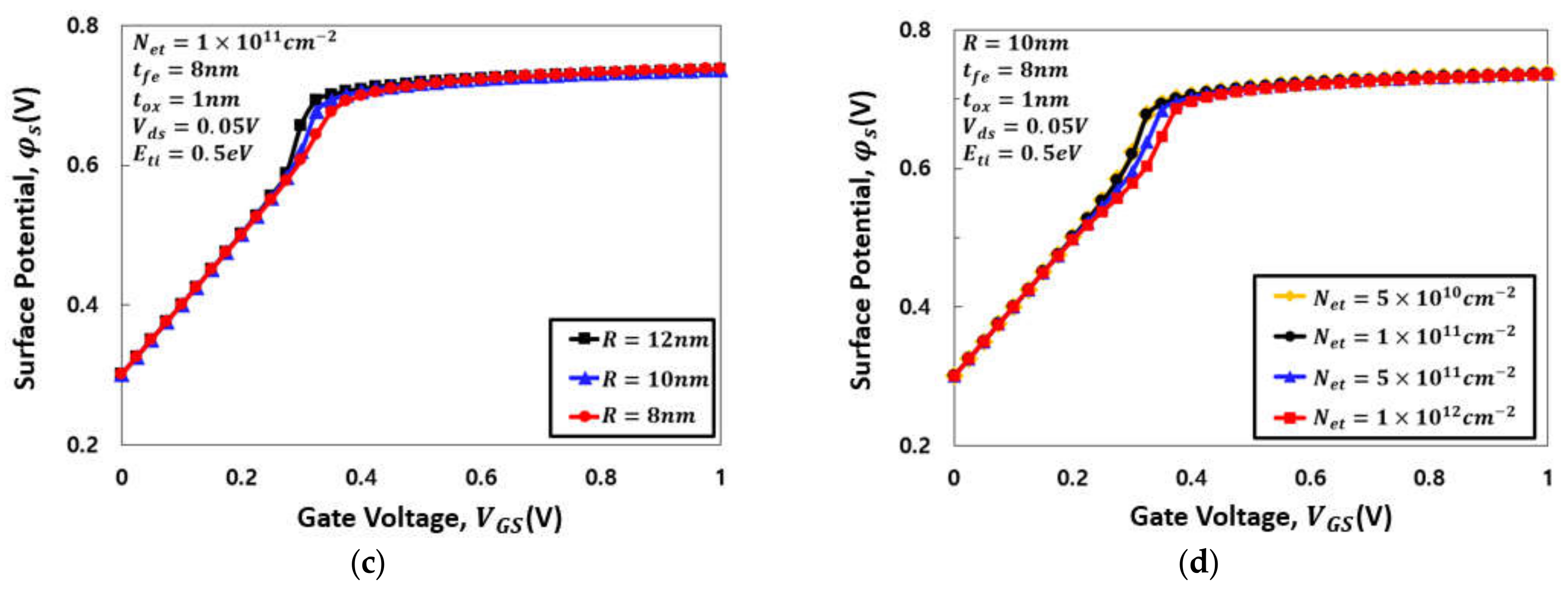
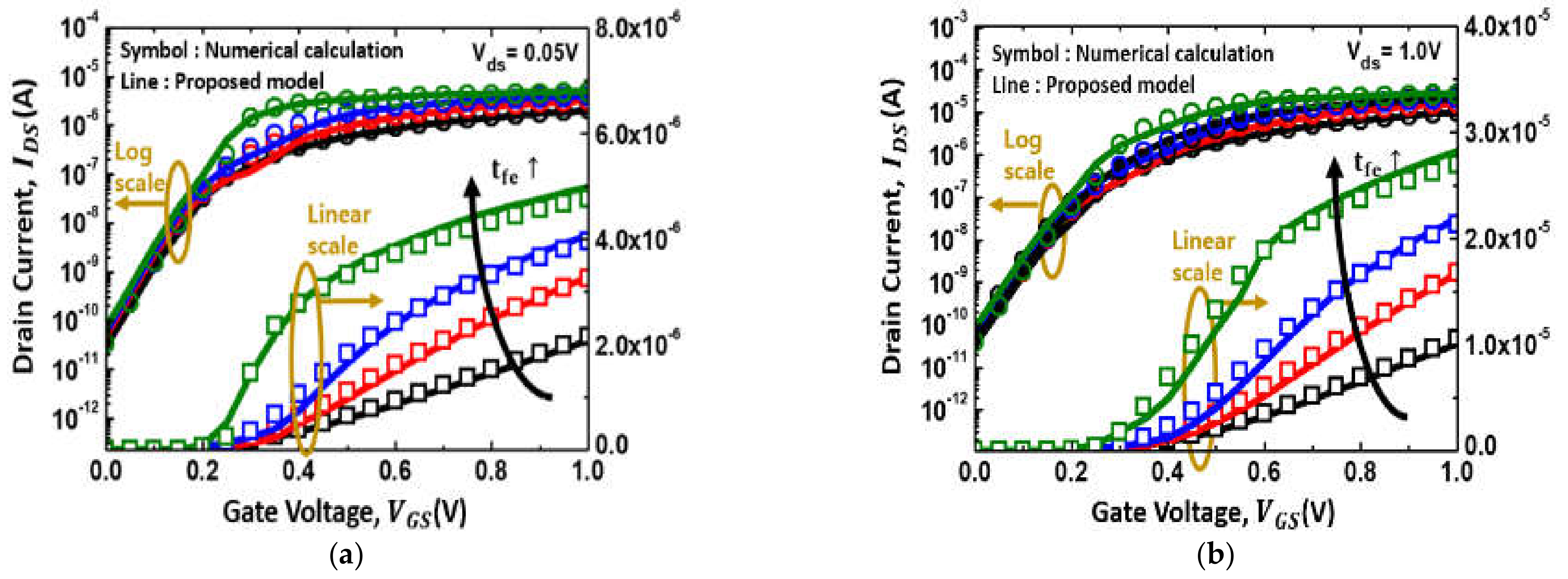
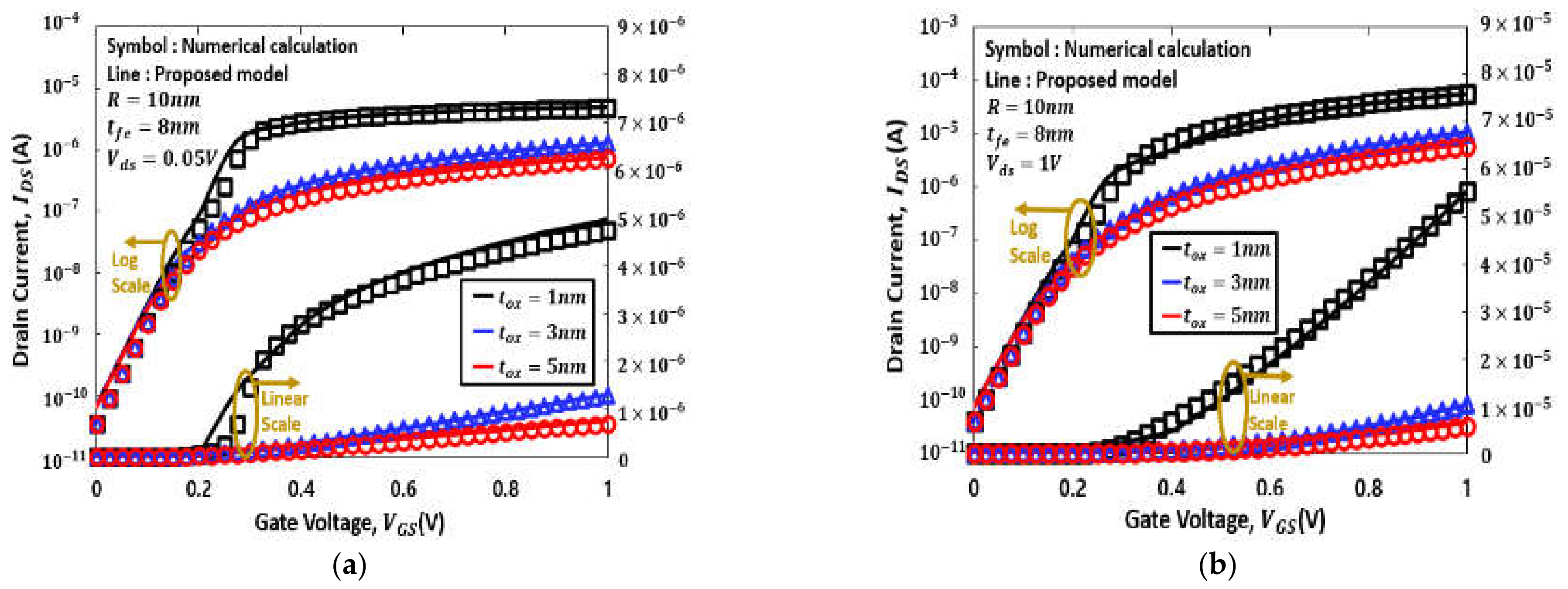
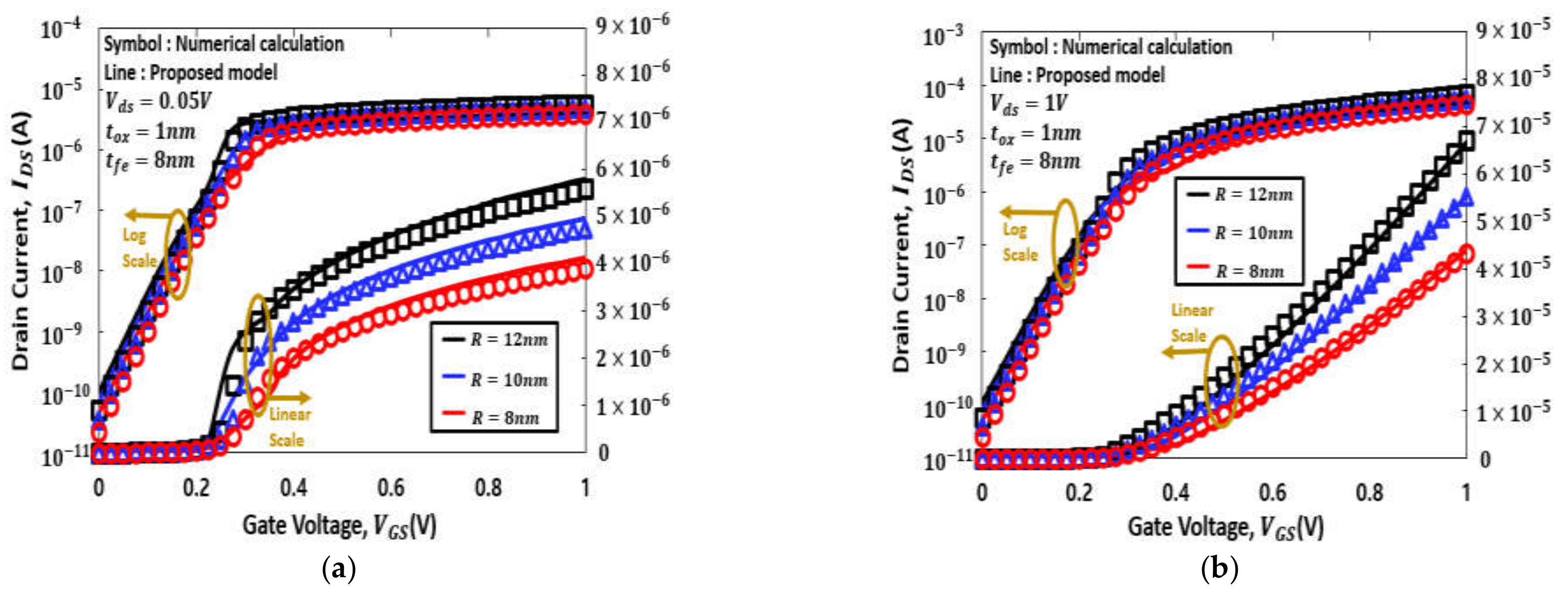
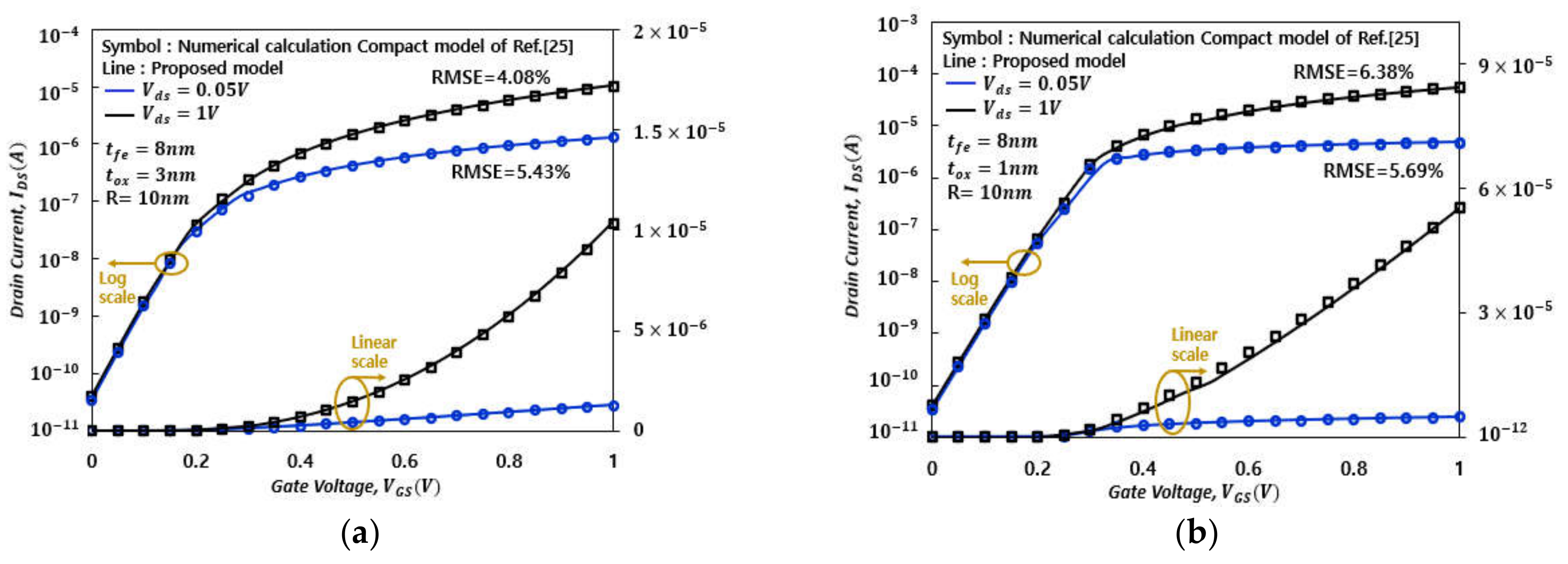
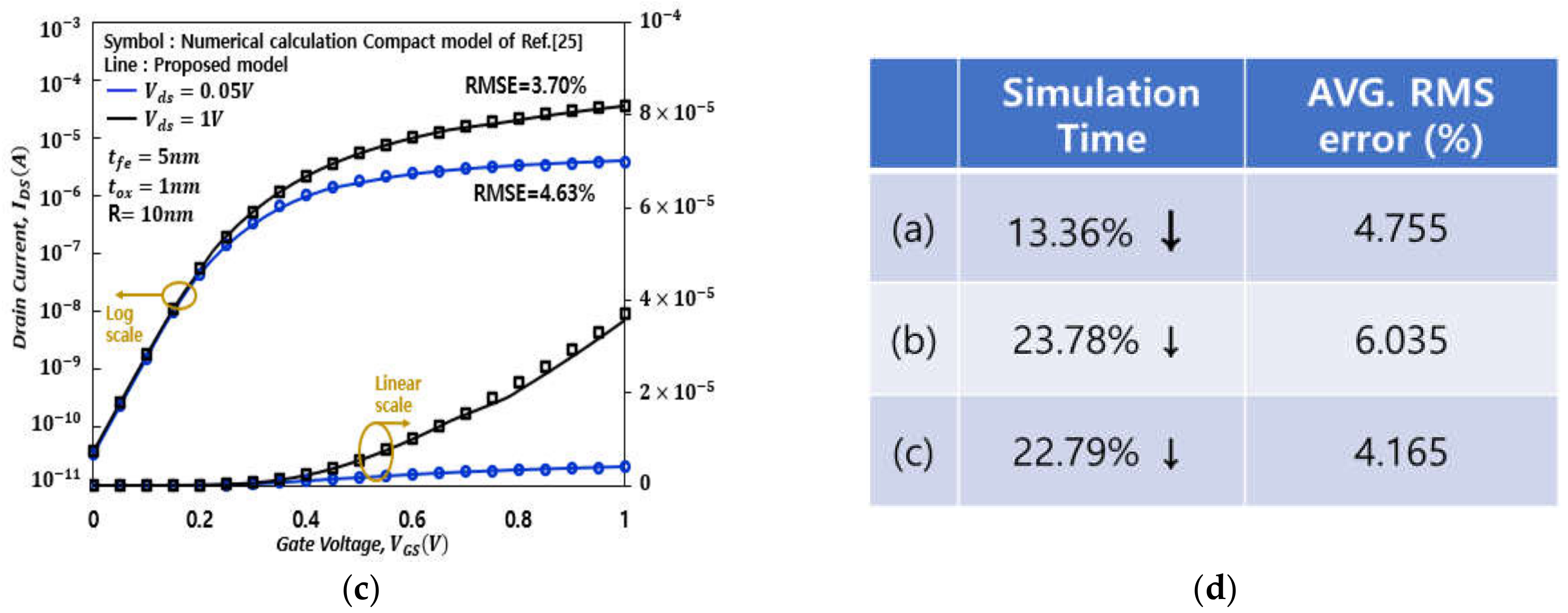
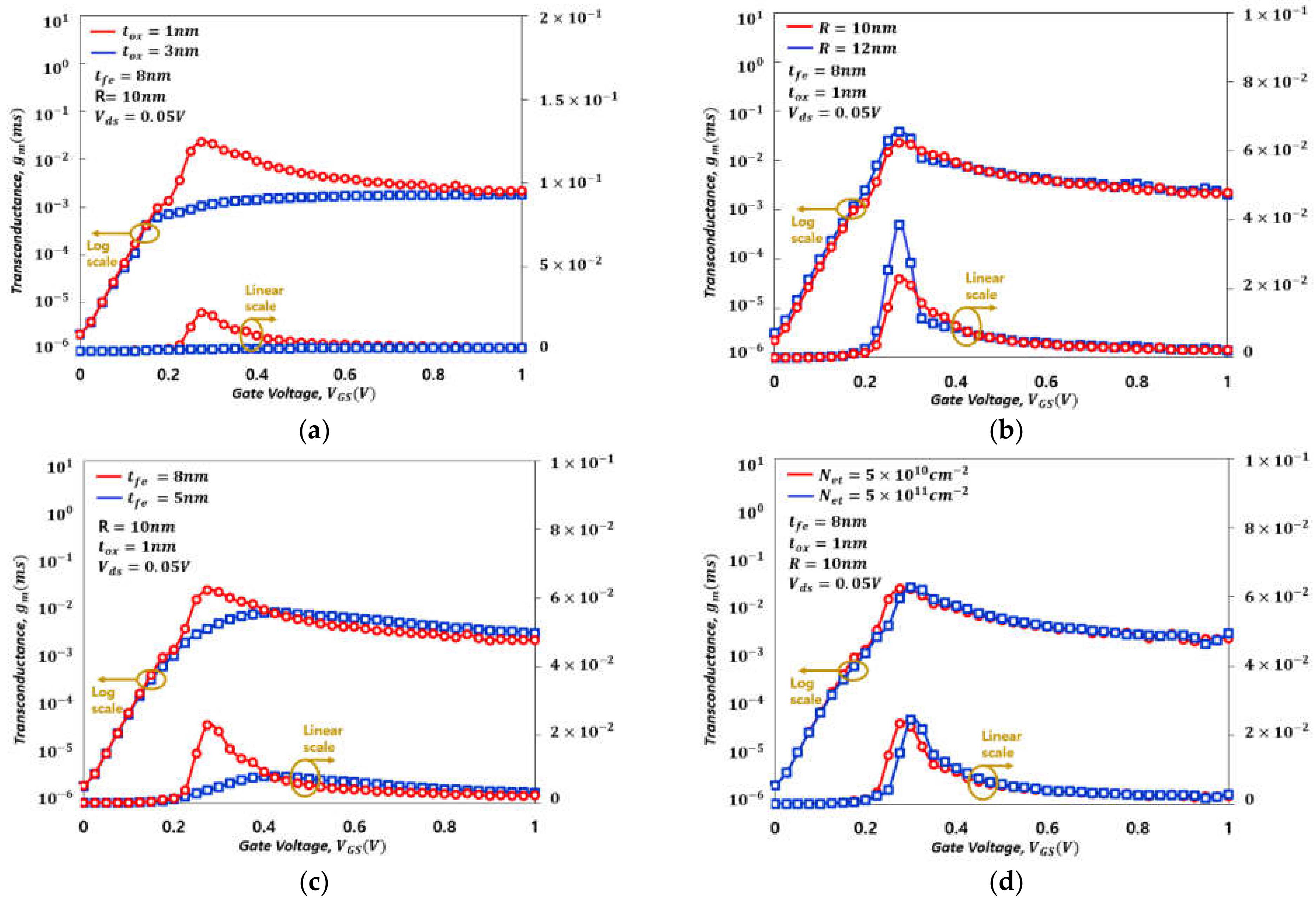
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, S.-Y.; Kim, S.-M.; Yoon, E.-J.; Oh, C.-W.; Chung, I.; Park, D.; Kim, K. A novel multibridge-channel MOSFET (MBCFET): Fabrication technologies and characteristics. IEEE Trans. Nanotechnol. 2003, 2, 253–257. [Google Scholar] [CrossRef]
- Barraud, S.; Lapras, V.; Previtali, B.; Samson, M.P.; Lacord, J.; Martinie, S.; Jaud, M.-A.; Athanasiou, S.; Triozon, F.; Rozeau, O.; et al. Performance and design considerations for gate-all-around stacked-nanowires FETs. In Proceedings of the 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2–6 December 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Bae, M.S.; Yun, I. Compact modeling of the subthreshold characteristics of junctionless double-gate FETs including the source/drain extentsion regions. Solid-State Electron. 2019, 156, 48. [Google Scholar] [CrossRef]
- Pezzimenti, F. Modeling of the Steady State and Switching Characteristics of a Normally Off 4H-SiC Trench Bi-polar-Mode FET. IEEE Trans. Electron Dev. 2013, 60, 1404. [Google Scholar] [CrossRef]
- Pezzimenti, F.; Bencherif, H.; Yousfi, A.; Dehimi, L. Current-voltage analytical model and multiobjective optimization of design of a short channel gate-all-around-junctionless MOSFET. Solid-State Electron. 2019, 161, 107642. [Google Scholar] [CrossRef]
- Xu, H.F.; Guan, B.G. Two-dimensional analytical model for hetero-juncion double-gate tunnel field-effect transistor with a stacked gate-oxide structure. Jpn. J. Appl. Phys. 2017, 56, 054201. [Google Scholar] [CrossRef]
- Jang, D.; Yakimets, D.; Eneman, G.; Schuddinck, P.; Bardon, M.G.; Raghavan, P.; Spessot, A.; Verkest, D.; Mocuta, A. Device Exploration of NanoSheet Transistors for Sub-7-nm Technology Node. IEEE Trans. Electron Devices 2017, 64, 2707–2713. [Google Scholar] [CrossRef]
- Yakimets, D.; Bardon, M.G.; Jang, D.; Schuddinck, P.; Sherazi, Y.; Weckx, P.; Miyaguchi, K.; Parvais, B.; Raghavan, P.; Spessot, A.; et al. Power aware FinFET and lateral nanosheet FET targeting for 3nm CMOS technology. In Proceedings of the 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2–6 December 2017; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017; pp. 20.4.1–20.4.4. [Google Scholar]
- Danowitz, A.; Kelley, K.; Mao, J.; Stevenson, J.P.; Horowitz, M. CPU DB: Recording Microprocessor History. Queue 2012, 10, 10–27. [Google Scholar] [CrossRef]
- Hilbert, M.; López, P. The World’s Technological Capacity to Store, Communicate, and Compute Information. Science 2011, 332, 60–65. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.H.; Fan, S.-T.; Tang, C.-H.; Chen, P.-G.; Chou, Y.-C.; Chen, H.-H.; Kuo, J.-Y.; Xie, M.-J.; Liu, S.-N.; Liao, M.-H.; et al. Physical thickness 1.x nm ferroelectric HfZrOx negative capacitance FETs. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 12.1.1–12.1.4. [Google Scholar]
- Khan, A.I.; Yeung, C.W.; Hu, C.; Salahuddin, S. Ferroelectric negative capacitance MOSFET: Capacitance tuning & antiferroelectric operation. In Proceedings of the 2011 International Electron Devices Meeting, Washington, DC, USA, 5–7 December 2011; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2011; pp. 11.3.1–11.3.4. [Google Scholar]
- Lin, C.-I.; Khan, A.I.; Salahuddin, S.; Hu, C. Effects of the Variation of Ferroelectric Properties on Negative Capacitance FET Characteristics. IEEE Trans. Electron Devices 2016, 63, 2197–2199. [Google Scholar] [CrossRef]
- Krishnamohan, T.; Kim, D.; Raghunathan, S.; Saraswat, K. Double-Gate Strained-Ge Heterostructure Tunneling FET (TFET) With record high drive currents and ≪ 60mV/dec subthreshold slope. In Proceedings of the 2008 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–3. [Google Scholar]
- Vishnoi, R.; Kumar, M.J. Compact Analytical Drain Current Model of Gate-All-Around Nanowire Tunneling FET. IEEE Trans. Electron. Devices 2014, 61, 2599–2603. [Google Scholar] [CrossRef]
- Knoch, J.; Mantl, S.; Appenzeller, J. Impact of the dimensionality on the performance of tunneling FETs: Bulk versus one-dimensional devices. Solid-State Electron. 2007, 51, 572–578. [Google Scholar] [CrossRef]
- Dunga, M.V.; Morshed, T.H.; Darsen, D.L.; Wenwei, Y.; Xuemei, X.; He, J.; Liu, W.; Cao, K.M.; Jin, X.; Ou, J.J.; et al. Bsim4. 6.0 Mosfet Model; University of California: Berkeley, CA, USA, 2006. [Google Scholar]
- Dunga, M.V.; Lin, C.-H.; Niknejad, A.M.; Hu, C. BSIM-CMG: A Compact Model for Multi-Gate Transistors. In FinFETs and Other Multi-Gate Transistors; Springer: Berlin/Heidelberg, Germany, 2007; pp. 113–153. [Google Scholar]
- Pahwa, G.; Dutta, T.; Agarwal, A.; Chauhan, Y.S. Compact Model for Ferroelectric Negative Capacitance Transistor with MFIS Structure. IEEE Trans. Electron Devices 2017, 64, 1366–1374. [Google Scholar] [CrossRef]
- Kobayashi, M.; Ueyama, N.; Jang, K.; Hiramoto, T. Experimental study on polarization-limited operation speed of negative capacitance FET with ferroelectric HfO2. In Proceedings of the 2016 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 3–7 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 12.3.1–12.3.4. [Google Scholar]
- Kim, T.; Shin, C. Effects of Interface Trap on Transient Negative Capacitance Effect: Phase Field Model. Electronics 2020, 9, 2141. [Google Scholar] [CrossRef]
- Lee, H.-P.; Tseng, K.-Y.; Su, P. Interface discrete trap induced variability for negative capacitance FinFETs. In Proceedings of the 2018 International Symposium on VLSI Technology, Systems and Application (VLSI-TSA), Hsinchu, Taiwan, 16–19 April 2018; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; pp. 1–2. [Google Scholar]
- Prakash, O.; Gupta, A.; Pahwa, G.; Henkel, J.; Chauhan, J.H.Y.S.; Amrouch, H. Impact of Interface Traps on Negative Capacitance Transistor: Device and Circuit Reliability. IEEE J. Electron Devices Soc. 2020, 8, 1193–1201. [Google Scholar] [CrossRef]
- Najam, F.; Yu, Y.S.; Cho, K.H.; Yeo, K.H.; Kim, D.-W.; Hwang, J.S.; Kim, S.; Hwang, S.W. Interface Trap Density of Gate-All-Around Silicon Nanowire Field-Effect Transistors with TiN Gate: Extraction and Compact Model. IEEE Trans. Electron Devices 2013, 60, 2457–2463. [Google Scholar] [CrossRef]
- Gaidhane, A.D.; Pahwa, G.; Verma, A.; Chauhan, Y.S. Compact Modeling of Drain Current, Charges, and Capacitances in Long-Channel Gate-All-Around Negative Capacitance MFIS Transistor. IEEE Trans. Electron Devices 2018, 65, 2024–2032. [Google Scholar] [CrossRef]
- Iniguez, B.; Fjeldly, T.; Lazaro, A.; Danneville, F.; Deen, M. Compact-Modeling Solutions for Nanoscale Double-Gate and Gate-All-Around MOSFETs. IEEE Trans. Electron Devices 2006, 53, 2128–2142. [Google Scholar] [CrossRef]
- Jimenez, D.; Iniguez, B.; Sune, J.; Marsal, L.; Pallares, J.; Roig, J.; Flores, D. Continuous Analytic I–V Model for Surrounding-Gate MOSFETs. IEEE Electron Device Lett. 2004, 25, 571–573. [Google Scholar] [CrossRef]
- Duarte, J.P.; Choi, S.-J.; Moon, D.-I.; Ahn, J.-H.; Kim, J.-Y.; Kim, S.; Choi, Y.-K. A Universal Core Model for Multiple-Gate Field-Effect Transistors. Part II: Drain Current Model. IEEE Trans. Electron Devices 2013, 60, 848–855. [Google Scholar] [CrossRef]
- Seon, Y.; Kim, J.; Kim, S.; Jeon, J. Analytical Current-Voltage Model for Gate-All-Around Transistor with Poly-Crystalline Silicon Channel. Electronics 2019, 8, 988. [Google Scholar] [CrossRef] [Green Version]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Advances in Computational mathematics. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Duarte, J.P.; Khandelwal, S.; Khan, A.I.; Sachid, A.; Lin, Y.-K.; Chang, H.-L.; Salahuddin, S.; Hu, C. Compact models of negative-capacitance FinFETs: Lumped and distributed charge models. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 30.5.1–30.5.4. [Google Scholar]


| Symbol (Units) | Value | Ferroelectric Parameter [31] |
|---|---|---|
| 1 | a = −3 × 109 m/F in Equation (4) b = 6 × 1011 m5/C2F in Equation (5) which is corresponding coercive field Ec = 1.15 MV/cm and remnant polarization Pr = 5 μC/cm2 | |
| 8–12 | ||
| 3–8 | ||
| 1–5 | ||
| −0.3 | ||
| 300 | ||
| 0–1 × | ||
| >1020 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Seon, Y.; Kim, S.; Kim, J.; Bae, S.; Yang, I.; Yoo, C.; Ham, J.; Hong, J.; Jeon, J. Analytical Current–Voltage Modeling and Analysis of the MFIS Gate-All-Around Transistor Featuring Negative-Capacitance. Electronics 2021, 10, 1177. https://doi.org/10.3390/electronics10101177
Kim Y, Seon Y, Kim S, Kim J, Bae S, Yang I, Yoo C, Ham J, Hong J, Jeon J. Analytical Current–Voltage Modeling and Analysis of the MFIS Gate-All-Around Transistor Featuring Negative-Capacitance. Electronics. 2021; 10(10):1177. https://doi.org/10.3390/electronics10101177
Chicago/Turabian StyleKim, Yeji, Yoongeun Seon, Soowon Kim, Jongmin Kim, Saemin Bae, Inkyung Yang, Changhyun Yoo, Junghoon Ham, Jungmin Hong, and Jongwook Jeon. 2021. "Analytical Current–Voltage Modeling and Analysis of the MFIS Gate-All-Around Transistor Featuring Negative-Capacitance" Electronics 10, no. 10: 1177. https://doi.org/10.3390/electronics10101177
APA StyleKim, Y., Seon, Y., Kim, S., Kim, J., Bae, S., Yang, I., Yoo, C., Ham, J., Hong, J., & Jeon, J. (2021). Analytical Current–Voltage Modeling and Analysis of the MFIS Gate-All-Around Transistor Featuring Negative-Capacitance. Electronics, 10(10), 1177. https://doi.org/10.3390/electronics10101177





