FPGA Implementation of High-Efficiency ECC Point Multiplication Circuit
Abstract
1. Introduction
- A field operation module compatible with four key lengths is designed to meet the requirements of system compatibility and improved flexibility of the system.
- The data path of group operation is optimized, the operation steps are reduced, and the speed of the system is improved.
- The field multiplier designed by combining partial product multiplication with Karatsuba–Offman (KO) algorithm multiplication improves the operation speed of the system, and can execute two m = 233 or 283 at the same time, which further improves the operation speed and reconfiguration efficiency of the system.
- By reusing the field operation module of the bottom layer, only two adders, two multipliers and two squarers are used to complete the requirements of the bottom layer operation of the system and save the system resources.
2. Related Works
3. Background
3.1. Binary Field Arithmetic Operations
b(z) = bm−1zm−1 + ⋯ + b2z2 + b1z1 + b0
3.1.1. Field Addition/Subtraction
| Algorithm 1 Addition in F2m |
| INPUT: Binary polynomials a(z) and b(z) of degree, at most, m−1. OUTPUT: c(z) = a(z) + b(z). |
| 1. For i from 0 to m−1 do 1.1 ci←ai⊕bi. 2. Return c(z). |
3.1.2. Polynomial Multiplication
| Algorithm 2 Processing columns for polynomial multiplication |
| INPUT: Binary polynomials a(z) and b(z) of degree, at most, m−1. OUTPUT: c(z) = a(z)·b(z). |
| 1. C←0. 2. For k from 0 to W−1 do 2.1 For j from 0 to t−1 do If the kth bit of A[j] is 1 then add B to C{j}. 2.2 If k ≠ (W−1) then B←B∙z. 3. Return(C). |
3.1.3. Modular Square
| Algorithm 3 Fast modular square f(z) = z233 + z74 + 1 (when m = 233) |
| INPUT: A binary polynomial a(z) of degree, at most, 232. OUTPUT: c(z) = a(z)2 mod f(z). |
| 1. For i from 1 to 231 do 1.1 c[i] ←a[117 + (i−1)/2]. 1.2 i←i + 2. 2. For i from 0 to 232 do 2.1 c[i] ←a[i/2]. 2.2 i←i + 2. 3. For i from 0 to 72 do 3.1 c[i] ←c[i]⊕a[196+i/2]. 3.2 i←i + 2. 4. For i from 74 to 146 do 4.1 c[i] ←c[i]⊕a[196 + (i−74)/2]. 4.2 i←i + 2 5. For i from 75 to 231 do 5.1 c[i] ←c[i]⊕a[117 + (i−75)/2]. 5.2 i←i + 2 6. Return c(z). |
3.1.4. Modular Reduction
| Algorithm 4 Fast reduction modulo f(z) = z571 + z10 + z5 + z2 + 1 (with W = 32) |
| INPUT: A binary polynomial c(z) of degree, at most, 1140. OUTPUT: c(z) mod f(z). |
| 1. For i from 35 down to 18 do {Reduce C[i]z32i modulo f (z)} 1.1 T← C[i]. 1.2 C[i−18]←C[i-18]⊕(T << 5)⊕(T<<7)⊕(T << 10)⊕(T << 15). 1.3 C[i−17]←C[i-17]⊕(T >> 27)⊕(T>>25)⊕(T >> 22)⊕(T >> 17). 2. T← C[17] >> 27. {Extract bits 27–31 of C[17]} 3. C[0]←C[0]⊕T⊕(T << 2)⊕(T << 5)⊕(T << 10). 4. C[17]←C[17] & 0×7FFFFFF. {Clear the reduced bits of C[17]} 5. Return(C[17], C[16], …, C[1], C[0]). |
3.1.5. Modular Inversion
| Algorithm 5 Inversion in F2m using Fermat’s Little Theorem (m odd) (Itoh–Tsujii inversion algorithm) |
| INPUT: a ∈ F2m(a ≠ 0). OUTPUT: a−1. |
| 1. Set A←a2, B←1, x←(m−1)/2. 2. While x ≠ 0 do 2.1 A←A·A2x. 2.2 If x is even then x←x/2. Else B←B∙A, A←A2, x← (x−1)/2. 3. Return (B). |
3.2. Elliptic Curve Overview
3.2.1. Point Addition
| Algorithm 6 Montgomery point addition (Madd) (standard projective coordinates) |
| INPUT: P = (x,y) in affine coordinates, P1 = (X1:Y1:Z1) and P2 = (X2:Y2:Z2) in standard projective coordinates on (E(F2m):y2 + xy = x3 + ax2 + b, P ∈ E(F2m)). OUTPUT: P1 + P2 = (X1:Y1:Z1) in standard projective coordinates. |
| 1. T1← x 2. X1← X1 × Z2 3. Z1← Z1 × X2 4. T2← X1 × Z1 5. Z1← Z1 + X1 6. Z1← Z12 7. X1← Z1 × T1 8. X1← X1 + T2 |
3.2.2. Point Doubling
| Algorithm 7 Montgomery point doubling (Mdouble) (standard projective coordinates) |
| INPUT: P = (X:Y:Z) in standard projective coordinates on (E(F2m) y2 + xy = x3 + ax2 + b, c2 = b, P ∈ E(F2m)). OUTPUT: 2P = (X:Y:Z) in standard projective coordinates. |
| 1. T1←c 2. X←X2 3. Z←Z2 4. T1←Z × T1 5. Z←Z × X 6. T1←T12 7. X←X2 8. X←X + T1 |
3.2.3. Coordinate Retransformation
| Algorithm 8 Montgomery point retransformation (Mxy) (standard projective coordinates) |
| INPUT: P = (x,y) in affine coordinates, P1 = (X1:Y1:Z1) and P2 = (X2:Y2:Z2) in standard projective coordinates on (E(F2m):y2 + xy = x3 + ax2 + b, P ∈ E(F2m)). OUTPUT: P1 = (xk,yk) = (X2,Z2) in affine coordinates. |
| 1. If Z1 = 0 then output (0,0) and stop. 2. If Z2 = 0 then output (x, x+y) and stop. 3. T1←x 4. T2←y 5. T3←Z1 × Z2 6. Z1←Z1 × T1 7. Z1←Z1 + X1 8. Z2←Z2 × T1 9. X1←Z2 × X1 10. Z2←Z2 + X2 11. Z2←Z2 × Z1 12. T4←T12 13. T4←T4 + T2 14. T4←T4 × T3 15. T4←T4 + Z2 16. T3←T3 × T1 17. T3←inverse(T3) 18. T4←T3 × T4 19. X2←X1 × T3 20. Z2←X2 + T1 21. Z2←Z2 × T4 22. Z2←Z2 + T2 |
3.3. Point Multiplication
| Algorithm 9 Montgomery point multiplication (standard projective coordinates) |
| INPUT: k = (km−1,…,k2,k1,k0)2,km−1 = 1,P = (x, y) ∈ E(F2m). OUTPUT: kP. |
| 1. X1←x, Z1←1, X2←x4 + b, Z2←x2. {Compute(P,2P)} 2. For i from m−2 downto 0 do 2.1 If ki = 1 then Madd(X1, Z1, X2, Z2), Mdouble(X2, Z2). 2.2 Else Madd(X2, Z2, X1, Z1), Mdouble(X1, Z1). 3. Return(Q = Mxy(X1, Z1, X2, Z2)). |
4. Hardware Design Architecture
4.1. PM Module Overview
4.2. VAU
4.2.1. Field Addition/Subtraction Module
4.2.2. Modular Square Module
4.2.3. Field Multiplication Module
b(z) = zm/2(zm/2–1bm−1 + ⋯ + bm/2)+(zm/2–1bm/2–1 + ⋯·+ b0) = zm/2BH + BL
4.3. FAUC
4.3.1. Point Addition Module
4.3.2. Point Doubling Module
4.3.3. Modular Inversion Module
4.3.4. Coordinate Retransformation Module
4.4. PMC
- The affine coordinates of base point P are transformed into standard projective coordinates, and the data initialization assignment of this module is completed.
- The private key k is scanned bit by bit to determine the value of each bit, and the point addition and point doubling operations are subject to the scanning results.
- According to the Montgomery method, the point adding and doubling modules are called upon to perform the iterative operation.
- Upon completion of the point multiplication operation in projective coordinates, coordinate retransformation is called upon to convert the outcome into affine coordinates.
5. Experimental Results and Discussion
5.1. Experiment Setup
5.2. Results Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Feki, M.A.; Kawsar, F.; Boussard, M.; Trappeniers, L. The Internet of Things: The Next Technological Revolution. Computer 2013, 46, 24–25. [Google Scholar] [CrossRef]
- Kai, Z.; Ge, L. A Survey on the Internet of Things Security. In Proceedings of the 2013 International Conference on Computational Intelligence and Security, Emeishan, China, 14–15 December 2013; pp. 663–667. [Google Scholar]
- Tsague, H.D.; Twala, B. Practical Techniques for Securing the Internet of Things (IoT) Against Side Channel Attacks. In Internet of Things and Big Data Analytics Toward Next-Generation Intelligence, 1st ed.; Springer: Cham, Germany, 2017; pp. 439–481. [Google Scholar]
- Herder, C.; Yu, M.; Koushanfar, F.; Devadas, S. Physical Unclonable Functions and Applications: A Tutorial. Proc. IEEE 2014, 102, 1126–1141. [Google Scholar] [CrossRef]
- Chen, S.; Li, B.; Cao, Y. Intrinsic Physical Unclonable Function (PUF) Sensors in Commodity Devices. Sensors 2019, 19, 2428. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Li, B.; Chen, Z.; Zhang, Y.; Wang, C.; Tao, C. Novel Strong-PUF-based Authentication Protocols Leveraging Shamir’s Secret Sharing. IEEE Internet Things J. 2021, in press. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, B.; Liu, B.; Hu, Y.; Zheng, H. A Privacy-Aware PUFs-Based Multi-Server Authentication Protocol in Cloud-Edge IoT Systems Using Blockchain. IEEE Internet Things J. 2021, in press. [Google Scholar] [CrossRef]
- Ulrich, R.; Jan, S.; Frank, S.; Xiaolin, X.; Ahmed, M.; Vera, S.; Gideon, D.; Jürgen, S.; Wayne, B.; Srinivas, D. PUF Modeling Attacks on Simulated and Silicon Data. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1876–1891. [Google Scholar]
- Imran, M.; Rashid, M.; Jafri, A.R.; Kashif, M. Throughput/area optimized pipelined architecture for elliptic curve crypto processor. IET Comput. Digit. Tech. 2019, 13, 361–368. [Google Scholar] [CrossRef]
- Sutter, G.; Deschamps, J.; Imana, J. Efficient elliptic curve point multiplication using digit-serial binary field operations. IEEE Trans. Ind. Electron. 2013, 60, 217–225. [Google Scholar] [CrossRef]
- Khan, Z.U.A.; Benaissa, M. High-Speed and Low-Latency ECC Processor Implementation Over GF(2m) on FPGA. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 165–176. [Google Scholar] [CrossRef]
- Li, L.; Li, S. High-performance pipelined architecture of point multiplication on Koblitz curves. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1723–1727. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A.; Springer, S.V. Guide to Elliptic Curve Cryptography, 1st ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Digital Signature Standard. FIPS Standard 186-4. 2013. Available online: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.186-4.pdf (accessed on 21 May 2021).
- Morioka, S.; Katayama, Y. O(log2m) Iterative Algorithm for Multiplicative Inversion in GF(2m). In Proceedings of the 2000 IEEE International Symposium on Information Theory (Cat. No.00CH37060), Sorrento, Italy, 25–30 June 2000; p. 449. [Google Scholar]
- Itoh, T.; Tsujii, S. A fast algorithm for computing multiplicative inverses in GF(2m) using normal bases. Inf. Comput. 1988, 78, 171–177. [Google Scholar] [CrossRef]
- Meher, P.K.; Lou, X. Low-Latency, Low-Area, and Scalable Systolic-Like Modular Multipliers for GF(2m) Based on Irreducible All-One Polynomials. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 399–408. [Google Scholar] [CrossRef]
- Renuka, G.; Shree, V.U.; Reddy, P.C. Comparison of AES and DES Algorithms Implemented on Virtex-6 FPGA and Microblaze Soft Core Processor. Int. J. Electr. Comput. Eng. 2018, 8, 3544–3549. [Google Scholar] [CrossRef][Green Version]
- Li, L. Research on Algorithms and Hardware Implementations for Elliptic Curve Cryptography over Binary Extension Fields. Ph.D. Thesis, Tsinghua University, Beijing, China, 2017. [Google Scholar]
- Hasbi, A.; Arif, S.; Yusuf, K. Implementation of ECC on Reconfigurable FPGA Using Hard Processor System. In Proceedings of the 2018 International Symposium on Electronics and Smart Devices (ISESD), Bandung, Indonesia, 23–24 October 2018; pp. 1–6. [Google Scholar]


















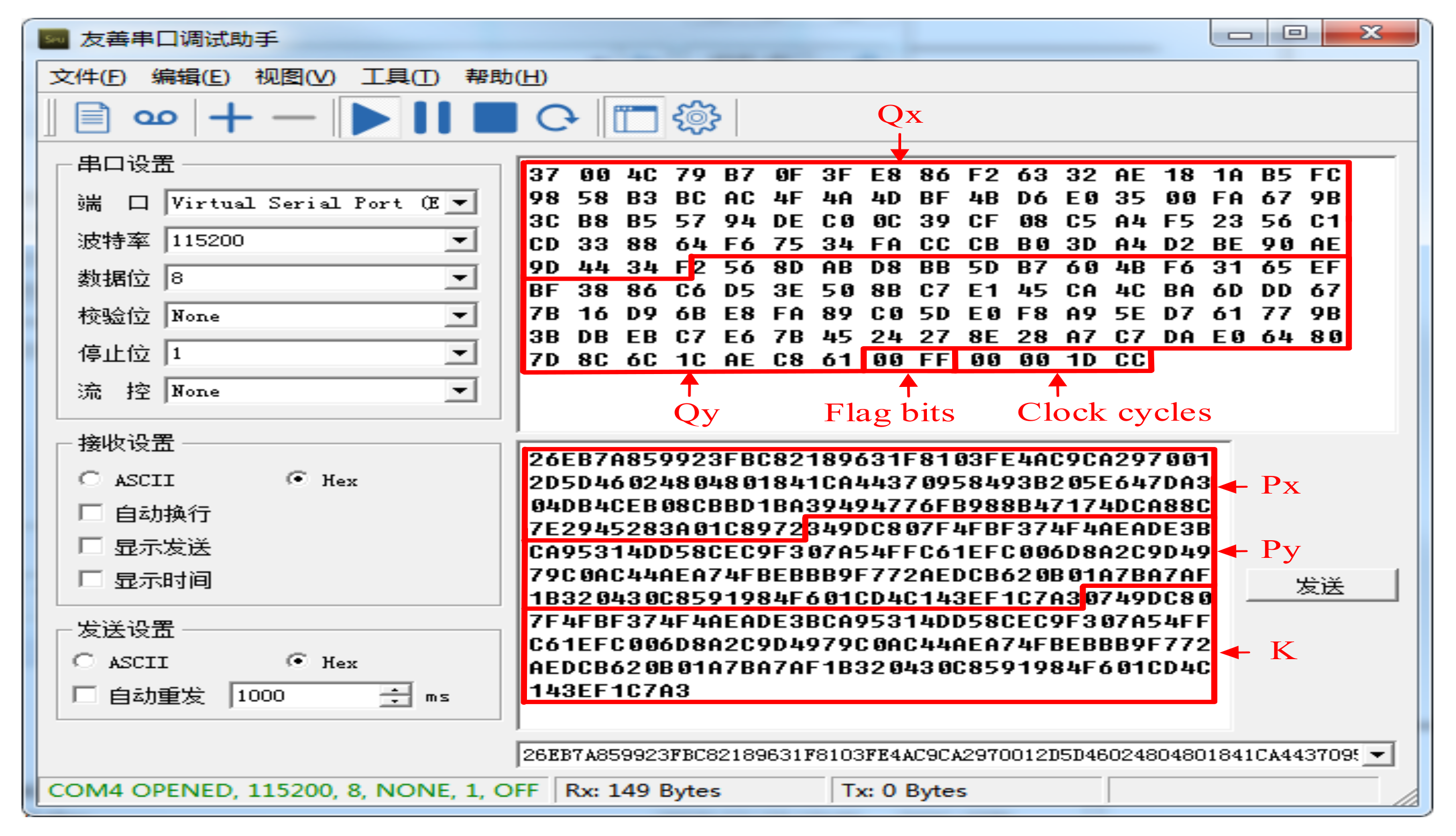
| Circuits | Digital Serial Multiplier | KO Multiplier |
|---|---|---|
| Freq. (MHz) | 141.920 | 188.253 |
| LUTs | 20,114 | 41,612 |
| Registers | 1757 | 3089 |
| Delay (Clock Cycles) (m = 233) | 16 | 1 |
| Delay (Clock Cycles) (m = 283) | 18 | 1 |
| Delay (Clock Cycles) (m = 409) | 26 | 2 |
| Delay (Clock Cycles) (m = 571) | 36 | 2 |
| Delay (Clock Cycles) (m = 233 & 233) | - | 1 |
| Delay (Clock Cycles) (m = 283 & 283) | - | 1 |
| The Range of Degree i | Modular Reduction Results |
|---|---|
| [0, 570] | zi |
| [571, 1131] | (z10 + z5 + z2 + 1)zi–571 |
| [1132, 1136] | (z566 + z563 + z561 + z10 + z5 + z2 + 1)zi–1132 |
| [1137, 1139] | (z568 + z566 + z15 + z7 + z2 + 1)zi–559 |
| [1140] | z569 + z18 + z3 + z2 + 1 |
| Key Length (m) | 233 | 283 | 409 | 571 | ||||
|---|---|---|---|---|---|---|---|---|
| Product | Cycles | Product | Cycles | Product | Cycles | Product | Cycles | |
| Step1 | 1 | 1 | 1 | 1 | ||||
| Step2 | 1 | 2 | 2 | 2 | ||||
| Step3 | 3 | 4 | 3 | 4 | ||||
| Step4 | a | 1 | 8 | 6 | 8 | |||
| Step5 | 7 | 1 | 12 | 1 | ||||
| Step6 | 14 | 17 | 1 | 17 | ||||
| Step7 | 1 | 1 | 25 | a | 1 | |||
| Step8 | 29 | 35 | 1 | 35 | ||||
| Step9 | 58 | 70 | 51 | 1 | ||||
| Step10 | 116 | 1 | 102 | 71 | ||||
| Step11 | 1 | 1 | 141 | 408 | 142 | |||
| Step12 | - | - | 1 | 1 | 1 | 1 | 1 | |
| Step13 | - | - | - | - | - | - | 285 | |
| Step14 | - | - | - | - | - | - | 1 | 1 |
| Solutions | m | FPGA | LUTs | Freq. (MHz) | Cycles | T (μs) | Key Length |
|---|---|---|---|---|---|---|---|
| [10] | 233 | V5 | 25,129 | 250 | 1375 | 5.50 | 233 |
| 283 | 25,030 | 189 | 6350 | 33.6 | 283 | ||
| 409 | 28,503 | 161 | 16,519 | 102.6 | 409 | ||
| 571 | 32,432 | 121 | 42,108 | 348 | 571 | ||
| [11] | 571 | V7 | 141,078 | 111 | 3780 | 34.05 | 571 |
| [12] | 233 | V5 | - | 173 | 708 | 4.09 | 233 |
| 283 | - | 154 | 895 | 5.81 | 283 | ||
| 409 | - | 143 | 1358 | 9.50 | 409 | ||
| 571 | - | 121 | 2240 | 18.51 | 571 | ||
| [19] | 233 | K7 | 95,799 | 120 | 2321 | 19.34 | 163,233, 283,367 |
| 283 | 2819 | 23.49 | |||||
| [20] | 163 | DE10 | - | 50 | 1,179,500 | 23,590 | 163,233, 283,409 |
| 233 | 2,546,000 | 50,920 | |||||
| 283 | 3,772,000 | 75,440 | |||||
| 409 | 9,287,000 | 185,740 | |||||
| Ours | 233 | V6 | 116,241 | 135 | 2609 | 19.33 | 233,283, 409,571 |
| 283 | 3018 | 22.36 | |||||
| 409 | 5784 | 41.36 | |||||
| 571 | 7628 | 56.50 | |||||
| 233 & 233 | 2609 | 19.33 | |||||
| 283 & 283 | 3018 | 22.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Li, B.; Zhang, L.; Wang, Y.; Zhang, Y.; Chen, R. FPGA Implementation of High-Efficiency ECC Point Multiplication Circuit. Electronics 2021, 10, 1252. https://doi.org/10.3390/electronics10111252
Zhao X, Li B, Zhang L, Wang Y, Zhang Y, Chen R. FPGA Implementation of High-Efficiency ECC Point Multiplication Circuit. Electronics. 2021; 10(11):1252. https://doi.org/10.3390/electronics10111252
Chicago/Turabian StyleZhao, Xia, Bing Li, Lin Zhang, Yazhou Wang, Yan Zhang, and Rui Chen. 2021. "FPGA Implementation of High-Efficiency ECC Point Multiplication Circuit" Electronics 10, no. 11: 1252. https://doi.org/10.3390/electronics10111252
APA StyleZhao, X., Li, B., Zhang, L., Wang, Y., Zhang, Y., & Chen, R. (2021). FPGA Implementation of High-Efficiency ECC Point Multiplication Circuit. Electronics, 10(11), 1252. https://doi.org/10.3390/electronics10111252







