1. Introduction
Because of the high output power [
1], low torque ripple [
2], low harmonic content [
3], and high reliability of the multiphase PMSM [
4,
5], this motor has broad application prospects in electric vehicles, ship propulsion, aerospace, and rail transit, all of which require high power and high reliability [
6,
7]. The traditional position detection method needs a position sensor which increases the volume and cost of production and also reduces the reliability; therefore, the sensorless position detection technology is a promising technical method [
8,
9].
Generally, there are two types of sensorless position detection techniques: the first is a high-frequency injection (HFI) method which is suitable for low speeds and uses the rotor salient effect of the motor rotor to estimate the position and speed [
10,
11]. The advantage of this control method is that it is not sensitive to the change of motor parameters, and the estimation accuracy has nothing to do with the speed; the biggest disadvantage is that it is only suitable for the motor with a salient effect, and because of the injection of high-frequency signals, there is the problem of high-frequency noise.
Li et al. [
12] proposed that, based on the high-frequency square wave voltage injection method, the extended state observer (ESO) should be used to estimate the rotor position and speed. Compared with the traditional sensorless control strategy, this method reduces the use of digital filters, simplifies the signal processing, and eliminates the influence of inverter nonlinearity on system performance. However, the position estimation accuracy and motor speed range obtained by this method are limited as this method is only suitable for low-speed motor operation.
The other position estimation method depends on the BEMF and is suitable for medium and high speeds. Examples include the extended Kalman filter method [
13,
14], the model reference adaptive control [
15,
16], and the sliding mode observer (SMO) method [
17,
18].
Kumar et al. [
19] proposed using a fractional order phase-locked loop instead of a traditional phase-locked loop in the sliding mode observer method, and the position information of the rotator can be obtained more accurately by choosing an appropriate fractional order factor. However, this method fails to analyze the robustness of the system when the parameters of the motor change.
Saadaoui et al. [
20] proposed using a continuous function instead of a traditional switching function in an SMO to solve chattering problems, as well as using an arctangent function to estimate the rotor position, but this still presents some problems such as low estimation accuracy and large speed errors.
Shao et al. [
21] proposed an integral SMO to compensate for the estimated BEMF error. Although it solves the problems of chattering and phase delay, this method has a weak resistance to load disturbance and is not practical.
Zhang et al. [
22] proposed a cascaded SMO using an adaptive sliding mode to observe the BEMF and compared three methods of angle estimation: phase-locked loop (PLL), second-order extended state observer (ESO), and non-smooth feedback observer (NSFO). The structure of second-order ESO is basically the same as that of PLL, and the comparison significance is not strong. The NSFO can resist disturbance, but the estimation error is large. Compared with PLL, the improvement is not obvious.
Wu et al. [
23] proposed a stable SMO which uses a new saturated state control (SSC) function instead of the sign function to reduce the chattering phenomenon and steady-state errors, but the simulation and experimental waveforms produced from this method are less defined, which is not convincing.
In this study, the dual Y shift 30° six-phase PMSM with an isolated neutral point was investigated, and a new sliding mode sensorless control strategy was used to estimate the speed and rotor position. Firstly, the frequency-variable tracker of the stator current (FVTSC) was added to the traditional SMO to solve the problem of the BEMF dynamic estimation, especially when the stator winding current frequency changes. This method can improve the estimation accuracy of the BEMF and at the same time introduce the FVTSC to replace the original switching function in the SMO, which solves the problem of chattering during the BEMF estimation. Secondly, in order to improve the estimation accuracy and resistance ability of the observer regarding rotor position, electromagnetic torque and load torque as disturbance terms, and taking rotor position error as input, a third-order extended state observer (ESO) was constructed to estimate the speed and rotor position through the mechanical motion equation of the motor. Finally, in order to verify the effectiveness of the method, the system simulation model and experimental platform were established and the experimental research was carried out. The results show that the control system with the new sliding mode variable structure and estimation method has a fast dynamic response and strong anti-interference ability.
This article mainly includes the following aspects:
Section 2 introduces the mathematical model of six-phase PMSM.
Section 3 proposes a new PMSM sensorless control strategy using FVTSC technology to solve the problem of dynamic estimation of the BEMF. In order to improve estimation accuracy and resistance to disturbances, a third-order ESO is designed to estimate the speed and rotor position, and the simulation analysis and robustness verification are carried out in
Section 4. In
Section 5, experiments are carried out to verify the practicability and feasibility of the new sensorless control strategy. Finally,
Section 6 summarizes the conclusions and future research directions.
2. Mathematical Model of the Six-Phase PMSM
The inverter topology is shown in
Figure 1 and
Figure 2 shows the distribution structure.
The six-phase PMSM is a six-dimensional system with six independent variables. Its mathematical model in the natural coordinate system has the disadvantages of high order, nonlinearity, and strong coupling. Flux is not only related to the phase current but also to the rotor position angle
, thereby making it difficult to realize effective control [
24,
25].
Through the transformation matrix in Equation (1), the electrical elements in the double three-phase motor are mapped to the fundamental plane (α-β space) and harmonic plane (z1-z2 space). In the matrix, the first and second vectors correspond to the α-β plane, the third and fourth vectors correspond to the z1-z2 plane, and the fifth and sixth vectors correspond to the zero-order plane (o1-o2 space). The conversion of electromechanical energy is only connected to the α-β subspace rather than z1-z2 and o1-o2 subspaces; thus, these two spaces are called harmonic subspaces.
As the neutral point of the dual Y shift 30° six-phase PMSM is not connected, the o1-o2 space has a zero-sequence variable, which is also called the zero-sequence space. The rotation coordinate transformation of the α-β space is performed, while the z1-z2 and o1-o2 subspaces are multiplied by the unit matrix and remain unchanged.
Thus, the transformation matrix is expressed as:
where
denotes the rotor electric degree. Using the transformation matrix, we can determine the flux, voltage, electromagnetic torque, and motion equations as follows:
Electromagnetic torque equation:
Motion equation:
where
Ld and
Lq are the inductance;
id and
iq are the currents;
ψd and
ψq are the stator flux; and
ud and
uq are the stator voltage. Further,
Te,
TL,
ψf,
B,
ωe,
J,
R, and
p represent electromagnetic torque, load torque, rotor permanent magnet flux, damping coefficient, electric angular velocity, moment of inertia of the motor, stator resistance, and pole pairs, respectively.
3. Sensorless Control of PMSM
3.1. Traditional Sliding Mode Observer
In the six-phase PMSM system, the mathematical model in the α-β coordinate system is:
where
eα and
eβ are components of the BEMF and can be expressed as:
The SMO can make the state variable trajectory move along the ideal sliding mode surface by changing the system structure dynamically [
26]. Taking the stator current components as the state variable, from Equation (7), we obtain:
According to the theory of the sliding mode variable structure, taking
,
as the sliding mode surface, the SMO of winding currents are:
where
and
are the estimated currents, and
and
represent the estimated BEMF and can be expressed as:
where
Ks is the sliding gain, and its selection must satisfy the requirements of existence, stability, and reachability of the SMO.
From Equations (9)–(11), the current deviation equation can be expressed as:
where
,
, represent the current estimation error of the observer.
The discrete switching characteristics of the symbolic functions in a traditional SMOs can easily lead to high-frequency chattering when estimating the BEMF. To solve this problem, this study introduces an FVTSC to replace the original switch sign function.
3.2. Frequency-Variable Tracker of the Stator Current (FVTSC)
An FVTSC method is introduced to estimate the BEMF to address the torque pulsation problem caused by the SMO. The FVTSC is an improvement for the traditional SMO. By optimizing the symbol function in the traditional SMO, the chattering problem is solved. Compared with the traditional SMO, the BEMF estimation of an FVTSC is more accurate by tracking the stator current frequency in real time. Simultaneously, the problems of phase lag and amplitude attenuation in the traditional SMO are solved. The main principle is to use the F function instead of the switching function in Equation (12), as shown in Equation (13).
where F() is a new sliding mode switching function used to track the fundamental wave of the stator current. Its specific manifestation is shown below.
Let
and
, then the FVTSC function can be expressed as:
Formula (14) shows that the main parameters Kp, Kr, ωc, and f affect the performance of the controller. Kp and Kr are the proportional gain and the peak gain at resonance frequency, respectively. ωc affects the resonance gain and bandwidth, and f is the tracking frequency of the stator current. The principle of parameter adjustment is to adjust Kp to eliminate dynamic errors, Kr to eliminate steady-state errors, and ωc to suppress frequency fluctuation. In the experiment, each parameter needs to be tuned online.
In order to facilitate calculation and combine the parameters of motor and observer, the frequency range of
ωc is 2000–4000 rad/s,
Kp and
Kr parameters can be adjusted according to the real-time response and frequency characteristics of the observer, and the appropriate parameters can be determined according to the expected experimental results. The stator current frequency
f can be obtained by PLL [
27]. Its structure block diagram is shown in
Figure 3.
Here, is the estimated angle, f is the operating frequency, Kp is the proportional gain, and is the angular frequency.
In order to adapt to the digital implementation, the transfer function in the time domain of Equation (14) must be transformed into the z domain:
State variables are defined as:
The state space equation can be obtained by deriving Equation (20) as:
Equation (21) provides the FVTSC function as follows:
Based on the above analysis, the structure diagram of the FVTSC is demonstrated in
Figure 4.
When the moving point converges on the sliding mode surface, the BEMF estimated
and
by the SMO is equivalent to:
3.3. Design of Third-Order ESO
Generally, in order to obtain the rotor position information, the arctangent function method is used:
Because the sliding mode control is accompanied by a high-frequency chattering in the sliding mode, there will be a high-frequency chattering phenomenon in the estimated BEMF. The rotor position estimation method based on the arctangent function directly introduces the chattering phenomenon into the division operation of the arctangent function, thus causing the error of angle estimation. In order to improve the estimation accuracy of the motor speed and rotor position information, this paper designed an ESO state equation to estimate motor speed and rotor position information so as to replace the traditional SMO method of obtaining rotor position information by an arctangent function. The specific implementation process is shown as follows:
For a system of the following form,
where
is the unknown nonlinear function in the system,
u(
t) is the control quantity of the system, and
,
, and
are state variables. Let
,
,
be the disturbance and
x3 be the expanded state variable, then the state equation is:
In the disturbance rejection control technology, the ESO can estimate the unknown disturbance in real time with high accuracy. The ESO is an idea that uses a state observer to expand unknown disturbance variables into new state variables and uses a special feedback mechanism to establish a new observer that can observe the expanded state. Its general form of expression is shown in Equation (27).
where
e is the deviation between the observed value
z1 and
x1,
z2 is the observer
x2,
z3 is the observed value of
x3,
a1,
a2 and
a3 are intermediate variables,
u is the control quantity, and
b is the compensation factor.
The characteristics of disturbance can be accurately observed with the ESO. The variables containing rotor position and speed information are taken as the disturbance quantity and the variables are observed to obtain the motor rotor position information. The rotor position realization block diagram based on the third-order ESO is shown in
Figure 5.
When
,
is considered valid, the following relationship can be obtained from
Figure 5:
According to the relationship between rotational speed and rotor position in the rotor motion equation shown in Equation (6), the state equation of the ESO with rotor position angle
θ as the main variable can be constructed as shown in Equation (29). Its structure diagram is shown in
Figure 6.
where
is the estimated electrical angular velocity,
J is the inertia,
p is the pole pairs,
TL is the load torque, and
Q is the total disturbance of the system.
Then, the closed-loop transfer function is:
where
β1,
β2, and
β3 are the coefficients of the third-order ESO, and
ωn is the bandwidth of the third-order ESO. In order to ensure the stability of the system, the three poles in the characteristic equation can be overlapped at the same point and arranged on the left half of the
s plane. The adjustable parameter
βi adopts the bandwidth-based configuration method so that
β1 = 3
ωn,
β2 = 3
ωn2,
β3 =
ωn3. According to the actual adjustment effect (dynamic response speed, steady-state accuracy) and using a reasonable selection of bandwidth, the reference range of
ωn is 100–1000 rad/s.
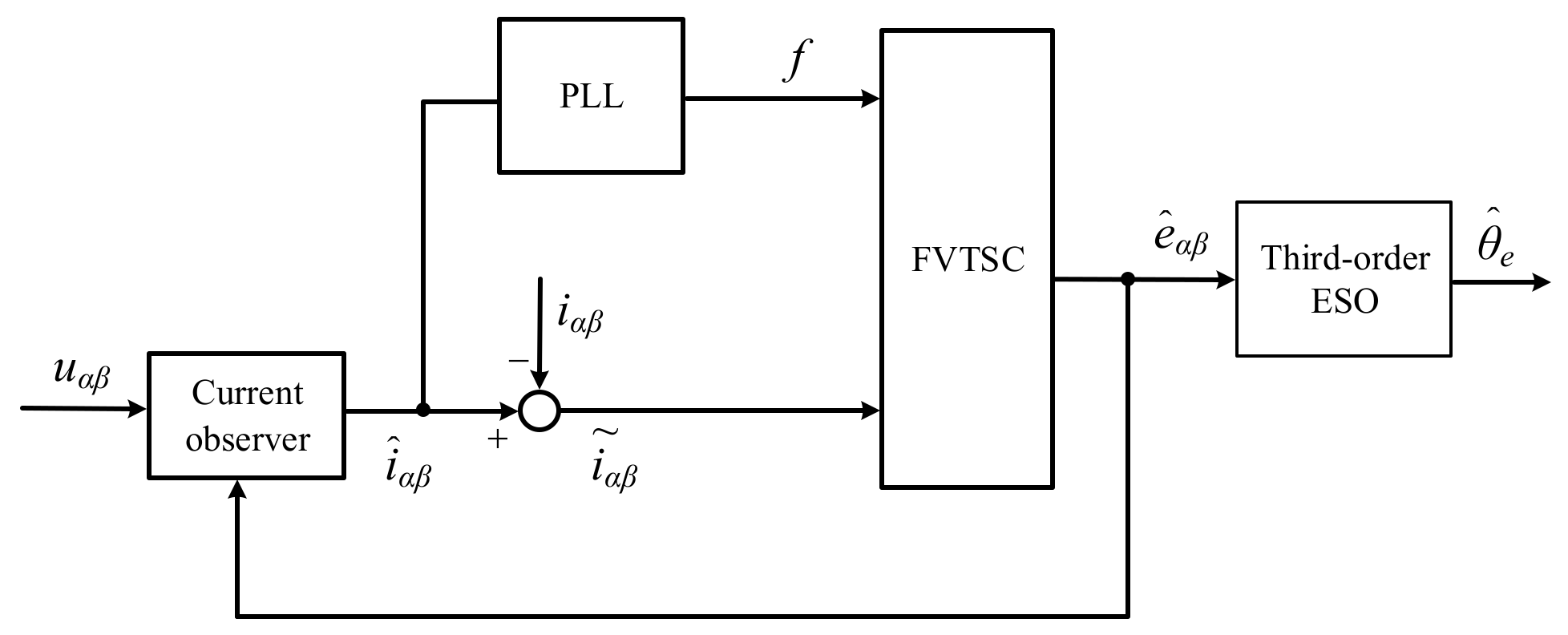
To summarize, the overall implementation block diagram of the new SMO is shown in
Figure 7. The estimated stator currents
and
are obtained by using the current observer and when compared with the measured values
iα and
iβ, the deviation values
,
of the stator current are obtained. Then, the deviation values
and
, together with the stator current frequency
f obtained through the PLL, are input into the FVTSC module to obtain the BEMF. Finally, the rotor position information is obtained through the third-order ESO module.
5. Experiment Study
To prove the accuracy and reliability of the six-phase PMSM control strategy in this study, a dual Y shift 30° six-phase PMSM with an isolated neutral point was taken as the research object. The six-phase motor parameters are shown in
Table 1. The experimental platform can be seen in
Figure 25.
The motor started with a 3 N·m load torque, and the given rotating speed was set to 500 r/min.
Figure 26 shows the motor speed and current waveform at 500 r/min, and
Figure 27 shows the motor speed and current waveform at 1000 r/min, from 500 r/min to 1000 r/min. As can be seen from
Figure 26 and
Figure 27, the phase current of the motor has a high sinusoidal degree, and the phase relationship conforms to the theoretical analysis. During the abrupt change of the motor speed, the phase current and rotor speed quickly returned to the steady state.
The waveforms of the estimated and actual rotor position of six-phase PMSM under 500 r/min steady-state operation and the experimental waveforms of the motor from 200 r/min to 1000 r/min are shown in
Figure 28 and
Figure 29, respectively, in which red represents the actual rotor position and blue represents the estimated rotor position of the improved SMO. The rotor position angle error waveforms at 500 r/min and rotor position error waveforms at the sudden change of rotation speed are shown in
Figure 30 and
Figure 31, respectively. From
Figure 28 and
Figure 31, we can see that the estimated angle can quickly and accurately track the rotor position, and that the rotor position error was ±0.06 rad, which demonstrated the feasibility of the SMO in this study.
6. Conclusions
In this paper, the mathematical model of the six-phase PMSM was established in the static coordinate system and the traditional sliding mode variable structure controls were improved by combining the FVTSC and the ESO. The problems of chattering, low estimation accuracy of the BEMF, and phase lag existing in the traditional SMO system were solved, and the ability to resist load disturbance was improved. Finally, simulation and experimental research was carried out and the results showed that the new detection and control strategies proposed in this paper could accurately estimate the rotor position, ensured that the motor had good dynamic performance, and the system had strong robustness when the motor parameters changed.
However, this paper ignored the multidimensional characteristics of the six-phase motor system; therefore, any future research directions should also include sensorless detection and control in the case of failure.