Finite-Time Adaptive Higher-Order SMC for the Nonlinear Five DOF Active Magnetic Bearing System
Abstract
:1. Introduction
- This work investigates an adaptive integral third-order SMC for five DOF AMB system under unknown bounded model uncertainties and time-varying harmonic disturbances;
- The proposed control law is formulated by employing an auxiliary input, which is the first-order derivative of the actual control input. The auxiliary input contains the discontinuous input, i.e., the signum function components of SMC is in the first-order derivative of the actual control input. As a result, the chattering problem is significantly reduced without compromising with the robustness, which is the case in the boundary layer technique;
- Unlike [34], the proposed approach implements two adaptive laws to relax the design assumption about a priori knowledge of upper bound of lumped disturbance;
- The system state trajectories are theoretically proved to be converging in finite-time under the proposed scheme;
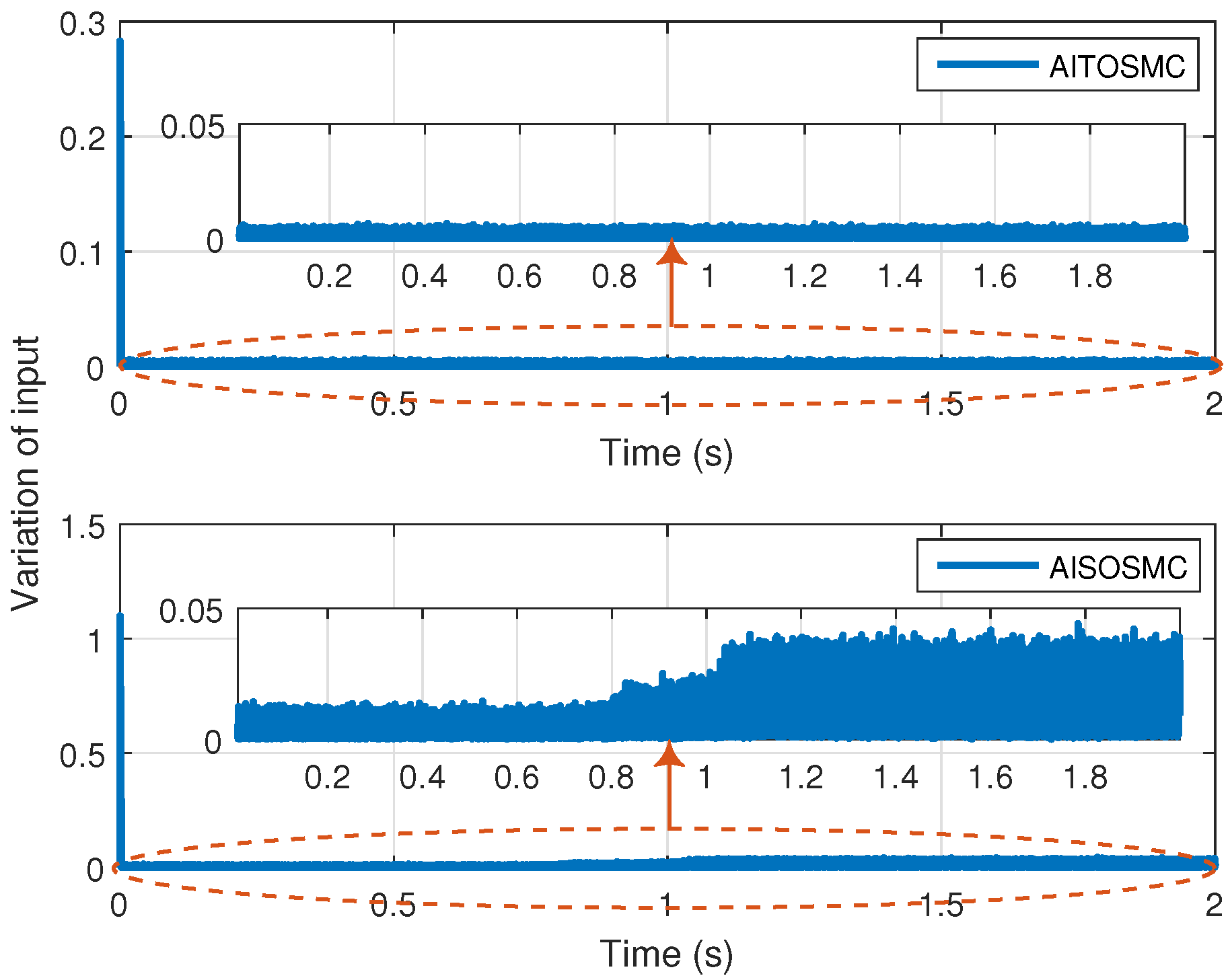
- The comparative simulation analysis illustrates the superiority of the proposed controller over the second order SMC and the PID control in terms of faster response and a significant reduction in the chattering.
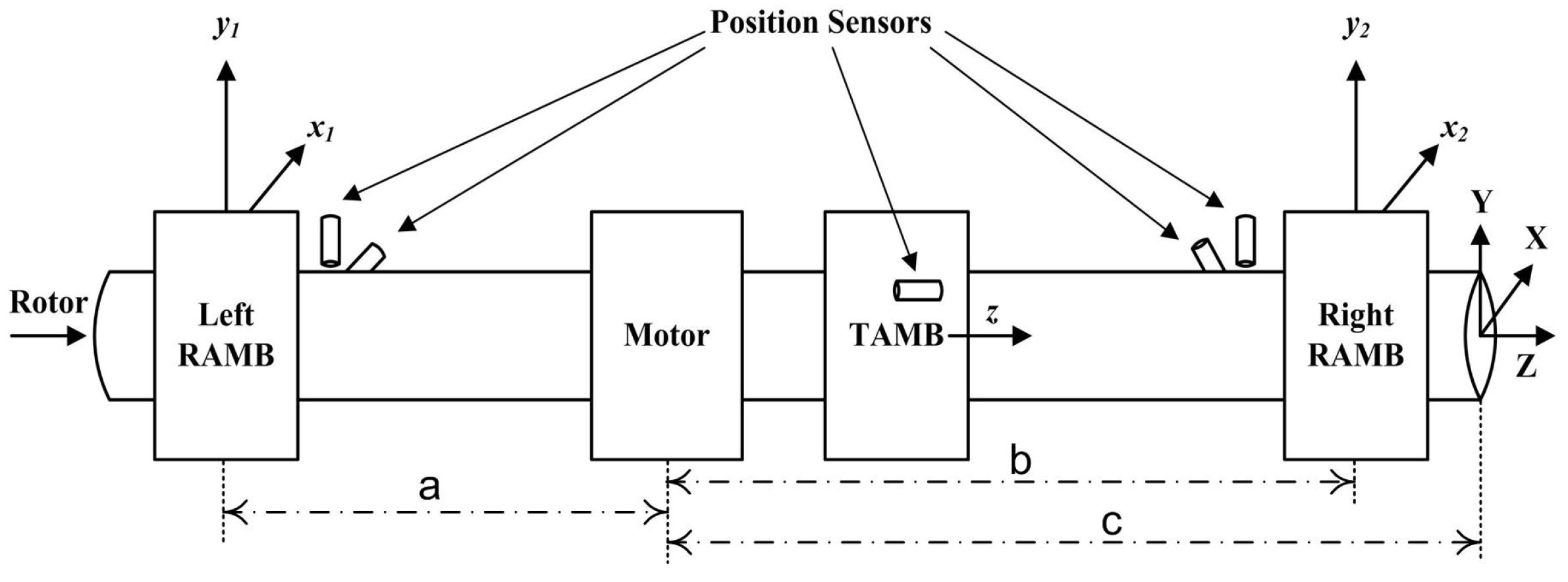
2. Modeling of the AMB System
Problem Statement
3. The Proposed Control Strategy
3.1. Problem Formulation
3.2. Proposed Control Design
4. Stability of the Closed-Loop System
5. Simulation Analysis With Comparative Study
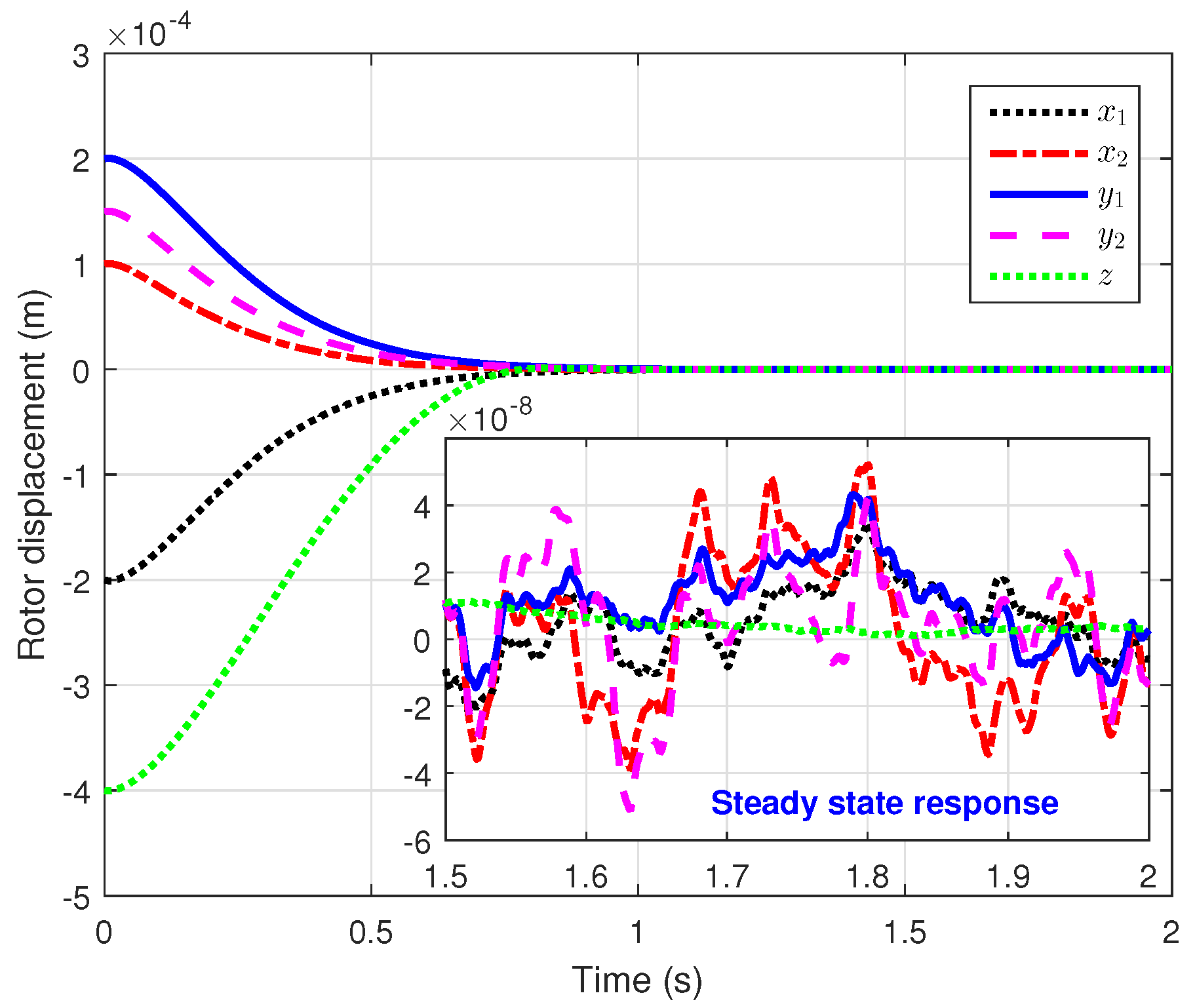
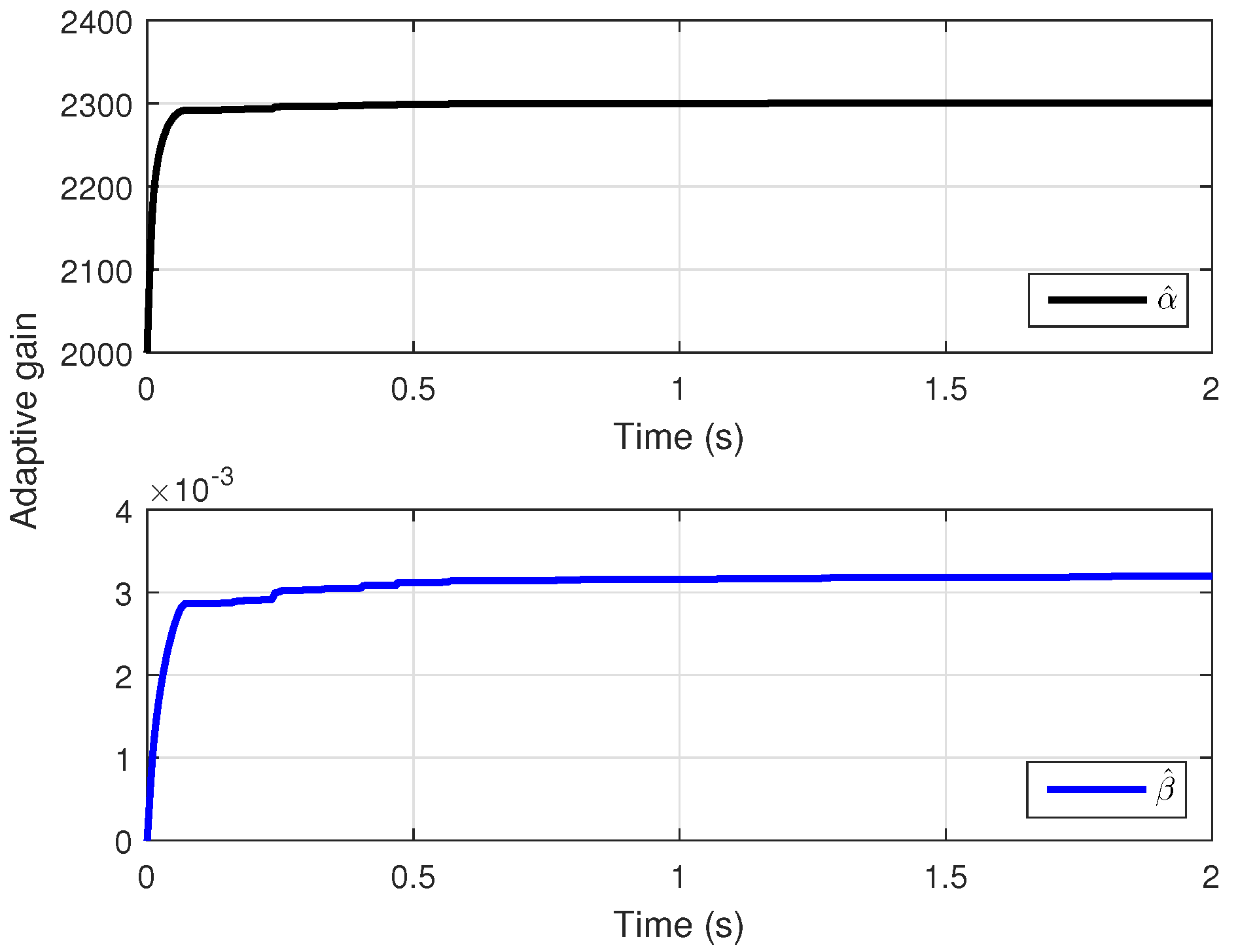
5.1. The Proposed AITOSMC Strategy
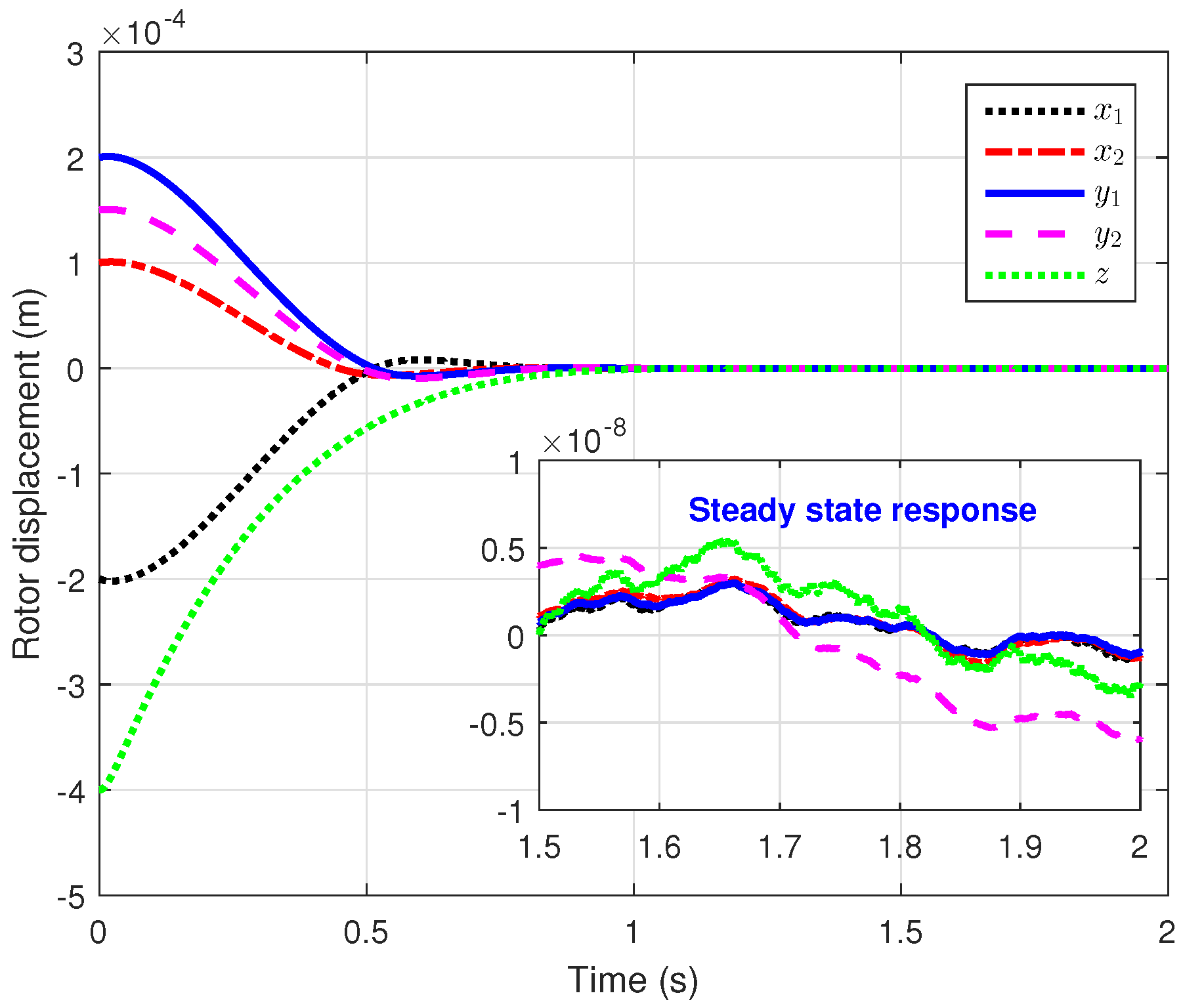
5.2. The AISOSMC Strategy
5.3. The PID Control Approach
5.4. Comparison between the Three Control Techniques
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bleuler, H.; Cole, M.; Keogh, P.; Larsonneur, R.; Maslen, E.; Okada, Y.; Schweitzer, G.; Traxler, A. Magnetic Bearings: Theory, Design, and Application to Rotating Machinery; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Saha, S.; Nabi, M. A review on active magnetic bearing and exploitation of parametric model order reduction. In Proceedings of the 2016 11th International Conference on Industrial and Information Systems (ICIIS), Roorkee, India, 3–4 December 2016; pp. 420–425. [Google Scholar]
- Saha, S.; Amrr, S.M.; Nabi, M.; Iqbal, A. Reduced Order Modeling and Sliding Mode Control of Active Magnetic Bearing. IEEE Access 2019, 7, 113324–113334. [Google Scholar] [CrossRef]
- Hutterer, M.; Schrödl, M. Control of active magnetic bearings in turbomolecular pumps for rotors with low resonance frequencies of the blade wheel. Lubricants 2017, 5, 26. [Google Scholar] [CrossRef] [Green Version]
- Han, B.; Liu, X.; Zheng, S. A novel integral 5-DOFs hybrid magnetic bearing with one permanent magnet ring used for turboexpander. Math. Probl. Eng. 2014, 2014, 18. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Zhu, C.; Wang, M.; Jiang, K. Vibration control for active magnetic bearing high-speed flywheel rotor system with modal separation and velocity estimation strategy. J. Vibroeng. 2015, 17, 757–775. [Google Scholar]
- Wan, L.; Yang, Z.; Sun, X.; Chen, Z.; Chen, L. Decoupling control of a 5-degree-of-freedom bearingless induction motor based on least squares support vector machine inverse. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef] [Green Version]
- Knospe, C.R. Active magnetic bearings for machining applications. Control Eng. Pract. 2007, 15, 307–313. [Google Scholar] [CrossRef]
- Wampler, R.K.; Lancisi, D.M. Active Magnetic Bearing System for Blood Pump. U.S. Patent 6,264,635, 3 December 1998. [Google Scholar]
- Burdet, L. Active Magnetic Bearing Design and Characterization for High Temperature Applications; Technical Report for EPFL; Epfl: Lausanne, Switzerland, 2006. [Google Scholar]
- Rajagopal, K.; Sivadasan, K. Low-stiction magnetic bearing for satellite application. J. Appl. Phys. 2002, 91, 6994–6996. [Google Scholar] [CrossRef]
- Pichot, M.; Kajs, J.; Murphy, B.; Ouroua, A.; Rech, B.; Hayes, R.; Beno, J.H.; Buckner, G.; Palazzolo, A. Active magnetic bearings for energy storage systems for combat vehicles. IEEE Trans. Magn. 2001, 37, 318–323. [Google Scholar] [CrossRef] [Green Version]
- Moon, F.C. Superconducting Levitation: Applications to Bearings and Magnetic Transportation; John Wiley & Sons: Weinheim, Germany, 2008. [Google Scholar]
- Turk, N.; Bulić, N.; Gruber, W. Nonlinear control of a bearingless flux-switching slice motor with combined winding system. IEEE/ASME Trans. Mechatron. 2019, 25, 152–163. [Google Scholar] [CrossRef]
- Polajžer, B.; Ritonja, J.; Štumberger, G.; Dolinar, D.; Lecointe, J.P. Decentralized PI/PD position control for active magnetic bearings. Electr. Eng. 2006, 89, 53–59. [Google Scholar] [CrossRef]
- Wei, C.; Söffker, D. Optimization strategy for PID-controller design of AMB rotor systems. IEEE Trans. Control Syst. Technol. 2015, 24, 788–803. [Google Scholar] [CrossRef]
- Chen, K.Y.; Tung, P.C.; Tsai, M.T.; Fan, Y.H. A self-tuning fuzzy PID-type controller design for unbalance compensation in an active magnetic bearing. Expert Syst. Appl. 2009, 36, 8560–8570. [Google Scholar] [CrossRef]
- Chang, L.Y.; Chen, H.C. Tuning of fractional PID controllers using adaptive genetic algorithm for active magnetic bearing system. WSEAS Trans. Syst. 2009, 8, 158–167. [Google Scholar]
- Ellis, G. Control System Design Guide: Using Your Computer to Understand and Diagnose Feedback Controllers; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- Nevaranta, N.; Jaatinen, P.; Vuojolainen, J.; Sillanpää, T.; Pyrhönen, O. Adaptive MIMO pole placement control for commissioning of a rotor system with active magnetic bearings. Mechatronics 2020, 65, 102313. [Google Scholar] [CrossRef]
- Geng, X.; Zhu, C. Sliding Mode Control Based on Linear Quadratic Regulator for an Active Magnetic Bearing Flexible Rotor Virtual Collocated System. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Cole, M.O.; Chamroon, C.; Keogh, P.S. H-infinity controller design for active magnetic bearings considering nonlinear vibrational rotordynamics. Mech. Eng. J. 2017, 4. [Google Scholar] [CrossRef] [Green Version]
- Saha, S.; Banerjee, A.; Amrr, S.M.; Nabi, M. Pseudospectral method-based optimal control for a nonlinear five degree of freedom active magnetic bearing system. Trans. Inst. Meas. Control 2021, 43, 1668–1679. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Edwards, C.; Spurgeon, S. Sliding Mode Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Jang, M.J.; Chen, C.L.; Tsao, Y.M. Sliding mode control for active magnetic bearing system with flexible rotor. J. Franklin Inst. 2005, 342, 401–419. [Google Scholar] [CrossRef]
- Nicola, M.; Nicola, C.I. Sensorless fractional order control of PMSM based on synergetic and sliding mode controllers. Electronics 2020, 9, 1494. [Google Scholar] [CrossRef]
- Kang, M.S.; Lyou, J.; Lee, J.K. Sliding mode control for an active magnetic bearing system subject to base motion. Mechatronics 2010, 20, 171–178. [Google Scholar] [CrossRef]
- Lin, F.J.; Chen, S.Y.; Huang, M.S. Intelligent double integral sliding-mode control for five-degree-of-freedom active magnetic bearing system. IET Control Theory Appl. 2011, 5, 1287–1303. [Google Scholar] [CrossRef]
- Yao, X.; Chen, Z. Sliding mode control with deep learning method for rotor trajectory control of active magnetic bearing system. Trans. Inst. Meas. Control 2019, 41, 1383–1394. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Xu, Q. Precision motion control of piezoelectric nanopositioning stage with chattering-free adaptive sliding mode control. IEEE Trans. Autom. Sci. Eng. 2016, 14, 238–248. [Google Scholar] [CrossRef]
- Bartolini, G.; Fridman, L.; Pisano, A.; Usai, E. Modern Sliding Mode Control Theory: New Perspectives and Applications; Springer: Cham, Switzerland, 2008. [Google Scholar]
- Kandil, M.S.; Dubois, M.R.; Bakay, L.S.; Trovao, J.P.F. Application of Second-Order Sliding-Mode Concepts to Active Magnetic Bearings. IEEE Trans. Ind. Electron. 2017, 65, 855–864. [Google Scholar] [CrossRef]
- Levant, A. Principles of 2-sliding mode design. Automatica 2007, 43, 576–586. [Google Scholar] [CrossRef] [Green Version]
- Boiko, I.M. Chattering in sliding mode control systems with boundary layer approximation of discontinuous control. Int. J. Syst. Sci. 2013, 44, 1126–1133. [Google Scholar] [CrossRef]
- Utkin, V. Discussion aspects of high-order sliding mode control. IEEE Trans. Autom. Control 2015, 61, 829–833. [Google Scholar] [CrossRef]
- Amrr, S.M.; Nabi, M. Finite-time fault tolerant attitude tracking control of spacecraft using robust nonlinear disturbance observer with anti-unwinding approach. Adv. Space Res. 2020, 66, 1659–1671. [Google Scholar] [CrossRef]
- Giap, V.N.; Huang, S.C.; Nguyen, Q.D.; Trinh, X.T. Time Varying Disturbance Observer Based on Sliding Mode Control for Active Magnetic Bearing System. In Proceedings of the 2nd Annual International Conference on Material, Machines and Methods for Sustainable Development (MMMS2020), Nha Trang, Vietnam, 12–15 November 2020; pp. 929–935. [Google Scholar]
- Amrr, S.M.; Banerjee, A.; Nabi, M. Time-Energy Efficient Finite Time Attitude Tracking Control of Spacecraft Using Disturbance Observer. IFAC-PapersOnLine 2020, 53, 5964–5969. [Google Scholar] [CrossRef]
- Levant, A. Homogeneity approach to high-order sliding mode design. Automatica 2005, 41, 823–830. [Google Scholar] [CrossRef]
- Davila, J.; Fridman, L.; Levant, A. Second-order sliding-mode observer for mechanical systems. IEEE Trans. Autom. Control 2005, 50, 1785–1789. [Google Scholar] [CrossRef]
- Slotine, J.-J.; Li, W. Applied Nonlinear Control; Prentice Hall: Hoboken, NJ, USA, 1991. [Google Scholar]
- Vo, A.T.; Kang, H.J. A chattering-free, adaptive, robust tracking control scheme for nonlinear systems with uncertain dynamics. IEEE Access 2019, 7, 10457–10466. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Yu, X. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer. IEEE Trans. Ind. Electron. 2012, 60, 160–169. [Google Scholar] [CrossRef]
- Amrr, S.M.; Nabi, M.; Tiwari, P.M. A fault-tolerant attitude tracking control of spacecraft using an anti-unwinding robust nonlinear disturbance observer. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 6005–6018. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Alanis, A.Y.; Munoz-Gomez, G.; Rivera, J. Nested High Order Sliding Mode Controller with Back-EMF Sliding Mode Observer for a Brushless Direct Current Motor. Electronics 2020, 9, 1041. [Google Scholar] [CrossRef]
- Merabet, A. Cascade second order sliding mode control for permanent magnet synchronous motor drive. Electronics 2019, 8, 1508. [Google Scholar] [CrossRef] [Green Version]
- Huynh, V.V.; Hoang, B.D. Second order sliding mode control design for active magnetic bearing system. In AETA 2015: Recent Advances in Electrical Engineering and Related Sciences; Springer: Cham, Switzerland, 2016; pp. 519–529. [Google Scholar]
- Chen, S.Y.; Lin, F.J. Robust nonsingular terminal sliding-mode control for nonlinear magnetic bearing system. IEEE Trans. Control Syst. Technol. 2010, 19, 636–643. [Google Scholar] [CrossRef]
- Chiang, H.K.; Fang, C.C.; Lin, W.B.; Chen, G.W. Second-order sliding mode control for a magnetic levitation system. In Proceedings of the 2011 8th Asian Control Conference (ASCC), Kaohsiung, Taiwan, 15–18 May 2011; pp. 602–607. [Google Scholar]
- Jain, S.; Mishra, J.P.; Talange, D. A robust control approach for magnetic levitation system based on super-twisting algorithm. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Kota Kinabalu, Malaysia, 31 May–3 June 2015; pp. 1–6. [Google Scholar]
- Wang, X.; Zhang, Y.; Gao, P. Design and Analysis of Second-Order Sliding Mode Controller for Active Magnetic Bearing. Energies 2020, 13, 5965. [Google Scholar] [CrossRef]
- Saha, S.; Amrr, S.M.; Nabi, M. Adaptive Second Order Sliding Mode Control for the Regulation of Active Magnetic Bearing. IFAC-PapersOnLine 2020, 53, 1–6. [Google Scholar] [CrossRef]
- Maslen, E.H.; Schweitzer, G. Magnetic Bearings: Theory, Design, and Application to Rotating Machinery; Springer: Cham, Switzerland, 2009. [Google Scholar]
- Sivrioglu, S. Adaptive backstepping for switching control active magnetic bearing system with vibrating base. IET Control Theory Appl. 2007, 1, 1054–1059. [Google Scholar] [CrossRef]
- Abooee, A.; Arefi, M.M. Robust finite-time stabilizers for five-degree-of-freedom active magnetic bearing system. J. Franklin Inst. 2019, 356, 80–102. [Google Scholar] [CrossRef]
- Lin, F.; Chen, S.; Huang, M. Tracking control of thrust active magnetic bearing system via hermite polynomial-based recurrent neural network. IET Electr. Power Appl. 2010, 4, 701–714. [Google Scholar] [CrossRef]
- Saidi, A.S. Investigation of Structural Voltage Stability in Tunisian Distribution Networks Integrating Large-Scale Solar Photovoltaic Power Plant. Int. J. Bifurc. Chaos 2020, 30, 2050259. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of homogeneous systems. In Proceedings of the 1997 American Control Conference, Albuquerque, NM, USA, 6 June 1997; Volume 4, pp. 2513–2514. [Google Scholar]
- Bhat, S.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Mondal, S.; Mahanta, C. Adaptive integral higher order sliding mode controller for uncertain systems. J. Control Theory Appl. 2013, 11, 61–68. [Google Scholar] [CrossRef]
- Taleb, M.; Plestan, F.; Bououlid, B. An adaptive solution for robust control based on integral high-order sliding mode concept. Int. J. Robust Nonlinear Control 2015, 25, 1201–1213. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Geometric homogeneity with applications to finite-time stability. Math. Control Signals Syst. 2005, 17, 101–127. [Google Scholar] [CrossRef] [Green Version]

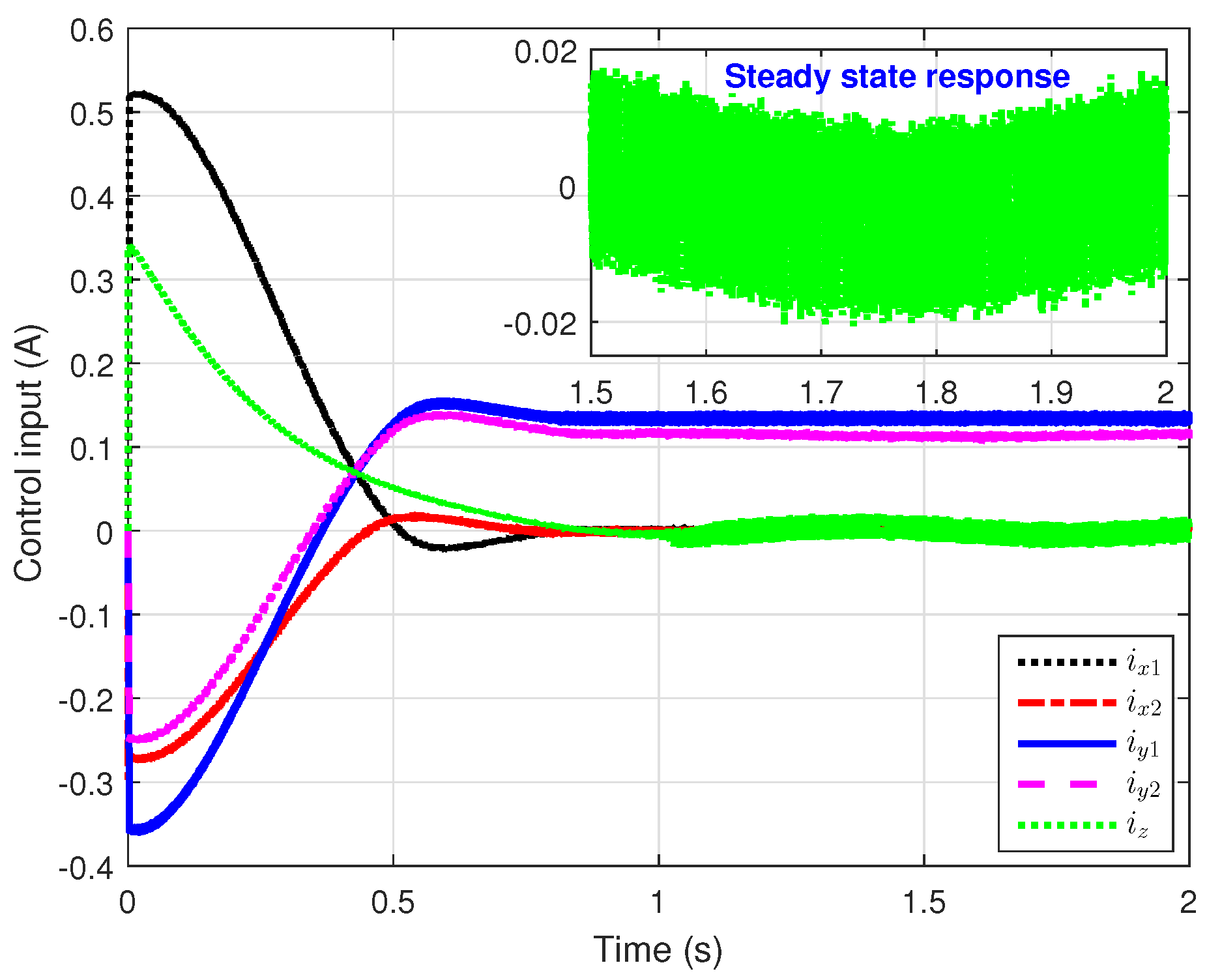
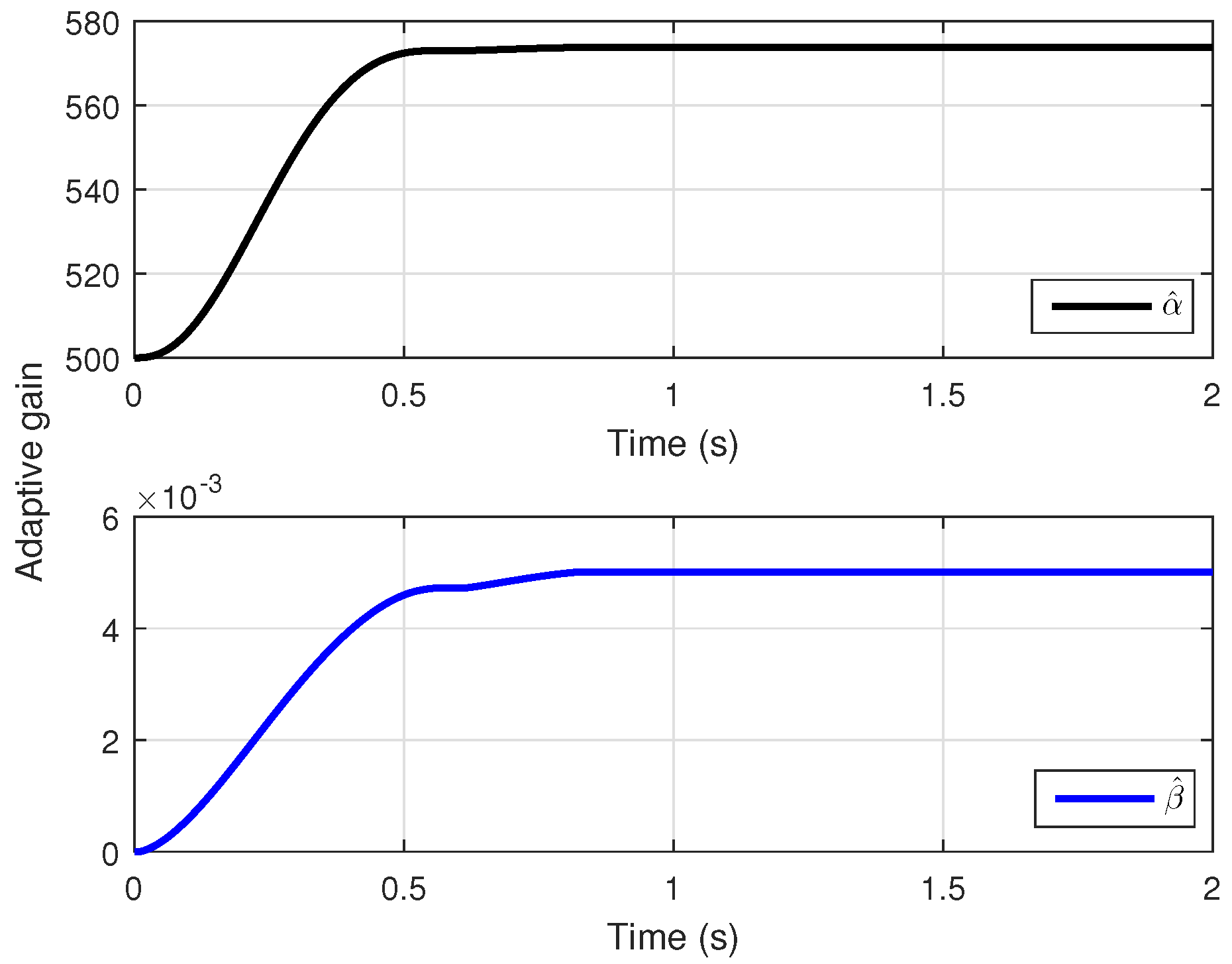
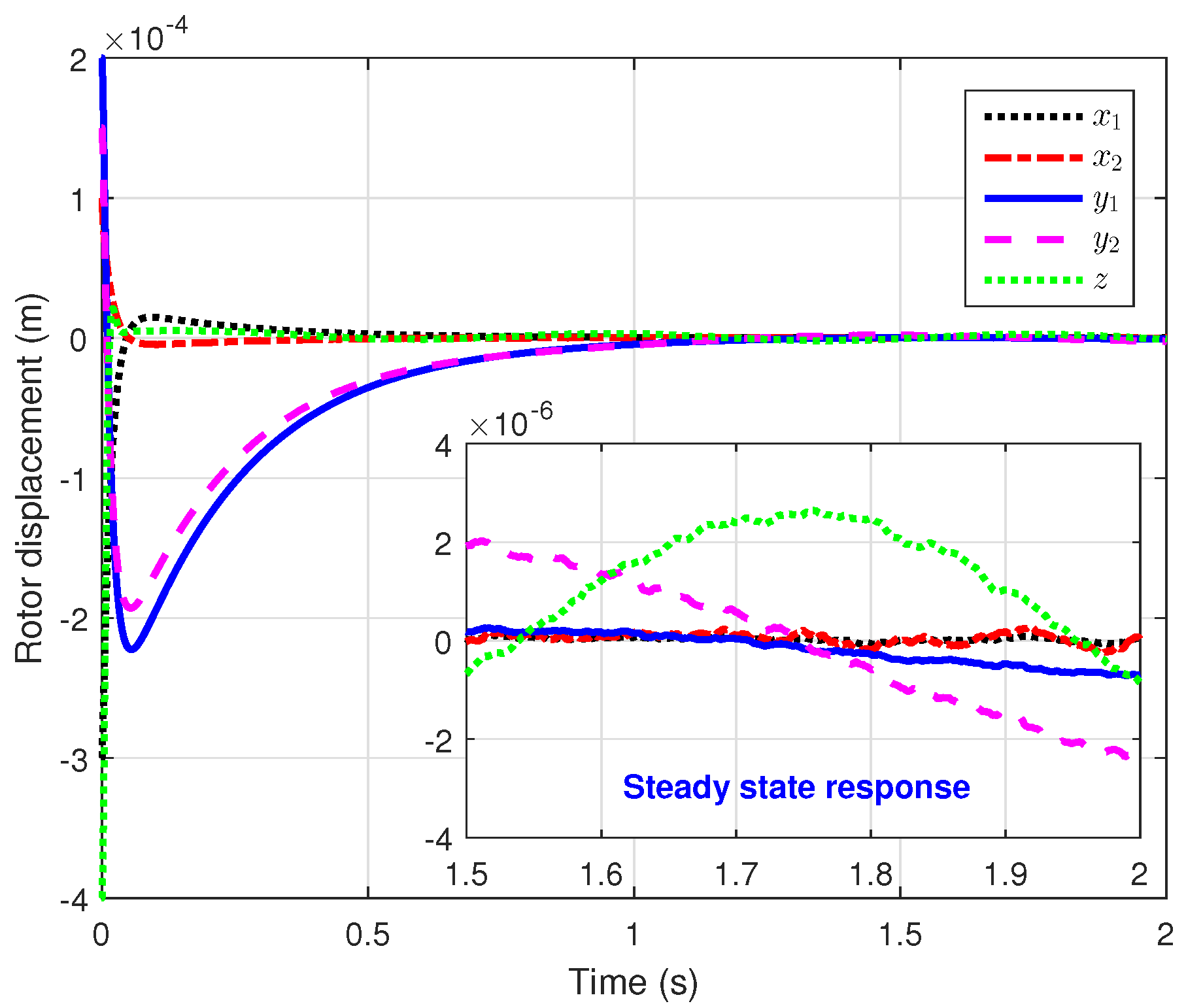
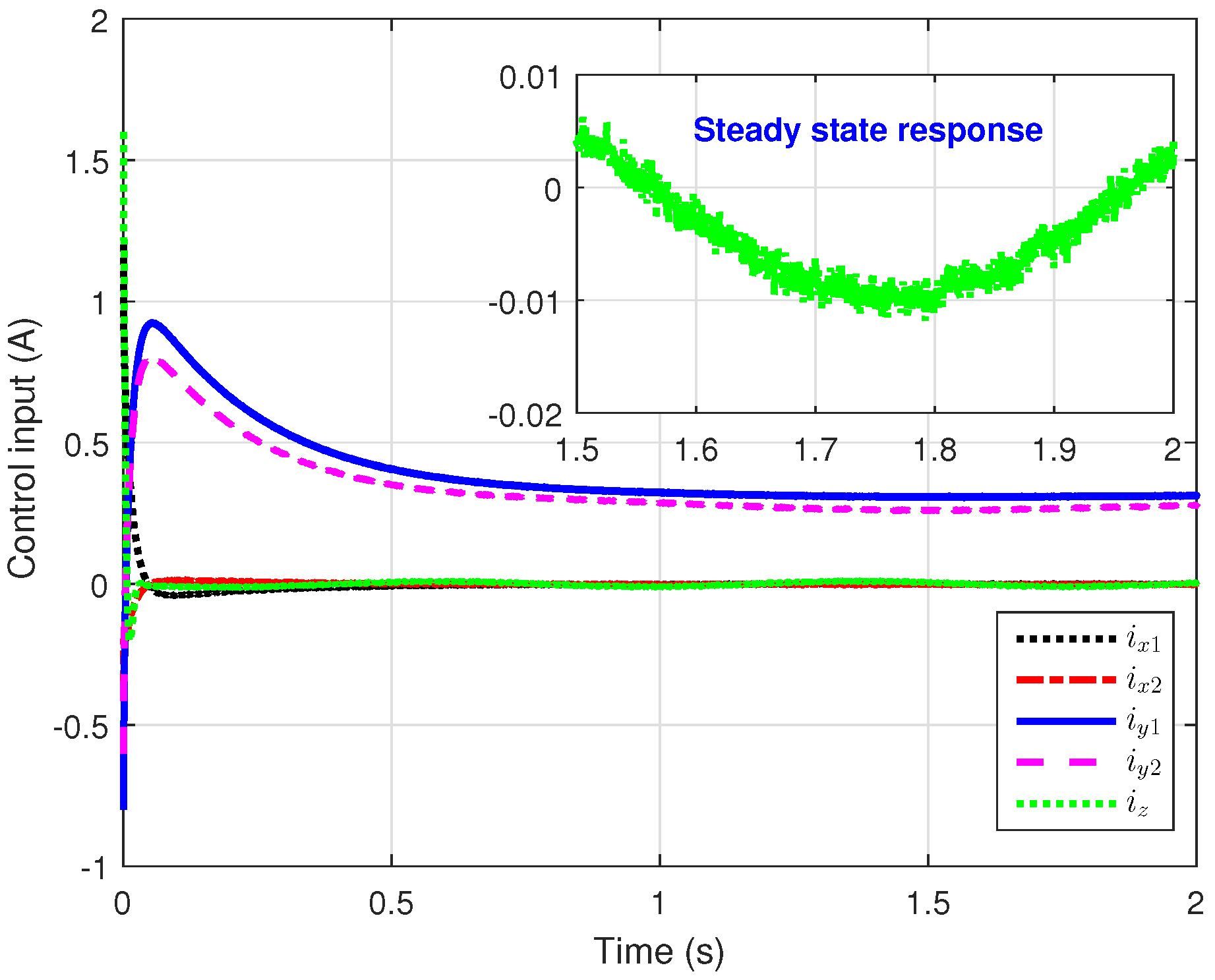
| Parameters | Value |
|---|---|
| Rotor (R) Mass () | 2.56478 kg |
| R Length () | 0.505 m |
| R Diameter (d) | 0.0166 m |
| R transverse mass moment of inertia about X and Y axis (J) | 0.04004 kg·m |
| R polar mass moment of inertia about Z axis () | 0.0006565 kg·m |
| Length between center of gravity and left RAMB () | 0.16 m |
| Length between center of gravity and right RAMB () | 0.19 m |
| Distance between left RAMB and right RAMB () | 0.35 m |
| Distance between center of gravity and end of rotor () | 0.263 m |
| Current stiffness for thrust AMB () | 40 N/A |
| Position stiffness for thrust AMB () | 36,000 N/m |
| Current stiffness for radial AMB () | 80 N/A |
| Position stiffness for thrust AMB () | 220,000 N/m |
| - |
| Control Schemes | Settling Time (s) | at Steady State | Order of Chattering | Total Variations |
|---|---|---|---|---|
| AITOSMC | ||||
| AISOSMC | ||||
| PID | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, S.; Amrr, S.M.; Saidi, A.S.; Banerjee, A.; Nabi, M. Finite-Time Adaptive Higher-Order SMC for the Nonlinear Five DOF Active Magnetic Bearing System. Electronics 2021, 10, 1333. https://doi.org/10.3390/electronics10111333
Saha S, Amrr SM, Saidi AS, Banerjee A, Nabi M. Finite-Time Adaptive Higher-Order SMC for the Nonlinear Five DOF Active Magnetic Bearing System. Electronics. 2021; 10(11):1333. https://doi.org/10.3390/electronics10111333
Chicago/Turabian StyleSaha, Sudipta, Syed Muhammad Amrr, Abdelaziz Salah Saidi, Arunava Banerjee, and M. Nabi. 2021. "Finite-Time Adaptive Higher-Order SMC for the Nonlinear Five DOF Active Magnetic Bearing System" Electronics 10, no. 11: 1333. https://doi.org/10.3390/electronics10111333
APA StyleSaha, S., Amrr, S. M., Saidi, A. S., Banerjee, A., & Nabi, M. (2021). Finite-Time Adaptive Higher-Order SMC for the Nonlinear Five DOF Active Magnetic Bearing System. Electronics, 10(11), 1333. https://doi.org/10.3390/electronics10111333






