Anti-Disturbance Fault-Tolerant Sliding Mode Control for Systems with Unknown Faults and Disturbances
Abstract
1. Introduction
2. System Description
3. Composite Observer Design
3.1. FDO Design
3.2. DO Design
3.3. Performance Analysis of Error System
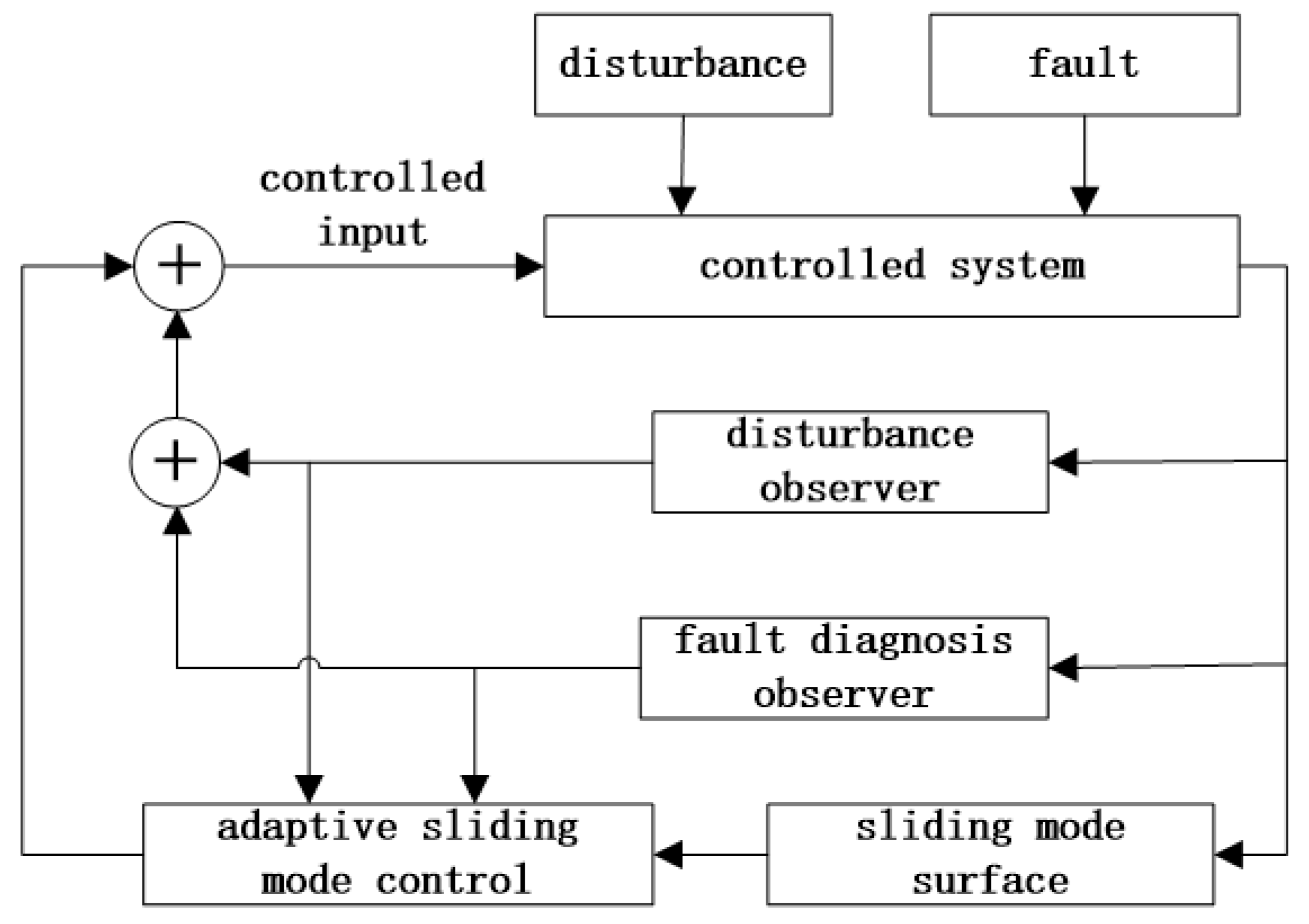
4. Controller Design and Dynamical Performance Analysis
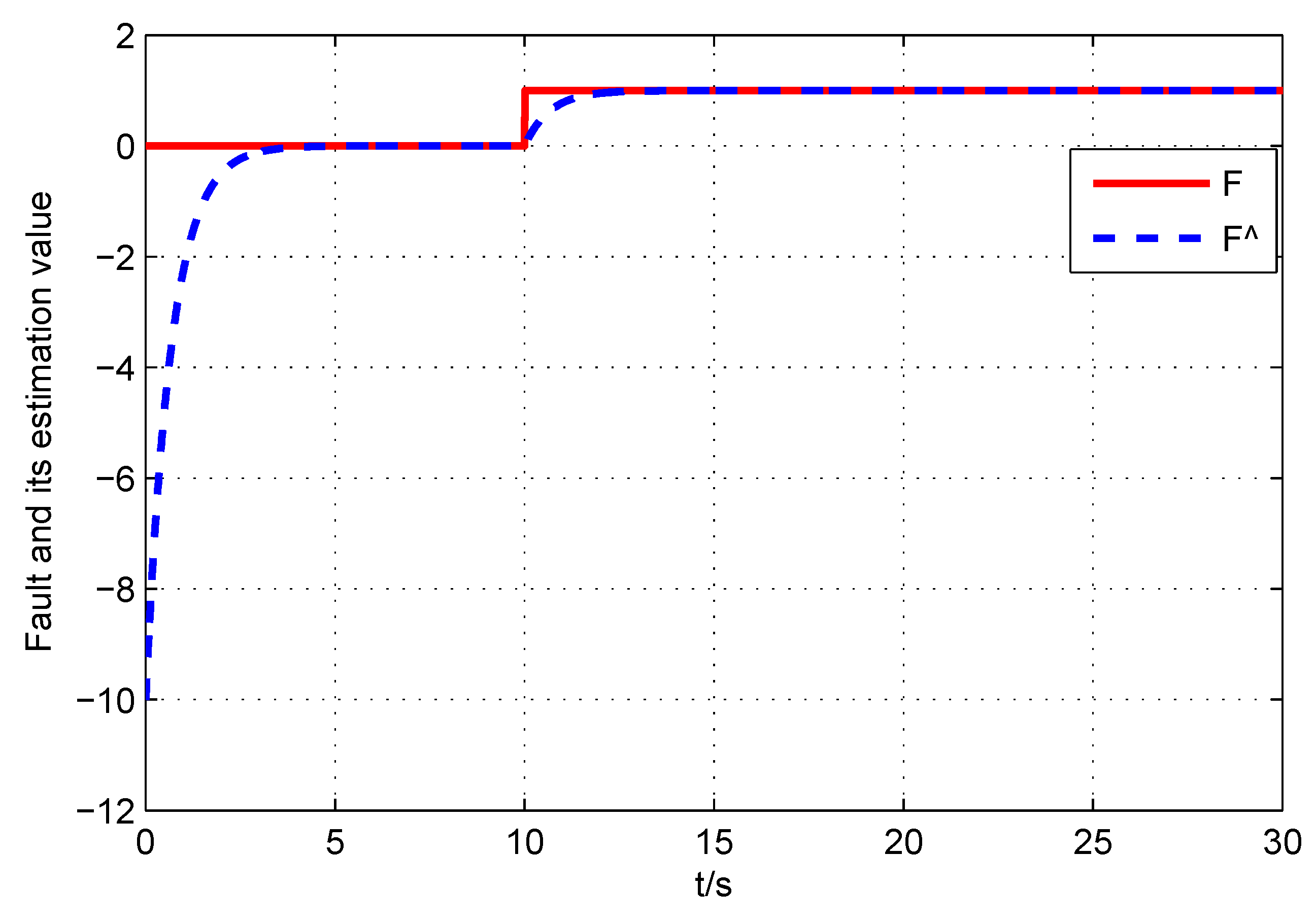
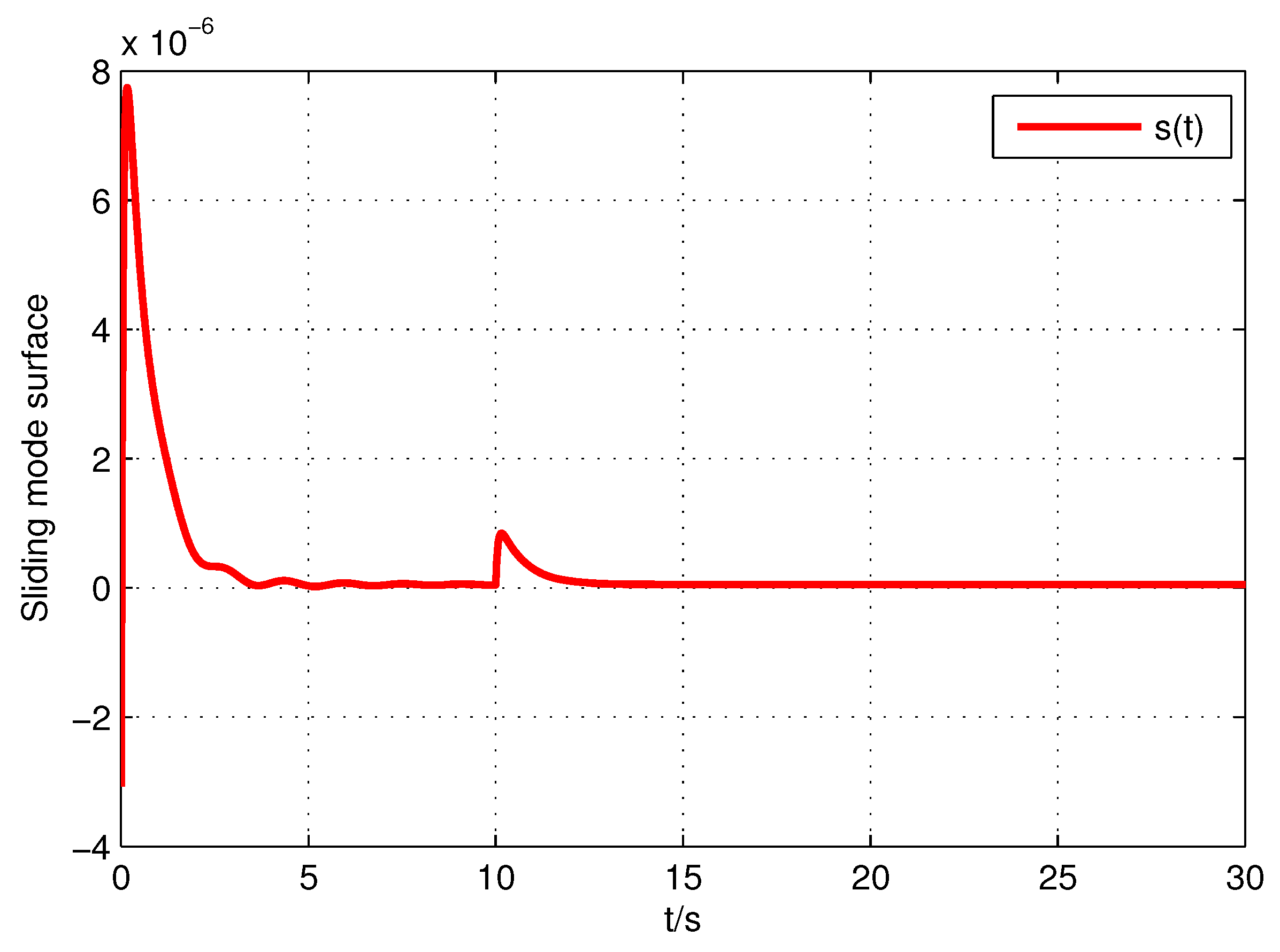
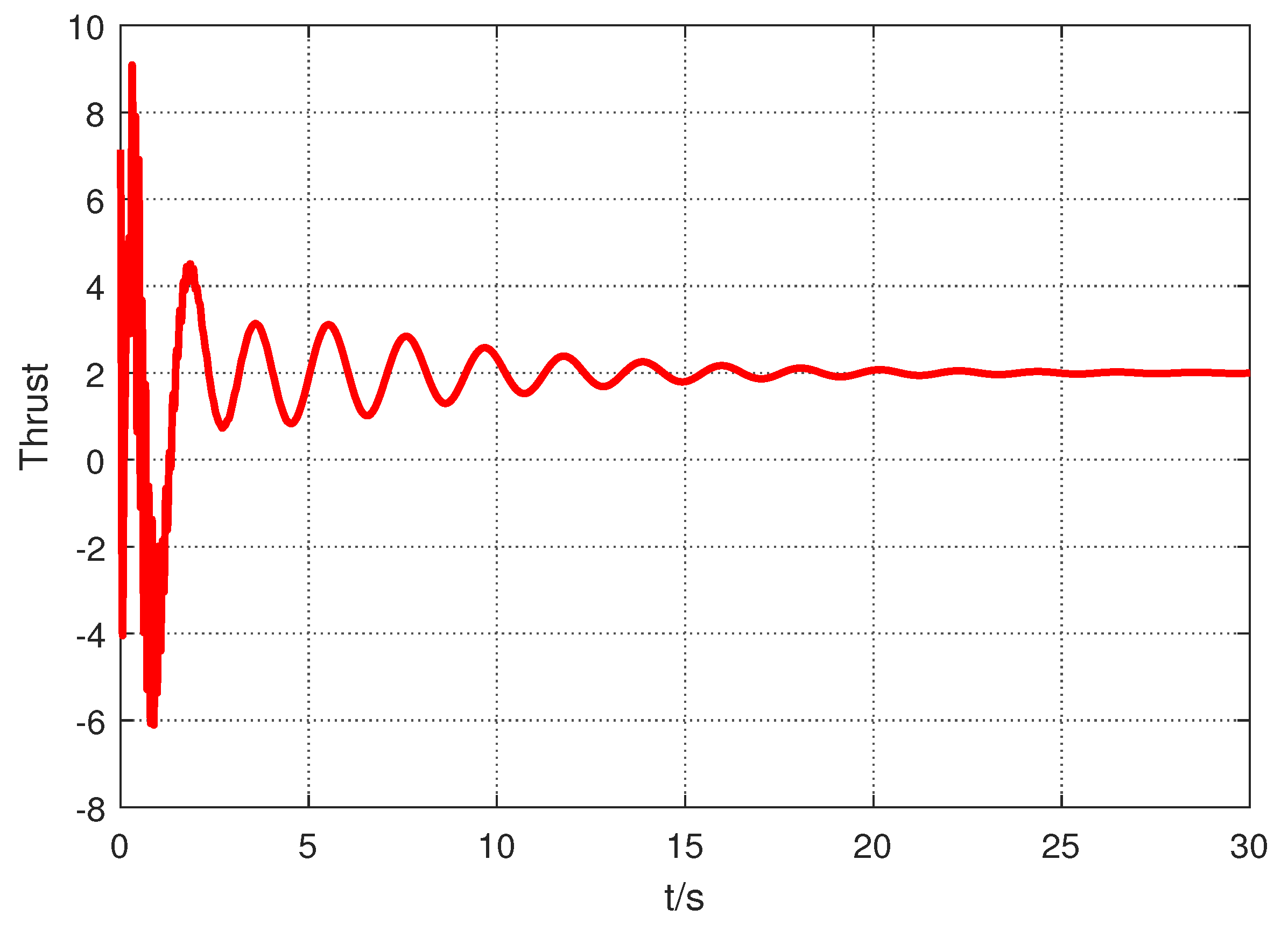
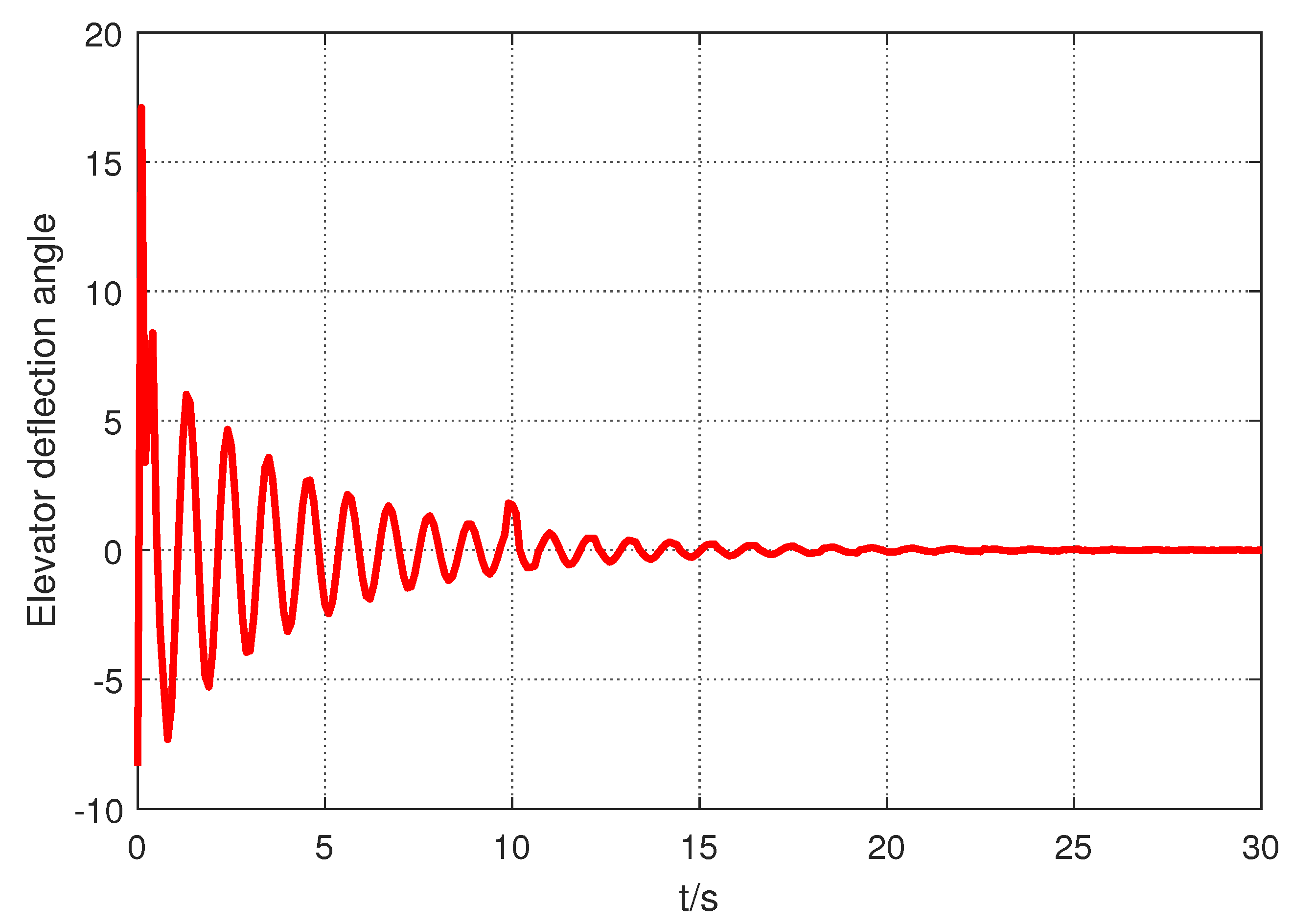
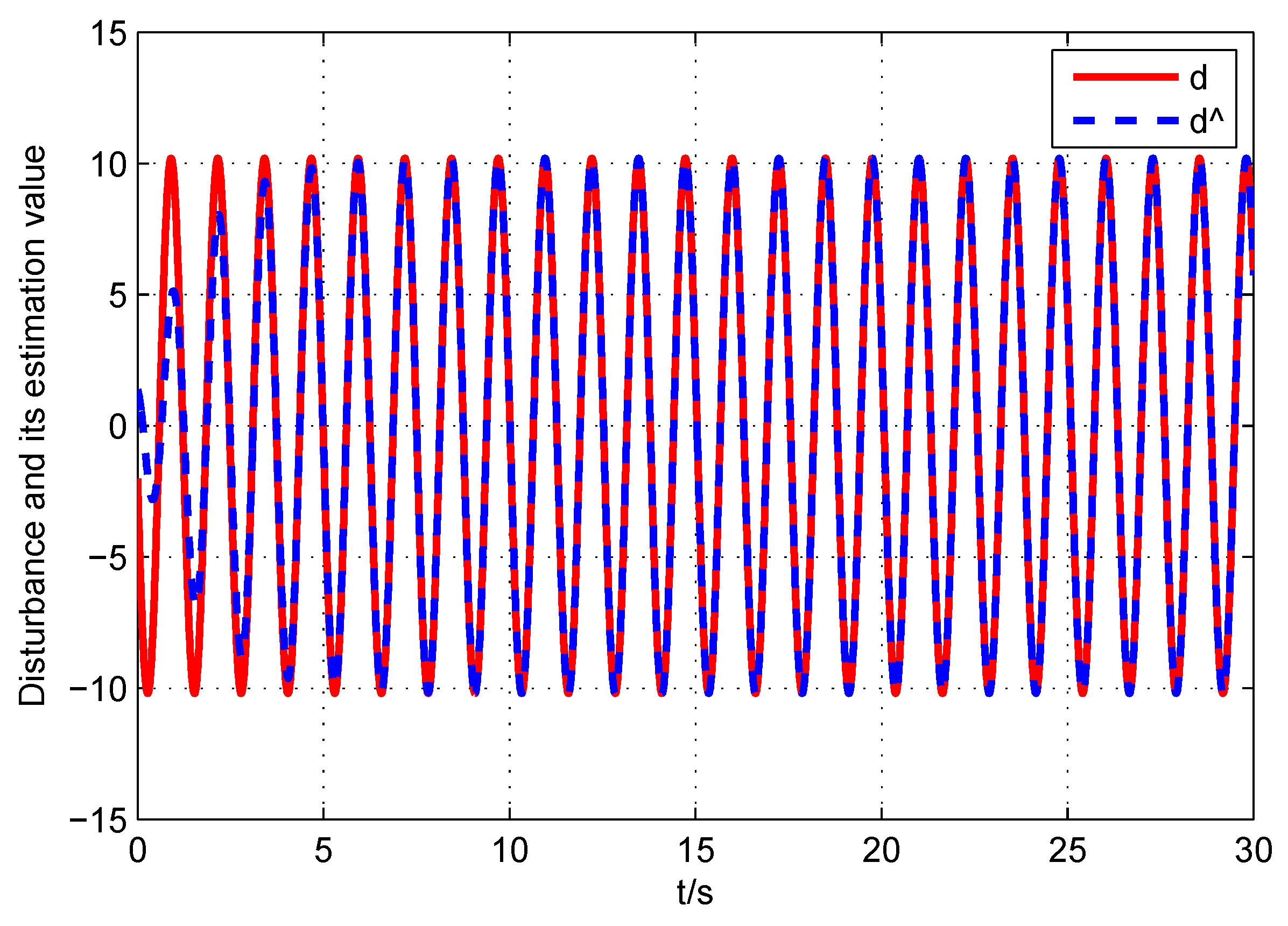
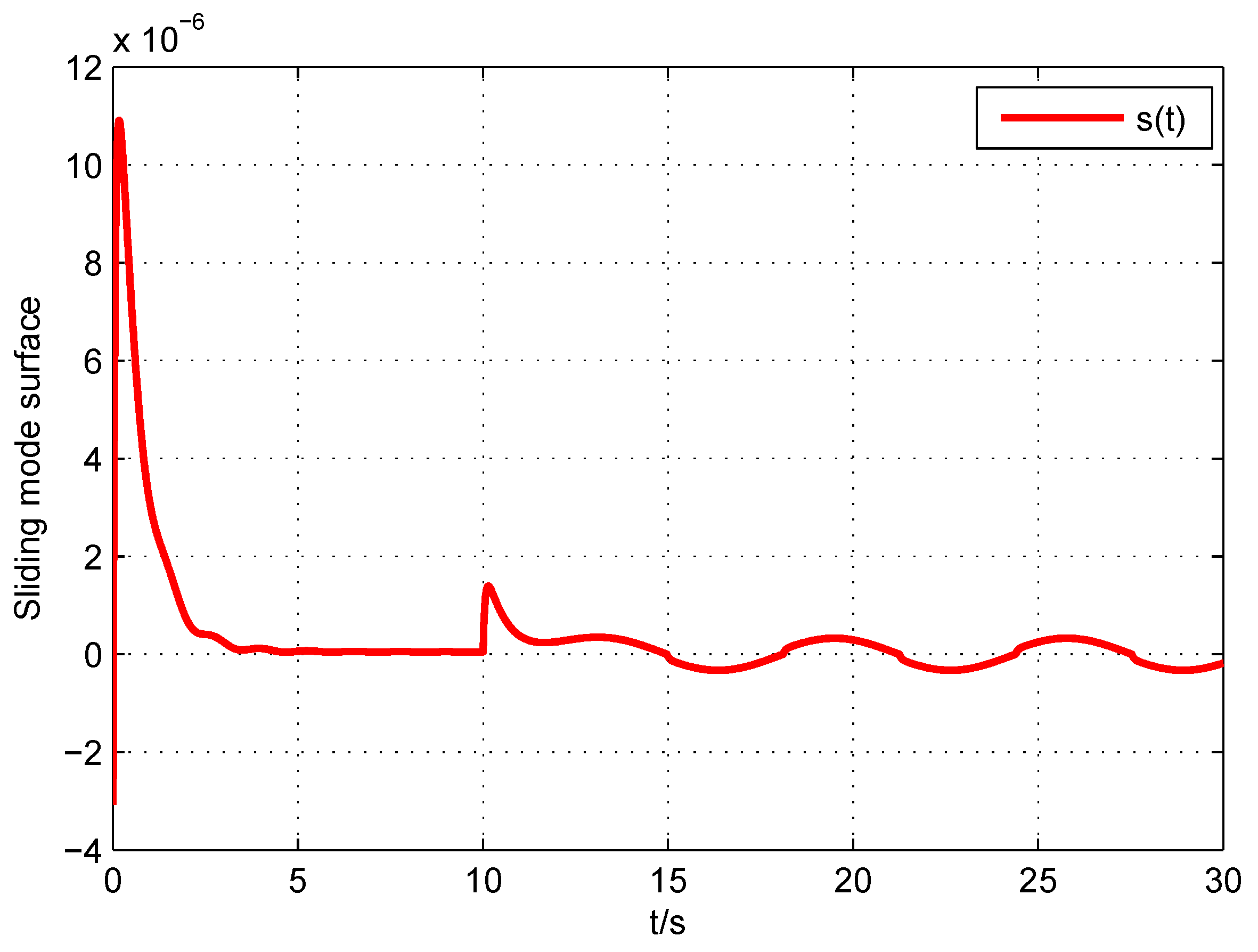
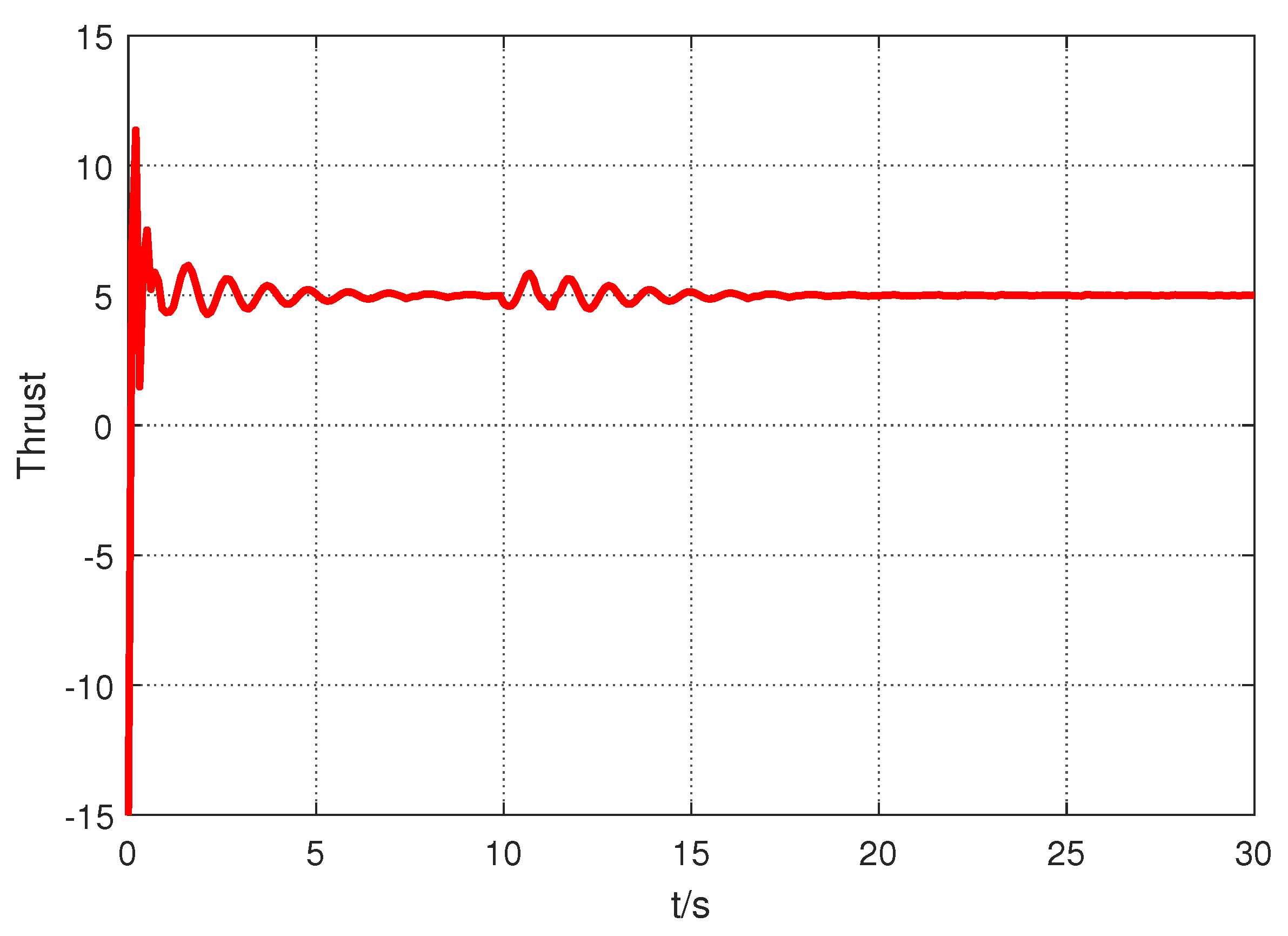
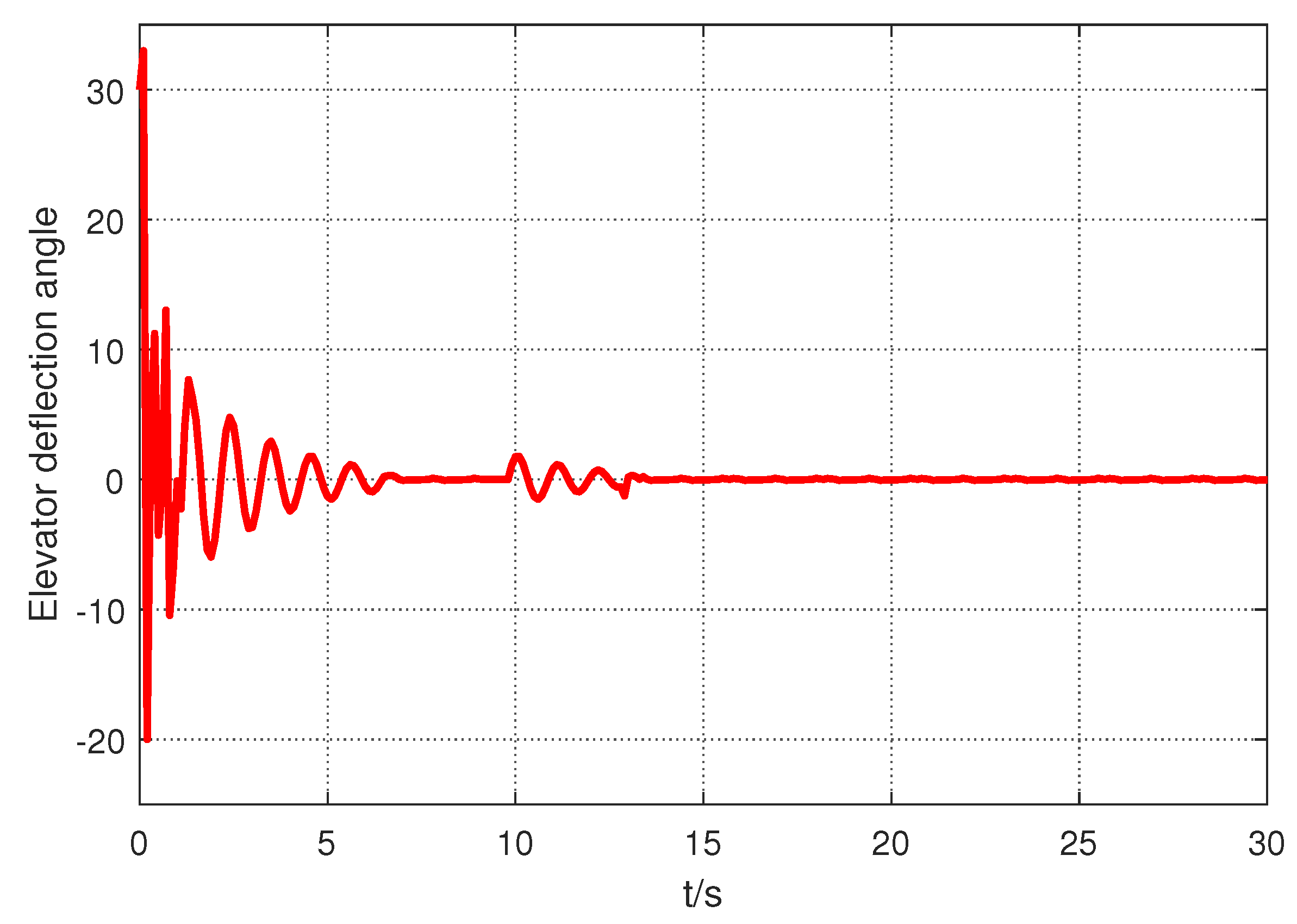
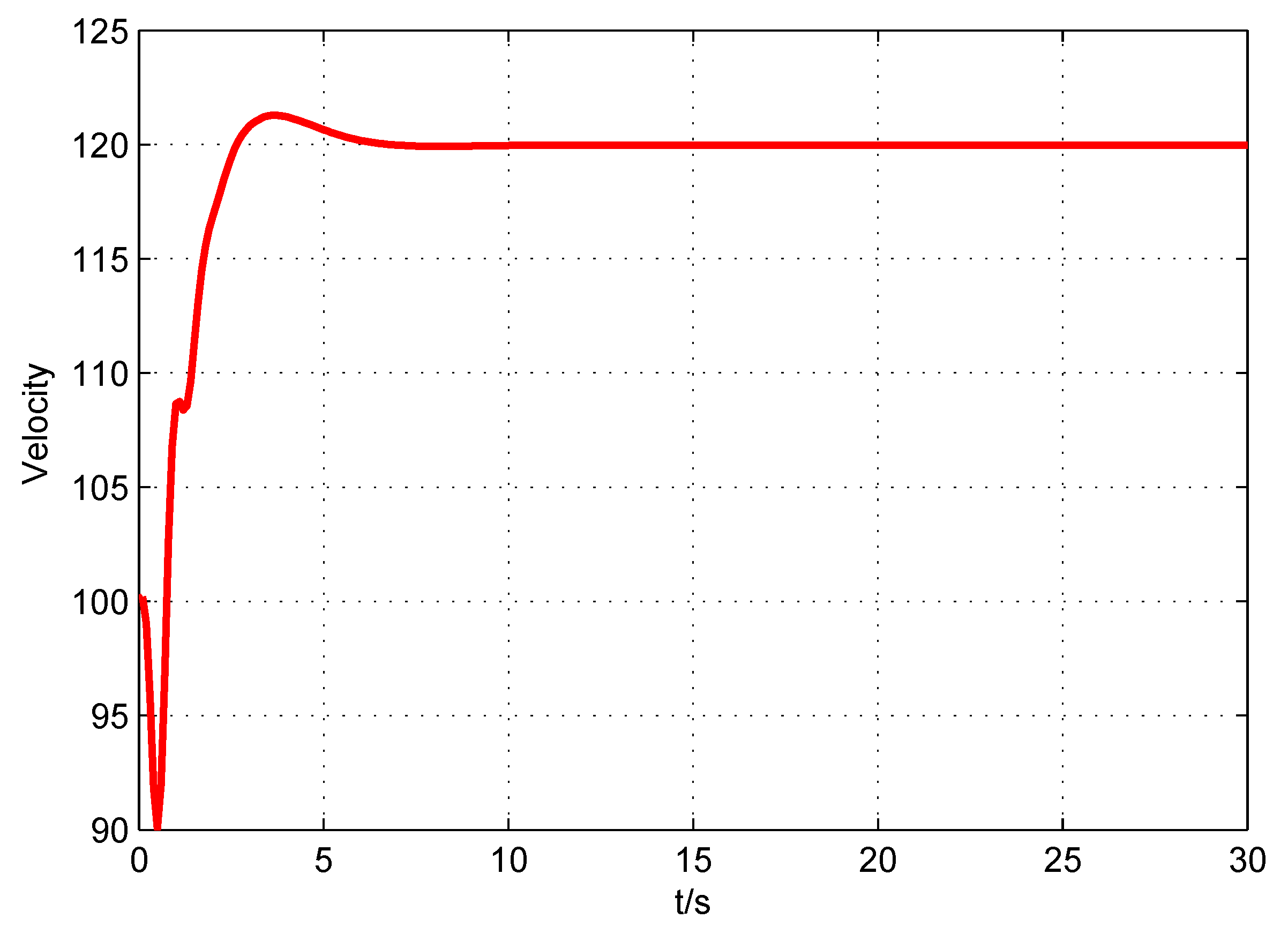
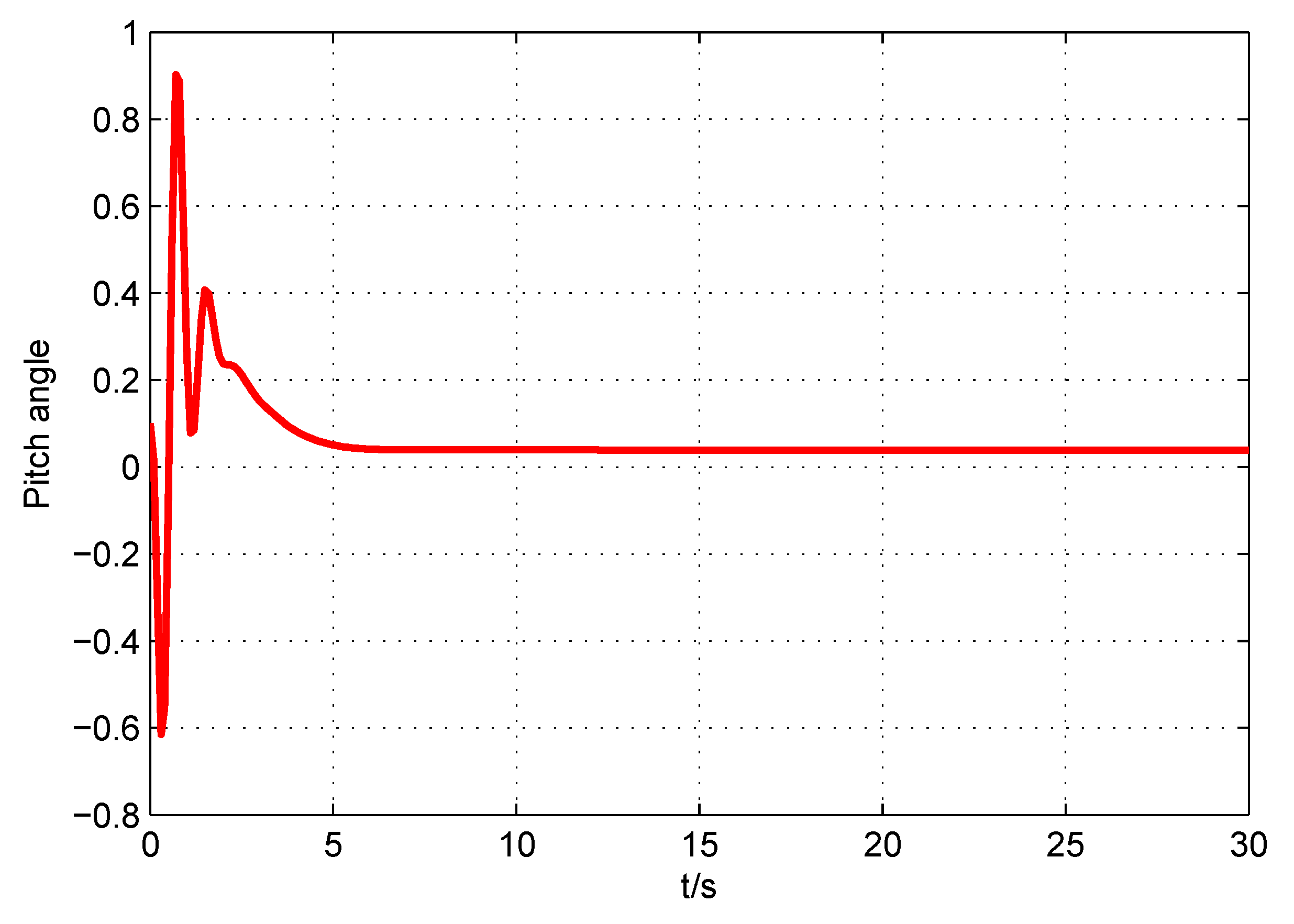
5. Numerical Illustrations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guo, L.; Cao, S.Y. Anti-disturbance Control for Systems with Multiple Disturbances; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Bittar, A.; Sales, R.M. H-2 and H-infinity control for MagLev vehicles. IEEE Control Syst. Mag. 1998, 18, 18–25. [Google Scholar]
- Li, Y.K.; Sun, H.B.; Zong, G.D. Disturbance-observer-based-control and L2-L∞ rsilient control for Markvian jump nonlinear systems with multiple disturbances and its application to single robot arm system. IET Control Theory Appl. 2016, 10, 226–233. [Google Scholar] [CrossRef]
- Gao, Z. Active disturbance rejection control for nonlinear fractionalorder systems. Int. J. Robust Nonlin. Control 2016, 26, 876–892. [Google Scholar] [CrossRef]
- Wu, Z.H.; Guo, B.Z. Approximate decoupling and output tracking for MIMO nonlinear systems with mismatched uncertainties via ADRC approach. J. Franklin Inst. 2018, 355, 3873–3894. [Google Scholar] [CrossRef]
- Isidori, A.; Byrnes, C.I. Output regulation of nonlinear systms. IEEE Trans. Autom. Control 1990, 35, 131–140. [Google Scholar] [CrossRef]
- Morawiec, M. The adaptive backstepping control of permanent magnet synchronous motor supplied by current source inverter. IEEE Trans. Ind. Inf. 2013, 8, 1047–1055. [Google Scholar] [CrossRef]
- Abdel-Rady, Y.; Mohamed, I. Design and implementation of a robust current-control scheme for a PMSM vector drive with a simple adaptive disturbance observer. IEEE Trans. Ind. Electron. 2007, 54, 1981–1988. [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Zhao, Z.H. Robust control of uncertain nonlinear systems: A nonlinear DOBC approach. J. Dyn. Syst. Meas. Control 2016, 138, 823–828. [Google Scholar] [CrossRef]
- Wang, X.Y.; Li, S.H.; Yu, X.H.; Yang, J. Distributed active anti-disturbance consensus for leader-follower higher-order multi-agent systems with mimatched disturbances. IEEE Trans. Autom. Control 2017, 62, 5795–5801. [Google Scholar] [CrossRef]
- Yang, J.; Cui, H.Y.; Li, S.H.; Zolotas, A. Optimized active disturbance rejection control DC-DC buck converters with uncertainties using a reduced-order GPI observer. IEEE Trans. Circuits Syst. I Reg. Papers 2018, 65, 832–841. [Google Scholar] [CrossRef]
- Liu, C.; Chen, W.H.; Andrews, J. Tracking control of small-scale helicopers using explicit nonlinear MPC augment with disturbance observers. Control Eng. Pract. 2012, 20, 258–268. [Google Scholar] [CrossRef]
- Yang, J.; Su, J.Y.; Li, S.H.; Yu, X.H. High-Order Mismatched Disturbance Compensation for Motion Control Systems Via a Continuous Dynamic Sliding-Mode Approach. IEEE Trans. Ind. Inform. 2014, 10, 604–614. [Google Scholar] [CrossRef]
- Hamayun, M.T.; Edwards, C.; Alwi, H. A fault tolerant control allocation scheme with output integral sliding modes. Automatica 2013, 49, 1830–1837. [Google Scholar] [CrossRef]
- Liu, J.; Vazquez, S.; Wu, L.; Marquez, A.; Gao, H.; Franquelo, L.G. Extended state observer-based sliding -mode control for three-phase power converters. IEEE. Trans. Ind. Election. 2017, 64, 22–31. [Google Scholar] [CrossRef]
- Tapia, A.; Bernal, M.; Fridman, L. Nonlinear sliding mode control design: An LMI approach. Syst. Control Lett. 2017, 104, 38–44. [Google Scholar] [CrossRef]
- Wu, L.; Gao, Y.; Liu, J.; Li, H. Event-triggered sliding mode control of stochastic systems via output feedback. Automatica 2017, 82, 79–92. [Google Scholar] [CrossRef]
- Yang, C.S.; Ni, S.F.; Dai, Y.C.; Huang, X.N.; Zhang, D.D. Anti-disturbance finite-time adaptive sliding mode backstepping control for PV inverter in master-slave-organized islanded microgrid. Energies 2020, 13, 4490. [Google Scholar] [CrossRef]
- Zhu, W.W.; Chen, D.B.; Du, H.B.; Wang, X.Y. Position control for permanent magnet synchronous motor based on neural network and terminal sliding mode control. Trans. Inst. Meas. Control 2020, 42, 1632–1640. [Google Scholar] [CrossRef]
- Lee, J.; Chang, P.H.; Jin, M. Adaptive integral sliding mode control with time-delay estimation for robot manipulators. IEEE Trans. Ind. Electron. 2017, 64, 6796–6804. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Yu, X. Sliding mode control for systems with mismatched uncertainties via a disturbance observer. IEEE Trans. Ind. Electron. 2013, 60, 160–169. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.H. Disturbance Observer-Based Control: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Thanh, H.L.N.N.; Vu, M.T.; Mung, N.X.; Nguyen, N.P.; Phuong, N.T. Perturbation observer-based robust control using a multiple sliding surfaces for nonlinear systems with influences of matched and unmatched uncertainties. Mathematics 2020, 8, 1371. [Google Scholar] [CrossRef]
- Vu, M.T.; Le, T.-H.; Thanh, H.L.N.N.; Huynh, T.-T.; Van, M.; Hoang, Q.-D.; Do, T.D. Robust position control of an over-actuated underwater vehicle under model uncertainties and ocean current effects using dynamic sliding mode surface and optimal allocation control. Sensors 2021, 21, 747. [Google Scholar] [CrossRef] [PubMed]
- Vu, M.T.; Thanh, H.L.N.N.; Huynh, T.-T.; Duc, T.; Hoang, Q.-D.; Le, T.-H. Station-keeping control of a hovering over-actuated autonomous underwater vehicle under ocean current effects and model uncertainties in horizontal plane. IEEE Access 2021, 9, 6855–6867. [Google Scholar] [CrossRef]
- Du, D.S.; Jiang, B.; Shi, P. Fault Tolerant Control for Control for Switched Linear Systems; Springer: London, UK, 2005. [Google Scholar]
- Blanke, M.; Kinnaert, M.; Lunze, M.; Staroswiecki, M. Diagnosis and Fault-Tolerant Control; Springer: London, UK, 2006. [Google Scholar]
- Li, B.; Hu, Q.; Ma, G.; Yang, Y. Fault Tolerant Attitude Stabilization Incorporating Closed-loop Control Allocation under Actuator Failure. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1989–2000. [Google Scholar] [CrossRef]
- Li, L.L.; Luo, H.; Ding, S.X.; Yang, Y.; Peng, K.X. Performance-based fault detection and fault-tolerant control for automatic control systems. Automatica 2019, 99, 308–316. [Google Scholar] [CrossRef]
- Cho, S.; Gao, Z.; Moan, T. Model-based fault detcetion, fault isolation and fault-tolerant control of a blade pitch system in floating wind turbines. Renew. Energy 2018, 120, 306–321. [Google Scholar] [CrossRef]
- Li, Q.; Yuan, J.P.; Sun, C. Robust fault-tolerant saturated control for spacecraft proximity operations with actuator saturations and faults. Adv. Space Res. 2018, 63, 1541–1553. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, X.; Ren, Z.; Cooper, J. Fault-tolerant control for commercial aircraft with actuator faults and constraints. J. Franklin Inst. 2019, 356, 3849–3868. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Guo, L.; Wang, H. Robust filtering for fault tolerant control using output PDFs of non-Gaussian systems. IET Theory Appl. 2007, 1, 636–645. [Google Scholar] [CrossRef]
- Spong, M.W. On the robust control of robot Manipulators. IEEE Trans. Autom. Control 1992, 37, 1782–1786. [Google Scholar] [CrossRef]
- Ducard, G.J. Fault-Tolerant Flight Control and Guidance Systems: Practical Methods for Small Unmanned Aerial Vehicles; Springer: London, UK, 2009. [Google Scholar]
- Wu, Q.; Saif, M. Robust fault diagnosis of a satellite system using a learning strategy and second order sliding mode observer. IEEE Syst. J. 2010, 4, 112–121. [Google Scholar]
- Sharifuddin, M.; Goutam, C.; Kingshook, B. LMI approach to robust unknown input observer design for continuous systems with noise and uncertainties. Int. J. Control Autom. Syst. 2010, 8, 210–219. [Google Scholar]
- Liu, Y.; Yang, G.H. Integrated design of fault estimation and fault-tolerant control for linear multi-agent systems using relative outputs. Neurocomputing 2019, 329, 468–475. [Google Scholar] [CrossRef]
- Du, D.S.; Xu, S.Y.; Cocquempot, V. Actuator fault estimation for discrete-time switched systems with finite-frequency. Syst. Control Lett. 2017, 108, 64–70. [Google Scholar] [CrossRef]
- Xie, X.P.; Yue, D.; Park, J.H. Robust fault estimation design for discrete-time nonliner systems via a modified fuzzy fault estimation observer. ISA Trans. 2018, 73, 22–30. [Google Scholar] [CrossRef]
- Zong, G.; Ren, H.; Karimi, H.R. Event-triggered communication and annular finite-time H∞ filtering for networked switched systems. IEEE Trans. Cybern. 2020, 51, 309–317. [Google Scholar] [CrossRef]
- Yu, P.; Liu, K.-Z.; Wu, M.; She, J. Improved equivalent-input disturbance approach based on H∞ control. IEEE Trans. Ind. Electron. 2020, 67, 8670–8679. [Google Scholar] [CrossRef]
- Rasouli, P.; Moattari, M.; Forouzantabar, A. Nonlinear disturbance observer-based fault-tolerant control for flexible teleoperation systems with actuator constraints and varying time delay. Trans. Inst. Meas. Control 2021, 43, 2246–2257. [Google Scholar] [CrossRef]
- Sun, S.X.; Wei, X.J.; Zhang, H.F.; Karimi, R.R.; Han, H. Composite fault-tolerant control with disturbance observer for stochastic systems with multiple disturbances. J. Fraklin Inst. 2018, 355, 4897–4915. [Google Scholar] [CrossRef]
- Ding, R.Q.; Cheng, M.; Jiang, L.; Hu, G.L. Active fault-tolerant control for electro-hydraulic systems with an independent metering valve against valve faults. IEEE Trans. Ind. Electron. 2021, 68, 7221–7232. [Google Scholar] [CrossRef]
- Xu, J.W.; Yu, X.; Qiao, J.Z. Hybrid disturbance observer-based anti-disturbance composite control with applications to mars landing mission. IEEE Trans. Syst. Man. Cybern. Syst. 2021, 51, 2885–2893. [Google Scholar] [CrossRef]




| Parameters | Values |
|---|---|
| Acceleration of gravity | 9.81 m/s |
| Air density | 1.205 kg/m |
| Mass of the UAV | 28 kg |
| Wing planform aera | 1.8 m |
| Mean aerodynamic chord | m |
| Pitch moment-of-inertia | 10.9(±0.05) kg· m |
| Lift force coefficient | |
| Lift force coefficient | |
| Drag force coefficient | |
| Drag force coefficient | |
| Drag force coefficient | |
| Pitch force coefficient | |
| Pitch force coefficient | |
| Pitch force coefficient | |
| Pitch force coefficient |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhu, Z.; Yi, Y. Anti-Disturbance Fault-Tolerant Sliding Mode Control for Systems with Unknown Faults and Disturbances. Electronics 2021, 10, 1487. https://doi.org/10.3390/electronics10121487
Zhang X, Zhu Z, Yi Y. Anti-Disturbance Fault-Tolerant Sliding Mode Control for Systems with Unknown Faults and Disturbances. Electronics. 2021; 10(12):1487. https://doi.org/10.3390/electronics10121487
Chicago/Turabian StyleZhang, Xiaoli, Zhengyu Zhu, and Yang Yi. 2021. "Anti-Disturbance Fault-Tolerant Sliding Mode Control for Systems with Unknown Faults and Disturbances" Electronics 10, no. 12: 1487. https://doi.org/10.3390/electronics10121487
APA StyleZhang, X., Zhu, Z., & Yi, Y. (2021). Anti-Disturbance Fault-Tolerant Sliding Mode Control for Systems with Unknown Faults and Disturbances. Electronics, 10(12), 1487. https://doi.org/10.3390/electronics10121487






