Small-Signal Stability Analysis for Multi-Terminal LVDC Distribution Network Based on Distributed Secondary Control Strategy

Abstract

This paper presents a detailed and accurate small-signal analysis model for a four-terminal low-voltage direct current (LVDC) distribution network with distributed secondary control strategy. To tackle the contradiction between power sharing accuracy and average voltage recovery ability of voltage source converters (VSCs), a distributed secondary control strategy is adopted, which is based on average consensus algorithm and local voting protocol. Furthermore, to analyze the stability of LVDC distribution network based on the proposed distributed secondary control strategy, a detailed and accurate small-signal analysis model is formulated which is derived from various non-linear state-space sub-models. The time-domain simulation and electromagnetic simulation are carried out to verify the validity and accuracy of the proposed model. Based on this model, the influence rules of main eigenvalues are summarized with the variation of PI control and DC line parameters. Time-domain simulations conducted in PSCAD are used to validate the operational limits of the secondary controllers and DC line obtained from the small-signal stability analysis.

1. Introduction

Recently, the DC distribution system has witnessed a vigorous development because the extensive application of power electronics and large-scale access of renewable energy sources [1]. The DC distribution system has larger power supply capacity and lower line losses with simpler control schemes over traditional AC distribution network [1,2,3]. Multi-terminal DC distribution network is mainly composed by DC converter stations, distributed generations (DGs), load and energy storage systems (ESSs). It has become a research hotspot for superiorities of easy DG access and high system efficiency. The coordinated control among DC converter stations is one of the key technologies to ensure stability, reliability and optimization of the system.

The control targets of the DC converter stations usually involve voltage regulation and power optimization. Generally, the DC converter stations adopt the droop method to implement power distribution according to their own capacity without communication, which can improve the operation reliability of the system [4,5,6]. However, even though the droop control can be implemented easily, it has a contradiction between voltage regulation and power distribution due to the existence of line impedance in the DC system [7]. Therefore, a secondary control for the droop-based DC system is necessary. At present, the centralized and decentralized methods are two main ways to implement secondary control. A single central controller is designed to collect information and send reference to each unit in centralized way [8,9,10,11]. However, the reliability of centralized method is poor due to the failure of the center node or link, and the capability in plug and play is weakened by centralized communication. The decentralized method is more practical than the centralized control, because its reliability and flexibility [12]. In [13], a decentralized droop control method based on virtual resistance in DC system is proposed to compensate power distribution deviations caused by line resistances. However, this method cannot eliminate the voltage deviation. To restore the bus voltage, a hierarchical coordination control based on local information is proposed for DC distribution system to realize smooth operation in steady state and secondary voltage recovery in harsh operating condition as well as global power optimization [14]. Although the simplicity and decentralized nature of the droop control are retained by decentralized method, the global power optimization cannot be realized by only the local information.

Compared with the above two methods, the distributed secondary control method that requires only local computation and information exchange among some neighboring units through a sparse communication network has drawn more attentions [15,16,17]. Reference [7] proposes a hierarchical distributed control strategy for the DC distribution network based on the distributed average algorithm. By designing different weights of the voltage control and power control, the effective balance between the two control objectives can be achieved. A distributed control paradigm based on the reverse droop controller is established to achieve voltage regulation and proportionate load current sharing in a DC network [18]. In [19], a distributed voltage control method for distribution network is proposed to compensate the reactive power and provide the stable voltage for distribution network by using the terminal load and its corresponding power factor correction device. Reference [20] designs a two-level distributed control strategy for the wind farms by regarding the active power utilization rate as the consistent variable. To sum up, although the centralized method can achieve more complex control objectives, it has the risk of system failure. The decentralized method has higher reliability and expansibility, the control effect is not satisfactory. The distributed method can be implemented by multiple distributed controllers working in parallel, which increases the reliability, flexibility, and scalability of the control system.

Table 1. Summaries on secondary control methods.

Secondary Control Methods	Advantages	Disadvantages
Centralized control	High control accuracy	Poor reliability, scalability
Decentralized control	High reliability, scalability	Poor control accuracy
Distributed control	High reliability, scalability, accuracy	Complicated control scheme

lists the advantages and disadvantages according to above three methods.

Therefore, the distributed manners are considered as promising options for the optimal control of the DC distribution network. In this case, a distributed secondary control strategy for enhancing the power distribution accuracy and recovering the average voltage of the DC converter stations is adopted in this paper. However, there are also many problems remained to be solved before the distributed schemes become more practical for DC distribution network. The stability of the system should be considered first, which is the foundation of voltage regulation and power distribution.

The most commonly used way for stability study is the small-signal analysis method [21]. The small-signal stability analysis of conventional power systems has been well established. More and more researches have focused on the stability analysis of low voltage DC microgrids [22,23,24,25,26] and HVDC transmission & distribution networks [21,27,28,29,30,31,32,33]. The small-signal model of the converter-based microgrid is established to investigate how circuit and control parameters give rise to the oscillatory modes and the damping performance of these modes [22]. Reference [23] establishes a small-signal model of DC microgrid and analyzes the influence laws of generation parameters to ensure the system stability. A reduced-order model of multi-terminal DC microgrid is established in [24], and the small signal stability of the system is closely related to the sag constant of the distributed generation. In [25], a general methodology considering four kinds of terminals for small-signal stability analysis is presented, which is useful for academic purposes and practical applications. An improved secondary control strategy is proposed for DC microgrid in [26], and the control parameters are optimized using small signal modeling. Similarly, the small signal model of the HV MTDC network is built in [27], and the stability of the system is analyzed. However, the stability influencing factors and countermeasures are not mentioned. Reference [28] presents a detailed state-space model of a more elaborated four-terminal VSC-MTDC system connecting two offshore wind farms to an AC network. Small-signal stability analysis is carried out to define the ranges for the gains of the VSC controllers that ensure dynamic stability. Reference [29] reviews various small-signal stability analysis tools, and the impedance stability analysis of the VSC-based HVDC transmission system is presented. Furthermore, the stability assessment of multi-terminal DC distribution system is performed through small-signal pole-zero analysis to investigate the key factors affecting the system stability in [30,31]. Additionally, a comprehensive small-signal model and stability analysis of VSC-based medium-voltage DC distribution system are performed to confirm that the proposed comprehensive model is more accurate than the simplified model and identify the guidance for the selection of PI parameters [32,33].

As discussed above, the most stability studies are based on the traditional primary control scheme or its improved one. The detailed small-signal model of multi-terminal DC distribution network should be established, and the stability analysis considering distributed secondary control needs further verification. The main contributions of this paper include:

• The detailed and accurate small-signal model of the whole multi-terminal LVDC system containing distributed secondary control is built.
• The stability of the entire LVDC distribution network is analyzed, and the effects of parameters variations on the small-signal stability are investigated by sensitivity analysis.
• The time-domain simulation by Simulink and the electromagnetic simulation by PSCAD are both conducted for the entire LVDC system to verify the accuracy of the model.

The rest of this paper is organized as follows: Section 2 introduces the structure and operation principle of the DC distribution network, including primary control and distributed secondary control. Section 3 proposes the non-linear state-space model of the DC distribution network containing secondary control. A small-signal model of the entire DC distribution network is established and verified for stability analysis in Section 4. Small-signal stability analysis is conducted in Section 5. At last, Section 6 and Section 7 present discussion and concluding remarks respectively.

2. Operation Principle of the LVDC Distribution Network

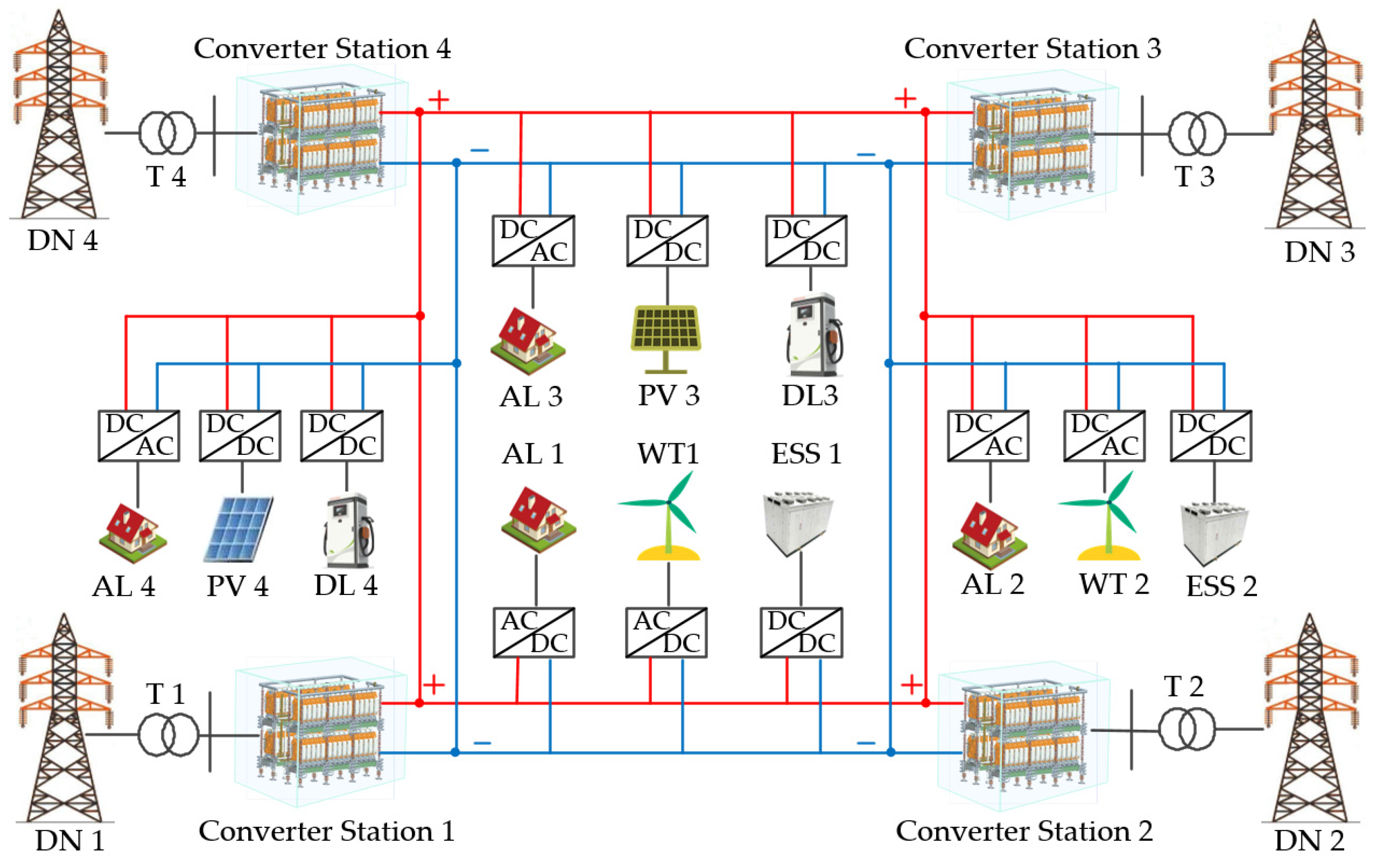
2.1. The Structure of LVDC Distribution Network

The common topology of LVDC distribution network usually includes chain structure, two-terminal structure, and ring structure. A typical multi-terminal low voltage LVDC distribution network topology is shown in Figure 1. The DC distribution system connects with the AC systems through converter stations, and it integrates the renewable resources, energy storage system, AC loads (ALs), DC loads (DLs), and so on. The renewable resources usually contain photovoltaic (PV) system and wind turbine (WT) system, which work in maximum power point tracking (MPPT) mode. The energy storage systems can absorb or inject active power from or to the network to optimize the load flow and keep the bus voltage stable when the converter stations broke down. The load can be classified into common load and important load, where the common load can be cut off to ensure the system stable in critical situation. As the converter station is dominant for the LVDC network, the coordinated control of converter stations is important for the stable and optimal operation of the whole system.

2.2. The Primary Control of VSC-Based Converter Station

In a multi-terminal LVDC distribution system, the coordinated control strategy of VSC-based converter station consists of primary control and secondary control. The primary control usually adopts droop method to distribute active power among all converter stations according to their capacity. The structure of a converter station and its primary control is shown in Figure 2. The primary control consists of P-V droop loop and inner loops, and the SPWM signals achieved by these control loops are applied to converter to accomplish the primary control target.

The P-V droop equation and voltage control loop can be expressed

$$\{\begin{array}{l}{U}_{dc}{}^{\ast }=U_{dc\_ref}-k\times P_{dc} \\ i_{fd}{}^{\ast }=(k_{P,U}+\frac{k_{I,U}}{s})(U_{dc}{}^{\ast }-U_{dc})\end{array}$$

(1)

where $U_{dc}{}^{\ast }$ is the reference output voltage of converter station, U_{dc_ref} is the rated voltage provided by secondary control level. The measurement unit of $U_{dc}{}^{\ast }$ and U_{dc_ref} is V. k is the droop coefficient. P_dc is the actual output power and the unit is kW. $i_{fd}{}^{\ast }$ is the d-axis current reference value of inductance L_f, U_dc is the actual output DC voltage and the unit is the same as $U_{dc}{}^{\ast }$. k_P,U and k_I,U are the parameters of the proportional-integral (PI) controller of the inner voltage loop.

The droop coefficient k can be designed as follows

$$k=\frac{U_{dcN}-U_{dc\min }}{P_{N\max }}$$

(2)

where U_dcN is the rated voltage of DC network, U_dcmin is the minimum voltage, which can be set to 95% of U_dcN. The unit of U_dcN and U_dcmin is V. P_Nmax is the maximum output power of converter station and the unit of it is kW. It can be seen from Equations (1) and (2) that the power sharing of different converter stations is in proportion to their maximum output power [34,35]. However, the DC output voltages of different converter stations are different, which causes the output power deviation between each station and decreases the utilization rate of whole stations. On the other hand, it can be concluded that the elimination of output power deviation will enhance the voltage drop level of different stations. This will increase the probability of voltage violation and the power loss in DC distribution network. Therefore, the primary control has a contradiction between voltage regulation and power distribution. In order to improve the power distribution accuracy and recover DC output voltage, a distributed secondary control strategy is implemented based on the primary control.

2.3. The Distributed Secondary Control for DC Distribution Network

As discussed above, the distributed control method requires only local computation and information exchange among some neighboring units through a sparse communication network. It can increase the reliability, flexibility, and scalability of the secondary control level. According to the secondary control target, the distributed secondary control structure of converter station is shown in Figure 3. It can be observed that the secondary control includes voltage secondary control and power secondary control. In voltage regulation step, the average DC output voltage of all converter stations is estimated, and the estimated average voltage U_ave is compared with rated voltage U_dcN to obtain the compensation item ΔV. In the power regulation step, the average per unit output power P_aveλ is estimated, and it is compared with the local value P_dcλ of each converter station to generate the compensation item ΔU. Finally, ΔV and ΔU are added to generate the rated voltage U_{dc_ref} for the primary level. Then, the primary control in this paper can be rewritten as follows

$$U_{dci}{}^{\ast }=U_{dcN}+\Delta V_i+\Delta U_i-k\times P_{dci}, i=1,2\dots ,n.$$

(3)

where ΔV_i and ΔU_i are the voltage compensation items.

As shown in Figure 3, the estimation of average voltage and per unit power are all realized by distributed algorithm. As the communication delay is too small that the sampling control cycle of the secondary level can be designed shorter. Thus, the continuous model is considered in this paper. The dynamic consensus algorithm is often used to estimate the average value of the whole measurements [36]. Let x_i represents the measurement of node i, while x_avei is the estimation value of global averaging. Then, the dynamic consensus algorithm can be described as follows

$$x_{avei}(t)=x_i(t)+{\displaystyle {\int }_0^t{\displaystyle \sum _{j\in N_i}{a}_{ij}(x_{avej}(\zeta )}}-x_{avei}(\zeta ))d\zeta$$

(4)

where a_ij is the element of adjacency matrix A. A = [a_ij] is a (0,1)-matrix with zeros on its diagonal, and the off-diagonal entry a_ij is one if node j∈N_i. N_i represents the set of adjacent nodes of node i, namely, a node j belongs to N_i if there exists a communication link between it and node i. It can be said that the nodes have reached a consensus if and only if x_avei = x_avej, for all i, j. If the communication is bidirectional, then all nodes will converge to the average value of all measurements. For converter station i, the measurements can be the DC output voltage, per unit output power, et al. Based on the dynamic consensus algorithm, the voltage regulation process can be described as follows

$$\{\begin{array}{l}{U}_{avei}=U_{dci}+C_E{\displaystyle {\int }_0^t{\displaystyle \sum _{j\in N_i}{a}_{ij}(U_{avej}}}-U_{avei})d\zeta \\ \Delta V_i=(k_{P,V}+\frac{k_{I,V}}{s})(U_{dcN}-U_{avei})\end{array}, i=1,2,\dots ,n.$$

(5)

where C_E is the control gain, k_P,V and k_I,V are the PI parameters of voltage secondary control. U_avei is the average voltage estimated by station i. On the other hand, in order to eliminate the deviation of per unit output power, the local voting protocol is used to estimate the average per unit value, thus the power regulation process can be described as follows

$$\{\begin{array}{l}{P}_{ave\lambda i}=d_{ii}{P}_{dc\lambda i}+{\displaystyle \sum _{j\in N_i}^n{d}_{ij}}{P}_{dc\lambda j}\\ \Delta U_i=(k_{P,P}+\frac{k_{I,P}}{s})(P_{ave\lambda i}-P_{dc\lambda i})\end{array}, i=1,2,\dots ,n.$$

(6)

where P_dcλi is the per unit power of station i, and can be calculated by

$$P_{dc\mathsf{\lambda }i}=\frac{P_{dci}}{P_{Ni}}, i=1,2,\dots ,n.$$

(7)

where P_Ni is the rated capacity of station i. P_aveλi is the average per unit output power estimated by station i. d_ij is the voting weight, where d_ij > 0 if node j belongs to N_i and d_ij = 0, otherwise. As the below steady state analysis shows, when the coefficient matrix D = [d_ij] is designed as a double-stochastic matrix, the power deviation between different stations will be eliminated asymptotically. k_P,P and k_I,P are the PI parameters of power secondary control.

The output voltage reference $U_{dc}{}^{\ast }$ then can be calculated according to (3), and the current control loop is used to follow the current reference $i_{fd}{}^{\ast }$ from the voltage control loop. The bandwidth of this loop is designed to be large enough to maintain the power balance of the converter station while load changes. Within the distributed secondary control, the average DC output voltage can be recovered and the per unit output power deviation of all stations can be eliminated, respectively.

2.4. Steady-State Analysis

Laplace Transform Method is often used to verify the steady control effect of the proposed control strategy. The Laplace Transform of Equations (3), (5) and (6) are shown as follows

$${\mathit{U}}_{dc}{}^{\ast }(\mathrm{s})={\mathit{U}}_{dcN}(\mathrm{s})+\Delta \mathit{V}(\mathrm{s})+\Delta \mathit{U}(\mathrm{s})-k{\mathit{P}}_N{\mathit{P}}_{dc\lambda }(\mathrm{s})$$

(8)

$$\{\begin{array}{l}{U}_{ave}\left(\mathrm{s}\right)=\mathrm{s}(\mathrm{s}{I}_n+C_E{L}_{n1}{)}^{-1}{U}_{dc}\left(\mathrm{s}\right)=H_{obs}{U}_{dc}\left(\mathrm{s}\right)\\ \Delta V\left(\mathrm{s}\right)=(k_{P,V}+\frac{k_{I,V}}{\mathrm{s}}\left)\right[U_{dcN}\left(\mathrm{s}\right)-U_{ave}\left(\mathrm{s}\right)]\\ \Delta U\left(\mathrm{s}\right)=(k_{P,P}+\frac{k_{I,P}}{\mathrm{s}})(D-I_n)P_{dc\lambda }\left(\mathrm{s}\right)\end{array}$$

(9)

where U_dcN(s) = (U_dcN/s)1, 1 is a n × 1 vector whose elements are all equal to one, P_N = diag{P_Ni}, P_dcλ(s) is the Laplace Transform of [P_dcλ1, P_dcλ2, …, P_dcλn]^T, U_dc(s) is the Laplace Transform of [U_dc1, U_dc2, …, U_dcn]^T.

Let L_n2 = D − I_n, I_n is the unit matrix, then L_n1 and L_n2 are all the so called Laplace matrix. Suppose the system is stable, then $U_{dc}{}^{\ast }$ = U_dc, and substitute Equation (9) into (8)

$$[{\mathit{I}}_n+H(\mathrm{s}){\mathit{H}}_{obs}]{\mathit{U}}_{dc}(\mathrm{s})=[{\mathit{I}}_n+H(\mathrm{s})]{\mathit{U}}_{dcN}(\mathrm{s})+[G(\mathrm{s}){\mathit{L}}_{n2}-k{\mathit{P}}_N]{\mathit{P}}_{dc\lambda }(\mathrm{s})$$

(10)

where H(s) = diag{k_P,V + k_I,V/s}, G(s) = diag{k_P,P + k_I,P/s}. Multiplying both sides of Equation (10) by s² and implementing the Final Value Theorem, (10) can be described as follows

$$k_{I,V}\left[\right(\underset{s\to 0}{lim}{H}_{obs})U_{dc}^s-U_{dcN}\underset{¯}{\mathbf{1}}\left)\right]=k_{I,P}{L}_{n2}{P}_{dc\lambda }^s$$

(11)

where ${\mathit{U}}_{dc}^s$ is the steady DC voltage vector, and ${\mathit{P}}_{dc\mathsf{\lambda }}^s$ is the steady per unit power vector. Since Equation (11) is guaranteed for any k_I,V and k_I,P, it can be derived that

$${\mathit{Q}\mathit{U}}_{dc}^{\mathrm{s}}=U_{dcN}\underset{¯}{\mathbf{1}}$$

(12)

$${\mathit{L}}_{n2}{\mathit{P}}_{dc\lambda }^{\mathrm{s}}=0$$

(13)

For Equation (12), according to [37], Q = $\underset{s\to 0}{lim}{\mathit{H}}_{obs}$ is the averaging matrix, whose elements are all equal to 1/n. Multiplying both sides by 1^T, Equation (12) can be expressed as follows

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{U}_{dci}{}^{\mathrm{s}}}=U_{dcN}$$

(14)

For Equation (13), because L_n2 is the Laplace matrix, (13) only has one solution, that is ${\mathit{P}}_{dc\lambda }^s$ = L^*1, in other words

$$P_{dc\lambda 1}{}^{\mathrm{s}}=P_{dc\lambda 2}{}^{\mathrm{s}}=\dots \dots =P_{dc\lambda n}{}^{\mathrm{s}}=L^{\ast }$$

(15)

The above analysis shows that the per unit output power of each converter station will converge to L^*, and its value is determined by the net load in the DC distribution network. That is, all converter stations will distribute their output power according to their rated capacity accurately. In addition, the average DC output voltage will converge to the rated value U_dcN.

3. Non-linear State-Space Model of the DC Distribution Network

3.1. State-Space Model of the Individual Converter Station with Primary Control

To obtain the model of the entire DC distribution system, the state-space model of an individual converter station with primary control needed to be first established. In this section, all elements in the converter station system shown in Figure 2 are expressed in terms of mathematical equations as a basis for the small-signal model.

• Phase Locked Loop Equations

In earlier studies, d_PLLq_PLL coordinate system based on the AC input voltage u_o is usually used for the small-signal modelling. However, when the transient process of PLL cannot be neglected, the state space equations should be established

$$\{\begin{array}{l}\frac{dz}{dt}=-u_{oq}\\ \frac{d{\delta }_{PLL}}{dt}=\omega -{\omega }_{PLL}=\omega -({\omega }_o+k_{I,PLL}z-k_{P,PLL}{u}_{oq})\end{array}$$

(16)

where u_oq is the input voltage of filter in the q_PLL-axis. ω and ω_o are the angular frequency of AC grid and rated angular frequency, respectively. The unit of ω_o is rad/s. ω_PLL is the output angular frequency of PLL. δ_PLL is the output angular of PLL, which is the phase deviation between u_o and e, as shown in Figure 2. z is an auxiliary state variable representing the integral part of the PI controller in the PLL, and the parameters of PI controller are k_P,PLL and k_I,PLL.

• Input Filter Equations

A typical LC filter is composed of the filter inductance L_f and its equivalent resistance R_f, and the filter capacitor, which is given by C_f. Based on the d_PLLq_PLL coordinate system, the state equations of the LC filter can be presented as

$$\{\begin{array}{l}\frac{d{i}_{fd}}{dt}=\frac{-R_f}{L_f}{i}_{fd}+\frac{1}{L_f}(u_{od}-u_{ed})+\omega i_{fq}\\ \frac{d{i}_{fq}}{dt}=\frac{-R_f}{L_f}{i}_{fq}+\frac{1}{L_f}(u_{oq}-u_{eq})-\omega i_{fd}\\ \frac{d{u}_{od}}{dt}=\frac{1}{C_f}(i_{od}-i_{fd})+\omega u_{oq}\\ \frac{d{u}_{oq}}{dt}=\frac{1}{C_f}(i_{oq}-i_{fq})-\omega u_{od}\end{array}$$

(17)

where i_fd and i_fq are the filter inductor current in the d_PLLq_PLL-axis. u_ed and u_eq are the input voltage of the converter in the d_PLLq_PLL-axis, respectively. u_od is the input voltage of filter in the d_PLL-axis. i_od and i_oq are the input current in the d_PLLq_PLL-axis. The units of R_f, L_f and C_f are mΩ, mH and μF, respectively.

• AC Connection Line Equations

The converter station is connected to the AC grid through a transmission line, which consists of resistance R_c and inductance L_c. As the AC grid is considered as an ideal source, the absolute stable d_Gq_G coordinate system based on it is used to establish the state space equations of the transmission line

$$\{\begin{array}{l}\frac{d{i}_{od\_G}}{dt}=\frac{-R_c}{L_c}{i}_{od\_G}+\frac{1}{L_c}(e_d-u_{od\_G})+\omega i_{oq\_G}\\ \frac{d{i}_{oq\_G}}{dt}=\frac{-R_c}{L_c}{i}_{oq\_G}+\frac{1}{L_c}(e_q-u_{oq\_G})-\omega i_{od\_G}\\ u_{od\_G}=u_{od}\cos ({\delta }_{PLL})+u_{oq}\sin ({\delta }_{PLL})\\ u_{oq\_G}=-u_{od}\sin ({\delta }_{PLL})+u_{oq}\cos ({\delta }_{PLL})\\ i_{od}=i_{od\_G}\cos ({\delta }_{PLL})-i_{oq\_G}\sin ({\delta }_{PLL})\\ i_{oq}=i_{od\_G}\sin ({\delta }_{PLL})+i_{oq\_G}\cos ({\delta }_{PLL})\end{array}$$

(18)

where e_d and e_q are the AC grid voltage in the d_Gq_G-axis, and they are constant values with e_q = 0. The unit of e_d and e_q is V. i_{od_G} and i_{oq_G} are the input current in the d_Gq_G-axis, respectively. u_{od_G} and u_{oq_G} are the input voltage of LC filter in the d_Gq_G-axis, respectively.

• Converter Equations

With the losses in switching elements (e.g., IGBTs and diodes) neglected, it can be assumed that the input voltage of the converter station will be equal to its reference value, as follows

$$\{\begin{array}{l}{u}_{ed}=u_e{{}_d}^{\ast }\\ u_{eq}=u_e{{}_q}^{\ast }\end{array}$$

(19)

where u_ed^* and u_eq^* are the voltage reference of the inverter in the d_PLLq_PLL-axis.

• DC Connection Line Equations

The converter station is also connected to the DC bus through the transmission line, with the line parameters consisting of resistance R_dc and inductance L_dc. The state space equations of the DC connection line are given as follows

$$\{\begin{array}{l}{C}_{dc}\frac{d{U}_{dc}}{dt}=I_g-I_{dc} \\ L_{dc}\frac{d{I}_{dc}}{dt}=U_{dc}-R_{dc}{I}_{dc}-U_b\end{array}$$

(20)

where I_dc is the current of transmission line, and U_dc is the DC output voltage of capacitor C_dc. I_g is the output current of converter and U_b is the voltage of DC bus. The measurement units of C_dc, L_dc and R_dc are F, mH and mΩ, respectively.

• Power Calculator

The power calculator is applied in this case for calculating the instantaneous active power. With the losses neglected in converter station, the AC active power is equal to the power transmitted to the DC port, which is shown in (21)

$$P_{dc}=\frac{w_c}{s+w_c}{U}_{dc}{I}_g=\frac{3}{2}\frac{w_c}{s+w_c}\left(u_{ed}{i}_{fd}+u_{eq}{i}_{fq}\right)$$

(21)

where ω_c is the cut-off frequency of low-pass filter and the unit is rad/s.

• Voltage and Current Loop Control

The voltage and current loop control block diagram are shown in Figure 4 in detail. k_P,U and k_I,U are the parameters of the PI controller of the outer voltage loop, and k_P,C and k_I,C are the parameters of the PI controllers of the inner current loop. The DC output voltage reference ($U_{dc}{}^{\ast }$) of converter station is obtained through droop equation and the secondary control value ΔV and ΔU, as mentioned in Section 2.2.

According to Figure 4, the space state equations of voltage and current loop control can be written

$$\{\begin{array}{l}{U}_{dc}{}^{\ast }=U_{dcN}+\Delta V+\Delta U-k\times P_{dc}\\ i_{fd}{}^{\ast }=k_{I,U}{\gamma }_d+k_{P,U}(U_{dc}{}^{\ast }-U_{dc})\\ u_{ed}{}^{\ast }=-k_{I,C}{\lambda }_d-k_{P,C}(i_{fd}{}^{\ast }-i_{fd})+u_{od}+{\omega }_{PLL}{L}_f{i}_{fq}\\ u_{eq}{}^{\ast }=-k_{I,C}{\lambda }_q-k_{P,C}(i_{fq}{}^{\ast }-i_{fq})+u_{oq}-{\omega }_{PLL}{L}_f{i}_{fd}\end{array}$$

(22)

where state variables γ and λ are defined to assess the dynamic properties of the PI controllers in the voltage and current loop, and the corresponding state equation in the d_PLLq_PLL-axis is shown as

$$\{\begin{array}{l}\frac{d{\gamma }_d}{dt}=U_{dc}{}^{\ast }-U_{dc}\\ \frac{d{\lambda }_d}{dt}=i_{fd}{}^{\ast }-i_{fd} \\ \frac{d{\lambda }_q}{dt}=-i_{fq} \end{array}$$

(23)

3.2. State-Space Model of the Distributed Secondary Control

According to the proposed distributed secondary control strategy described by (5) and (6), the space state model is described as follows

$$\{\begin{array}{l}\Delta V=k_{P,V}(U_{dcN}-U_{ave})+k_{I,V}{\Phi }_v\\ \Delta U=k_{P,P}{L}_{n2}{P}_{dc\lambda }+k_{I,P}{\Phi }_p\\ U_{ave}=U_{dc}+U_{es}\end{array}$$

(24)

The state variable Φ_v = [Φ_v1, Φ_v2, …, Φ_vn]^T is defined to describe the error accumulation between estimated voltage and rated voltage, while Φ_p = [Φ_p1, Φ_p2, …, Φ_pn]^T is defined to describe the error accumulation between estimated per unit power and local per unit power. The corresponding state equation is

$$\{\begin{array}{l}\frac{d{\Phi }_v}{dt}=U_{dcN}-U_{ave}\\ \frac{d{\Phi }_p}{dt}=L_{n2}{P}_{dc\lambda }\\ \frac{d{U}_{es}}{dt}=-C_E{L}_{n1}{U}_{ave}\end{array}$$

(25)

where U_dcN = U_dcN1, U_ave = [U_ave1, U_ave2, …, U_aven]^T, U_es = [U_es1, U_es2, …, U_esn]^T.

3.3. State-Space Model of the DC Distribution Line and Load

As different DC network topologies have different state space models, the four-terminal ring topology DC distribution network is taken for the example in this paper to establish the state space model, as shown in Figure 1. On the other hand, the wye-delta transform is adopted to simplify the DC distribution line and load model, thus the equivalent model of the DC distribution network line and inner constant power load (CPL) is shown in Figure 5.

• DC Distribution Line Equations

As Figure 5a shows, all the converter stations are connected to each other through DC distribution lines. The state space equations of lines are written as follows

$$\{\begin{array}{l}{L}_{l1}\frac{d{I}_{l1}}{dt}=U_{b4}-U_{n1}-R_{l1}{I}_{l1}, L_{l2}\frac{d{I}_{l2}}{dt}=U_{n1}-U_{b1}-R_{l2}{I}_{l2} \\ L_{l3}\frac{d{I}_{l3}}{dt}=U_{b1}-U_{n2}-R_{l3}{I}_{l3}, L_{l4}\frac{d{I}_{l4}}{dt}=U_{n2}-U_{b2}-R_{l4}{I}_{l4} \\ L_{l5}\frac{d{I}_{l5}}{dt}=U_{n3}-U_{b2}-R_{l5}{I}_{l5}, L_{l6}\frac{d{I}_{l6}}{dt}=U_{b3}-U_{n3}-R_{l6}{I}_{l6} \\ L_{l7}\frac{d{I}_{l7}}{dt}=U_{n4}-U_{b3}-R_{l7}{I}_{l7}, L_{l8}\frac{d{I}_{l8}}{dt}=U_{b4}-U_{n4}-R_{l8}{I}_{l8} \\ C_{b1}\frac{d{U}_{b1}}{dt}=I_{dc1}+I_{l2}-I_{l3}, C_{b2}\frac{d{U}_{b2}}{dt}=I_{dc2}+I_{l4}+I_{l5} \\ C_{b3}\frac{d{U}_{b3}}{dt}=I_{dc3}+I_{l7}-I_{l6}, C_{b4}\frac{d{U}_{b4}}{dt}=I_{dc4}-I_{l1}-I_{l8}\\ I_{CPL1}=I_{l1}-I_{l2}, I_{CPL2}=I_{l3}-I_{l4}, I_{CPL3}=I_{l6}-I_{l5}, I_{CPL4}=I_{l8}-I_{l7} \end{array}$$

(26)

where U_n is the node voltage of the equivalent constant power load, I_l is the branch current, L_l and R_l are line inductance and resistance, respectively. C_b represents the grounded capacitance. I_CPL is the current of CPL. The measurement units of L_l, R_l and C_b are mH, Ω and μF, respectively

• Constant Power Load Equations

As Figure 5b shows, the equivalent constant power load in the DC distribution system is modeled as DC/DC bulk converter. The state space equations are as follows

$$\{\begin{array}{l}{C}_{ni}\frac{d{U}_{ni}}{dt} =I_{CPLi}-D_i{I}_{Li}\\ L_{Di}\frac{d{I}_{Li}}{dt}=D_i{U}_{ni}-U_{Li}\\ C_{Di}\frac{d{U}_{Li}}{dt} =I_{Li}-\frac{U_{Li}}{R_i}\\ \frac{d{X}_i}{dt}=U_{L\_ref}-U_{Li}\\ D_i=k_{p,L}(U_{L\_ref}-U_{Li})+k_{I,L}{X}_i \end{array}$$

(27)

where C_n, L_D, C_D are the parameters of DC/DC bulk converter, respectively. U_L and I_L are the capacity voltage and inductor current of resistance side. U_{L_ref} is the rated voltage, and R is the equivalent resistance of load. D is the duty ratio of control signal, k_P,L and k_I,L are the parameters of the PI controller of the converter. The measurement units of L_D, C_D and C_n are mH, mF and mF, respectively.

4. Small-Signal Model of the DC Distribution Network Based on Distributed Secondary Control

4.1. Small-Signal Model of the DC Distribution Lines and Loads

Based on (26) and (27), the small-signal state space model contains 28 state variables and 4 output variables, which are given by

$$\begin{array}{l}\Delta {\mathit{x}}_s{}_0= [\Delta U_b{}_1, \Delta U_b{}_2,\Delta U_b{}_3, \Delta U_b{}_4,\Delta I_l{}_1,\Delta I_l{}_2,\Delta I_l{}_3,\Delta I_l{}_4,\Delta I_l{}_5,\Delta I_l{}_6,\Delta I_l{}_7,\Delta I_l{}_8,\Delta U_n{}_1,\Delta U_n{}_2,\\ \Delta U_n{}_3,\Delta U_n{}_4,\Delta I_L{}_1,\Delta I_L{}_2,\Delta I_L{}_3,\Delta I_L{}_4,\Delta U_L{}_1,\Delta U_L{}_2,\Delta U_L{}_3,\Delta U_L{}_4,\Delta X_1,\Delta X_2,\Delta X_3,\Delta X_4{]}^{\mathrm{T}}\end{array}$$

(28)

$$\Delta U_b={\left[\Delta U_b{}_1,\Delta U_b{}_2,\Delta U_b{}_3,\Delta U_b{}_4\right]}^T$$

(29)

Thus, the small-signal equation and the output equation are as follows

$$\Delta {\dot{x}}_{s0}={\mathit{A}}_{s0}\Delta {\mathit{x}}_{s0}+{\mathit{B}}_{s0}\Delta {\mathit{I}}_{dc}+{\mathit{C}}_{s0}\Delta \mathit{R}$$

(30)

$$\Delta {\mathit{U}}_b={\mathit{D}}_{s0}\Delta {\mathit{x}}_{s0}$$

(31)

where ΔI_dc = [ΔI_dc1, ΔI_dc2, ΔI_dc3, ΔI_dc4]^T and ΔR = [ΔR₁, ΔR₂, ΔR₃, ΔR₄]^T. Both of them are the input variables. Appendix A shows the coefficient matrix A_s0, B_s0, C_s0, D_s0.

4.2. Small-Signal Model of the Multiple Converter Stations

As previously discussed, all the state space equations needed for modeling the converter stations have been introduced. Based on (16)–(23), the state space model of i-th converter station without proposed distributed secondary control contains 14 state variables and 3 output variables (ΔI_dci, ΔP_dci, ΔU_dci)

$$\Delta x_{vsci}=[\Delta P_{dci},\Delta {\gamma }_{di},\Delta {\lambda }_{di},\Delta {\lambda }_{qi},\Delta i_{fdi},\Delta i_{fqi},\Delta u_{odi},\Delta u_{oqi},\Delta i_{od\_Gi},\Delta i_{oq\_Gi},\Delta U_{dci},\Delta I_{dci},\Delta z_i,\Delta {\delta }_{PLLi}{]}^{\mathrm{T}}$$

(32)

The small-signal equation of i-th converter station then can be described as follows

$$\Delta {\dot{x}}_{vsci}={\mathit{A}}_{vsci}\Delta {\mathit{x}}_{vsci}+{\mathit{B}}_{vsci}\Delta U_{bi}+{\mathit{C}}_{vsci}\Delta {\omega }_i+{\mathit{D}}_{vsci}\Delta {\mathit{U}}_i+{\mathit{E}}_{vsci}\Delta {\mathit{E}}_i$$

(33)

where U_i = [ΔV_i, ΔU_i]^T, E_i = [e_di, e_qi]^T. As there are four converter stations in the DC system, the entire small-signal model is established as follows:

$$\Delta {\dot{\mathit{x}}}_{s1}={\mathit{A}}_{s1}\Delta {\mathit{x}}_{s1}+{\mathit{B}}_{s1}\Delta {\mathit{U}}_b+{\mathit{C}}_{s1}\Delta \omega +{\mathit{D}}_{s1}\Delta \mathit{U}+{\mathit{E}}_{s1}\Delta \mathit{E}$$

(34)

where Δx_s1 = [Δx_vsc1^T, Δx_vsc2^T, Δx_vsc3^T, Δx_vsc4^T]^T, ΔU_b = [ΔU_b1, ΔU_b2, ΔU_b3, ΔU_b4]^T, Δω = [Δω₁, Δω₂, Δω₃, Δω₄]^T, U = [ΔV₁, ΔU₁, ΔV₂, ΔU₂, ΔV₃, ΔU₃, ΔV₄, ΔU₄]^T, ΔE = [Δe_d1, Δe_q1, Δe_d2, Δe_q2, Δe_d3, Δe_q3, Δe_d4, Δe_q4]^T. A_s1 = diag(A_vsc1, A_vsc2, A_vsc3, A_vsc4), B_s1= diag(B_vsc1, B_vsc2, B_vsc3, B_vsc4), C_s1 = diag(C_vsc1, C_vsc2, C_vsc3, C_vsc4), D_s1 = diag(D_vsc1, D_vsc2, D_vsc3, D_vsc4), E_s1 = diag(E_vsc1, E_vsc2, E_vsc3, E_vsc4).

The output equations are as follows

$$\{\begin{array}{l}\Delta {\mathit{I}}_{dc}={\mathit{F}}_{s1}\Delta {\mathit{x}}_{s1}\\ \Delta {\mathit{P}}_{dc}={\mathit{G}}_{s1}\Delta {\mathit{x}}_{s1}\\ \Delta {\mathit{U}}_{dc}={\mathit{H}}_{s1}\Delta {\mathit{x}}_{s1}\end{array}$$

(35)

where ΔI_dc = [ΔI_dc1, ΔI_dc2, ΔI_dc3, ΔI_dc4]^T, ΔP_dc = [ΔP_dc1, ΔP_dc2, ΔP_dc3, ΔP_dc4]^T, ΔU_dc = [ΔU_dc1, ΔU_dc2, ΔU_dc3, ΔU_dc4]^T. Appendix B shows the coefficient matrix A_vsci, B_vsci, C_vsci, D_vsci, E_vsci, F_s1, G_s1, H_s1.

4.3. Small-Signal Model of the Proposed Distributed Secondary Control

According to (24) and (25), there are 12 state variables and 4 output variables in the state space model, which are Δx_s2 = [Δϕ_v1, Δϕ_v2, Δϕ_v3, Δϕ_v4, Δϕ_p1, Δϕ_p2, Δϕ_p3, Δϕ_p4, ΔU_ave1, ΔU_ave2, ΔU_ave3, ΔU_ave4]^T and ΔP_dc = [ΔP_dc1, ΔP_dc2, ΔP_dc3, ΔP_dc4]^T. The small-signal equation and output equation are described as follows

$$\Delta {\dot{\mathit{x}}}_{s2}={\mathit{A}}_{s2}\Delta {\mathit{x}}_{s2}+{\mathit{B}}_{s2}\Delta {\mathit{U}}_{dc}+{\mathit{C}}_{s2}\Delta P_{dc}$$

(36)

$$\Delta \mathit{U}={\mathit{D}}_{s2}\Delta {\mathit{x}}_{s2}+{\mathit{E}}_{s2}\Delta {\mathit{U}}_{dc}+{\mathit{F}}_{s2}\Delta P_{dc}$$

(37)

Finally, the small-signal model of the entire DC distribution network can be obtained as follows

$$\Delta {\dot{\mathit{x}}}_s={\mathit{A}}_s\Delta {\mathit{x}}_s+{\mathit{B}}_s\Delta \mathit{R}+{\mathit{C}}_s\Delta \omega +{\mathit{D}}_s\Delta \mathit{E}$$

(38)

where Δx_s = [Δx_s0^T, Δx_s1^T, Δx_s2^T]^T and represents all state variables in the DC distribution network. ΔR represents the small variation of constant power load. Δω represents the small frequency variation of AC grid, and ΔE represents the small voltage magnitude variation of AC grid. Appendix C shows the coefficient matrix A_s2, B_s2, C_s2, D_s2, E_s2, F_s2, A_s, B_s, C_s, D_s.

4.4. Verification of the Established Small-Signal Model

In this section, the results from the time-domain simulation in MATLAB/Simulink and electromagnetic simulation in PSCAD are presented for the verification of the proposed small-signal model. The structure of the LVDC distribution network for case study is shown as Figure 1. There are four converter stations, and the DC sources (PV, WT, DC loads) are integrated as a constant power load for simplicity. Thus, there are four CPLs in the network. The parameters of the DC distribution network and four converter stations are shown in

Table 2. The parameters of DC distribution system.

Parameter	Value	Parameter	Value
Rf/mΩ	2	Lf/mH	2
Cf/uF	50	UdcN/V	800
ed/V	311	eq/V	0
k1	0.44	k2, k3, k4	0.88
PN1/kW	180	PN2, PN3, PN4/kW	90
Ldc1~Ldc4/mH	0.1	Rdc1~Rdc4/mΩ	50
Cdc1~Cdc4/F	0.02	Cb1~Cb4/uF	50
Rc1~Rc4/mΩ	50	Cn1~Cn4/mF	2
Lc1~Lc4/mH	0.2	R1~R4/Ω	0.6
Ll1~Ll8/mH	0.32	Rl1~Rl8/Ω	0.1
LD1~LD4/mH	3	CD1~CD4/mF	3
ωo/rad/s	314	ωc/Hz	50
kP,U	0.3	kI,U	15
kP,C	10	kI,C	10,000
kP,V	2	kI,V	10
kP,P	200	kI,P	2000
kP,PLL	50	kI,PLL	900

. The communication topology of the stations is a ring, and its corresponding adjacency matrix A and coefficient matrix D are shown in Figure 6.

Initially, all the DC loads (about 323 kW) are connected to the network, and all converter stations are accessed to low voltage AC grid. The main steady operation points of the system obtained by Simulink are that ${\mathit{U}}_{dc}^s$ is equal to [808 V, 798 V, 796 V, 798 V], ${\mathit{P}}_{dc}^s$ is equal to [135.2 kW, 67.6 kW, 67.6 kW, 67.6 kW]. It is clearly that the average voltage of DC side is 800 V, and the per unit output power of all converters are all 0.75. Thus, the effectiveness of the distributed secondary control is verified. The introduced small disturbance is a 5 kW step change of the CPL1 from 80 kW to 85 kW at 3.5 s. The curves of different state variables (U_n1, P_dc1, U_dc1, I_dc1, u_oq1, u_od1, i_fq1, i_fd1) obtained using the small-signal model and electromagnetic simulation are compared in Figure 7. It can be seen from Figure 7 that the time-domain responses of different state variables calculated by the established small-signal model using MATLAB coincide with those obtained by PSCAD simulation. This indicates that the accuracy of the established small-signal model is suitable for the stability analysis of the DC distribution network.

5. Small-Signal Stability Analysis

The system eigenvalues are calculated and listed in

Table 3. The system eigenvalues.

Mode	Re	Im	Frequency (Hz)	Damping Ratio	Major Participants
λ1, λ2	−3116.8, −1483.5	0	0	1.0	λd1, ifd1
λ3	−3359.5	0	0	1.0	ifd2, ifd3, ifd4
λ4	−3245.7	0	0	1.0	ifd2, ifd3, ifd4, λd3
λ5, λ6	−3292.8, −1450.4	0	0	1.0	ifd2, λd2, ifd4, λd4
λ7, λ8	−3571.2, −1388.5	0	0	1.0	ifq1, λq1
λ9, λ10, λ11	−3596.6	0	0	1.0	ifq2, ifq3, ifq4, λq2, λq4
λ12	−1460.4	0	0	1.0	ifd3, λd1, λd3
λ13	−1434.8	0	0	1.0	ifd2, λd2, ifd3, λd3, ifd4, λd4
λ14, λ15, λ16	−1384.7	0	0	1.0	ifq4, λq2, λq3, λq4
λ17,18, λ19,20 λ21,22, λ23,24	−213.5	±18,068.4	2876	0.01	Ub1~Ub4 Idc1~Idc4
λ25,26 λ27,28	−127.2 −132.2	±10,359.0 ±9725.9	1648.7 1547.9	0.01 0.01	uod1, uoq1 iod_G1, ioq_G1
λ29,30, λ31,32 λ33,34 λ35,36	−120.5 −122.2 −123.9	±10,333.5 ±9705.4 ±9704.9	1644.6 1544.7 1544.6	0.01 0.01 0.01	uod3, uoq3 iod_G3, ioq_G3
λ37,38 λ39,40	−120.2 −123.0	±10,333.4 ±9705.1	1644.6 1544.7	0.01 0.01	uod2, uoq2, iod_G2, ioq_G2 uod4, uoq4, iod_G4, ioq_G4
λ41,42 λ43,44, λ45,46 λ47,48	−338.6 −328.8 −319.9	±2149.0 ±2131.0 ±2120.5	342 339.2 337.5	0.16 0.15 0.15	UL1~UL4 IL1~IL4
λ49,50	−85.5	±1714.1	272.8	0.05	Un1~Un4 Il1~Il8
λ51,52 λ53,54, λ55,56	−145.1 −111.8	±1424.3 ±1574.2	226.7 250.5	0.1 0.07	Un1~Un4
λ57,58	−208.9	±410.7	65.4	0.45	Udc1~Udc4
λ59,60	−191.1	±307.4	48.9	0.53	Udc1, Udc3
λ61,62	−190.5	±304.2	48.4	0.53	Udc2, Udc4
λ63	−312.5	0	0	1.0	Il1~Il8
λ64,65	−11.7	±31.5	5.0	0.35	Udc1~Udc4, γd1~γd4
λ66,67	−5.5	±4.8	0.8	0.75	Φp1, Φp3, γd1, γd3
λ68,69	−7.1	±4.1	0.7	0.87	Φp2, Φp4, γd2, γd4
λ70,71	−10.7	±5.5	0.9	0.89	Φp3, γd3
λ72,73	−26.1	±16.0	2.5	0.85	z1, δPLL1
λ74,75, λ76,77, λ78,79	−25.5	±16.3	2.6	0.84	z2, δPLL2, z3, δPLL3, z4, δPLL4
λ80	−22.8	0	0	1.0	Ues1~Ues4, γd2~γd4
λ81	−13.8	0	0	1.0	Ues2, Ues4, γd2, γd4
λ82	−12.7	0	0	1.0	Ues1, Ues3, γd1, γd3
λ83	−3.3	0	0	1.0	Φv1~Φv4
λ84, λ85, λ86, λ87	−19.5	0	0	1.0	X1~X4
λ88	−50	0	0	1.0	Pdc3, Pdc4, γd3, γd4
λ89,90	−50	±1.3	0.2	1.0	Pdc2, Pdc4
λ91	−50	0	0	1.0	Pdc1, Pdc3
λ92,93, λ94, λ95,96	0	0	/	/	Ues1, Ues3, Φv1, Φv3, Φv4, Φp3

based on the parameters in Table 2. In the small-signal analysis, it is necessary to quantify the contribution of each state to a specific eigenvalue according to [38]. Thus, the major participants of each eigenvalue are exhibited in Table 3 as well.

As shown in Table 3, all eigenvalues have negative real parts indicating a stable operating condition for the system. It can be also seen that these eigenvalues fall in to three different clusters, namely, the high damped modes, the medium damped modes and low damped modes. The participation factor indicates that the inductive current of LC filter and inner current loop influence greatly the high damped modes λ₁–λ₁₆. These modes are not detrimental to the system stability. The medium damped modes λ₁₇–λ₆₃ are associated with the states of DC network (DC line currents, bus voltages, node voltages) and their effects on the AC side input currents and voltages. Additionally, the low damped modes considered as the dominate modes are associated with the states of secondary control. These dominate modes are greatly influenced by the parameters of secondary control and PLL. Moreover, the DC line parameters can be also selected to optimize the transient behavior of the DC network.

By plotting the eigenvalue loci in the complex plane, the impacts of the main parameters (such as the PI parameters of the secondary control, communication delay, the parameters of PLL, and the impedance parameters of DC distribution) on system dynamics can be observed. The eigenvalue loci in the complex plane with parameters variations are shown in Figures 8, 12, 13 and 15. In Figures 8, 12, 13 and 15, the eigenvalues are marked with stars. The arrows indicate the direction of the parameter variation and black circles indicate the parameters of critical stability. For simple analysis, only the important eigenvalues are plotted. The following subsections emphasize on the influence of these parameters on the system dynamics.

5.1. Distributed Secondary Controller Effect

This section presents the impact of the secondary voltage and power controller parameters k_P,V, k_I,V, k_P,P and k_I,P on the small-signal stability and the verification of the stable region through PSCAD simulation results. When the individual parameter is considered and changed for plotting eigenvalue loci, the other parameters are all consistent with the value as presented in Table 1. The varying range of individual parameter k_P,V, k_I,V, k_P,P and k_I,P is 1 to 50, 1 to 150, 1 to 10,000 and 1 to 300,000, respectively. The eigenvalue loci are shown in Figure 8, and Figure 9 shows the time-domain simulation results through PSCAD.

With a variation of proportional parameter k_P,V, which changed from 1 to 50, the parametric eigenvalue analysis is repeated. In the overview of the eigenvalue loci shown in Figure 8a, λ_80–82 move towards the left half of the complex plane along the real axis. The eigenpair λ_64,65 also move towards left, which indicates that the real part of λ_64,65 decrease while the damping ratio increase. Eigenvalue λ₈₃ moves towards the original point along the real axis, and the eigenpair λ_53,54 move towards the right part of the complex plane with the real part increasing dramatically. Furthermore, when the value of k_P,V is larger than 39.8, an obvious vibration appeared, and the λ_53,54 enter into the unstable region of the complex plane that bringing about the instability of the system.

Figure 8b exhibits the eigenvalue loci of the integral parameter k_I,V changing from 1 to 150, where eigenpair λ_53-54 are neglected due to unobvious changes in their locations and are not discussed in the following. With the increasing of k_I,V, it is clear that eigenvalues λ_80–83 all approach the original point along the real axis and the eigenpair λ_64,65 move towards the right half of the complex plane gradually. When the value of k_I,V is larger than 118.5, the λ_53,54 cross the imaginary axis, which means that they enter into the unstable region of the complex plane, generating the instability of the system.

Figure 8c shows the eigenvalue loci of the parameter k_P,P changing from 1 to 10000. For the power secondary control, eigenpairs λ_53,54, λ_66,67, λ_68,69 and λ_70,71 are discussed and analyzed here. It can be seen that with the k_P,P increasing, λ_70,71 move towards the left direction with the imaginary part becoming zero, which indicates that the oscillation of the output power disappears gradually. Meanwhile, λ_66,67 and λ_68,69 move towards the opposite direction with the imaginary part becoming zero and real part increasing. In addition, λ_53,54 move towards the right part of the complex plane fast and as soon as k_P,P is more than 7500, λ_53,54 cross the imaginary axis immediately, resulting in unstable operating state.

The integral parameter of power secondary control k_I,P is also the main parameter influencing the system stability. Figure 8d reveals the eigenvalue loci with k_I,P varying from 1 to 300,000. Eigenpair λ_53,54 is neglected while λ_64,65 is added in the following analysis. In Figure 8d, λ_66,67 turn to the left part of complex plane with moving towards the right direction at first. Eigenvalues λ_64,65, λ_68,69 and λ_70,71 have the same changing patterns, that is the imaginary parts move up and down respectively and the absolute value of imaginary parts increase with the parameter adding up, which means the system would experience a slow response.

To verify the eigenvalue loci shown in Figure 8, the time-domain responses of the multi-terminal LVDC distribution network simulated in PSCAD are plotted, as presented in Figure 9. Figure 9a shows that when k_P,V steps from 2 to 45 at 3.5 s, the state variable U_n1 experiences an amplitude oscillation, which corroborates the results obtained in Figure 8a. Similarly, Figure 9b indicates that when k_I,V steps from 10 to 2000 at 3.5 s, the DC voltage U_dc1 experiences an amplitude oscillation. However, this oscillation happens at 3.7 s and the value of k_I,V in this period is far larger than 118.5 shown in Figure 8b. Furthermore, Figure 9c shows the time-domain simulation results when k_P,P changes from 200 to 65,000. It can obviously be seen that state variable U_n1 undergoes an amplitude oscillation as well. Nevertheless, the value of k_P,P is still well over the stable region shown in Figure 8c. It indicates that the accuracy of MATLAB simulation is a little higher than the results simulated in PSCAD. As shown clearly in Figure 9d, when k_I,P varys from 2000 to 500,000, the curve of U_dc1 stay unchanged, which is in agreement with the results obtained in Figure 8d.

According to the above analysis, the design rule of PI parameters of secondary control for the system stability can be concluded as follows:

• The augment of k_P,V and k_I,V may decrease the relative damping with low-frequency eigenvalues, which goes against the system stability. Too large a value of k_P,V and k_I,V can cause low-frequency oscillation in the multi-terminal LVDC distribution network.
• Within the range of system stability, the gradual increase of k_I,P will decrease the damping ratio of the low-frequency eigenvalues. Furthermore, system also has the possibility of losing stability in the condition of large value of k_P,P.

5.2. Time Delay Effect

This section presents the impact of the time delay on the small-signal stability and the verification by PSCAD simulation. The impact of time delay cannot be neglected when the sampling rate of the secondary control level is very high. In order to study the impact on system stability, the expression of delay e^−τs should be simplified firstly. Using the first-order approximation of the Taylor series expansion, the e^−τs can be written as follows

$$e^{-\tau s}=\frac{1}{e^{\tau s}}=\frac{1}{1+\tau s+\frac{{\tau }^2{s}^2}{2!}+\frac{{\tau }^3{s}^3}{3!}+\dots }\approx \frac{1}{1+\tau s}$$

(39)

When the delay is small, the equation above stands. Obviously, the equation is a first-order lag function, which will bring a state variable. Based on the simplified equation, the distributed secondary control with communication delay τ can be described as follows

$$\{\begin{array}{l}{U}_{avei}=U_{dci}+C_E{\displaystyle {\int }_0^t{\displaystyle \sum _{j\in N_i}{a}_{ij}({\overline{U}}_{avej}}}-U_{avei})d\zeta \\ P_{ave\lambda i}=d_{ii}{P}_{dc\lambda i}+{\displaystyle \sum _{j\in N_i}^n{d}_{ij}}{\overline{P}}_{dc\lambda j}\\ {\overline{U}}_{avei}=\frac{1}{1+\tau s}{U}_{avei}, {\overline{P}}_{dc\lambda i}= \frac{1}{1+\tau s}{P}_{dc\lambda i} \end{array}$$

(40)

Finally, replace the original state-space model of the distributed secondary control with Equation (40), the small-signal model of the entire DC distribution network with time delay can be obtained as follows

$$\Delta {\dot{\overline{\mathit{x}}}}_s={\overline{\mathit{A}}}_s\Delta {\overline{\mathit{x}}}_s+{\overline{\mathit{B}}}_s\Delta \mathit{R}+{\overline{\mathit{C}}}_s\Delta \omega +{\overline{\mathit{D}}}_s\Delta \mathit{E}$$

(41)

where, Δ${\overline{\mathit{x}}}_s$ is the state variable including the new variable Δ${\overline{U}}_{ave}$ and Δ${\overline{P}}_{dc\lambda }$, which are related to time delay. These eigenvalues related to time delay are calculated and listed in

Table 4. The new eigenvalues.

Mode	Re	Im	Frequency (Hz)	Damping Ratio	Major Participants
λ97	−345.6	0	0	1.0	${\overline{U}}_{ave1}$~${\overline{U}}_{ave4}$, Δ${\overline{P}}_{dc\lambda 1}$, Δ${\overline{P}}_{dc\lambda 3}$
λ98	−340.8	0	0	1.0	Δ${\overline{P}}_{dc\lambda 1}$, ~Δ${\overline{P}}_{dc\lambda 4}$
λ99	−323.4	0	0	1.0	${\overline{U}}_{ave1}$~${\overline{U}}_{ave4}$
λ100	−323.9	0	0	1.0	Δ${\overline{P}}_{dc\lambda 1}$, ~Δ${\overline{P}}_{dc\lambda 4}$
λ101,102	−333.3	±0.0	0	1.0	Δ${\overline{P}}_{dc\lambda 2}$, Δ${\overline{P}}_{dc\lambda 4}$
λ103,104, λ105,106	−333.3	±0.0	0	1.0	Δ${\overline{P}}_{dc\lambda 2}$, Δ${\overline{P}}_{dc\lambda 4}$, ${\overline{U}}_{ave1}$, ${\overline{U}}_{ave3}$
λ107,108	−333.3	±0.0	0	1.0	${\overline{U}}_{ave1}$, ${\overline{U}}_{ave3}$
λ109	−333.3	±0.0	0	1.0	Δ${\overline{P}}_{dc\lambda 2}$, Δ${\overline{P}}_{dc\lambda 4}$
λ110	−333.3	±0.0	0	1.0	${\overline{U}}_{ave3}$
λ111	−333.3	±0.0	0	1.0	Δ${\overline{P}}_{dc\lambda 2}$, Δ${\overline{P}}_{dc\lambda 4}$, ${\overline{U}}_{ave1}$, ${\overline{U}}_{ave3}$
λ112	−333.3	±0.0	0	1.0	${\overline{U}}_{ave2}$, ${\overline{U}}_{ave4}$

based on the parameters of DC distribution network and τ = 3 ms.

As shown in Table 4, all new eigenvalues have negative real parts indicating a stable operating condition for the system when τ = 3 ms. That is, the small delay has little impact on the stability of the system. In order to study the impact of large delay, the eigenvalue loci are plotted according to different time delay. The varying range of time delay is 3 ms to 50 ms, and the eigenvalue loci are shown in Figure 10.

With the increasing of τ, it is clear that all eigenvalues approach the original point along the real axis first. Then, all the eigenvalues are equal to −50 at τ = 20 ms. From then on, some eigenvalues’ imaginary parts begin to increase, and they move towards the right half of the complex plane gradually. From Figure 10, it can be indicated that the system is still stable during 3 ms to 50 ms, however, the stability of the DC distribution network is weakened. With the increasing of τ, the oscillation will appear on the estimated average voltages, and the damping ratio decrease gradually. Furthermore, the simulation by PSCAD is implemented as shown in Figure 11. From Figure 11, it can be seen that the ${\overline{U}}_{ave}$ will appear low-frequency oscillation after a small disturbance when τ = 30 ms, while the responses are smooth when τ = 3 ms. The damped time of the oscillation is about 0.42 s, which is similar with the result in Figure 10. Thus, the time domain simulation verifies the results from eigenvalue analysis in Figure 10.

5.3. Phase Locked Loop Effect

This part mainly discusses the effects of PI parameters of phase locked loop on system stability. The secondary control parameters are all original parameters presented in Table 2 when PI parameters of PLL are studied. The changing range of PI parameters are 1 to 520 and 1 to 1000 respectively. The eigenvalues loci are plotted in Figure 12.

For phase locked loop, with k_P,PLL and k_I,PLL varying, the eigenvalue loci are shown in Figure 12. In Figure 12a, it is clearly found that λ_88,91 move towards the left direction, which means they have little impacts on system stability when k_P,PLL changes. Apart from these, eigenvalue λ_81,82,83 as well as eigenpairs λ_25,26, λ_29,30, λ_31,32 and λ_37,38 move towards the right part of complex plane with k_P,PLL varying gradually. One point to note is that, when the value of k_P,PLL is up to 502.5, the stablity of system will face threats due to eigenpairs λ_25,26, λ_29,30, λ_31,32 and λ_37,38 cross the imaginary axis.

Figure 12b shows the eigenvalue loci with k_I,PLL varying from 1 to 1000. Eigenvalues λ_81,82,83 all move towards the left direction along the negative real axis while λ_89,91 move towards the opposite direction. Furthermore, the absolute values of imaginary part of eigenpairs λ_72,73, λ_74,75, λ_76,77 and λ_76,77 increase as k_I,PLL changed from 1 to 1000, which means that the damping ratio decrease slowly. Although the response speed of the system declines, the stability of it still can be ensured.

According to the above analysis, the design rule of PI parameters of phase locked loop for the system stability can be concluded as follows:

• The augment of k_P,PLL has an important effect on the medium damped modes. Too large a value of k_P,PLL can cause an unstable state of system.
• The parameter k_I,PLL has something to do with the system oscillation. And the increase of k_I,PLL may decrease the damping ratio with high-frequency eigenvalues without affecting the system stability.

5.4. DC Distribution Line Effect

According to the analysis above, the DC line parameters also have an impact on the system’s stability. Here, the effects of DC inductance L_l1–L_l8 and DC resistance R_l1–R_l8 are considered and studied shown in Figure 13, where the varying scopes of L_l1–L_l8 and R_l1–R_l8 are 3.2 × 10⁻⁵ H to 3.2 × 10⁻³ H and 0.01 Ω to 1 Ω respectively. Simulations in PSCAD with parameters varying confirm the correctness of stable region as shown in Figure 14.

In Figure 13a, all eigenvalues including λ_49–63 move towards the right part of complex plane as parameters L_l1-L_l8 changed from 3.2 × 10⁻⁵ H to 3.2 × 10⁻³ H. When L_l1–L_l8 are all set to 1.28 × 10⁻³ H, the eigenpairs λ_49,50, λ_53,54 and λ_55,56 all enter into the right part of complex plane, indicating that system lose stability. It is noted that when the parameters of L_l1–L_l8 are 1.28 × 10⁻³ H, the first eigenvalues crossing the imaginary axis are λ_49,50, whose major participants are U_n1–U_n4.

Figure 13b shows the eigenvalue loci in the parametric sweep of R_l1–R_l8 varying in the range of 0.01 Ω to 1 Ω. Eigenvalues λ_49–63 all move towards the imaginary axis or along the imaginary axis in a left direction. Especially, when the value of R_l1–R_l8 is less than 0.04 Ω, the eigenpairs λ_49,50 exist in the right part of the coordinate system, causing system unstable.

Figure 14a indicates that when L_l1–L_l8 steps from 0.32 mH to 5 mH at 3.5 s, the voltage of CPL1 U_n1 experiences an amplitude oscillation. This oscillation is unobvious at the beginning and becomes conspicuous after 3.7 s and it is a divergent oscillation, which demonstrates that there is small-signal instability appearing in the system when inductance parameter is larger than 1.28 mH. Similarly, in Figure 14b, when R_l1–R_l8 step from 0.1 Ω to 0.001 Ω at 3.5 s, the state variable U_n1 also experiences an amplitude oscillation apparently. The unstable state after 3.5 s demonstrates that the time-domain simulation results are in agreement with the stable region obtained in Figure 13b and small value of R_l1–R_l8 might cause instability. Moreover, the influence of R_l1–R_l8 is not as obvious as that of L_l1–L_l8.

According to the above analysis, the design rule of parameters L_l1–L_l8 and R_l1–R_l8 of DC line for the system stability can be concluded as follows:

• The increase of L_l1–L_l8 has significant influences on the medium damped modes and low damped modes. Too large a value of L_l1–L_l8 can cause an unstable state of system.
• The augment of R_l1–R_l8 may increase the relative damping with low-frequency and medium-frequency eigenvalues. Too small a value of R_l1–R_l8 has a tendency of causing system to lose stability.

These rules are significant for parameters design and optimization of the multi-terminal LVDC system such as PI parameters of the secondary control, which are the key parameters for VSC control. During the parameters design based on the small-signal model analysis, it must be ensured that all the eigenvalues of the system in every frequency range are provided with enough damping. The parameter design for the multi-terminal LVDC system must combine the stability of the eigenvalues in every frequency range.

5.5. Different Load Effect

This part mainly discusses the effects of constant power load (CPL) and resistance load on system stability. The CPL is the load whose electricity power does not change, while the resistance load will change according to the voltage. The eigenvalues of the system are used to explain the influence of different loads on system stability. Further, the simulation in time domain is implemented to illustrate the stability problem. Firstly, the DC distribution network with CPL and the DC distribution network with resistance load are modeled respectively based on the small signal modeling method presented in this paper. Then, the eigenvalues can be calculated based on A_{s_CPL} and A_{s_RES}, where A_{s_CPL} is the state matrix of the CPL system, and A_{s_RES} is the state matrix of the resistance system. The eigenvalues or modes that are related to U_dc, I_dc, U_n and I_l are shown in Figure 15.

From Figure 15, it can be seen that the number of eigenvalues of A_{s_CPL} is more than that of A_{s_RES}, because the CPL will bring extra modes from DC/DC converter. The both systems are stable, however, the extra modes that the CPL generated have a large imaginary part, and they are closer to real axis. Thus, it can be indicated that the variation of CPL will bring higher oscillation (about 239 Hz), and the damped time will be longer. However, the modes of resistance system have a smaller imaginary part, and the oscillation frequency is about 80 Hz. Moreover, the damped speed is faster. From the distribution of eigenvalues of different systems, the resistance load has a less impact on the stability of the system. Additionally, the simulation by PSCAD is implemented as shown in Figure 16. From Figure 16, it can be seen that the U_dc, I_dc, and U_n will appear high-frequency oscillation after a 4 kW CPL is connecting to network. The damped time of the oscillation mode is about 0.046 s, which is similar with the result in Figure 15. In the same condition, the voltage and current change gently after the 4 kW resistance load is connecting to network. Thus, the time domain simulation verifies the results from eigenvalue analysis in Figure 15.

6. Discussion

In this paper, a small-signal modeling procedure of a four-terminal LVDC distribution network with distributed secondary control is presented and analyzed. The main focus is the small-signal analysis where eigenvalue analysis and major participants analysis are adopted. The benefit of modular method is the rapidity and scalability of the small-signal modeling. In other words, the procedure of modeling is suitable for multi-terminal LVDC system. The presented procedure of modeling considers three main aspects containing individual converter stations, distributed control part and DC distribution line/load.

With the established small-signal model, the rules of system eigenvalues varying caused by the change of some parameters are carried out and analyzed. In Section 5, distributed secondary controller effect, phase locked loop effect and DC distribution line and load effect on system small-signal stability are considered. On the basis of presented results, some important influence laws are displayed in paper which indicate that PI control parameters of distributed secondary control and DC distribution line parameters such as inductance and resistance have a relative significant effect on system voltage stability through eigenvalue loci and simulations on PSCAD. Moreover, the operational limits of studied parameters are given in this study. The time-domain simulation by PSCAD is conducted for the entire LVDC system to verify the operational limits of the model, and the design rules are given for main parameters of the four-terminal LVDC distribution network, which gives a guideline for future practical parameter selection. The presented analysis only considered some important parameters, and the analysis with some other parameters varying can be studied in the future research.

7. Conclusions

A distributed secondary control method for VSCs and a detailed and accurate small-signal analysis model for a four-terminal LVDC distribution network are presented in this paper. Compared with traditional control method, the adopted secondary control strategy based on average consensus algorithm and local voting protocol can promote the power distribution accuracy while increasing the average voltage. This paper focuses on the small-signal stability analysis for the multi-terminal LVDC distribution network. Firstly, various non-linear state-space models of individual entities including individual VSC with primary control, distributed secondary control and DC distribution line/load are built. Secondly, small-signal model of the entire system is established based on individual non-linear state-space model. The accuracy of the proposed model is further assessed through a comparison between the results from the electromagnetic simulation in PSCAD and small-signal model in MATLAB. At last, eigenvalue analysis and major participants analysis are adopted to study the effects of main parameters on the stability of the system involving PI control, time delay and DC distribution line or load. However, the presented results are valid for LVDC distribution network only. If the system’s voltage is higher than the studied one in this paper, the MMC structure should be adopted for the converter station. Then, the modeling will be more complicated and the small-signal analysis need more consideration. Furthermore, the time-domain simulation results will be supplemented and verified through laboratory simulation for the next research direction.