A 0.18-ns Response Time Digital LDO Regulator with Adaptive PI Controller in 180-nm CMOS
Abstract
:1. Introduction
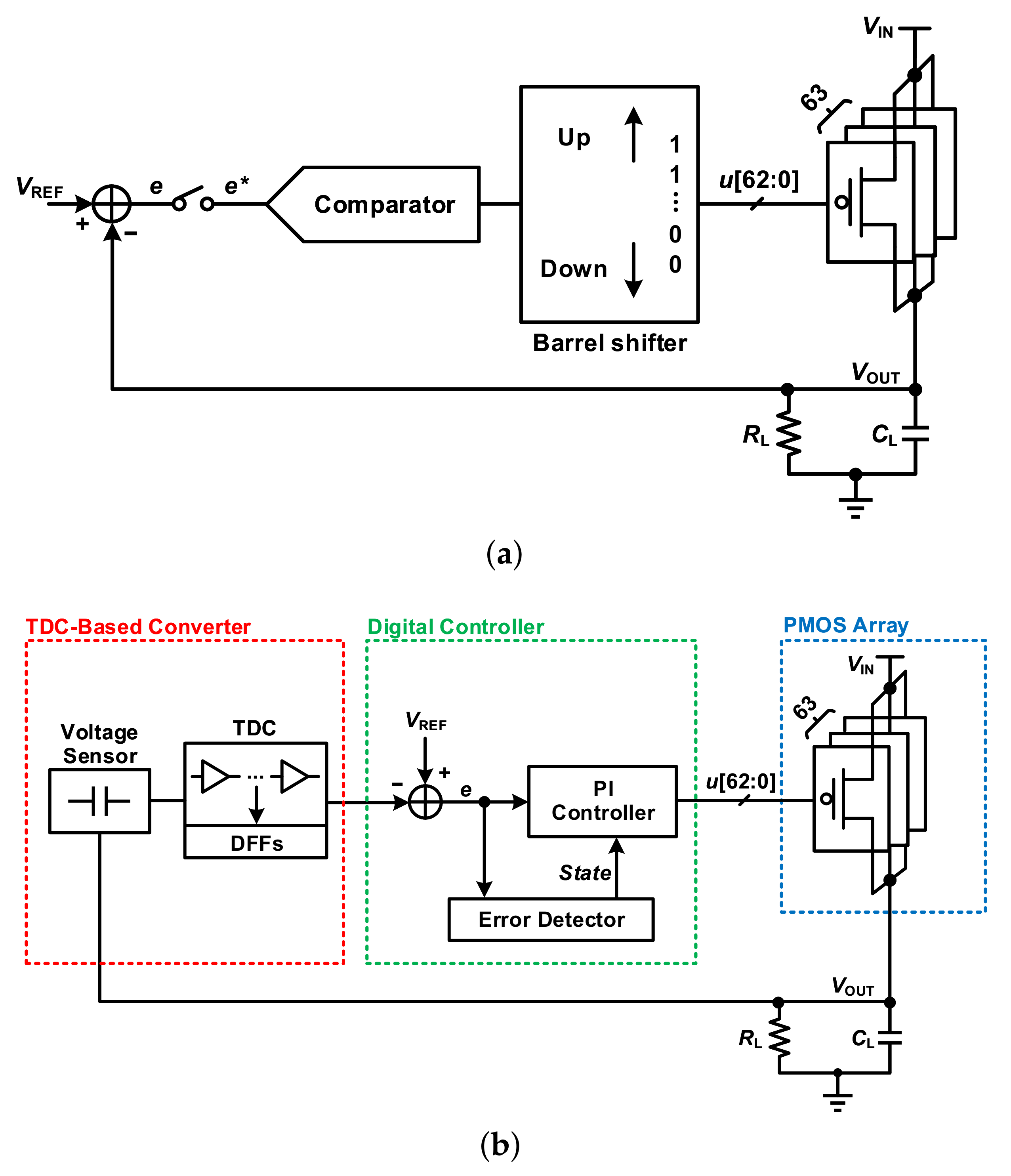
2. Architecture of the Proposed D-LDO
2.1. Topology
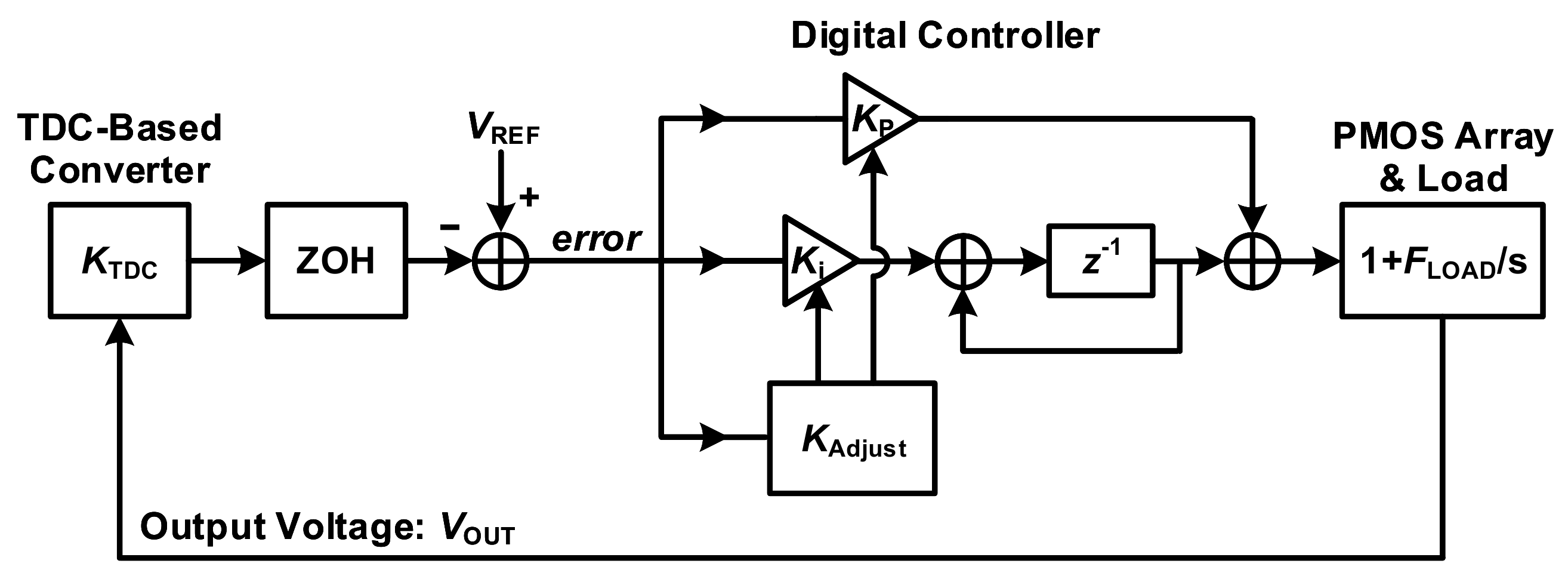
2.2. Transfer Function of the Control Loop
3. Circuit Implementation
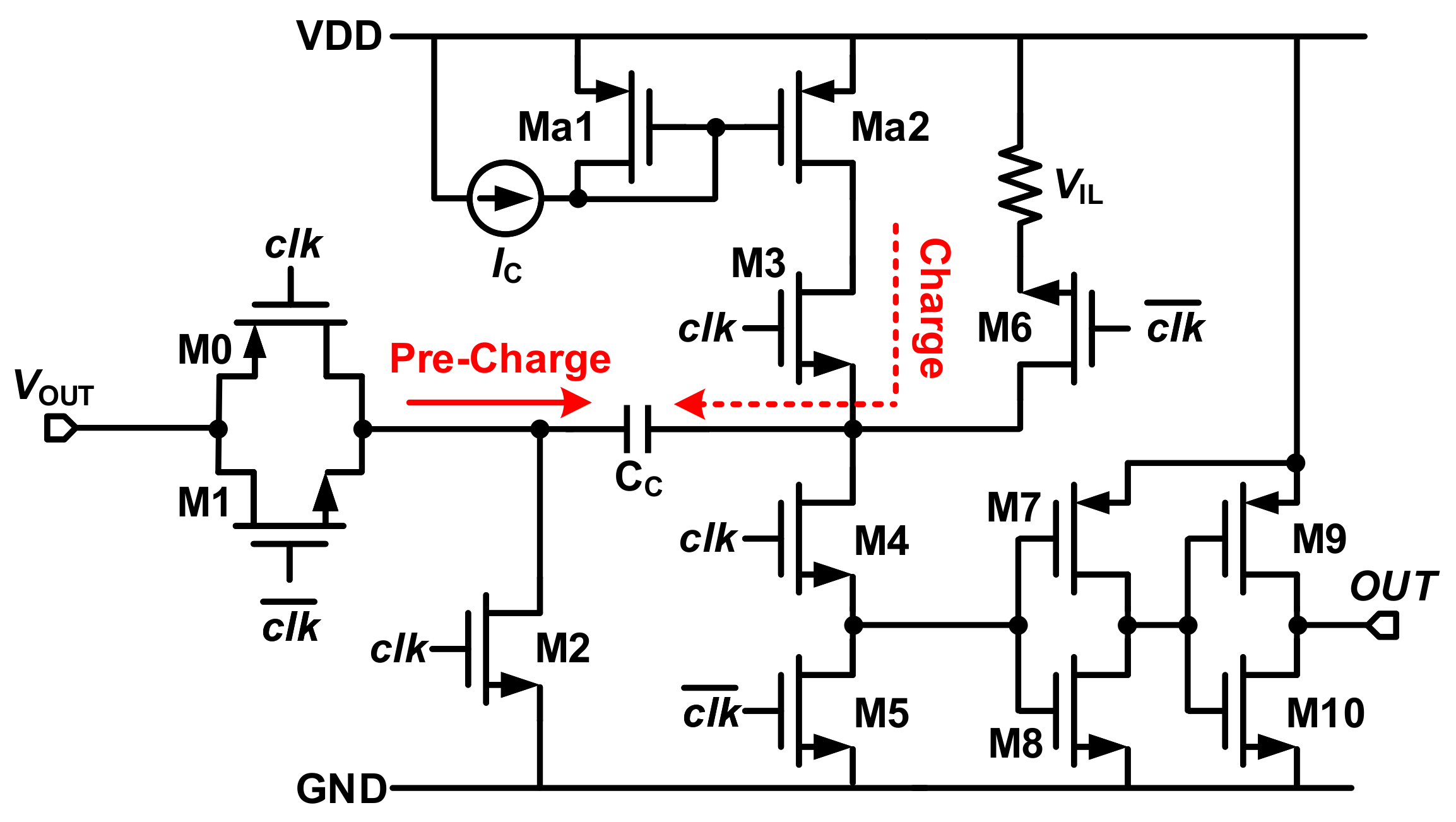
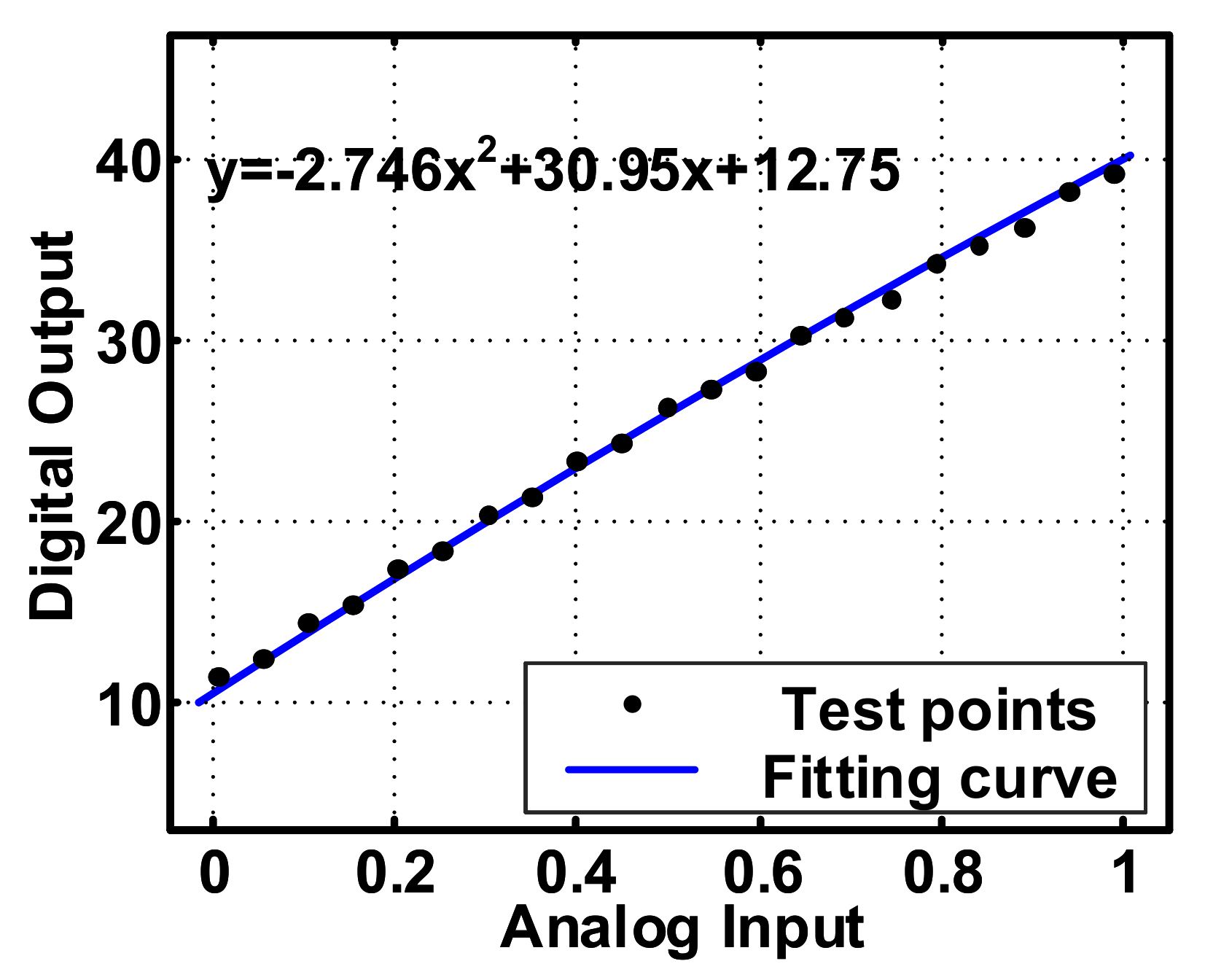
3.1. Time-to-Digital Based Converter
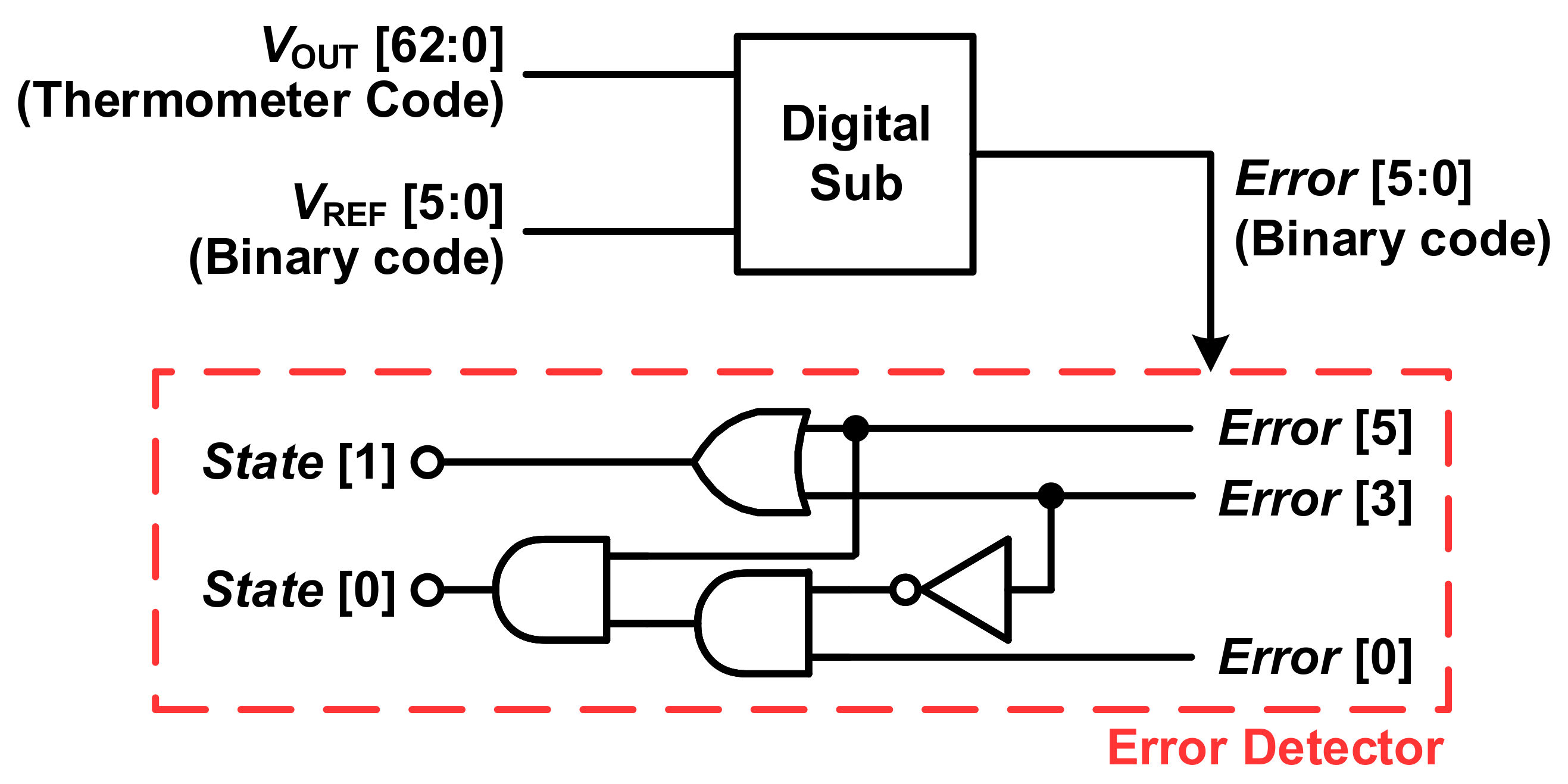
3.2. Error Detector
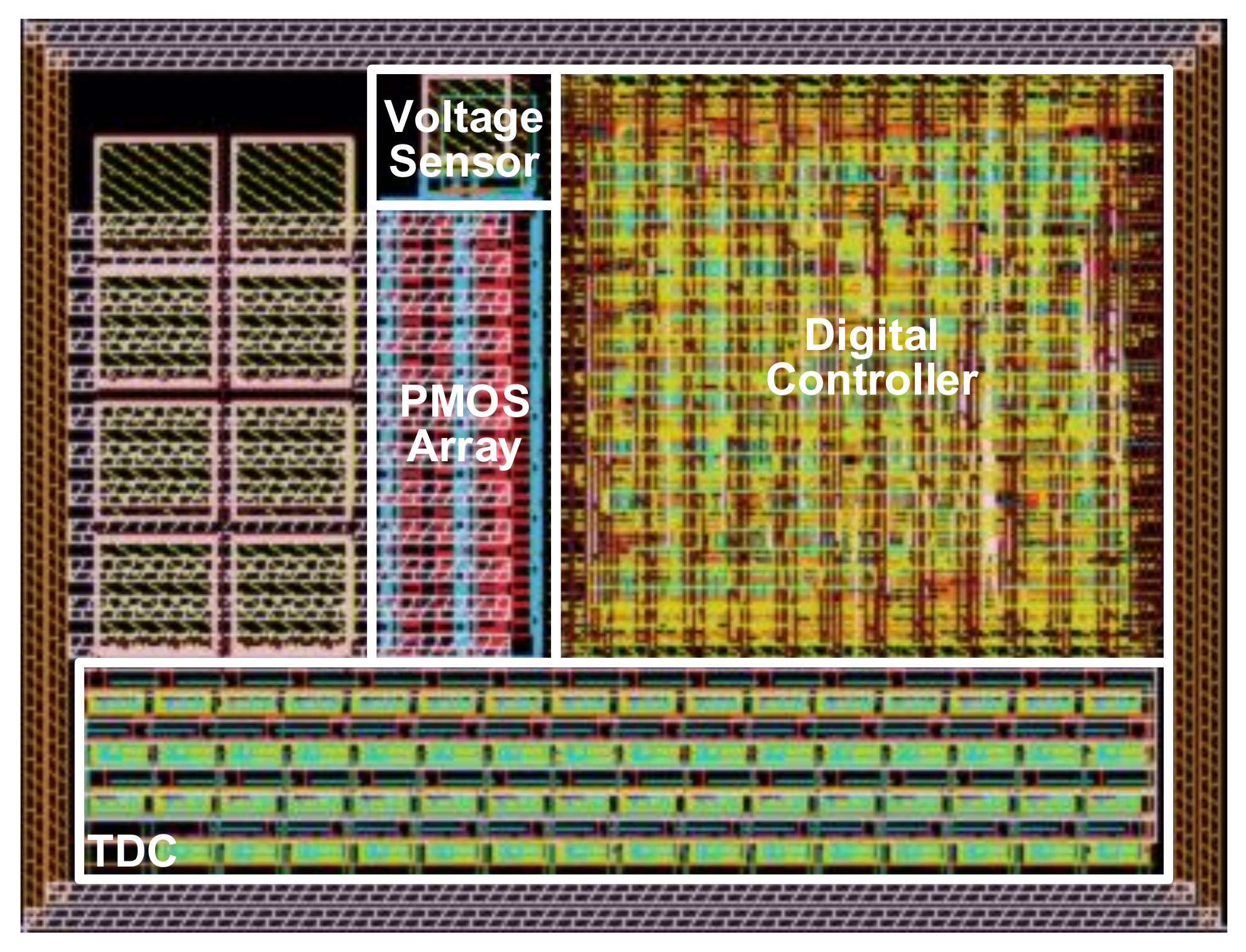
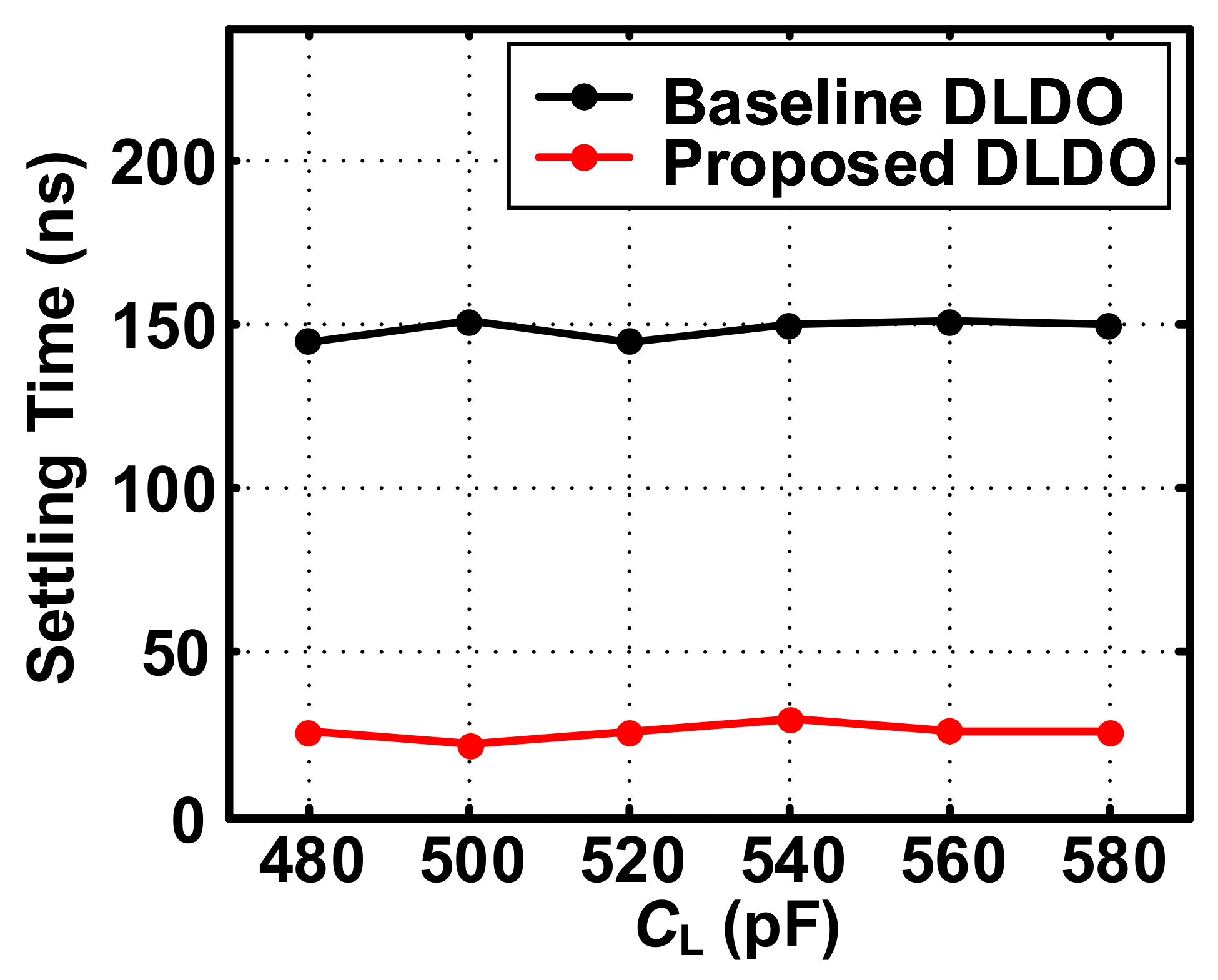
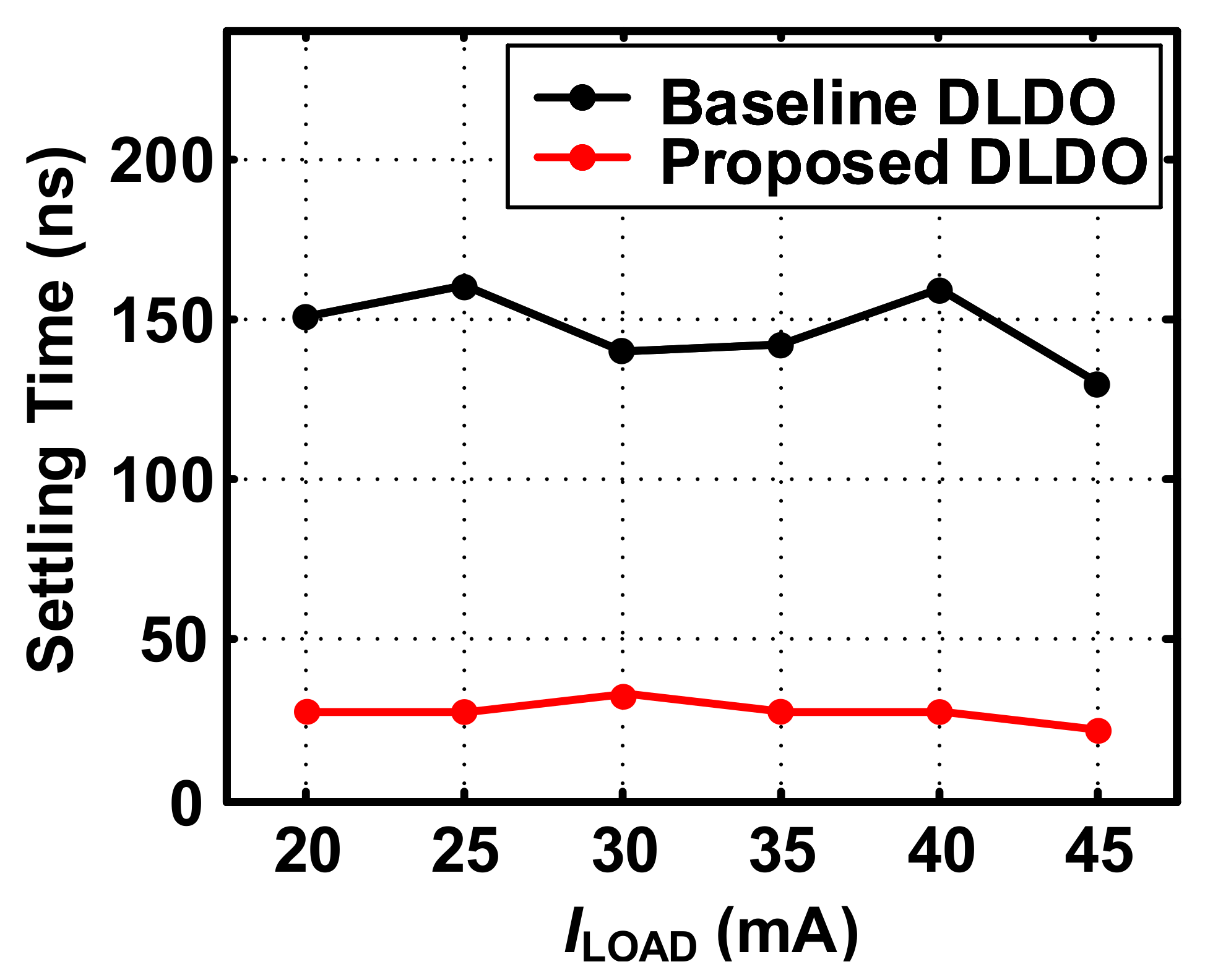
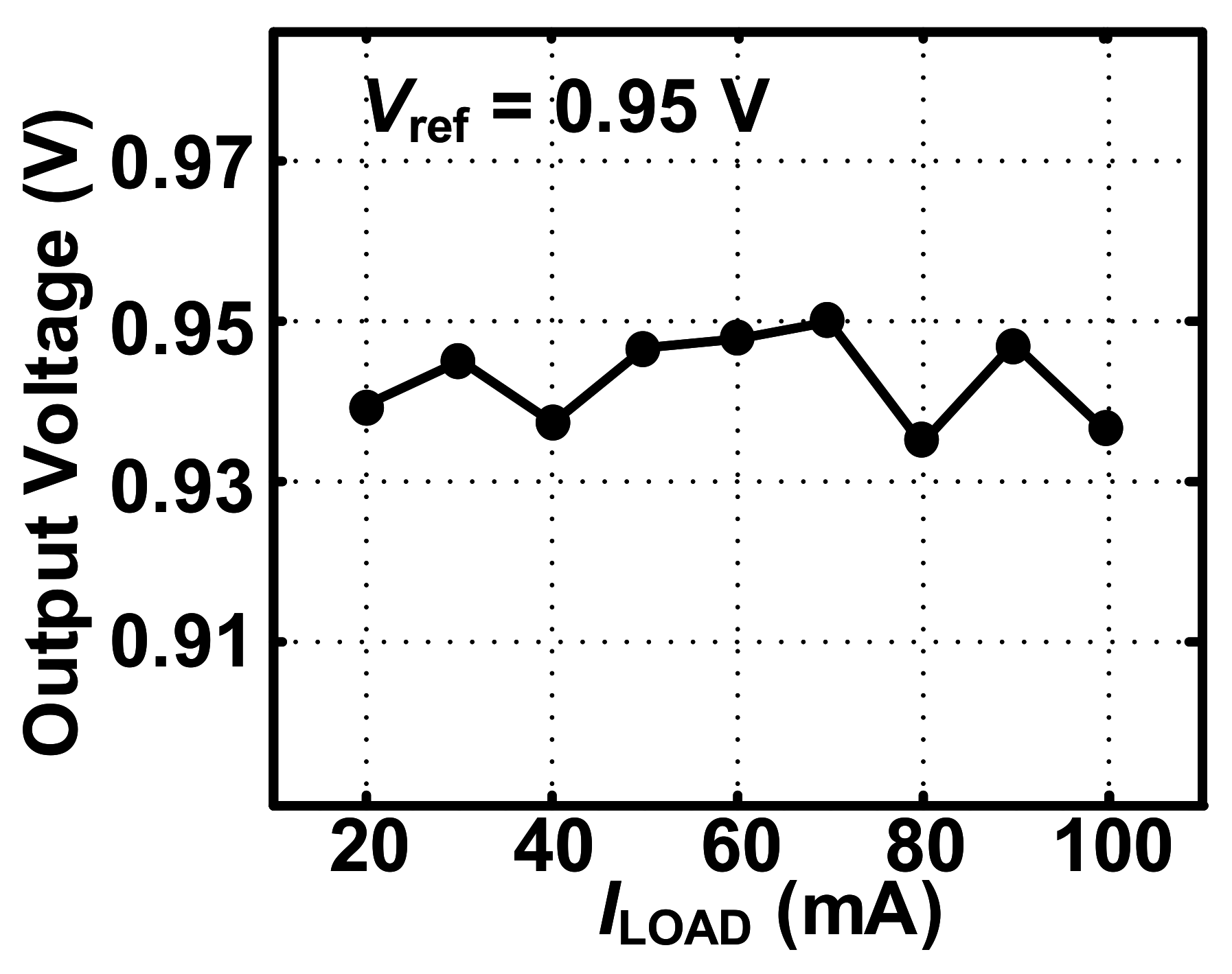
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lam, Y.H.; Ki, W.H. A 0.9 V 0.35 µm Adaptively Biased CMOS LDO Regulator with Fast Transient Response. In Proceedings of the 2008 IEEE International Solid-State Circuits Conference—Digest of Technical Papers, San Francisco, CA, USA, 3–7 February 2008; pp. 442–626. [Google Scholar]
- Milliken, R.J.; Silva-Martinez, J.; Sanchez-Sinencio, E. Full On-Chip CMOS Low-Dropout Voltage Regulator. IEEE Trans. Circuits Syst. I Regular Pap. 2007, 54, 1879–1890. [Google Scholar] [CrossRef]
- Nasir, S.B.; Gangopadhyay, S.; Raychowdhury, A. All-Digital Low-Dropout Regulator With Adaptive Control and Reduced Dynamic Stability for Digital Load Circuits. IEEE Trans. Power Electron. 2016, 31, 8293–8302. [Google Scholar] [CrossRef]
- Ojima, N.; Nakura, T.; Iizuka, T.; Asada, K. A Synthesizable Digital Low-Dropout Regulator Based on Voltage-to-Time Conversion. In Proceedings of the 2018 IFIP/IEEE International Conference on Very Large Scale Integration (VLSI-SoC), Verona, Italy, 8–10 October 2018; pp. 55–58. [Google Scholar]
- Woo, K.; Kim, T.; Hwang, S.; Kim, M.; Yang, B. A fast-transient digital LDO using a double edge-triggered comparator with a completion signal. In Proceedings of the 2018 International Conference on Electronics, Information, and Communication (ICEIC), Honolulu, HI, USA, 24–27 January 2018; pp. 1–4. [Google Scholar]
- Salem, L.G.; Warchall, J.; Mercier, P.P. A 100 nA-to-2 mA successive-approximation digital LDO with PD compensation and sub-LSB duty control achieving a 15.1 ns response time at 0.5 V. In Proceedings of the 2017 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 5–9 February 2017; pp. 340–341. [Google Scholar]
- Amayreh, M.; Leicht, J.; Manoli, Y. A 200ns settling time fully integrated low power LDO regulator with comparators as transient enhancement. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, USA, 22–25 May 2016; pp. 494–497. [Google Scholar]
- Ding, Z.; Rhee, W.; Wang, Z. A VCO-dedicated digital LDO with multi-comparator coarse loop and 1-bit Δ∑ fine loop for robust frequency generation. In Proceedings of the 2018 IEEE MTT-S International Wireless Symposium (IWS), Chengdu, China, 6–10 May 2018; pp. 1–4. [Google Scholar]
- Lu, Y.; Huang, M.; Martins, R.P. PID Control Considerations for Analog-Digital Hybrid Low-Dropout Regulators (Invited Paper). In Proceedings of the 2019 IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC), Xi’an, China, 12–14 June 2019; pp. 1–3. [Google Scholar]
- Kim, D.; Seok, M. A fully integrated digital low-dropout regulator based on event-driven explicit time-coding architecture. IEEE J. Solid State Circuits 2017, 52, 3071–3080. [Google Scholar] [CrossRef]
- Lim, C.; Mandal, D.; Bakkaloglu, B.; Kiaei, S. A 50-mA 99.2% Peak Current Efficiency, 250-ns Settling Time Digital Low-Dropout Regulator with Transient Enhanced PI Controller. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2017, 25, 2360–2370. [Google Scholar] [CrossRef]
- Santos, M.; Dormido, S.; de la Cruz, J.M. Fuzzy-PID controllers vs. fuzzy-PI controllers. In Proceedings of the IEEE 5th International Fuzzy Systems, New Orleans, LA, USA, 11 September 1996; Volume 3, pp. 1598–1604. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 116–132. [Google Scholar] [CrossRef]
- Hazucha, P.; Karnik, T.; Bloechel, B.A.; Parsons, C.; Finan, D.; Borkar, S. Area-efficient linear regulator withultra-fast load regulation. IEEE J. Solid State Circuits 2005, 40, 933–940. [Google Scholar] [CrossRef]
- Yuan, Z.; Fan, S.; Geng, L. A 225-mA Binary Searching Digital LDO with Transient Enhancement. In Proceedings of the 2019 IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC), Xi’an, China, 12–14 June 2019; pp. 1–2. [Google Scholar]
- Yuan, Z.; Fan, S.; Yuan, C.; Geng, L. A 100 MHz, 0.8-to-1.1 V, 170 mA Digital LDO with 8-Cycles Mean Settling Time and 9-Bit Regulating Resolution in 180-nm CMOS. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1664–1668. [Google Scholar] [CrossRef]
- Chen, W.-J.; Huang, C.-H. Fast-Turnaround Design and Modeling Techniques for a Fast-Transient Digital Low-Dropout Regulator With 3 mV Ripples. IEEE Trans. Power Electron. 2021, 36, 6824–6837. [Google Scholar] [CrossRef]





| Error Levels | Input | Output | |||
|---|---|---|---|---|---|
| Error[5] | Error[3] | Error[0] | State[1] | State[0] | |
| Error ≥ 32 | 1 | X | X | 1 | 1 |
| Error ≥ 8 | 0 | 1 | X | 1 | 0 |
| Error ≥ 1 | 0 | 0 | 1 | 0 | 1 |
| Error = 0 | 0 | 0 | 0 | 0 | 0 |
| Input | Output | ||
|---|---|---|---|
| State[1] | State[0] | P | I |
| 0 | 0 | Hold on | Hold on |
| 0 | 1 | 0.8 | 4 |
| 1 | 0 | 1 | 0.7 |
| 1 | 1 | 1.2 | 0.1 |
| Design | Yuan [15], EDSSC’19 | Yuan [16], TCSII’20 | Chen [17], TPEL’21 | This Work |
|---|---|---|---|---|
| Process | 180-nm | 180-nm | 110-nm | 180-nm |
| (V) | 1 | 0.8–1.1 | 0.8–1.2 | 1–1.2 |
| (V) | 0.9 | 0.7–1.0 | 0.7–1.1 | 0.95 |
| Load Regulation (mV/mA) | 0.053 | 0.11 | 0.422 | 0.3 |
| Current Consumption (A) | 500 | 500 | 188.8–197.9 | 34.68 |
| Total | Not available | 390 pF | 40 pF | 0.5 nF |
420 mV @216 mA | 267 mV @160 mA | 360 mV @47.5 mA | 36 mV @40 mA | |
| Load Transient Edge Time (ns) | NA | 65 | <1 | 1 |
| Recovery Under/Over-shoot Time (ns) | 80/80 | 80/80 | 67/250 | 143/186 |
| Peak Current Efficiency (%) | 99.78 | 99.71 | 92.98–99.61 | 99.64 |
| Response Time (ns) | 0.95 | 0.52 | 0.2 | 0.18 |
| FOM1 (ps) | 2.1 | 2.03 | 1.26 | 0.65 |
| FOM2 (pF) | Not available | 0.362 | 0.0706 | 0.068 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, S.; Wan, P.; Zhang, H.; Geng, J.; Wen, J.; Yao, Y.; Chen, Z. A 0.18-ns Response Time Digital LDO Regulator with Adaptive PI Controller in 180-nm CMOS. Electronics 2021, 10, 1668. https://doi.org/10.3390/electronics10141668
Lv S, Wan P, Zhang H, Geng J, Wen J, Yao Y, Chen Z. A 0.18-ns Response Time Digital LDO Regulator with Adaptive PI Controller in 180-nm CMOS. Electronics. 2021; 10(14):1668. https://doi.org/10.3390/electronics10141668
Chicago/Turabian StyleLv, Shengping, Peiyuan Wan, Hongda Zhang, Jiarong Geng, Jiabao Wen, Yiming Yao, and Zhijie Chen. 2021. "A 0.18-ns Response Time Digital LDO Regulator with Adaptive PI Controller in 180-nm CMOS" Electronics 10, no. 14: 1668. https://doi.org/10.3390/electronics10141668
APA StyleLv, S., Wan, P., Zhang, H., Geng, J., Wen, J., Yao, Y., & Chen, Z. (2021). A 0.18-ns Response Time Digital LDO Regulator with Adaptive PI Controller in 180-nm CMOS. Electronics, 10(14), 1668. https://doi.org/10.3390/electronics10141668






