Prescribed Performance-Based Event-Driven Fault-Tolerant Robust Attitude Control of Spacecraft under Restricted Communication
Abstract
:1. Introduction
- A robust attitude regulation control using an SMC-based PPC technique is proposed to tackle model uncertainties, disturbances, and actuator faults for the spacecraft system.
- The PPF enables the spacecraft to achieve a predefined transient and steady-state response without repeated tuning of control parameters.
- The constraint on the communication network is also considered while designing the control law. Therefore, an event trigger strategy is integrated with the proposed PPC-based SMC scheme. Moreover, the event-triggering rule is established using the negative definiteness rule of the Lyapunov theory, unlike [29,30,31,32,33,34], where a predefined relative threshold function is used. Therefore, the proposed ET approach is more promising and convenient for other sets of dynamics as well.
- The theoretical analysis establishes the convergence of sliding surface, transformed attitude state, and state trajectories. The overall closed-loop system analysis under the ET-based PPF-SMC strategy guarantees the uniformly ultimately bounded (UUB) convergence of the preceding signals. Moreover, precluding the Zeno phenomenon is also proved under the proposed ET strategy.
2. Attitude Model of Spacecraft
2.1. The Attitude Model of Spacecraft
2.2. Control Objectives
- Design a robust fault-tolerant control for the attitude regulation of the spacecraft under various uncertainties.
- The transient and the steady-state response of attitude should satisfy a priori prescribed performance without repeated attempts in tuning the gain parameters of the control. In other words, the predefined performance measures (rate of convergence, maximum overshoot, accurate steady-state precision) should be achieved.
- The controller and actuator modules interact with each other minimally to update the control data. Thus, the rate of control update through the restricted communication channel is lesser.
- All the internal and output signals must be bounded.
3. Design of Prescribed Performance Approach
3.1. Prescribed Performance Function
- (i)
- The and monotonically decaying.
- (ii)
- .
3.2. Attitude State Transformation
4. Proposed Controller Design
4.1. Proposed PPF Based SMC
4.2. Stability Analysis
5. Proposed Event-Trigger Mechanism
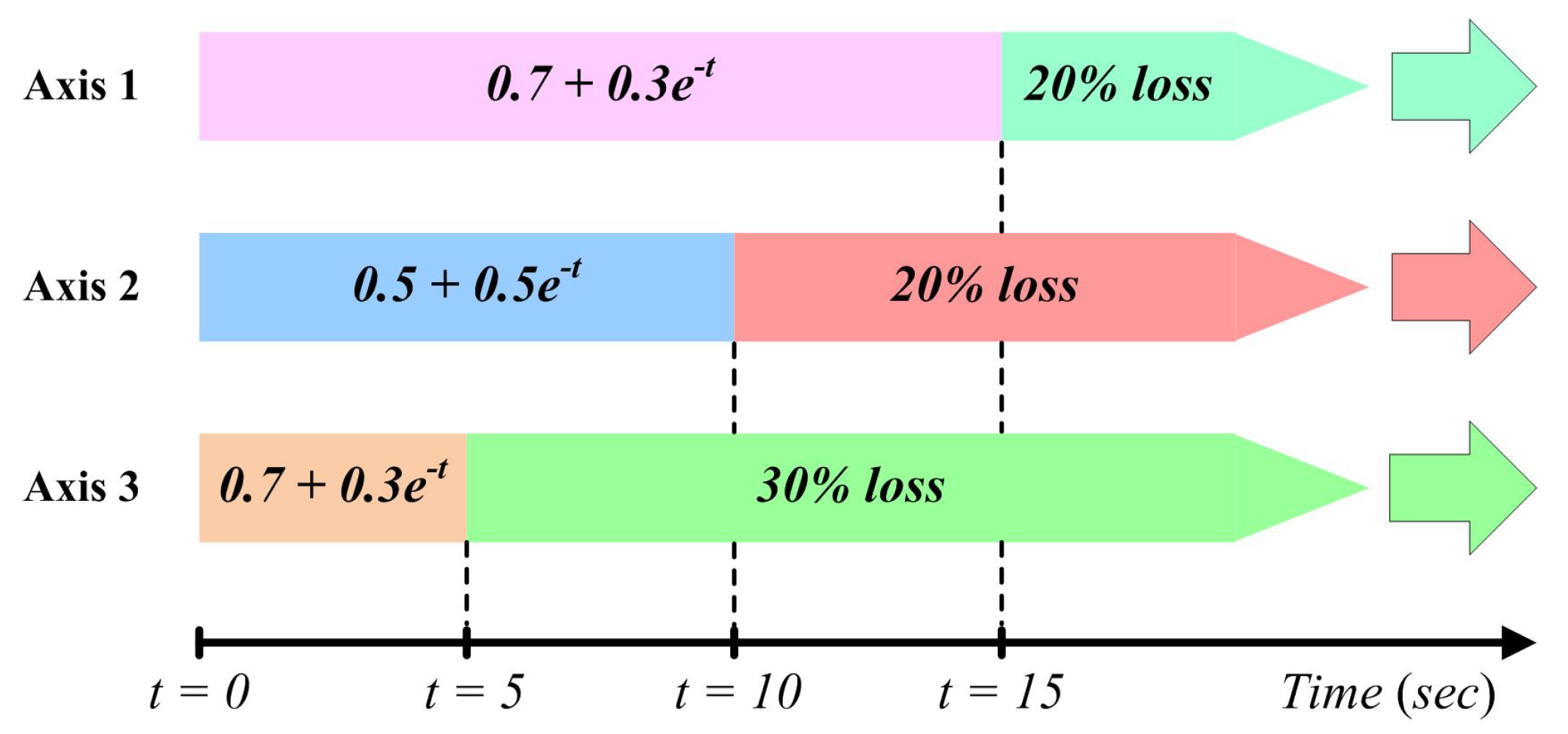
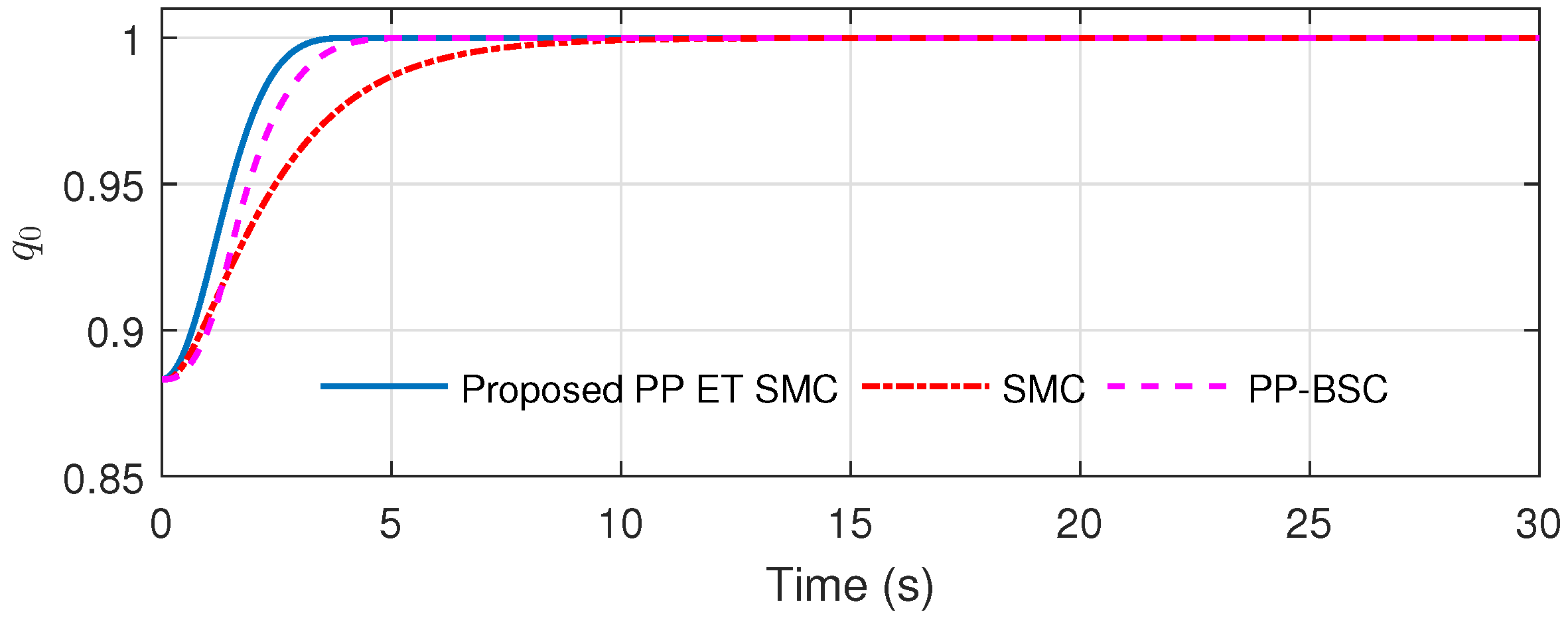
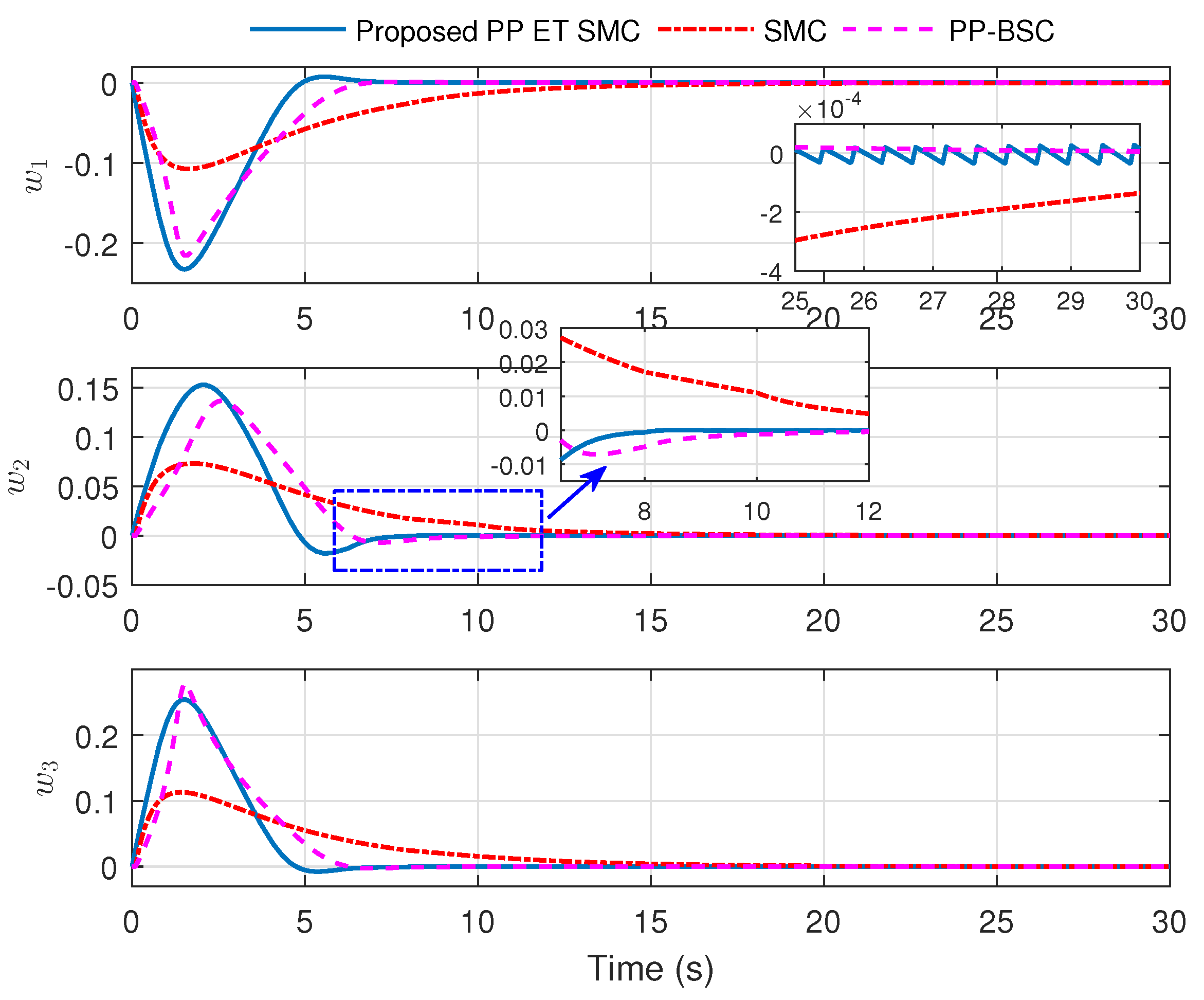
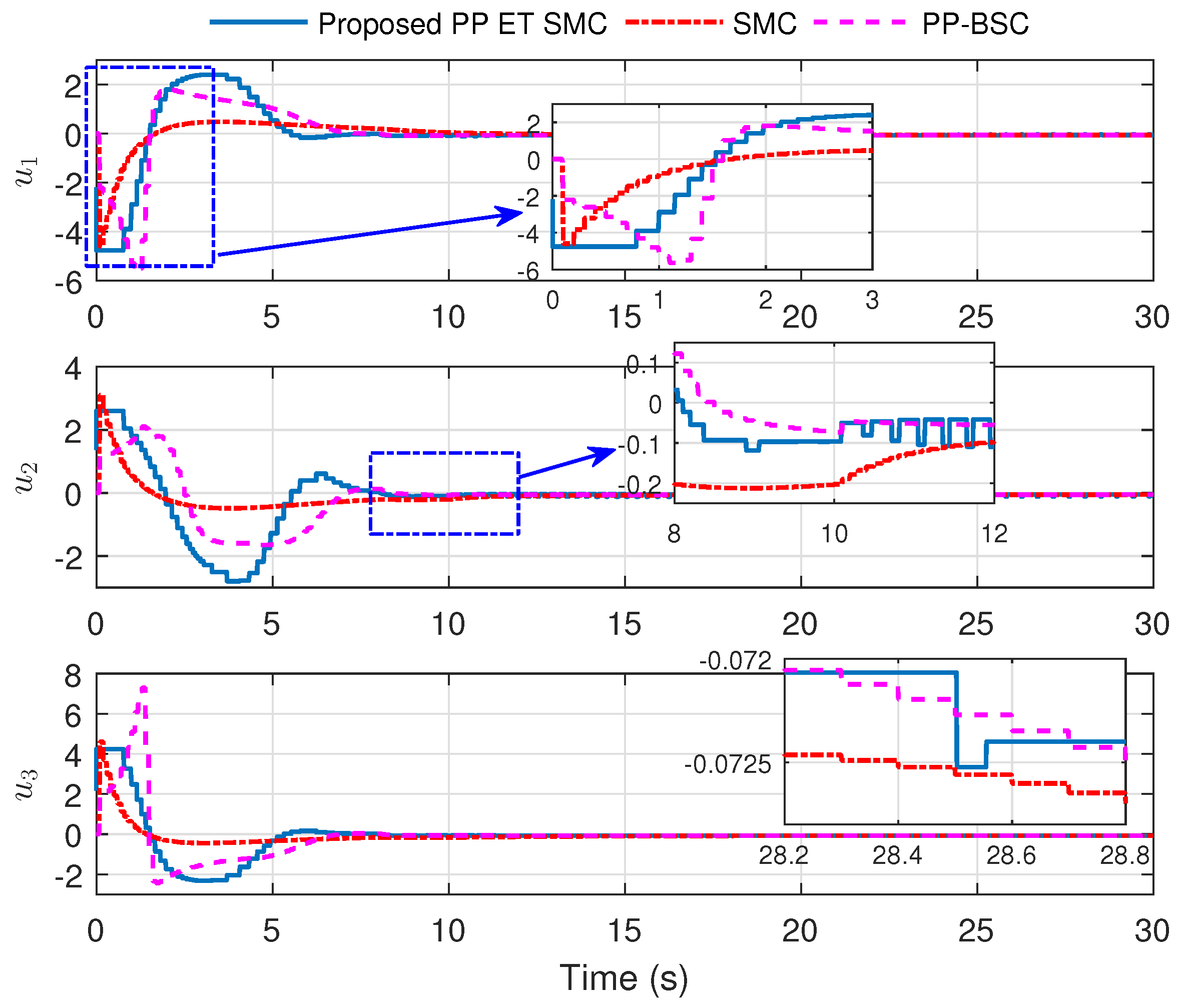
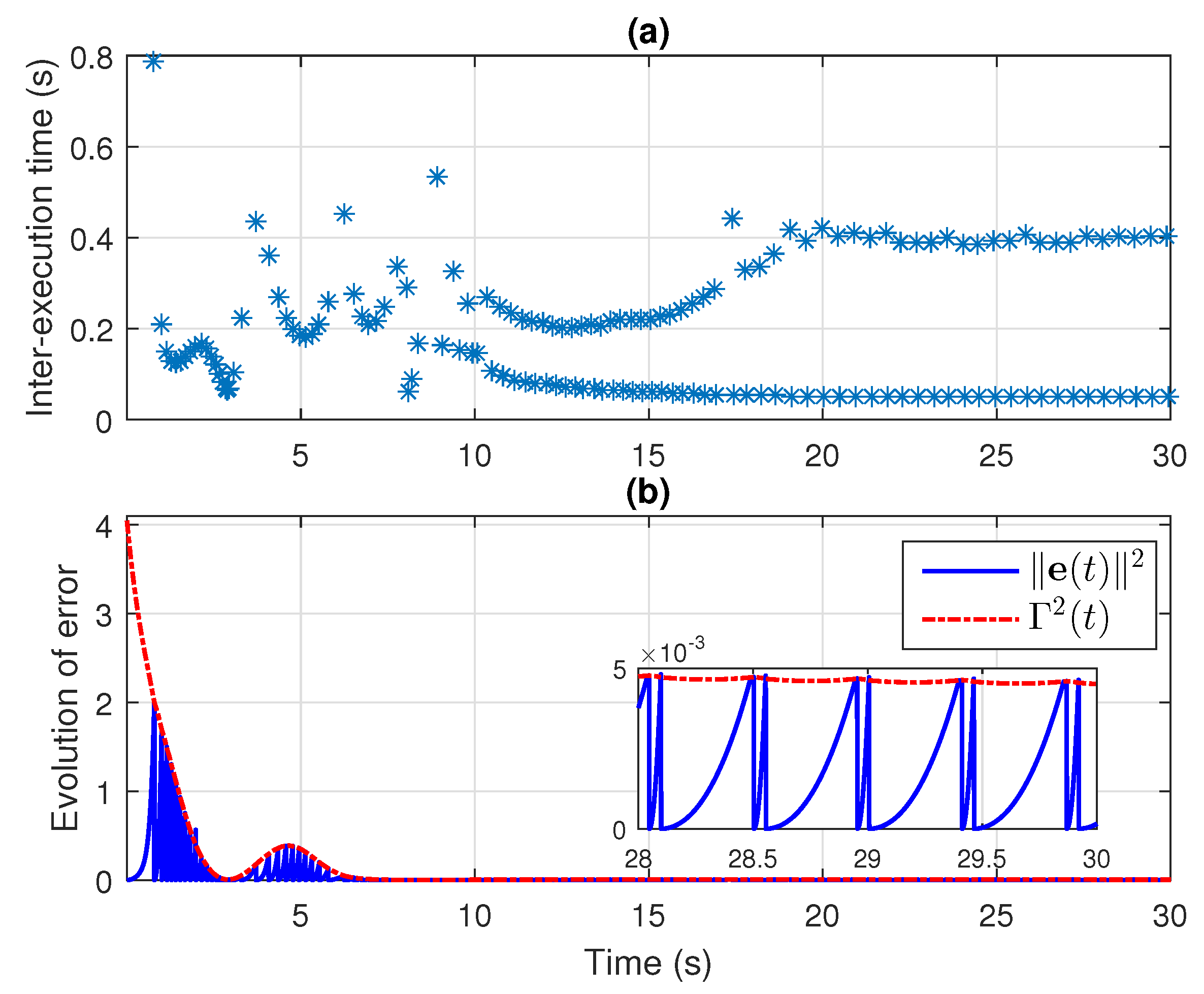
6. Numerical Analysis
Simulation Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wertz, J.R. Spacecraft Attitude Determination and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 73. [Google Scholar]
- Vadali, S.R. Variable-structure control of spacecraft large-angle maneuvers. J. Guid. Control. Dyn. 1986, 9, 235–239. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shijun, M. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 1999; Volume 34. [Google Scholar]
- McDuffie, J.; Shtessel, Y.; McDuffie, J.; Shtessel, Y. A sliding mode controller and observer for satellite attitude control. In Proceedings of the Guidance, Navigation, and Control Conference, New Orleans, LA, USA, 11–13 August 1997; p. 3755. [Google Scholar]
- Massey, T.; Shtessel, Y. Continuous traditional and high-order sliding modes for satellite formation control. J. Guid. Control. Dyn. 2005, 28, 826–831. [Google Scholar] [CrossRef]
- Luo, W.; Chu, Y.C.; Ling, K.V. H-infinity inverse optimal attitude-tracking control of rigid spacecraft. J. Guid. Control Dyn. 2005, 28, 481–494. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Y.; Fu, M. Adaptive sliding mode control for attitude stabilization with actuator saturation. IEEE Trans. Ind. Electron. 2011, 58, 4898–4907. [Google Scholar] [CrossRef]
- Xia, Y.; Zhu, Z.; Fu, M.; Wang, S. Attitude tracking of rigid spacecraft with bounded disturbances. IEEE Trans. Ind. Electr. 2011, 58, 647–659. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Z. Disturbance-observer-based robust backstepping attitude stabilization of spacecraft under input saturation and measurement uncertainty. IEEE Trans. Ind. Electr. 2017, 64, 7994–8002. [Google Scholar] [CrossRef]
- Amrr, S.M.; Nabi, M.; Tiwari, P.M. A fault-tolerant attitude tracking control of spacecraft using an anti-unwinding robust nonlinear disturbance observer. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 6005–6018. [Google Scholar] [CrossRef]
- Amrr, S.M.; Nabi, M. Finite-time fault tolerant attitude tracking control of spacecraft using robust nonlinear disturbance observer with anti-unwinding approach. Adv. Space Res. 2020, 66, 1659–1671. [Google Scholar] [CrossRef]
- Lyke, J.C. Plug-and-play satellites. IEEE Spectr. 2012, 49, 36–42. [Google Scholar] [CrossRef]
- Viel, C.; Bertrand, S.; Kieffer, M.; Piet-Lahanier, H. Distributed event-triggered control for multi-agent formation stabilization. IFAC-PapersOnLine 2017, 50, 8025–8030. [Google Scholar] [CrossRef]
- Wu, B. Spacecraft attitude control with input quantization. J. Guid. Control Dyn. 2015, 39, 176–181. [Google Scholar] [CrossRef]
- Wu, B.; Cao, X. Robust attitude tracking control for spacecraft with quantized torques. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 1020–1028. [Google Scholar] [CrossRef]
- Gao, H.; Lv, Y.; Nguang, S.K.; Ma, G. Finite-time attitude quantised control for rigid spacecraft. Int. J. Syst. Sci. 2018, 49, 2328–2340. [Google Scholar] [CrossRef]
- Amrr, S.M.; Srivastava, J.P.; Nabi, M. Robust Attitude Stabilization of Spacecraft under Constrained Network with Hysteresis Quantizer. IEEE J. Miniaturization Air Space Syst. 2020. [Google Scholar] [CrossRef]
- Amrr, S.M.; Nabi, M.; Srivastava, J.P. Quantized Attitude Control of Rigid Spacecraft without Unwinding. IFAC-PapersOnLine 2020, 53, 105–110. [Google Scholar] [CrossRef]
- Tallapragada, P.; Chopra, N. On event triggered tracking for nonlinear systems. IEEE Trans. Autom. Control 2013, 58, 2343–2348. [Google Scholar] [CrossRef] [Green Version]
- Guerrero-Castellanos, J.; Vega-Alonzo, A.; Durand, S.; Marchand, N.; Gonzalez-Diaz, V.R.; Castañeda-Camacho, J.; Guerrero-Sánchez, W.F. Leader-following consensus and formation control of VTOL-UAVs with event-triggered communications. Sensors 2019, 19, 5498. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cucuzzella, M.; Incremona, G.P.; Ferrara, A. Event-triggered variable structure control. Int. J. Control 2020, 93, 252–260. [Google Scholar] [CrossRef] [Green Version]
- Nowzari, C.; Garcia, E.; Cortés, J. Event-triggered communication and control of networked systems for multi-agent consensus. Automatica 2019, 105, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Incremona, G.P.; Ferrara, A. Adaptive model-based event-triggered sliding mode control. Int. J. Adapt. Control Signal Process. 2016, 30, 1298–1316. [Google Scholar] [CrossRef]
- Al Issa, S.; Chakravarty, A.; Kar, I. Improved event-triggered adaptive control of non-linear uncertain networked systems. IET Control Theory Appl. 2019, 13, 2146–2152. [Google Scholar] [CrossRef]
- Al Issa, S.; Kar, I. Event-triggered adaptive control of uncertain non-linear systems under input delay and limited resources. Int. J. Dyn. Control 2021. [Google Scholar] [CrossRef]
- Postoyan, R.; Tabuada, P.; Nešić, D.; Anta, A. A framework for the event-triggered stabilization of nonlinear systems. IEEE Trans. Autom. Control 2015, 60, 982–996. [Google Scholar] [CrossRef] [Green Version]
- Abdelrahim, M.; Postoyan, R.; Daafouz, J.; Nešić, D. Robust event-triggered output feedback controllers for nonlinear systems. Automatica 2017, 75, 96–108. [Google Scholar] [CrossRef] [Green Version]
- Xing, L.; Wen, C.; Liu, Z.; Su, H.; Cai, J. Event-triggered adaptive control for a class of uncertain nonlinear systems. IEEE Trans. Autom. Control. 2016, 62, 2071–2076. [Google Scholar] [CrossRef]
- Wu, B.; Shen, Q.; Cao, X. Event-triggered attitude control of spacecraft. Adv. Space Res. 2018, 61, 927–934. [Google Scholar] [CrossRef]
- Amrr, S.M.; Banerjee, A.; Nabi, M. Robust attitude control of rigid spacecraft based on event-triggered approach with anti-unwinding. In Proceedings of the IEEE 2019 Fifth Indian Control Conference (ICC), New Delhi, India, 9–11 January 2019; pp. 510–515. [Google Scholar]
- Amrr, S.M.; Nabi, M. Attitude Stabilization of Flexible Spacecraft under Limited Communication with Reinforced Robustness. Trans. Inst. Meas. Control 2019, 41, 4475–4487. [Google Scholar] [CrossRef]
- Amrr, S.M.; Nabi, M.; Iqbal, A. An Event-Triggered Robust Attitude Control of Flexible Spacecraft with Modified Rodrigues Parameters under Limited Communication. IEEE Access 2019, 7, 93198–93211. [Google Scholar] [CrossRef]
- Chenliang, W.; Yun, L.; Qinglei, H.; Huang, J. Event-triggered adaptive control for attitude tracking of spacecraft. Chin. J. Aeronaut. 2019, 32, 454–462. [Google Scholar]
- Xing, L.; Zhang, J.; Liu, C.; Zhang, X. Fuzzy-logic-based adaptive event-triggered sliding mode control for spacecraft attitude tracking. Aerosp. Sci. Technol. 2021, 108, 106394. [Google Scholar] [CrossRef]
- Ning, K.; Wu, B.; Xu, C. Event-triggered adaptive fuzzy attitude takeover control of spacecraft. Adv. Space Res. 2020, 67, 1761–1772. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Hu, Q.; Shao, X.; Guo, L. Adaptive fault-tolerant attitude tracking control of spacecraft with prescribed performance. IEEE/ASME Trans. Mechatron. 2018, 23, 331–341. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, G.; Sun, Y.; Li, C. Simple model-free attitude control design for flexible spacecraft with prescribed performance. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 2760–2771. [Google Scholar] [CrossRef]
- Wei, C.; Chen, Q.; Liu, J.; Yin, Z.; Luo, J. An overview of prescribed performance control and its application to spacecraft attitude system. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2020, 235, 435–447. [Google Scholar] [CrossRef]
- Wu, X.; Luo, S.; Wei, C.; Liao, Y. Observer-based fault-tolerant attitude tracking control for rigid spacecraft with actuator saturation and faults. Acta Astronaut. 2021, 178, 824–834. [Google Scholar] [CrossRef]
- Wang, C.; Lei, G.; Hu, Q.; Qiao, J. Event-triggered adaptive attitude tracking control for spacecraft with unknown actuator faults. IEEE Trans. Ind. Electron. 2020, 67, 2241–2250. [Google Scholar] [CrossRef]
- Wie, B.; Weiss, H.; Arapostathis, A. Quarternion feedback regulator for spacecraft eigenaxis rotations. J. Guid. Control. Dyn. 1989, 12, 375–380. [Google Scholar] [CrossRef]
- Amrr, S.M.; Banerjee, A.; Nabi, M. Fault-Tolerant Attitude Control of Small Spacecraft using Robust Artificial Time Delay Approach. IEEE J. Miniaturization Air Space Syst. 2020, 1, 179–187. [Google Scholar] [CrossRef]
- Hu, Q.; Xiao, B.; Wang, D.; Poh, E.K. Attitude control of spacecraft with actuator uncertainty. J. Guid. Control Dyn. 2013, 36, 1771–1776. [Google Scholar] [CrossRef]
- Cai, W.; Liao, X.; Song, Y. Indirect robust adaptive fault-tolerant control for attitude tracking of spacecraft. J. Guid. Control. Dyn. 2008, 31, 1456–1463. [Google Scholar] [CrossRef]
- Jia, Z.; Hu, Z.; Zhang, W. Adaptive output-feedback control with prescribed performance for trajectory tracking of underactuated surface vessels. ISA Trans. 2019, 95, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Karayiannidis, Y.; Doulgeri, Z. Model-free robot joint position regulation and tracking with prescribed performance guarantees. Robot. Auton. Syst. 2012, 60, 214–226. [Google Scholar] [CrossRef]
- Wei, C.; Luo, J.; Dai, H.; Bian, Z.; Yuan, J. Learning-based adaptive prescribed performance control of postcapture space robot-target combination without inertia identifications. Acta Astronaut. 2018, 146, 228–242. [Google Scholar] [CrossRef]
- Sontag, E.D. Mathematical Control Theory: Deterministic Finite Dimensional Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 6. [Google Scholar]
- Mei, J.; Ren, W.; Ma, G. Distributed coordination for second-order multi-agent systems with nonlinear dynamics using only relative position measurements. Automatica 2013, 49, 1419–1427. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Al Issa, S.; Kar, I. Design and implementation of event-triggered adaptive controller for commercial mobile robots subject to input delays and limited communications. Control Eng. Pract. 2021, 114, 104865. [Google Scholar] [CrossRef]
- Ha, Q.P.; Nguyen, Q.; Rye, D.C.; Durrant-Whyte, H.F. Fuzzy sliding-mode controllers with applications. IEEE Trans. Ind. Electr. 2001, 48, 38–46. [Google Scholar] [CrossRef]
- Krstic, M.; Kokotovic, P.V.; Kanellakopoulos, I. Nonlinear & Adaptive Control Design, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Hu, Q.; Shi, Y.; Shao, X. Adaptive fault-tolerant attitude control for satellite reorientation under input saturation. Aerosp. Sci. Technol. 2018, 78, 171–182. [Google Scholar] [CrossRef]


| Para. | Value | Para. | Value | Para. | Value | Para. | Value |
|---|---|---|---|---|---|---|---|
| 0.5 | 1 | 2 | 0.001 | ||||
| 0.5 | 1 | 0.2 | |||||
| 0.005 | 0.15 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amrr, S.M.; Alturki, A.; Kumar, A.; Nabi, M. Prescribed Performance-Based Event-Driven Fault-Tolerant Robust Attitude Control of Spacecraft under Restricted Communication. Electronics 2021, 10, 1709. https://doi.org/10.3390/electronics10141709
Amrr SM, Alturki A, Kumar A, Nabi M. Prescribed Performance-Based Event-Driven Fault-Tolerant Robust Attitude Control of Spacecraft under Restricted Communication. Electronics. 2021; 10(14):1709. https://doi.org/10.3390/electronics10141709
Chicago/Turabian StyleAmrr, Syed Muhammad, Abdulrahman Alturki, Ankit Kumar, and M. Nabi. 2021. "Prescribed Performance-Based Event-Driven Fault-Tolerant Robust Attitude Control of Spacecraft under Restricted Communication" Electronics 10, no. 14: 1709. https://doi.org/10.3390/electronics10141709






