Multi-Kernel Polar Codes versus Classical Designs with Different Rate-Matching Approaches ^†

Abstract

Polar codes, which have been proposed as a family of linear block codes, has garnered a lot of attention from the scientific community, owing to their low-complexity implementation and provably capacity-achieving capability. Thus, they have been proposed to be used for encoding information on the control channels in the upcoming 5G wireless networks. The basic approach introduced by Arikan in his landmark paper to polarize bit channels of equal capacities to those of unequal capacities can be used to design only codewords of length $N=2^n$, which is a major limitation when codewords of different lengths are required for the underlying applications. In the predecessor paper, this aspect was partially addressed by using a $3\times 3$ kernel circuit (used to generate codewords of length $M=3^m$), along with downsizing techniques such as puncturing and shortening to asses the optimal design and resizing techniques based on the underlying system parameters. In this article, we extend this research to include the assessment of multi-kernel rate-matched polar codes for applicability over a much wider range of codeword lengths.

1. Introduction

As polar codes of length $N=2^n$ might not always be suitable for an underlying system, developing techniques to generate more versatile codeword lengths is very important to realize their utilities in a wider range of practical systems. They are proposed to be used for encoding/decoding data over the 5G control channels with certain utilitarian criteria and challenges mentioned in [1]. In the latest version of 3GPP 5G NR specifications [2], three resizing techniques for polar codes have been used, namely, repetition (upsizing) or puncturing and shortening (downsizing). In this article, we only investigate the downsizing aspect. These techniques w.r.t 5G, however, have been proposed only over codewords of length $N=2^n$. Additionally, we perform a comparative analysis with polar codes generated by a $3\times 3$ polarization circuit (same as the one used in [3]), resulting in codewords of length $M=3^m$, and use the $2\times 2$ and $3\times 3$ circuits to design multi-kernel polar codes, as shown in the series of articles [4,5,6,7,8,9,10]. By assessing the error rate performances and complexities of polar code designs generated by these different construction and downsizing techniques, we determine the effect of different parameters and how to optimally design polar codes for a given set of parameter values. This expands the scope of practical applications of polar codes to include scenarios when nonconventional ($2^n$) codeword lengths are desirable.

The rest of the article is organized as follows. In Section 2, we provide an overview of the polarization kernels of sizes 2 and 3, which correspond to the same circuits used in [3]. Additionally, the design technique for multi-kernel codes is also provided. In Section 3, a brief description of the downsizing techniques used in this article, namely, puncturing and shortening is provided. In Section 4, a comparative analysis of downsized single kernel codes to multi-kernel codes is presented, based on bit error rate (BER) performance and complexity, to determine the conditions on system parameters for optimal design of polar codes of desired codeword lengths. The open questions that have arisen owing to the research conducted for this article are stated in Section 5. Finally, the concluding remarks are provided in Section 6.

Notations and Remarks: N and M denote codeword lengths (corresponding to the exponents n and m of 2 and 3, respectively, (i.e., $N=2^n$ and $M=3^m$) of codewords generated by $2\times 2$ and $3\times 3$ kernels, respectively, whereas K is used to denote codeword lengths of multi-kernel codes (i.e., $K=2^n\times 3^m$) generated by $2\times 2$ and $3\times 3$ kernels. G denotes generator matrix, with a subscript denoting the codeword length generated by G. $R_d$ denotes code rate. Z denotes the z-parameter (Bhattacharyya parameter) value of a given bit channel, with a subscript denoting the channel number. z-parameter indicates the inverse of the capacity of a bit channel (refer to [11] for details) and is used to determine the effect of channel polarization. All the BER simulations have been performed over additive white Gaussian noise channel (AWGNC) with binary phase shift keying (BPSK) modulation scheme and z-parameter value $Z=0.5$ for channel polarization. Amongst all the available polar decoding options, successive cancellation (SC) decoder is used.

2. Polarization Circuits

2.1. $2\times 2$ Kernel Circuit

In his landmark paper [11], Arikan proposed the method of channel polarization to design a family of block codes called polar codes. He proposed using a $2\times 2$ circuit (as shown by the dashed red boxes in Figure 1 and Figure 2) to polarize 2 bit channels of equal capacities to 2 bit channels of unequal capacities.

We denote the z-parameter value of the real channel ($\overrightarrow{x}$ to $\overrightarrow{y}$ in Figure 1 and Figure 2) as Z. The virtual bit channels obtained from the transformation by the $2\times 2$ polarization circuit (three sets from $\overrightarrow{u}$ to $\overrightarrow{\tilde{x}}$ in Figure 1 or three sets from $\overrightarrow{\tilde{x}}$ to $\overrightarrow{x}$ in Figure 2) are denoted as $Z_1$ and $Z_2$ and are given by (1) and (2) over a binary erasure channel (BEC).

$$\begin{array}{cc}\hfill Z_1& =2Z-Z^2\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill Z_2& =Z^2\hfill \end{array}$$

(2)

where $Z_1+Z_2=2Z$, resulting in the conservation of channel capacity after polarization. Clearly as $Z_1\ge Z$ and $Z_2\le Z$, one virtual channel has higher capacity than the real channel, while the other one has a lower capacity. Although the equality in Equations (1) and (2) are valid just for BECs, the concept of channel transformation to polarize their effective capacity holds true for any given channel model. Due to the recursive nature of constructing polar code circuits using the $2\times 2$ kernel element, only codewords of length $N=2^n$ can be obtained. For more details, the reader is recommended to refer to Section IIA of [3] or [11].

2.2. $3\times 3$ Kernel Circuit

The idea of channel polarization to transform multiple bit channels with equal capacities to the same number of bit channels with unequal capacities can be expanded to any number of bit channels. In this subsection, we will look into polarizing 3 bit channels simultaneously, using a $3\times 3$ circuit. There have been multiple proposals in the literature as to how to polarize the three channels (or how to design a $3\times 3$ circuit) similar to the ones either in the set of articles [4,5,6,7,8,9,10] or, alternatively, in [12,13,14] or [15]. Within the scope of this article, we only use the circuit structure proposed in [12], owing to easier implementation and proximity of design to Arikan’s original circuit, and it has also been used in [3]. It is shown by the dashed blue boxes in Figure 1 and Figure 2.

Here, we denote the z-parameter value of the real channel ($\overrightarrow{x}$ to $\overrightarrow{y}$ in Figure 1 and Figure 2) as Z and the corresponding virtual bit channels by a $3\times 3$ polarization circuit (two sets from $\overrightarrow{\tilde{x}}$ to $\overrightarrow{x}$ in Figure 1 or two sets from $\overrightarrow{u}$ to $\overrightarrow{\tilde{x}}$ in Figure 2) as $Z_1$, $Z_2$, and $Z_3$. Equations (3)–(5) provide the corresponding z-parameter transformation over a BEC.

$$\begin{array}{cc}\hfill Z_1& =3Z-3Z^2+Z^3\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill Z_2& =2Z^2-Z^3\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill Z_3& =Z^2\hfill \end{array}$$

(5)

Clearly, as $Z_1+Z_2+Z_3=3Z$, the channel capacity is conserved, and this results in valid channel polarization. Thus, the aforementioned circuit can be used recursively to design channel polarization circuits to generate polar codewords of length $M=3^m$. For more details, the reader is recommended to refer to Section IIB of [3].

2.3. Multi-Kernel Circuit

For channel polarization, one need not be limited to the recursive usage of a single kernel circuit to polarize bit channels. The polarization effect can also be achieved by using multiple kernel sizes simultaneously within the same encoding/decoding circuits, called multi-kernel polar codes. The concept of channel polarization using different kernel designs within the same polar circuit and the theoretical analysis of channel polarization aspects of such multi-kernel designs have been investigated in a series of papers [4,5,6,7,8,9,10]. In this section and within the scope of this article, we investigate multi-kernel polar codes generated by the combination of circuit kernels of sizes 2 and 3 to obtain codeword lengths of the form $K=2^n\times 3^m$. Using $n=1$ and $m=1$, we can obtain $6\times 6$ polarization circuits. The generator matrices are denoted by G. In this section, the circuit design with $2\times 2$ kernels in the first stage and $3\times 3$ kernels in the second stage is denoted as the A version, whereas the one with $3\times 3$ kernels in the first stage and $2\times 2$ kernels in the second stage is denoted as the B version.

The circuit design for $G_{6A}=\mathit{perm}(G_2\otimes G_3)$ (where perm denotes the permutation of rows of G to establish the correct connection between stages of polarization; perm = bit-reversal for $G_{2^n}$) is shown in Figure 1, with the dashed red and blue boxes encapsulating the $2\times 2$ and $3\times 3$ polarization circuits, respectively.

The generator matrix for the circuit in Figure 1 is given as

$$G_{6A}=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 1& 0& 0& 1& 0& 0\\ 1& 1& 0& 0& 0& 0\\ 1& 1& 0& 1& 1& 0\\ 0& 1& 1& 0& 0& 0\\ 0& 1& 1& 0& 1& 1\end{array}\right]$$

(6)

through which the codeword $\overrightarrow{x}=[x_1,x_2,x_3,x_4,x_5,x_6]$ is generated from the input bit vector $\overrightarrow{u}=[u_1,u_2,u_3,u_4,u_5,u_6]$ by (7).

$$\overrightarrow{x}=\overrightarrow{u}·G_{6A}$$

(7)

Using the same convention as in Section 2.1 and Section 2.2, Equations (8)–(13) provide the z-parameter transformation by the polarization circuit in Figure 1.

$$\begin{array}{cc}\hfill Z_1& =6Z-15Z^2+20Z^3-15Z^4+6Z^5-Z^6\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill Z_2& =8Z^2-16Z^3+14Z^4-6Z^5+Z^6\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill Z_3& =4Z^2-4Z^3+Z^4\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill Z_4& =3Z^2-3Z^4+Z^6\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill Z_5& =2Z^4-Z^6\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill Z_6& =Z^4\hfill \end{array}$$

(13)

Clearly, as, $Z_1+Z_2+Z_3+Z_4+Z_5+Z_6=6Z$, the channel capacity is conserved, and this results in valid channel polarization. Thus, the aforementioned circuit can be used recursively to design channel polarization circuits to generate polar codewords of length $K=6^k$.

The circuit design for $G_{6B}=\mathit{perm}(G_3\otimes G_2)$ is shown in Figure 2.

The generator matrix for the circuit in Figure 2 is given as

$$G_{6B}=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 1& 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 1& 0\\ 1& 1& 0& 0& 0& 0\\ 1& 1& 1& 1& 0& 0\\ 0& 0& 1& 1& 1& 1\end{array}\right]$$

(14)

through which the codeword $\overrightarrow{x}=[x_1,x_2,x_3,x_4,x_5,x_6]$ is generated from the input bit vector $\overrightarrow{u}=[u_1,u_2,u_3,u_4,u_5,u_6]$ by (15).

$$\overrightarrow{x}=\overrightarrow{u}·G_{6B}$$

(15)

Using the same convention as before, Equations (16)–(21) provide the z-parameter transformation by the polarization circuit in Figure 2.

$$\begin{array}{cc}\hfill Z_1& =6Z-15Z^2+20Z^3-15Z^4+6Z^5-Z^6\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill Z_2& =4Z^2-2Z^3-4Z^4+4Z^5-Z^6\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill Z_3& =2Z^2-Z^4\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill Z_4& =9Z^2-18Z^3+15Z^4-6Z^5+Z^6\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill Z_5& =4Z^4-4Z^5+Z^6\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill Z_6& =Z^4\hfill \end{array}$$

(21)

Here too, $Z_1+Z_2+Z_3+Z_4+Z_5+Z_6=6Z$, implying conservation of channel capacity resulting in valid channel polarization, and using it recursively can help design polarization circuits to generate codewords of length $K=6^k$.

Using a different number of circuit elements in each stage or different order of kernel elements in different stages, one can generate different polarization circuits for the same codeword length $K=2^n\times 3^m$. Note from the set of Equations (8)–(13) and (16)–(21) that they are different. This signifies that, as the order of kernel elements within the polarization circuit differs, so do the z-parameter values of the virtual bit channels as well as the generator matrices. Therefore, based on the required system parameter values such as K, $R_d$m and Z, there exists an optimal choice of designing the polarization circuit or ordering the kernel elements within a multi-kernel circuit design, such that the bit channels chosen to encode the information bits have the maximum possible capacity. Within the scope of this article, amongst the various algorithms available in the literature, we would use the density evolution (DE) technique for polar code construction, as provided in the set of articles [16,17,18] and is also used in [4]. Note that w.r.t. to Figure 1 and Figure 2 the size of $\overrightarrow{u}$ and $\overrightarrow{y}$ is constant and is equal to the codeword length. Based on $R_d$, a subset of $R_d·K$ bits in $\overrightarrow{u}$ is used to encode the information bits, whereas the remaining $(1-R_d)·K$ bits are used to encode the frozen bits (generally 0 s). The choice of the set of bit indices for the information and frozen bits is also determined by the DE technique.

3. Resizing Polar Codes

In this section, we provide a brief description of two downsizing techniques for polar codes, namely, puncturing and shortening. These techniques are quite well known in the research community, and multiple variations/approaches exist in the literature.

3.1. Puncturing

Puncturing of channel codes is a well-known technique to reduce the number of codeword bits that are eventually transmitted over the channel. There exist some puncturing techniques for polar codes in the literature, such as those in [19,20,21]. For the implementation in this article, the simplest approach of puncturing scheme, as discussed in [19], has been used.

In puncturing, the punctured codeword bits are not transmitted over the channel, i.e., the bits are entirely avoided during an ongoing transmission. The decoder typically handles such punctured bits as bits erased by the channel. Thus, the choice of bits to be punctured should be such that only the frozen bit channels at the encoder input are affected by it, because decapitating any of the information bit channels would result in an unnecessary loss of performance and degradation of the error-correcting capability of the codes on top of introducing an error floor. Ideally, the bits with the lowest capacity (or highest z-parameter values) should be targeted to minimize the loss of total capacity while puncturing. For details regarding the encoding or decoding of punctured polar codes generated for analysis in this article, the reader is recommended to refer to Section IIIA of [3] or [19].

Puncturing some bits results in degradation of total the capacity of input bit channels. This fact is justified by the channel polarization method, in which the channel capacity is conserved from input to output of the polarizing circuit. Thus, the overall reduction in capacity corresponds to the total capacity of punctured bits. Therefore, it is justified to use the least capacity bit channels for puncturing to minimize the loss of total capacity. The effective code rate of the transmitted codewords is increased by puncturing, due to the utilization of some bit channels for puncturing. This leads to a reduction in channel capacity and consequently worse error rate performance.

3.2. Shortening

Similar to puncturing, shortening is another way of downsizing channel codes. Shortening is usually applied to codes of the systematic form; however, in the case of polar codes, shortening can be easily applied to the nonsystematic form as well. There exist some shortening techniques for polar codes in the literature, such as those in [19,22]. For the implementation in this article, we focus only on the shortening of nonsystematic codes, as shown in [19], for a fair comparison to downsizing by puncturing in Section 3.1.

Similar to puncturing, in the case of shortening, one or more codeword bits are not transmitted over the channel, i.e., the bits are entirely avoided during an ongoing communication. However, contrary to puncturing, the decoder handles these nontransmitted bits as bits known with complete confidence at the receiver instead of erased bits, i.e., they are reconstructed at the receiver as apriori bits. Hence, it is advantageous to utilize bit channels with the highest capacities for shortening to minimize error in the prediction/assignment of apriori bits at the receiver. Using low-capacity channels for shortening would result in unnecessary errors owing to falsely predicted bits at the receiver, thus resulting in an error floor and loss in error-correcting capability. For details regarding the encoding or decoding of shortened polar codes generated for analysis in this article, the reader is recommended to refer to Section IIIB of [3] or [19].

Shortening some bits results in degradation of total the capacity of input bit channels, due to the absence of highest-capacity bits being shortened; some lower-capacity bits need to be used for encoding the information bits, i.e., the overall capacity of information bit channels is reduced. This fact is justified by the channel polarization method, in which the channel capacity is conserved from input to output of the polarizing circuit. The effective code rate of the transmitted codewords is increased by shortening. This leads to a reduction in channel capacity and consequently worse error rate performance.

4. Analysis of Optimal Design Techniques

In this section, we perform a comparative analysis of polar codes over different sets of parameter settings and assess them based on the error rate performances (Section 4.1) and complexities (Section 4.2). From the discussions in Section 2 and Section 3, we can conclude that the following techniques for designing polar codes are at our disposal:

• A $2\times 2$ circuit of kernel size 2;
• A $3\times 3$ circuit of kernel size 3;
• Multi-kernel circuit composed of $2\times 2$ and $3\times 3$ circuits;
• Puncturing;
• Shortening.

In [3], we analyzed the performance of downsized (punctured/shortened) codewords generated by the $2\times 2$ kernel circuit, compared to codewords generated by the $3\times 3$ kernel circuit and vice versa. In this article, we analyze the performance of downsized (punctured/shortened) codewords generated by either $2\times 2$ or $3\times 3$ kernel circuits to a corresponding multi-kernel design. We use two scenarios with differing codeword lengths for such analysis. A summary of the corresponding parameter settings is provided in

Table 1. Parameter settings for the simulation environment.

	Scenario 1			Scenario 2
	$\mathit{N}$	$\mathit{M}$	$\mathit{K}$	$\mathit{N}$	$\mathit{M}$	$\mathit{K}$
Encoding/Decoding length	1024	729	648	512	729	432
Number of downsized bits	376	81	0	80	297	0
Z	$0.5$			$0.5$
Modulation Scheme	BPSK			BPSK
Coderates $R_d$	{$1/4$, $1/2$, $3/4$}			{$1/4$, $1/2$, $3/4$}

. We perform the analysis over AWGNC and $Z=0.5$, which corresponds to $designSN{R}_{dB}\approx -1.6$ dB as per the metric for polar code construction shown in [23].

From the results in [3] and per the specifications provided in [2] for using downsized polar codes for encoding over the 5G control channels, we observed that for low code rates, puncturing tends to be the preferable downsizing option, while for high code rates, shortening tends to be the preferable downsizing option. In [24], this aspect has been validated for multi-kernel polar codes as well, using a downsizing type selection (DTS) parameter, also based on DE, which provides a more accurate prediction of the optimality of choice of downsizing technique based on the desired system parameter settings.

4.1. Error Rate Performance

In this section, we perform the comparative analysis using error rate performance as the quantifier of optimality of code design and performance.

4.1.1. Scenario 1

In this subsection, we examine the error rate performance of multi-kernel polar codes of length $K=648$, compared to polar codewords of length $N=1024$ generated using only the $2\times 2$ kernel circuit (as in Figure 1 from [3]) and downsized (punctured/shortened) by 376 bits, as well as polar codewords of length $M=729$ generated using only the $3\times 3$ kernel circuit (as in Figure 2 from [3]) and downsized (punctured/shortened) by 81 bits. Code rate values of $R_d=1/4$, $1/2$, and $3/4$, i.e., low, half, and high code rates are used for a comparative analysis of the error rate performance. Using the DE technique, mentioned in Section 2.3, we determine the optimal configuration for the arrangement of kernel designs within the polar code circuits for a given code rate value, i.e., $G_{648}^{R_d}=perm\left(f\left(G\right)\right)$. Details of the figures corresponding to respective $R_d$ and $f\left(G\right)$ are provided in

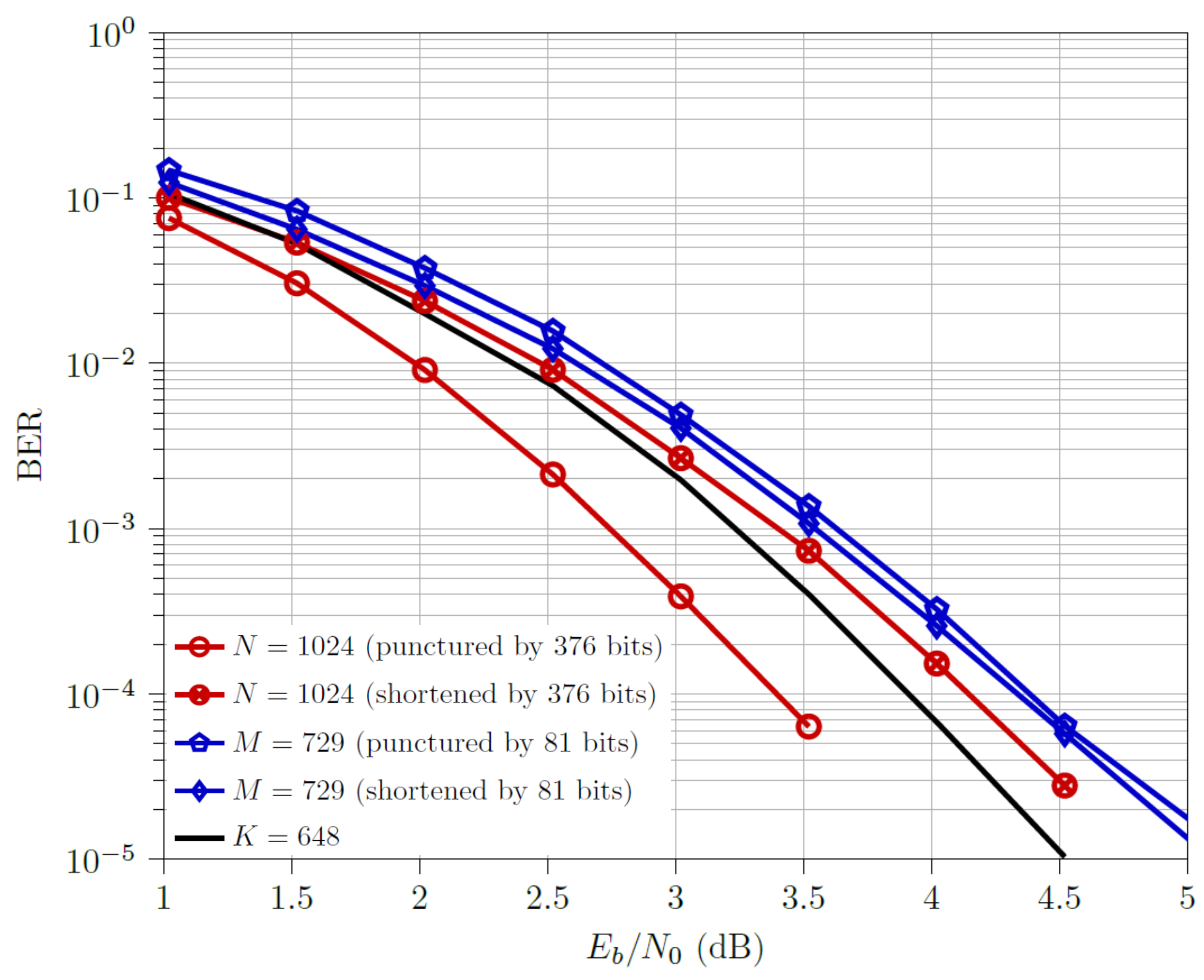
Table 2. Simulation cases for Scenario 1.

	Figure 3	Figure 4	Figure 5
Coderates $R_d$	$1/4$	$1/2$	$3/4$
Arrangement $G_{648}^{R_d}$	$G_3^{\otimes 4}\otimes G_2^{\otimes 3}$	$G_2^{\otimes 2}\otimes G_3\otimes G_2\otimes G_3^{\otimes 3}$	$G_2^{\otimes 2}\otimes G_3\otimes G_2\otimes G_3^{\otimes 3}$

.

From Figure 3, Figure 4 and Figure 5, the following conclusions can be made:

• For the low code rate, $R_d=1/4$, punctured $N=1024$ codewords outperform the shortened ones. The multi-kernel $K=648$ codewords outperform all but punctured $N=1024$ codewords, with a $\approx 0.5$ dB difference. One interesting observation is w.r.t. downsized $M=729$ codewords. Although at low $R_d$, one would expect the punctured ones to be better than the shortened ones, the performance difference is marginal with shortened ones narrowly outperforming the punctured ones. This corresponds to the observations made in [3], where shortened $M=729$ codewords outperform the punctured ones even at low code rates.
• For the half code rate, $R_d=1/2$, shortened $N=1024$ and $M=729$ codewords outperform the respective punctured ones. The multi-kernel $K=648$ codewords outperform nearly all but shortened $N=1024$, with just a $\approx 0.25$ dB difference.
• For the high code rate, $R_d=3/4$, shortened $N=1024$ and $M=729$ codewords outperform the respective punctured ones. The multi-kernel $K=648$ codewords outperform all but shortened $N=1024$ codewords, with just a $\approx 0.25$ dB difference.

From all three plots in Scenario 1, we observe that with an exception at the low code rate, the assumption that puncturing for low code rates and shortening for high code rates are better options for downsizing holds true. When the number of bits used for downsizing is relatively high, this assumption has higher validity, and the performance difference between the corresponding punctured and shortened codewords is higher. The downsized N codewords are always better than their corresponding downsized M codewords. At low and half code rates, both the punctured and shortened N codewords are better than both the downsized M codewords. Although the number of downsized bits for N codewords is much higher than M codewords in this scenario, it follows the observations in [3] about $2\times 2$ kernel being a better design choice than the $3\times 3$ kernel. A multi-kernel code design is evidently a good design choice when the corresponding K codeword length is desirable.

4.1.2. Scenario 2

In this subsection, we investigate the error rate performance of multi-kernel polar codes of length $K=432$, compared to polar codewords of length $N=512$ generated using only the $2\times 2$ kernel circuit (as in Figure 1 from [3]) and downsized (punctured/shortened) by 80 bits, as well as polar codewords of length $M=729$ generated using only the $3\times 3$ kernel circuit (as in Figure 2 from [3]) and downsized (punctured/shortened) by 297 bits. Code rate values as in Section 4.1.1, i.e., $1/4$, $1/2$, and $3/4$ are used. Furthermore, using the DE technique, the optimal configuration $f\left(G\right)$ for the multi-kernel design of $G_{432}^{R_d}=perm\left(f\left(G\right)\right)$ is determined. Details of the figures corresponding to respective $R_d$ and $f\left(G\right)$ are provided in

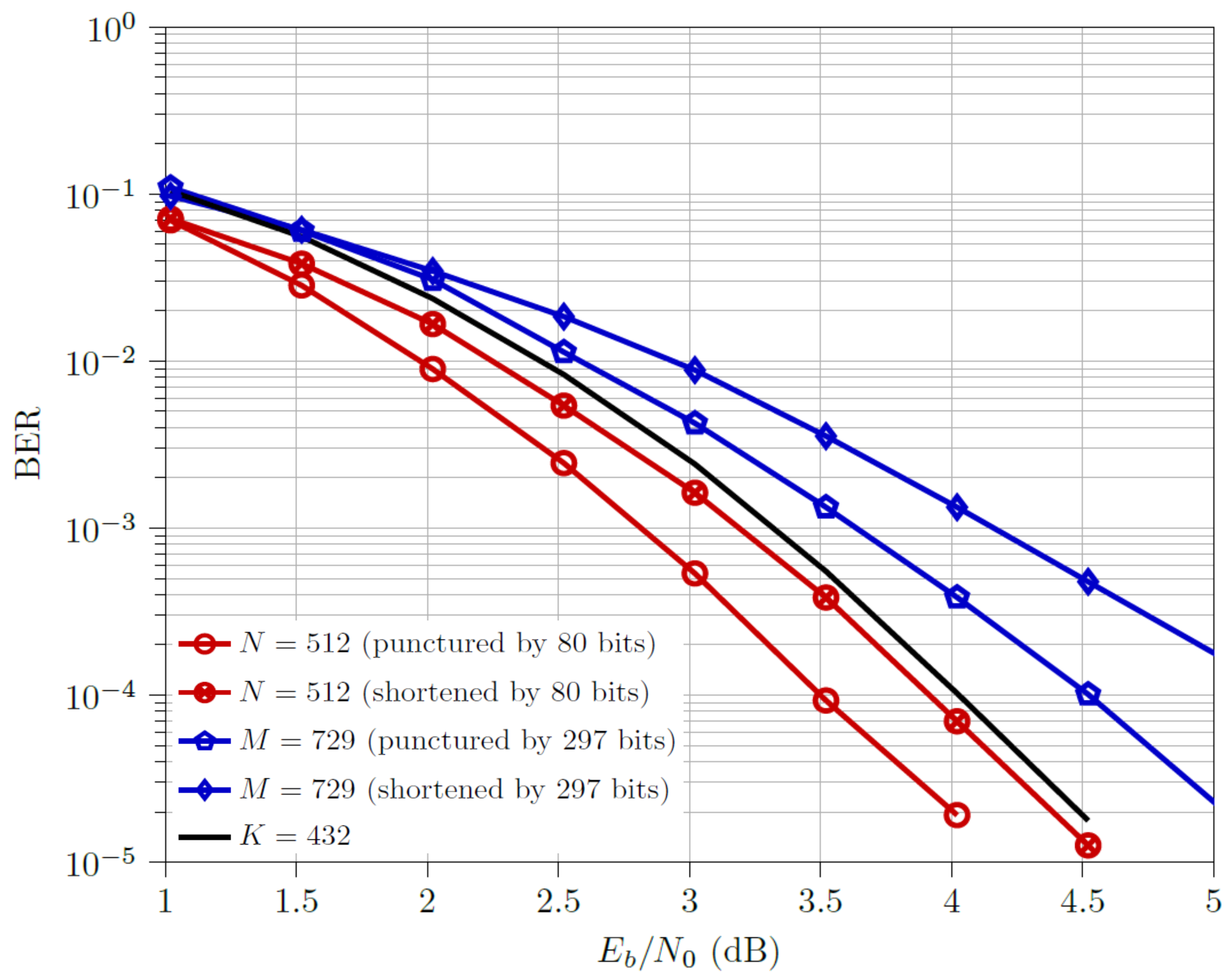
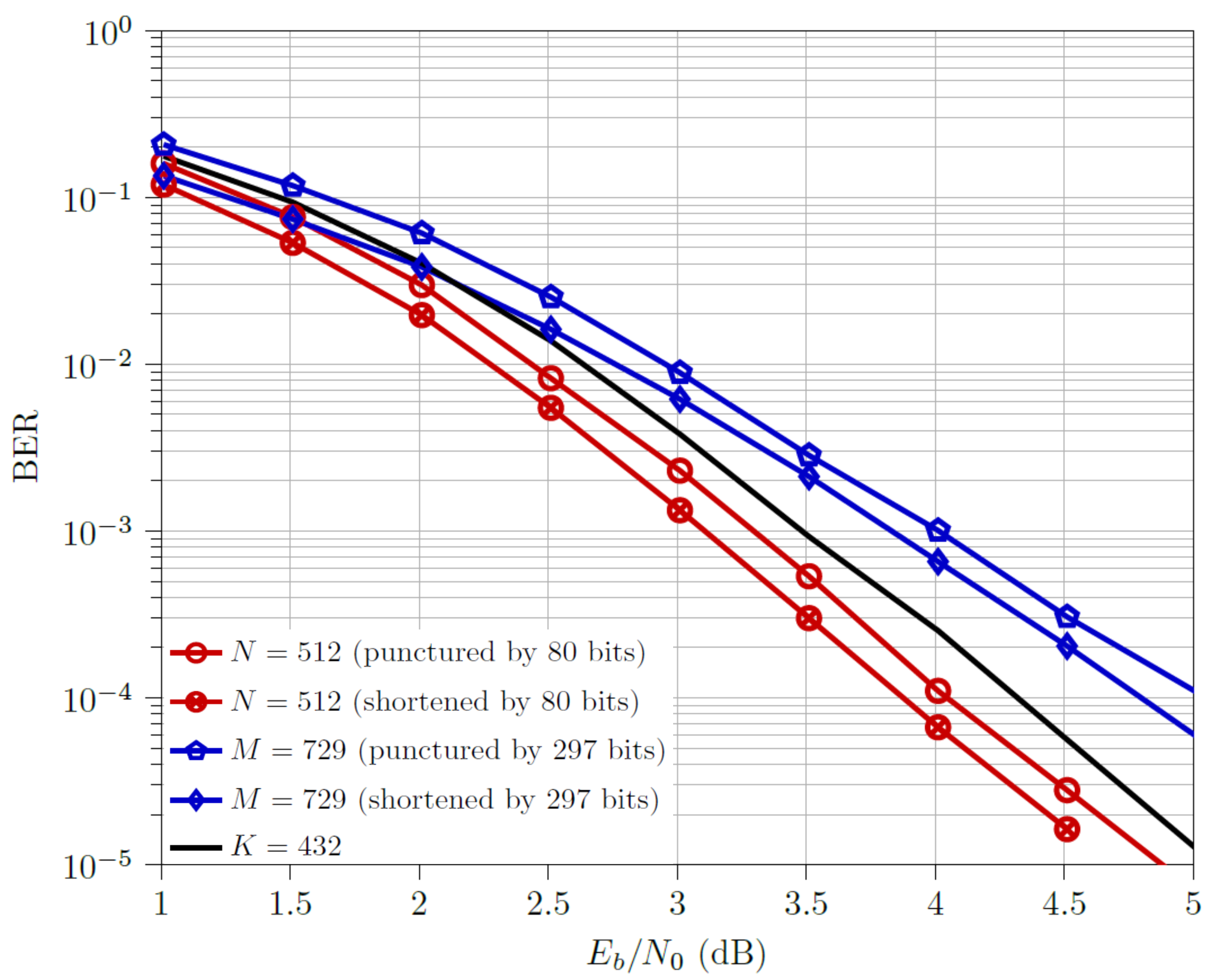
Table 3. Simulation cases for Scenario 2.

	Figure 6	Figure 7	Figure 8
$R_d$	$1/4$	$1/2$	$3/4$
$G_{432}^{R_d}$	$G_3^{\otimes 2}\otimes G_2\otimes G_3\otimes G_2^{\otimes 3}$	$G_2^{\otimes 2}\otimes G_3\otimes G_2\otimes G_3\otimes G_2\otimes G_3$	$G_2^{\otimes 2}\otimes G_3\otimes G_2^{\otimes 2}\otimes G_3^{\otimes 2}$

.

From Figure 6, Figure 7 and Figure 8, the following conclusions can be made:

• For the low code rate, $R_d=1/4$, punctured $N=1024$ and $M=729$ codewords outperform the corresponding shortened ones. This phenomenon of punctured M being better than their shortened counterparts had not been observed in any plots of [3]. Note that here, downsizing of $M=729$ codewords was carried out by 297 bits, whereas in [3], downsizing was performed by 217 bits, indicating that a higher number of downsized bits improves the prediction of using code rate value for determining optimal downsizing technique, as observed in Scenario 1 as well. The multi-kernel $K=432$ codewords outperform both the downsized $M=729$ codewords but are outperformed by both the downsized $N=512$ codewords, with a performance gap of ≈0.5 dB from the optimal design (i.e., punctured $N=512$ codewords).
• For the half code rate, $R_d=1/2$, shortened $N=512$ and $M=729$ codewords outperform the respective punctured ones. The multi-kernel $K=432$ codewords outperform both the downsized $M=729$ codewords but are outperformed by both the downsized $N=512$ codewords, with a performance gap of ≈0.5 dB from the optimal design (i.e., shortened $N=512$ codewords).
• For the high code rate, $R_d=3/4$, shortened $N=512$ and $M=729$ codewords outperform the respective punctured ones. The multi-kernel $K=432$ codewords outperform all but the shortened $N=512$ codewords, with a ≈0.3 dB difference.

From all three plots in Scenario 2, we observe that the assumption of downsizing by puncturing for low code rates and by shortening for high code rates being better options holds true. The downsized N codewords are always better than their corresponding downsized M codewords. At low and half code rates, both the punctured and shortened N codewords are better than both the downsized M codewords. In spite of the fact that, in this scenario, the number of downsized bits for $M=729$ codewords is much higher than $N=512$ codewords, the downsized $N=512$ codewords perform better than the downsized $M=729$ ones, thus following the observations in [3] about $2\times 2$ kernel being a better design choice than the $3\times 3$ kernel. A multi-kernel code design is evidently a good design choice when the corresponding K codeword length is desirable.

4.2. Computational Complexity

In this section, we discuss the complexity of polar code design for both scenarios 1 and 2. The encoding and decoding complexity of $2\times 2$ polar codes is given as $\mathcal{O}(N·lo{g}_{2}N)$, i.e., dependent on codeword length and number of stages within the polarization circuit [11]. Similarly, it can be quantified for M (for $3\times 3$ circuit) and K (for multi-kernel circuit). Effectively, at the encoder, the XOR gate (as seen in Figure 1 and Figure 2) generates a modulo 2 sum operation. At the decoder, this corresponds to one boxplus and one summation operation of the log-likelihood ratios (LLRs). For simplicity, we consider one XOR gate contributing one unit of complexity to the code design. Using this convention, we state that the complexity of polar circuits shown in Figure 1 and Figure 2 is 7 units.

The complexities of polar codes in scenarios 1 and 2 are tabulated in

Table 4. Complexity comparison of the polar code designs.

	Scenario 1			Scenario 2
	$\mathit{N}$	$\mathit{M}$	$\mathit{K}$	$\mathit{N}$	$\mathit{M}$	$\mathit{K}$
Encoding/Decoding length	1024	729	648	512	729	432
Number of downsized bits	376	81	0	80	297	0
Complexity units	5120	2916	2700	2304	2916	1728

. Note that higher values of complexity units indicate a more complex unit, i.e., worse design choice. We observe that the complexity is directly proportional to the number of downsized bits. This is because, although the downsized (punctured/shortened) bits are not transmitted/received across the channel, they still need to be encoded and decoded at the transmitter and receiver, respectively. Thus, if a corresponding codeword length is required, such that a multi-kernel circuit can directly generate it, then using a design based on downsizing from a single kernel circuit results in a more complex design. Thus, a less complex alternative to downsizing single kernel polar codewords at a small performance degradation could be an acceptable compromise if it suffices the desired quality-of-service (QoS).

4.3. Assessment

Based on the analysis performed in Section 4.1 and Section 4.2, we can derive some conclusions regarding the comparisons of error rate performances and complexities of the polar code design techniques implemented for simulation scenarios 1 and 2. The corresponding summaries of observations are provided in

Table 5. Tabulated observations from Scenario 1.

	Punctured N	Shortened N	K	Punctured M	Shortened M
BER at $R_d=1/4$	$++$	−	0	$--$	$--$
BER at $R_d=1/2$	0	+	0	$--$	0
BER at $R_d=3/4$	$--$	+	0	$--$	−
Complexity	$--$		0	−

and

Table 6. Tabulated observations from Scenario 2.

	Punctured N	Shortened N	K	Punctured M	Shortened M
BER at $R_d=1/4$	$++$	+	0	$--$	$--$
BER at $R_d=1/2$	+	$++$	0	$--$	−
BER at $R_d=3/4$	−	+	0	$--$	0
Complexity	−		0	$--$

, respectively. We use the multi-kernel design as a reference (0), with $++$, +, −, or $--$ indicating better to worse choices.

Clearly, the desired code rate is a key parameter used to determine the optimal choice of polar code design. Nevertheless, if a codeword length that can be obtained by a multi-kernel design is required, then the multi-kernel design is a good approach, providing near-optimal BER performance with reduced complexity. Additionally, it extends the scope of polar codeword lengths that can be generated without the requirement of any downsizing mechanism.

For instance, for code rates $R_d=1/2$ and $3/4$ in Scenario 1, multi-kernel design is able to reach the performance of the optimal (shortened) $2\times 2$ kernel design, with a gap of $0.25$ dB with $47.3\%$ complexity reduction (refer to Figure 4 and Figure 5). Simultaneously, it outperforms all other design techniques.

5. Future Work

Within the scope of research conducted for this article, we have polarization kernels of sizes 2 and 3 to generate single and multi-kernel polarization circuit designs. Nevertheless, the idea of channel polarization is not limited to only $2\times 2$ and $3\times 3$ kernel sizes. It would be interesting to study the comparative error rate performance with higher kernel sizes such as 5, 7, etc. or even non-prime standalone kernel sizes (i.e., not composed of smaller divisible kernel circuits), examples of which are available in [8]. Additionally, these higher-ordered kernel sizes can be used to generate polar codes of an even wider range of codeword lengths without the need for resizing.

In this article, we only used the SC decoder to assess the comparative BER performance; however, better variations exist such as the SC List (shown in [25]) or Flip (shown in [26]) decoders. Soft decoding techniques such as belief propagation (BP) have also been developed for polar codes. Recently, some interesting polar code construction techniques have been proposed, such as using the information bottleneck method (shown in [27]) or deep learning (shown in [28]). Additionally, some efficient simulation methods to analyze polar codes performance via importance-sampling techniques exist, such as those provided in [29,30]. Analyzing the error rate performance over these different techniques for downsized and multi-kernel designs can help identify the effects of specific system parameter settings. This, in turn, would aid in the generalization of polar code design and standardized use for practical applications.

6. Conclusions

In this article, we have discussed downsizing techniques such as puncturing, shortening, and using a different kernel size (such as 3) to design single- or multi-kernel polar codes of length other than $2^n$ form. The disadvantage of a limited choice of codeword lengths is a major obstacle for utilizing polar codes over a wide range of applications. Thus, when resizing is necessary, depending on availability, one may use alternatives to the classical $2\times 2$ polar circuit design such as higher-ordered kernel sizes, by themselves or within a multi-kernel framework, to generate polar codes without the need for resizing at all. Additionally, certain design aspects may prove to be optimal for given underlying system parameter settings. The threshold value of $R_d=7/16$, mentioned in [2], used for determining the downsizing choice, is not a very accurate assumption (also observed in [24]), and one also needs to take into account other parameters such as codeword length, the number of downsized bits, channel conditions, etc. as well to determine optimal code design for the desired application. In the case of multi-kernel codes, the order of kernel elements amongst the stages within the polar circuit is also a key design factor to be accounted for optimal performance as the selection of sets of information/frozen bits would vary for a different order of kernels. Using a multi-kernel design provides a higher degree of freedom for choosing codeword lengths without the requirement for downsizing while providing near-optimal performance.