A New 4D Hyperchaotic System and Its Analog and Digital Implementation
Abstract
:1. Introduction
2. Basic Analysis and Characterization of New Hyperchaotic System
2.1. Symmetry
2.2. Dissipativity and Existence of Attractor
+ (2by2 + a − c − 2ac − 2bz + bcz)λ
+ 2by2 − bz − ac + bcz − 2bcy2 = 0.
2.3. Bicurcation Analysis
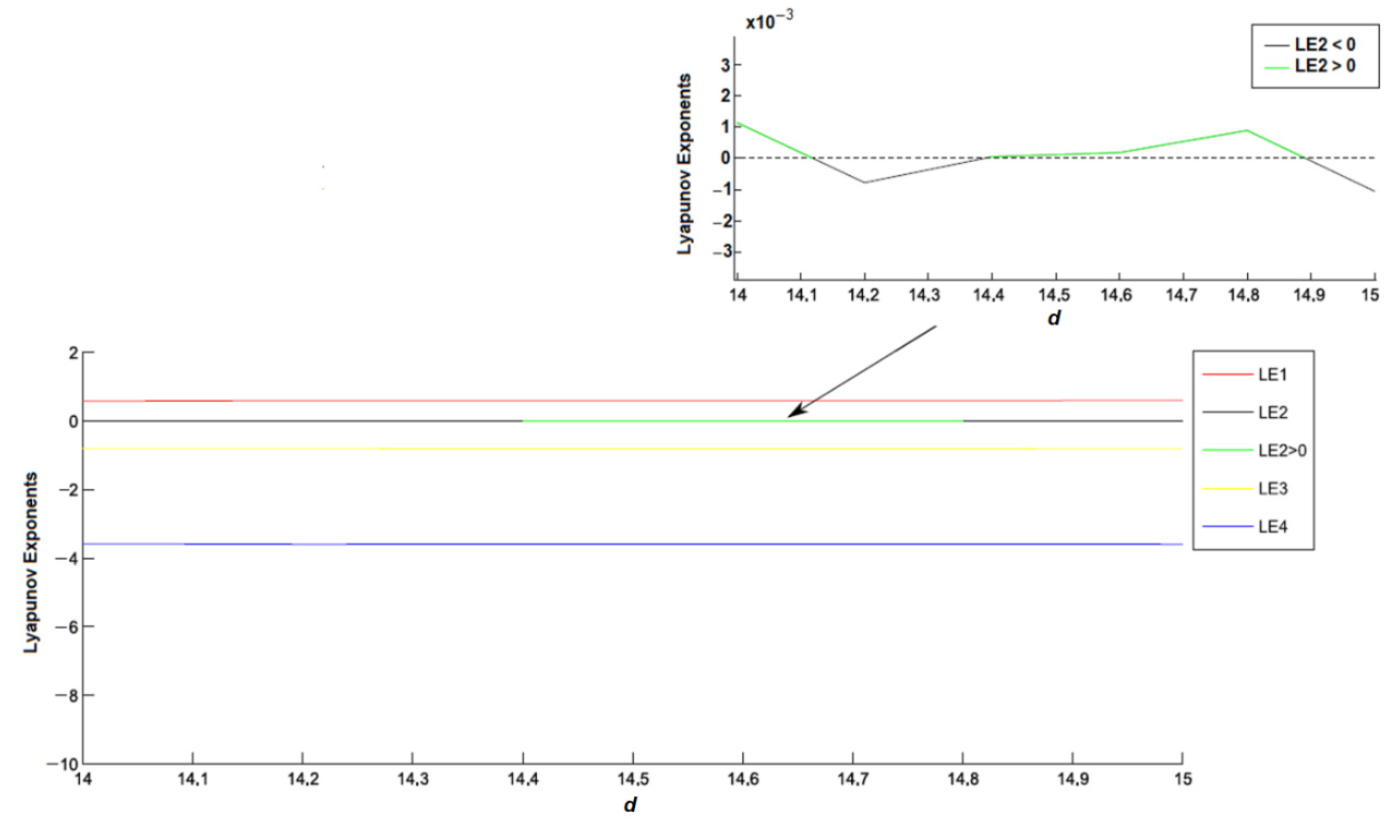
2.4. Lyapunov Exponents
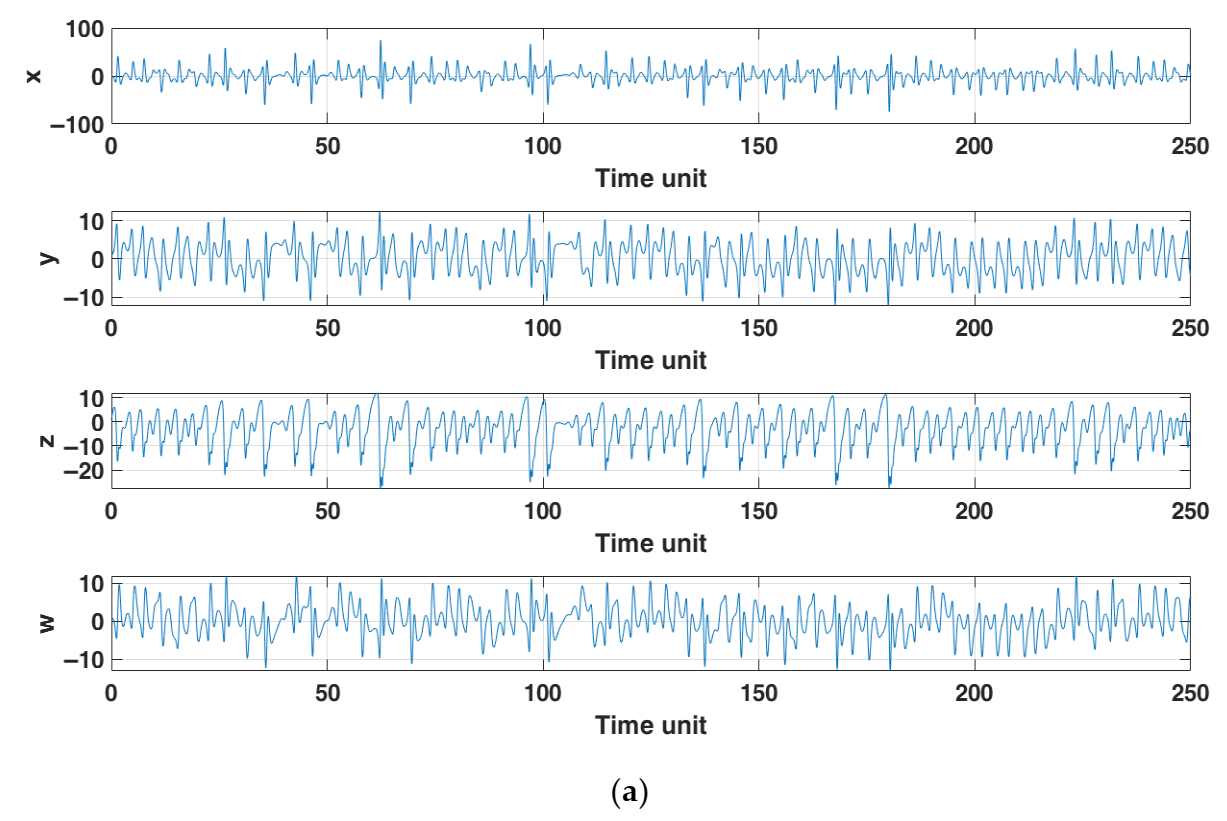
2.5. Numerical Simulations
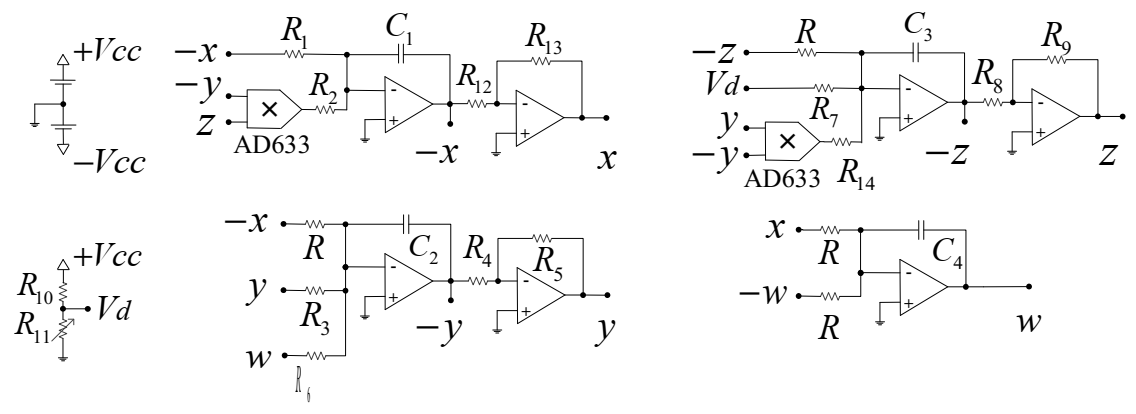
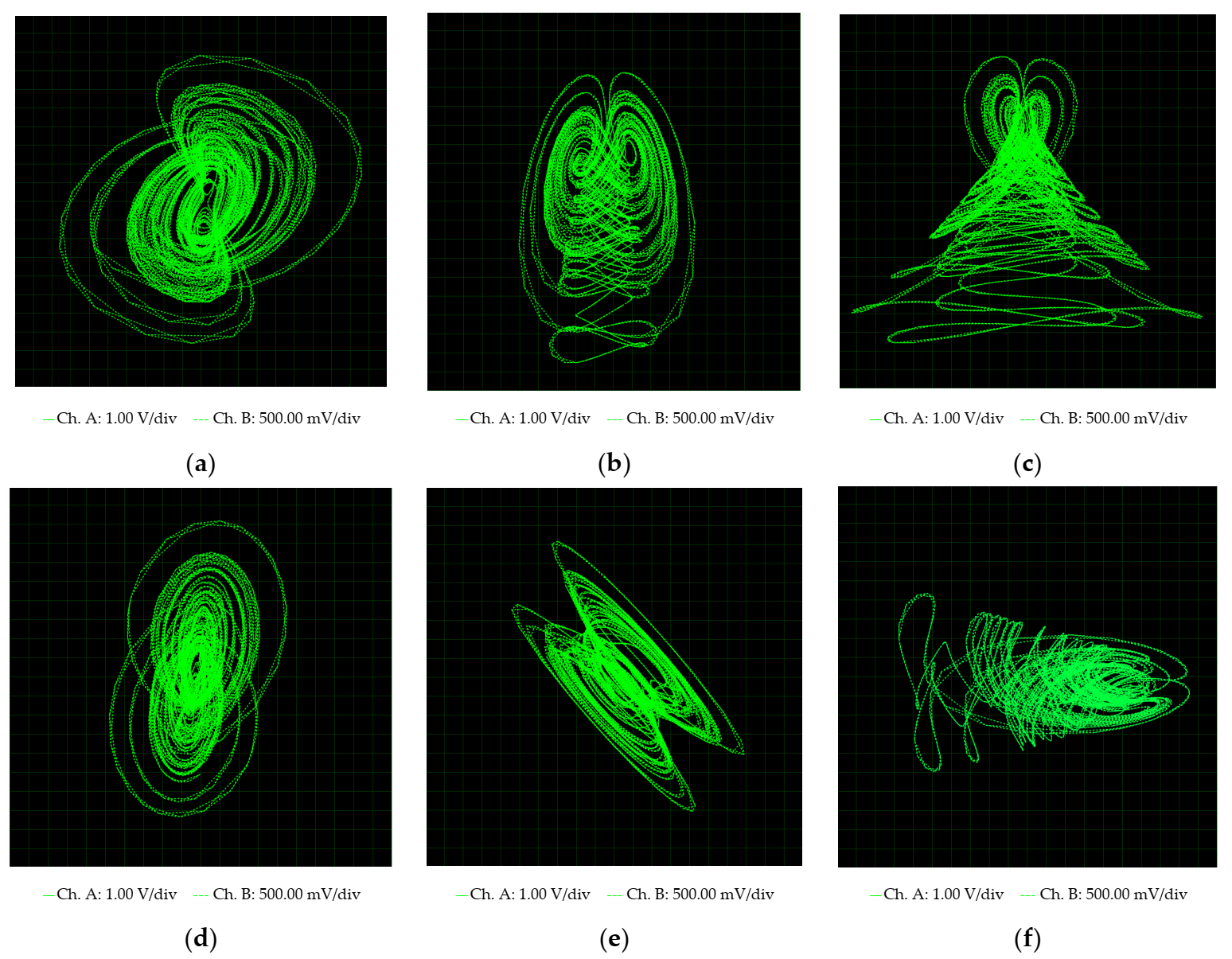
3. Electronic Implementations
3.1. Continuous Version and Its Electronic Circuit Design
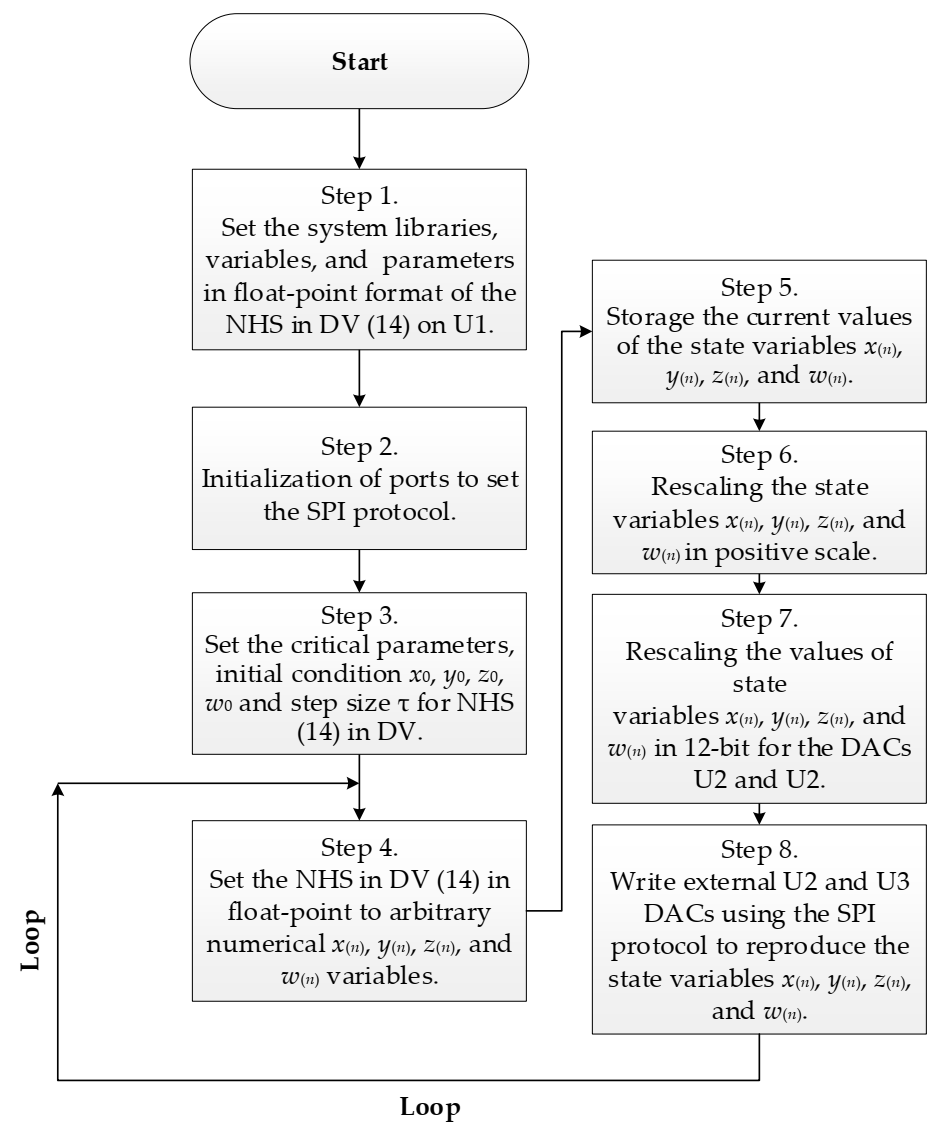
3.2. Discretized Version and Embedded System Design
y(n + 1) = y(n) + τ(−x(n) + cy(n) + cw(n)),
z(n + 1) = z(n) + τ(d − y(n)2 − z(n)),
w(n + 1) = w(n) + τ(x(n) − w(n)).
3.2.1. Circuit Design of an Embedded System
3.2.2. Implementation of the DV of NHS in Floating-Point
3.2.3. Implementation of the DV of NHS in Fixed-Point Q1.15
p(n + 1) = p(n) − τo (n) + cτp(n) + cτr(n),
q(n + 1) = q(n) + dτ − τp(n)2 − τq(n),
r(n + 1) = r(n) + τo (n) − τr(n),
p(n + 1) = − 0.02o(n) + 0.505p(n) + 0.505p(n) + 0.01r(n),
q(n + 1) = 0.0145 + 0.98q(n) − 0.4p(n)2,
r(n + 1) = 0.02o (n) + 0.98r(n).
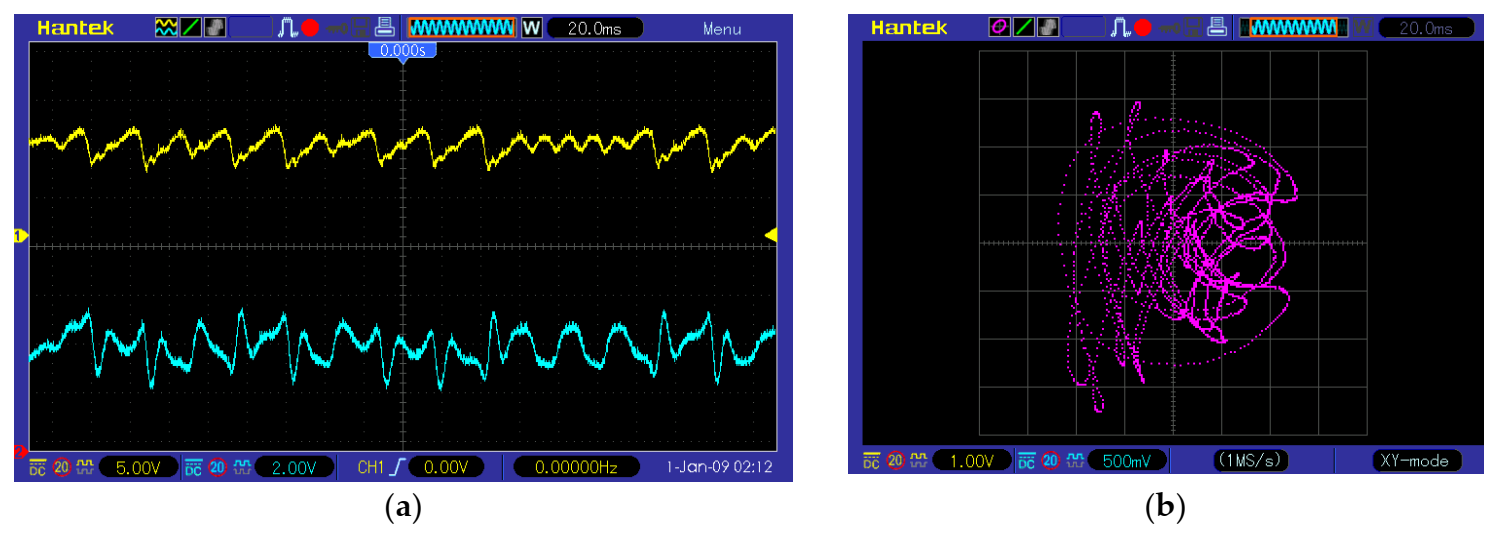
3.2.4. Comparison of the Digital Implementations of the DV of NHS Algorithm in dsPIC
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| 4D | Four-dimensional |
| MACM | Méndez-Arellano-Cruz-Martínez |
| NHS | New hyperchaotic system |
| CV | Continuous version |
| OA | Operational amplifiers |
| DV | Discretized Version |
| DSP | Digital Signal Processor |
| DACs | Digital-to-analog converters |
| ES | Embedded System |
| NA | Numerical algorithm |
References
- Eckmann, J.-P.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 1985, 57, 617–656. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Alligood, K.T.; Sauer, T.D.; Yorke, J.A. Chaos: An Introduction to Dynamical Systems; Springer: Berlin, Germany, 1996. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Perseus Books: Boston, MA, USA, 1994. [Google Scholar]
- Liu, J.; Wang, Z.; Shu, M.; Zhang, F.; Leng, S.; Sun, X. Secure Communication of Fractional Complex Chaotic Systems Based on Fractional Difference Function Synchronization. Complexity 2019, 2019, 7242791. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, Y.; Sekiguchi, A. The chaotic mobile robot. IEEE Trans. Robot. Autom. 2001, 17, 898–904. [Google Scholar] [CrossRef]
- Arellano-Delgado, A.; López-Gutiérrez, R.; Cruz-Hernández, C.; Posadas-Castillo, C.; Cardoza-Avendaño, L.; Serrano-Guerrero, H. Experimental network synchronization via plastic optical fiber. Opt. Fiber Technol. 2016, 19, 93–98. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Abundiz-Pérez, F.; López-Gutiérrez, R.M. A robust embedded biometric authentication system based on fingerprint and chaotic encryption. Expert Syst. Appl. 2015, 42, 8198–8211. [Google Scholar] [CrossRef]
- Méndez-Ramírez, R.; Arellano-Delgado, A.; Cruz-Hernández, C.; Abundiz-Perez, F.; Martinez-Clark, R. Chaotic digital cryptosystem by using SPI protocol and its dsPICs implementation. Front. Inf. Technol. Electron. Eng. 2018, 19, 165–179. [Google Scholar] [CrossRef]
- Méndez-Ramírez, R.; Arellano-Delgado, A.; Murillo-Escobar, M.; Cruz-Hernández, C. Multimedia contents encryption using the chaotic MACM system on a smart-display. In Cryptographic and Information Security Approaches for Images and Videos; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2019; 10th chapter. [Google Scholar]
- Lorenz, E. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for Hyperchaos. Phys. Lett. A 1979, 71, 155–157. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Rajagopal, K.; Sambas, A.; Kacar, S.; Cavusoglu, U. A new hyperchaotic temperature fluctuations model, its circuit simulation, FPGA implementation and an application to image encryption. Int. J. Simul. Process. Model. 2018, 13, 281–296. [Google Scholar] [CrossRef]
- Kamdem Kuate, P.D.; Lai, Q.; Fotsin, H. Complex behaviors in a new 4D memristive hyperchaotic system without equilibrium and its microcontroller-based implementation. Eur. Phys. J. Spec. Top. 2019, 228, 2171–2184. [Google Scholar] [CrossRef]
- Rajagopal, K.; Vaidyanathan, S.; Karthikeyan, A.; Srinivasan, A. Complex novel 4D memristor hyperchaotic system and its synchronization using adaptive sliding mode control. Alex. Eng. J. 2018, 57, 683–694. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A.; Duraisamy, P. Hyperchaotic Chameleon: Fractional Order FPGA Implementation. Complexity 2017, 16, 8979408. [Google Scholar] [CrossRef] [Green Version]
- Vicente, R.; Daudén, J.; Colet, P.R. Toral Analysis and Characterization of the Hyperchaos Generated by a Semiconductor Laser Subject to a Delayed Feedback Loop. IEEE J. Quantum Electron. 2005, 41, 541–548. [Google Scholar] [CrossRef] [Green Version]
- Panga, S.; Liu, Y. A new hyperchaotic system from the Lü system and its control. J. Comput. Appl. Math. 2011, 235, 2775–2789. [Google Scholar] [CrossRef] [Green Version]
- Li-Xin, J.; Hao, D.; Meng, H. A new four-dimensional hyperchaotic Chen system and its generalized synchronization. Chin. Phys. B 2010, 19, 100501. [Google Scholar] [CrossRef]
- Ding, L.; Ding, Q. A Novel Image Encryption Scheme Based on 2D Fractional Chaotic Map, DWT and 4D Hyper-chaos. Electronics 2020, 9, 1280. [Google Scholar] [CrossRef]
- Kapitaniak, T.; Maistrenko, Y.; Popovych, S. Chaos-hyperchaos transition. Phys. Rev. E 2000, 62, 1972. [Google Scholar] [CrossRef] [Green Version]
- Li, G.L.; Chen, X.Y.; Liu, F.C.; Mu, X.M. Hyper-chaotic Canonical 4-D Chua’s Circuit. In Proceedings of the 2009 International Conference on Communications, Circuits and Systems, Milpitas, CA, USA, 23–25 July 2009; p. 10879007. [Google Scholar]
- Wang, X.; Wang, M. A hyperchaos generated from Lorenz system. Phys. A Stat. Mech. Appl. 2008, 387, 3751–3758. [Google Scholar] [CrossRef]
- Chen, B.; Yu, S.; Chen, P.; Xiao, L. Design and Virtex-7-Based Implementation of Video Chaotic Secure Communications. Int. J. Bifurc. Chaos 2020, 30, 24. [Google Scholar] [CrossRef]
- Méndez-Ramírez, R.; Arellano-Delgado, A.; Murillo-Escobar, M.; Cruz-Hernández, C. Degradation Analysis of Chaotic Systems and their Digital Implementation in Embedded Systems. Complexity 2019, 22, 9863982. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L. Fixed-point FPGA model-based design and optimization for Henon map chaotic generator. In Proceedings of the 2017 IEEE 8th Latin American Symposium on Circuits & Systems (LASCAS), Bariloche, Argentina, 20–23 February 2017; p. 16964391. [Google Scholar]
- Flores-Vergara, A.; Inzunza-González, E.; García-Guerrero, E.E.; López-Bonilla, O.; Rodríguez-Orozco, E.; Hernández-Ontiveros, J.M.; Cárdenas-Valdez, J.R.; Tlelo-Cuautle, E. Implementing a Chaotic Cryptosystem by Performing Parallel Computing on Embedded Systems with Multiprocessors. Entropy 2019, 21, 268. [Google Scholar] [CrossRef] [Green Version]
- Chuan Qin, K.S.; Shaobo, H. Characteristic Analysis of Fractional-Order Memristor-Based Hypogenetic Jerk System and Its DSP Implementation. Electronics 2021, 10, 841. [Google Scholar] [CrossRef]
- Mendez-Ramirez, R.; Arellano-Delgado, A.; Cruz-Hernandez, C.; Lopez-Gutierrez, R.M. Degradation analysis of generalized Chua’s circuit generator of multi-scroll chaotic attractors and its implementation on PIC32. In Proceedings of the Future Technologies Conference (FTC), San Francisco, CA, USA, 6–7 December 2016; pp. 1034–1039. [Google Scholar]
- Koulamas, C.; Lazarescu, M.T. Real-Time Embedded Systems: Present and Future. Electronics 2018, 7, 205. [Google Scholar] [CrossRef] [Green Version]
- Méndez-Ramírez, R.; Cruz-Hernández, C.; Arellano-Delgado, A.; Martínez-Clark, R. A new simple chaotic Lorenz-type system and its digital realization using a TFT touch-screen display embedded system. Complexity 2017, 2017, 6820492. [Google Scholar] [CrossRef] [Green Version]
- Nik, H.S.; Golchaman, M. Chaos Control of a Bounded 4D Chaotic System. Neural Comput. Applic. 2014, 25, 683–692. [Google Scholar]
- Qinghai, S.; Hui, C.; Yuxia, L. Complex Dynamics of a Novel Chaotic System Based on an Active Memristor. Electronics 2020, 9, 410. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.Y.; Cao, W.; Chung, T.-S.; Morris, J. Applied Numerical Methods Using Matlab; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Microchip Technology Inc. 16-Bit Language Tools Libraries, Reference Manual; Microchip Technology Inc.: Chandler, AZ, USA, 2014; DS0001456J.1–155. [Google Scholar]


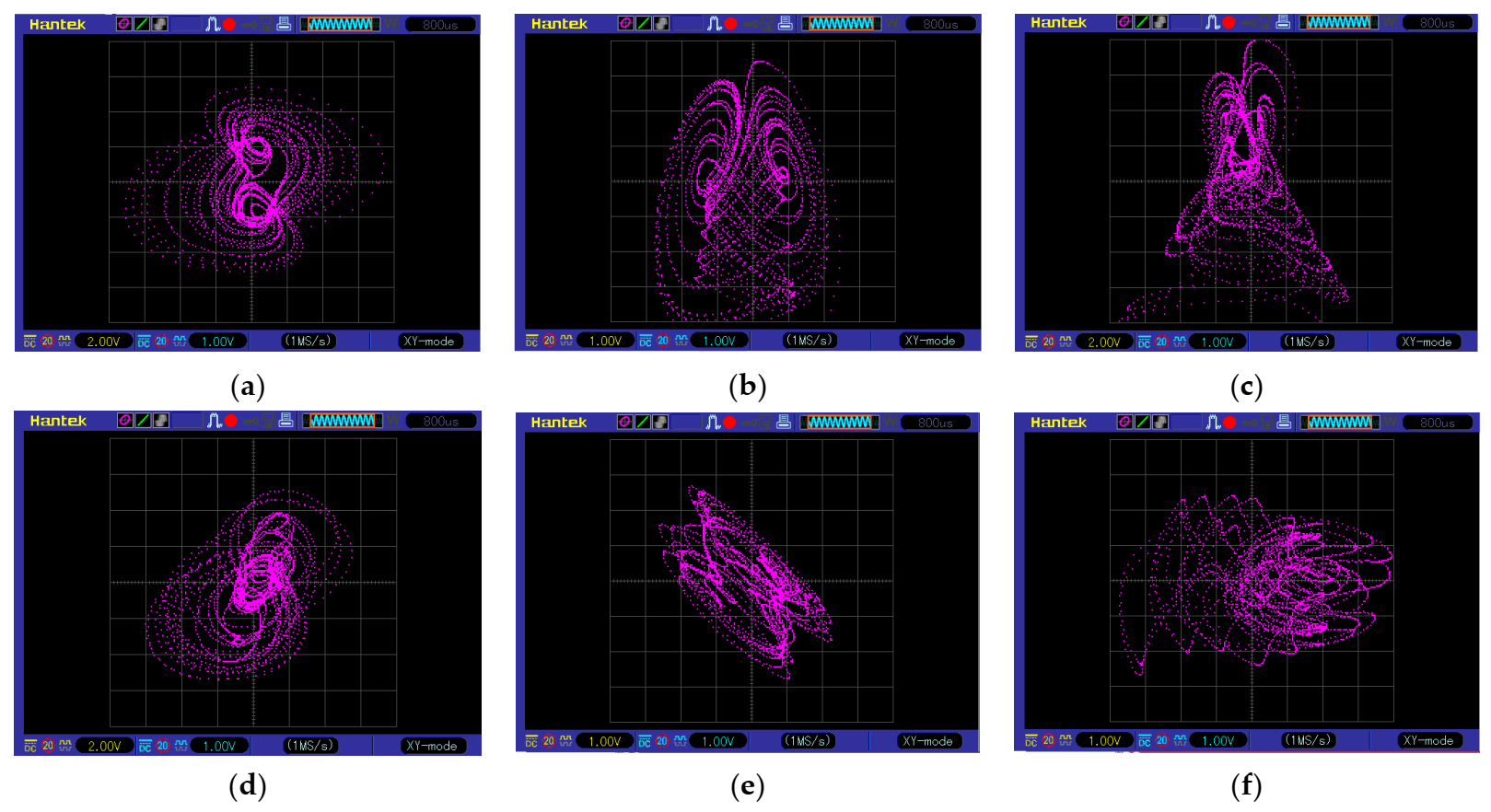




| Point | Eigenvalues | Stability |
|---|---|---|
| P0 | λ1 = −0.5247 λ2 = −1 λ3 = 4.5361 λ4 = −6.5113 | λ1, λ2, λ4 < 0, and λ3 > 0, unstable saddle point |
| P1–4 | λ1 = −0.4939 λ2 = 0.94767 − 3.4506i λ3 = 0.94767 + 3.4506i λ4 = −4.9014 | λ1, λ4 < 0, and the real part λ2, λ3 > 0, unstable saddle point |
| P5–6 | λ1 = −0.4918 λ2 = 1.5384 λ3 = 2.7915 λ4 = −7.3381 | λ1, λ4 < 0, and λ2, λ3 > 0, unstable saddle point |
| P7–8 | λ1 = 0 λ2 = −1 λ3 = −1.25 + 0.9682i λ4 = −1.25 − 0.9682i | λ2 < 0, and the real part λ2, λ3 < 0, Spiral stable point |
| Peripheral Number | Hardware Description |
|---|---|
| U1 | Master, microcontroller dsPIC33FJ32MC204 |
| U2 | Slave 1, DAC MCP4922 shows x(t) and y(t) |
| U3 | Slave 2, DAC MCP4922 shows z(t) and w(t) |
| U1 Pin | Description |
|---|---|
| RB14—SCK | Serial clock signal to synchronize U2 and U3 |
| RB13—SDO | Serial data output to enable U2 and U3 |
| RC2—EDAC1 | Chip Select to enable U2 |
| RC1—EDAC2 | Chip Select to enable U3 |
| RC0—LDAC | Enable U2–U3 simultaneously to depict the state variables x(n), y(n), z(n), and w(n) |
| Parameter | Result |
|---|---|
| τ | 0.02 |
| tc1 | 56 µs |
| tTg1 | 34.4 µs |
| TTd1 | 90.4 µs |
| fTd1 | 11061 ips |
| QT1 | 221.22 tu |
| Parameter | Result |
|---|---|
| τ | 0.02 |
| tc2 | 6 µs |
| tTg2 | 34.4 µs |
| TTd2 | 40.4 µs |
| fTd2 | 24752 ips |
| QT2 | 495.04 tu |
| Parameter | Floating-Point System (14) Result | Fixed-Point System (17) Result |
|---|---|---|
| τ | 0.02 | 0.02 |
| tc | 56 µs | 6 µs |
| tTg | 34.4 µs | 34.4 µs |
| TTd | 90.4 µs | 40.4 µs |
| fTd | 11061 ips | 24752 ips |
| QT | 221.22 tu | 495.04 tu |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Méndez-Ramírez, R.D.; Arellano-Delgado, A.; Murillo-Escobar, M.A.; Cruz-Hernández, C. A New 4D Hyperchaotic System and Its Analog and Digital Implementation. Electronics 2021, 10, 1793. https://doi.org/10.3390/electronics10151793
Méndez-Ramírez RD, Arellano-Delgado A, Murillo-Escobar MA, Cruz-Hernández C. A New 4D Hyperchaotic System and Its Analog and Digital Implementation. Electronics. 2021; 10(15):1793. https://doi.org/10.3390/electronics10151793
Chicago/Turabian StyleMéndez-Ramírez, Rodrigo Daniel, Adrian Arellano-Delgado, Miguel Angel Murillo-Escobar, and César Cruz-Hernández. 2021. "A New 4D Hyperchaotic System and Its Analog and Digital Implementation" Electronics 10, no. 15: 1793. https://doi.org/10.3390/electronics10151793
APA StyleMéndez-Ramírez, R. D., Arellano-Delgado, A., Murillo-Escobar, M. A., & Cruz-Hernández, C. (2021). A New 4D Hyperchaotic System and Its Analog and Digital Implementation. Electronics, 10(15), 1793. https://doi.org/10.3390/electronics10151793







