Inferring the Hidden Cascade Infection over Erdös-Rényi (ER) Random Graph
Abstract
:1. Introduction
- First, the recovering hidden cascade infection problem is studied on the well-known ER random graph under the IC model. As shown in Figure 1, for a given number of nodes, the shape of the ER random graph varies greatly depending on the average degree . Hence, the effect of this parameter on the recovery performance was investigated for the first time.
- Second, to solve the problem, an algorithm that detects whether the node is infected with only neighboring infection information is first designed, which gives the local infection status of the graph. For this, the possibilities that can occur with the infected neighbor nodes are parameterized by a single parameter, and the method of selecting the best parameter is investigated. Next, as global information regarding infection, an efficient algorithm is proposed that uses the location of the estimated cascade sources. The infection probabilities from the sources are used, which is a new method that has yet to be approached.
- Third, various simulations are conducted to obtain the recovering performance of the two proposed algorithms. As a result, although the first one uses only local information of the neighboring infection status, it recovers the hidden cascade infection well compared with other baseline algorithms. Further, it is shown that the detection performance of the second graph is also good if the ER random graph has a local tree structure.
2. Related Work
- (1)
- Hidden node (structure) Inference. For the graph structure learning, Netrapalli et al. [4] considered the graph inference problem, where only the infection times of the nodes are given. In this study, the authors tried to estimate which neighbors are influential through multiple cascades spreading throughout the graph. To do this, they suggested a MLE for recovering influential connections, which guarantees a necessary cascade sample complexity for the IC model. Pouget et al. [15] studied the graph structure learning from the sparse recovery framework for a general discrete cascade model. They first formulated the problem as a general Linear Threshold (LT) model and proposed an algorithm that recovers the true edges in the graph with high probability. The authors of Reference [16] considered the graph learning problem for continuous-time cascade models. For this, they first introduced the concept of a trace complexity as the number of distinct traces required to achieve high fidelity in reconstructing the topology of an unobserved network. Based on this, they proposed a simple but efficient algorithm for inferring the graph structures. He et al. [9] proposed an algorithm that effectively recovers a graph with partial cascade samples by considering a generative model, referred to as the MultiCascades Model. As the key idea of this model, it uses the commonality between highly correlated diffusion graphs. He et al. [17] also designed some algorithms inferring the influence function from the partial observations of the node activation in the graph. To do so, they considered a probably approximately correct learnability of the influence functions for the missing observations. Rozenshtein et al. [18] has studied the reconstruction of cascades from partial timestamps. They designed an effective algorithm called a CULT to recover from epidemics by formulating a temporal Steiner tree problem. Xiao et al. [7] formulated a cascade-reconstruction problem as a variant of the Steiner tree problem. With their approach, they first estimate a tree that spans all reported active nodes, which satisfies some temporal consistency constraints. Furthermore, they proposed several algorithms and showed that one of them achieves a linear time -approximation guarantee, where k is the number of active nodes. Some researchers have studied the graph learning without the explicit time of infection. Gripon et al. [19] proposed an algorithm that recovers infection edges, which are the edges in the graph that are involved in the infection process from an unordered set of infected nodes. They designed an algorithm to infer such edges in order by comparing each trace into a path using information in which pairs of nodes in the path co-occur most frequently in the observations. Amin et al. [20] investigated the problem of reconstructing the node connectivity using only the initial source nodes and the final diffusion snapshot of infected nodes for the IC model, without any time information of the nodes. Wu et al. [8] considered an EM approach for the Continuous Independent Cascade (CIC) model using partial information on the infection status of the graph, and proposed algorithms that estimate the influence parameters of edges based on the EM. The authors of Reference [5] investigated the problem of recovering missing infected nodes and the source nodes of an epidemic. To do so, they proposed an algorithm called NETFILL, which solves these two inference problems simultaneously. The authors of Reference [6] considered a problem that reconstructs the underlying cascade that is likely to generate observations of infections in the graph. They estimated the infection probabilities by generating a sample of the probable cascades, proposed several algorithms for sampling directed Steiner trees with a given set of terminals.
- (2)
- Cascade Source Detection. Next, some of the cascade source detection problems are summarized in the following sections. Zhu et al. [21] considered the cascade source detection problem using an ER random graph. They proposed a new source localization algorithm for the IC model, called the Short-Fat Tree algorithm, which selects the node of the Breadth-First Search (BFS) tree, which has the minimum depth but the maximum number of leaf nodes. In addition, they also proposed a new source localization algorithm, called an Optimal-Jordan-Cover (OJC) in Reference [22], which extends the source inferring problem to the case of multiple sources in the graph. The OJC first extracts a subgraph using a candidate selection algorithm that selects the source candidates based on the number of observed infected nodes in their neighborhoods. Considering the heterogeneous SIR diffusion in the ER random graph, they proved that OJC can locate all sources with a probability of 1 asymptotically with partial observations. Next, some studies have utilized partial information on when a random node is infected. The authors of Reference [23] studied the problem of partial timestamps of infection. They solved this problem by formulating a ranking problem on graphs using the likelihood of being the source. In the opposite direction as the previous source detection problem, Fanti et al. [24] first studied how to spread as many anonymous messages as possible while hiding the source. They designed a message-propagation protocol, called an adaptive diffusion model, and then obtained analytical results of the hiding performance of the model. The authors of Reference [25] considered the source-finding problem with observation time information , which contains some set S of nodes with the first infection timestamps . Tang et al. [26] investigated the problem based on the network topology and a subset of infection timestamps. For a tree network, they first derived the maximum likelihood estimator of the source and unknown diffusion parameters. Using this, they considered an optimization over a parametrized family of Gromov matrices in the design of an estimation algorithm for general graphs. Kumar et al. [27] considered a problem with additional relative information about the infection times of a fraction of node pairs.
3. Model and Goal
3.1. Models
- Graph Model. The recovery problem of a hidden cascade node for the ER random graph G, as represented by some graph parameters, is considered. An ER random graph, which is usually denoted by on the vertex set V, is a random graph that connects each pair of nodes with probability . This model is parameterized by the number of nodes, and p. The expected number of degrees of a node is then computed by (see Figure 1). Most results for ER graphs suppose that this is fixed (e.g., or ) or increases slowly (e.g., ). Although it is a synthetic graph, the ER random graph may have a local tree-like structure with a large diameter or an extremely dense graph structure with a small diameter as the parameter varies.
- Cascade and Observation Models. As a cascade model, a well-known independent cascade model is considered. With this model, three possible states of nodes are considered: Susceptible (S), Active (A), or Inactive (I). First, a susceptible state means that a node can be activated. Next, if a node in the susceptible state is activated at the previous time slot, it becomes an active node, which is in a state in which other susceptible child nodes are activated. The inactive state denotes a state in which a node was activated once earlier, but no longer able to activate other susceptible nodes. In the proposed model, the cascade starts from a subset of seed nodes that have been initially infected in the network. The cascade occurs in a discrete round, At round , the seed nodes are active, and the others are inactive. Then, if a node u receives the information or is infected from one of its infected nodes at time t, the node spreads its own information (or a virus) to its neighbor v with probability at the next time . It is assumed that the activated nodes are active for only one time slot, and they become inactive in the next time slot. Once a node becomes inactive, it maintains the state until reaching the end of the cascade process. The process stops when no more nodes are infected. For a simpler expression, the probability is also used, where is the edge among the nodes in the network. When some neighbors are already infected, the probability of infection is regarded as zero. Let be the diffusion vector over each edge An infected node v is considered to report its status of infection with probability , labelled based on an observation probability and denoted as . The node represents the information source, which acts as a node that initiates diffusion, and the set indicates the set of observed (reported) infected nodes. Further, represents the observed snapshot of the cascade graph at time Finally, assume that the number of cascade sources is given as a prior by for a certain analytical tractability. We summarize the explanations of notations used in the paper in Table 1.
3.2. Goal: Estimation of an Infection
- Performance metric. As a performance measure for the true recovery of the proposed estimation algorithm, the following precision-based accuracy is used: Let be the set of hidden infected nodes (ground truth) and be the estimated recovery set of infected nodes by the estimator . As a measure of the hidden cascade recovery, a precision metric is defined bywhere is an indicator function that has only one function for ; otherwise, it is zero. The notion is the number of infected nodes for . This metric measures the rate at which the number of recovered nodes is truly infected among the estimated recovered set for the observed snapshot at time . To obtain this, two classification algorithms are proposed. The first is a neighbor-based approach that uses local infection status information. The second approach is a source-location-based approach that uses global infection status information from the cascade source nodes. Various simulations are then conducted, and the results are obtained by varying the model parameters described in Section 6.
4. Neighbor-Based Recovery Algorithm
Neighbor-Based Recovery
- Algorithm. In NBRA(), the algorithm first initializes the recovering set as an empty set. Then, for the nodes , it counts the number of observed infected neighbor nodes, denoted by , and sets the minimum diffusion probability among by . Next, a heuristic infection probability is defined from the infected neighbor nodes of node v. In this algorithm, the probability is set to zero when there are no infected neighbor nodes, i.e., Otherwise, it setswhere is a trade-off parameter. Finally, the algorithm puts the node v into the recovering set if the probability is greater than (this approach implies that, if the heuristic infection probability from the infected neighbor nodes is larger than , it is regarded as an infected node).
- Case I: Single candidate neighbor . When , it results in . This is the case in which there is only one possible candidate, i.e., already infected neighbor, with the minimum diffusion probability among all infected neighbors . In this case, it is considered that one neighbor node is infected first, node v is then infected by the neighbor node, and the remaining infected neighbor nodes are, thus, consequently infected. This is the lowest probability of all possible cases of infection order among , except for the case in which node v is infected first because only one possible infection is considered.
- Case II: Multiple candidate neighbors . When , occurs. This is the case in which all nodes in are infected before the infection of v. Hence, there are many possibilities of infection from the infected neighbors, i.e., the node v will be infected if there exists at least one infection successfully among the infected neighbor nodes. This is the greatest probability from , except that the infection to node v comes from other hidden infection nodes because infection from all infected neighboring nodes is considered.
- Case III: Relaxation case (). When only the infected node v and the infection snapshots for neighboring infected nodes are given, it is difficult to estimate the path of the infection. Hence, in this algorithm, various choices of can be considered. As depicted above, when the value reaches 1, it estimates that the infection comes from only one possible node that has the minimum diffusion probability among the infected neighbor set . However, if the value of reaches zero, the infection occurs in at least one neighbor infected node. In the numerical section, some simulation results show how the hidden infection changes according to .
| Algorithm 1 Neighbor-based Recovery Algorithm (NBRA()) |
|
5. BFST Source-Based Recovery Algorithm
5.1. Source Estimation
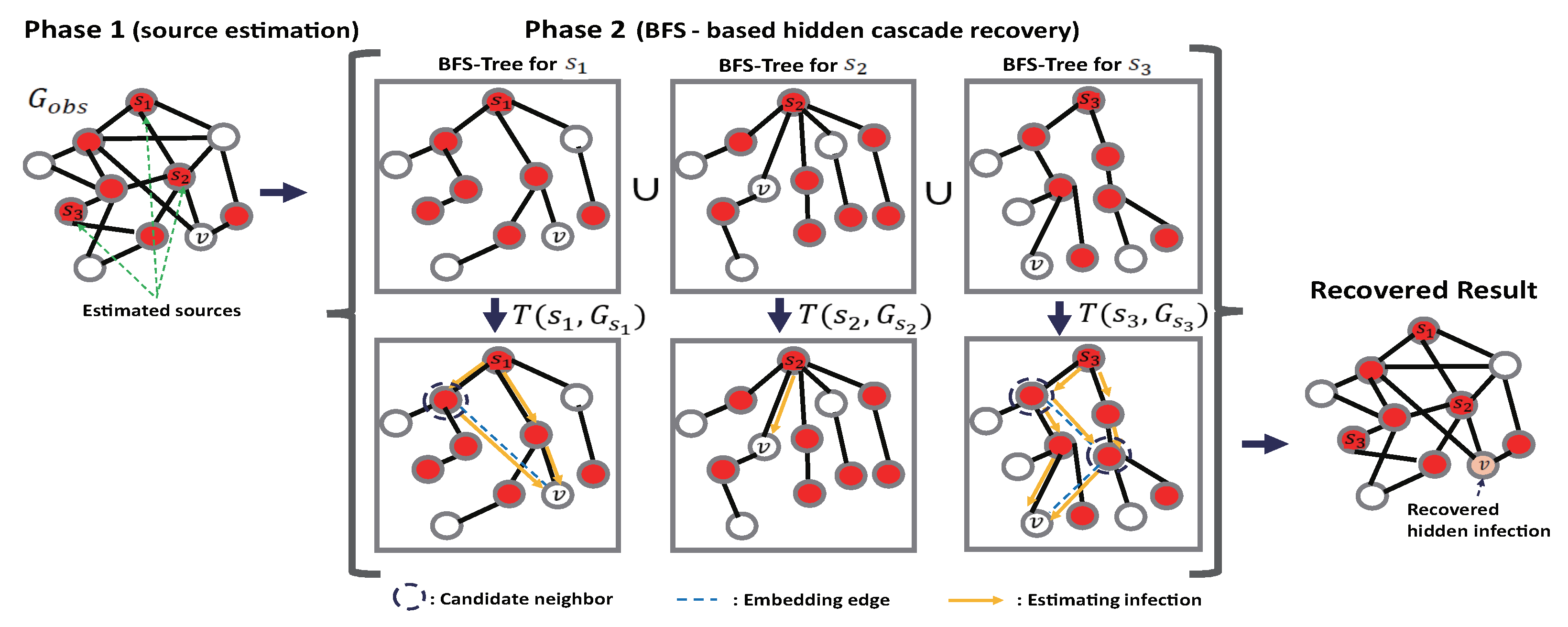
- Step 1 (Candidate Set Selection): In this step, the algorithm first selects the candidate source nodes by considering the number of infected (observed) neighbors. To do that, let be a positive integer, which is called the selection threshold. Then, define a candidate set of the cascade sources W as the set of nodes whose number of infected neighbors is greater than the predefined threshold . Next, the algorithm sets by the union of the candidate sets W and the observed infection set . This procedure considers a node that is not an infected node in a limited observation, but is infected with many neighbor nodes. It then sets by a connected sub-graph of induced by the node set . Such a reconstructed graph is called an induced graph. An induced graph is a subset of nodes in a graph with all edges having endpoints in the node subset. This refers to the part in which the graph is reconstructed as new nodes are added to the infection graph created from the original infected node. However, the induced graph may not be fully connected because of the hidden infected nodes or multiple sources. This becomes a problem when it is necessary to determine the infection eccentricity in the infection graph. Therefore, if the induced graph is separated, a node is selected with minimum eccentricity for each sub-graph (component) and connects it to connect the entire induced graph. Subsequently, the minimum eccentricity of the induced graph is computed. This is a modified part of the OJC, which randomly selects such nodes in each component. This modification is considered to ensure that the central node of each cluster of the cascade does not lose its high probability of becoming a candidate source (although, considering a hidden infection, this will be a natural step to guessing that the high centrality node of a cluster may have a high possibility of becoming a source due to the randomness of hiding its status of infection in the proposed model). The pseudo-code of the candidate selection algorithm for selecting W and can be found in Reference [22].
- Step 2 (Jordan Cover Selection): Using the result of the candidate set W in Step 1, the algorithm computes the infection eccentricity of the node set with , as defined in Equation (4) on the sub-graph . Next, a combination is selected with the minimum infection eccentricity as a set of sources. Then, the m-Jordan cover is chosen byTies are broken by the total distance from the observed infection to the node set, that is, .
5.2. BFS Tree-Based Recovery Hidden Infection
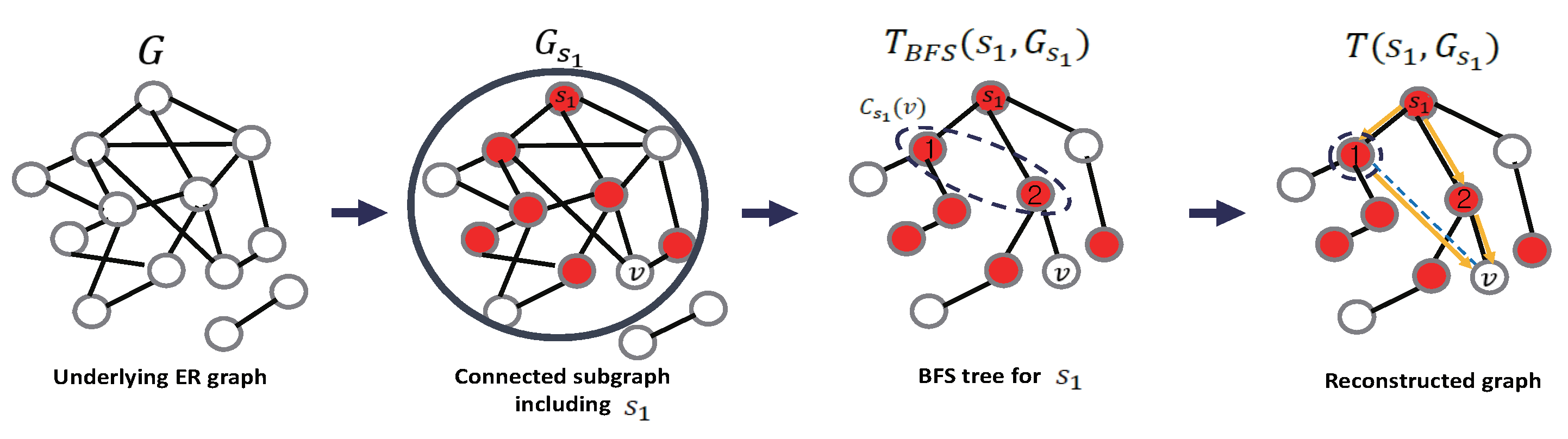
- Step 1 (Candidate Infection Path Selection): In this step, the algorithm first constructs BFS trees based on the estimated source node from Phase 1. To do this, let be the connected subgraph of G as in Figure 3, which contains the source and let be the BFS tree with respect to the (Because the underlying graph is a random graph, some disconnections may exist. If there is no separation of is equal to G.). Then, m such BFS trees are obtained on the underlying graph G because there are m sources. If , i.e., G is disconnected, the BFS tree is generated only on the connected subgraph . However, the BFS tree generates a unique candidate infection path from the source to node This is quite limited in general graphs that can have multiple paths. With the proposed algorithm, to guarantee such multiple infection paths, some candidate neighbors (here, the candidate neighbor means a neighbor node that can infect the node v among the neighbors in the original graph) of each node from v to the source node are first found among the infected nodes based on the BFS tree. To this end, the candidate neighbor set is defined in each BFS tree aswhere is the hop distance from node to . The algorithm then embeds an edge from a candidate infected neighbor node to v. Next, for the chosen nodes in , the candidate neighbor procedure is repeated. It performs this procedure until the candidate neighbor is exactly the estimated source. The graph reconstructed by is then denoted as in Figure 3. As the reason for this approach, the BFS preserves the infection path in the IC model. Further, it removes the loops in the original graph from the estimated source node to v while guaranteeing the candidate infection paths.
- Step 2 (Recovery Hidden Infection): Next, the algorithm computes the infection probability for the given cascade sources with the corresponding BFS based on the reconstructed graphs under the IC diffusion model. To do this, let be the set of infected nodes (including the observed infection set and unobserved infection set ) by the cascade from The objective is then to compute the probability , i.e., the probability of infection of node v from the source S. However, it is not easy to compute this probability in a general loopy graph because of the computational complexity, as described above. Hence, the probability is approximated by over T, where . To compute this in the IC model, let be the path between node v and the source node in Then, we havewhere is the probability that a diffusion will occur over the edge in . For example, if the diffusion is an IC model with a successful probability of , the probability in Equation (7) becomeswhere is the number of edges over the path in Using this, the algorithm determines a node as a cascade-infected node if the diffusion probability is greater than a predefined threshold, i.e., as a cascade infected node. Then, it remains how to choose such a parameter For this, is set. Here, and are the maximum and minimum infection probabilities over , respectively. The reason for the threshold is that it can be a measure of how the diffusion spreads from the current observation.
| Algorithm 2 BFST Source-based Recovery Algorithm (BSRA) |
|
6. Simulation Results
6.1. Results
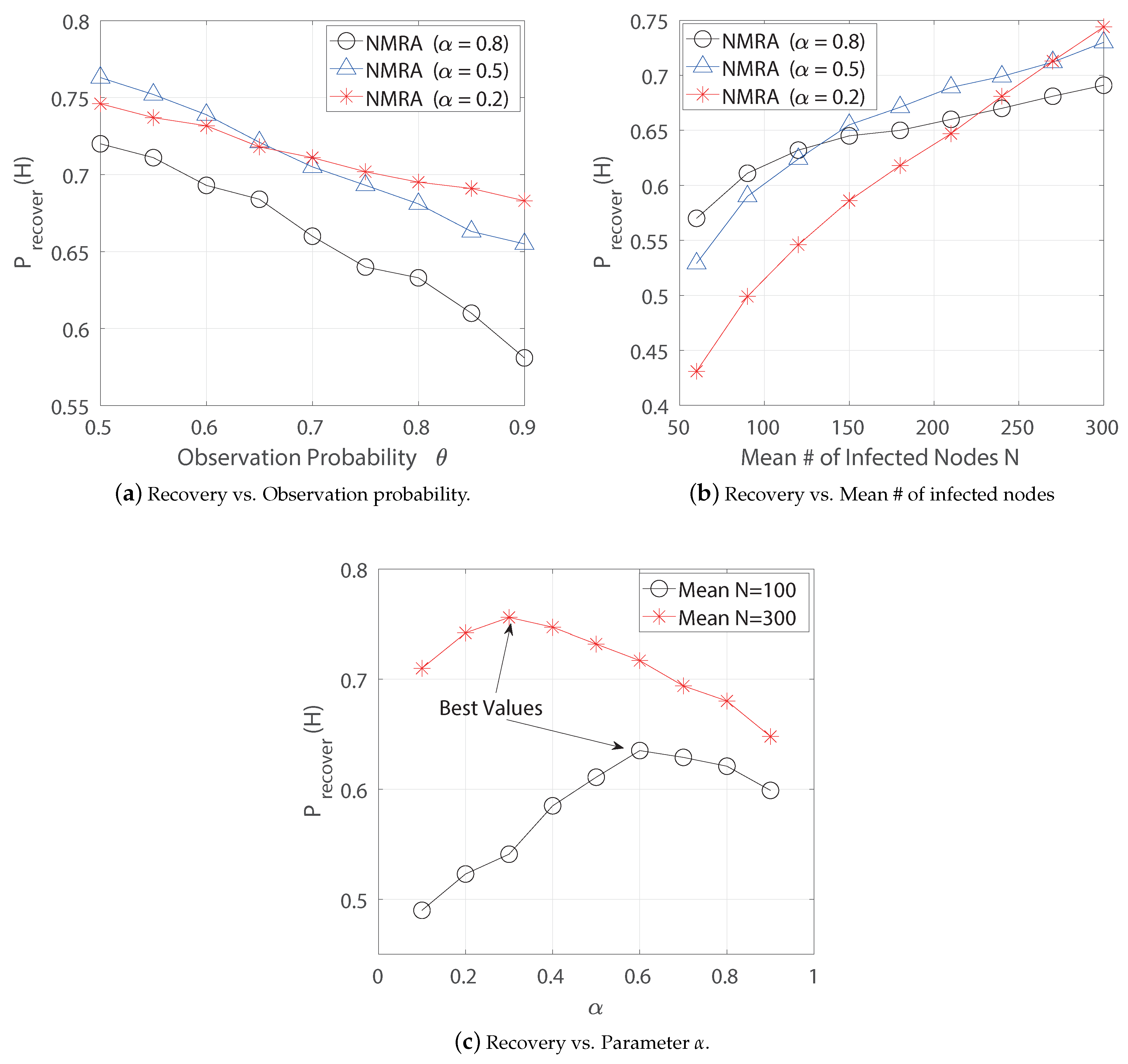
6.1.1. Neighbor-Based Recovery Algorithm
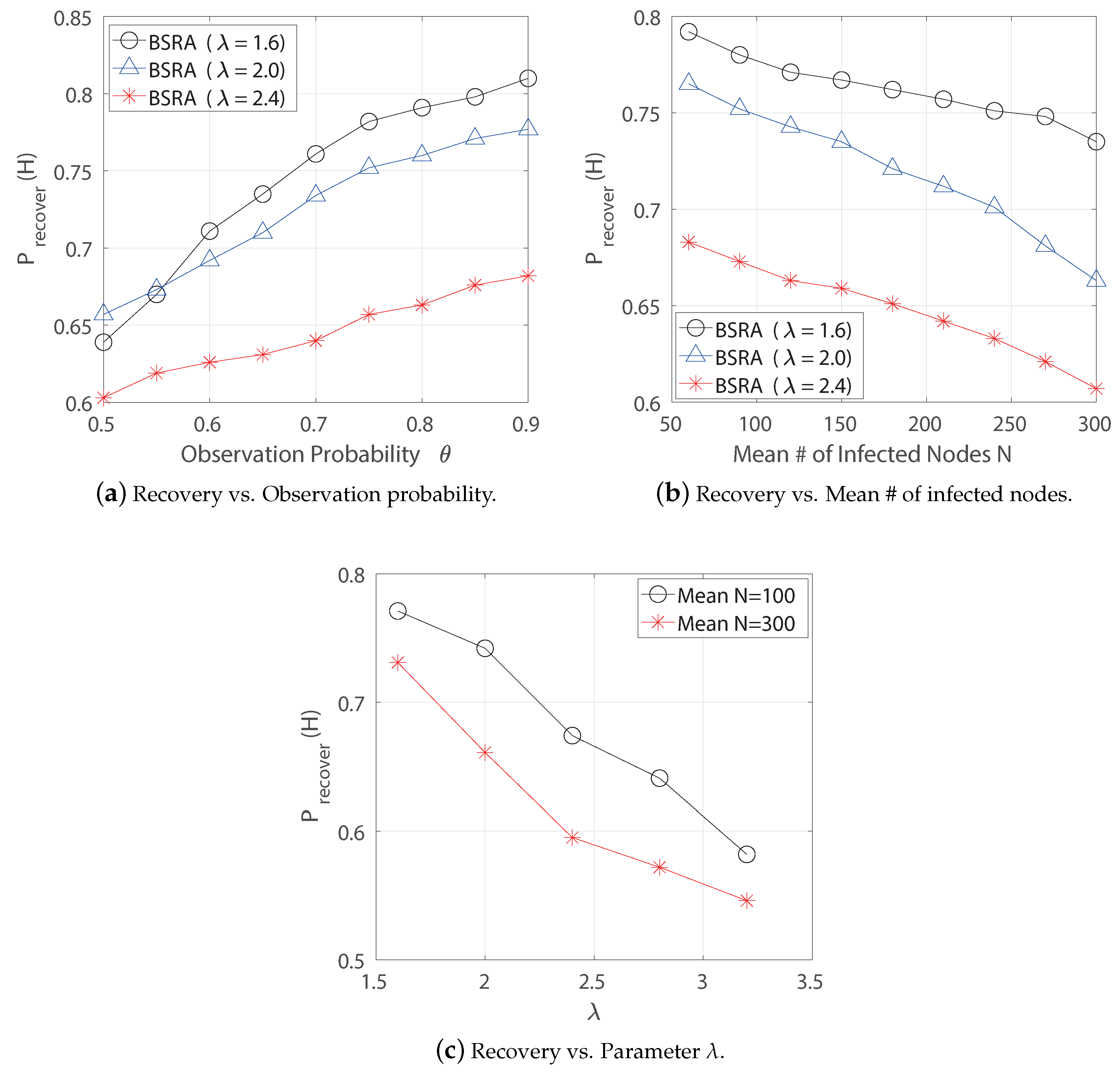
6.1.2. BFST Source-Based Recovery Algorithm
6.1.3. Performance Comparison
7. Conclusions
8. Limitations and Future Works
Funding
Conflicts of Interest
Appendix A. Proof of Theorem 1
References
- Woo, J.; Ok, J.; Yi, Y. Iterative learning of graph connectivity from partially-observed cascade samples. In Proceedings of the Twenty-First International Symposium on Theory, Algorithmic Foundations, and Protocol Design for Mobile Networks and Mobile Computing (Mobihoc ’20), online. 11–14 October 2020. [Google Scholar]
- Liu, Y.; Bao, Z.; Zhang, Z.; Tang, D.; Xiong, F. Information cascades prediction with attention neural network. Hum. Cent. Comput. Inf. Sci. 2020, 10, 13. [Google Scholar] [CrossRef]
- Feng, X.; Zhao, Q.; Liu, Z. Prediction of information cascades via content and structure proximity preserved graph level embedding. Inf. Sci. 2021, 560, 424–440. [Google Scholar] [CrossRef]
- Netrapalli, P.; Sanghavi, S. Finding the Graph of Epidemic Cascades. ACM SIGMETRICS Perform. Eval. Rev. 2012, 40, 211–222. [Google Scholar] [CrossRef]
- Sundareisan, S.; Vreeken, J.; Prakash, B.A. Hidden Hazards: Finding Missing Nodes in Large Graph Epidemics. In Proceedings of the 2015 SIAM International Conference on Data Mining (SDM), Vancouver, BC, Canada, 30 April–2 May 2015. [Google Scholar]
- Xiao, H.; Aslay, C.; Gionis, A. Robust Cascade Reconstruction by Steiner Tree Sampling. In Proceedings of the IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2017. [Google Scholar]
- Xiao, H.; Rozenshtein, P.; Tatti, N.; Gionis, A. Reconstructing a cascade from temporal observations. In Proceedings of the 2018 SIAM International Conference on Data Mining (SDM), San Diego, CA, USA, 3–5 May 2018. [Google Scholar]
- Wu, X.; Kumar, A.; Sheldon, D.; Zilberstein, S. Parameter Learning for Latent Network Diffusion. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013. [Google Scholar]
- He, X.; Liu, Y. Not Enough Data? Joint Inferring Multiple Diffusion Networks via Network Generation Priors. In Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, Cambridge, UK, 6–10 February 2017. [Google Scholar]
- Choi, J. Identification of Individual Infection Over Networks With Limit Observation: Random vs. Epidemic? IEEE Access 2021, 9, 74234–74245. [Google Scholar] [CrossRef]
- Huang, Y.; Feamster, N.; Teixeira, R. Practical Issues with Using Network Tomography for Fault Diagnosis. ACM SIGCOMM Comp. Commun. Rev. 2008, 38, 53–58. [Google Scholar] [CrossRef]
- Tosic, T.; Thomos, N.; Frossard, P. Distributed sensor failure detection in sensor networks. Signal Process. 2013, 93, 399–410. [Google Scholar] [CrossRef] [Green Version]
- Nasiri, M.; Mobayen, S.; Zhu, Q. Super-Twisting Sliding Mode Control for Gearless PMSG-Based Wind Turbine. Complexity 2019, 2019, 6141607. [Google Scholar] [CrossRef]
- Jafari, M.; Mobayen, S. Second-order sliding set design for a class of uncertain nonlinear systems with disturbances: An LMI approach. Math. Comput. Simul. 2019, 156, 110–125. [Google Scholar] [CrossRef]
- Abadie, J.P.; Horel, T. Inferring Graphs from Cascades: A Sparse Recovery Framework. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015. [Google Scholar]
- Abrahao, B.; Chierichetti, F.; Kleinberg, R.; Panconesi, A. Trace Complexity of Network Inference. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013. [Google Scholar]
- He, X.; Xu, K.; Kempe, D.; Liu, Y. Learning Influence Functions from Incomplete Observations. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS 2016), Barcelon, Spain, 5–10 December 2016. [Google Scholar]
- Rozenshtein, P.; Gionis, A.; Prakash, B.; Vreeken, J. Reconstructing an Epidemic Over Time. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Gripon, V.; Rabbat, M. Reconstructing a Graph from Path Traces. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013. [Google Scholar]
- Amin, K.; Heidari, H.; Kearns, M. Learning from Contagion (Without Timestamps). In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014. [Google Scholar]
- Zhu, K.; Ying, L. Information source detection in networks: Possibility and impossibility result. In Proceedings of the IEEE INFOCOM 2016—The 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2017. [Google Scholar]
- Zhu, K.; Chen, Z.; Ying, L. Catch’Em All: Locating Multiple Diffusion Sources in Networks with Partial Observations. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence (AAAI-17), San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Zhu, K.; Chen, Z.; Ying, L. Locating the contagion source in networks with partial timestamps. Data Min. Knowl. Discov. 2016, 30, 1217–1248. [Google Scholar] [CrossRef]
- Fanti, G.; Kairouz, P.; Oh, S.; Ramchandran, K.; Viswanath, P. Metadata-Conscious Anonymous Messaging. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016. [Google Scholar]
- Liu, X.; Fu, L.; Jiang, B.; Lin, X.; Wang, X. Information Source Detection with Limited Time Knowledge. In Proceedings of the Twentieth ACM International Symposium on Mobile Ad Hoc Networking and Computing, Catania, Italy, 2–5 July 2019. [Google Scholar]
- Tang, W.; Ji, F.; Tay, W. Estimating Infection Sources in Networks Using Partial Timestamps. IEEE Trans. Inf. Forensics Secur. 2018, 13, 3035–3049. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Borkar, V.S.; Karamchandani, N. Temporally Agnostic Rumor-Source Detection. IEEE Trans. Signal Inf. Process. Netw. 2017, 3, 316–329. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm as 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]


| Notation | Explanation |
|---|---|
| ER random graph with two parameters n and p | |
| Average degree of a node in | |
| Infection probability from node u to v | |
| Infection probability over edge e | |
| Infection reporting probability for node v | |
| Infection probability vector for all edges | |
| Infection-reporting probability vector for all nodes | |
| , S | (True) Cascade source, Set of cascade sources |
| Set of observed (reported) infected nodes | |
| Observed cascade snapshot at time t | |
| m | Number of cascade sources |
| , | Estimated (i-th) cascade source, Estimated set of cascade sources |
| Infection status of a node v | |
| Estimator of | |
| recovery probability of | |
| Set of hidden (not reported)-infected nodes | |
| Estimated recovering set | |
| Set of (reported) infected neighbors of a node v | |
| Minimum diffusion probability among for all | |
| Infection eccentricity of node set S over | |
| Selection threshold | |
| W | Set of nodes with more than observed infected neighbors |
| Union of W and | |
| Induced graph (connected subgraph of ) from | |
| Connected sub-graph of G including | |
| BFS tree over w.r.t. | |
| Candidate neighbor (infected) set of v in | |
| Reconstructed graph from | |
| Union of and | |
| T | Union of reconstructed graphs |
| Path between node v and source node in | |
| Pre-defined threshold for determining the infection of node v | |
| () | Maximum (minimum) infection probability over T from S |
| NBRA() | BSRA | Steiner | NETFILL | |
|---|---|---|---|---|
| 0.69 | 0.65 | 0.71 | 0.61 | |
| 0.68 | 0.67 | 0.69 | 0.57 | |
| 0.65 | 0.72 | 0.67 | 0.55 | |
| 0.62 | 0.75 | 0.64 | 0.53 | |
| 0.61 | 0.77 | 0.63 | 0.54 |
| NBRA() | BSRA | Steiner | NETFILL | |
|---|---|---|---|---|
| 0.59 | 0.73 | 0.69 | 0.64 | |
| 0.62 | 0.71 | 0.67 | 0.56 | |
| 0.65 | 0.67 | 0.63 | 0.51 | |
| 0.64 | 0.63 | 0.59 | 0.48 | |
| 0.65 | 0.58 | 0.55 | 0.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J. Inferring the Hidden Cascade Infection over Erdös-Rényi (ER) Random Graph. Electronics 2021, 10, 1894. https://doi.org/10.3390/electronics10161894
Choi J. Inferring the Hidden Cascade Infection over Erdös-Rényi (ER) Random Graph. Electronics. 2021; 10(16):1894. https://doi.org/10.3390/electronics10161894
Chicago/Turabian StyleChoi, Jaeyoung. 2021. "Inferring the Hidden Cascade Infection over Erdös-Rényi (ER) Random Graph" Electronics 10, no. 16: 1894. https://doi.org/10.3390/electronics10161894
APA StyleChoi, J. (2021). Inferring the Hidden Cascade Infection over Erdös-Rényi (ER) Random Graph. Electronics, 10(16), 1894. https://doi.org/10.3390/electronics10161894






