A Low-Power CMOS Bandgap Voltage Reference for Supply Voltages Down to 0.5 V
Abstract
:1. Introduction
2. LV Bandgap Voltage Reference
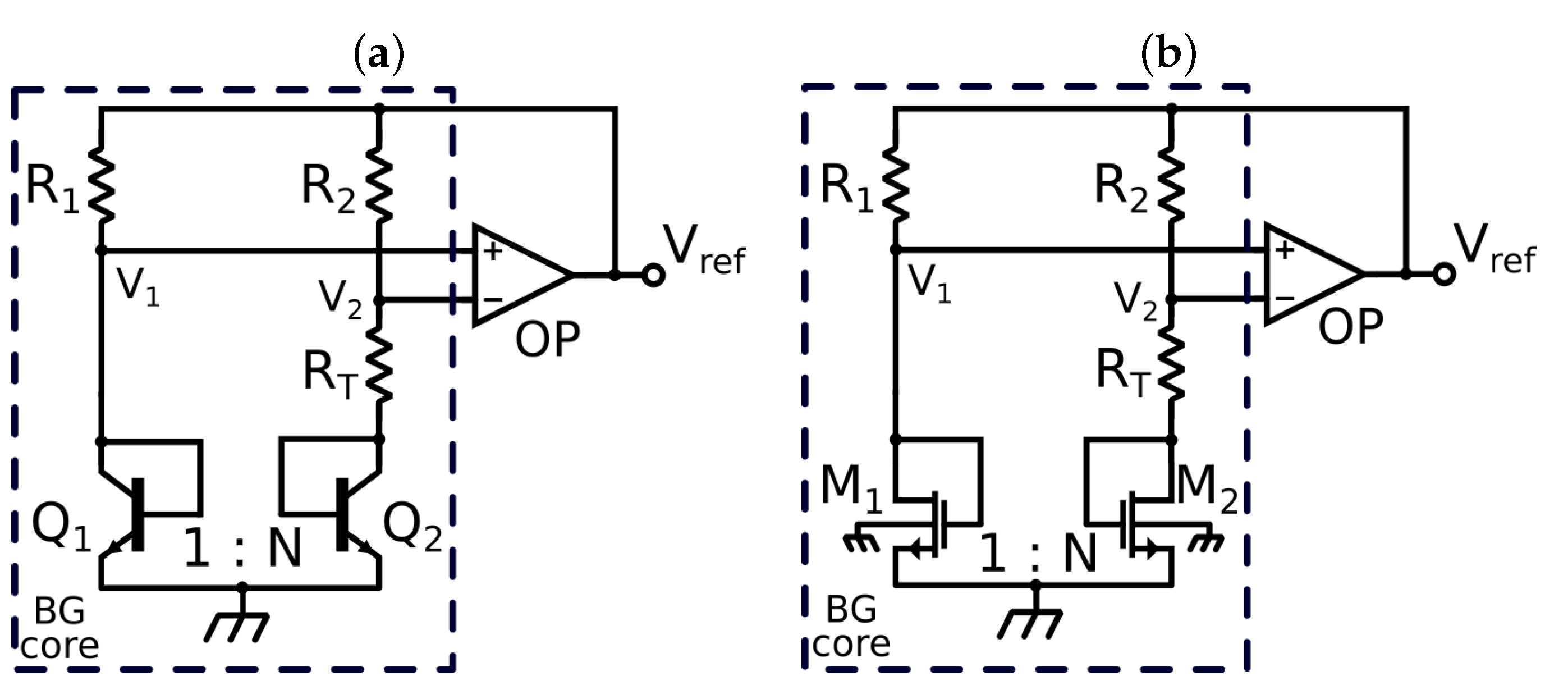
2.1. MOSFET-Based Voltage Reference
2.2. Proposed BG Core
2.3. Offset and Noise Contribution of the Amplifier
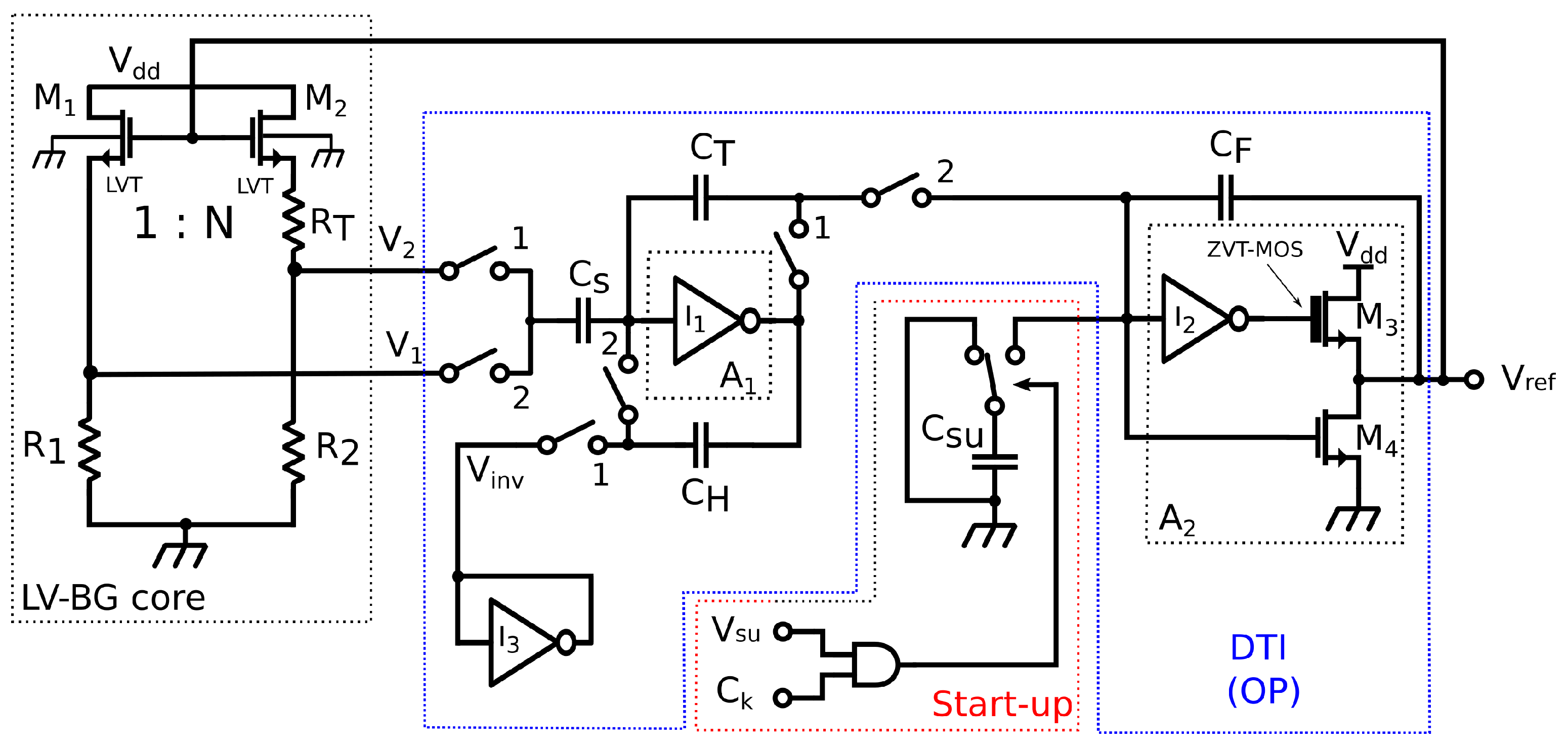
3. Prototype Design
3.1. Start-Up Circuit
3.2. Device Sizing
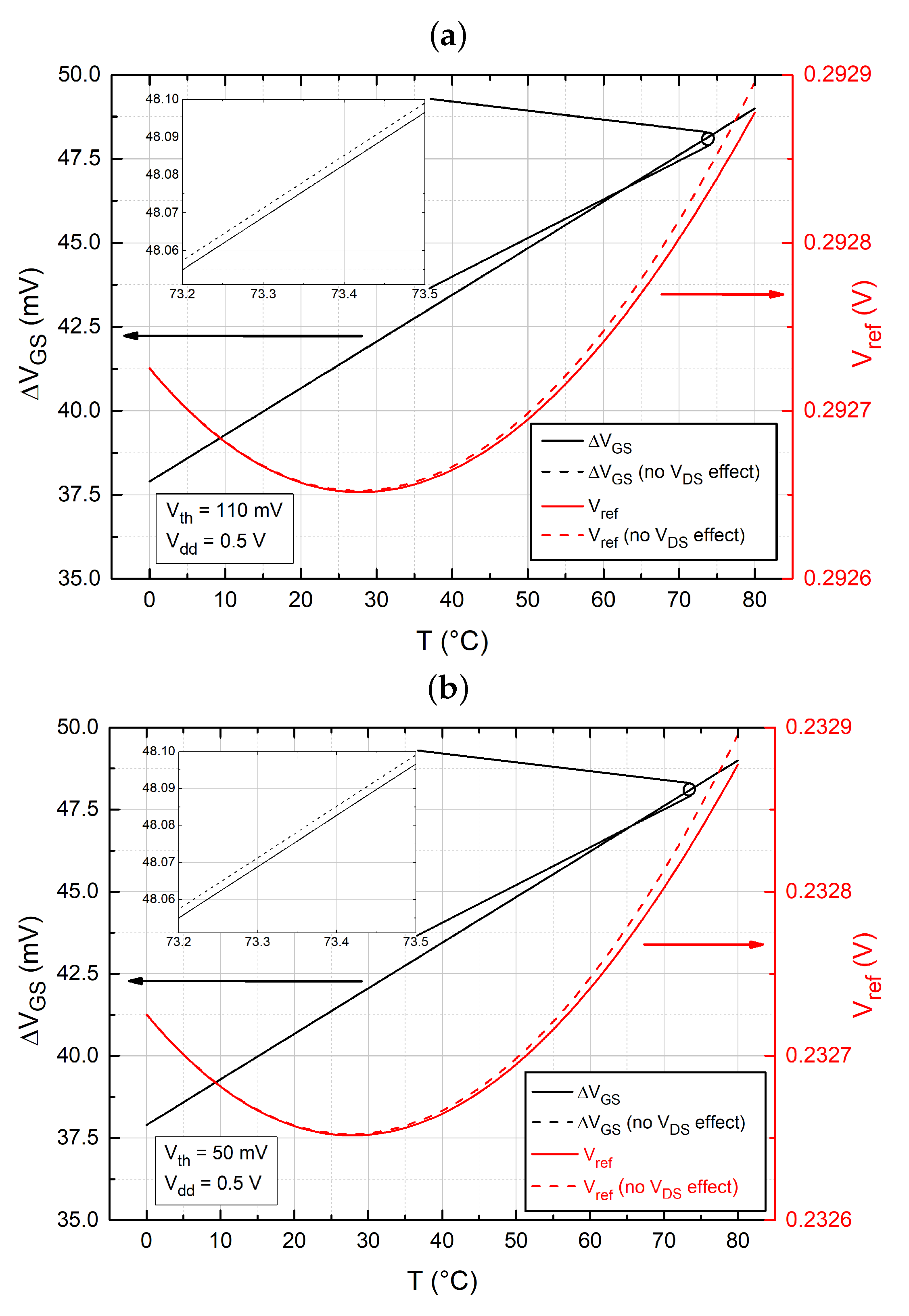
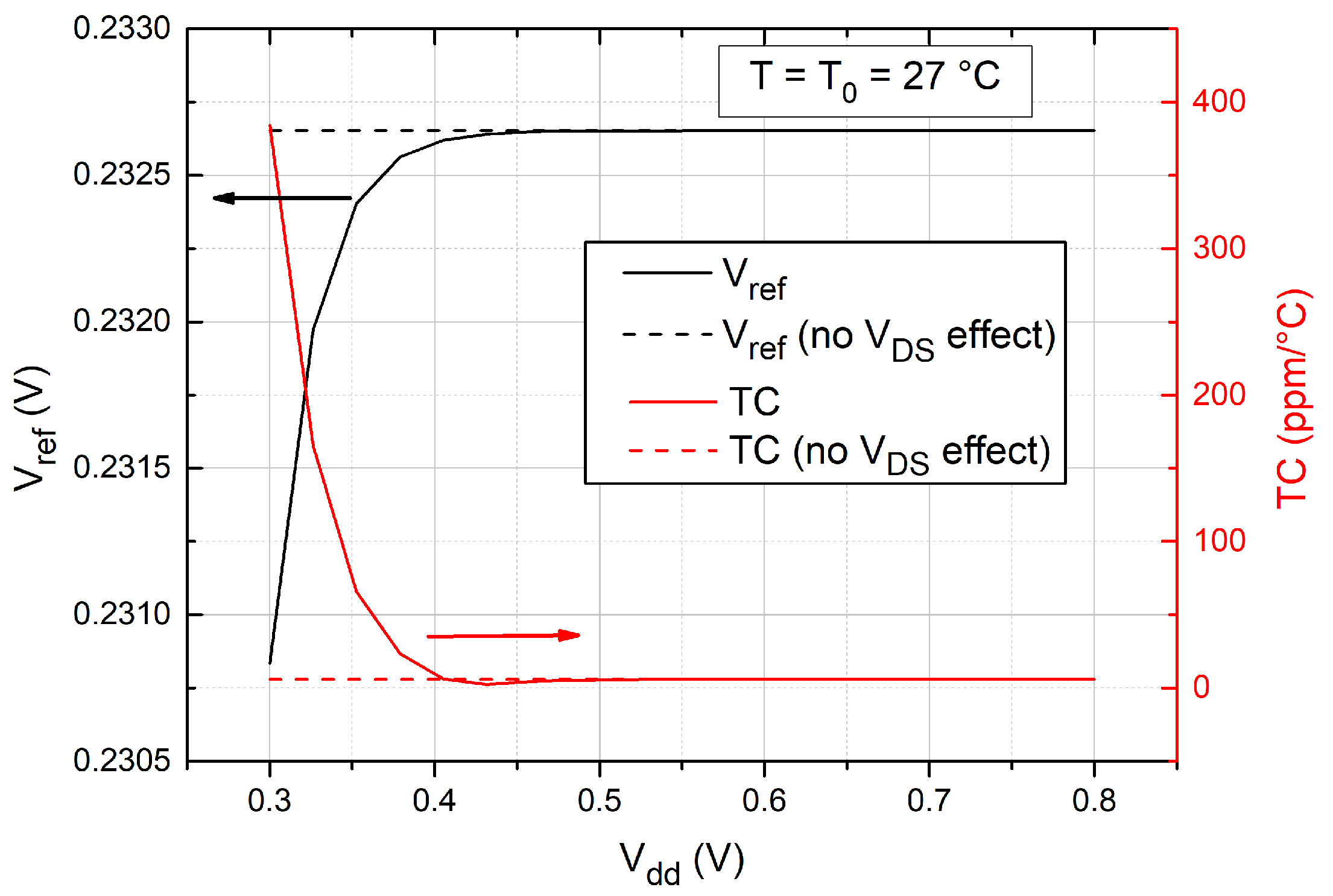
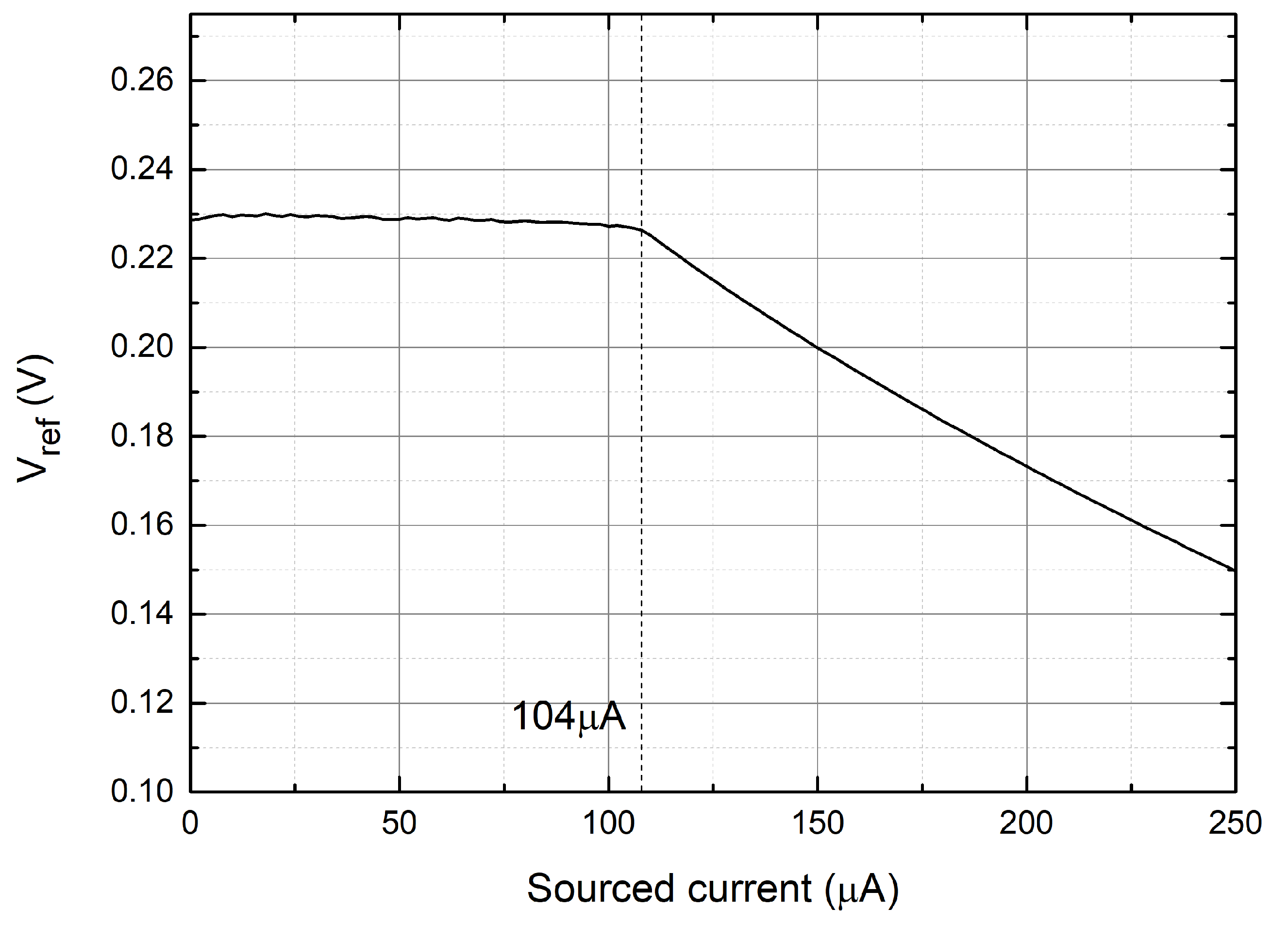
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Qiu, S.; Wang, Z.; Zhao, H.; Hu, H. Using Distributed Wearable Sensors to Measure and Evaluate Human Lower Limb Motions. IEEE Trans. Instrum. Meas. 2016, 65, 939–950. [Google Scholar] [CrossRef] [Green Version]
- Selvam, A.P.; Muthukumar, S.; Kamakoti, V.; Prasad, S. A wearable biochemical sensor for monitoring alcohol consumption lifestyle through Ethyl glucuronide (EtG) detection in human sweat. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef]
- Saraereh, O.A.; Alsaraira, A.; Khan, I.; Choi, B.J. A Hybrid Energy Harvesting Design for On-Body Internet-of-Things (IoT) Networks. Sensors 2020, 20, 407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lo Presti, D.; Carnevale, A.; D’Abbraccio, J.; Massari, L.; Massaroni, C.; Sabbadini, R.; Zaltieri, M.; Di Tocco, J.; Bravi, M.; Miccinilli, S.; et al. A Multi-Parametric Wearable System to Monitor Neck Movements and Respiratory Frequency of Computer Workers. Sensors 2020, 20, 536. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bariya, M.; Nyein, H.Y.Y.; Javey, A. Wearable sweat sensors. Nat. Electron. 2018, 1, 160–171. [Google Scholar] [CrossRef]
- Dei, M.; Aymerich, J.; Piotto, M.; Bruschi, P.; del Campo, F.J.; Serra-Graells, F. CMOS Interfaces for Internet-of-Wearables Electrochemical Sensors: Trends and Challenges. Electronics 2019, 8, 150. [Google Scholar] [CrossRef] [Green Version]
- Oktavius, A.K.; Gu, Q.; Wihardjo, N.; Winata, O.; Sunanto, S.W.; Li, J.; Gao, P. Fully-Conformable Porous Polyethylene Nanofilm Sweat Sensor for Sports Fatigue. IEEE Sens. J. 2021, 21, 8861–8867. [Google Scholar] [CrossRef]
- Wang, H.; Wang, G.; Ling, Y.; Qian, F.; Song, Y.; Lu, X.; Chen, S.; Tong, Y.; Li, Y. High power density microbial fuel cell with flexible 3D graphene–nickel foam as anode. Nanoscale 2013, 5, 10283–10290. [Google Scholar] [CrossRef]
- Talkhooncheh, A.H.; Yu, Y.; Agarwal, A.; Kuo, W.W.T.; Chen, K.C.; Wang, M.; Hoskuldsdottir, G.; Gao, W.; Emami, A. A Biofuel-Cell-Based Energy Harvester With 86% Peak Efficiency and 0.25-V Minimum Input Voltage Using Source-Adaptive MPPT. IEEE J. Solid-State Circuits 2021, 56, 715–728. [Google Scholar] [CrossRef]
- Tanwar, A.; Lal, S.; Razeeb, K.M. Structural Design Optimization of Micro-Thermoelectric Generator for Wearable Biomedical Devices. Energies 2021, 14, 2339. [Google Scholar] [CrossRef]
- Khan, S.; Kim, J.; Roh, K.; Park, G.; Kim, W. High power density of radiative-cooled compact thermoelectric generator based on body heat harvesting. Nano Energy 2021, 87, 106180. [Google Scholar] [CrossRef]
- Proto, A.; Vondrak, J.; Schmidt, M.; Kubicek, J.; Gorjani, O.M.; Havlik, J.; Penhaker, M. A Flexible Thermoelectric Generator Worn on the Leg to Harvest Body Heat Energy and to Recognize Motor Activities: A Preliminary Study. IEEE Access 2021, 9, 20878–20892. [Google Scholar] [CrossRef]
- Alioto, M. Enabling the Internet of Things: From Integrated Circuits to Integrated Systems; Springer: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Widlar, R. New developments in IC voltage regulators. IEEE J. Solid-State Circuits 1971, 6, 2–7. [Google Scholar] [CrossRef] [Green Version]
- Kuijk, K.E. A precision reference voltage source. IEEE J. Solid-State Circuits 1973, 8, 222–226. [Google Scholar] [CrossRef]
- Kok, C.W.; Tam, W.S. CMOS Voltage References: An Analytical and Practical Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Ferro, M.; Salerno, F.; Castello, R. A floating CMOS bandgap voltage reference for differential applications. IEEE J. Solid-State Circuits 1989, 24, 690–697. [Google Scholar] [CrossRef]
- Banba, H.; Shiga, H.; Umezawa, A.; Miyaba, T.; Tanzawa, T.; Atsumi, S.; Sakui, K. A CMOS bandgap reference circuit with sub-1-V operation. IEEE J. Solid-State Circuits 1999, 34, 670–674. [Google Scholar] [CrossRef] [Green Version]
- Malcovati, P.; Maloberti, F.; Fiocchi, C.; Pruzzi, M. Curvature-compensated BiCMOS bandgap with 1-V supply voltage. IEEE J. Solid-State Circuits 2001, 36, 1076–1081. [Google Scholar] [CrossRef] [Green Version]
- Boni, A. Op-amps and startup circuits for CMOS bandgap references with near 1-V supply. IEEE J. Solid-State Circuits 2002, 37, 1339–1343. [Google Scholar] [CrossRef] [Green Version]
- Sanborn, K.; Ma, D.; Ivanov, V. A Sub-1-V Low-Noise Bandgap Voltage Reference. IEEE J. Solid-State Circuits 2007, 42, 2466–2481. [Google Scholar] [CrossRef]
- Ivanov, V.; Brederlow, R.; Gerber, J. An Ultra Low Power Bandgap Operational at Supply From 0.75 V. IEEE J. Solid-State Circuits 2012, 47, 1515–1523. [Google Scholar] [CrossRef]
- Chi-Wa, U.; Zeng, W.L.; Law, M.K.; Lam, C.S.; Martins, R.P. A 0.5-V Supply, 36 nW Bandgap Reference With 42 ppm/°C Average Temperature Coefficient Within -40 °C to 120 °C. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 3656–3669. [Google Scholar] [CrossRef]
- Tzanateas, G.; Salama, C.; Tsividis, Y. A CMOS bandgap voltage reference. IEEE J. Solid-State Circuits 1979, 14, 655–657. [Google Scholar] [CrossRef]
- Vittoz, E.; Neyroud, O. A low-voltage CMOS bandgap reference. IEEE J. Solid-State Circuits 1979, 14, 573–579. [Google Scholar] [CrossRef]
- Giustolisi, G.; Palumbo, G.; Criscione, M.; Cutri, F. A low-voltage low-power voltage reference based on subthreshold MOSFETs. IEEE J. Solid-State Circuits 2003, 38, 151–154. [Google Scholar] [CrossRef]
- Zhuang, H.; Zhu, Z.; Yang, Y. A 19-nW 0.7-V CMOS Voltage Reference with No Amplifiers and No Clock Circuits. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 830–834. [Google Scholar] [CrossRef]
- Yang, Y.; Binkley, D.M.; Li, L.; Gu, C.; Li, C. All-CMOS subbandgap reference circuit operating at low supply voltage. In Proceedings of the 2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 893–896. [Google Scholar] [CrossRef]
- Yang, B.D. 250-mV Supply Subthreshold CMOS Voltage Reference Using a Low-Voltage Comparator and a Charge-Pump Circuit. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 850–854. [Google Scholar] [CrossRef]
- Blauschild, R.; Tucci, P.; Muller, R.; Meyer, R. A new NMOS temperature-stable voltage reference. IEEE J. Solid-State Circuits 1978, 13, 767–774. [Google Scholar] [CrossRef]
- De Vita, G.; Iannaccone, G. A Sub-1-V, 10 ppm/°C, Nanopower Voltage Reference Generator. IEEE J. Solid-State Circuits 2007, 42, 1536–1542. [Google Scholar] [CrossRef]
- Dong, Q.; Yang, K.; Blaauw, D.; Sylvester, D. A 114-pW PMOS-only, trim-free voltage reference with 0.26% within-wafer inaccuracy for nW systems. In Proceedings of the 2016 IEEE Symposium on VLSI Circuits (VLSI-Circuits), Honolulu, HI, USA, 15–17 June 2016; pp. 1–2. [Google Scholar] [CrossRef]
- Fassio, L.; Lin, L.; De Rose, R.; Lanuzza, M.; Crupi, F.; Alioto, M. Trimming-Less Voltage Reference for Highly Uncertain Harvesting Down to 0.25 V, 5.4 pW. IEEE J. Solid-State Circuits 2021. [Google Scholar] [CrossRef]
- Bruschi, P.; Catania, A.; Del Cesta, S.; Piotto, M. A Two-Stage Switched-Capacitor Integrator for High Gain Inverter-Like Architectures. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 210–214. [Google Scholar] [CrossRef]
- Del Cesta, S.; Ria, A.; Simmarano, R.; Piotto, M.; Bruschi, P. A compact programmable differential voltage reference with unbuffered 4 mA output current capability and ±0.4% untrimmed spread. In Proceedings of the ESSCIRC 2017—43rd IEEE European Solid State Circuits Conference, Leuven, Belgium, 11–14 September 2017; pp. 11–14. [Google Scholar] [CrossRef]
- Ria, A.; Catania, A.; Cicalini, M.; Benvenuti, L.; Piotto, M.; Bruschi, P. A Sub-1V CMOS Switched Capacitor Voltage Reference with high output current capability. In Proceedings of the 2019 15th Conference on Ph.D Research in Microelectronics and Electronics (PRIME), Lausanne, Switzerland, 15–18 July 2019; pp. 9–12. [Google Scholar] [CrossRef]
- Enz, C.C.; Krummenacher, F.; Vittoz, E.A. An analytical MOS transistor model valid in all regions of operation and dedicated to low-voltage and low-current applications. Analog Integr. Circuits Signal Process. 1995, 8, 83–114. [Google Scholar] [CrossRef]
- Enz, C.C.; Vittoz, E.A. Charge-Based MOS Transistor Modeling: The EKV Model for Low-Power and RF IC Design; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Majumder, S.; Mondal, T.; Deen, M.J. Wearable Sensors for Remote Health Monitoring. Sensors 2017, 17, 130. [Google Scholar] [CrossRef]
- Magnelli, L.; Crupi, F.; Corsonello, P.; Pace, C.; Iannaccone, G. A 2.6 nW, 0.45 V Temperature-Compensated Subthreshold CMOS Voltage Reference. IEEE J. Solid-State Circuits 2011, 46, 465–474. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Z.; Yao, J.; Yang, Y. A 0.45-V, 14.6-nW CMOS Subthreshold Voltage Reference With No Resistors and No BJTs. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 621–625. [Google Scholar] [CrossRef]







| Device | Type | W (m) | L (m) | m |
|---|---|---|---|---|
| LVT | 3 | 3 | 1 | |
| LVT | 3 | 3 | 5 | |
| ZVT | 3.5 | 0.35 | 4 | |
| RVT | 1.8 | 0.18 | 2 | |
| ZVT | 0.5 | 0.5 | 1 | |
| RVT | 3 | 3 | 10 | |
| RVT | 2 | 2 | 1 | |
| RVT | 2 | 2 | 4 | |
| RVT | 2 | 2 | 1 | |
| RVT | 2 | 2 | 4 | |
| RVT | 2 | 2 | 1 | |
| RVT | 2 | 2 | 4 | |
| RVT | 0.28 | 0.18 | 1 | |
| RVT | 0.28 | 0.18 | 4 | |
| RVT | 0.28 | 0.18 | 1 | |
| RVT | 0.28 | 0.18 | 4 |
| Device | Value | Device | Value |
|---|---|---|---|
| 616 k | 1 pF | ||
| 616 k | 1 pF | ||
| 154 k | 1 pF | ||
| 1 pF | 200 fF |
| This Work | [22] | [40] | [23] | [41] | [29] | [33] | [27] | |
|---|---|---|---|---|---|---|---|---|
| Technology (nm) | 180 | 130 | 180 | 65 | 180 | 110 | 180 | 180 |
| Power (nW) | 315 | 170 | 2.6 | 38 | 14 | 5.35 | 5.4 | 19 |
| (V) | 0.5 | 0.75 | 0.45 | 0.5 | 0.45 | 0.242 | 0.25 | 0.7 |
| (V) | 0.233 | 0.256 | 263.5 | 0.495 | 0.118 | 0.195 | 0.091 | 0.438 |
| PSRR (dB) | −44@100 Hz | N.A | −40@30 Hz | −50@DC | −40@100 Hz | N.A. | −70@100 Hz | N.A. |
| Temperature range (°C) | 10–50 | −20–85 | 0–125 | −40–120 | −40–125 | N.A. | 0–120 | −25–85 |
| TC (ppm/°C) | 45 | 40 | 165 | 42 | 63.6 | 134 | 265 | 22.1 |
| Trimmed | NO | YES | NO | YES | YES | YES | NO | YES |
| LR (mV/V) | 1.44 | 0.013 | 1.16 | 3.2 | 1.2 | 8 | 0.145 | 0.571 |
| Area (mm2) | 0.015 | 0.055 | 0.043 | 0.0522 | 0.012 | 0.013 | 0.0022 | 0.041 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ria, A.; Catania, A.; Bruschi, P.; Piotto, M. A Low-Power CMOS Bandgap Voltage Reference for Supply Voltages Down to 0.5 V. Electronics 2021, 10, 1901. https://doi.org/10.3390/electronics10161901
Ria A, Catania A, Bruschi P, Piotto M. A Low-Power CMOS Bandgap Voltage Reference for Supply Voltages Down to 0.5 V. Electronics. 2021; 10(16):1901. https://doi.org/10.3390/electronics10161901
Chicago/Turabian StyleRia, Andrea, Alessandro Catania, Paolo Bruschi, and Massimo Piotto. 2021. "A Low-Power CMOS Bandgap Voltage Reference for Supply Voltages Down to 0.5 V" Electronics 10, no. 16: 1901. https://doi.org/10.3390/electronics10161901
APA StyleRia, A., Catania, A., Bruschi, P., & Piotto, M. (2021). A Low-Power CMOS Bandgap Voltage Reference for Supply Voltages Down to 0.5 V. Electronics, 10(16), 1901. https://doi.org/10.3390/electronics10161901









