Miller Plateau Corrected with Displacement Currents and Its Use in Analyzing the Switching Process and Switching Loss

Abstract

This paper reveals the relationship between the Miller plateau voltage and the displacement currents through the gate–drain capacitance ($C_{\mathit{GD}}$) and the drain–source capacitance ($C_{\mathit{DS}}$) in the switching process of a power transistor. The corrected turn-on Miller plateau voltage and turn-off Miller plateau voltage are different even with a constant current load. Using the proposed new Miller plateau, the turn-on and turn-off sequences can be more accurately analyzed, and the switching power loss can be more accurately predicted accordingly. Switching loss models based on the new Miller plateau have also been proposed. The experimental test result of the power MOSFET (NCE2030K) verified the relationship between the Miller plateau voltage and the displacement currents through $C_{\mathit{GD}}$ and $C_{\mathit{DS}}$. A carefully designed verification test bench featuring a power MOSFET written in Verilog-A proved the prediction accuracy of the switching waveform and switching loss with the new proposed Miller plateau. The average relative error of the loss model using the new plateau is reduced to 1/2∼1/4 of the average relative error of the loss model using the old plateau; the proposed loss model using the new plateau, which also takes the gate current’s variation into account, further reduces the error to around 5%.

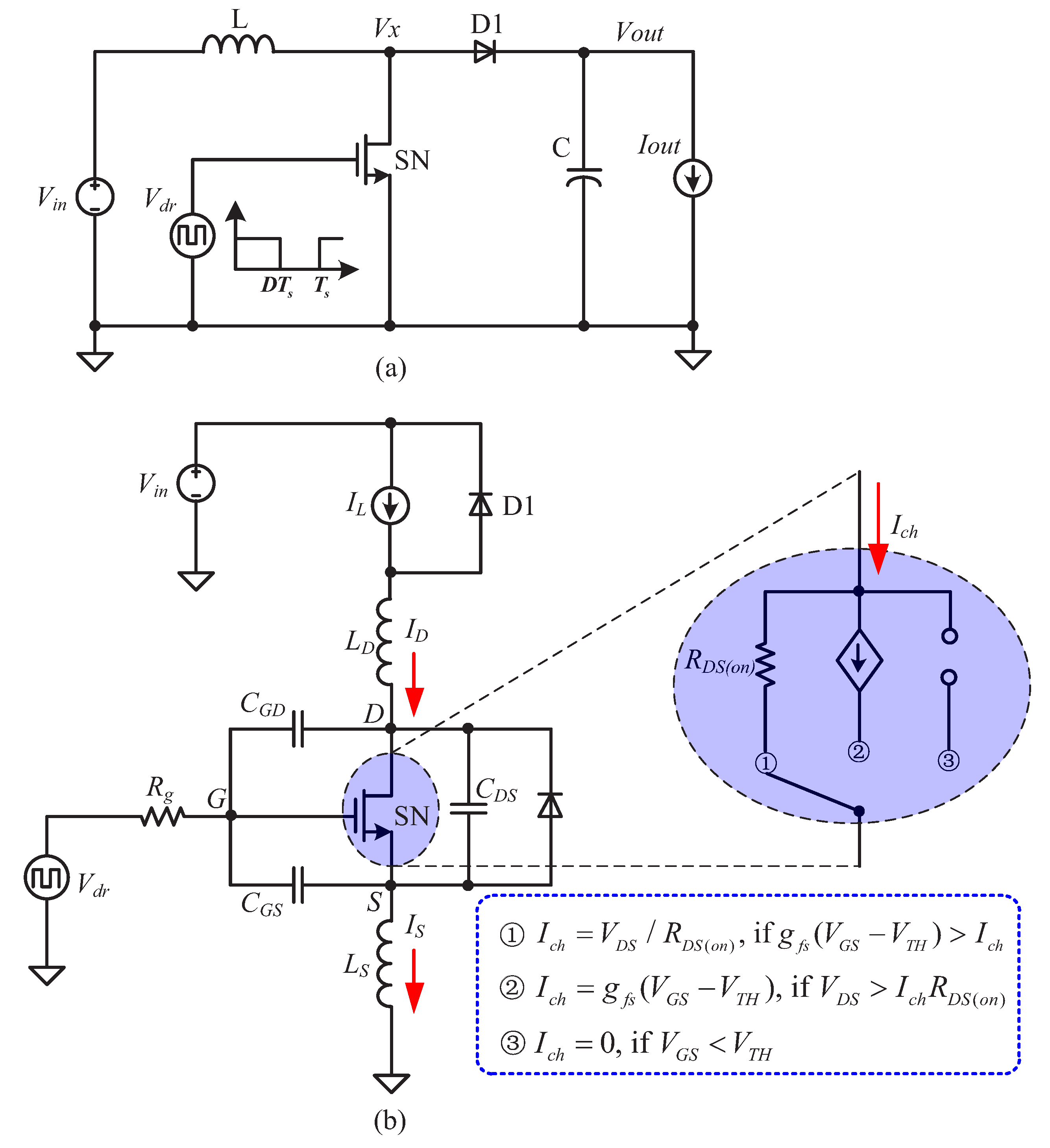
1. Introduction

Integrated power management and conversion circuitry is a fundamental block in many emerging applications such as Internet of Things (IoT) systems [1,2] and wearable healthcare devices, which are usually powered by batteries and energy harvesters [3,4]. The power consumption of these devices needs to be minimized to prolong the battery lifetime and improve the usability in inaccessible environments, requiring highly efficient DC-DC converters. In recent years, the operating frequency of the converter has been continuously increasing [5,6,7,8] to achieve higher power efficiency, faster speed, and higher power density. In addition to the consideration of topologies and control strategies [9,10,11,12], the switching process and the switching loss of the power switches are playing more important roles in a high-frequency DC-DC converter. The transient behavior of a power transistor can cause power dissipation and overvoltage, overcurrent, or even ringing [13,14,15,16,17], which are related to the system efficiency, maximum voltage or current ratings of the power transistor, and the electromagnetic interference (EMI) property of the system. Therefore, in-depth analysis of the switching process and more accurate switching loss models are necessary to ensure better performance and maintain the high efficiency of the switching mode power supply (SMPS) working at a higher and higher switching frequency.

Obviously, the switching behavior can be reproduced accurately with simulators such as Spectre and HSpice, but the simulation-based approach fails to provide intuitive understanding [18,19], which is helpful in circuit design. On the other hand, an analytical model with reasonable simplifications provides closed-form mathematical equations, which show the relationship between the device loss and key parameters. These equations can be further used to optimize the power transistors. The conventional piecewise-linear model [20,21,22] is simple and effective in a capacitance-limited case, but not suitable for the latest generation of low-voltage power MOSFETs where the parasitic inductance limits the switching process. Many new analytical models [18,23,24,25,26,27,28] with different tradeoffs between accuracy and complexity have been proposed to analyze the switching process and switching loss. These analytical models are more application-specific and may even include the nonlinearity of the capacitors of the devices. Reference [27] aimed at superjunction MOSFETs and demanded the unusual extraction of electrical characteristics from regular datasheets. Reference [28] only analyzed output capacitance-related losses in wide-bandgap transistors and did not include other kinds of switching losses. Effective figures of merit (FOMs) [29,30] of the power transistors have also been proposed to measure the device performance and help to select the right design parameters of power transistors. Nevertheless, providing an analytical model of the power transistor’s switching process and switching power loss with high accuracy is still very challenging. With the least added complexity, loss models developed directly from the classical piecewise-linear model that can still provide accurate prediction are especially attractive.

One major reason for the limited accuracy of the analytical switching loss models is that the so-called Miller plateau is difficult to predict. The Miller effect has long been a well-known phenomenon, and the Miller plateau observed in the switching process of a power transistor is related to this effect. In the conventional or the newly proposed analytical models [20,24,27,30], the Miller plateau voltage $V_{\mathit{pl}}$ has proven to be useful in analyzing the switching process and calculating switching loss. In existing analytical models, the value of $V_{\mathit{pl}}$ is defined as the gate–source voltage $V_{\mathit{GS}}$ when the channel current $I_{\mathit{ch}}$ equals the load current. However, as revealed in this paper, the Miller plateau voltage also relates to the gate driving voltage $V_{\mathit{dr}}$ and the displacement currents through $C_{\mathit{GD}}$ and $C_{\mathit{DS}}$. A more precise Miller plateau voltage will improve the accuracy of the calculated switching loss.

In this paper, we analyze the Miller effect in the switching operation of power MOSFETs thoroughly and provide a more accurate Miller plateau including the displacement currents through the parasitic capacitances. As a result, the switching process and the switching loss can be analyzed more accurately: the average relative error of the loss model using the new Miller plateau is reduced to 1/2∼1/4 of the one obtained by the traditional Miller plateau. The rest of the paper is structured as follows: the new model for accurate Miller plateau estimation is proposed in Section 2. Based on the corrected Miller plateau voltage, the switching process and the switching power loss are analyzed in Section 3. Experimental and simulation results are provided in Section 4, verifying the proposed analysis method using the new Miller plateau. Finally, the conclusion is given in Section 5.

2. Miller Plateau Corrected with Displacement Currents

Figure 1a shows a traditional boost converter, which is a widely used step-up DC-DC converter. Since the duration of the turn-on time $T_{\mathit{r}}$ or turn-off time $T_{\mathit{f}}$ is much smaller than the switching period $T_{\mathit{s}}$, the inductance L may be considered to be a constant current source and the output capacitance C a constant voltage source during the switching transitions. With these assumptions and a simple rearrangement of the circuit elements, the equivalent circuit shown in Figure 1b is obtained, which is used to analyze the switching process in this paper. It has been proven that this equivalent circuit can also be utilized to analyze the switching process of other SMPS topologies [18,31,32].

As was clarified in [32] that the basic transistor action is fast enough, which makes solving the physical equations governing the device behavior simultaneously with the circuit equations unnecessary, and we can safely rely on the fact that what decides the switching process is the time required to establish voltage changes across the parasitic capacitances and current changes in the parasitic inductances. The parasitic capacitances mainly comprise the three interelectrode capacitances, namely $C_{\mathit{GS}}$, $C_{\mathit{GD}}$, and $C_{\mathit{DS}}$. The parasitic inductances of the drain and source leads, $L_D$ and $L_S$, must also be considered in high-frequency SMPS. These parasitic capacitances and inductances are also indicated in Figure 1b. Although the capacitances of the devices manifest great nonlinearity, methods as shown in [24] can be adopted to estimate the effective value of each capacitance. To simplify the discussion, we here use the effective values of $C_{\mathit{GS}}$, $C_{\mathit{GD}}$, and $C_{\mathit{DS}}$ and omit their nonlinearity.

In Figure 1b, the transistor SN used as a power switch is a MOSFET. In a monolithic low-voltage DC-DC converter, those integrated power switches are no more than standard CMOS MOSFETs, only that there are thousands of elementary cells in parallel with each other and usually bearing at least 1 A current in the ON state [33]. Figure 1b also gives the equivalent circuit of the MOSFET and its three states.

Both the source inductor $L_{\mathit{S}}$ and the gate–drain capacitor $C_{\mathit{GD}}$ form negative feedbacks from the drain circuit to the gate circuit. The former slows down the gate circuit, creating more switching loss, while the latter causes the Miller effect [34,35,36]. The Miller effect shows that the equivalent input capacitance related to $C_{\mathit{GD}}$ is multiplied by $1+A$, where A denotes the voltage gain from $V_{\mathit{G}}$ to $V_{\mathit{D}}$. The observed Miller plateau in the switching process of a power transistor is a result of the Miller effect. When the load current of the power transistor is $I_{\mathit{L}}$, the Miller plateau of $V_{\mathit{GS}}$ is traditionally [20,21,22,24] defined as:

$$V_{\mathit{pl}}=V_{\mathit{TH}}+\frac{I_L}{g_{\mathit{fs}}}$$

(1)

where $g_{\mathit{fs}}$ is the MOSFET’s transconductance and $V_{\mathit{TH}}$ is its typical threshold voltage.

According to (1), the turn-on Miller plateau voltage and turn-off Miller plateau voltage are the same with a constant current load, and few papers have mentioned the impact of the displacement currents through $C_{\mathit{GD}}$ and $C_{\mathit{DS}}$ on the Miller plateau. Reference [27] defined a current $I_{\mathit{p}}$ that correlates with the displacement current, but its value was calculated empirically by observing $I_{\mathit{p}}$ patterns in the simulated waveforms, and only the displacement current through $C_{\mathit{DS}}$ was considered.

During the switching process, the current flowing through the transistor is not equal to the load current, namely $I_{\mathit{ch}}\ne I_{\mathit{L}}$. As shown in Figure 1b, the displacement currents flowing through $C_{\mathit{GD}}$ and $C_{\mathit{DS}}$ must also be included. According to Kirchhoff’s current law (KCL) for node D in Figure 1b, it is derived that:

$$I_{\mathit{ch}}=I_L+C_{\mathit{GD}}\frac{d{V}_{\mathit{GD}}}{dt}-C_{\mathit{DS}}\frac{d{V}_{\mathit{DS}}}{dt}$$

(2)

With an ideal current source load, the voltage gain $A=g_m{R}_{\mathit{out}}\to \infty$, and this equals an infinite capacitance according to the Miller effect. When $V_{\mathit{GS}}$ reaches the Miller plateau $V_{\mathit{pl}\_\mathit{on}}$ during the turn-on process, all the gate current $(V_{\mathit{dr}}-V_{\mathit{pl}\_\mathit{on}})/R_g$ flows into $C_{\mathit{GD}}$, but there is no voltage increase of $V_{\mathit{GS}}$. As a result, the voltages of the gate node G and the source node S are both constant, and their rate of change is zero. Therefore, $d{V}_{\mathit{GD}}=d{V}_G-d{V}_D=-d{V}_D$, and $d{V}_{\mathit{DS}}=d{V}_D-d{V}_S=d{V}_D$. Then,

$$\frac{d{V}_{\mathit{GD}}}{dt}=-\frac{d{V}_{\mathit{DS}}}{dt}$$

(3)

The current flowing into $C_{\mathit{GD}}$ is now $\left(V_{\mathit{dr}}-V_{\mathit{pl}\_\mathit{on}}\right)/R_g$, and the current flowing out of $C_{\mathit{DS}}$ and $C_{\mathit{GD}}$ in parallel is now $(I_{\mathit{ch}}-I_{\mathit{L}})$. Substituting $I_{\mathit{ch}}=g_{\mathit{fs}}(V_{\mathit{pl}\_\mathit{on}}-V_{\mathit{TH}})$ and the capacitor’s current–voltage relationship $I=CdV/dt$ into (3), it is deduced that:

$$\frac{V_{\mathit{dr}}-V_{\mathit{pl}\_\mathit{on}}}{R_g{C}_{\mathit{GD}}}=\frac{g_{\mathit{fs}}(V_{\mathit{pl}\_\mathit{on}}-V_{\mathit{TH}})-I_L}{C_{\mathit{GD}}+C_{\mathit{DS}}}$$

(4)

This equation reveals the relationship between the turn-on Miller plateau and the two displacement currents through $C_{\mathit{GD}}$ and $C_{\mathit{DS}}$.

Similarly, when $V_{\mathit{GS}}$ reaches the Miller plateau $V_{\mathit{pl}\_\mathit{off}}$ during the turn-off process, the current flowing out of $C_{\mathit{GD}}$ is $V_{\mathit{pl}\_\mathit{off}}/R_g$ and the current flowing into $C_{\mathit{DS}}$ and $C_{\mathit{GD}}$ in parallel is $(I_{\mathit{L}}-I_{\mathit{ch}})$. Substituting $I_{\mathit{ch}}=g_{\mathit{fs}}(V_{\mathit{pl}\_\mathit{off}}-V_{\mathit{TH}})$ and the capacitor’s current–voltage relationship $I=CdV/dt$ into (3), it is deduced that:

$$\frac{V_{\mathit{pl}\_\mathit{off}}}{R_g{C}_{\mathit{GD}}}=\frac{I_L-g_{\mathit{fs}}(V_{\mathit{pl}\_\mathit{off}}-V_{\mathit{TH}})}{C_{\mathit{GD}}+C_{\mathit{DS}}}$$

(5)

This equation reveals the relationship between the turn-off Miller plateau and the two displacement currents through $C_{\mathit{GD}}$ and $C_{\mathit{DS}}$.

From (4) and (5), the Miller plateau voltages of the turn-on process and turn-off process are derived as:

$$\left\{\begin{array}{cc}\hfill V_{\mathit{pl}\_\mathit{on}}& =\frac{V_{\mathit{TH}}{g}_{\mathit{fs}}{R}_g{C}_{\mathit{GD}}+I_L{R}_g{C}_{\mathit{GD}}+V_{\mathit{dr}}(C_{\mathit{GD}}+C_{\mathit{DS}})}{(1+g_{\mathit{fs}}{R}_g)C_{\mathit{GD}}+C_{\mathit{DS}}}\hfill \\ \hfill V_{\mathit{pl}\_\mathit{off}}& =\frac{V_{\mathit{TH}}{g}_{\mathit{fs}}{R}_g{C}_{\mathit{GD}}+I_L{R}_g{C}_{\mathit{GD}}}{(1+g_{\mathit{fs}}{R}_g)C_{\mathit{GD}}+C_{\mathit{DS}}}\hfill \end{array}\right.$$

(6)

This equation shows that the two Miller plateau voltages of the turn-on and turn-off processes are different even with a constant current load. This can be better explained by realizing that a Miller plateau voltage of $V_{\mathit{GS}}$ also means a Miller plateau current of $I_{\mathit{ch}}$. Since the MOSFET is in the ACTIVE state during the Miller time, the turn-on Miller plateau current $I_{\mathit{pl}\_\mathit{on}}$ and turn-off Miller plateau current $I_{\mathit{pl}\_\mathit{off}}$ are:

$$\left\{\begin{array}{cc}\hfill I_{\mathit{pl}\_\mathit{on}}& =g_{\mathit{fs}}(V_{\mathit{pl}\_\mathit{on}}-V_{\mathit{TH}})\hfill \\ \hfill I_{\mathit{pl}\_\mathit{off}}& =g_{\mathit{fs}}(V_{\mathit{pl}\_\mathit{off}}-V_{\mathit{TH}})\hfill \end{array}\right.$$

(7)

With the capacitances being considered, the channel current $I_{\mathit{ch}}$ must be larger than the load current $I_{\mathit{L}}$ during the turn-on process and smaller than the load current $I_{\mathit{L}}$ during the turn-off process to provide the extra displacement currents through $C_{\mathit{GD}}$ and $C_{\mathit{DS}}$. The traditional value of $V_{\mathit{pl}}$ in (1) does not take the displacement currents into account and assumes that $I_{\mathit{ch}}=I_{\mathit{L}}$ when $V_{\mathit{GS}}$ reaches the Miller plateau $V_{\mathit{pl}}$ during the switching process; thus, the Miller plateau is the same in both the turn-on and turn-off process. As will be shown in the following sections, using the new assessment of the Miller plateau voltage, the switching process and switching power loss can be more accurately analyzed, especially for the low-voltage, high-frequency SMPS.

3. Analyzing the Switching Process and Switching Loss with the New Miller Plateau

The new Miller plateau voltage shown in (6) can be easily applied to the conventional piecewise-linear model or other analytical models. In the turn-on process, the traditional Miller plateau voltage $V_{\mathit{pl}}$ should be replaced by $V_{\mathit{pl}\_\mathit{on}}$; in the turn-off process, $V_{\mathit{pl}}$ should be replaced by $V_{\mathit{pl}\_\mathit{off}}$.

3.1. Switching Waveform Analysis Using the New Miller Plateau

The turn-on or turn-off transition of a power transistor follows several distinct intervals [18,20,32]. Figure 2 illustrates the switching waveforms of a power MOSFET with a clamped current load. Both the turn-on and the turn-off switching processes are divided into five intervals. In Figure 2, each interval of the turn-on sequence is marked by $T_{*}\mathit{r}$, and each interval of the turn-off sequence is marked by $T_{*}\mathit{f}$. On the top of the figure, the corresponding state of the MOSFET in each interval is also indicated with the same mark (three states of the MOSFET: 1 → ON, 2 → ACTIVE, 3 → OFF) in Figure 1b.

In the turn-on sequence, the first interval is the delay time $T_{1\mathit{r}}$, during which $V_{\mathit{GS}}$ ramps up to $V_{\mathit{TH}}$. Next comes the current increase phase, during which $V_{\mathit{GS}}$ continues ramping up to the Miller voltage $V_{\mathit{pl}\_\mathit{on}}$. The channel current $I_{\mathit{ch}}$ also reaches its Miller plateau, a value larger than the load current $I_{\mathit{L}}$. $T_{3\mathit{r}}$ is the Miller time, and $V_{\mathit{DS}}$ falls from $V_{\mathit{in}}$ to zero with a constant rate $K_r=(V_{\mathit{dr}}-V_{\mathit{pl}\_\mathit{on}})/\left(R_g{C}_{\mathit{GD}}\right)$. Entering $T_{4\mathit{r}}$, the MOSFET has already gone into the ON state. This is the time $I_{\mathit{ch}}$ needs to change from its Miller value to its final state. The time constant $\tau$ in this interval is $R_{\mathit{DS}}\left(\mathit{on}\right)C_{\mathit{DS}}$. The final interval sees $V_{\mathit{GS}}$ complete its rise toward $V_{\mathit{dr}}$.

In the turn-off sequence, the first interval is the delay time $T_{1\mathit{f}}$, during which $V_{\mathit{GS}}$ ramps down to $V_{\mathit{pl}}$. Next comes the interval during which $V_{\mathit{GS}}$ continues ramping down to the Miller voltage $V_{\mathit{pl}\_\mathit{off}}$. The channel current $I_{\mathit{ch}}$ also reaches its Miller plateau, a value smaller than the load current $I_{\mathit{L}}$. $T_{3\mathit{f}}$ is the Miller time, and $V_{\mathit{DS}}$ rises from zero to $V_{\mathit{in}}$ with a constant rate $K_f=V_{\mathit{pl}\_\mathit{off}}/\left(R_g{C}_{\mathit{GD}}\right)$. Entering $T_{4\mathit{f}}$, the MOSFET is still in the ACTIVE state. This is the time $I_{\mathit{ch}}$ needs to change from its Miller value to zero. The final interval sees $V_{\mathit{GS}}$ complete its fall toward zero.

According to the above analysis, the equivalent circuit of each interval is first-order, whose solution can be easily obtained. For example, during the delay time $T_{1\mathit{r}}$, the gate–source voltage $V_{\mathit{GS}}$ rises exponentially towards $V_{\mathit{dr}}$ with a time constant given by $R_g{C}_{\mathit{iss}}$ ($C_{\mathit{iss}}=C_{\mathit{GS}}+C_{\mathit{GD}}$), that is,

$$V_{\mathit{GS}}=V_{\mathit{dr}}(1-e^{-\frac{t}{R_g{C}_{\mathit{iss}}}})$$

(8)

The delay time $T_{1\mathit{r}}$ lasts until $V_{\mathit{GS}}=V_{\mathit{TH}}$. Thus, $T_{1\mathit{r}}$ is derived as follows:

$$T_{1\mathit{r}}=R_g{C}_{\mathit{iss}}ln\frac{V_{\mathit{dr}}}{V_{\mathit{dr}}-V_{\mathit{TH}}}$$

(9)

Table 1. Duration of each interval of the switching process of a power MOSFET with a clamped current load.

Turn-On		Turn-Off
$T_{1\mathit{r}}$	$R_g{C}_{\mathit{iss}}ln\frac{V_{\mathit{dr}}}{V_{\mathit{dr}}-V_{\mathit{TH}}}{}^{*}$	$T_{1\mathit{f}}$	$R_g{C}_{\mathit{iss}}ln\frac{V_{\mathit{dr}}}{V_{\mathit{pl}}}$
$T_{2\mathit{r}}$	$R_g{C}_{\mathit{iss}}ln\frac{V_{\mathit{dr}}-V_{\mathit{TH}}}{V_{\mathit{dr}}-V_{\mathit{pl}\_\mathit{on}}}$	$T_{2\mathit{f}}$	$R_g{C}_{\mathit{iss}}ln\frac{V_{\mathit{pl}}}{V_{\mathit{pl}\_\mathit{off}}}$
$T_{3\mathit{r}}$	$V_{\mathit{in}}/K_r$	$T_{3\mathit{f}}$	$V_{\mathit{in}}/K_f-T_{2\mathit{f}}$
$T_{4\mathit{r}}$	$5R_{\mathit{DS}\left(\mathit{on}\right)}{C}_{\mathit{DS}}$	$T_{4\mathit{f}}$	$R_g{C}_{\mathit{iss}}ln\frac{V_{\mathit{pl}\_\mathit{off}}}{V_{\mathit{TH}}}$
$T_{5\mathit{r}}$	$R_g{C}_{\mathit{iss}}ln\frac{V_{\mathit{dr}}-V_{\mathit{pl}\_\mathit{on}}}{(1-0.99)V_{\mathit{dr}}}-T_{4\mathit{r}}$	$T_{5\mathit{f}}$	$R_g{C}_{\mathit{iss}}ln\frac{V_{\mathit{TH}}}{0.01V_{\mathit{TH}}}$

* C_iss = C_GS + C_GD.

gives the duration of each interval of the switching process. As $T_{5\mathit{r}}$ and $T_{5\mathit{f}}$ indicate, when $V_{\mathit{GS}}$ is larger than $0.99V_{\mathit{dr}}$, the turn-on sequence is believed to be over; when $V_{\mathit{GS}}$ is smaller than $0.01V_{\mathit{TH}}$, the turn-off sequence is believed to be over.

Figure 2 and Table 1 analyze the switching process of the capacitance-limited (the parasitic $L_D$ and $L_S$ are small enough to be neglected) case with a clamped current load. However, the proposed new Miller plateau can be used to analyze the switching process under other conditions only if some revisions are made.

For example, with a resistive load $R_L$, $T_{1\mathit{r}}$ remains unchanged. However, the duration of the following intervals must be changed since the load current now varies during the switching process. $T_{2\mathit{r}}$ can be calculated with the same equation in Table 1 with a new value of $V_{\mathit{pl}\_\mathit{on}1}$ @ $I_L=0$. The value of $V_{\mathit{pl}\_\mathit{on}2}$ @ $I_L=V_{\mathit{in}}/R_L$, together with $V_{\mathit{pl}\_\mathit{on}1}$, can be used to calculate $T_{3\mathit{r}}$:

$$\begin{array}{c}\hfill T_{3\mathit{r}}=R_g[C_{\mathit{GS}}+(1+g_{\mathit{fs}}{R}_L)C_{\mathit{GD}}]ln\frac{V_{\mathit{dr}}-V_{\mathit{pl}\_\mathit{on}1}}{V_{\mathit{dr}}-V_{\mathit{pl}\_\mathit{on}2}}\end{array}$$

(10)

If $L_D$ cannot be ignored, the time constant of $T_{\mathit{1}}\mathit{r}$ is $R_g(C_{\mathit{GS}}+C_{\mathit{GD}}//C_{\mathit{DS}})$ instead of $R_g(C_{\mathit{GS}}+C_{\mathit{GD}})$ since $L_D$ acts as a current source during this interval. Reference [32] showed that, in the turn-on sequence, depending on which, the gate circuit and drain circuit, is faster, the drain voltage will collapse before there is any appreciable rise in current, or the current will reach its Miller value before the drain voltage collapses. This actually equals whether there is a Miller plateau in the turn-on sequence or not. If $L_D$ is small, there will be a Miller plateau in the turn-on sequence and the channel current will finish its rise earlier. From the analysis of [32], $V_{\mathit{GS}}$ varies according to a quadratic function during the main transition interval. Then, the rate of the $V_{\mathit{GS}}$ rise will accelerate, and this means an abrupt change when it enters its Miller plateau. With the new value of $V_{\mathit{pl}\_\mathit{on}}$, we can make it rise smoothly since $V_{\mathit{GS}}$ still needs to change from $V_{\mathit{pl}}$ to $V_{\mathit{pl}\_\mathit{on}}$ during $T_{\mathit{2}}\mathit{r}$ in Figure 2.

There will always be a Miller plateau in the turn-off process even in the inductance-limited case (the drain voltage collapses before the channel current finishes its rise in the turn-on process). However, during $T_{\mathit{4}}\mathit{f}$, $V_{\mathit{DS}}$ must rise above $V_{\mathit{in}}$ to discharge $L_D$. Using the same method as in [32] with the new Miller plateau $V_{\mathit{pl}\_\mathit{off}}$ of the turn-off process to analyze the switching action during $T_{\mathit{4}}\mathit{f}$,

$$\begin{array}{c}\hfill V_{\mathit{GS}}=V_{\mathit{pl}\_\mathit{off}}(1-\frac{t^2}{{\tau }_m{\tau }_{G\prime }})\end{array}$$

(11)

where ${\tau }_m=g_{\mathit{fs}}{L}_D$ and ${\tau }_{G\prime }=R_G{C}_{\mathit{GD}}$. Thus:

$$\begin{array}{c}\hfill T_{\mathit{4}}\mathit{f}=\sqrt{{\tau }_m{\tau }_{G\prime }\frac{V_{\mathit{pl}\_\mathit{off}}-V_{\mathit{TH}}}{V_{\mathit{pl}\_\mathit{off}}}}\end{array}$$

(12)

In all, using the new Miller plateau voltages $V_{\mathit{pl}\_\mathit{on}}$ and $V_{\mathit{pl}\_\mathit{off}}$, the switching waveforms can be analyzed under various load conditions. Parasitic inductances can also be included. No detail is missed; each interval has its own physical meaning, and the duration thereof can be easily calculated, which greatly helps to comprehend the switching process of the power MOSFET.

3.2. Switching Loss Analysis Using the New Miller Plateau

The above analysis shows that it is rather easy to use the new Miller plateau voltages $V_{\mathit{pl}\_\mathit{on}}$ and $V_{\mathit{pl}\_\mathit{off}}$ to analyze the switching process of a power transistor. With the switching waveforms being known, it is straightforward to calculate the corresponding turn-on and turn-off losses by calculating the integral of $V_{\mathit{DS}}\times I_{\mathit{ch}}$ over the switching time. Since the analyzed switching waveforms are accurate, the calculated switching losses will be accurate as well.

To simplify the discussion and make a better comparison, we here directly cite the closed-form loss model of [30]:

$$\left\{\begin{array}{cc}\hfill P_{\mathit{on}}& =\frac{V_{\mathit{in}}{I}_{\mathit{L}}{f}_{\mathit{sw}}}{2}\frac{C_{\mathit{iss}}(V_{\mathit{pl}}-V_{\mathit{TH}})+C_{\mathit{GD}}{V}_{\mathit{in}}}{(V_{\mathit{dr}}-V_{\mathit{pl}})/R_g}\hfill \\ \hfill P_{\mathit{off}}& =\frac{V_{\mathit{in}}{I}_{\mathit{L}}{f}_{\mathit{sw}}}{2}\frac{C_{\mathit{iss}}(V_{\mathit{pl}}-V_{\mathit{TH}})+C_{\mathit{GD}}{V}_{\mathit{in}}}{V_{\mathit{pl}}/R_g}\hfill \end{array}\right.$$

(13)

where $C_{\mathit{iss}}=C_{\mathit{GS}}+C_{\mathit{GD}}$; $P_{\mathit{on}}$ and $P_{\mathit{off}}$ represent turn-on switching loss and turn-off switching loss, respectively, and $f_{\mathit{sw}}$ is the switching frequency. This equation differs a little from its original expression in [30]. In [30], the gate charge was used instead of the capacitance. Although the capacitances of a power transistor manifest great nonlinearity, methods as shown in [24] can be adopted to estimate the effective value of each capacitance. After the new Miller plateau is calculated with the capacitance’s effective value, the gate charge can still be used. To simplify the discussion, we here use the effective values of $C_{\mathit{GS}}$, $C_{\mathit{GD}}$, and $C_{\mathit{DS}}$ and omit their nonlinearity.

Based on (13), the new $V_{\mathit{pl}\_\mathit{on}}$ and $V_{\mathit{pl}\_\mathit{off}}$ in (6) are used instead of the conventional $V_{\mathit{pl}}$, and the corresponding $I_{\mathit{pl}\_\mathit{on}}$ and $I_{\mathit{pl}\_\mathit{on}}$ in (7) are also used to replace the load current $I_{\mathit{L}}$. Then,

$$\left\{\begin{array}{cc}\hfill P_{\mathit{on}}& =\frac{V_{\mathit{in}}{I}_{\mathit{pl}\_\mathit{on}}{f}_{\mathit{sw}}}{2}\frac{C_{\mathit{iss}}(V_{\mathit{pl}\_\mathit{on}}-V_{\mathit{TH}})+C_{\mathit{GD}}{V}_{\mathit{in}}}{(V_{\mathit{dr}}-V_{\mathit{pl}\_\mathit{on}})/R_g}\hfill \\ \hfill P_{\mathit{off}}& =\frac{V_{\mathit{in}}{I}_{\mathit{pl}\_\mathit{off}}{f}_{\mathit{sw}}}{2}\frac{C_{\mathit{iss}}(V_{\mathit{pl}\_\mathit{off}}-V_{\mathit{TH}})+C_{\mathit{GD}}{V}_{\mathit{in}}}{V_{\mathit{pl}\_\mathit{off}}/R_g}\hfill \end{array}\right.$$

(14)

In (13) and (14), the gate current was assumed to be constant during the switching process, namely $(V_{\mathit{dr}}-V_{\mathit{pl}\_\mathit{on}})/R_g$ in the turn-on process and $V_{\mathit{pl}\_\mathit{off}}/R_g$ in the turn-off process. However, this makes sense only during the Miller time of the switching process. When $V_{\mathit{GS}}$ changes from $V_{\mathit{TH}}$ to $V_{\mathit{pl}\_\mathit{on}}$ in the turn-on process or from $V_{\mathit{pl}\_\mathit{off}}$ to $V_{\mathit{TH}}$ in the turn-off process, the gate current varies greatly. It is necessary to make a more accurate assessment of the gate current during this time to further improve the prediction accuracy of the switching power loss, especially for the low-voltage, high-frequency SMPS.

Using the average gate current when $V_{\mathit{GS}}$ changes from $V_{\mathit{TH}}$ to $V_{\mathit{pl}\_\mathit{on}}$ in the turn-on process or from $V_{\mathit{pl}\_\mathit{off}}$ to $V_{\mathit{TH}}$ in the turn-off process, (14) can be further written as:

$$\left\{\begin{array}{cc}\hfill P_{\mathit{on}}& =\frac{V_{\mathit{in}}{I}_{\mathit{pl}\_\mathit{on}}{f}_{\mathit{sw}}}{2}[\frac{C_{\mathit{iss}}(V_{\mathit{pl}\_\mathit{on}}-V_{\mathit{TH}})}{I_{\mathit{avg}\_\mathit{on}}}+\frac{C_{\mathit{GD}}{V}_{\mathit{in}}}{(V_{\mathit{dr}}-V_{\mathit{pl}\_\mathit{on}})/R_g}]\hfill \\ \hfill P_{\mathit{off}}& =\frac{V_{\mathit{in}}{I}_{\mathit{pl}\_\mathit{off}}{f}_{\mathit{sw}}}{2}[\frac{C_{\mathit{GD}}{V}_{\mathit{in}}}{V_{\mathit{pl}\_\mathit{off}}/R_g}+\frac{C_{\mathit{iss}}(V_{\mathit{pl}\_\mathit{off}}-V_{\mathit{TH}})}{I_{\mathit{avg}\_\mathit{off}}}]\hfill \end{array}\right.$$

(15)

in which $I_{\mathit{avg}\_\mathit{on}}$ and $I_{\mathit{avg}\_\mathit{off}}$ are the average gate current when $V_{\mathit{GS}}$ changes from $V_{\mathit{TH}}$ to $V_{\mathit{pl}\_\mathit{on}}$ in the turn-on process and the average gate current when $V_{\mathit{GS}}$ changes from $V_{\mathit{pl}\_\mathit{off}}$ to $V_{\mathit{TH}}$ in the turn-off process, respectively. Their values are approximated as:

$$\left\{\begin{array}{cc}\hfill I_{\mathit{avg}\_\mathit{on}}& =[V_{\mathit{dr}}-\frac{1}{2}(V_{\mathit{TH}}+V_{\mathit{pl}\_\mathit{on}})]/R_g\hfill \\ \hfill I_{\mathit{avg}\_\mathit{off}}& =\frac{1}{2}(V_{\mathit{TH}}+V_{\mathit{pl}\_\mathit{off}})/R_g\hfill \end{array}\right.$$

(16)

which is a simple linear approximation.

Simply replacing the traditional Miller plateau with the proposed new Miller plateau will improve the prediction accuracy of the existing loss models. In addition, unlike previous works, we here directly analyzed $I_{\mathit{ch}}$ instead of $I_D$. In this way, it is clear that the widely accepted output capacitance loss term is redundant [25]. If the capacitance’s effect on the switching duration has already been included, there is no need to further add the output capacitance loss to the final calculation of the switching loss.

4. Experimental and Simulation Verification

4.1. Experimental Test Result of the Miller Plateau

Shown in Figure 3, the experimental validation of the newly calculated Miller plateau was carried out by testing NCE2030K [37] with an equivalent load current $I_{\mathit{L}}=0.1$ A. The input voltage $V_{\mathit{in}}$ was 10 V, and the gate driving voltage $V_{\mathit{dr}}$ was 3 V. The nominal values of NCE2030K’s key parameters were: $g_{\mathit{fs}}=10\mathrm{S}$, $V_{\mathit{TH}}=0.7\mathrm{V}$, $C_{\mathit{iss}}=900\mathrm{pF}$ (@ $V_{\mathit{ds}}=10\mathrm{V}$), $C_{\mathit{oss}}=162\mathrm{pF}$ (@ $V_{\mathit{ds}}=10\mathrm{V}$), $C_{\mathit{rss}}=105$ pF (@ $V_{\mathit{ds}}=10\mathrm{V}$).

The circuit was driven directly by the signal generator whose 50 $\mathsf{\Omega }$ output impedance served as $R_{\mathit{g}}$. The driving signal was 100 kHz with a 50% duty cycle. An external 2 nF capacitance $C_{\mathit{GS}\_\mathit{ext}}$ was also connected in parallel with the power MOSFET.

The relatively low-frequency operation and the added capacitors made the gate circuit slow and reduced the effect of parasitic inductances, which ensured that the Miller plateau voltages could be accurately measured.

The measured switching waveforms of $V_{\mathit{GS}}$ and $V_{\mathit{DS}}$ are shown in Figure 4, where the Miller plateau of $V_{\mathit{GS}}$ can be readily identified from its waveform. As shown in this figure, the turn-on Miller plateau voltage $V_{\mathit{pl}\_\mathit{on}}$ and the turn-off Miller plateau voltage $V_{\mathit{pl}\_\mathit{off}}$ are different, which cannot be explained by the existing calculation method of the Miller plateau in (1). In contrast, the proposed calculation method of the Miller plateau in (6) shows that the two Miller plateau voltages of the turn-on and turn-off processes are different even with a constant current load. (6) also reveals that the Miller plateau correlates with the relevant capacitances.

Table 2. The measured (Meas.) Miller plateau, the predicted Miller plateau by the existing (Exist.) method, and the predicted Miller plateau by the proposed (Prop.) method when the relevant capacitance changes.

	When $C_{\mathit{DS}\_\mathit{ext}}=1\mathbf{nF}$			When $C_{\mathit{DS}\_\mathit{ext}}=5\mathbf{nF}$
	Meas.	Exist.	Prop.	Meas.	Exist.	Prop.
$V_{\mathit{pl}\_\mathit{on}}$	1070 mV	710 mV	760 mV	1230 mV	710 mV	922 mV
$V_{\mathit{pl}\_\mathit{off}}$	950 mV	710 mV	695 mV	909 mV	710 mV	644 mV

shows the measured (Meas.) Miller plateau, the predicted Miller plateau by the existing (Exist.) method, and the predicted Miller plateau by the proposed (Prop.) method when the relevant capacitance changes. Substituting the above circuit parameters into (1), the predicted Miller plateau $V_{\mathit{pl}}$ by the existing method is 710 mV in both the turn-on and turn-off switching processes and has no relationship with the relevant capacitances. Substituting the above circuit parameters into (6), the predicted Miller plateau voltages are: $V_{\mathit{pl}\_\mathit{on}}=760$ mV and $V_{\mathit{pl}\_\mathit{off}}=695$ mV when $C_{\mathit{DS}\_\mathit{ext}}=1\mathrm{nF}$; $V_{\mathit{pl}\_\mathit{on}}=922$ mV and $V_{\mathit{pl}\_\mathit{off}}=644$ mV when $C_{\mathit{DS}\_\mathit{ext}}=5\mathrm{nF}$. Apart from the measurement errors, as (6) indicates, the values of $V_{\mathit{pl}\_\mathit{on}}$ and $V_{\mathit{pl}\_\mathit{off}}$ greatly depend on $V_{\mathit{TH}}$ whose real value may be larger than the nominal one given in [37]. This explains why the difference between the measured Miller plateau and the predicted Miller plateau is quite large.

However, as

Table 3. Variation of the Miller plateau when $C_{\mathit{DS}\_\mathit{ext}}$ changes from $1\mathrm{nF}$ to $5\mathrm{nF}$.

	Measured	Existing	Proposed
$\Delta V_{\mathit{pl}\_\mathit{on}}$	160 mV	0 mV	162 mV
$\Delta V_{\mathit{pl}\_\mathit{off}}$	41 mV	0 mV	51 mV

shows, the measured voltage difference of $V_{\mathit{pl}\_\mathit{on}}$ (@ $C_{\mathit{DS}\_\mathit{ext}}=1\mathrm{nF}$) and $V_{\mathit{pl}\_\mathit{on}}$ (@ $C_{\mathit{DS}\_\mathit{ext}}=5\mathrm{nF}$) is 160 mV and the calculated voltage difference by the proposed method is 162 mV; the measured voltage difference of $V_{\mathit{pl}\_\mathit{off}}$ (@ $C_{\mathit{DS}\_\mathit{ext}}=1\mathrm{nF}$) and $V_{\mathit{pl}\_\mathit{off}}$ (@ $C_{\mathit{DS}\_\mathit{ext}}=5\mathrm{nF}$) is 41 mV and the calculated voltage difference by the proposed method is 51 mV. The calculated variation trend of plateau voltage as $C_{\mathit{DS}}$ changes agrees well with the measurement result, which verifies the correctness of (6) in revealing the relationship of the Miller plateau and the relevant capacitance. In contrast, the existing calculation method of the Miller plateau in (1) fails to predict the relationship of the Miller plateau and the relevant capacitance.

4.2. Verification of Analyzing the Switching Waveform

The SPICE model of a MOSFET always includes the corresponding capacitors, which makes it impossible to separate $I_{\mathit{ch}}$ from $I_{\mathit{D}}$, and it is difficult to measure the actual switching loss and make a loss breakdown analysis of an experimental prototype. As a result, an ideal MOSFET with the equivalent circuit in Figure 1b was written in Verilog-A. The key source code is as in Algorithm 1:

Algorithm 1

if (vov < 0) begin     mosfet_state = ‘OFF;   end   else if (gfs * vov < V(vd, vs)/ron) begin    mosfet_state = ‘ACTIVE;   end   else begin    mosfet_state = ‘ON;   end   if (mosfet_state == ‘OFF) begin    I(vd,vs) <+ 0.0;   end   else if (mosfet_state == ‘ACTIVE) begin    I(vd,vs) <+ gfs * vov;   end   else begin    I(vd,vs) <+ V(vd, vs)/ron;   end

The relevant parasitic capacitances and parasitic inductances can then be added to this ideal power MOSFET.

Based on this ideal power MOSFET, several test benches were set up to verify the effectiveness of the proposed analysis method using the new Miller plateau voltages $V_{\mathit{pl}\_\mathit{on}}$ and $V_{\mathit{pl}\_\mathit{off}}$. The parameters of the power MOSFET were: $V_{\mathit{TH}}=1$ V, $g_{\mathit{fs}}=10$ S, and $R_{\mathit{DS}}\left(\mathit{on}\right)=0.02$$\mathsf{\Omega }$. The parasitic capacitors of the power MOSFET were: $C_{\mathit{GS}}=0.6$ nF, $C_{\mathit{GD}}=0.1$ nF, and $C_{\mathit{DS}}=0.2$ nF. The gate driver was a voltage source driver with $V_{\mathit{dr}}=5$ V and $R_{\mathit{g}}=2$$\mathsf{\Omega }$. The switching frequency was 10 MHz.

Substituting the above circuit parameters into (1) and (6), $V_{\mathit{pl}}$, $V_{\mathit{pl}\_\mathit{on}}$, and $V_{\mathit{pl}\_\mathit{off}}$ were calculated to be 2 V, $2.39$ V, and $1.74$ V, respectively, when $I_{\mathit{L}}=10$ A and $V_{\mathit{in}}=10$ V. In the turn-on process, the new Miller plateau was larger than the traditional value; in the turn-off process, the new Miller plateau was smaller than the traditional value.

The simulated switching waveforms of $V_{\mathit{GS}}$, $I_{\mathit{ch}}$, and $V_{\mathit{DS}}$ in a capacitance-limited (the parasitic $L_D$ and $L_S$ were small enough to be neglected) case are shown in Figure 5. The simulated turn-on Miller plateau voltage ($2.391$ V) and turn-off Miller plateau voltage ($1.746$ V) were different, and they accorded with the predicted values from (6) very well.

The calculation (Cal.) and simulation (Sim.) results of the duration of each switching interval are shown in

Table 4. Calculation and simulation results of switching interval duration.

Turn-On				Turn-Off
On	Cal.	Sim.	Error	Off	Cal.	Sim.	Error
$T_{1\mathit{r}}$	312 ps	313 ps	$0.31\%$	$T_{1\mathit{f}}$	1.28 ns	1.29 ns	$0.77\%$
$T_{2\mathit{r}}$	598 ps	577 ps	$3.6\%$	$T_{2\mathit{f}}$	195 ps	240 ps	$18\%$
$T_{3\mathit{r}}$	767 ps	772 ps	$0.65\%$	$T_{3\mathit{f}}$	954 ps	1.05 ns	$9.1\%$
$T_{4\mathit{r}}$	20.0 ps	22 ps	$9.0\%$	$T_{4\mathit{f}}$	775 ps	785 ps	$1.3\%$
$T_{5\mathit{r}}$	5.52 ns	5.50 ns	$0.36\%$	$T_{5\mathit{f}}$	6.44 ns	6.45 ns	$0.15\%$

, in which the calculation result is based on the equations in Table 1.

The solution of Table 1 and the calculation result of Table 4 are accurate to the first-order. Compared with the simulation result, the accuracy of the calculation result of each interval in Table 4 is generally satisfactory with the exceptions of $T_{4\mathit{r}}$, $T_{2\mathit{f}}$, and $T_{3\mathit{f}}$. The duration of $T_{4\mathit{r}}$ is particularly small compared with other intervals. The time constant of this interval is $R_{\mathit{DS}}\left(\mathit{on}\right)C_{\mathit{DS}}$ since the MOSFET is now in the ON state. The MOSFET is also in the ON state during $T_{1\mathit{f}}$, but the ending of $T_{1\mathit{f}}$ is marked by when $V_{\mathit{GS}}$ falls to $V_{\mathit{pl}\_\mathit{off}}$. Moreover, $I_{\mathit{ch}}$ goes through a substantial change in $T_{4\mathit{r}}$, but both $I_{\mathit{ch}}$ and $V_{\mathit{DS}}$ only change a little in $T_{1\mathit{f}}$. The errors of $T_{2\mathit{f}}$ and $T_{3\mathit{f}}$ come from the first-order linear approximation. During $T_{2\mathit{f}}$, $V_{\mathit{DS}}$ and $I_{\mathit{ch}}$ vary simultaneously. It is better to use a quadratic function for the approximation [32].

Figure 6 shows the switching waveform of $V_{\mathit{GS}}$, $I_{\mathit{ch}}$, and $V_{\mathit{DS}}$ with a partially clamped current load ($L_D=1$ nH). Now, the drain voltage changes faster than the drain current, and there is no Miller voltage in the turn-on process, which also means that this is an inductance-limited case. Instead, we can use $I_D=0$ to obtain an approximate $V_{\mathit{pl}\_\mathit{on}}$ (1.52 V) to calculate $T_{2\mathit{r}}$ and $T_{3\mathit{r}}$, which were 195 ps and 575 ps, respectively. Compared with the simulated data (203 ps and 687 ps, respectively) in Figure 6, the relatively larger error of $T_{3\mathit{r}}$ also comes from the first-order linear approximation. As was analyzed earlier, during $T_{\mathit{4}}\mathit{f}$ of the turn-off sequence, $V_{\mathit{DS}}$ must rise above $V_{\mathit{in}}$ to discharge $L_D$. Using (12), the calculated $T_{4\mathit{f}}$ was 1.30 nS, which is also an accurate value according to the simulated result in Figure 6.

4.3. Verification of Analyzing Switching Loss

In this part, the simulation result of the switching loss was still based on the power MOSFET written in Verilog-A, and the circuit parameters were the same as in the preceding subsection. The simulated turn-on and turn-off switching losses were calculated by integrating $V_{\mathit{DS}}\times I_{\mathit{ch}}$ over the switching time directly.

Using the above circuit parameters, the loss model in (13), which uses the traditional Miller plateau, the loss model in (14), which uses the proposed new Miller plateau (denoted by Proposed Model 1), and the loss model in (15), which uses the proposed new Miller plateau and further takes the gate current’s variation into account (denoted by Proposed Model 2), were calculated and compared. These three models were based on the loss calculation method in [30]. The Proposed Model 1 and Proposed Model 2 here do not indicate specific loss models, and they can be developed by other loss calculation methods only if the traditional Miller plateau is replaced by the proposed new Miller plateau, and the effect of the gate current’s variation was further included for the Proposed Model 2. For example, the corresponding Proposed Model 1 and Proposed Model 2 using the loss calculation method in [20] were also calculated and compared to the original piecewise-linear model in [20]. The aim was to verify the improvement of the prediction accuracy by replacing the traditional Miller plateau with the proposed new Miller plateau.

Figure 7a,b shows the curves of the turn-on and turn-off switching losses as a function of the load current for the Verilog-A simulation, the original Model in [20], the Proposed Model 1, and the Proposed Model 2, respectively. Based on the loss calculation method in [20], the Proposed Model 1 uses the new Miller plateau, while the original Model in [20] uses the conventional Miller plateau. As

Table 5. The average relative error of different loss models based on two calculation methods when the load current $I_L$ changes from 4.0 A to 14 A at 10 MHz, 10 V input voltage, and 5 V gate driving voltage.

	The Loss Calculation Method in [20]			The Loss Calculation Method in [30]
	Original Model in [20]	Proposed Model 1	Proposed Model 2	Original Model in [30]	Proposed Model 1	Proposed Model 2
$P_{\mathit{on}}$	42.1%	09.9%	8.0%	43.0%	15.8%	5.2%
$P_{\mathit{off}}$	35.7%	10.1%	9.7%	29.8%	08.7%	1.6%

shows, replacing the conventional Miller plateau by the new Miller plateau can improve the prediction accuracy of the switching loss: the average relative error of the Proposed Model 1 was almost reduced to 1/3 of the average relative error of the original Model in [20]. The Proposed Model 2, which further takes the gate current’s variation into account, had the smallest prediction error.

Figure 8a,b shows the curves of the turn-on and turn-off switching losses as a function of the gate driving voltage for the Verilog-A simulation, the original Model in [20], the Proposed Model 1, and the Proposed Model 2, respectively. As

Table 6. The average relative error of different loss models based on two calculation methods when the gate driving voltage $V_{dr}$ changes from 4.0 V to 6.5 V at 10 MHz, 10 V input voltage, and 10 A load current.

	The Loss Calculation Method in [20]			The Loss Calculation Method in [30]
	Original Model in [20]	Proposed Model 1	Proposed Model 2	Original Model in [30]	Proposed Model 1	Proposed Model 2
$P_{\mathit{on}}$	39.3%	7.2%	2.9%	39.3%	15.8%	4.3%
$P_{\mathit{off}}$	18.8%	4.4%	5.3%	18.9%	09.8%	1.5%

shows, compared with the loss model based on conventional Miller plateau, the loss model based on new Miller plateau again better followed the trend of the simulation result: the average relative error of the Proposed Model 1 was almost reduced to 1/4 of the average relative error of the original Model in [20]; the Proposed Model 2, which further takes the gate current’s variation into account, had the smallest prediction error.

Figure 9a,b shows the curves of the turn-on and turn-off switching losses as a function of the load current for the Verilog-A simulation, the original Model in [30], the Proposed Model 1, and the Proposed Model 2, respectively. Based on the loss calculation method in [30], the Proposed Model 1 uses the new Miller plateau, while the original Model in [30] uses the conventional Miller plateau. As Table 5 shows, replacing the conventional Miller plateau by the new Miller plateau can improve the prediction accuracy of the switching loss: the average relative error of the Proposed Model 1 was almost reduced to 1/3 of the average relative error of the original Model in [30]. The Proposed Model 2, which further takes the gate current’s variation into account, had the smallest prediction error: the average relative error is within 5.5%.

Figure 10a,b shows the curves of the turn-on and turn-off switching losses as a function of the gate driving voltage for the Verilog-A simulation, the original Model in [30], the Proposed Model 1, and the Proposed Model 2, respectively. As Table 6 shows, compared with the loss model based on conventional Miller plateau, the loss model based on new Miller plateau again better followed the trend of the simulation result: the average relative error of the Proposed Model 1 was almost reduced to 1/2 of the average relative error of the original Model in [30]; the Proposed Model 2, which further takes the gate current’s variation into account, had the smallest prediction error and its average relative error is within 4.5%.

5. Conclusions

In order to estimate the switching loss of SMPS accurately, the relationship between the Miller plateau voltage and the displacement currents through parasitic capacitance of a power MOSFET was analyzed and a quantitative model was derived in this paper. Based on the proposed model, the Miller plateau should have different voltage levels during turn-on/-off, and it also changes according to different load conditions. Using the new Miller plateau, the switching waveform and switching loss can be analyzed and calculated more accurately. Experiment and simulation were performed to verify the proposed new Miller plateau and its use in analyzing switching process. For switching loss prediction, the benchmarking table shows that the achieved average relative error of the proposed Miller plateau-based loss model (Model 1) can be reduced to well below 10%, which is a 50∼75% reduction of the one obtained by the traditional Miller plateau-based model. Moreover, the error can be further reduced to around 5%, the lowest among these loss models, by using the proposed Miller plateau-based model (Model 2), taking into consideration the gate current’s variation. The proposed new Miller plateau can be further used to measure the device performance and to help to select the right device and gate driver for designing a high-frequency SMPS.