An 8-bit Radix-4 Non-Volatile Parallel Multiplier
Abstract
:1. Introduction
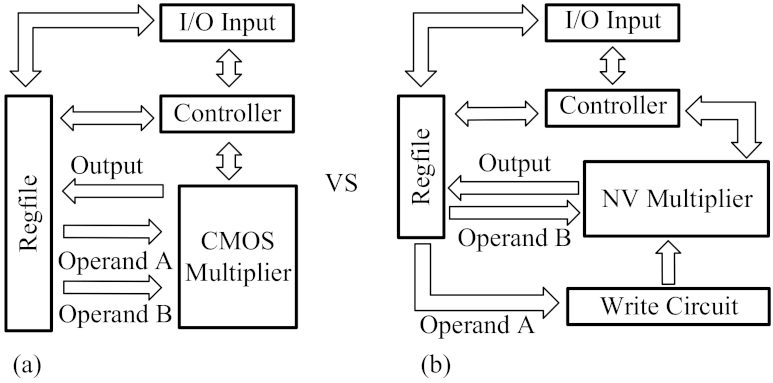
2. Background and Related Work
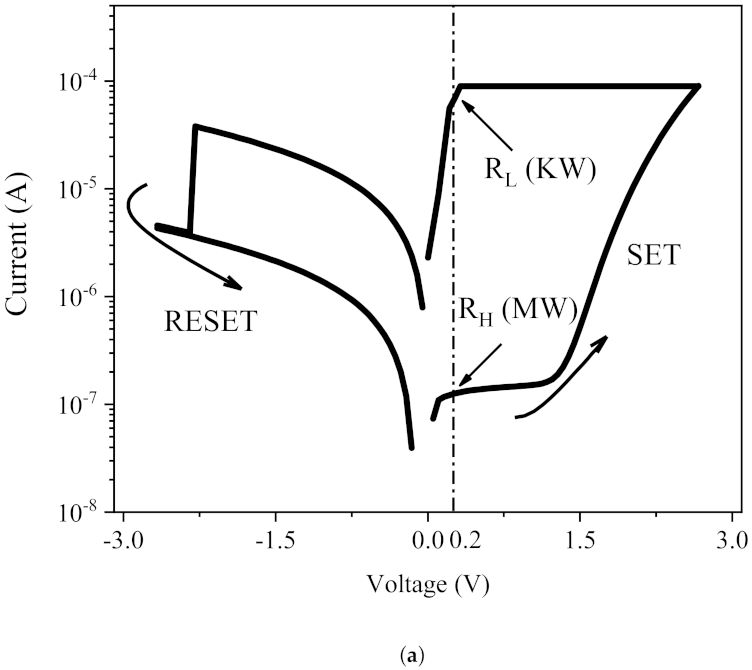
2.1. Resistive Non-Volatile Memory
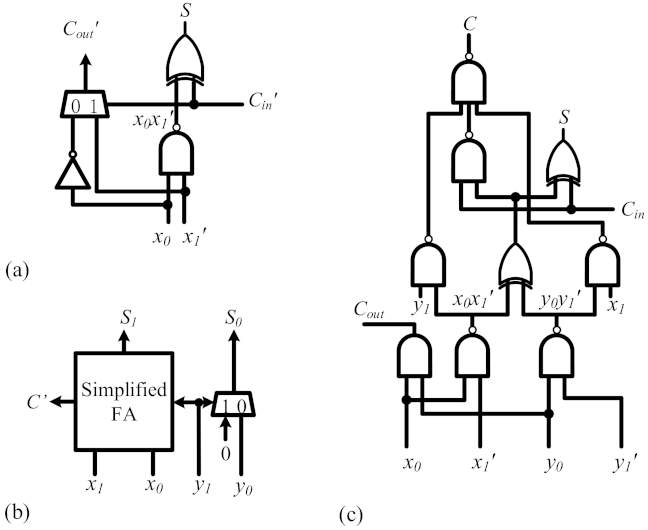
2.2. Booth Multiplier
3. Proposed 8-bit Non-Volatile Booth Multiplier
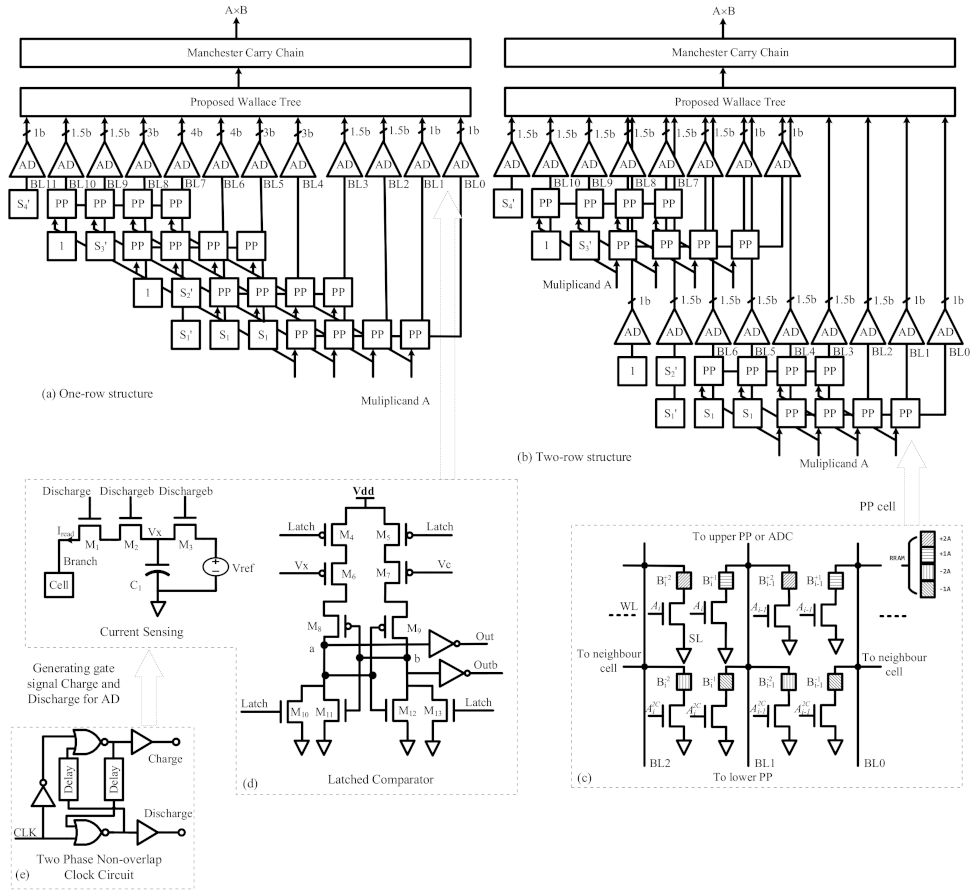
3.1. Booth Encoding and Partial Product Generator
- 1.
- ‘−1A’ RRAM is LRS, others types are HRS;
- 2.
- ‘+1A’ RRAM is LRS, others types are HRS;
- 3.
- ‘−2A’ RRAM is LRS, others types are HRS;
- 4.
- ‘+2A’ RRAM is LRS, others types are HRS.
3.2. Sign Bit
3.3. Readout Circuit
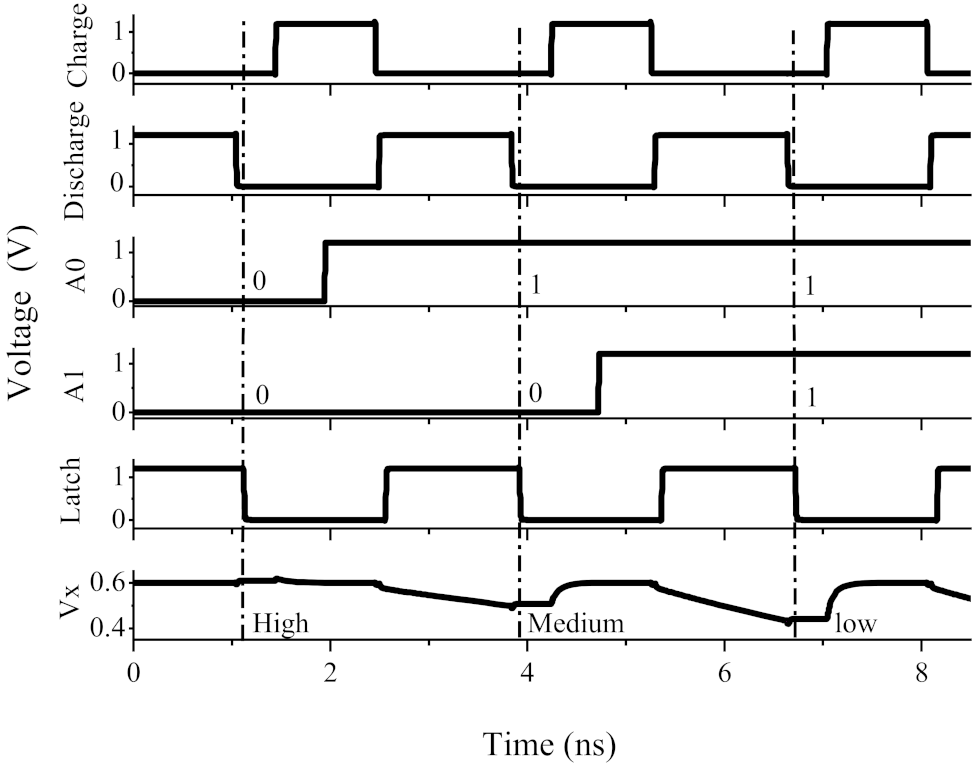
3.3.1. Current Sensing Circuit
3.3.2. Latched Comparator
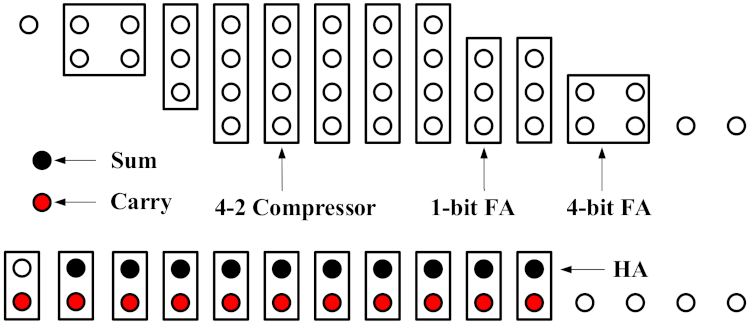
3.4. Proposed Wallace Tree
3.5. Manchester Carry Chain
3.6. Structure of Partial Product Generator
4. Simulation Result and Comparison
4.1. RRAM Circuit Simulation
4.2. AD Circuit Simulation
4.3. Multiplier Circuit Simulation
4.3.1. Transient Simulation Analysis
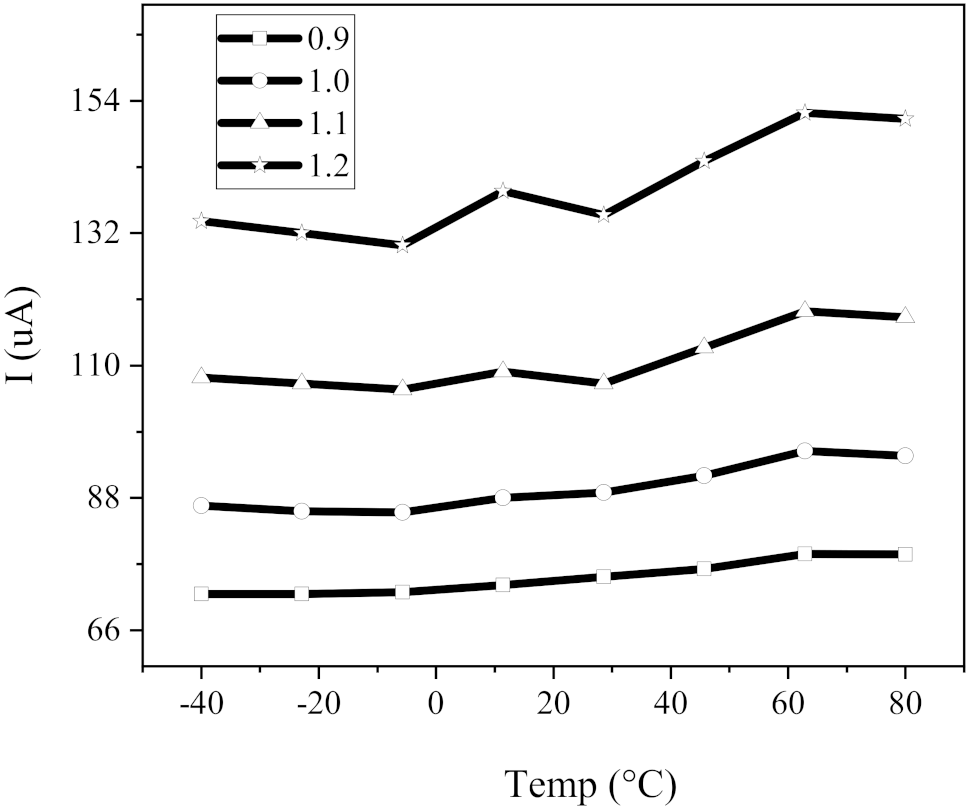
4.3.2. PVT Analysis
4.4. Performance Analysis and Comparison
4.5. System Power Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Silver, D.; Huang, A.; Maddison, C.; Guez, A.; Sifre, L.; Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Guo, H.; Lin, Q.; Xia, Y.; Zhang, X.; Zhang, F.; Fan, D. An In-Memory-Computing Design of Multiplier Based on Multilevel-Cell of Resistance Switching Random Access Memory. Chin. J. Electron. 2018, 27, 1151–1157. [Google Scholar] [CrossRef]
- Von Neumann, J. First draft of a report on the EDVAC. IEEE Ann. Hist. Comput. 1993, 15, 27–75. [Google Scholar] [CrossRef]
- Reuben, J. Rediscovering Majority Logic in the Post-CMOS Era: A Perspective from In-Memory Computing. J. Low Power Electron. Appl. 2020, 10, 28. [Google Scholar] [CrossRef]
- Yuhao, W.; Xin, L.; Hao, Y.; Leibin, N.; Wei, Y.; Chuliang, W.; Junfeng, Z. Optimizing Boolean embedding matrix for compressive sensing in RRAM crossbar. In Proceedings of the 2015 IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED), Rome, Italy, 22–24 July 2015; pp. 13–18. [Google Scholar] [CrossRef]
- Cui, X.; Ma, Y.; Wei, F.; Cui, X. The Synthesis Method of Logic Circuits Based on the NMOS-Like RRAM Gates. IEEE Access 2021, 9, 54466–54477. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, K.; Shen, H. A Robust 8-Bit Non-Volatile Computing-in-Memory Core for Low-Power Parallel MAC Operations. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 1867–1880. [Google Scholar] [CrossRef]
- Zahoor, F.; Zulkifli, T.Z.A.; Khanday, F.A.; Zainol Murad, S.A. Carbon Nanotube and Resistive Random Access Memory Based Unbalanced Ternary Logic Gates and Basic Arithmetic Circuits. IEEE Access 2020, 8, 104701–104717. [Google Scholar] [CrossRef]
- Sahay, S.; Bavandpour, M.; Mahmoodi, M.R.; Strukov, D. Energy-Efficient Moderate Precision Time-Domain Mixed-Signal Vector-by-Matrix Multiplier Exploiting 1T-1R Arrays. IEEE J. Explor. Solid-State Comput. Devices Circuits 2020, 6, 18–26. [Google Scholar] [CrossRef]
- Ellaithy, D.M.; El-Moursy, M.A. A 90-nm CMOS Low-Energy Dual-Channel Serial/Parallel Multiplier. In Proceedings of the 2019 6th International Conference on Advanced Control Circuits and Systems (ACCS) 2019 5th International Conference on New Paradigms in Electronics Information Technology (PEIT), Hurgada, Egypt, 17–20 November 2019; pp. 132–135. [Google Scholar] [CrossRef]
- Huang, Z. High-Level Optimization Techniques for Low-Power Multiplier Design; University of California: Los Angeles, CA, USA, 2003. [Google Scholar]
- Oskuii, S. Design of Low-Power Reduction-Trees in Parallel Multipliers; Norwegian University of Science and Technology: Trondheim, Norway, 2008. [Google Scholar]
- Mishra, S. Design and Implementation of Faster and Low Power Multipliers; National Institute Of Technology: Rourkela, India, 2009. [Google Scholar]
- Jain, S.; Ranjan, A.; Roy, K.; Raghunathan, A. Computing in Memory With Spin-Transfer Torque Magnetic RAM. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2018, 26, 470–483. [Google Scholar] [CrossRef]
- Kingra, S.K.; Vivek, P.; Che-Chia, C.; Hudec, B.; Tuo-Hung, H.; Manan, S. SLIM: Simultaneous Logic-in-Memory Computing Exploiting Bilayer Analog OxRAM Devices. Sci. Rep. 2020, 10, 2567. [Google Scholar] [CrossRef] [Green Version]
- Govoreanu, B.; Piazza, L.; Ma, J.; Conard, T.; Vanleenhove, A.; Belmonte, A.; Radisic, D.; Popovici, M.; Alin, V.; Redolfi, A.; et al. Advanced a-VMCO resistive switching memory through inner interface engineering with wide (>102) on/off window, tunable μA-range switching current and excellent variability. Dig. Tech. Pap.-Symp. VLSI Technol. 2016, 1–2. [Google Scholar] [CrossRef]
- Redolfi, A.; Goux, L.; Jossart, N.; Yamashita, F.; Nishimura, E.; Urayama, D.; Fujimoto, K.; Witters, T.; Lazzarino, F.; Jurczak, M. A novel CBRAM integration using subtractive dry-etching process of Cu enabling high-performance memory scaling down to 10 nm node. In Proceedings of the 2015 Symposium on VLSI Technology (VLSI Technology), Kyoto, Japan, 16–18 June 2015; p. 134. [Google Scholar] [CrossRef]
- Huang, K.; Zhao, R.; He, W.; Lian, Y. High-Density and High-Reliability Nonvolatile Field-Programmable Gate Array with Stacked 1D2R RRAM Array. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2016, 24, 139–150. [Google Scholar] [CrossRef]
- Goux, L.; Fantini, A.; Kar, G.; Chen, Y.; Jossart, N.; Degraeve, R.; Clima, S.; Govoreanu, B.; Lorenzo, G.; Pourtois, G.; et al. Ultralow sub-500 nA operating current high-performance TiN∖Al2O3∖HfO2∖Hf∖TiN bipolar RRAM achieved through understanding-based stack-engineering. In Proceedings of the 2012 Symposium on VLSI Technology (VLSIT), Honolulu, HI, USA, 12–14 June 2012; pp. 159–160. [Google Scholar] [CrossRef]
- ChiaHua, H.; Shen, T.Y.; Hsu, P.Y.; Chang, S.C.; Wen, S.Y.; Lin, M.H.; Wang, P.K.; Liao, S.C.; Chou, C.S.; Peng, K.M.; et al. Random soft error suppression by stoichiometric engineering: CMOS compatible and reliable 1Mb HfO2-ReRAM with 2 extra masks for embedded IoT systems. In Proceedings of the 2016 IEEE Symposium on VLSI Technology, Honolulu, HI, USA, 14–16 June 2016; pp. 1–2. [Google Scholar] [CrossRef]
- Waser, R.; Dittmann, R.; Staikov, G.; Szot, K. Redox-Based Resistive Switching Memories – Nanoionic Mechanisms, Prospects, and Challenges. Adv. Mater. 2009, 21, 2632–2663. [Google Scholar] [CrossRef]
- Wong, H.P.; Lee, H.; Yu, S.; Chen, Y.; Wu, Y.; Chen, P.; Lee, B.; Chen, F.T.; Tsai, M. Metal–Oxide RRAM. Proc. IEEE 2012, 100, 1951–1970. [Google Scholar] [CrossRef]
- Li, X.; Lai, L. Nonvolatile Memory and Computing Using Emerging Ferroelectric Transistors. In Proceedings of the 2018 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Hong Kong, China, 8–11 July 2018; pp. 750–755. [Google Scholar]
- Amirany, A.; Rajaei, R. Fully Nonvolatile and Low Power Full Adder Based on Spin Transfer Torque Magnetic Tunnel Junction with Spin-Hall Effect Assistance. IEEE Trans. Magn. 2018, 54, 1–7. [Google Scholar] [CrossRef]
- Huang, K.; Lian, Y. A Low-Power Low-VDD Nonvolatile Latch Using Spin Transfer Torque MRAM. IEEE Trans. Nanotechnol. 2013, 12, 1094–1103. [Google Scholar] [CrossRef]
- Meena, J.S.; Sze, S.M.; Chand, U.; Tseng, T.Y. Overview of emerging nonvolatile memory technologies. Nanoscale Res. Lett. 2014, 9, 526. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ho, C.; Hsu, C.L.; Chen, C.C.; Liu, J.T.; Wu, C.S.; Huang, C.C.; Hu, C.; Yang, F.-L. 9 nm half-pitch functional resistive memory cell with 1 μA programming current using thermally oxidized sub-stoichiometric WOx film. In Proceedings of the 2010 International Electron Devices Meeting, San Francisco, CA, USA, 6–8 December 2010; pp. 19.1.1–19.1.4. [Google Scholar] [CrossRef]
- Govoreanu, B.; Kar, G.S.; Chen, Y.; Paraschiv, V.; Kubicek, S.; Fantini, A.; Radu, I.P.; Goux, L.; Clima, S.; Degraeve, R.; et al. 10 × 10 nm2 Hf/HfOx crossbar resistive RAM with excellent performance, reliability and low-energy operation. In Proceedings of the 2011 International Electron Devices Meeting, Washington, DC, USA, 5–7 December 2011; pp. 31.6.1–31.6.4. [Google Scholar] [CrossRef]
- Tsunoda, K.; Kinoshita, K.; Noshiro, H.; Yamazaki, Y.; Iizuka, T.; Ito, Y.; Takahashi, A.; Okano, A.; Sato, Y.; Fukano, T.; et al. Low Power and High Speed Switching of Ti-doped NiO ReRAM under the Unipolar Voltage Source of less than 3 V. In Proceedings of the 2007 IEEE International Electron Devices Meeting, Washington, DC, USA, 10–12 December 2007; pp. 767–770. [Google Scholar] [CrossRef]
- Banno, N.; Tada, M.; Sakamoto, T.; Miyamura, M.; Okamoto, K.; Iguchi, N.; Nohisa, T.; Hada, H. A fast and low-voltage Cu complementary-atom-switch 1 Mb array with high-temperature retention. In Proceedings of the 2014 Symposium on VLSI Technology (VLSI-Technology): Digest of Technical Papers, Honolulu, HI, USA, 9–12 June 2014; pp. 1–2. [Google Scholar] [CrossRef]
- Cheng, C.H.; Tsai, C.Y.; Chin, A.; Yeh, F.S. High performance ultra-low energy RRAM with good retention and endurance. In Proceedings of the 2010 International Electron Devices Meeting, San Francisco, CA, USA, 6–8 December 2010; pp. 19.4.1–19.4.4. [Google Scholar] [CrossRef]
- Kim, W.; Park, S.I.; Zhang, Z.; Yang-Liauw, Y.; Sekar, D.; Wong, H.P.; Wong, S.S. Forming-free nitrogen-doped AlOX RRAM with sub-uA programming current. In Proceedings of the 2011 Symposium on VLSI Technology—Digest of Technical Papers, Kyoto, Japan, 14–16 June 2011; pp. 22–23. [Google Scholar]
- Govoreanu, B.; Redolfi, A.; Zhang, L.; Adelmann, C.; Popovici, M.; Clima, S.; Hody, H.; Paraschiv, V.; Radu, I.P.; Franquet, A.; et al. Vacancy-modulated conductive oxide resistive RAM (VMCO-RRAM): An area-scalable switching current, self-compliant, highly nonlinear and wide on/off-window resistive switching cell. In Proceedings of the 2013 IEEE International Electron Devices Meeting, Washington, DC, USA, 9–11 December 2013; pp. 10.2.1–10.2.4. [Google Scholar] [CrossRef]
- Liu, S.; Wang, W.; Li, Q.; Zhao, X.; Li, N.; Xu, H.; Liu, Q.; Liu, M. Highly improved resistive switching performances of the self-doped Pt/HfO2:Cu/Cu devices by atomic layer deposition. Sci. China Phys. Mech. Astron. 2016, 59, 127311. [Google Scholar] [CrossRef]
- Jameson, J.R.; Blanchard, P.; Cheng, C.; Dinh, J.; Gallo, A.; Gopalakrishnan, V.; Gopalan, C.; Guichet, B.; Hsu, S.; Kamalanathan, D.; et al. Conductive-bridge memory (CBRAM) with excellent high-temperature retention. In Proceedings of the 2013 IEEE International Electron Devices Meeting, Washington, DC, USA, 9–11 December 2013; pp. 30.1.1–30.1.4. [Google Scholar] [CrossRef]
- Goux, L.; Belmonte, A.; Celano, U.; Woo, J.; Folkersma, S.; Chen, C.Y.; Redolfi, A.; Fantini, A.; Degraeve, R.; Clima, S.; et al. Retention, disturb and variability improvements enabled by local chemical-potential tuning and controlled Hour-Glass filament shape in a novel W∖WO3∖Al2O3∖Cu CBRAM. In Proceedings of the 2016 IEEE Symposium on VLSI Technology, Honolulu, HI, USA, 14–16 June 2016; pp. 1–2. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Li, Y.; Zhou, Y.; Chu, T.; Chang, K.; Chang, T.; Tsai, T.; Sze, S.M.; Miao, X. Functionally Complete Boolean Logic in 1T1R Resistive Random Access Memory. IEEE Electron Device Lett. 2017, 38, 179–182. [Google Scholar] [CrossRef]
- Chen, P.; Yu, S. Compact Modeling of RRAM Devices and Its Applications in 1T1R and 1S1R Array Design. IEEE Trans. Electron Devices 2015, 62, 4022–4028. [Google Scholar] [CrossRef]
- Zheng, L.; Haimin, C.; Xianwen, Y. A hardware multiplier design of embedded microprocessor. In Proceedings of the 2010 IEEE International Conference on Information Theory and Information Security, Beijing, China, 17–19 December 2010; pp. 38–41. [Google Scholar] [CrossRef]
- Yeh, W.C.; Jen, C.W. High-speed Booth encoded parallel multiplier design. IEEE Trans. Comput. 2000, 49, 692–701. [Google Scholar] [CrossRef] [Green Version]
- Ping-hua, C.; Juan, Z. High-speed Parallel 32 × 32-b Multiplier Using a Radix-16 Booth Encoder. In Proceedings of the 2009 Third International Symposium on Intelligent Information Technology Application Workshops, Nanchang, China, 21–22 November 2009; pp. 406–409. [Google Scholar] [CrossRef]
- Xiaoping, C.; Wei, H.; Xin, C.; Shumin, W. A New Redundant Binary Partial Product Generator for Fast 2n-Bit Multiplier Design. In Proceedings of the 2014 IEEE 17th International Conference on Computational Science and Engineering, Chengdu, China, 19–21 December 2014; pp. 840–844. [Google Scholar] [CrossRef]
- Xue, H.; Patel, R.; Boppana, N.V.V.K.; Ren, S. Low-power-delay-product radix-4 8*8 Booth multiplier in CMOS. Electron. Lett. 2018, 54, 344–346. [Google Scholar]
- Kumar, G.G.; Sahoo, S.K. Implementation of a high speed multiplier for high-performance and low power applications. In Proceedings of the 2015 19th International Symposium on VLSI Design and Test, Ahmedabad, India, 26–29 June 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Lee, J.; Eshraghian, J.K.; Cho, K.; Eshraghian, K. Adaptive Precision CNN Accelerator Using Radix-X Parallel Connected Memristor Crossbars. arXiv 2019, arXiv:1906.09395. [Google Scholar]
- Kuang, S.; Wang, J.; Guo, C. Modified Booth Multipliers With a Regular Partial Product Array. IEEE Trans. Circuits Syst. II Express Briefs 2009, 56, 404–408. [Google Scholar] [CrossRef]
- Balaji, V.S.; Upadhyay, H.N. FPGA implemenation of high speed and low power carry save adder. IIOAB J. 2016, 7, 151–159. [Google Scholar]
- Ghosh, A.; Ghosh, D. Optimization of Static Power, Leakage Power and Delay of Full Adder Circuit Using Dual Threshold MOSFET Based Design and T-Spice Simulation. In Proceedings of the 2009 International Conference on Advances in Recent Technologies in Communication and Computing, Kottayam, India, 27–28 October 2009; pp. 903–905. [Google Scholar] [CrossRef]
- Aradhya, H.V.R.; Madan, H.R.; Suraj, M.S.; Mahadikar, M.T.; Muniraj, R.; Moiz, M. Design and performance comparison of adiabatic 8-bit multipliers. In Proceedings of the 2016 IEEE Distributed Computing, VLSI, Electrical Circuits and Robotics (DISCOVER), Mangalore, India, 13–14 August 2016; pp. 141–147. [Google Scholar]
- Subash, T.; Ajaiyan; Subha, T. Performance Comparison of 64-bit Carry Look-Ahead Adders Using 32 nm CMOS Technology. Mater. Today Proc. 2017, 4, 4153–4168. [Google Scholar] [CrossRef]
- Takayanagi, T.; Nogami, K.; Hatori, F.; Hatanaka, N.; Takahashi, M.; Ichida, M.; Kitabayashi, S.; Higashi, T.; Klein, M.; Thomson, J.; et al. 350 MHz time-multiplexed 8-port SRAM and word size variable multiplier for multimedia DSP. In Proceedings of the 1996 IEEE International Solid-State Circuits Conference, Digest of TEchnical Papers, ISSCC, San Francisco, CA, USA, 10 February 1996; pp. 150–151. [Google Scholar] [CrossRef]







| Shift & Add | Array Multiplier | Modified Booth Multiplier | Modified Booth Wallace Multiplier | |
|---|---|---|---|---|
| Serial/Parallel | Serial | Parallel | Parallel | Parallel |
| Area | Small | Large | Medium | Medium |
| Power Consumption | Small | Large | Medium | Medium |
| Delay | Large | Medium | Small | Smallest |
| Complexity | Simple | Simple | Complex | Complex |
| Implementation | Easy | Easy | Medium | Difficult |
| Type | (mV) | One-Row | Two-Row | Coding |
|---|---|---|---|---|
| AD1b | 253 | 3 | 6 | 0,1 |
| AD1.5b | 183 | 4 | 17 | 00,10,11 |
| AD3b | 132 | 3 | 0 | 000,001,011,111 |
| AD4b | 100 | 5 | 0 | 0000,0001,0011,0111,1111 |
| (W) | 4.92 | 4.99 | - | |
| Resistance | X0 | X1 | Cin | S | Cout |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 0 | |
| / | 0 | 1 | 0 | X | X |
| / | 0 | 1 | 1 | X | X |
| 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 |
| Parameter | Description | Default Value |
|---|---|---|
| L | Oxide thickness | 5 nm |
| gap_min | Min. gap distance | 0.1 nm |
| gap_max | Max. gap distance | 1.7 nm |
| gap_ini | Initial gap distance | 1.367 nm |
| a0 | Atomic distance | 0.25 nm |
| Eag | Activation energy for vacancy generation | 1.501 eV |
| Ear | Activation energy for vacancy recombination | 1.5 eV |
| I0 | I-V fitting parameter | |
| g0 | I-V fitting parameter | |
| V0 | I-V fitting parameter | 4.3 |
| Gap dynamics fitting parameter | 150 | |
| Gap dynamics fitting parameter | 16.5 | |
| Gap dynamics fitting parameter | ||
| Gap dynamics fitting parameter | 1.25 |
| Process | MC | FF | SS |
|---|---|---|---|
| Average Current (A) | 89.8 | 134.0 | 75.4 |
| Delay (ns) | 1.05 | 0.90 | 1.38 |
| Process (nm) | (V) | Delay (ns) | Power (W) | PDP (fJ) | Area (m) | Memory | PDP Save (%) | ||
|---|---|---|---|---|---|---|---|---|---|
| [44] | 90 | 1.2 | 1.04 | 435.9 | 453 | – | regular CMOS | 0 | |
| [3] | 65 | 1.2 | 1.03 | 335 | 345.05 | 738.23 | RRAM | 23 | |
| [45] | 65 | 1.32 | 1.04 | 358 | 372 | 749.12 | regular CMOS | 17 | |
| [46] | 180 | 1.2 | – | 1200 | – | – | RRAM | – | |
| Proposed | two-row | 45 | 1.2 | 0.83 | 161.19 | 133.80 | 785.20 | RRAM | 70 |
| one-row | 45 | 1.2 | 0.83 | 135.72 | 112.65 | 749.61 | RRAM | 75 | |
| two-row | 45 | 1 | 1.05 | 87.25 | 91.52 | 785.20 | RRAM | 79 | |
| two-row | 45 | 1 | 1.05 | 79.19 | 83.15 | 749.61 | RRAM | 81 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Zhu, X.; Huang, K.; Gu, Z. An 8-bit Radix-4 Non-Volatile Parallel Multiplier. Electronics 2021, 10, 2358. https://doi.org/10.3390/electronics10192358
Fu C, Zhu X, Huang K, Gu Z. An 8-bit Radix-4 Non-Volatile Parallel Multiplier. Electronics. 2021; 10(19):2358. https://doi.org/10.3390/electronics10192358
Chicago/Turabian StyleFu, Chengjie, Xiaolei Zhu, Kejie Huang, and Zheng Gu. 2021. "An 8-bit Radix-4 Non-Volatile Parallel Multiplier" Electronics 10, no. 19: 2358. https://doi.org/10.3390/electronics10192358
APA StyleFu, C., Zhu, X., Huang, K., & Gu, Z. (2021). An 8-bit Radix-4 Non-Volatile Parallel Multiplier. Electronics, 10(19), 2358. https://doi.org/10.3390/electronics10192358






