LogicSNN: A Unified Spiking Neural Networks Logical Operation Paradigm

Abstract

LogicSNN, a unified spiking neural networks (SNN) logical operation paradigm is proposed in this paper. First, we define the logical variables under the semantics of SNN. Then, we design the network structure of this paradigm and use spike-timing-dependent plasticity for training. According to this paradigm, six kinds of basic SNN binary logical operation modules and three kinds of combined logical networks based on these basic modules are implemented. Through these experiments, the rationality, cascading characteristics and the potential of building large-scale network of this paradigm are verified. This study fills in the blanks of the logical operation of SNN and provides a possible way to realize more complex machine learning capabilities.

1. Introduction

Spiking neural networks (SNN) originated in brain science and has received extensive attention in the field of brain-like computing, due to its rich spatiotemporal dynamics, diverse coding schemes, and event-driven characteristics. With continuous efforts in studying the structure and mechanism of biological neural networks [1,2], more and more research results have been applied to computational neuroscience and brain-like computing. The research and development of SNN is also the process to understand, simulate and make better use of the brain. To achieve these goals, the capability of doing logical operations that the brain can do is basic and essential for SNN.

Logical operations are the basis of complex operations and advanced intelligence. The essence of biological neural activities is the process of computing external input signals and self-excited signals. Logical operations play an important role in this process. In the biological context, pattern-matching and coincidence-detection share the same characteristics with logical operation AND [3].

As far as we know, there are few studies in the direction of SNN logical operation, not to mention the construction of a paradigm of SNN logical operation or a complete set of methods and systems. This paper aims to construct a unified logical operation paradigm of SNN. Based on this unified paradigm, all kinds of logical operations can be implemented through SNN, including basic logical operations, the combined logical networks and other more complicated logical operations. This unified paradigm may lay a foundation for constructing large-scale SNN and a computing system based on SNN.

This paper focuses on constructing LogicSNN, a unified SNN logical operation paradigm, including the definition of logical variables, the chosen of the spike neuron model, the cascading “building block” network structure, which is used to build logical operation modules and the spike-timing–dependent plasticity (STDP) rule to train the modules. According to LogicSNN, we constructed several logical operations as experiments to verify the feasibility of this paradigm.

In summary, the contributions of this paper include the following: (1) logical variables under the semantics of SNN are defined; (2) a unified logical operation paradigm network structure of SNN is designed; (3) using spike-timing-dependent plasticity (STDP), six basic SNN binary logical operation modules, including AND, OR, NAND, NOR, XOR, XNOR, are trained; and (4) using the basic modules trained in (3), we build the combined logical networks such as adder, and realize the corresponding logical functions.

The remainder of this paper is organized as follows: related work in the direction of SNN logical operation is introduced in Section 2. The methods of the proposed LogicSNN are described in detail in Section 3. The experimental design and results are presented in Section 4. In Section 5, important issues of the proposed paradigm and future research plans are discussed. The conclusion is drawn in Section 6.

2. Related Work

In 1943, McCulloch and Pitts believed that the brain is composed of reliable logic gates, similar to the logic at the core of computers [4]. The impact of this framework on neuroscience is limited because neurons have richer dynamic characteristics.

Shoshana Guberman et al. proposed a computational paradigm for dynamic logic-gates (DLGs) in neuronal activity [5]. They believe that the brain is composed of DLGs, and DLGs are controlled by time-dependent logic patterns. The truth table of DLGs depends on their historical activity and the stimulation frequency of input neurons. However, neurons that are continuously stimulated inevitably increase their response delay. As a result, the delays of different paths of the DLGs must be within a certain range in order to work normally. Moreover, unlike static logic gates, functions of DLGs will change over time. This computational paradigm has made many innovative attempts in the construction of DLGs, but the above problems remain.

Tim P. Vogels and L. F. Abbott studied the signal transmission and logic gate of the integrate-and-fire (IF) neuron network [6]. They found that for rate-encoded signals, if the synaptic strength is appropriately adjusted, a sparse and randomly connected SNN can support robust and accurate signal replication. The depth of this network can reach up to six layers. In this kind of network, multiple signals can propagate along different paths at the same time. Using this feature, by strengthening specific synapses, different types of logic gates can be generated in a random network structure. They encoded neuronal pulses with frequency, and manually specified different numbers, types, and different firing characteristics of excitatory and inhibitory neurons when constructing different types of logic gates. The synaptic strength of each type of neuron is adjusted to different multiples of the reference intensity. They built four types of logic gates: NOT, Switch, XOR, and Flip-Flop. However, due to frequency coding, the various states of the logic gate are not sufficiently clear, and it is difficult to judge the true state of the logic gate. The pulse firing frequency is a statistic, which means it is calculated by the number of pulses divided by the time window length. Under the condition of a certain period of time and a certain number of pulses, different time window length values will result in different pulse firing frequencies. Thus, it is prone to state confusion. Especially when the neuron pulse firing frequency is near the dividing line, it may cause an erroneous output.

Geoflly L. Adonias et al. have published a series of papers related to the digital logic of SNN. They designed a logic gate model based on neuron molecular communication engineering, using multi-cell Boolean logic operations to design AND gates and OR gates [7]. However, in the experimental part, only the influence of different inter-spike interval (ISI) on the logic gate function is considered. Moreover, the highest accuracy of the AND gates is less than 50%, and only one OR gate reaches 100%. This result is far from the causal characteristics of logic gates. The authors also studied how synthetic neurons are used as digital logic gates to perform biological calculations in the brain and their effects on epileptic behavior [8]. They adopted the relatively more reasonable biological Hodgkin–Huxley (HH) model and established eight neuron logic gates, including five different OR gates and three different AND gates. Compared with the previous work [7], the performance of constructed logic gates is improved, but the performance decreases as the pulse firing threshold and pulse firing frequency increase. The authors also proposed a reconfigurable logic gate design based on small neuronal networks, which can change the type of logic gate by changing the synapse weight [9]. The neuron logic circuit in this design can also be used to construct a digital filter with a reconfigurable cut-off frequency to filter abnormal high-frequency activities, such as epilepsy and other neurodegenerative diseases. However, the above three works only designed AND gates and OR gates, and did not cover more diverse logical operations. Moreover, the accuracy of the logic gates’ output has not reached a satisfactory level yet.

Zhe Wang et al. proposed a dendritic neuron model (DMASs) with adaptive synapses based on differential evolution algorithm training [10]. According to the order of signal transmission, a dendritic neuron model can be divided into four parts: synaptic layer, dendritic layer, cell membrane layer and soma layer. It can be converted into a logic circuit, which can be implemented and deployed on hardware by deleting useless synapses and dendrites after training. After design, the converted logic circuit can use only four basic logic devices (comparator, AND, OR, and NOT) to solve complex nonlinear problems. However, the model does not actually use the spike neuron model, but uses the sigmoid function in the synaptic layer. Through parameter adjustment and learning, the connection state is set to one of the four possible connecting states: direct-connecting state, opposite-connecting state, constant-1 state, and constant-0 state. The subsequent layers adopt mathematical models, such as continuous addition and continuous multiplication, respectively, to simulate operations such as OR, AND.

There are still some problems, especially as the types of logic gates are not comprehensive enough, and the accuracy and stability of logic gates can be improved. Moreover, a complete set of methods and systems of SNN logical operation have not been formed, and the above studies are not able to realize the function of complex logical operations through SNN. This study focuses on solving the above problems and attempts to construct a unified logical operation paradigm of SNN.

3. Methods

This section provides the methods of the proposed LogicSNN. First, Section 3.1 talks about the definition and encoding method of the logical operation. In particular, we define the two values of the logic variables as Logic 0 and Logic 1. After comparing two possible encoding methods, we adopt the better one, which is indicated in Figure 1. In Section 3.2, we compare two spike neuron models and introduce the chosen one and give the network structure of LogicSNN, which is shown in Figure 2. Furthermore, Section 3.3 details the training method STDP; Figure 3 shows the STDP curve.

3.1. Definition and Encoding Method of Logical Operation

To build LogicSNN, the first thing that needs to be clear is the basic concept of logical operation and how to define logical operation under the semantics of SNN.

The mathematical foundation of logical operations is logical algebra. Logical algebra, also known as Boolean algebra, is the summary of thinking logic expounded by the British mathematician George Boole in [11]. It is the mathematical foundation of logic theory and probability theory. Logical algebra is an algebra used to process logical operations, and its variables are called logical variables. For binary logic, logical variables have two values, namely Logic 0 and Logic 1. Here, 0 and 1 are symbols that indicate the contradictions of things, such as true or false of the proposition, presence or absence of a signal, or a high or low voltage level. Therefore, Logic 0 and Logic 1 have no significance in terms of numerical value [12].

According to the definition above, for binary logic, it is necessary to find a pair of contradictory things in SNN, or specify a pair of contradictory relations as Logic 0 and Logic 1 of logical variables.

Since SNN uses spiking to transmit signals, for a single neuron, a spike fired or not represented as Logic 1 and Logic 0, respectively, becomes the easiest encoding method to come up with. This method conforms to the definition of logical variables, and it also conforms to human intuition. However, this encoding method has some problems when facing actual logical operations. Take the logic NOT as an example. The NOT operation is also called the inversion operation, which means that when the condition that determines the occurrence of the event occurs, the event is false; otherwise, it is true. In other words, when the input is Logic 0/1, the output is Logic 1/0. In this definition, when the input is Logic 1 and the output is Logic 0, it is reasonable and easy to implement. For mapping to neuron, the input spike is not enough to make the post-synaptic neuron membrane potential reach the firing threshold potential, and thus, the post-synaptic neuron does not spike. When the input is Logic 0, that is, when the pre-synaptic neuron does not spike, it becomes extremely difficult for the post-synaptic neuron to generate a continuous spike output, which means Logic 1. This situation is similar to the symptoms of epilepsy in neurological diseases, for which the nervous system loses its homeostasis and is in an abnormal state.

In this paper, another logical variable encoding method is adopted, and Logic 0 and Logic 1 are defined as two different neurons firing a spike, that is, the two states of each logical variable are represented by two independent neurons. The two neurons are named Neuron 0 and Neuron 1, respectively. When only Neuron 0 is firing a spike, it is regarded as Logic 0; when only Neuron 1 is firing a spike, it is regarded as Logic 1, as shown in Figure 1. In this way, for N-ary logical operations, 2N neurons are needed to represent all the states of the N logical variables. In order to ensure that this pair of prescribed logic contradicts with each other, mutually exclusive encoding is used to encode the input, which means that the encoded input signal does not make Neuron 0 and Neuron 1 of the same group in the input layer fire at the same time. What needs to be pointed out is that Logic 0 and Logic 1 are mutually exclusive but do not need to be complementary. This logical variable encoding method does not prevent both Neuron 0 and Neuron 1 of the same group in the input layer from being non-active at the same time. If both of them do not give a signal, there is no Logic 0 nor Logic 1. The network is silent, or in other words, there is no logical signal transmitting through the network. With the guidance of the teacher layer, there is only one output neuron (0 or 1) spike at a time. The details of the teacher layer are described in the next section.

3.2. Spike Neuron Model and Network Structure

In addition to the encoding method of logical operation defined in Section 3.1, LogicSNN also requires a specific network structure to carry its functions. This section introduces the spike neuron model and the network structure of the LogicSNN.

3.2.1. Spike Neuron Model

The leaky-integrate-and-fire (LIF) neuron model [13] is a computationally friendly model with partial characteristics of biological neurons, and is widely used in SNN research. Its characteristics (as its name suggests) are connected mainly to three processes: leakage, integration and firing spike. The LIF neuron model can be simplified as the integrate-and-fire (IF) without the leakage process, but this would make the neurons less dynamic and lose their memory potential, which is not acceptable in this work. Thus, the LIF neuron model is chosen as the spike neuron model to build the network. The differential equation of the LIF neuron membrane potential is shown as Equation (1):

$$C_m\frac{dV}{dt}=-G_L\left(V-E_L\right)+I$$

(1)

where V is the membrane potential, $C_m$ is the membrane capacitance, $G_L$ is the leakage conductance, $E_L$ is the passive equilibrium voltage, which is generally the resting potential, and I is the external input current. In the absence of external current input I, Equation (1) can be rewritten as a time constant version as follows:

$$\frac{dV}{dt}=\frac{V_{rest}-V}{{\tau }_m}$$

(2)

where V is the membrane potential. $V_{rest}$ is the resting potential, the same as the $E_L$ in Equation (1). ${\tau }_m$ is the membrane potential time constant, which is equal to $C_m$/$G_L$ in Equation (1). As shown in Equation (2), when there is no external input, V will gradually decay to $V_{rest}$.

When the presynaptic spike arrives, the presynaptic membrane releases neurotransmitters through the vesicles. The neurotransmitters binding to the corresponding receptor proteins on the postsynaptic membrane cause the ion channels to open and the membrane potential of the postsynaptic neurons to change. For the convenience of calculation, the above synaptic behavior is simplified, and the details of the intermediate process are ignored. Therefore, the presynaptic spike directly causes the membrane potential of the postsynaptic neuron to increase. The synaptic behavior is described as Equation (3):

$$V_{post}(t+1)=V_{post}\left(t\right)+w\times \Delta Vif{V}_{pre}\left(t\right)>V_{th}$$

(3)

where $V_{post}$ is the membrane potential of the postsynaptic neuron, $V_{pre}$ is the membrane potential of the presynaptic neuron, $V_{th}$ is the firing threshold potential, $\Delta V$ is the delta value of membrane potential, and w is the synaptic weight. When $V_{pre}$ exceeds $V_{th}$, $V_{post}$ gets updated.

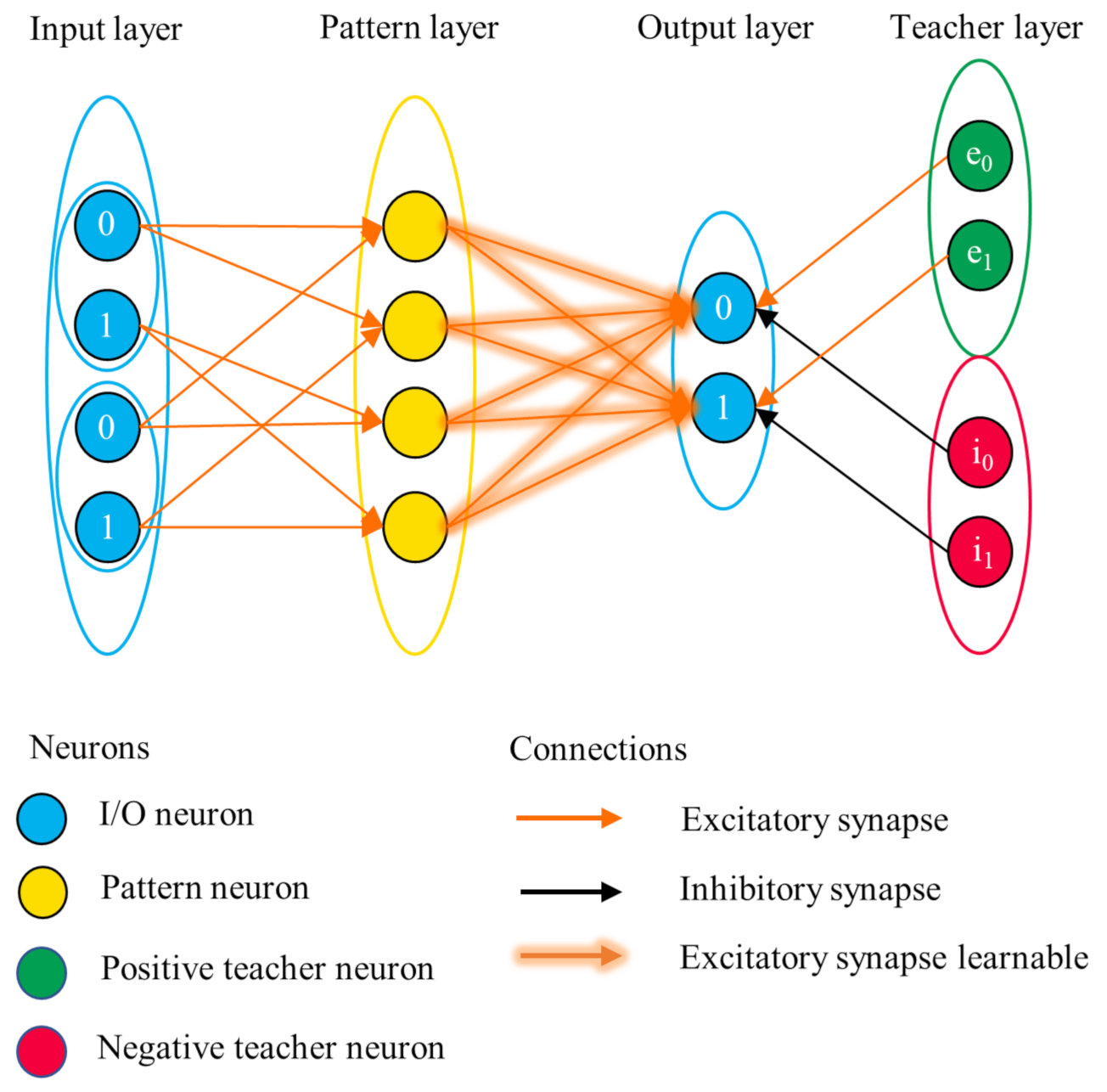
3.2.2. Network Structure

Many previous SNN and artificial neural networks (ANN) were constructed and trained in an end-to-end manner. In this way, the network structure can be optimized and adjusted for the corresponding tasks, achieving good results, but this effect is at the expense of its versatility. For example, one-pixel attacks created with the proposed algorithm in [14], which successfully fooled three types of deep neural networks (DNNs), trained on the CIFAR-10 datasets: the AllConv, NiN, and VGG. To design a unified logical operation paradigm of SNN, we must consider its versatility, replaceability and scalability. We adopt the “building block” style to design this paradigm so that it has the ability to build large-scale SNN and the potential to build a computing system based on SNN.

Figure 2 shows the network structure of the SNN logical operation module. The SNN logical operation module is designed as a four-layer structure, which includes the input layer, the pattern layer, the output layer, and the teacher layer. Among them, the teacher layer, which is in the dotted box of Figure 2, only exists in the training process, and is removed after training to facilitate the cascade between the modules. The logical operation module that is finally trained and applied has a three-layer structure. The network structure of the SNN logical operation module and the teacher layer are partly inspired by [15].

With the encoding method of logical variables defined in Section 3.1, the number of input layer neurons is twice that of the logical variables. For N-ary logical operations, the input layer is composed of $2^N$ neurons, forming N input logical neurons groups, representing N logical variables.

The design of the pattern layer refers to some prior knowledge. According to the truth table of logical operations, N-ary logic operations have $2^N$ input–output pairs. The pattern layer is composed of $2^N$ neurons, and each pattern neuron is only connected to the input layer neuron related to the specific pattern. The simultaneous firing of the input layer neurons related to the specific pattern cause the corresponding pattern layer neurons to fire. Each pattern is projected to the corresponding neuron and separated from each other, which is beneficial for learning the latter layer.

The output layer generally has only one logical variable, which is composed of two neurons, namely the output Neuron 0 and output Neuron 1, forming an output logical neuron group. The output logical neuron group and the input are the same in structure and characteristics. The only difference is that they are located in different positions of the single module. This makes composing a more complex network structure easily by cascading modules, that is, making a one-to-one connection of the former module’s output to the latter module’s input.

The synapses between the pattern layer neurons and output layer ones are fully connected. These synapses obey the spike-timing dependent plasticity (STDP) that satisfies the Hebb rule, and their weights are learnable. In the training phase, a teacher layer is added after the output layer. The teacher layer is composed of two kinds of neurons: one is the positive teacher neuron, and the other is the negative teacher neuron. The spikes emitted by the positive/negative teacher neuron increase/decrease the membrane potential of the corresponding output layer neuron. For the general case where the output layer has only one logical neuron group, the teacher layer is composed of two positive teacher neurons and two negative ones. Each teacher neuron group is connected with the output neuron group in a one-to-one way. This ensures that each output layer neuron has a positive and a negative teacher neuron to guide its behavior. When training is done, the teacher layer and its connection with the output layer are removed, and the learned synapse weights between the pattern layer and output layer are fixed. The above is the process to construct the SNN logical operation module.

It is worth noting that for the logical operation NOT, its definition is the inversion of the signal, and its network structure can be simplified based on this feature, that is, a two-layer network structure of the input layer and output layer is adopted, and each layer contains a logical neuron group. The wiring is done a in crossed way: the input layer Neuron 0 is connected to the output layer Neuron 1, and the input layer Neuron 1 is connected to the output layer Neuron 0. By fixing the value of w × $\Delta$V in Equation (3) as $V_{th}$−$V_{rest}$, the logical operation NOT can be realized. This structure can be cascaded with the logical operation paradigm, and can be used as network middleware to realize signal inversion at the specific position on demand.

3.3. Training Method

In the network structure defined in Section 3.2.2, the synapses between the pattern layer and the output layer are fully connected. These synapses are based on the STDP rule, and their weights are variable during the learning process. In other words, these synapses are plastic. The synaptic weights are adjusted with input signals and the guidance of the teacher layer. Therefore, the corresponding mode can be learned. In this section, the STDP rule is mainly introduced.

STDP is an attractive learning rule, which captures the essence of the Hebb rule: “cells that fire together wire together” [16]. STDP is affected by the close temporal correlation between the spikes of pre-synaptic and post-synaptic neurons [17].

In the above network structure, the synapses between the pattern layer and the output layer use the archetypical form of STDP [18], as shown in Equation (4):

$$\Delta w=\left\{\begin{array}{c}{a}^{+}·exp\left(\frac{-ISI}{{\tau }^{+}}\right)ifISI\ge 0\left(\mathrm{LTP}\right)\hfill \\ -a^{-}·exp\left(\frac{ISI}{{\tau }^{-}}\right)ifISI<0\left(\mathrm{LTD}\right)\hfill \end{array}\right.$$

(4)

$$ISI=t_{post}-t_{pre}$$

(5)

where w is the synaptic weight, and $ISI$ is the abbreviation of the inter-spike interval, which means the difference between the last spike firing time of the post-synaptic and pre-synaptic neuron, as shown in Equation (5). $a^{+}$ and $a^{-}$ are the amplitudes of the exponential functions. The parameters ${\tau }^{+}$ and ${\tau }^{-}$ are time constants, which determine the ranges of pre-to-postsynaptic interspike intervals over which synaptic strengthening and weakening occur. LTP and LTD are the abbreviations of long-term potentiation and long-term depression, respectively. Figure 3 shows the STDP curve.

4. Experiments and Results

In this section, a series of experiments of the logical operation module based on LogicSNN mentioned in Section 3 are carried out on the Brian 2 platform [19]. The STDP rule of Equation (4) is adjusted with the corresponding code implementation provided by the platform [20]. The experiments mainly include the following:

(1)

The construction, learning and testing of six kinds of basic SNN binary logical operation modules: AND, OR, NAND, NOR, XOR, XNOR, in Section 4.1.

(2)

The building and testing of simple combinational logic networks in Section 4.2: the rounding logic network of 8421-binary-coded decimal (BCD) code, half adder, full adder, which takes the basic SNN binary logical operation modules in (1) as the basic components.

4.1. Basic SNN Binary Logical Operation Modules

According to the designed LogicSNN in Section 3.2 and Section 3.3, binary logical operation modules are built and trained.

Table 1. The truth table of six kinds of binary logic operations.

A	B	${\mathit{P}}_{\mathit{AND}}$	${\mathit{P}}_{\mathit{OR}}$	${\mathit{P}}_{\mathit{NAND}}$	${\mathit{P}}_{\mathit{NOR}}$	${\mathit{P}}_{\mathit{XOR}}$	${\mathit{P}}_{\mathit{XNOR}}$
0	0	0	0	1	1	0	1
0	1	0	1	1	0	1	0
1	0	0	1	1	0	1	0
1	1	1	1	0	0	0	1

is the truth table of six binary logical operations (AND, OR, NAND, NOR, XOR, XNOR), A and B represent binary logic inputs, and $P_{logic}$ represents the output of the corresponding logic operation, where logic ∈ {AND, OR, NAND, NOR, XOR, XNOR}.

The training data need to be prepared before training. The training data mainly contain two types: one is the input signal of the input layer, and the other is the guidance signal of the teacher layer. $N_{size}$ group input signals of the input layer are randomly generated from the four binary logic input patterns: 00, 01, 10, and 11, and are encoded according to the encoding method defined in Section 3.1. The interval between each group of input pattern is $t_{interval}$. The guidance signal of the teacher layer is determined according to the output of the four input modes corresponding to each logical operation in Table 1. For example, for the logic AND, when the input signal of the input layer is 00, the theoretical output should be 0, and the corresponding teacher Neuron $e_0$ and $i_1$ emit spikes so that the output Neuron 0 is depolarized, and the output Neuron 1 is hyperpolarized. Under the action of the two signals, the synapse between the pattern layer and the output layer will be correctly strengthened by LTP, which is induced by the intra-group signal, and weakened by LTD, which is induced by the inter-group signal so as to learn the corresponding logic function.

It is worth noting that the output of the four logical operations of AND, OR, NAND, NOR is unbalanced. If the input pattern is generated in a purely random manner, the probability of one kind of output is 25%, and the other is 75%. The pattern that generates the output with less probability gets fewer spike pairs in the training process. As a consequence, the pattern convergence speed slows down or does not even converge. Therefore, the input patterns are generated based on the principle of “output balance”.

Figure 4 is part of the training data generated for the logical module AND. For clearer display, the spikes for the first 100 ms are shown.

The difference between different logical operation modules lies in the synaptic weights between the pattern layer and the output layer. The initial value of all learnable synapse weights is $w_0$:

$$w_0=\frac{w_{max}}{N_{fan\_in}}$$

(6)

where $w_{max}$ is the maximum value of the synapse weight, and $N_{fan\_in}$ is the number of fan-in, which indicates the number of synapses that each output layer neuron has with pattern layer neurons. This way of initialization makes all learnable synapses initially equal.

The parameter values used in training are shown in

Table 2. The parameter values used in training.

${\mathit{V}}_{\mathit{t}\mathit{h}}$	${\mathit{V}}_{\mathit{r}\mathit{e}\mathit{s}\mathit{t}}$	${\mathit{\tau }}_{\mathit{m}}$	${\mathit{w}}_{\mathit{m}\mathit{a}\mathit{x}}$	$\mathit{l}\mathit{r}$	${\mathit{a}}^{+}$
−50 mV	−80 mV	5 ms	1	0.005	$lr$ * $w_{max}$ = 0.005
$a^{-}$	${\tau }^{+}$	${\tau }^{-}$	$N_{fan\_in}$	$N_{size}$	$t_{interval}$
$a^{+}$ ∗ 1.05 = 0.00525	20 ms	20 ms	4	1400, 2000	5 ms

. The neuron-related parameters $V_{th}$, $V_{rest}$, ${\tau }_m$ refer to the values of biological neuron and LIF neuron models. The former are appropriately adjusted. The synaptic-related parameters $w_{max}$, $lr$ (learning rate), $a^{+}$, $a^{-}$, ${\tau }^{+}$, ${\tau }^{-}$ refer to the classic STDP settings, and the other mode construction related parameters ($N_{fan\_in}$, $N_{size}$, $t_{interval}$) are chosen through experiments.

Figure 5 shows the change of synaptic weights between the pattern layer and output layer during training. Figure 5a–f shows that the graphs of the weight changes for six kinds of SNN logical operations: AND, OR, NAND, NOR, XOR, XNOR. For the first four kinds of logical operations, $N_{fan\_in}$ is set to 4, $N_{size}$ is set to 1400, and the correspond training time is 7000 ms; for the last two, $N_{size}$ is set to 2000, and the correspond training time is 10,000 ms. After training, the synaptic weights of all six modules converge.

Figure 6 shows the test result of the SNN logical operation module AND. In order to show the state of each neuron more clearly, the color of the legend is different from that in Figure 2, and a richer color is used. The test spike inputs consist of four input patterns of 00, 01, 10, 11 in the truth table, which are reflected in the input layer neuron indices as 02, 03, 12, 13 in Figure 6a. The four input patterns cause the pattern layer neurons, 0, 1, 2, and 3, to spike, respectively, in Figure 6b,c. It can be seen from Figure 6d,e that after training, the SNN logical operation module AND converges, and the output is 0, 0, 0, 1, which is consistent with the expected output of the truth table. The trained module has the characteristics of a logic function, and meets the design requirements. The dashed box shows the fourth case in the truth table: the input is 11, and the output is 1, which is mapped to the network structure for display. The other five kinds of logical operation modules also meet the design requirements after training, and the input layer spikes and the output layer spikes of each module are displayed in Figure 7, with the same form and color of Figure 6a,d. The results of six SNN logical operation modules showed in Figure 6 and Figure 7 all match their truth table which is shown in Table 1.

In order to facilitate the representation of the basic SNN logical operation module, appropriate modifications are made on the basis of the internationally commonly used symbols of logic gates, and combined with the spike symbol. The icons of the basic SNN logical operation modules are designed as shown in Figure 8.

4.2. Combinational Logic Networks

Based on the unified paradigm LogicSNN, the SNN logical operation modules are designed as a “building block” at the beginning. One of its characteristics is that multiple modules can be easily cascaded to establish large-scale networks and achieve more complex functions. In this section, imitating the combinational logic in some digital circuits, the basic SNN logical operation modules built in Section 4.1 are used to construct combinational logic networks. The cascade characteristics of the SNN logical operation modules is tested.

4.2.1. Rounding Logic Network of 8421-BCD Code

BCD is the abbreviation of the binary-coded decimal. It uses four binary digits to represent one decimal number. The 8421-BCD code is a basic and the most commonly used form. It is similar to a 4-bit binary code. The weight of each bit is 8, 4, 2, 1, so it is a weighted BCD code. Different from the 4-bit binary code, it only selects the first 10 groups of codes, that is, 0000∼1001, to represent the corresponding decimal numbers, and the remaining six groups of codes are not used.

Table 3. The correspondence between 8421-BCD codes and decimal numbers.

8421-BCD	Decimal Number	8421-BCD	Decimal Number
0000	0	0101	5
0001	1	0110	6
0010	2	0111	7
0011	3	1000	8
0100	4	1001	9

shows the correspondence between 8421-BCD codes and decimal numbers.

Rounding is an accurate counting retention method. For a large amount of data that need to be retained, the error sum of this retention method is the smallest, so this method is also used as a basic retention method.

Table 4. The truth table of a rounding logic network in the 8421-BCD code.

A	B	C	D	P	A	B	C	D	P
0	0	0	0	0	0	1	0	1	1
0	0	0	1	0	0	1	1	0	1
0	0	1	0	0	0	1	1	1	1
0	0	1	1	0	1	0	0	0	1
0	1	0	0	0	1	0	0	1	1

is the truth table of a rounding logic network in the 8421-BCD code.

In Table 4, A, B, C and D respectively represent the logic variables corresponding to the 4-bit binary numbers of the 8421-BCD code from high to low, and P represents the output corresponding to the rounding logic network. According to the rules of logical algebra, the relationship between the input and output is simplified to the simplest OR-AND type as follows:

$$P\left(A,B,C,D\right)=(A+B)·(A+C+D)$$

(7)

The symbols in Equation (7) are all defined under logical operations, that is, “+” means logic OR (logical addition), and “·” means logic AND (logical multiplication). Equation (7) can be transformed to the NOR type, as follows:

$$P\left(A,B,C,D\right)=\overline{\overline{\left(A+B\right)}+\overline{(A+C)+D}}$$

(8)

According to Equation (8), three NOR modules and one OR module are needed to build the 8421-BCD code rounding logic network. The network structure is shown in Figure 9.

The results are shown in Figure 10. Because multiple logical operation modules are involved and the test results of a single logical operation module are shown in the previous section, only the input and output spikes are shown in Figure 10. The color table is consistent with Figure 6. Because each logic variable has two states, the logic variables A, B, C, and D correspond to the input neuron index 0∼7. The test inputs are the 10 possible input situations in Table 4. From Figure 10, it can be seen that when the decimal number corresponding to the input is less than five, the output Neuron 0 emits spikes; when it is greater than or equal to five, the output Neuron 1 emits spikes. The network outputs are consistent with the expected outputs, having the rounding logic function under the 8421-BCD code.

4.2.2. Half Adder and Full Adder

Half adder and full adder are the basic components of combinational circuits in digital circuits, and are also the core of the CPU for processing addition operations. Whether a half adder and a full adder can be built with the basic SNN logical operation module has become one of the verification experiments for building a calculation system based on SNN.

The half adder is a logic circuit that can add two 1-bit binary numbers to obtain the sum and the carry to the higher bit. Suppose the summand and addend are represented by A and B, and the sum and carry to the higher bit are represented by S and C.

Table 5. The truth table of the half adder.

A	B	S	C
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

is the truth table of the half adder. The output function expression can be obtained from the truth table as follows:

$$\left\{\begin{array}{c}S(A,B)=\overline{A}B+A\overline{B}=A\oplus B\hfill \\ C(A,B)=AB\hfill \end{array}\right.$$

(9)

The symbol “⊕” in Equation (9) is defined under logical operations, which means logic XOR (logic exclusive or). It can be seen from Equation (9) that the half adder can be composed of one XOR module and one AND module. The network structure of the half adder is shown in Figure 11.

The full adder is a logic circuit that can realize the addition of two 1-bit binary numbers and the carry from the lower bit, that is, the addition of three 1-bit binary numbers, to obtain the sum and the carry to the higher bit. Let the summand and addend of the i-th bit be represented by $A_i$ and $B_i$, $C_{i-1}$ represent the carry from the lower bit, and the calculated sum and the carry to the higher bit be represented by $S_i$,$C_i$.

The experimental test results are shown in Figure 12; the summand A and addend B correspond to the input neuron subscript 0∼3, and the color table is consistent with Figure 6. The test inputs are the four possible input conditions in Table 5. The network outputs are consistent with the expected outputs, and it has the logic function of a half adder.

Table 6. The truth table of the full adder.

${\mathit{A}}_{\mathit{i}}$	${\mathit{B}}_{\mathit{i}}$	${\mathit{C}}_{\mathit{i}-1}$	${\mathit{S}}_{\mathit{i}}$	${\mathit{C}}_{\mathit{i}}$
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

is the truth table of the full adder. The output function expression can be obtained from the truth table as follows:

$$\left\{\begin{array}{c}{S}_i(A_i,B_i,C_{i-1})=A_i\oplus B_i\oplus C_{i-1}\hfill \\ C_i(A_i,B_i,C_{i-1})=(A_i\oplus B_i)C_{i-1}+A_i{B}_i\hfill \end{array}\right.$$

(10)

It can be seen from Equation (10) that the full adder can be composed of two XOR modules, two AND modules and two OR modules. The network structure of the full adder is shown in Figure 13.

The experimental test results are shown in Figure 14. The summand, addend, and low-bit carry $A_i$,$B_i$,$C_{i-1}$ correspond to input neuron subscripts 0∼5. The color table is consistent with Figure 6. The test inputs are the eight possible input conditions in Table 6, the network outputs are consistent with the expected outputs, and it has the logic function of a full adder.

The full adder network structure shown in Figure 13 can be further encapsulated, as shown in Figure 15. The encapsulated full adder can be cascaded, and the carry output CO of the lower full adder is connected with the carry input CI of the higher full adder to transmit carry information, thereby realizing the function of multi-bit binary addition.

The above three experiments are all carried out based on the SNN logical operation modules, and have reached the logic function corresponding to the design requirements. The cascading characteristics of the SNN logical operation modules are verified, as well as the potential of building large-scale networks and constructing a computing system based on SNN.

5. Discussion

In this section, we have some discussion about the proposed paradigm LogicSNN. The cascading characteristics of LogicSNN enables it to have the potential of building large-scale networks and constructing a computing system based on SNN. In addition, LogicSNN also has flexibility. For example, according to the definition of this paradigm, it is possible to design and train not just binary, but multiple logical operation modules based on task requirements, reducing the number of modules to build a network, and balancing the network structure. Furthermore, when the task is relatively simple but the task may change under different conditions, a minimal network can be used to solve multiple tasks. The synaptic weight group or connection mode of the minimal network can be changed according to needs. This feature not only reduces the network scale, but also further cuts down the energy consumption of SNN.

Moreover, the SNN logical operation modules which are built in LogicSNN also have the ability to overcome the logic hazard in traditional combinational logic circuits. The reason for the logic hazard is the delay of the logic gate. In a spiking neural network, if the pre-synaptic spike does not make the membrane potential of the post-synaptic neuron reach the firing threshold, the membrane potential gradually decays to the resting potential. This process is different from the instantaneous jump of the digital circuit level. This gradual attenuation is equivalent to the record of the previous spike activity, allowing the network to have memory. This enables SNN to produce the correct response within a certain tolerance period (related to the membrane potential time constant ${\tau }_m$) and synchronize the signal to the time point of the later arriving spike, even if the signals of two logical variables do not arrive at the same time during the processing of the logical operations.

Future research plans include constructing more complex network structures by using the LogicSNN proposed in this paper, and realizing more complex non-linear functions, classification functions, fitting functions and other machine learning capabilities. In addition, it is necessary to introduce the recurrent connection structure, which is ubiquitous in the biological nervous system, as well as more flexible and diverse models of neurons and synapses to solve more complex tasks, thus making the system more rich and complete. With the development of neuromorphic hardware, we also expect to be able to deploy the research results to build a more mature, brain-like intelligence.

6. Conclusions

In this paper, we propose a unified SNN logical operation paradigm, namely LogicSNN. In this paradigm, logical variables and logical operations are first defined in the context of SNN. LIF neurons are used to design and build the network structure, according to the characteristics of logical operation and SNN. STDP is used for training, and the feasibility and development potential of this paradigm are verified by experiments of basic SNN logical operation modules and combinatorial logic networks. This paradigm has very high uniformity. Different logical operation modules have the same structure, but the difference only lies in the weight of synapses. It has the potential to realize “small network, multi-function”. At the same time, the input layer and the output layer adopt the same interface, and the “building block” structure is conducive to the cascade between modules, which is convenient for the construction and assembly of a large-scale network. This paper fills in the blanks of logical operation in SNN and lays the foundation for further research in the direction of SNN logical operation and the exploration of computing system construction based on SNN.